On the pernicious effects of oil price uncertainty on US real economic activities

Abstract

The last five decades have witnessed dramatic changes in crude oil price dynamics. We identify the influence of extreme oil shocks and changing oil price uncertainty dynamics associated with economic and political events. Neglecting these features of the data can lead to model misspecification that gives rise to: firstly, an explosive volatility process for oil price uncertainty, and secondly, erroneous output growth dynamic responses to oil shocks. Unlike past studies, our results show that the sharp increase in oil price uncertainty after mid-1985 has a pernicious effect on output growth. There is evidence that output growth responds symmetrically (asymmetrically) to positive and negative shocks in the period when oil price uncertainty is lower (higher) and more (less) persistent before (after) mid-1985. These results highlight the importance of accounting for outliers and volatility breaks in oil price and output growth and the need to better understand the response of economic activity to oil shocks in the presence of oil price uncertainty. Our results remain qualitatively unchanged with the use of real oil price.

Appendices

Appendix A: Impulse response function

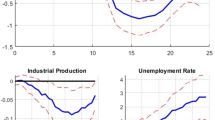
To study the response of endogenous variables to the impact of a unit or standard deviation shock in the VAR system we use the impulse response function. Elder (2003) provides an analytical representation of the impulse responses in a VAR model with GARCH-in-Mean. The impulse response function captures the time profile of the effect of a shock on the $m-$th variable, $m\in \{1,2\},$ at time t, being $e_{mt}$, on the expected value of $y_{v,t+n}$ where $n\ge 0$. Note that in the case of our model, $m=1$ denotes $\mathrm{IPI}$ while $m=2$ denotes $\mathrm{Oil}$. Mathematically, we write the impulse response function of $y_{v,t+n}$ at horizon n given information up to $\mathcal {F}_{t-1}$ as:

$$\begin{aligned} \frac{\partial E(y_{v,t+n}|e_{m,t},\mathcal {F}_{t-1})}{\partial e_{m,t}}. \end{aligned}$$

(5)

The impulse response for $y_{v,t+n}$ stemming from a shock $e_{m,t}$ takes the following analytical expression

$$\begin{aligned} \frac{\partial E(y_{v,t+n}|e_{m,t},\mathcal {F}_{t-1})}{\partial e_{m,t}}= & {} \left( \Theta _{n}A^{-1}\right) _{\{v,m\}}+\sum _{i=0}^{n-1}\left( \Theta _{i}A^{-1}\Lambda \left( A_{2}+A_{3}\right) ^{n-i-1}A_{2}\right) _{\{v,:\}}\left( \Upsilon _{1}+\Upsilon _{0}\right) \nonumber \\ \end{aligned}$$

(6)

where $\Upsilon _{1}$ is an $4\times 1$ vector such that its $\left( 2(m-1)+m\right)$th row contains $2e_{mt}$ and zeros elsewhere, and $\Upsilon _{0}$ is an $4\times 1$ vector such that its $\left( \left( j-1\right) 2+i\right)$th row and its $\left( 2\left( i-1\right) +1+(j-1\right)$th row contain $e_{jt}$ for $i,j=1,2$ and $i\ne j$. The subscripts $\{v,m\}$ indicate elements in the vth row and mth column of a matrix and $\{v,:\}$ indicates the vth row vector. Here, $\Xi _{i}$ and $\Theta _{i}$ are sub-matrices of $\Omega _{i}^{*}$ where $\Omega _{i}^{*}=$ $\left[ \begin{array}{cc} \widetilde{\Xi }_{i} &{} \widetilde{\Theta }_{i} \\ \Xi _{i} &{} \Theta _{i} \end{array} \right]$ and is a product of $\Omega _{1}$ and $\Omega _{i-1}^{*}$ with $\Omega _{0}^{*}=I_{3}$ and $\Omega _{s}^{*}=0$ for $s<0$. Note also that $\Omega (L)=I-\left[ \begin{array}{cc} \Phi (L) &{} \Psi ^{*}(L) \\ 0 &{} A^{-1}\Gamma (L) \end{array} \right]$ where $\Psi ^{*}$ is an null matrix. It is important to highlight that the coefficient estimates of the GARCH process $h_{\mathrm{Oil},t}$ given by $\hat{a}_{22}^{2}+\hat{a}_{22}^{3}$ need to be strictly less than unity to ensure that the effect of oil shock on output growth will dissipate over time. In this regard, it is important that any outliers and regime changes in the underlying oil price volatility are identified and accounted for appropriately to ensure that the GARCH parameter estimates are not biased towards an integrated or even an explosive GARCH process. An evaluation of the response of output growth to oil price shocks critically relies on unbiased parameter estimates of the model.

Appendix B: Detecting additive outliers

There are methods for detecting outliers in GARCH-type models based on interventional analysis approach which was first put forward by Box and Tiao (1975). We apply the semi-parametric procedure to detect additive outliers proposed by Laurent et al. (LLP) (2016).⁷ They assume that the returns $r_{t}$ are described by the ARMA(p,q)-GARCH(1,1) model, which is defined in Eqs. (7)–(9).

Consider the return series with an independent outlier component $a_{t}I_{t}$ , defined as

$$\begin{aligned} r_{t}^{*}=r_{t}+a_{t}I_{t} \end{aligned}$$

(7)

where $r_{t}^{*}$ denotes observed returns, $I_{t}$ is a dummy variable taking the value 1 in the case of an additive outlier on day t and 0 otherwise while $a_{t}$ is the outlier size. The model for $r_{t}^{*}$ has the properties that an additive outlier $a_{t}I_{t}$ will not affect $\sigma _{t+1}^{2}$ (the conditional variance of $r_{t+1}$), and it allows for non-Gaussian fat-tailed conditional distributions of $r_{t}^{*}$. LLP then use the bounded innovation propagation (BIP)-ARMA model proposed by Muler et al. (2009) and the BIP-GARCH(1,1) model proposed by Muler and Yohai (2008) to obtain robust estimations of $\mu _{t}$ and $\sigma _{t}^{2}$, respectively. These are shown in Eqs. (7)–(9) as $\widetilde{\mu }_{t}$ and $\widetilde{\sigma }_{t}$, respectively and that they are robust to potential presence of additive outliers $a_{t}I_{t}$. In other words, the model is estimated based on $r_{t}^{*}$ and not on $r_{t}$. The BIP-ARMA and BIP-GARCH(1,1) are defined as

$$\begin{aligned} \widetilde{\mu }_{t}= & {} \mu +\sum _{i=1}^{\infty }\xi _{i}\widetilde{\sigma } _{t-i}\omega _{k_{\Delta }}^{MPY}(\widetilde{J}_{t-i}) \end{aligned}$$

(8)

$$\begin{aligned} \widetilde{\sigma }_{t}^{2}= & {} \omega +\alpha _{1}\widetilde{\sigma } _{t-1}^{2}c_{\Delta }\omega _{k_{\Delta }}^{MPY}\left( \widetilde{J} _{t-1}\right) ^{2}+\beta _{1}\widetilde{\sigma }_{t-1}^{2}, \end{aligned}$$

(9)

respectively where $\xi _{i}$ are the coefficients of the AR(p ) and MA(q) polynomials defined in Eq. (8), $\omega _{k_{\Delta }}^{MPY}(.)$ is the weight function, and $c_{\Delta }$ a factor which ensures that the conditional expectation of the weighted squared unexpected shocks is the conditional variance of $r_{t}$ in the absence of outliers (Boudt et al. 2013).

Consider the standardised return on day t, which is given by

$$\begin{aligned} \widetilde{J}_{t}=\frac{r_{t}^{*}-\widetilde{\mu }_{t}}{\widetilde{ \sigma }_{t}}. \end{aligned}$$

(10)

To detect the presence of additive outliers they test the null hypothesis $H_{0}:a_{t}I_{t}=0$ against the alternative $\hbox {H} _{1}:a_{t}I_{t}\ne 0$. The null is rejected if

$$\begin{aligned} \max _{T}|\widetilde{J}_{t}|>g_{T,\lambda },\quad t=1,\ldots ,T \end{aligned}$$

(11)

where $g_{T,\lambda }$ is the suitable critical value.⁸ If $H_{0}$ is rejected, a dummy variable is defined as follows

$$\begin{aligned} \widetilde{I}_{t}=I\left( |\widetilde{J}_{t}|>k\right) \end{aligned}$$

(12)

where I(.) is the indicator function, with $\widetilde{I}_{t}=1$ when an additive outlier is detected at time t and 0 otherwise. LLP show that their test does not suffer from size distortions irrespective of the parameter values of the GARCH model from Monte Carlo simulations. The filtered returns or adjusted data are obtained as follows:

$$\begin{aligned} \widetilde{r}_{t}=r_{t}^{*}-(r_{t}^{*}-\widetilde{\mu }_{t}) \widetilde{I}_{t}. \end{aligned}$$

(13)

Appendix C: Detecting variance changes

Having identified and adjusted the data for possible additive outliers, we apply the CUSUM-type test of Sansó et al. (2004) to the series $\Delta \mathrm{IPI}_{t}$ and $\Delta \mathrm{Oil}_{t}$. The test is based on the iterative cumulative sum of squares (ICSS) algorithm developed by Inclan and Tiao (1994). This algorithm makes it possible to detect multiple breakpoints in variance.

Define $\tilde{y}_{t}$ as the mean-adjusted series for $y_{t}$ so that it has a mean of zero for $y_{t}=\{\Delta \mathrm{IPI}_{t},\Delta \mathrm{Oil}_{t}\}$. Further assume that $\{\tilde{y}_{t}\}$ is a series of independent observations from a normal distribution with zero mean and unconditional variance $\sigma _{t}^{2}$ for $t=1,\ldots ,T$. We know from the data summary statistics that both $\Delta \mathrm{IPI}_{t}$ and $\Delta \mathrm{Oil}_{t}$ display serial dependence/correlation (see Sect. 3) and that the violation of the independence property of the series will cause serious size distortions to the ICSS test statistic (Sansó et al. 2004). Sansó et al. (2004), therefore, propose a test that explicitly takes into consideration the fourth moment properties of $\tilde{y }_{t}$ and the conditional heteroskedasticity. The non-parametric adjustment to the test statistic allows for $\tilde{y}_{t}$ to obey a wide class of dependent processes under the null hypothesis. This is discussed below.

Assume that the variance within each interval is denoted by $\sigma _{j}^{2}$ for $j=0,1,\ldots ,N_{T}$ where $N_{T}$ is the total number of variance changes with $1<\kappa _{1}<\kappa _{2}<\cdots<\kappa _{N_{T}}<T$ being the set of breakpoints. Accordingly, the variances over the $N_{T}$ intervals are defined as:

$$\begin{aligned} \sigma _{t}^{2}=\left\{ \begin{array}{c} \sigma _{0}^{2}, \quad 1<t<\kappa _{1} \\ \sigma _{1}^{2}, \quad \kappa _{1}<t<\kappa _{2} \\ \cdots \\ \sigma _{N_{T}}^{2},\quad \kappa _{N_{T}}<t<T \end{array} \right. \end{aligned}$$

(14)

The cumulative sum of the squared observations, $C_{k},$ is used to estimate the number of variance changes and to identify the point in time when the variance shifts such that $C_{k}=\sum _{t=1}^{k}$ $\tilde{y}_{t}^{2}$ for $k=1,\ldots ,T$. Sansó et al. (2004) propose the adjusted test statistic – non-parametric adjustment based on the Bartlett kernel—given by:

$$\begin{aligned} AIT=\sup _{k}\left| (T/2)^{0.5}G_{k}\right| \end{aligned}$$

(15)

where $G_{k}=\hat{\lambda }^{-0.5}\left[ C_{k}-\left( \frac{k}{T}\right) C_{T} \right]$ and $\hat{\lambda }=\hat{\gamma }_{0}+2\sum _{l=1}^{m}\left[ 1-l(m+1)^{-1}\right] \hat{\gamma }_{l}$.

Here, $\hat{\gamma }_{l}=T^{-1}\sum _{t=l+1}^{T}\left( \tilde{y}_{t}^{2}-\hat{\sigma }^{2}\right) \left( \tilde{y}_{t-l}^{2}-\hat{\sigma }^{2}\right)$ and $\hat{\sigma }^{2}=T^{-1}C_{T}$, with $C_{T}=$ $\sum _{t=1}^{T}$ $\tilde{y}_{t}^{2}$. The lag truncation parameter m is selected using the Newey and West (1994) procedure. Under general conditions, the asymptotic distribution of AIT is also given by $\sup _{r}\left| W^{*}(r)\right|$ and the finite sample critical values are obtained from simulation.

Appendix D: The Carrion-Kim-Perron (CKP) test

Carrion-i-Silvestre et al. (2009) propose a testing procedure which allows for multiple structural breaks in the level and/or slope of the trend function under both the null and alternative hypotheses. The model is given by

$$\begin{aligned} y_{t}= & {} d_{t}+u_{t},\quad t=1,\ldots ,T, \end{aligned}$$

(16)

$$\begin{aligned} u_{t}= & {} \alpha u_{t-1}+v_{t},\quad t=2,\ldots ,T,\quad u_{1}=v_{1} \end{aligned}$$

(17)

with $d_t$ denotes the deterministic component given by

$$\begin{aligned} d_t = z_t^{\prime }(T_0^{0})\psi _0 + z_t^{\prime }(T_1^{0})\psi _1 + \cdots + z_t^{\prime }(T_m^{0})\psi _m \equiv z_t^{\prime 0})\psi \end{aligned}$$

(18)

where $z_t(T_0^{0})=(1,t)^{\prime }$, $\psi _0=(\mu _0,\beta _0)^{ \prime })$, and $z_t(T_j^{0})=\left( DU_t(T_j^{0}),DT_t(T_j^{0})\right) ^{\prime }$ for $1\le j \le m$, with m is the number of breaks. $DU_{t}(T_j^{0})=1$ and $DT_t(T_j^{0})=(t-T_j^{0})$ for $t>T_j^{0}$ and 0 elsewhere, with $T_j^{0}=[T\lambda _j^0]$ is the jthe break date, with [.] the integer part and $\lambda _j^0\equiv T_j^{0}/T \in (0,1)$ the break fraction parameter.

Carrion-i-Silvestre et al. (2009) consider extensions of the M class of unit root tests analysed in Ng and Perron (2001) and the feasible point optimal statistic of Elliott et al. (1996). The GLS-detrended unit root test statistics are based on using the quasi-differenced variable $y_{t}{\bar{ \alpha }}=(1-\bar{\alpha }L)y_{t}$ and $z_{t}{\bar{\alpha }}(\lambda ^{0})=(1- \bar{\alpha }L)z_{t}(\lambda ^{0})$ for $t=2,\ldots ,T$, with $\bar{\alpha }=1+ \bar{c}/T$ and $\bar{c}=-13.2$ when $z_{t}(T_{0}^{0})=(1,t)^{\prime }$. The feasible point optimal statistic is given by

$$\begin{aligned} P_{T}^{\mathrm{GLS}}(\lambda ^{0})=\left\{ S\left( \bar{\alpha },\lambda ^{0}\right) - \bar{\alpha }S\left( 1,\lambda ^{0}\right) \right\} /s^{2}(\lambda ^{0}) \end{aligned}$$

where $S \left( \bar{\alpha },\lambda ^0\right)$ is the minimum of the following sum of squared residuals from the quasi-differenced regression $S \left( \psi ,\bar{\alpha },\lambda ^0\right) =\sum _{t=1}^T \left( y_t{\bar{ \alpha }} - \psi ^{\prime }y_t{\bar{z}}(\lambda ^0) \right) ^2$, and $s^2(\lambda ^0)$ is an estimate of the spectral density at frequency zero of $v_t$ defined by

$$\begin{aligned} s^2(\lambda ^0) = s^2_{ek} / \left( 1-\sum _{j=1}^{k}\hat{b}_j \right) ^2 \end{aligned}$$

(19)

where $s^2_{ek}=(T-k)^{-1}\sum _{t=k+1}^{T}\hat{e}_{t,k}^2$ and $\{ \hat{b}_j,\hat{e}_{t,k}\}$ are obtained from the following OLS regression

$$\begin{aligned} \Delta \tilde{y}_t = b_0\tilde{y}_{t-1} + \sum _{j=1}^k b_j\tilde{y}_{t-j} + e_{t,k} \end{aligned}$$

(20)

with $\tilde{y}_t=y_t \hat{\psi }'z_t(\lambda ^0)$, where $\hat{\psi }$ minimises $S \left( \psi ,\bar{\alpha },\lambda ^0\right)$. The lag order k is selected using the modified information criteria suggested by Ng and Perron (2001) with the modification proposed by Perron and Qu (2007).

The M-class of tests are defined by

$$\begin{aligned} MZ_{\alpha }^{\mathrm{GLS}}(\lambda ^{0})= & {} \left( T^{-1}\tilde{y}_{T}^{2}-s(\lambda ^{0})^{2}\right) \left( 2T^{-1}\sum _{t=1}^{T}\tilde{y}_{t-1}^{2}\right) ^{-1} \end{aligned}$$

(21)

$$\begin{aligned} MZ_{t}^{\mathrm{GLS}}(\lambda ^{0})= & {} \left( T^{-1}\tilde{y}_{T}^{2}-s(\lambda ^{0})^{2}\right) \left( 4s(\lambda ^{0})^{2}T^{-2}\sum _{t=1}^{T}\tilde{y} _{t-1}^{2}\right) ^{-1/2} \end{aligned}$$

(22)

$$\begin{aligned} MP_{T}^{\mathrm{GLS}}(\lambda ^{0})= & {} \left[ \bar{c}^{2}T^{-2}\sum _{t=1}^{T}\tilde{y} _{t-1}^{2}+(1-\bar{c}T^{-1}\tilde{y}_{T}^{2}\right] /s(\lambda ^{0})^{2} \end{aligned}$$

(23)