Abstract
What proportion of Australian business cycle fluctuations are caused by international shocks? We address this question by estimating a panel VAR model that has time-varying parameters and a common stochastic volatility factor. The time-varying parameters capture the inter-temporal nature of Australia’s various bilateral trade relationships, while the common stochastic volatility factor captures various episodes of volatility clustering among macroeconomic shocks, e.g., the 1997/98 Asian Financial Crisis and the 2007/08 Global Financial Crisis. Our main result is that international shocks from Australia’s five largest trading partners: China, Japan, the EU, the USA and the Republic of Korea, have caused around half of all Australian business cycle fluctuations over the past two decades. We also find important changes in the relative importance of each country’s economic impact. For instance, China’s positive contribution increased throughout the mining boom of the 2000s, while the overall US influence has almost halved since the 1990s.

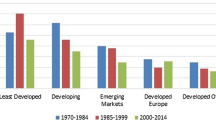
(Source: Australian Department of Foreign Affairs and Trade (DFAT) 2017)




Similar content being viewed by others
Notes
When choosing the model for our study, we also considered estimating international factor-augmented VAR (FAVAR) (e.g., Mumtaz and Surico 2009) and global VAR (GVAR) (e.g., Dees et al. 2007) models. The primary reason for choosing the PVAR framework is that it allows us to estimate time-varying coefficients in an economically meaningful way (Canova et al. 2007). We provide further details of this estimation method in Sect. 2.2. For a more detailed survey of the benefits of the panel VAR approach to FAVARs and GVARs, see Canova and Ciccarelli (2013).
Volatility clustering is a phenomenon whereby large changes in observations tend to be followed by large changes and small changes are followed by small changes.
Our reason for limiting the analysis to this set of countries is due to a lack of data availability. We would ideally include the top 10 trading partners but could not obtain quarterly time series data for Singapore, Thailand and India. We therefore decided to limit the analysis to Australia’s top five trading partners.
All statistics and data used in this paragraph are based on historical trade and economic data available from the Australian Department of Foreign Affairs and Trade (DFAT) website. Link: https://dfat.gov.au/trade/resources/trade-statistics/Pages/trade-time-series-data.aspx. Due to data availability, the EU proportion of the statistics is represented by Belgium, Finland, France, Germany, Ireland, Italy, Netherlands and Sweden. Importantly, the data used in the empirical application cover all 28 EU countries.
For details underlying the nature of the dramatic change in the Australia–China trade relationship, we refer the interested reader to Sheng and Song (2008).
In online appendix, we provide model results with conventional user choices of hyperparameters in time-varying PVAR models as in Poon (2018b). The results suggest that such choices may provide different results compared to the modern hierarchical prior framework. Specifically, the time-varying parameter results under the hierarchical prior framework are smoother and therefore show less time variation compared to conventional user choices. Interestingly, the estimated common stochastic volatility factor is almost identical under both estimation methods.
We provide a 95% credible interval for each of the figures in online appendix. The results are similar to those presented here. Interestingly, the common factor becomes less significant when using a two standard deviation credible set; however, the country-specific factors and stochastic volatility factor remain significant.
We are extremely grateful to a referee for this suggestion.
Note that \(\varvec{\kappa }_{X}\) will be a scalar when associated with \(\varvec{\varvec{\Sigma }}_{u}\) or \(\sigma _{h}^{2}\) and a vector when associated with \(\varvec{\Omega }\).
We set the tuning parameter \(\sigma _{\kappa _{X}}=0.001\), and we found that the acceptance ratio is between 80 and 90% for each of the models used in the paper.
References
Amir-Ahmadi P, Matthes C, Wang M-C (2018) Choosing prior hyperparameters: with applications to time-varying parameter models. J Bus Econ Stat. https://doi.org/10.1080/07350015.2018.1459302
Australian Department of Foreign Affairs and Trade (DFAT) (2017) Australia’s trade in goods and services 2014–15. https://dfat.gov.au/about-us/publications/trade-investment/australias-trade-in-goods-and-services/Pages/australias-tradein-goods-and-services-2016.aspx
Bańbura M, Giannone D, Reichlin L (2010) Large bayesian vector auto regressions. J Appl Econom 25(1):71–92
Canova F, Ciccarelli M (2009) Estimating multicountry var models. Int Econ Rev 50(3):929–959
Canova F, Ciccarelli M (2012) Clubmed? cyclical fluctuations in the mediterranean basin. J Int Econ 88(1):162–175
Canova F, Ciccarelli M (2013) Panel vector autoregressive models: a survey. In: VAR models in macroeconomics-new developments and applications: essays in honor of christopher A. Sims. Emerald Group Publishing Limited, pp 205–246
Canova F, Ciccarelli M, Ortega E (2007) Similarities and convergence in G-7 cycles. J Monet Econ 54(3):850–878
Canova F, Ciccarelli M, Ortega E (2012) Do institutional changes affect business cycles? Evidence from Europe. J Econ Dyn Control 36(10):1520–1533
Carriero A, Clark TE, Marcellino M (2016) Common drifting volatility in large bayesian vars. J Bus Econ Stat 34(3):375–390
Chan JC (2018) Large bayesian vars: a flexible kronecker error covariance structure. J Bus Econ Stat (just-accepted). https://doi.org/10.1080/07350015.2018.1451336
Chan JC, Grant AL (2015) Pitfalls of estimating the marginal likelihood using the modified harmonic mean. Econ Lett 131:29–33
Chan JC, Hsiao CY (2014) Estimation of stochastic volatility models with heavy tails and serial dependence. Wiley, New York, pp 155–176
Chan JC, Jeliazkov I (2009) Efficient simulation and integrated likelihood estimation in state space models. Int J Math Model Numer Optim 1(1–2):101–120
Chib S (1995) Marginal likelihood from the gibbs output. J Am Stat Assoc 90(432):1313–1321
Chib S, Greenberg E (1995) Hierarchical analysis of sur models with extensions to correlated serial errors and time-varying parameter models. J Econom 68(2):339–360
Claus E, Dungey M, Fry R (2008) Monetary policy in illiquid markets: options for a small open economy. Open Econ Rev 19(3):305–336
Corsetti G, Pesenti P, Roubini N (1999) What caused the asian currency and financial crisis? Jpn World Econ 11(3):305–373
De Mol C, Giannone D, Reichlin L (2008) Forecasting using a large number of predictors: Is bayesian shrinkage a valid alternative to principal components? J Econom 146(2):318–328
Dees S, Mauro F, Pesaran MH, Smith LV (2007) Exploring the international linkages of the euro area: a global var analysis. J Appl Econom 22(1):1–38
Dungey M, Fry R (2003) International shocks on Australia-the Japanese effect. Aus Econ Pap 42(2):158–182
Dungey M, Pagan A (2000) A structural var model of the Australian economy. Econ Rec 76(235):321–342
Dungey M, Pagan A (2009) Extending a svar model of the Australian economy. Econ Rec 85(268):1–20
Dungey M, Osborn D, Raghavan M (2014) International transmissions to Australia: the roles of the USA and Euro area. Econ Rec 90(291):421–446
Frühwirth-Schnatter S, Wagner H (2008) Marginal likelihoods for non-Gaussian models using auxiliary mixture sampling. Comput Stat Data Anal 52(10):4608–4624
Gelfand AE, Dey DK (1994) Bayesian model choice: asymptotics and exact calculations. J R Stat Soc Ser B (Methodological) 56(3):501–514
Geweke J, Amisano G (2011) Hierarchical markov normal mixture models with applications to financial asset returns. J Appl Econom 26(1):1–29
Kass RE, Raftery AE (1995) Bayes factors. J Am Stat Assoc 90(430):773–795
Kim S, Shephard N, Chib S (1998) Stochastic volatility: likelihood inference and comparison with arch models. Rev Econ Stud 65(3):361–393
Kose MA, Prasad ES, Terrones ME (2003) How does globalization affect the synchronization of business cycles? Am Econ Rev 93(2):57–62
Kroese DP, Chan JC et al (2014) Statistical modeling and computation. Springer, Berlin
Leu SC-Y (2011) A new keynesian svar model of the Australian economy. Econ Model 28(1):157–168
Leu SC-Y, Sheen J (2011) A small new keynesian state space model of the Australian economy. Econ Model 28(1):672–684
Liu P (2010) The effects of international shocks on Australia’s business cycle. Econ Rec 86(275):486–503
Mian A, Sufi A (2010) The great recession: lessons from microeconomic data. Am Econ Rev 100(2):51–56
Mumtaz H, Surico P (2009) The transmission of international shocks: a factor-augmented var approach. J Money Credit Bank 41(s1):71–100
Nimark KP (2009) A structural model of australia as a small open economy. Aust Econ Rev 42(1):24–41
Poon A (2018a) The transmission mechanism of Malaysian monetary policy: a time-varying vector autoregression approach. Empir Econ 55(2):417–444
Poon, A. (2018b) Assessing the synchronicity and nature of australian state business cycles. Economic Record 94(307):372–390
Sheng Y, Song L (2008) Comparative advantage and Australia–China bilateral trade. Econ Pap J Appl Econ Policy 27(1):41–56
Voss G, Willard L (2009) Monetary policy and the exchange rate: evidence from a two-country model. J Macroecon 31(4):708–720
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Sharada Davidson and Yiqiao Sun for useful comments on the paper.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix A. Appendices
Appendix A. Appendices
1.1 Appendix A.1 Markov Chain Monte Carlo algorithm
In appendix, we present the Markov chain Monte Carlo (MCMC) algorithm used to estimate the TVP-PVAR model. All alternative models considered in this paper are nested versions of this model and can therefore be estimated by straightforward modifications of the MCMC procedure. To detail the MCMC procedure, let \(\varvec{Y}=(\varvec{Y}_{1},\ldots ,\varvec{Y}_{T})'\), \(\varvec{\theta }=(\varvec{\theta }_{1},\ldots ,\varvec{\theta }_{T})'\), \(\varvec{h}=(\varvec{h}_{1},\ldots ,\varvec{h}_{T})'\) and \(\varvec{\lambda }=(\lambda _{1},\ldots ,\lambda _{T})'\). The posterior draws are obtained through a six-block Metropolis-within-Gibbs sampler that sequentially samples each variable from their respective full conditional distribution:
-
1.
Draw from \(p\left( \varvec{\theta }\mid {\mathbf {Y}},{\mathbf {h}},\varvec{\Sigma }_{u},\varvec{\Omega },\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
-
2.
Draw from \(p\left( \varvec{\Sigma }_{u}\mid {\mathbf {Y}},\varvec{\theta },{\mathbf {h}},\varvec{\Omega },\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
-
3.
Draw from \(p\left( \varvec{\Omega }\mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},{\mathbf {h}},\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
-
4.
Draw from \(p\left( {\mathbf {h}}\mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},\varvec{\Omega },\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
-
5.
Draw from \(p\left( \rho \mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},{\mathbf {h}},\varvec{\Omega },\sigma _{h}^{2},\varvec{\kappa }\right) \)
-
6.
Draw from \(p\left( \sigma _{h}^{2}\mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},{\mathbf {h}},\varvec{\Omega },\rho ,\varvec{\kappa }\right) \)
-
7.
Draw from \(p\left( \varvec{\kappa }\mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},{\mathbf {h}},\varvec{\Omega },\rho ,\sigma _{h}^{2}\right) \)
In our analysis, we use 35,000 posterior draws, discarding the first 15,000 to allow for convergence of the Markov chain to its stationary distribution. Under the previously defined conjugate priors, Steps 2, 3 and 6 can be directly sampled from their resulting posterior distributions. Next, following Canova et al. (2007, 2012), the latent states in Step 1 can be sampled using standard Kalman filter algorithms as in Chib and Greenberg (1995). In this paper, we instead follow Poon (2018b) and make use of an efficient precision sampling algorithm. The increased efficiency of the algorithm comes from exploiting the fact that the precision matrices of the latent states are block banded and sparse. This means that computational savings can be made in necessary operations when solving linear systems—such as taking a Cholesky decomposition, matrix multiplication and forward–backward substitution. Next, Step 4 involves a nonlinear non-Gaussian measurement equation, and the standard linear Kalman filter cannot be applied. To overcome this issue, we follow Poon (2018a) and make use of the auxiliary mixture sampler developed by Kim et al. (1998) along with an efficient sampling algorithm in Chan and Hsiao (2014). The auxiliary mixture sampler uses a seven-Gaussian mixture to convert the nonlinear measurement equation in the stochastic volatility model, into a log-linear equation that is conditionally Gaussian. Chan and Hsiao (2014) then show how to adapt to sample the log-volatilities using an efficient precision sampling algorithm. Finally, the full conditional distribution in Steps 5 results in nonstandard distribution. Sampling is therefore achieved through an independence chain Metropolis–Hastings Algorithm adapted from the univariate models in Chan and Hsiao (2014). For completeness, we now discuss the derivation of the conditional posterior distribution of each block in the Gibbs sampler. In each case, we use the fact that the posterior distribution for a parameter of interest can be obtained by working with the kernel of the resulting product from the prior and likelihood functions.
Step 1: Sample from \(p\left( \varvec{\theta }\mid {\mathbf {Y}},{\mathbf {h}},\varvec{\Sigma }_{u},\varvec{\Omega },\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
To sample \(\varvec{\theta }\), first note that (4) can be rewritten as:
where \(\varvec{Z}=\text {diag}\left( \varvec{Z}_{1},\dots ,\varvec{Z}_{T}\right) \), \(\varvec{u}=\left[ \begin{array}{cccc} \varvec{u}_{1}^{'}&\varvec{u}_{2}^{'}&\dots&\varvec{u}_{T}^{'}\end{array}\right] '\)and \(\varvec{\Sigma }=\text {diag}\left( e^{h_{1}}\varvec{\Sigma }_{u},\dots ,e^{h_{T}}\varvec{\Sigma }_{u}\right) \). By a change of variable:
Next, rewrite (5) as:
where \(\tilde{\varvec{\alpha }}_{\theta }=\left[ \begin{array}{cccc} \varvec{\theta }_{0}^{'}&{\mathbf {0}}&\dots&{\mathbf {0}}\end{array}\right] \), \({\varvec{\eta }}=({\varvec{\eta }}_{1},\ldots ,{\varvec{\eta }}_{T})'\), \({\mathbf {S}}_{\theta }=\text {diag}({\mathbf {V}}_{\theta },\varvec{\Omega },\dots ,\varvec{\Omega })\) and \({\mathbf {H}}_{\theta }\) is a \(Tm\times Tm\) block diagonal matrix, where \(m=N_{1}+N+G\), with \({\mathbf {I}}_{m}\) on the main diagonal, \(-{\mathbf {I}}_{m}\) on the lower diagonal and \({\mathbf {0}}_{m}\) elsewhere. Since \({\mathbf {H}}_{\theta }\) is a lower triangular matrix with ones along the main diagonal, \(\left| {\mathbf {H}}_{\theta }\right| =1\), implying that it is invertible. Using this result, (A.3) can be rewritten as:
where \(\varvec{\alpha }_{\theta }={\mathbf {H}}_{\theta }^{-1}\tilde{\varvec{\theta }}_{0}\). By a change of variable:
Combining (A.2) and (A.5) gives the conditional posterior distribution:
Thus, by standard linear regression results (Kroese et al. 2014, pp. 237–240):
where \(\hat{\varvec{\theta }}={\mathbf {D}}_{\beta }^{^{-1}}\left( {\mathbf {Z}}'{\varvec{\Sigma }}^{-1}{\mathbf {Y}}+{{\mathbf {H}}_{\theta }^{'}}\varvec{S}_{\theta }^{-1}{{\mathbf {H}}_{\theta }\varvec{\alpha }_{\theta }}\right) \) and \({\mathbf {D}}_{\beta }={\mathbf {Z}}'\varvec{\varvec{\Sigma }}^{-1}{\mathbf {Z}}+{{\mathbf {H}}_{\theta }^{'}}{\mathbf {S}}_{\theta }^{-1}{{\mathbf {H}}_{\theta }}\). Following Poon (2018b), sampling from this distribution is conducted with the precision sampling algorithm in Chan and Jeliazkov (2009).
Step 2: Sample from \(p\left( \varvec{\Sigma }_{u}\mid {\mathbf {Y}},\varvec{\theta },{\mathbf {h}},\varvec{\Omega },\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
To sample, \(\varvec{\Sigma }_{u}\), combine the inverse-Wishart prior distribution with the Gaussian likelihood function. Since this is a conjugate distribution, it is easy to show that:
Step 3: Sample from \(p\left( \varvec{\Omega }\mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},{\mathbf {h}},\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
To sample \(\varvec{\Omega }\), we combine the inverse-Wishart prior distribution with the Gaussian likelihood function to get
Step 4: Sample from \(p\left( {\mathbf {h}}\mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},\varvec{\Omega },\rho ,\sigma _{h}^{2},\varvec{\kappa }\right) \)
To sample \({\mathbf {h}}\), we follow Poon (2018b) and apply the auxiliary mixture sampler from Kim et al. (1998) along with the precision sampler from Chan and Hsiao (2014). To this end, note that the measurement equation in (4) can be written as:
where \({\varvec{P}}\) is the (lower) Cholesky factor of \(\varvec{\Sigma }_{u}\). Squaring both sides of (A.9) and taking the (natural) logarithm give the log-linear equation:
where \(\varvec{y}_{t}^{*}=\ln \left( \left( {\varvec{P}}^{-1}\left( {\mathbf {Y}}_{t}-{\mathbf {X}}_{t}\Xi \varvec{\theta _{t}}\right) \right) ^{2}\right) \), \(\varvec{\iota }_{NG}\) is a \(NG\times 1\) unit vector and \(\varvec{\epsilon }_{t}^{*}=\left[ \begin{array}{ccc} \ln \left( \varvec{\epsilon }_{1,t}^{2}\right)&\dots&\ln \left( \varvec{\epsilon }_{n,t}^{2}\right) \end{array}\right] '\). In practice, it is common to set some small constant, c, to \(\varvec{y}_{t}^{*}\) to avoid numerical problems when \(\varvec{y}_{t}^{*}\) is close to zero—in this paper, we set \(c=0.0001\). Note that the resulting disturbance term in (A.10) is no longer Gaussian distributed but instead follows a \(\log \chi _{1}^{2}\) distribution. This means that despite being linear in the log-volatility term, standard linear Gaussian state–space algorithms cannot be directly applied. To overcome this difficulty, Kim et al. (1998) show that the moments of the \(\log \chi _{1}^{2}\) distribution can be well approximated through a seven-Gaussian mixture, in which an auxiliary random variable, denoted \(s_{t}\), serves as the mixture component indicator—hence the name of the algorithm, that is,
where \(p_{j}=P\left( s_{t}=j\right) \), \(j=1,\dots ,7\), \(f_{N}\left( \cdot |\mu ,\sigma ^{2}\right) \) is a Gaussian density with mean \(\mu \) and variance \(\sigma ^{2}\) and the values of the probabilities and moments associated with each Gaussian distribution are given in Table 3.
In summary, given the vector of mixture component indicators, \(\varvec{s}=\left[ \begin{array}{ccc} s_{1}&\dots&s_{T}\end{array}\right] '\), and parameter values in Table 3, the state–space model in (A.10) and (9) is linear and conditionally Gaussian; thus, standard sampling methods can be used. Instead of adopting traditional Kalman filter-based algorithms, we follow Poon (2018b) and implement the efficient precision sampling-based algorithm in Chan and Jeliazkov (2009) and Chan and Hsiao (2014).
To summarize, define \(\varvec{y}^{*}=\left( \varvec{y}_{1}^{*},\dots ,\varvec{y}_{T}^{*}\right) '\), \({\mathbf {h}}=(h_{1},...,h_{T})'\) is a \(T\times 1\) and \(\varvec{\epsilon }^{*}=(\varvec{\epsilon }_{1}^{*},\ldots \varvec{\epsilon }_{t}^{*})'\). Stacking the measurement equation in (A.10) over dates \(t=1,\dots ,T\) gives:
where \({\mathbf {X}}_{h}={\mathbf {I}}_{T}\otimes \varvec{\iota }_{NG}\) and \(\varvec{\epsilon }^{*}\sim N({\mathbf {d}}_{s},\varvec{\Sigma }_{\varvec{y}^{*}})\) where \({\mathbf {d}}_{s}=(\varvec{\mu }_{s_{1}},\dots ,\varvec{\mu }_{s_{T}})'\) and \(\varvec{\Sigma }_{\varvec{y}^{*}}=\text {diag}(\varvec{\sigma }_{s_{1}},\dots ,\varvec{\sigma }_{s_{T}})\) in which \(\varvec{\mu }_{s_{t}}=\left( {\mu _{s_{t}^{1}}-1.2704,\dots ,\mu _{s_{t}^{n}}-1.2704}\right) \) and \(\varvec{\sigma }_{s_{t}}=\left( {\sigma _{s_{t}^{1}}^{2},\dots ,\sigma _{s_{t}^{n}}^{2}}\right) \). Thus, by a change of variable:
To complete the state–space representation, stack the state equation for the log stochastic volatility factor in (9) over all dates \(t=1,\dots ,T\) to get:
where \(\varvec{\alpha }_{h}={\mathbf {H}}_{h}^{-1}\left( \begin{array}{cccc} h_{0}&0&\dots&0\end{array}\right) '\), \(\varvec{\Phi }=\text {diag}\left( \frac{\sigma _{h}^{2}}{(1-\rho ^{2})},\sigma _{h}^{2},\ldots ,\sigma _{h}^{2}\right) \) and
By a change of variable:
Finally, combining (A.13) and (A.15) gives the conditional posterior distribution:
where \(\hat{{\mathbf {h}}}={\mathbf {K}}_{h}^{-1}({\mathbf {H}}_{h}^{'}\varvec{\Phi }^{-1}{\mathbf {H}}_{h}^{'}\varvec{\alpha }_{h}+{\mathbf {X}}_{h}^{'}\varvec{\Sigma }_{{\mathbf {y}}_{i}^{*}}^{-1}({\mathbf {y}}^{*}-{\mathbf {d}}_{s}))\) and \({\mathbf {K}}_{h}={\mathbf {H}}_{h}^{'}\varvec{\Phi }^{-1}{\mathbf {H}}_{h}+{\mathbf {X}}_{h}^{'}\varvec{\Sigma }_{{\mathbf {y}}_{i}^{*}}^{-1}{\mathbf {X}}_{h}\). As in Step 1, sampling from this distribution is conducted with the precision sampling algorithm in Chan and Jeliazkov (2009).
Step 5: Sample from \(p\left( \rho \mid {\mathbf {Y}},\varvec{\theta },\varvec{\Sigma }_{u},{\mathbf {h}},\varvec{\Omega },\sigma _{h}^{2},\varvec{\kappa }\right) \)
To sample \(\rho \), first note that combining the prior with (9) gives:
where \(g(\rho )=(1-\rho ^{2})^{\frac{1}{2}}\text{ exp }(-\frac{1}{2\sigma _{h}^{2}}(1-\rho ^{2})(h_{1}-h_{0})^{2})\) and \(p(\rho )\) is a truncated normal. Since this conditional distribution is nonstandard, we follow Chan and Hsiao (2014) and implement an independence chain Metropolis–Hastings step with a truncated normal distribution. More precisely, \(\rho \sim N(\hat{\rho },D_{\rho })1(|\rho |<1)\), where \(D_{\rho }=\left( V_{\rho }+{\varvec{X}}'_{\rho }{\varvec{X}}_{\rho }/\sigma _{h}^{2}\right) ^{-1}\) and \(\hat{\rho }=D_{\rho }\left( V_{\rho }^{-1}\mu _{\rho }+{\varvec{X}}'_{\rho }\varvec{{\mathbf {z}}}_{\rho }/\sigma _{h}^{2}\right) \), in which \(\mathbf {\varvec{X}}_{\rho }=\left( h_{1},...,h_{T-1}\right) '\) and \(\mathbf {\varvec{z}}_{\rho }=\left( h_{2},...,h_{T}\right) '\). Then, given the current draw \(\rho ^{d}\), a proposal draw \(\rho ^{c}\) is accepted with probability \(\min \left\{ 1,\frac{g(\rho ^{c})}{g(\rho ^{d})}\right\} \); otherwise, the Markov chain stays at the current draw.
Step 6: Sample from \(p\left( \sigma _{h}^{2}\mid {\mathbf {Y}},\varvec{\theta },\varvec{\varvec{\Sigma }}_{u},{\mathbf {h}},\varvec{\Omega },\rho ,\varvec{\kappa }\right) \)
To sample \(\sigma _{h}^{2}\), we combine the inverse-Gamma prior distribution with the Gaussian likelihood function to get
Step 7: Sample from \(p\left( \varvec{\kappa }\mid {\mathbf {Y}},\varvec{\theta },\varvec{\varvec{\Sigma }}_{u},{\mathbf {h}},\varvec{\Omega },\rho ,\sigma _{h}^{2}\right) \)
Finally, to sample the hyperparameters in \(\varvec{\kappa }\) we follow Amir-Ahmadi et al. (2018) and employ a version of the (Gaussian) random walk Metropolis–Hastings algorithm for the proposal variance in a burn-in phase. In what follows, we describe the sampling procedure for a generic scaling factor \(\varvec{\kappa }_{X}\) where \(X\in \left\{ \varvec{\varvec{\Sigma }}_{u},\varvec{\Omega },\sigma _{h}^{2}\right\} \).Footnote 9 Starting from an initial condition in which we set \(\varvec{\kappa }_{X}^{0}\) to be the unit vector, the details are as follows:
-
1.
At step i, take a candidate draw \(\varvec{\kappa }_{X}^{c}\) from \(N\left( \varvec{\kappa }_{X}^{i-1},\sigma _{\kappa _{X}}^{2}{\mathbf {I}}\right) \) where \(\sigma _{\kappa _{X}}^{2}\) is a tuning parameter which is changed in the burn-in phase to achieve a target acceptance rate.Footnote 10
-
2.
Calculate the acceptance probability \(p^{i}=\left\{ 1,\frac{p\left\langle X|\varvec{\kappa }_{X}^{c}\right\rangle p\left( \varvec{\kappa }_{X}^{c}\right) }{p\left\langle X|\varvec{\kappa }_{X}^{i-1}\right\rangle p\left( \varvec{\kappa }_{X}^{i-1}\right) }\right\} \)
-
3.
Accept the candidate draw by setting \(\varvec{\kappa }_{X}^{i}=\varvec{\kappa }_{X}^{c}\) with probability \(p^{i}\). Otherwise set \(\varvec{\kappa }_{X}^{i}=\varvec{\kappa }_{X}^{i-1}\).
1.2 Appendix A.2 Model comparison
In appendix, we discuss how to compute the marginal likelihood using the one-step-ahead predictive likelihood. To this end, let \(\varvec{Y}_{t}^{o}\) denote a vector of observed variables up to date t. Following Geweke and Amisano (2011), the one-step- ahead predictive likelihood for model \(M_{i}\), given data up to date \(t-1\), is given by:
where \(t=1\) is evaluated by:
which is entirely driven by the marginal data density: \(p\left( {\mathbf {Y}}_{1}^{o}\right) \). Given this value, we then approximate \(p\left( {\mathbf {Y}}_{t}|{\mathbf {Y}}_{t-1}^{o},M_{i}\right) \) for dates \(t=2,\dots ,T\) by the Monte Carlo average:
where \(\left\{ \varvec{\Theta }_{i,t-1}^{\left( r\right) }\right\} _{r=1}^{R}\) is a sequence of draws from then Metropolis–Hastings within Gibbs sampler described in “Appendix A.1.”
Finally, to see how the predictive likelihood is related to the Bayes factor, note that the marginal likelihood of the model \(M_{i}\) is given by:
Thus, the Bayes factor between models \(M_{i}\) and \(M_{j}\) is:
Rights and permissions
About this article
Cite this article
Cross, J.L., Poon, A. On the contribution of international shocks in Australian business cycle fluctuations. Empir Econ 59, 2613–2637 (2020). https://doi.org/10.1007/s00181-019-01752-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-019-01752-y