The arbitrage-free generalized Nelson–Siegel term structure model: Does a good in-sample fit imply better out-of-sample forecasts?

Abstract

At the zero lower bound, the dynamic Nelson–Siegel (DNS) model and even the Svensson generalization of the model have trouble in fitting the short maturity yields and fail to grasp the characteristics of the Japanese government bonds (JGBs) yield curve. During the zero interest rate policy regime, the short end of the yield curve is flat and yields corresponding to various maturities have asymmetric movements. Therefore, closely related generalized versions of Nelson–Siegel model—with and without no-arbitrage restriction (GAFNS and GDNS)—that have two slopes and curvatures factors are considered and compared empirically in terms of in-sample fit as well as out-of-sample forecasts with the standard Nelson–Siegel model—with and without no-arbitrage restriction (AFNS and DNS). The affine-based models provide a more attractive fit of the yield curve than their counterpart DNS-based models. Both extended models are capable to restrict the estimated rates from becoming negative at the short end of the curve and distill the JGBs term structure of interest rate quite well. The affine-based extended model leads to a better in-sample fit than the simple GDNS model. In terms of out-of-sample accuracy, both non-affine models outperform the affine models at least for 1- and 6-month horizons. The out-of-sample predictability of the GDNS for the 1- and 6-month-ahead forecasts is superior to the GAFNS for all maturities, and for longer horizons, i.e., 12-month-ahead, the former is still compatible to the latter, particularly for short- and medium-term maturities.

Appendices

Appendix-I

1.1 Principal component analysis of the JGBs yields

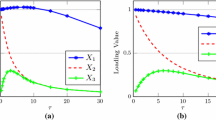
Consider the JGB zero rates with maturities of 3, 6, 9, 12, 15, 18, 21, 24, 30, 36, 48, 60, 72, 84, 96, 108, 120, 180, 240 and 300 months (20 maturities) from January 1996 through December 2013, the principal component analysis is carried out and the results are reported in Table 11 and Fig. 5. Table 11 reports the eigenvectors that correspond to the first five principal components of the sample. Figure 5 displays the scatter plot of loadings of first five principal components against maturity.

Table 11 Principal component analysis and factor loadings of JGBs yields during ZIRP

Fig. 5

Loadings of the first five principal components. The figure presents the loadings for the first five eigenvalues (eigenvectors) of the principal component analysis of the JGBs zero rates for 20 maturities. The sample consists of monthly observations from January 1996 to December 2013

Appendix-II

2.1 Coefficients and latent variable in the general state-space form

In the statistical formulation of the models in Sect. 2.3, the matrices and vectors for the state and observations equations should be considered as follows. In the state-space framework (23–25) for GDNS, the matrices can be defined as:

$$ \begin{array}{*{20}l} {B = \varLambda \left( {\lambda_{1} ,\lambda_{2} } \right);\,\,\left( {N \times 5} \right)} \hfill & {X_{t} = \left( {\beta_{1t} ,\beta_{2t} ,\beta_{3t} ,\beta_{4t} ,\beta_{5t} } \right)^{\prime } ;\,\, \left( {5 \times 1} \right)} \hfill & {w_{t} = \varepsilon_{t} ;\,\,\left( {N \times 1} \right)} \hfill \\ {C = \left( {I_{5} - F} \right)\mu ;\,\,\left( {5 \times 1} \right)} \hfill & {H = F;\,\,\left( {5 \times 5} \right)} \hfill & {u_{t} = v_{t} ;\,\,\left( {5 \times 1} \right)} \hfill \\ {\varOmega = \varOmega ;\,\,\left( {N \times N} \right)} \hfill & {Q_{t} = \varSigma_{v} ;\,\,\left( {5 \times 5} \right)} \hfill & {\tilde{A} = 0;\,\,\left( {N \times 1} \right)} \hfill \\ \end{array} $$

while for the GAFNS model the matrices and vectors can be written as:

$$ \begin{array}{*{20}l} {B = \varLambda \left( {\lambda_{1} ,\lambda_{2} } \right): \, \left( {N \times 5} \right)} \hfill & {X_{t} = \left( {X_{t}^{1} , X_{t}^{2} ,X_{t}^{3} ,X_{t}^{4} ,X_{t}^{5} } \right)^{'} :\left( {5 \times 1} \right)} \hfill & {w_{t} = \varepsilon_{t} : \, \left( {N \times 1} \right)} \hfill \\ {C = \left( {I_{5} - e^{ - K\Delta t} } \right)\theta : \, \left( {5 \times 1} \right)} \hfill & {H = e^{ - K\Delta t} : \, \left( {5 \times 5} \right)} \hfill & {u_{t} = v_{t} : \, \left( {5 \times 1} \right)} \hfill \\ {\varOmega = \varOmega :\left( {N \times N} \right)} \hfill & {Q_{t} = \varSigma_{v} : \, \left( {5 \times 5} \right)} \hfill & {\tilde{A} = - A: \, \left( {N \times 1} \right)} \hfill \\ \end{array} $$

In both models, the matrix $\varOmega$ is assumed to be diagonal for computational traceability, while the covariance matrix $\varSigma_{v}$ is considered non-diagonal.

Appendix-III

3.1 Data description

We consider JGB yields with maturities of 3, 6, 9, 12, 15, 18, 21, 24, 30, 36, 48, 60, 72, 84, 96, 108, 120, 180, 240 and 300 months. The yields are derived from bid/ask average price quotes, from January 1996 through December 2013, using the Fama and Bliss (1987) methodology.

Table 12 provides summary statistics for the dataset. For each maturity, we report mean, standard deviation, minimum, maximum, skewness, kurtosis, and autocorrelation coefficients at various displacements. The summary statistics reveal that the average yield curve is upward sloping. Unconditional volatility increases by maturity and yields for all maturities are persistent; however, relatively short rates persistency is higher than those of the long rates.

Table 12 Descriptive statistics of yields data across maturities

In addition to the findings in Table 12, we see few interesting characteristics in Fig. 6, which plots cross section of yields over time. The first noticeable fact is that long-term yields vary significantly over time. Second, the short rates are almost zero during the prolonged period except with a little rise in late 2006 and early 2007 that causes a fall in the slope of the curves. Moreover, when short rates are stuck at zero, the long end seems more volatile than the short end of the curves.

Fig. 6

The figure shows the yield curves, 1996:01–2013:12. The sample consists of monthly yield data from January 1996 to December 2013 (216 months) for maturities of 3, 6, 9, 12, 15, 18, 21, 24, 30, 36, 48, 60, 72, 84, 96, 108, 120, 180, 240 and 300 months (20 maturities)