Skip to main content
SpringerLink
Log in

Modeling US historical time-series prices and inflation using alternative long-memory approaches

  • Published:
Empirical Economics Aims and scope Submit manuscript

Abstract

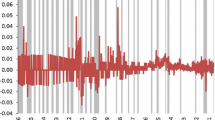
We consider two important features of the historical US price data (1774–2015), namely the data’s persistence and cyclical structure. We first consider the persistence of the series and focus on standard long-memory models that incorporate a peak at the zero frequency. We examine different models with respect to the deterministic terms, including nonlinear deterministic trends of the Chebyshev form. Then, we investigate a more general model that includes both persistence and cyclicality of the series and, thus, includes two fractional integration parameters, one at the zero (long-run) frequency and the other at the nonzero (cyclical) frequency. We model the cyclical structure as a Gegenbauer process. This specification outperforms the standard long-memory specifications. We find that the order of integration at the zero frequency is about 0.5, and the one at the cyclical frequency is about 0.2 with cycles repeating approximately every 6 years, producing mean-reverting long-memory effects at both the zero and cyclical frequencies. Fitting the values to this model, however, we discover the presence of a break that, according to the methods employed, takes place at around 1940–1941. The results indicate the prevalence of the long-run or zero component with a much higher degree of persistence during the second post-1940–1941 subsample, suggesting important implications for monetary policy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. As the existing literature frequently notes, inflation persistence plays an important role in the conduct of monetary policy as well as the development of the underlying macroeconomic theories. Inflation persistence measures the speed with which the inflation rate returns to its equilibrium level after an inflationary shock. If the inflation rate returns to its equilibrium level quickly (i.e., the inflation rate exhibits less persistence) after a shock, then the monetary authorities can more effectively reduce inflation fluctuations, all else equal (Fuhrer 1995). High inflation persistence, on the other hand, causes shocks to exert long-lasting effects and may require a strong policy response to affect the dynamics of inflation and bring it under control. In the worst case, inflation may follow a random-walk I(1) process, making it impossible for central banks to control inflation. In the best case, inflation may follow a stationary I(0) process, implying that it reverts to its equilibrium level rapidly after a random shock. In this latter case, the response to the inflationary shock may not require an active monetary policy. Thus, the optimal timing and size of monetary policy crucially depend on not only knowledge of how shocks affect the dynamics of inflation but also on the degree of persistence that identifies the inflation process. In this regard, we note that inflation persistence plays an important role in the current debate on inflation targeting. When a central bank successfully anchors inflationary expectations by its inflation targeting policy, it reduces or eliminates inflation persistence, since well-anchored inflationary expectations depend less on past inflation.

  2. Hassler et al. (2009) propose a similar procedure based on a LM test in the time domain to detect general forms of fractional integration at the long-run and/or the cyclical component of a time series.

  3. These regularity conditions are rather mild, involving the behavior of \( u_{t} \) and specific technical assumptions on the two polynomials in Eq. (2).

  4. See Hamming (1973) and Smyth (1998) for a detailed description of these polynomials.

  5. See Cuestas and Gil-Alana (2016) for further details on the choice of m.

  6. One can download the data from: http://liberalarts.oregonstate.edu/spp/polisci/research/inflation-conversion-factors.

  7. For the exponential spectral model of Bloomfield (1973), we tried different orders from 1 to 3. The results were similar in the three cases. Thus, we report the results only with m = 1.

  8. Similar to the nonlinear case above, expressing the two equations in (8) in a single equation produces I(0) errors, implying that t values apply.

  9. Using other types of nonlinear deterministic terms such as Hermite polynomials does not produce any evidence of nonlinearities in the data.

  10. In particular, we perform tests of no serial correlation, functional form, normality, and homoscedasticity using Microfit 5.0. For serial correlation, we use a Lagrange Multiplier test of residuals serial correlation (Godfrey 1978a, b): test statistic, 0.356; for the functional form, the Ramsey’s (1969) RESET test using powers of the fitted values: test statistic, 1.145 and 1.177 with squared and cubic terms, respectively; for normality, a test based on skewness and kurtosis of residuals, (Bera and Jarque 1981): test statistic, 3.490; and for homoscedasticity, we use Koenker (1981) modified LM test of Breusch and Pagan (1979): test statistic, 1.906.

References

  • Abadir KM, Distaso W, Giraitis L (2007) Nonstationarity-extended local Whittle estimation. J Econ 141(2):1353–1384

    Article  Google Scholar 

  • Andre C, Gil-Alana LA, Gupta R (2014) App Econ 46(18):2127–2138

    Article  Google Scholar 

  • Anděl J (1986) Long memory time series models. Kybernetika 22(2):105–123

    Google Scholar 

  • Bai J, Perron P (2003) Computation and analysis of multiple structural change models. J Appl Econ 18(1):1–22

    Article  Google Scholar 

  • Baillie RT (1996) Long memory processes and fractional integration in econometrics. J Econ 73(1):5–59

    Article  Google Scholar 

  • Ben Nasr A, Ajmi AN, Gupta R (2014) Modeling the volatility of the Dow Jones Islamic market world index using a fractionally integrated time varying GARCH (FITVGARCH) model. App FIn Econ 24(14):993–1004

    Article  Google Scholar 

  • Bera AK, Jarque NM (1981) Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Monte Carlo Evid 7(4):313–318

    Google Scholar 

  • Bierens HJ (1997) Testing the unit root with drift hypothesis against nonlinear trend stationarity with an application to the US price level and interest rate. J Econ 81(1):29–64

    Article  Google Scholar 

  • Bloomfield P (1973) An exponential model in the spectrum of a scalar time series. Biometrica 60(2):217–226

    Article  Google Scholar 

  • Bos CS, Franses PH, Ooms M (1999) Long memory and level shifts: Re-analyzing inflation rates. Empir Econ 24(3):427–449

    Article  Google Scholar 

  • Boubaker H, Canarella G, Gupta R, Miller SM (2017) Time-varying persistence of inflation: evidence from a wavelet-based approach. Stud Nonlinear Dyn Econ 21(4):1–18

    Google Scholar 

  • Breusch T, Pagan A (1979) A simple test for heterocedasticity and random coefficient variation. Econometrica 47(5):1287–1294

    Article  Google Scholar 

  • Burns F, Mitchell W (1946) Measuring business cycles. NBER, New York

    Google Scholar 

  • Canarella G, Miller SM (2016) Inflation persistence and structural breaks: the experience of inflation targeting countries and the US. J Econ Stud 43(6):980–1005

    Article  Google Scholar 

  • Canarella G, Miller SM (2017a) Inflation persistence before and after inflation targeting: a fractional integration approach. East Econ J 43(1):1–26

    Article  Google Scholar 

  • Canarella G, Miller SM (2017b) Inflation targeting: new evidence from fractional integration and cointegration. J Econ Bus 92(Jul/Aug):45–62

    Article  Google Scholar 

  • Caporale GM, Gil-Alana LA (2002) Fractional integration and mean reversion in stock prices. Q Rev Econ Finance 42(3):599–609

    Article  Google Scholar 

  • Caporale GM, Gil-Alana LA (2005) Fractional cointegration and aggregate money demand functions. Manch Sch 73(6):737–753

    Article  Google Scholar 

  • Caporale GM, Gil-Alana LA (2007) Nonlinearities and fractional integration in the US unemployment rate. Oxford Bull Econ Stat 69(4):521–544

    Article  Google Scholar 

  • Caporale GM, Gil-Alana LA (2010) Fractional integration and data frequency. J Stat Comput Simul 80(2):121–132

    Article  Google Scholar 

  • Caporale GM, Gil-Alana LA (2013) Long memory and fractional integration in high frequency data on the US dollar/British pound spot exchange rate. Int Rev Financ Anal 29:1–9

    Article  Google Scholar 

  • Caporale GM, Gil-Alana LA (2014) Long-run and cyclical dynamics in the US stock market. J Forecast 33(2):147–161

    Article  Google Scholar 

  • Chung C-F (1996a) A generalized fractionally integrated autoregressive moving-average process. J Time Ser Anal 17(2):111–140

    Article  Google Scholar 

  • Chung C-F (1996b) Estimating a generalized long memory process. J Econ 73(1):237–259

    Article  Google Scholar 

  • Cuestas JC, Gil-Alana LA (2016) Testing for long memory in the presence of non-linear deterministic trends with Chebyshev polynomials. Stud Nonlinear Dyn Econ 20(1):57–74

    Google Scholar 

  • Dahlhaus R (1989) Efficient parameter estimation for self-similar processes. Ann Stat 17(4):1749–1766

    Article  Google Scholar 

  • Dalla V, Hidalgo J (2005) A parametric bootstrap test for cycles. J Econ 129(1–2):219–261

    Article  Google Scholar 

  • Demetrescu M, Kuzin V, Hassler U (2008) Long memory testing in the time domain. Econ Theory 24(1):176–215

    Article  Google Scholar 

  • Diebold F, Inoue A (2001) Long memory and regime switching. J Econ 105(1):131–159

    Article  Google Scholar 

  • Diebold FX, Mariano RS (1995) Comparing predictive accuracy. J Bus Econ Stat 13(3):253–326

    Google Scholar 

  • Fuhrer JC (1995) The persistence of inflation and the cost of disinflation. New Engl Econ Rev (Jan/Feb):3–16

  • Gadea MD, Mayoral L (2006) The persistence of inflation in OECD countries: a fractionally integrated approach. Int J Cent Bank 4(1):51–104

    Google Scholar 

  • Geweke J, Porter-Hudak S (1983) The estimation and application of long memory time series models. J Time Ser Anal 4(4):221–237

    Article  Google Scholar 

  • Gil-Alana LA (2001) Testing stochastic cycles in macroeconomic time series. J Time Ser Anal 22(4):411–430

    Article  Google Scholar 

  • Gil-Alana LA (2004) The use of the Bloomfield (1973) model as an approximation to ARMA processes in the context of fractional integration. Math Comput Model 39(4–5):429–436

    Article  Google Scholar 

  • Gil-Alana LA (2005a) Fractional cyclical structures and business cycles in the specification of the US real output. Euro Res Stud J 8(1–2):99–126

    Google Scholar 

  • Gil-Alana LA (2005b) Testing and forecasting the degree of integration in the US inflation rate. J Forecast 24(3):173–187

    Article  Google Scholar 

  • Gil-Alana LA (2008) Fractional integration and structural breaks at unknown periods of time. J Time Ser Anal 29(1):163–185

    Article  Google Scholar 

  • Gil-Alana LA, Gupta R (2014) Persistence and cycles in historical oil price data. Energy Econ 45:511–516

    Article  Google Scholar 

  • Gil-Alana LA, Robinson PM (1997) Testing of unit roots and other nonstationary hypotheses in macroeconomic time series. J Econ 80(2):241–268

    Article  Google Scholar 

  • Giraitis L, Leipus R (1995) A generalized fractionally differencing approach in long memory modeling. Lith Math J 35(1):65–81

    Article  Google Scholar 

  • Godfrey LG (1978a) Testing against general autoregressive and moving average error models when the regressors include lagged dependent variables. Econometrica 46(6):1293–1301

    Article  Google Scholar 

  • Godfrey LG (1978b) Testing for higher order serial correlation in regressor equations when the regressors include lagged dependent variables. Econometrica 46(6):1303–1310

    Article  Google Scholar 

  • Granger CWJ (1980) Long memory relationships and the aggregation of dynamic models. J Econ 14(2):227–238

    Article  Google Scholar 

  • Granger CWJ (1981) Some properties of time series data and their use in econometric model specification. J Econ 16(1):121–131

    Article  Google Scholar 

  • Granger CWJ, Hyung N (2004) Occasional structural breaks and long memory with an application to the S&P 500 absolute stock returns. J Empir Finance 11(3):213–228

    Article  Google Scholar 

  • Granger CWJ, Joyeux R (1980) An introduction to long-memory time series models and fractional differencing. J Time Ser Anal 1(1):15–29

    Article  Google Scholar 

  • Gray HL, Yhang N, Woodward WA (1989) On generalized fractional processes. J Time Ser Anal 10(3):233–257

    Article  Google Scholar 

  • Gray HL, Yhang N, Woodward WA (1994) On generalized fractional processes. A correction. J Time Ser Anal 15(5):561–562

    Article  Google Scholar 

  • Hamming RW (1973) Numerical methods for scientists and engineers. McGraw-Hill, New York

    Google Scholar 

  • Hansen PR, Lunde A, Nason JM (2011) The model confidence set. Econometrica 79(2):453–497

    Article  Google Scholar 

  • Harvey DI, Leybourne SJ, Newbold P (1997) Testing the equality of prediction mean squared errors. Int J Forcast 13(2):281–291

    Article  Google Scholar 

  • Hassler U, Meller B (2014) Detecting multiple breaks in long memory. The case of US inflation. Empir Econ 46(2):653–680

    Article  Google Scholar 

  • Hassler U, Rodrigues P, Rubia A (2009) Testing for general fractional integration in the time domain. Econ Theory 25(6):1793–1828

    Article  Google Scholar 

  • Hipel KW, McLeod AI (1978) Preservation of the rescaled adjusted range. Simulation studies using Box–Jenkins models. Water Resour Res 14(3):509–516

    Article  Google Scholar 

  • Hosking JRM (1981) Fractional differencing. Biometrika 68(1):165–176

    Article  Google Scholar 

  • Hou J, Perron P (2014) Modified local Whittle estimator for long memory processes in the presence of low frequency (and other) contaminations. J Econom 182(2):309–328

    Article  Google Scholar 

  • Koenker R (1981) A note on studentizing a test for heteroscedasticity. J Econ 17(1):107–112

    Article  Google Scholar 

  • Kumar MS, Okimoto T (2007) Dynamics of persistence in international inflation rates. J Money Credit Bank 39(6):1457–1479

    Article  Google Scholar 

  • Kydland FE, Prescott EC (1982) Time to build and aggregate fluctuations. Econometrica 50(6):1345–1370

    Article  Google Scholar 

  • Lee J, Strazicich MC (2003) Minimum Lagrange Multiplier unit root test with one structural break. Rev Econ Stat 85(4):1082–1089

    Article  Google Scholar 

  • Long JB, Plosser CI (1983) Real business cycles. J Polit Econ 91(1):39–69

    Article  Google Scholar 

  • Lucas RE (1972) Expectations and the neutrality of money. J Econ Theory 4(2):103–124

    Article  Google Scholar 

  • Lucas RE (1975) An equilibrium model of the business cycle. J Polit Econ 83(6):1113–1144

    Article  Google Scholar 

  • Mankiw NG (1989) Real business cycles: a new Keynesian perspective. J Econ Perspect 3(3):79–90

    Article  Google Scholar 

  • Nelson CR, Plosser CI (1982) Trends and random walks in macroeconomic time series: some evidence and implications. J Monet Econ 10(2):139–162

    Article  Google Scholar 

  • Ouliaris S, Park JY, Phillips PCB (1989) Testing for a unit root in the presence of a maintained trend. In: Raj B (ed) Advances in econometrics and modelling. Kluwer Academic Publishers, Norwell, pp 7–28

    Chapter  Google Scholar 

  • Phillips PCB (2007) Unit root log periodogram regression. J Econ 138(1):104–124. Original version (March 1999) Cowles Foundation Discussion Paper (CFDP) No. 1243, Cowles Foundation for Research in Economics, Yale University

  • Ramsey JB (1969) Test for specification errors in classical linear least squares regression analysis. J R Stat Soc Ser B 31(2):350–371

    Google Scholar 

  • Robinson PM (1994) Efficient tests of nonstationary hypotheses. J Am Stat Assoc 89(42):1420–1437

    Article  Google Scholar 

  • Robinson PM (1995) Gaussian semi-parametric estimation of long range dependence. Ann Stat 23(5):1630–1661

    Article  Google Scholar 

  • Smyth GK (1998) Polynomial approximation. Wiley, Chichester

    Google Scholar 

  • Tomasevic NM, Stanivuk T (2009) Regression analysis and approximation by means of Chebyshev polynomial. Informatologia 42(3):166–172

    Google Scholar 

  • Velasco C (1999) Gaussian semiparametric estimation of nonstationary time series. J Time Ser Anal 20(1):87–127

    Article  Google Scholar 

  • Velasco C (2000) Non-Gaussian log-periodogram regression. Econ Theory 16(1):44–79

    Article  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge the comments from the Editor and two anonymous reviewers. Luis A. Gil-Alana gratefully acknowledges financial support from the Ministerio de Economía y Competitividad (ECO2017-85503-R).

Author information

Authors and Affiliations

  1. Department of Economics, University of Nevada, Las Vegas, 4505 S. Maryland Parkway, Las Vegas, NV, USA

    Giorgio Canarella & Stephen M. Miller

  2. Faculty of Economics, University of Navarra, Pamplona, Spain

    Luis A. Gil-Alana

  3. University of Pretoria, Pretoria, South Africa

    Rangan Gupta

Authors
  1. Giorgio Canarella
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luis A. Gil-Alana
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rangan Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Stephen M. Miller
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stephen M. Miller.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Canarella, G., Gil-Alana, L.A., Gupta, R. et al. Modeling US historical time-series prices and inflation using alternative long-memory approaches. Empir Econ 58, 1491–1511 (2020). https://doi.org/10.1007/s00181-018-1597-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00181-018-1597-2

Keywords

JEL Classification

Search

Navigation