Abstract
This paper uses data for the UK and the Netherlands (1983q4–2011q4) to test if hysteresis occurs in these economies, and through what mechanisms. The novelty of the paper resides in the use of a VAR-IRF that encompasses previous hysteresis studies, using long-term unemployment, productivity, capital stock and real long-term interest rates, and in the use of specific Labour Market Institutions shocks, such as benefits, taxation or unions’ power. This allows us to disentangle what specific demand and supply-variables affect unemployment in the long-run, i.e. the NAIRU. Our findings suggest that there is hysteresis in both countries, and that it happens through several channels. Further, we find that the influence of Labour Market Institutions on unemployment depend on their impact on the real wages-productivity gap. These results have implications for structural and macroeconomic policies that we also discuss. Finally, we investigate the impact of different supply and demand-shock on long-term unemployment and discuss the relevant policy implications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
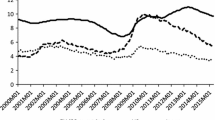
This paper investigates if hysteresis occurs in the UK and the Netherlands and what demand variables make this phenomenon possible. It is usually argued that Labour Market Institutions (LMI) can explain the evolution of unemployment in these economies since the 1980s (Nickell 1998; Nickell and Ours 2000; Broersma et al. 2000). These authors argue that high-trade union power, generous benefits systems and high taxation contributed to high unemployment during the 1980s, and that reforms of these LMIs have made unemployment reductions possible afterwards. In the UK, these reforms include Thatcher’s programmes of liberalization and Blair’s “New Deal”, and in the Netherlands, the “Wassenaar Agreements” and later reforms of the benefits and tax systems. However, if we examine the response of variables, such as long-term unemployment and capital accumulation to the recessions of the last three decades, here presented in Fig. 1, we observe that these variables recover very slowly, if at all, after these shocks occur. According to Blanchard and Summers (1986) and Arestis and Sawyer (2005), this can influence wage and price-setting behaviour, and in turn the NAIRU, generating hysteresis effects. This paper examines this hypothesis, we test if there is hysteresis in the UK and the Netherlands and what demand variables cause such phenomenon.
Several approaches have been used to test the hysteresis hypothesis in country-specific studies. Some authors apply unit root and stationarity tests to study the properties of unemployment series. If unemployment is found to be mean reverting it is interpreted as evidence in favour of the NAIRU a la Layard et al. (1991, Ch. 8). Alternatively, if unemployment exhibits a unit root, it is taken as evidence of hysteresis. Some recent reviews of this literature can be found in Romero-Avila and Usabiaga (2008) or Fosten and Ghoshray (2011). Evidence for the UK and the Netherlands is mixed and sensitive to the inclusion of structural breaks and changes in the sample period. Furthermore, this approach cannot disentangle what demand-factors, e.g., long-term unemployment or capital stock, propitiate unit roots.
This problem does not arise in other branches of the literature that aim at testing specific hysteresis mechanisms rather than the properties of unemployment series. This is the case of the wage-equation literature that examines the response of real wages to unemployment duration. This serves to test Blanchard and Summers (1986) hypothesis that shocks that increase the share of long-term unemployment increase wage pressure and in turn the NAIRU, creating hysteresis. Available evidence for the UK is mixed, Nickell (1987), Manning (1994) and Arulampalam et al. (2000) find support for this hypothesis, but this is disputed by Blanchflower and Oswald (1994) and Bell and Blanchflower (2014). In the Netherlands, this hypothesis is rejected by Graafland (1991, 1992). However, this literature focuses on the wage-equation and does not control for demand-factors that affect the price-setting behaviour of firms, which could also cause hysteresis, such as, capital stock (Bean 1989; Arestis and Sawyer 2005) or interest rates (Fitoussi and Phelps 1988, p. 57; Rowthorn 1999). These omissions are problematic because they can bias results.
Other authors use time-varying estimation methods to identify the structural breaks on unemployment and the variables that cause such shifts, e.g. Logeay and Tober (2006) and Srinivasan and Mitra (2014) for Germany and the UK, respectively. Srinivasan and Mitra find no evidence of hysteresis in the UK, although they only use labour-supply measures to control for hysteresis. Further, this single-equation approach does not take account of the interactions that shocks generate in the labour market. To control for these interactions, researchers use VAR-systems to model the labour market and then use the associated Impulse Response Functions (IRF) to evaluate the impact of shocks. Carstensen and Hansen (2000), Gambetti and Pistoresi (2004) and Binotti and Ghiani (2008) apply this approach to Germany and ItalyFootnote 1. They simulate labour supply-shocks to tests Blanchard and Summers’ hypothesis, and productivity shocks to evaluate claims that this variable can reduce unemployment permanently (Stiglitz 1997; Ball and Mankiw 2002). However, these studies might also be subject to biases as they overlook the potential influence of capital stock and real long-term interest rates on unemployment.
Our paper extends available literature by estimating a VAR-IRF that allows us to test for hysteresis effects through unemployment duration, productivity, capital stock and real long-term interest rates. This helps us disentangle what specific demand-factors affect unemployment in the long run while controlling for the interactions in the labour market and avoiding potential biases that existing literature might be subject to. We use the most recent data for the UK and the Netherlands to estimate a Cointegrated-VAR model for each country and simulate different demand-shocks, using the associated IRFs, to test different hysteresis hypothesis. Further, we also consider the impact of specific LMI-shocks to investigate the LMI-unemployment link. This is in contrast to existing VAR-IRF literature, where this link is studied by simulating generic wage-shocks. Our approach seems more adequate for policy design given that available evidence suggests that not all LMI increase the NAIRU (Nickell 1997; OECD 2006; Layard and Nickell 2011, Ch. 7). Finally, we also study the impact of different supply and demand-shocks on long-term unemployment.
The paper proceeds as follows. Section 2 presents our theoretical model. Section 3 explains our methodology. Section 4 examines the data. Section 5 presents our estimations. Section 6 presents our IRF-simulations. Section 6 summarizes our findings and their implications.
2 Wage and price-setting model
Our theoretical model draws from the well-known NAIRU model presented in Layard et al. (1991, Ch. 8) and Layard and Nickell (2011, Ch. 1–2), LNJ hereafterFootnote 2. We extend this model to account for the following hysteresis factors, long-term unemployment, productivity, capital stock and real long-term interest rates. We assume that the labour and goods market operate under imperfect competition, which gives workers and firms price-making power. In the labour market, imperfect competition is usually characterized by the presence of unions or efficiency wagesFootnote 3. Accordingly, workers negotiate a nominal wage based on their price expectation that allows them to achieve certain “target” real wage \((w-p^{e})\), which grows with expected productivity \((y-l )^{e}\) and is moderated by slack in the labour market, i.e. unemployment (u). Equation (1) illustrates this (all the variables are in logarithm):
As in LNJ’s model, workers’ “Target” is also pushed-up by several LMIs, viz-a-viz, unemployment benefits (grr), the tax-wedge \((t^{w})\) and unions’ power (up). We do not consider other LMIs, such as employment legislation or minimum wages because existing evidence is generally not supportive of their influence on unemployment (OECD 2006, p. 59–107; Layard and Nickell 2011, Ch. 7). Further, Eq. (1) also grows with long-term unemployment (lu) reflecting Blanchard and Summers (1986) hypothesis, BS hereafter, that is, increases in unemployment duration raises insiders bargaining power and wages, which in turn increases the NAIRU. See also Ball (1999, 2009) or Krueger et al. (2014).
In the goods market, imperfect competition takes the form of monopolistic or oligopolistic competitionFootnote 4. This allows firms to set prices as a mark-up over expected wages \((p-w^{e})\) moderated by unemployment and expected productivity, hence, the term “feasible” real wage to refer to this mark-up, here illustrated by Eq. (2).
Equation (2) is also a negative function of capital stock (k) to account for hysteresis through capital-scrapping. Bean (1989) and Arestis and Sawyer (2005) argue that after a negative shock, capital accumulation slows-down scrapping part of the productive capacity of the economy. As a result, some of the workers that lost their jobs cannot be re-employed and add-up to the existing unemployment equilibrium, i.e. the NAIRUFootnote 5. Further, Eq. (2) is a positive function of real long-term interest rates \((i-\Delta p)\) to reflect claims by Fitoussi and Phelps (1988, p. 57) and Rowthorn (1999), that firms’ (real) long-term cost of borrowing increases firms mark-up, and in turn the NAIRU.
Assuming expectations are fulfilled in the long-run and equating (1) and (2) to solve for unemployment, we find Eq. (3), the unemployment level that makes workers and firms income claims compatible, i.e. the NAIRU. Further, solving for \(w-p\), we find the long-run real wage equilibrium associated with this NAIRU, Eq. (4).
Where, \(\beta _{12}=\frac{\omega _{2}-\varphi _{3}}{\omega _{1}+\varphi _{1}},\quad \beta _{14}=\frac{\omega _{11}}{\omega _{1}+\varphi _{1}},\quad \beta _{15}=\frac{\omega _{4}}{\omega _{1}+\varphi _{1}},\quad \beta _{16}=\frac{\omega _{5}}{\omega _{1}+\varphi _{1}}, \beta _{17}=\frac{\omega _{6}}{\omega _{1}+\varphi _{1}},\quad \beta _{18}=-\frac{\varphi _{2}}{\omega _{1}+\varphi _{1}},\quad \beta _{19}=\frac{\varphi _{5}}{\omega _{1}+\varphi _{1}}\)
Where, \(\beta _{22}=\left( \omega _{2}-\omega _{1}\frac{\omega _{2}-\varphi _{3}}{\omega _{1}+\varphi _{1}} \right) ,\quad \beta _{24}=\varphi _{1}\frac{\omega _{11}}{\omega _{1}+\varphi _{1}},\quad \beta _{25}=\varphi _{1}\frac{\omega _{4}}{\omega _{1}+\varphi _{1}},\quad \beta _{26}=\varphi _{1}\frac{\omega _{5}}{\omega _{1}+\varphi _{1}},\quad \beta _{27}=\varphi _{1}\frac{\omega _{6}}{\omega _{1}+\varphi _{1}},\quad \beta _{28}=\omega _{1}\frac{\varphi _{2}}{\omega _{1}+\varphi _{1}},\quad \beta _{29}=-\omega _{1}\frac{\varphi _{5}}{\omega _{1}+\varphi _{1}}\)
The NAIRU described by Eq. (3) is a function of LMI and demand variables. If \(\beta _{{12}}=\beta _{{14}}=\beta _{{18}}=\beta _{{19}}=0\), the NAIRU is exclusively determined by LMI, as argued by LNJ. In our case, \(grr,\, t^{w}\) and up. These \(\beta \)-restrictions imply the following restrictions in Eqs. (1) and (2). First, \(\beta _{{12}}=0\) meaning that the NAIRU is neutral to productivity, requires \(\omega _{{2}}=\varphi _{{3}}\), i.e. productivity gains are fully reflected in workers real wages. However, if wages are slow to react to changes in productivity, i.e. \(\omega _{{2}}<\varphi _{{3}}\) for long lapses of time, productivity reduces the NAIRU \((\beta _{{12}}<0)\) as argued by Stiglitz (1997) and Ball and Mankiw (2002)Footnote 6. Second, \(\beta _{{14}}=0\) requires \(\omega _{11}=0\), meaning that there is no hysteresis through unemployment duration. However, if \(\omega _{11}>0\), then greater long-term unemployment increases wage claims and the NAIRU \((\beta _{{14}}>0)\) as proposed by BS. Third, \(\beta _{{18}}=0\) requires \(\varphi _{2}=0\), ruling out capital-scrapping. However, if \(\varphi _{2}>0\), then more productive capacity reduces firms mark-up and the NAIRU \((\beta _{{18}}<0)\) as advocated by the capital-scrapping hypothesis. Fourth, \(\beta _{{19}}=0\) requires \(\varphi _{5}=0\), the cost of borrowing does neither affect the “feasible” real wage, nor the NAIRU. However, if \(\varphi _{5}>0\), then real long-term interest rates raises firms’ mark-up and in turn the NAIRU \((\beta _{{19}}>0)\).
On the other hand, if any of the restrictions \(\beta _{{12}}=\beta _{{14}}=\beta _{{18}}=\beta _{{19}}=0\) does not hold, then the NAIRU is determined by either \(y-l\) or lu or k or \(i-\Delta p\), respectively. These variables are sensitive to the evolution of demand (and macroeconomic policy); thus, there is hysteresisFootnote 7. This paper tests these restrictions to evaluate whether there is hysteresis or not and what mechanisms in the wage and price-setting equations make this possible.
In the short-run, expectations might not be fulfilled, and unemployment and real wages will deviate from their long-run equilibria noted above. To find their short-run levels, we need to solve the expectations terms in (1) and (2). We adopt adaptive expectations on the basis that in our sample price and wage-inflation, as well as productivity, seem to have a unit rootFootnote 8. Hence, considering adaptive expectation and short-run mistakes, Eqs. (1) and (2) can be rewritten as followsFootnote 9:
Solving for unemployment and real wages, we obtain their short-run values as followsFootnote 10:
3 Methodology
A VAR-IRF approach is particularly well equipped to study hysteresis in the labour market. IRF-simulations allow us to simulate different demand-shocks to investigate what variables have a long-term impact on unemployment, i.e. affect the NAIRU and cause hysteresis, and what variables only have temporary or cyclical influence (Dolado and Jimeno 1997; Fabiani et al. 2001). Further, the system nature of the VAR-IRF provides a wealth of estimates capturing not only the influence of a specific variable on unemployment, but also on the rest of variables of the system, e.g. real wages and productivity, to assess the mechanism that permits the relationship with unemployment. That is, it allows us to test the restrictions on \(\beta \), together with those for \(\omega \) and \(\varphi \). Finally, the VAR accommodates the potential endogeneity between our macroeconomic and labour variables.
We estimate a VAR for the vector \(z_{t}\) that contains all the variables included in Eqs. (1)–(4), i.e. \(z_{t}=( w_{t}-p_{t},\, y_{t}-l_{t},\, u_{t},\, {lu}_{t},\, {\, grr}_{t},\, t_{t}^{w},{up}_{t},{\, k}_{t},\, i_{t}-\Delta p_{t} )^{'}\). Unit root and stationarity tests suggest that we should treat these variables as I(1), see “Appendix C”. Hence, we adopt a cointegrated-VAR approach illustrated by the following Vector Error Correction Model (VECM):
where \({\Delta }\) is the first difference operator, \(z_{t}\) is a \((9\times 1)\) vector of I(1) variables. \(c_{0}\) is a vector of intercepts. \(\Delta z_{t-n+1}\) is the higher lag of \(\Delta z_{t}\), where n denotes the lag order of the underlying VAR. \(\gamma \beta ^{'}\big [ {\begin{array}{*{20}c} z_{t-1} \\ T\\ \end{array}}\big ]\) is the Error Correction Mechanism (ECM) of the system, with \(\beta ^{'}\) and \(\gamma \) denoting the matrix of long-run and loading coefficients, respectively. T is a vector of time-trends that account for the deterministic trends that some variables exhibit, see Figs. 2, 3, 4, 5, 6 discussed in the next section. We restrict T to the ECM-term to avoid quadratic trends. \(x_{t}\) is a \((h\times 1)\) vector of exogenous I(0) variables that controls for past external cost-shocks with two lags of \(\Delta p_{t}^\mathrm{vm}\)Footnote 11. In the Dutch case, \(x_{t}\) also contains two dummies D95q2 and D07q2 that accommodate outliers, which caused autocorrelation and normality issues in preliminary estimationsFootnote 12. \(\varepsilon _{t}\) is a vector of error terms, Normally and Independently Distributed (NID).
Drawing from AIC and SBC selection criteria, we favour a lag order \(n=2\). This choice and the composition of \(x_{t}\) are the result of experimenting with several specifications, until a parsimonious but informative lag structure that provides satisfactory diagnostic test results is found. Hence, our empirical specification is the following:
where \(x_{t,\mathrm{UK}}=(\Delta p_{t-1}^\mathrm{vm},\, \Delta p_{t-2}^\mathrm{vm} )^{'}\), \(x_{t,\mathrm{Neth}}=(\Delta p_{t-1}^\mathrm{vm},\, \Delta p_{t-2}^\mathrm{vm},\, D95q2,\, D07q2 )^{'}\).
Our empirical strategy proceeds as follows. First, we test for cointegration in \(z_{t}\) using the Maximum Eigenvalue \((\lambda _\mathrm{max})\) and Trace \((\lambda _\mathrm{trace})\) tests. Second, we identify the long-run relationships that exist among our variables using restrictions drawn from economic theory, as suggested by Pesaran and Shin (2002) and Garrat et al. (2006, Ch. 6). This provides an initial test of the \(\beta \)-restrictions by identifying what variables have a long-run relationship with unemployment. Third, we estimate the short-run dynamics of the system, evaluate the goodness of the fit and the stability of the estimated VAR. Fourth, we use IRF to simulate different demand and supply-shocks (of one standard deviation of the residuals, \(\sigma _{{\upvarepsilon }}\)) and test the hysteresis hypothesis embedded in the \(\beta \), \(\omega \) and \(\varphi \) coefficients. It should be noted that all IRF reported in Sect. 6 are Generalized-IRF (GIRF), to ensure that the ordering of variables in the VAR-system does not affect the outcome of our simulations (Garrat et al. 2006, p. 142).
These are the IRF-simulations presented below: (i) Shocks in unemployment \((\sigma _{{\hat{\varepsilon }}_{\Delta u}})\) and long-term unemployment \((\sigma _{{\hat{\varepsilon }}_{\Delta lu}})\) to assess BS hysteresis hypothesis, \(\omega _{11}=0\) and \(\beta _{{14}}=0\). (ii) Productivity shock \((\sigma _{{\hat{\varepsilon }}_{\Delta y-l}})\) to evaluate its impact on unemployment and real wages, i.e. \(\beta _{{12}}=0\), \(\omega _{{2}}=\varphi _{{3}}\). (iii) Capital stock shock \((\sigma _{{\hat{\varepsilon }}_{\Delta k}})\) to assess the capital-scrapping hypothesis, \(\beta _{{18}}=0\). (iv) Shock in real long-term interest rates \((\sigma _{{\hat{\varepsilon }}_{\Delta (i-\Delta p)}})\) to evaluate the response of unemployment, \(\beta _{{19}}=0\). (v) Three LMI-shocks, unemployment benefits \((\sigma _{{\hat{\upvarepsilon }}_{\Delta grr}})\), labour taxation \((\sigma _{{\hat{\upvarepsilon }}_{\Delta tw}})\), and unions power \((\sigma _{{\hat{\upvarepsilon }}_{\Delta up}})\) to assess the response of unemployment (\(\beta _{15}>0\), \(\beta _{16}>0\) and \(\beta _{17}>0\)). (vi) We examine the response of long-term unemployment to the above-mentioned demand and supply-shocks.
4 Data
Our dataset contains quarterly data for the UK and the Netherlands from 1983q4 to 2011q4. The sample period is determined by data availability. The main source of data is OECD’s statistical office, although we also employ data from UK’s Office of National Statistics and the IMF, see “Appendix A” for further details. The following figures examine our data (in logarithm scale). Figure 2 shows the evolution of unemployment. In both countries, unemployment seems to trend downwards after peaking in the early-1980s, and despite hikes in the early-1990s, early-2000s, and after 2007.
Figure 3 shows the evolution of our LMIs (solid line) against unemployment (dotted line). Unemployment benefits (grr) in panels (a) and (b), the tax-wedge \((t^{w})\) in panels (c) and (d), and unions’ power (up) in panels (e) and (f), all trend downwards for most of the sample period. This reflects the labour market reforms introduced in both countries since the 1980s (Siebert 1997; Nickell and Ours 2000; Brandt et al. 2005; OECD 2000, 2006). The downward trends of LMI and unemployment since the 1980s seem to suggest that there is a positive relationship between these variables. However, close examination shows that only unemployment benefits, particularly in the UK, moved with unemployment over the sample period. The tax-wedge, panels (c) and (d), moves downwards with unemployment up to the late-1980s, but for most of the 1990s and 2000s labour taxation and unemployment move in opposite directions. Similarly, unions’ power shown in panels (e) and (f). Our IRFs will confirm that only unemployment benefits have a positive long-run relationship with unemployment.
We turn now to demand-factors that could cause hysteresis. Figure 4, panels (a) and (b), present the evolution of long-term unemployment (lu) against total unemployment (u). In both countries, lu mirrors the behaviour of overall unemployment with some delay. This suggests that demand-shocks can increase (and reduce) long-term unemployment in line with BS hypothesis. In panels (c) and (d), we observe the evolution of capital accumulation \((\Delta k)\) along with unemployment (u). In both countries, there seems to be a negative relationship between \(\Delta k\) and u, as periods of greater accumulation coincide with reductions of unemployment, e.g. the second half of the 1980s and 1990s. And periods of lower investment come with rising unemployment, e.g. the early-1980s, early-1990s and after 2007. This behaviour is consistent with the capital-scrapping hypothesis. Our IRFs will suggest that this relationship is statistically significant.
Figure 5, panels (a) and (b), compare the evolution of productivity \((y-l)\) and unemployment (u). The former exhibits a clear upward trend in both countries, despite marked falls in 2007, and several periods of stagnation in the early 1980s, between 1988–1992, early 2000s, and in the UK, after 2008. Some of these slowdowns in \(y-l\) coincide with hikes in unemployment, suggesting that there is a negative relationship between these variables, which our IRFs will confirm. Looking at panel (c), in the UK, this relationship could be the result of real wages lagging behind productivity, as the reductions in unemployment during the late 1980s, and from mid-1990s to 2007, are characterized by \(y-l\) growing faster than \(w-p\). This is unclear in the Dutch case, panel (d), where \(w-p\) grow above \(y-l\) in periods of rising but also falling unemployment. Further, in the Netherlands the relationship between \(y-l\) and \(w-p\) seems weaker than in the UK.
Finally, Fig. 6 compares the evolution of real long-term interest rates \((i-\Delta p)\) and unemployment. In both countries, there is an initial period of relatively high but stable interest rates until the early-1990s, period in which the highest levels of unemployment were recorded. The rest of the sample period is characterized by an intense fall in \(i-\Delta p\) that coincides with falling unemployment from the mid-1990s to the early-2000s, but also with rising joblessness in the 2000s. Hence, from these figures, it is unclear whether there is a relationship between these variables and whether this is positive or negative.
5 Model estimation
We start our empirical analysis by testing for cointegration in \(z_{t}=( w_{t}-p_{t},\, y_{t}-l_{t},u_{t},\, {lu}_{t},\,{grr}_{t},\, t_{t}^{w},{up}_{t},{\, k}_{t},\, i_{t}-\Delta p_{t})^{'}\). Table 1 presents our results. In both countries, Maximum Eigenvalue \((\lambda _\mathrm{max})\) and Trace \((\lambda _\mathrm{trace})\) tests support the existence of cointegration, as the null \(r=0\) is rejected at one per cent significance level for both testsFootnote 13. However, tests differ with regard to the number of long-run relationships. In the UK’s case, \(\lambda _\mathrm{max}\) fails to reject the null hypothesis of having two long-run relationships, while \(\lambda _\mathrm{trace}\) fails to reject having four cointegrated vectors, both at one per cent. For the Netherlands, \(\lambda _\mathrm{max}\) and \(\lambda _\mathrm{trace}\), fail to reject the null of having two and five cointegrated vectors, respectively. Weighting these results against the predictions from our theoretical model, which suggest that there are two cointegrated vectors among our variables, Eqs. (3) and (4), it seems reasonable to proceed under the assumption of \(r=2\). This choice is vindicated by the diagnostic tests for our short-run equations, reported in Table 3 below, which suggest that the model is specified satisfactorily.
Next, we study what variables take part in these two cointegrated vectors by identifying the matrix of long-run coefficients, \(\beta \) in Eq. (10). For this purpose, we draw from economic theory and experiment with several schemes. These include \(\beta \hbox {s}\) exclusively determined by LMIs and extensions of these with demand variables, see “Appendix B” for further details. In both countries, there is little support for a \(\beta \) exclusively determined by LMIs, as restrictions excluding all demand-factors are insignificant for both countries. In the UK, the Likelihood Ratio (LR) statistic is \(X_{\mathrm{LR}_{(10)}}^{2}=52.351\), and in the Netherlands \(X_{\mathrm{LR}_{(10)}}^{2}=69.395\). In both cases, \(p\;\hbox {value}=0.000\).
Further, excluding \({lu}_{t}\) and \(k_{t}\) from the unemployment vector pushes \(\beta \) into rejection in both countries, suggesting that these variables are cointegrated with unemployment. Unit-proportionality between real wages and productivity seems supported in the UK but not in the Netherlands. Further, the co-trending hypothesis (excluding T from the cointegrated vector) seems to hold in both vectors for the UK, but only in the unemployment vector for the Netherlands. Using this information we experiment until we find a significant \(\beta \)-matrix of long-run coefficients for each country that we adopt as our preferred long-run specifications, here reported in Table 2. These cointegrated vectors are clearly significant. In the UK, the LR-statistic is \(X_{\mathrm{LR}_{(10)}}^{2}=10.307\) with p values=0.414, and in the Netherlands, \(X_{\mathrm{LR}_{(6)}}^{2}= 4.135\) with p value=0.658.
According to Table 2, in the UK unemployment is cointegrated with long-term unemployment and capital stock, with long-run elasticities of 0.83 and \(-\,\)0.15, respectively. These findings are in accordance with previous cointegration analysis of British unemployment (Arestis and Biefang-Frisancho Mariscal 1998, 2000). Results for the Netherlands are similar, an increase in lu of 1% increases the overall unemployment rate by 1.9% in the long-run, whereas an increase in k of one per cent reduces unemployment by 2%. Arestis et al. (2007) report similar results. Further, in the Netherlands, we find unemployment cointegrated with real long-term interest rates, with an elasticity of \(-\,\)1.2. This sign is unexpected because the cost of borrowing and unemployment are usually thought to have a positive relationship. We investigate this further in our IRF section.
Finally, in the second cointegrated vector, real wages are positively cointegrated with productivity in the UK, where we find a long-run one-to-one relationship between real wages and productivity as also reported by Arestis and Biefang-Frisancho Mariscal (1998). In the Netherlands, unit-proportionality is rejected and the unrestricted coefficient suggests that there is a very modest long-run relationship between real wages and productivity, in contrasts to Schreiber (2012) estimates. Differences in the \(w-p\) to \(y-l\) relationship, was anticipated in Fig. 5c, d, and reflect the well-documented stability of the wage-share in the UK and its fall in the Netherlands. In sum, Table 2 provides evidence of long-run links between unemployment and demand-factors, in line with hysteresis effects, we examine these links in more depth in our IRF section.
Next, we estimate the short-run dynamics of the system and evaluate our VAR-model. Table 3, presents the reduced ECM-form for \(\Delta u_{t}\) and \(\Delta {(w-p)}_{t}\) contained in Eq. (10). These estimates provide valuable information about the short-run dynamics of unemployment and real wages that will be helpful to understand the IRF below. Our estimates of the coefficient of \(\hat{\xi }_{1,t-1}\), suggest that deviations from unemployment’s long-run equilibrium imply modest adjustments, below 5% every quarter, in both countries. Further, this coefficient is only significant for \({\Delta }u_{t}\), in the Netherlands. Estimates for \({\hat{\xi }}_{2,t-1}\), imply larger adjustments in both unemployment and real wages, but this coefficient is only significant at 5% in the UK for \({\Delta }u_{t}\) and in the Netherlands for \({\Delta }{(w-p)}_{t}\). Estimates for \({\hat{\xi }}_{1,t-1}\) and \({\hat{\xi }}_{2,t-1}\) will be helpful in interpreting the response of unemployment to the shocks that we examine below.
The regressions, presented in Table 3, pass all the diagnostic tests at the standard 5% significance level, this suggests that our model is specified satisfactorily. Overall, our fitted values seem to do a good job in describing unemployment fluctuations in both countries, this is reflected in the adjusted R-squares for both countries, reported in Table 3, which are reasonably high, 0.52 for the UK, and 0.80 for the Netherlands. See also Fig. 15 in Appendix B, which compares changes in unemployment implied by our estimations against actual data. Further, the eigenvalues, of the companion matrix, see “Appendix B”, are within the unit circle, which suggests that our VAR-system is stable and adequately specified. Thus, we conclude that our estimations capture satisfactorily the long-run and short-run properties of unemployment in both countries and proceed with our IRF-simulations.
Unemployment duration-shock. Note: Solid lines denote IRF point estimates and dashed lines 95% confidence interval (CI). a \(w-p\) response to u-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta u}} =0.0249)\). b \(w-p\) response to u-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta u}} =0.0208)\). c \(w-p\) response to lu-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta lu}} =0.0149)\). d \(w-p\) response to lu-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta lu} } =0.0341)\). e \(y-l\) response to lu-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta lu}} =0.0149)\). f \(y-l\) response to lu-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta lu}} =0.0341)\)
6 Impulse response analysis
6.1 Hysteresis hypothesis
We start by testing BS hypothesis that long-term unemployment increases real wages and the NAIRU \((\omega _{11}>0,\, \beta _{{14}}>0)\). Figure 7 shows the response of real wages \((w-p)\) to a shock on overall unemployment (u) and long-term unemployment (lu). Panels (a) and (b) show that an increase in u moderates real wages by about 5 and 1.5%, in the UK and the Netherlands, respectively. The fall in Dutch real wages is more modest, and stabilizes faster, after 16 quarters for 24 of the UK, reflecting differences in our estimates for the coefficient of \(\hat{\xi }_{2,t-1}\) in Table 3. On the other hand, a rise in lu, panels (c) and (d), has no significant impact in the UK, but it increases \(w-p\) in the Netherlands. This suggests that demand-shocks that modify the share of long-term unemployment generate hysteresis in the Netherlands, i.e. \(\omega _{11}>0\) and \(\beta _{{14}}>0\), but not in the UK, where \(\omega _{11}=\beta _{{14}}=0\). Our results for the UK are in line with Blanchflower and Oswald (1994) and Bell and Blanchflower (2014), but our findings for the Netherlands are in contrast to studies with data from the 1980s (Graafland 1991, 1992).
Productivity-shock. Note: Solid lines denote IRF point estimates and dashed lines 95% CI. a u response to \(y-l\) shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta (y-l)}} =0.0106)\). b u response to \(y-l\) shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta (y-l)}} =0.0095)\). c \(w-p\) and \(y-l\) response to \(y-l\) shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta (y-l)}} =0.0106)\). d \(w-p\) and \(y-l\) response, \(y-l\) shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta (y-l)}} =0.0095)\)
Figure 7 panels (e) and (f) present the response of productivity to the lu-shock and help understand why real wages behave differently in these economies. In the UK, a rise in lu does not affect productivity, but in the Netherlands, the shock raises \(y-l\) pushing real wages with it, as per our estimate of their long-run relationship reported in Table 2.
Figure 8 evaluates the effect of a productivity shock on unemployment and real wages. Panels (a) and (b) show that, in both countries, a rise in productivity reduces unemployment permanently, i.e. reduces the NAIRU. In the UK, the unemployment rate falls on impact until it stabilizes at its new equilibrium at a rate 17% lower, eight quarters after the shock. In the Netherlands, unemployment stabilizes at a rate approximately 20% lower than its baseline. Hence, Fig. 8, suggests that \(\beta _{{12}}<0\) for both countries. Previous results are mixed, but our findings reinforce evidence of a negative relationship between productivity and the NAIRU in both countries (Broersma et al. 2000; Hatton 2007).
Capital stock shock. Note: Solid lines denote IRF point estimates and dashed lines 95% CI. a u response to k-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta k} } =0.0001)\). b u response to \(k-\)shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta k}} =0.0007)\). c k response to u-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta u} } =0.0249)\). d k response to u-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta u}} =0.0208)\)
To test whether this productivity-NAIRU link is due to workers sluggishness to adapt their income claims to changes in productivity, panels (c) and (d), compare the evolution of productivity \((y-l)\) and real wages \((w-p)\) after the above-mentioned productivity shock. In both countries, the initial response of \(w-p\) falls short to the rise in \(y-l\), this gap makes \(\hat{\xi }_{2,t-1}\) negative and reduces unemployment as per our estimates for \({\Delta }u_{t}\) from Table 3. Further, unemployment does not stabilize at its new equilibrium until real wages start to close the gap with \(y-l\), eight quarters after the shock in the UK, twelve in the Netherlands. Hence, Fig. 7 suggests that productivity influences the NAIRU because, workers income claims react slowly to improvements in productivity, that is, \(\omega _{{2}}<\varphi _{{3}}\) for long lapses of time, as suggested by Stiglitz (1997) and Ball and Mankiw (2002). It is worth noting that in the UK the shock is eventually fully absorbed by real wages, but not in the Netherlands, in line with our estimates of the long-run elasticity of real wages to productivity presented in Table 2.
Figure 9, panels (a) and (b), present the response of unemployment to a shock in capital stock. In both countries, greater accumulation reduces unemployment permanently providing support for \(\beta _{{18}}<0\). British unemployment falls for about 24 quarters until it stabilizes at a rate 17% lower than its baseline, whereas, in the Netherlands, the shock pushes unemployment to a minimum after eight quarters and then stabilizes at its new equilibrium, at a rate approximately 25% below its pre-shock level. These findings reinforce available evidence of a negative long-run relationship between capital stock and unemployment in the UK and the Netherlands (Dreze and Bean 1990; Arestis and Biefang-Frisancho Mariscal 1998, 2000; Arestis et al. 2007).
Interest rates-shock. Note: Solid lines denote IRF point estimates and dashed lines 95% CI. a u response to \(i-\Delta p\) shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta ({i-\Delta p})}} =0.1930)\). b u response, \(i-\Delta p\) shock \((\sigma _{\hat{\varepsilon } _{\Delta (i-\Delta p)}} =0.1648)\). c \(w-p\) and \(y-l\) response to \(i-\Delta p\) shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta (i-\Delta p)}} =0.1930)\). d \(w-p\) and \(y-l\) response, \(i-\Delta p\) shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta (i-\Delta p)}} =0.1648)\)
To assess whether this link is due to capital-scrapping during downturns, Fig. 9, panels (c) and (d) assess the response of k to a rise in unemployment. We find that effectively, increases in unemployment reduce capital stock permanently between 2.8 and 5% depending on the country. Hence, our results endorse the view that unemployment will persist after a shock unless pre-shock capital stock levels are restored, as suggested by the capital-scrapping hypothesis.
Figure 10 evaluates the influence of real long-term interest rates on unemployment. Panels (a) and (b) show that a rise in the cost of borrowing reduces unemployment permanently by around 10% in both countries. In the UK, unemployment falls for eight quarters until it stabilizes at a rate approximately 11% below its benchmark, whereas Dutch unemployment reaches a new equilibrium, 9% below its pre-shock level after 20 quarters. This evidence suggests that \(\beta _{{19}}<0\) for both countries. The sign of these IRFs is unexpected because Fitoussi and Phelps (1988, p. 57) and Rowthorn (1999) predict a positive relationship and available panel data evidence seems to support it, e.g. Gianella et al. (2008). However, these studies do not control for capital stock. Hence, a possible explanation for this sign discrepancy is that their positive real interest rate coefficient is, in fact, capturing the negative influence of capital stock over the NAIRU. This highlights the importance of controlling for different hysteresis factors.
To investigate the sign of our IRFs, we examine the response of real wages and productivity to the \(i-\Delta p\) shock. In the UK, panel (c), the interest rates-shock increases productivity by a larger amount than real wages for the first 8 quarters, this gap makes \({\hat{\xi }}_{2,t-1}\) negative, which according to Table 3 reduces unemployment, as we observe in panel (a). Afterwards, \(y-l\) stabilizes while \(w-p\) converges towards it, which coincides with unemployment stabilizing. Hence, the unexpected sign of unemployment seems to be due to the response of real wages and productivity to the shock.
grr-shock. Note: Solid lines denote IRF point estimates and dashed lines 95% CI. a u response to grr-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta grr} } =0.0031)\). b u response to grr-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta grr} } =0.0070)\). c \(w-p\) and \(y-l\) response to grr-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta grr} } =0.0031)\). d \(w-p\) and \(y-l\) response, grr-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta grr}} =0.0070)\). e k response to grr-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta grr} } =0.0031)\). f k response to grr-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta grr}} =0.0070)\)
\(t^{w}\)-shock. Note: Solid lines denote IRF point estimates and dashed lines 95% CI. a u response to \(t^{w}\)-shock (\(\sigma _{\hat{{\upvarepsilon }}_{\Delta tw}} =0.0036)\) b u response to \(t^{w}\)-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta tw}} =0.0117)\). c \(w-p \) and \(y-l\) response to \(t^{w}\)-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta tw}} =0.0036)\). d \(w-p \) and \(y-l\) response, \(t^{w}\)-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta tw}} =0.0117)\). e k response to \(t^{w}\)-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta tw}} =0.0036)\). f k response to \(t^{w}\)-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta tw}} =0.0117)\)
up-shock. Note: Solid lines denote IRF point estimates and dashed lines 95% CI. a u response to up-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta up} } =1.206)\). b u response to up-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta up} } =0.0047)\). c \(w-p\) and \(y-l\) response to up-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta up} } =1.206)\). d \(w-p\) and \(y-l\) response, up-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta up}} =0.0047)\). e k response to up-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta up} } =1.206)\). f k response to up-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta up} } =0.0047)\)
In the Netherlands, Fig. 10d, the shock also creates a negative gap between real wages and productivity that could filter into unemployment through \({\hat{\xi }}_{2,t-1}\); however, both IRFs are insignificant. Hence, it seems more reasonable to believe that the response of Dutch unemployment is due to the direct impact of real long-term interest rates on the unemployment cointegrated vector, see Table 2, which would also reduce unemployment indirectly through \({\hat{\xi }}_{1,t-1}\). It is worth noting that differences in the size of the estimated coefficient of \({\hat{\xi }}_{2,t-1}\), for the UK, and \({\hat{\xi }}_{1,t-1}\), for the Netherlands, can also explain why British unemployment stabilizes faster.
In sum, according to our impulse response analysis, there is hysteresis in both countries through productivity, capital stock and real long-term interest rates, and in the Netherlands, also via long-term unemployment.
6.2 Unemployment and LMI
Next, we investigate the LMI-unemployment link by simulating three supply-shocks, namely unemployment benefits (grr), labour taxation \((t^{w})\) and unions’ power (up). Figure 11 presents the impact of a grr-shock. In the UK, panel (a), unemployment increases on impact, until it stabilizes 20 quarters after the shock at a rate 20% above its initial equilibrium. In the Netherlands, panel (b), unemployment describes a J-curve, and after an initial fall it stabilizes at a rate 2% greater than its baseline, although this rise is only marginally significant. Layard et al. (1991, p. 441), Nickell and Bell (1995), Broersma et al. (2000) and Gianella et al. (2008) also find that unemployment benefits increase the NAIRU in both countries.
Figure 11c shows that in the UK, the grr-shock causes a larger fall in productivity than in real wages for the first 8 quarters, which feeds into higher unemployment through the positive coefficient of \(\hat{\xi }_{2,t-1}\), see Table 3. The shock also reduces accumulation, see panel (e), which reinforces the rise in unemployment. In the Netherlands, panel (d), the shock reduces productivity below real wages throughout, which should raise unemployment by making \({\hat{\xi }}_{2,t-1}\) positive. However, this is somehow compensated in the first 8 quarters by a modest increase in accumulation, panel (f), which allows unemployment to fall in the short-run, as we observe in panel (b).
Figure 12 shows the impact of a shock in labour taxation. Panels (a) and (b) show that this results in permanent reductions of unemployment in both countries. The fall in British unemployment seems to be driven by a larger rise in productivity than in real wages on impact during the first eight quarters, see panel (c), which reduces unemployment through \({\hat{\xi }}_{2,t-1}\). Further, the shock also results in a faster accumulation, see panel (e), which reinforces the fall in unemployment. In the Netherlands, in panel (d), the shock has no significant impact on real wages or productivity for the first twelve quarters, while unemployment falls. Hence, it seems more reasonable to believe that the response of Dutch unemployment is due to the direct influence of labour taxation on the unemployment cointegrated vector, see Table 2, which could reduce unemployment through \({\hat{\xi }}_{1,t-1}\), aided by rising accumulation that follows the \(t^{w}\)-shock after four quarters, see panel (f).
On the other hand, a rise in up, shown in Fig. 13, also reduces unemployment permanently in both countries, see panels (a) and (b). This seems to result from the real wages-productivity gap caused by the shock. In the UK, the rise in up pushes productivity above real wages for the first 12 quarters, see panel (c). This makes \({\hat{\xi }}_{2,t-1}\) negative and reduces unemployment until the gap is closed and unemployment stabilizes. In the Netherlands, panel (c), real wages falls below productivity making \({\hat{\xi }}_{2,t-1}\) negative, which reduces unemployment. The shock also increases accumulation, see panels (e) and (f), which reinforces the reduction in unemployment.
Thus, after performing our three supply-shocks, only unemployment benefits have the expected long-run positive relation with unemployment. These results reinforce available evidence that not all LMI have a pernicious impact on unemployment (Nickell 1997; OECD 2006; Layard and Nickell 2011, Ch.7) and highlight the importance of considering specific shocks to inform policy design, a novelty of our paper. Further, our results also highlight that the impact of LMI on unemployment does not depend on the impact of LMI on real wages, but the impact of institutions on the real wages-productivity gap and other macroeconomic variables, such as accumulation.
LMI and demand-shocks. Note: Solid lines denote IRF point estimates and dashed lines 95% CI. a lu response to grr-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta grr} } =0.0031)\). b lu response to grr-shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta grr} } =0.0070)\). c lu response to \(t^{w}\)-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta tw} } =0.0036)\). d lu response to \(t^{w}\)-shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta tw}} =0.0117)\). e lu response to \(y-l\) shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta ( {y-l} )} } =0.0106)\). f lu response to \(y-l\) shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta ( {y-l} )} } =0.0095)\). g lu response to \(k-\)shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta k} } =0.0001)\). h lu response to \(k-\)shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta k} } =0.0007)\). i lu response to \(i-\Delta p\) shock \((\sigma _{\hat{{\upvarepsilon }} _{\Delta ( {i-\Delta p} )} } =0.1930)\). j lu response, \(i-\Delta p\) shock \((\sigma _{\hat{{\upvarepsilon }}_{\Delta ( {i-\Delta p} )} } =0.1629)\)
6.3 Long-term unemployment
We close our IRF-analysis by studying the impact of different supply and demand-shocks on long-term unemployment. It is sometimes argued that correcting hysteresis caused by unemployment duration requires supply-policies that increase incentives to work, reducing benefits or taxes, rather than positive demand-shocks (de Koning et al. 2003; Tatsiramos and Ours 2014). To assess this claim, Fig. 14 presents the response of long-term unemployment to shocks on unemployment benefits, labour taxation, productivity, capital stock and interest rates.
In the UK, none of these shocks have significant effects on long-term unemployment for the first 4–8 quarters, but after that, lu responds in the same fashion as overall unemployment. That is, benefits-shocks increases long-term unemployment permanently, panel (a), whereas shocks in labour taxation, productivity, capital stock and real long-term interest rates, panels (c), (e), (g) and (i) respectively, reduce long-term unemployment permanently. This delay in the response of lu suggests that it takes time for shocks to modify the composition of unemployment. Hence, suggesting that quick interventions to prevent changes in unemployment duration can help to prevent hysteresis, as argued by Ball (1999, 2009) Stockhammer and Sturn (2012). Further, our results suggest that if these preventive measures were not taken, both supply and demand-shocks can be used to reduce long-term unemployment.
In the Netherlands, the response of long-term unemployment, to shocks on productivity and capital stock, panels (f) and (h), also follows the response of overall unemployment with some delay. This is not the case for the rest shocks. Figure 14b shows that after a grr-shock, lu falls from quarters 4–20, until it stabilizes at a level, barely significant, below its benchmark. This behaviour is contrary to that of overall unemployment, shown in Fig. 11b, and suggests that higher benefits generosity increases unemployment by raising short-term not long-term unemployment. The opposite happens in response to a \(t^{w}\)-shock, Fig. 14d, where the shock increases the proportion of long-term unemployment, despite reducing overall unemployment, see Fig. 12b. This implies that those unemployed for more than one year do not benefit of positive shocks and need targeted policies. The \(i-\Delta p\) shock, Fig. 14j, has a similar effect, although it only increases long-term unemployment in the short-run.
Overall, Fig. 14 suggests that labour market reforms can reduce long-term unemployment, although these need to be country-specific. Further, demand policies can achieve similar results either by preventing that temporary shocks have permanent effects, or reversing the long-term effects of negative shocks.
7 Summary
This paper investigated whether there is hysteresis in the UK and the Netherlands and what demand-factors can cause such phenomenon. Further, we also investigated what specific LMIs affect the NAIRU and the impact of supply and demand-shocks on long-term unemployment. We used a VAR-IRF model that extends available studies by testing for hysteresis through unemployment duration, productivity, capital stock and real long-term interest rates, and by considering specific LMIs.
We find evidence of hysteresis in the UK and the Netherlands since the 1980s. Our results suggest that hysteresis happens because of the impact of productivity, capital stock and real long-term interest rates on the NAIRU. In the Netherlands, the proportion of long-term unemployed can also cause hysteresis. Further, exploiting the wealth of estimates provided by our VAR-system, we find that productivity reduces the NAIRU because workers are sluggish to absorb improvements in productivity. The capital stock-NAIRU link seems to be the result of capital-scrapping during downturns, and the impact of long-term unemployment in the Netherlands is due to the influence of unemployment duration on real wages and productivity.
On the other hand, we find that the only LMI that increases unemployment permanently is unemployment benefits, although this effect is only marginally significant in the Netherlands. Interestingly, we find that the LMI-unemployment link depends, not on the impact of LMI-shocks on real wages, but on the impact of institutions on the real wages-productivity gap and other macroeconomic factors. Finally, we find that long-term unemployment can be brought down by country-specific labour market reforms, as well as, positive productivity or capital stock shocks.
Thus, our results contradict the belief that LMI alone can explain the evolution of unemployment in the UK and the Netherlands, since the 1980s. This means that policy makers aiming to reduce current levels of unemployment, have a choice between labour market reforms, which must be selective and country specific, and macroeconomic policies that encourage productivity, investment and the reduction of long-term unemployment.
Notes
For some authors, the interest rates-NAIRU link does not create a monetary policyNAIRU link (Hian Teck and Phelps 1992, p. 896; Gianella et al. 2008, p. 21). They argue that changes in real long-term interest rates are not the result of changes in monetary policy but the evolution of financial markets along with governments’ fiscal position. This claim is at odds with Central Bank pass-through estimates in the UK (Gulmaraes 2012) and the Netherlands (ECB 2009). Hence, we treat real long-term interest rates as a demand variable.
“Appendix C” presents unit roots/stationarity test results for \(\Delta w\), \(\Delta p\), \(\Delta (y-l)\).
“Appendix D” provides further details of our expectations and short-run considerations.
Where, \(\delta _{11}=\frac{1}{\omega _{1}+\varphi _{1}}\), \(\delta _{12}=\frac{1}{\omega _{1}+\varphi _{1}}\), \(\delta _{13}=\frac{\omega _{2}-\varphi _{3}}{\omega _{1}+\varphi _{1}}\), and \(\delta _{21}=\frac{\varphi _{1}}{\omega _{1}+\varphi _{1}}\), \(\delta _{22}=-\frac{\omega _{{1}}}{\omega _{1}+\varphi _{1}}\), \(\delta _{23}=\omega _{2}-\omega _{1}\frac{\omega _{2}-\varphi _{3}}{\omega _{1}+\varphi _{1}}\).
We tested if \(p_{t}^\mathrm{vm}\) enters our cointegrated vectors. However, imposing the restriction of a zero coefficient for \(p_{t}^\mathrm{vm}\) on our cointegrated vectors could not be rejected in either country, with \(X_{\mathrm{LR}_{(12)}}^{2}=\)13.919 and p value\(=\)0.306 in the UK, and \(X_{\mathrm{LR}_{(9)}}^{2}=21.287\) with p value\(=\)0.011 in the Netherlands. Hence, we restrict its influence to the short-run dynamics. We thank an anonymous referee for this suggestion.
We speculate this could be the result of temporary changes in policy, such as the unusually expansionary budget for 2007 set by the interim 3rd Balkenende Cabinet.
Given the well-known size problems of these tests we use 1% critical values rather than standard 5%.
For a formal demonstration of how a unit root justifies adaptive expectations see Wooldridge (2009, p. 388–392). We are grateful to an anonymous referee that has pointed out that a unit root would also be consistent with the weak formulation of rational expectations, see for instance Forsells and Kenny (2002).
References
Arestis P, Baddeley M, Sawyer M (2007) The relationship between capital stock, unemployment and wages in nine EMU countries. Bull Econ Res 59(2):125–148
Arestis P, Biefang-Frisancho Mariscal I (1998) Capital shortages and asymmetries in UK unemployment. Struct Change Econ Dyn 9(2):189–204
Arestis P, Biefang-Frisancho Mariscal I (2000) Capital Stock, Unemployment and Wages in the UK and Germany. Scott J Policy Econ 47(5):487–503
Arestis P, Sawyer M (2005) Aggregate demand, conflict and capacity in the inflationary process. Camb J Econ 29(6):959–974
Arulampalam W, Booth A, Taylor M (2000) Unemployment persistence. Oxf Econ Pap 52(1):24–50
Ball L (1999) Aggregate demand and long-run unemployment. Brook Pap Econ Act 1999(2):189–251
Ball L (2009) Hysteresis in unemployment: old and new evidence. In: NBER Working paper no. 14818 National Bureau of Economic Research
Ball L, Mankiw NG (2002) The NAIRU in theory and practice. J Econ Perspect 16(4):115–136
Bean CR (1989) Capital shortages and persistent unemployment. Econ Policy 4(1):11–53
Bell DNF, Blanchflower DG (2014) Labour market slack in the UK. Natl Inst Econ Rev 229(1):F4–F11
Binotti AM, Ghiani E (2008) Changes in aggregate supply conditions in Italy: a small econometric model and its policy implications. J Policy Model 30(6):1017–1039
Blanchard O (1988) Unemployment: getting the questions right and some of the answers. In: NBER Working paper no. 2698 National Bureau of Economic Research
Blanchard OJ, Summers LH (1986) Hysteresis and the European unemployment problem. NBER Macroecon Annu 1:15–78
Blanchflower DG, Oswald AJ (1994) The wage curve. MIT Press, Cambridge
Brandt N, Burniaux J, Duval R (2005) Assessing the OECD jobs strategy: past developments and reforms. In: OECD Economics Department Working Papers, No. 429, OECD Publishing, Paris
Broersma L, Koeman J, Teulings C (2000) Labour supply, the natural rate, and the welfare state in The Netherlands: the wrong institutions at the wrong point in time. Oxf Econ Pap 52(1):96–118
Carstensen K, Hansen G (2000) Cointegration and common trends on the West German labour market. Empir Econ 25(3):475–493
de Koning J, Layard R, Nickell S, Westergaard-Nielsen N (2003) Policies for Full Employment. UK Department for Work and Pensions, London
Dolado JJ, Jimeno JF (1997) The causes of Spanish unemployment: a structural VAR approach. Eur Econ Rev 41(7):1281–1307
Dreze J, Bean C (1990) European unemployment: lessons from a multicountry econometric study. Scand J Econ 92(2):135–165
ECB (2009) Recent developments in the retail bank interest rate pass-through in the Euro Area. In: Monthly bulleting. August. European Central Bank (ECB), Frankfurt
Elliot G, Rothenberg TJ, Stock JH (1996) Efficient tests for an autoregressive unit root. Econmetrica 64:813–836
Fabiani S, Locarno A, Oneto GP, Sestito P (2001) The sources of unemployment fluctuations: an empirical application to the Italian case. Labour Econ 8(2):259–289
Fitoussi J-P, Phelps E (1988) The slump in Europe. Reconstructing open economy theory. Basil Blackwell, Oxford
Forsells M, Kenny G (2002) The rationality of consumer’s inflation expectations: surey-based evidence for the Euro area. In: ECB working papers No. 163. European Central Bank (ECB), Frankfurt
Fosten J, Ghoshray A (2011) Dynamic persistence in the unemployment rate of OECD countries. Econ Modell 28(3):948–954
Gambetti L, Pistoresi B (2004) Policy matters. The long run effects of aggregate demand and mark-up shocks on the Italian unemployment rate. Empir Econ 29(2):209–226
Garrat A, Lee K, Pesaran MH, shin Y (2006) Global and national macroeconometrics modelling. A long-run structural approach. Oxford University Press, Oxford
Gianella C, Koske I, Rusticelli E, Chatal O (2008) What drives the NAIRU? Evidence from a panel of OECD countries. In: OECD Economics Department Working Papers. No 649. OECD, Paris
Graafland JJ (1991) On the causes of Hysteresis in long-term unemployment in the Netherlands. Oxf Bull Econ Stat 53(2):155–170
Graafland JJ (1992) Insiders and outsiders in wage formation: the dutch case. Empir Econ 17(4):583–602
Gulmaraes R (2012) What accounts for the fall in UK ten-year government bond yields? In: Bank of England Quarterly Bulletin Interest Rates Articles, Q3. Bank of England, London
Hatton TJ (2007) Can productivity growth explain the NAIRU? Long-run evidence from Britain, 1871–1999. Economica 74(295):475–491
Hian Teck H, Phelps ES (1992) Macroeconomic shocks in a dynamized model of the natural rate of unemployment. Am Econ Rev 82(4):889–900
Krueger AB, Cramer J, Cho D (2014) Are the long-term unemployed on the margins of the labor market? In: Spring conference of brookings panel on economic activity
Kwiatkowski D, Phillips PCB, Schmidt P, Shin Y (1992) Testing the null hypothesis of stationarity against the alternative of a unit root. J Econ 54:159–178
Layard R, Nickell S (2011) Combatting unemployment. Oxford University Press, Oxford
Layard R, Nickell S, Jackman R (1991) Unemployment: macroeconomic performance and the labour market. Oxford University Press, Oxford
Logeay C, Tober S (2006) Hysteresis and the NAIRU in the Euro area. Scott J Political Econ 53(4):409–429
Manning A (1993) Wage bargaining and the Phillips curve: the identification and specification of aggregate wage equations. Econ J 103(416):98–118
Manning A (2011) Chapter 11-Imperfect competition in the labor market. In: David C, Orley A (eds) Handbook of labor economics. Elsevier, Amsterdam, pp 973–1041
Manning N (1994) Are higher long-term unemployment rates associated with lower earnings? Oxf Bull Econ Stat 56(4):383–397
Nickell S (1987) Why is wage inflation in Britain so high? Oxf Bull Econ Stat 49(1):103–128
Nickell S (1997) Unemployment and labor market rigidities: Europe versus North America. J Econ Perspect 11(3):55–74
Nickell S (1998) Unemployment: questions and some answers. Econ J 108(448):802–816
Nickell S, Bell B (1995) The Collapse in demand for the unskilled and unemployment across the OECD. Oxf Rev Econ Policy 11(1):40–62
Nickell S, Van Ours J (2000) The Netherlands and the United Kingdom: a European unemployment miracle? Econ Policy 15(30):135–180
OECD (2000) Recent labour-market performance and structural reforms. In: OECD Economic Outlook 67. OECD, Paris
OECD (2006) Boosting jobs and income. In: OECD Employment outlook. OECD, Paris
Pesaran MH, Shin Y (2002) Long-run structural modelling. Econ Rev 21(1):49–87
Phelps E (2000) Lessons in natural-rate dynamics. Oxf Econ Pap 52(1):51–71
Pissarides CA (2000) Equilibrium unemployment Theory. MIT Press, Cambridge Mass
Romero-Avila D, Usabiaga C (2008) On the persistence of Spanish unemployment rates. Empir Econ 35(1):77–99
Rowthorn R (1995) Capital formation and unemployment. Oxf Rev Econ Policy 11(1):26–39
Rowthorn R (1999) Unemployment, wage bargaining and capital-labour substitution. Camb J Econ 23(4):413–425
Sawyer MC (1982) Collective bargaining, oligopoly and macro-economics. Oxf Econ Pap 34(3):428–448
Schreiber S (2012) Estimating the natural rate of unemployment in euro-area countries with co-integrated systems. Appl Econ 44(10):1315–1335
Siebert H (1997) Labor market rigidities: at the root of unemployment in Europe. J Econ Perspect 11(3):37–54
Srinivasan N, Mitra P (2014) The European unemployment problem: its cause and cure. Empir Econ 47(1):57–73
Stiglitz J (1997) Reflections on the natural rate hypothesis. J Econ Perspect 11(1):3–10
Stockhammer E, Sturn S (2012) The impact of monetary policy on unemployment hysteresis. Appl Econ 44(21):2743–2756
Tatsiramos K, van Ours JC (2014) Labour market effects of unemployment insurance design. J Econ Surv 28(2):284–311
Wooldridge JM (2009) Introductory Econometrics. A modern Approach. Mason, OH45040. South-Western
Author information
Authors and Affiliations
Corresponding author
Additional information
We would like to thank the referee and the editor for their comments and useful suggestions. We are also grateful to Malcolm Sawyer, Kausik Chaudhuri, Engelbert Stockhammer, David Spencer, Suman Seth, Annina Kaltenbrunner and Luisa Zanchi for their valuable comments on earlier versions of this paper. Any remaining errors are the authors.
Appendices
Appendix A: Data
See Table 4.
Appendix B: Complementary results
See Table 5, Fig 15, Tables 6, 7 and Fig 16.
Appendix C: Unit root and stationarity tests
Appendix D: Expectations and the short-run
We adopt adaptive expectations on the grounds that, as shown in “Appendix C”, price and wage-inflation, as well as productivity, seem to have a unit rootFootnote 14. From the evidence of a unit root on inflation, we can write inflation as:
where \(\Delta p_{t-1}\) is the lagged change in inflation, and v is a white noise. Then:
Taking expectations:
Adding and subtracting p to obtain price surprises:
Similarly, wage surprises:
Productivity also has a unit root, hence:
Taking expectations:
Adding and subtracting \((y-l)\) and multiplying by minus one both sides of the equality, we obtain productivity surprises:
We can now, re-write Eqs. (1) and (2) in terms of price, wage and productivity surprises by adding and subtracting the p into (1), w into (2) and \(y-l\) into both:
We can see that when expectations are fulfilled, in the long-run, surprise terms cancel out and unemployment and real wages take the values indicated by Eqs. (3) and (4):
when expectations are not fulfilled, in the short-run, we solve the surprise terms in (1’) and (2’) using (i), (ii) and (iii), we obtain the following:
Solving for unemployment and real wages, we obtain their short-run values as follows:
where \(\delta _{11}=\frac{1}{\omega _{1}+\varphi _{1}}\), \(\delta _{12}=\frac{1}{\omega _{1}+\varphi _{1}}\), \(\delta _{13}=\frac{\omega _{2}-\varphi _{3}}{\omega _{1}+\varphi _{1}}\)
where \(\delta _{21}=\frac{\varphi _{1}}{\omega _{1}+\varphi _{1}}\), \(\delta _{22}=-\frac{\omega _{{1}}}{\omega _{1}+\varphi _{1}}\), \(\delta _{23}=\omega _{2}-\omega _{1}\frac{\omega _{2}-\varphi _{3}}{\omega _{1}+\varphi _{1}}\)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rodriguez-Gil, A. Hysteresis and labour market institutions. Evidence from the UK and the Netherlands. Empir Econ 55, 1985–2025 (2018). https://doi.org/10.1007/s00181-017-1338-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-017-1338-y