Hospital efficiency under global budgeting: evidence from Taiwan

Abstract

Global budgeting sets a predetermined cap to restrain health expenditure, but the fixed budget for medical providers could result in less efficient services. This paper measures hospital efficiency under global budgeting using simultaneous stochastic frontier analysis, stressing that physicians and dentists within a hospital were under separate budgets in Taiwan. Empirical results show that hospital efficiency was not improved after global budgeting, and physicians were found to be less efficient than dentists. The physicians and dentists within the same hospital were also found to be less integrated after global budgeting. Empirical results show that a joint analysis improves the estimation efficiency from separate analysis and suggest that the aggregate inefficiency came mostly from physicians in hospitals that were small, public, non-teaching, located in small markets and had a low market share. Except for public hospitals, physicians and dentists in the above hospitals were also found to be less integrated.

1 Introduction

More than 100 countries around the world are pursuing universal healthcare coverage for their citizens. Since 2014, the World Health Organization and the World Bank Group have made universal healthcare coverage their priority to improve global health.¹ However, the increasing coverage could also result in more health expenditures. For example, various studies using data from Taiwan have found that health expenditure was greatly increased after universal health care was implemented.² The New York Times (Sanger-Katz 2014) and The Economist (2015) also questioned whether the Affordable Care Act had reduced health expenditure in the USA. For example, McGlynn et al. (2010) argued that this healthcare reform could hardly reduce health expenditure, likely due to political reasons.

By setting a predetermined cap on health expenditure, global budgeting was found to be an effective policy to address the above concern. For instance, Kan et al. (2014) showed that global budgeting in Taiwan effectively reduced the growth rate of health expenditure by nearly 3%. Although Poterba (1994) was suspicious of its effect in the USA due to political reasons, National Public Radio (Cornish 2015) recently reported that Maryland has successfully controlled its increasing health expenditure by changing from fee-for-service payments to global budgeting in 2014. But cutting costs is not the ultimate goal of any universal healthcare system. What if this cost containment forces medical providers to trade off the quality and efficiency of their services?

The answer to the above question was hardly found in the existing literature, likely because few countries have adopted global budgeting within a universal healthcare system. This study focuses on the case of Taiwan, which adopts a price adjustment mechanism that is also used in Germany and Canada.³ Since 1995, Taiwan began its National Health Insurance with a single payer system that reimburses medical providers on a fee-for-services basis. To control its increasing expanses, the authority implemented global budgeting since 1999, which maintains the fee-for-services reimbursement but with price adjust mechanism. In particular, medical providers in Taiwan receive certain points at the time of their services instead of the actual price. The value of these points is determined by dividing the predetermined budget by the total points of services provided in a sector. Consequently, the actual reimbursements for services are determined retrospectively, conditional on the volumes of services in the market (Chen and Fan 2015).

Related literature studying global budgeting focuses on either the effect on quantity or quality of healthcare services. Theoretical studies agree that medical providers have an incentive to increase their quantity of services after global budgeting due to the prisoner’s dilemma or the tragedy of commons (Feldman and Lobo 1997; Fan et al. 1998; Benstetter and Wambach 2006). However, Chen et al. (2007), Cheng et al. (2009), and Chen and Fan (2015) analyzed Taiwanese data and found that the effect of global budgeting on service quantity varies with patients’ disease and the size of hospitals. While Hurley et al. (1997) found the service quantity increased after Canada implemented global budgeting, Redmon and Yakoboski (1995) found opposite results using French data. Regarding the effect of global budgeting on the quality of medical services, Mougeot and Naegelen (2005) showed that global budgeting could reduce the quality of medical service in theory. Most empirical studies confirmed this prediction using data from Taiwan (Chang and Hung 2008; Chang et al. 2011; Chen and Fan 2015; Kan et al. 2014).

While hospital efficiency has been extensively studied (Hollingsworth 2008; Rosko and Mutter 2008), we found only one paper (Wu et al. 2013) that investigated hospital efficiency under global budgeting. The authors applied a non-radial data envelopment analysis (DEA) on Taiwanese data and found that hospital efficiency decreased after global budgeting. One estimation problem of Wu et al. (2013) is that they adopt a two-stage approach, where efficiency is estimated by the nonparametric DEA approach, and then the estimated efficiencies are regressed on environment variables by a Tobit model. Simar and Wilson (2007) have pointed out that the DEA efficiency estimates are serially correlated and criticized that the statistical interpretation of the second stage estimation is meaningless since the data-generating process (DGP) was not described. Therefore, they proposed a bootstrap approach for the statistical inference in the second step estimation. Extension of their approach to our two-division model is not so straightforward and needs more investigation. Moreover, the DEA-based efficiency measure is relatively sensitive to the extreme value than the efficiency measure of stochastic frontier analysis (SFA), because the DEA efficiency is measured by the distance between the observed output and the output envelope curve. Our objective here is not only to estimate the hospital efficiency, but also to investigate how the inefficiencies are different between hospitals, how they change due to the implementation of global budgeting, and how they related to the environment variables. Therefore, we adopt the one-step SFA approach to investigate hospital efficiency in this study.

Empirically, global budgeting may cause reallocation of the input resources from the viewpoint of profit maximization or cost minimization and it changes the relationship between inputs and outputs. Examining the effects of global budget on allocative efficiency is plausible for our current objective; however, it requires more information about inputs prices when profit maximization or cost minimization is considered. For instance, see Kumbhakar et al. (2015) for more discussion. Due to the data constraint, we focus on the production frontier to investigate the output efficiency and assume the allocation of inputs to be exogenously decided or already at the optimal efficient level in our following analysis.⁴

Since the dentist and physician sectors of the same hospital are quite different in their nature, we consider the two-equation system for the stochastic frontier analysis, stressing that dentists and physicians in the same hospital are under separate budget caps in Taiwan. In particular, dentists in Taiwan are under the same budget cap regardless of their affiliations.⁵ Physicians practicing Western medicine, however, are under two separate caps for community clinics and hospitals. The intention of these separate caps is to encourage patients with less severe conditions to visit community clinics, while preserving hospital resources for patients with more severe conditions. Accordingly, the global budgeting in Taiwan imposes separate budget caps for hospitals with both dentist and physician divisions.⁶

We incorporated the aforementioned institutional features in this analysis using the system regression model of Lai and Huang (2013), where they used the copula approach to estimate the seemingly unrelated stochastic frontier system. Each frontier regression in the system corresponds to the output function of each division within a decision-making unit. A prior assumption we made here is that we assume the physician and dentist divisions have different technologies due to the nature of the provided medical services. Furthermore, the two divisions of the same hospital share some common characteristics, such as the same managerial factors or common resources, which may or may not be observed in the sample. Although the two divisions are under separate budget caps, these common factors have effects on the input allocations between the two divisions and thus the joint estimation of the two-division production functions is more appropriate than the single equation approach for our study. Furthermore, joint estimation of the system not only improves the estimation efficiency, but also allows us to model the cross-dependence between the divisions within a hospital. Thus, this study contributes to the existing literature by showing how to simultaneously consider hospitals’ multiple outputs when estimating hospital efficiency. Hauck and Street (2006) applied the seemingly uncorrelated regression analysis based on the least squares method to account for the correlations between various objectives of English health authorities. Alternatively, Gerdtham et al. (1999) considered a reimbursement scheme change from budget-based allocation to output-based reimbursement in Sweden. Although their empirical model allows hospitals to have multi-output technology based on a stochastic ray frontier production function, which enables simultaneous estimation of hospital efficiency, their single equation approach may not be appropriate when the outputs are produced for different objectives or under different constraints, as pointed out by Hauck and Street (2006).

Our empirical specification includes hospital characteristics that were found to be important determinants of hospital efficiency, such as hospital ownership (for-profit, public, private), market size and location, and teaching status (Hollingsworth 2008; Rosko and Mutter 2011). A measure of market share of each medical provider was also included to control the effect of hospital competition on hospital efficiency. Empirical results show that a joint estimation considering the correlation between dentists and physicians within hospitals has a greater statistical efficiency of estimates than separate estimations. We found that dentists’ efficiency was reduced after global budgeting for hospitals in 2002, despite the fact that dentists were not subject to this budget cap. The separate estimation did not reveal this pattern. Physicians’ efficiency remained similar before and after global budgeting, but was lower than their dentist colleagues. These results suggest that the aggregate hospital efficiency was not improved after global budgeting in 2002, if not reduced. The results also suggest that the estimated hospital inefficiency came mostly from the physicians in hospitals that are small, public, non-teaching, located in small markets, and have a low market share. Regarding the correlation between physicians and dentists within the same hospital, we found these two divisions became less integrated after global budgeting. They were more integrated in the hospitals that had a high physician services market share and the hospitals that had a low dental services market share. Public hospitals, academic medical centers, teaching hospitals, and hospitals located in large markets had higher correlations between their physicians and dentists.

This paper proceeds as follows: the next section describes the global budgeting system in Taiwan. Section 3 discusses how our sample was assembled and the resulting descriptive statistics. Section 4 describes our empirical model, while the estimation results are presented in Sect. 5. Section 6 concludes.

2 Global Budgeting in Taiwan

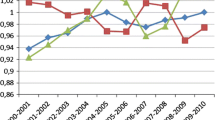
The global budgeting system in Taiwan is a sectoral expenditure cap system with a price adjustment mechanism (Chen et al. 2007; Chang and Hung 2008; Chen and Fan 2015). Essentially, the total budget for a given year is determined in the previous year, conditional on the expenditure last year, the age structure of population, and the consultation with representatives from each sector including dentistry, Chinese medicine, community clinics, and hospitals. The national budget is then divided into sub-budgets by quarter, sector, and six regions across Taiwan. Because the budget is predetermined, the price of each service is calculated using a “point value” system and the value of each point is determined ex post by dividing the total budget by the total services served by all medical providers in each region and sector. In the system, the points are designed in such a way that 1 New Taiwan Dollar (NTD) per point is considered a fair value to healthcare providers.⁷ Figure 1 shows the point values of each sector by year since 2000. As discussed previously, most of the point values are under 1 NTD except for the Chinese medicine sector in the early 2000s. Among the four groups, dentists maintained a stable point value close to 1 NTD. They also had the least variation of this point value, where the standard deviation is 0.019. On the other hand, hospitals have the lowest average point value among the four sectors, which is 0.87. This suggests that hospitals were likely competing against each other by increasing their volume of services.

Fig. 1

Point value trends by sectors

In addition to the potential competition in the healthcare services, hospitals in Taiwan have been reimbursed on a fee-for-service basis before and after the implementation of global budgeting. Accordingly, this study investigates the technical efficiency of hospitals in Taiwan regarding their number of services provided. This measure displays the effects of global budgeting on hospitals’ behavioral change and is a natural outcome measure considering hospitals as a firm with services as their products.⁸ Since the existing studies investigate either the quantity or quality effects, our paper contributes to the literature by studying the effects on hospital efficiency.

Fig. 2

Average number of physician services and average cost per service

Fig. 3

Average number of dental services and average cost per service

The trend of hospital services and the associated costs are shown in Figs. 2 and 3 for physicians and dentists, respectively. The amount of services was recorded by each medical claim hospitals applied for reimbursement purpose. We considered only outpatient services because the analysis controls the competition from community clinics that provide no inpatient services; dentists also provided mainly outpatient services. Both figures display a decreasing trend of medical services during 2002–2004, right after the implementation of global budgeting on hospital physicians. But Fig. 2 reveals that the average points applied per outpatient service were not reduced with fewer outpatient visits, which was also mentioned in Cheng et al. (2009). Thus, hospitals likely became less efficient in outpatient services after global budgeting.⁹ On the contrary, Fig. 3 shows the trends of dental services and the associated points applied are similar, except in 2003. Because dentists were not subject to the global budgeting for hospitals implemented in 2002, Fig. 3 shows this policy nevertheless might have a negative effect on dentists’ average points applied per service.

While global budgeting was implemented on the hospital sector in 2002, three noteworthy events also happened during 2002–2004. First, hospital inpatient services were restricted during the SARS epidemic outbreak from April to July 2003. This could relate to the significant drop of outpatient visits during 2003 due to the fear of hospital transmission. However, the outbreak is a temporary shock while the effect of global budgeting would sustain afterwards. Thus, our sample period covers five more years after the outbreak to show the long-term effect of global budgeting. Second, the Bureau of National Health Insurance (BNHI) raised the copayment of outpatient visits to hospitals in September 2002. This policy effect was insignificant because the increase was small. According to Kan et al. (2014), the copayment was raised from US$5 to US $7 for medical center and US $3.3 to US$4.7 for regional hospital. Third, Yan et al. (2010) reported that 6% of the hospitals went bankrupt after global budgeting was implemented. The quality of medical services also decreased due to the increased quantity of services after global budgeting. The BNHI thus launched a self-management project in 2004 to help hospitals control their expenditure and resource allocation, and 80% of the hospitals had joined. Because this program could increase hospital efficiency and reduce quantity of services, our estimate of hospital efficiency in 2004 should be interpreted with these events in mind. However, the shock was temporary because the program was terminated within a year.¹⁰ Our sample periods cover five more years after this program and would be able to display the long-term effect of global budgeting on hospital efficiency.

3 Data

Two datasets were used to estimate hospital efficiency under global budgeting in Taiwan. The National Health Insurance Research Database (NHIRD) provides information on hospital output variables, including the number of outpatient visits to dentists and physicians per hospital. These variables were constructed from the medical claims that hospitals filed for reimbursement. We calculated hospital market share by dividing the total medical claims filed by a hospital by the total number of such claims filed by all medical providers within a sector and region, including clinics. Information on hospital characteristics, such as hospital age, type, and location, is also included in this database.¹¹ The NHIRD sample was then merged with the hospital survey data provided by the Division of Statistics, Ministry of Health and Welfare (MHW). The later dataset provides information on hospital input variables, including the numbers of medical personnel, doctor’s offices and pieces of medical equipment per hospital.

Because hospital identification codes were not provided in both datasets, we merged these two datasets as follows. First, all the clinics’ data were dropped. Second, hospitals with the same located city, ownership, and type in both datasets were merged.¹² Third, only hospitals with similar number of workers, fields, and hospital accreditation level were used for empirical analysis.¹³ Table 1 lists the variable definitions and summary statistics. The number of nurses in a hospital and the number of doctor’s offices in a hospital were allocated to dentists and physicians by their ratios in the hospital because the MHW survey provides no such information.¹⁴

Table 1 Variable definitions and summary statistics

Table 1 shows that our sample includes 1614 observations on 233 hospitals during 2000–2008, with an average of 7-year observations per hospital. An average hospital in our sample received about 0.32 million visits annually, where 3% of them were visits to dentists. The average market share for physician outpatient services is about 1.5% within a branch, where the maximum market share of a hospital is 27%. The average market share of outpatient visits to dentists in hospitals is much lower, where the maximum is 5% in a region. These numbers show that the outpatient services market in Taiwan is fairly competitive and patients went to dentists in clinics more often than those in hospitals. Besides, the average cost per physician service is nearly twice as much as the average dental service, while the number of physicians is roughly 15 times much as then number of dentists.

Regarding the inputs and other hospital characteristics, an average hospital in the sample has been operating for 16 years, with roughly 280 nurses, 25 offices and 20 pieces of equipment shared by physicians and dentists. There were about 43 other medical assistants and 20 pharmacists to aid in physicians’ services. Most of the hospitals were private and/or local community hospitals. Half of the hospitals in the sample were located in large markets, and half of the hospitals were teaching hospitals. As previously mentioned, Taiwan implemented its global budgeting for hospitals in July 2002. Our sample thus consists of nearly three years of observations before this policy implementation.

4 The Empirical Model

Suppose the production operations of a hospital consist of two divisions, physicians and dentists, each producing a single output under the Cobb–Douglas type of production technology. The production frontiers of the two divisions are represented by a system of stochastic frontier (SF) regressions,

$$\begin{aligned} y_{it}^{1}&=\beta _{1}^{\text {T}}x_{it}^{1}+v_{it}^{1}-u_{it}^{1},\nonumber \\ y_{it}^{2}&=\beta _{2}^{\text {T}}x_{it}^{2}+v_{it}^{2}-u_{it}^{2}, \end{aligned}$$

(1)

where $i= 1,2,\ldots ,N$; $t=1,\ldots ,T$. $y_{it}^{j}$ and $x_{it}^{j}$ denote the log output and the log inputs of the jth division ($j= 1,2$) of the hospital i at time t; $v_{it}^{j}\sim N(0,\sigma _{vj}^{2})$ and $u_{it}^{j}\sim N^{+}(0,\sigma _{uj}^{2})$, respectively, represent the noise component and the nonnegative inefficiency component. For a given j, the division’s $v_{it}^{j}$ and $u_{it}^{j}$ are assumed to be mutually independent. Thus, for any given SF regression, the noise component is uncorrelated with the inefficiency component, which is a standard assumption in a single stochastic frontier modeling. For a more general setting, one may allow $\sigma _{uj}^{2}$ to be heteroskedastic, i.e.,

$$\begin{aligned} \sigma _{uj}^{2}=\exp (\delta _{j}^{\text {T}}q_{it}^{j}), \end{aligned}$$

(2)

where $q_{it}^{j}$ may include time variant or time invariant exogenous variables for sector j. When the composite error is defined as $\varepsilon _{it}^{j}=v_{it}^{j} -u_{it}^{j}$, the correlations among the composite errors $\varepsilon _{it}^{j}$ are the consequence of the correlation in $v_{it}^{j}$ and $u_{it}^{j}$. Across the SF regressions in (1), $u_{it}^{1}$ and $u_{it}^{2}$ are correlated due to the sharing of the same common characteristics among the two divisions within a hospital. Similarly, across the SF regressions, $v_{it}^{1}$ and $v_{it}^{2}$ are allowed to be correlated, possibly due to common stochastic shocks to the hospitals and its physician and dentist divisions. Let $\theta _{j}=(\beta _{j}^{\text {T}},\sigma _{vj},\sigma _{uj})^{\text {T}}$ be a vector of parameters in the jth SF regression, and $F(\varepsilon _{it}^{j};\theta _{j})$ be the cumulative distribution function (cdf) of the composite error of the jth SF regression with the vector of parameters $\theta _{j}$. In order to simplify the notation in our following analysis, we suppress $\theta _{j}$ in the marginal cdf $F(\varepsilon _{it}^{j};\theta _{j})$ and use the subscript j to indicate the jth SF regression, so $F_{j}(\varepsilon _{it}^{j})$ will be used instead in our following analysis. Derivation of the joint cdf of $\varepsilon _{it}^{1}$ and $\varepsilon _{it}^{2}$ may rely on the results of Sklar’s theorem (Sklar 1959; Schweizer and Sklar 1983), by which the joint cdf can be expressed as a function of its own one-dimensional margins. The function binding the margins together is referred to as the copula. Accordingly, the joint cdf of the composite errors $\varepsilon _{it}=\left( {\varepsilon _{it}^{1} ,\varepsilon _{it}^{2}}\right)$ can be represented as

$$\begin{aligned} F\left( {\varepsilon _{it}^{1},\varepsilon _{it}^{2}}\right) =C\left( {F_{1}(\varepsilon _{it}^{1}),F_{2}(\varepsilon _{it}^{2});\rho }\right) , \end{aligned}$$

(3)

where $\rho$ is called the dependence parameter and captures the dependence between the marginal cdfs. In order to capture dynamics of the dependence structure due to the policy change in our empirical study, we allow the dependence parameter ${\rho }$ to be a function of some exogenous variables $\omega _{it}$, i.e.,

$$\begin{aligned} \rho _{it}=g(\gamma ^{\text {T}}\omega _{it}), \end{aligned}$$

(4)

where $g(\cdot )$ is a function with the value bounded between $[-1,1].$ For instance, we may let

$$\begin{aligned} g(a)=\frac{\exp (2a)-1}{\exp (2a)+1}, \end{aligned}$$

(5)

where $g^{\prime }(a)>0$ implies $g(\cdot )$ is a monotonic increasing function. By taking partial derivatives of (3) with respect to $\varepsilon _{it} ^{1}$ and $\varepsilon _{it}^{2}$, we may obtain the corresponding joint probability density function (pdf),

$$\begin{aligned} f\left( {\varepsilon _{it}^{1},\varepsilon _{it}^{2}}\right) =c\left( {F_{1}\left( {\varepsilon _{it}^{1}}\right) ,F_{2}\left( {\varepsilon _{it}^{2}}\right) ;\rho _{it}}\right) \times \prod {}_{j=1}^{2}f_{j}\left( {\varepsilon _{it}^{j}}\right) , \end{aligned}$$

(6)

where $c\left( {F_{1}\left( {\varepsilon _{it}^{1}}\right) ,F_{2}\left( {\varepsilon _{it}^{2}}\right) ;\rho _{it}}\right) ={\frac{{\partial ^{2}C\left( {F_{1}\left( {\varepsilon _{it}^{1}}\right) ,F_{2}\left( {\varepsilon _{it}^{2}}\right) ;\rho _{it}}\right) }}{{\partial F_{1}\left( {\varepsilon _{it}^{1}}\right) \partial F_{2}\left( {\varepsilon _{it}^{2}}\right) }}}$ is the copula density and$^{\,}f_{j}(\varepsilon _{it}^{j})$ is the marginal pdf. Let $\phi _{p}\left( .;\eta ,\Psi \right)$ and $\Phi _{p}\left( .;\eta ,\Psi \right)$ denote the pdf and cdf of the p-dimensional normal distribution with mean $\eta$ and variance $\Psi .$ Under the assumptions, $v_{it}^{j}\sim N(0,\sigma _{vj}^{2})$ and $u_{it}^{j}\sim N^{+}(0,\sigma _{uj}^{2})$, it is straightforward to show that ${\varepsilon _{it}^{j}}$ follows a closed skew normal (CSN) distribution

$$\begin{aligned} {\varepsilon _{it}^{j}}\sim \hbox {CSN}_{1,1}\left( {0,\sigma _{vj}^{2}+\sigma _{uj} ^{2},\frac{-\sigma _{uj}}{\sigma _{vj}^{2}+\sigma _{uj}^{2}},0,\frac{\sigma _{vj}^{2}}{\sigma _{vj}^{2}+\sigma _{uj}^{2}}}\right) {,} \end{aligned}$$

which has the pdf

$$\begin{aligned} f\left( {\varepsilon _{it}^{j}}\right) =\frac{\phi _{1}\left( {\varepsilon _{it}^{j};0,\sigma _{vj}^{2}+\sigma _{uj}^{2}}\right) \Phi _{1}\left( \frac{-\sigma _{uj}}{\sigma _{vj}^{2}+\sigma _{uj}^{2}}{\varepsilon _{it}^{j};0,}\frac{\sigma _{vj}^{2}}{\sigma _{vj}^{2}+\sigma _{uj}^{2}}\right) }{\Phi _{1}\left( 0{;0,}1\right) } \end{aligned}$$

and the cdf

$$\begin{aligned} F\left( {\varepsilon _{it}^{j}}\right) =\frac{\Phi _{2}\left( \left( \begin{array} [c]{c}{\varepsilon _{it}^{j}}\\ 0 \end{array} \right) ;\left( \begin{array} [c]{c}{0}\\ 0 \end{array} \right) ,\left( \begin{array} [c]{cc}{\sigma _{vj}^{2}+\sigma _{uj}^{2}} &{} \sigma _{uj}\\ \sigma _{uj} &{} 1 \end{array} \right) \right) }{\Phi _{2}\left( \left( \begin{array} [c]{c}{0}\\ 0 \end{array} \right) ;\left( \begin{array} [c]{c}{0}\\ 0 \end{array} \right) ,\left( \begin{array} [c]{cc}{\sigma _{vj}^{2}+\sigma _{uj}^{2}} &{} \sigma _{uj}\\ \sigma _{uj} &{} 1 \end{array} \right) \right) }. \end{aligned}$$

Under the Gaussian copula specification, the joint cdf of ${\varepsilon _{it}^{1}}$ and ${\varepsilon _{it}^{2}}$ has the representation

$$\begin{aligned} C\left( {\gamma _{it}^{1},\gamma _{it}^{2};}\Omega \right)= & {} \Phi _{z,2}\left( \left( \begin{array} [c]{c} {\Phi _{z}^{-1}(\gamma _{it}^{1})}\\ {\Phi _{z}^{-1}(\gamma _{it}^{2})} \end{array} \right) {;}\left( \begin{array} [c]{cc} 1 &{} \rho _{it}\\ \rho _{it} &{} 1 \end{array} \right) \right) \\ \nonumber= & {} \int \limits _{-\infty }^{\Phi _{z}^{-1}(\gamma _{it}^{1})}{\int \limits _{-\infty }^{\Phi _{z}^{-1}(\gamma _{it}^{2})}{\frac{1}{\left( {2\pi }\right) |\Omega _{it}|^{1/2}}e^{-\frac{1}{2}z^{\text {T}}{\Omega }_{it}^{-1}z} dz_{1}dz_{2}}} \end{aligned}$$

(7)

where $\Phi _{z}\left( \cdot \right)$ is the CDF of the standard normal distribution and $\Phi _{z,2}\left( \cdot \right)$ is the CDF of a standard bivariate normal distribution of the random variables with the $2\times 2$ correlation matrix

$$\begin{aligned} \Omega _{it}=\left( \begin{array} [c]{cc} 1 &{} \rho _{it}\\ \rho _{it} &{} 1 \end{array} \right) , \end{aligned}$$

of which the off-diagonal element is the correlation coefficient between two variables, $\Phi _{z}^{-1}(\gamma _{it}^{1})$ and $\Phi _{z}^{-1}(\gamma _{it} ^{2})$. The corresponding Gaussian copula density of (7) is

$$\begin{aligned} c\left( {\gamma _{it}^{1},\gamma _{it}^{2};\Omega }_{it}\right) =\frac{1}{|\Omega _{it}|^{1/2}}e^{-\frac{1}{2}\zeta _{it}^{\text {T}}\left( {\Omega _{it}^{-1}-I_{2}}\right) \zeta _{it}}, \end{aligned}$$

(8)

where $\zeta _{it}=\left( {\Phi _{z}^{-1}(\gamma _{it}^{1}),\Phi _{z}^{-1} (\gamma _{it}^{2})}\right) ^{\text {T}}$ and $I_{2}$ is a $2\times 2$ identity matrix. Replacing $\gamma _{it}^{j}=F_{j}\left( {\varepsilon _{it}^{j}}\right)$ in (7), the joint CDF of the composite errors in (3) becomes

$$\begin{aligned} F\left( {\varepsilon _{it}^{1},\varepsilon _{it}^{2}}\right) =\Phi _{z,2}\left( {\Phi _{z}^{-1}\left( {F_{1}(\varepsilon _{it}^{1})}\right) ,\Phi _{z}^{-1}\left( {F_{2}(\varepsilon _{it}^{2})}\right) ;\Omega } _{it}\right) . \end{aligned}$$

(9)

The corresponding joint PDF of the composite errors in (6) becomes

$$\begin{aligned} f\left( {\varepsilon _{it}^{1},\varepsilon _{it}^{2}}\right) =\frac{1}{|\Omega _{it}|^{1/2}}e^{-\frac{1}{2}\zeta _{it}^{\text {T}}\left( {\Omega ^{-1}-I_{2}}\right) \zeta _{it}}\times \prod {}_{j=1}^{2}f_{j}\left( {\varepsilon _{it}^{j}}\right) , \end{aligned}$$

(10)

where $\zeta _{i}=\left( {\Phi _{z}^{-1}\left( {F_{1}(\varepsilon _{it}^{1} )}\right) ,\Phi _{z}^{-1}\left( {F_{2}(\varepsilon _{it}^{2})}\right) }\right) ^{\text {T}}$. Note that the off-diagonal elements of $\Omega _{it}$ measure the correlation coefficients between two variables, $\Phi _{z} ^{-1}\left( {F_{1}(\varepsilon _{it}^{1})}\right)$ and $\Phi _{z}^{-1}\left( {F_{2}(\varepsilon _{it}^{2})}\right)$. Thus, if the off-diagonal elements of $\Omega _{it}$ are all zeros, $\Omega _{it}$ becomes a $2\times 2$ identity matrix, i.e., $\Omega _{it}=I_{2}$. In this case, the Gaussian copula density $c\left( \cdot \right) =1$ and $f\left( {\varepsilon _{it}^{1},\varepsilon _{it}^{2}}\right) =\prod {}_{j=1}^{2}f_{j}\left( {\varepsilon _{it}^{2} }\right)$, which implies the mutual independence of the composite errors $\varepsilon _{it}=\left( {\varepsilon _{it}^{1},\varepsilon _{it}^{2}}\right)$, and hence the mutual independence of the SF regressions in (1). Here, the dependence parameter $\rho _{it}$ in (3) is defined as the diagonal element of $\Omega _{it}$ . Therefore, based on (10) we may write the log-likelihood function of the two multiple SF regressions of (1) as

$$\begin{aligned} \ln L(\theta )= & {} \sum \limits _{i=1}^{N}{\sum \limits _{t=1}^{T}{\ln f\left( {\varepsilon _{it}^{1},\varepsilon _{it}^{2}}\right) }}\nonumber \\= & {} \sum \limits _{i=1}^{N}{\sum \limits _{t=1}^{T}{\ln c\left( {F_{1}\left( {\varepsilon _{it}^{1}}\right) ,F_{2}\left( {\varepsilon _{it}^{2}}\right) ;\Omega }_{it}\right) }}+\sum \limits _{i=1}^{N}{\sum \limits _{t=1}^{T} {\sum \limits _{j=1}^{2}{\ln f_{j}\left( {\varepsilon _{it}^{j}}\right) }}}\end{aligned}$$

(11)

$$\begin{aligned}= & {} -\frac{NT}{2}\ln |\Omega _{it}|-\frac{1}{2}\sum \limits _{i=1}^{N}{\zeta _{it}^{\text {T}}\left( {\Omega _{it}^{-1}-I_{2}}\right) \zeta _{it}} +\sum \limits _{i=1}^{N}{\sum \limits _{t=1}^{T}{\sum \limits _{j=1}^{2}{\ln f_{j}\left( {\varepsilon _{it}^{j}}\right) }}},\nonumber \\ \end{aligned}$$

(12)

where $\theta =\left( {\theta _{1}^{\text {T}},\theta _{2}^{\text {T}} ,\delta ^{\text {T}}}\right) ^{\text {T}}$ and $\theta _{j}$’s are vectors of parameters of the jth SF regression. Therefore, the ML estimator of $\theta$ is defined as

$$\begin{aligned} \hat{{\theta }}=\arg {\max }_{\theta \in \Theta }\ln L(\theta ), \end{aligned}$$

where $\Theta$ denotes the parameter space of $\theta$. Under the regularity conditions for the asymptotic maximum likelihood theory, the ML estimator can be shown to be consistent, asymptotic efficient and asymptotic normal (Serfling 1980). That is,

$$\begin{aligned} \sqrt{N}\left( {\hat{{\theta }}-\theta _{0}}\right) \rightarrow N\left( {0,I^{-1}(\theta _{0})}\right) , \end{aligned}$$

where $I(\theta _{0})$ is the usual Fisher’s information matrix and $\theta _{0}=\left( {\theta _{1,0},\theta _{2,0},\delta }\right)$ denotes the vector of true parameters. Finally, some measures of the dependence structure between the two SF regressions can be obtained by the transformations from the Gaussian copula parameter matrix $\Omega _{it}$ (or equivalently ${\rho }_{it}$). Taking the transformation according to the distribution function (Cherubini et al. 2004), one can show that the linear correlation between $F_{1}(\varepsilon _{it}^{1})$ and $F_{2}(\varepsilon _{it}^{2})$ is

$$\begin{aligned} \rho _{F_{1},F_{2}}=\frac{6}{\pi }\arcsin \left( {\frac{\rho _{it}}{2}}\right) , \end{aligned}$$

(13)

which measures the correlation of the two SF regressions in terms of the cdf’s of $\varepsilon _{it}^{1}$and $\varepsilon _{it}^{2}$, and is also called the Spearman’s rank correlation coefficient of $\varepsilon _{it}^{1}$ and $\varepsilon _{it}^{2}$. Alternatively, another dependence measure is the concordance. For example, two observations $(\varepsilon _{it_{1}}^{1},\varepsilon _{it_{1}}^{2})$ and $(\varepsilon _{it_{2}}^{1},\varepsilon _{it_{2}}^{2})$ of a pair $(\varepsilon _{it}^{1},\varepsilon _{it}^{2})$ of composite errors are concordant if both values of one pair are greater than the corresponding values of the other pair, that is if $\varepsilon _{it_{1}}^{1}>\varepsilon _{it_{2}}^{1}$ and $\varepsilon _{it_{1}}^{2}>\varepsilon _{it_{2}}^{2}$, or $\varepsilon _{it_{1}}^{1}<\varepsilon _{it_{2}}^{1}$and $\varepsilon _{it_{1}}^{2}<\varepsilon _{it_{2}}^{2}$. The discordance is defined in the opposite way; in other words, $\varepsilon _{it}^{1}$ and $\varepsilon _{it}^{2}$ are said to be discordant if $\varepsilon _{it_{1}}^{1}>\varepsilon _{it_{2}}^{1}$ and $\varepsilon _{it_{1}}^{2}<\varepsilon _{it_{2}}^{2}$, or $\varepsilon _{it_{1}}^{1}<\varepsilon _{it_{2}}^{1}$and $\varepsilon _{it_{1}}^{2}>\varepsilon _{it_{2}}^{2}$. The measure of the concordance is also called the Kendall’s coefficient, which is defined as

$$\begin{aligned} \tau _{it}=\Pr \left( {\left( \varepsilon _{it_{1}}^{1}-\varepsilon _{it_{2}} ^{1}\right) \left( \varepsilon _{it_{1}}^{2}-\varepsilon _{it_{2}}^{2}\right) >0}\right) -\Pr \left( {\left( \varepsilon _{it_{1}}^{1}-\varepsilon _{it_{2}}^{1}\right) \left( \varepsilon _{it_{1}}^{2}-\varepsilon _{it_{2}} ^{2}\right) <0}\right) . \end{aligned}$$

(14)

Table 2 Separate and joint estimation results of hospital production—(A) Frontier, (B) Inefficiency term and (C) Correlation

Intuitively, Kendall $\tau$ measures the difference between the probability of concordance and that of discordance for two composite errors. It can be shown that Kendall $\tau$ can also be transformed from the Gaussian copula parameter $\Omega$. The concordance between $\varepsilon _{it}^{1}$ and $\varepsilon _{it}^{2}$ of the two SF regressions is

$$\begin{aligned} \tau _{it}=\frac{2}{\pi }\arcsin \left( \rho _{it}\right) . \end{aligned}$$

(15)

Although we may obtain certain dependence measures of the SF regressions through the direct transformation of the copula parameter $\Omega$, the interpretation of the measure is limited to the composite errors. How much correlation between $\varepsilon _{it}^{1}$ and $\varepsilon _{it}^{2}$ is attributed to $(v_{it}^{1},v_{it}^{2})$ or $(u_{it}^{1},u_{it}^{2})$ cannot be further identified. Once we obtain the estimates for the model parameters, we are also interested in predicting the technical efficiencies (TE) and the effects of global budgeting, managerial characteristics and some exogenous variables on the technical efficiencies. The technical efficiency of the sector j is the conditional expectation

$$\begin{aligned} E\left( \left. e^{-u_{it}^{j}}\right| \varepsilon _{it}^{1} ,\varepsilon _{it}^{2}\right) , \end{aligned}$$

(16)

which requires estimating the conditional density $f\left( \left. u_{it} ^{j}\right| \varepsilon _{it}^{1},\varepsilon _{it}^{2}\right)$. Since how much of the correlation between $\varepsilon _{it}^{1}$ and $\varepsilon _{it}^{2}$ is attributed to $(v_{it}^{1},v_{it}^{2})$ or $(u_{it}^{1} ,u_{it}^{2})$ is not identified, the conditional marginal density $f\left( \left. u_{it}^{j}\right| \varepsilon _{it}^{1},\varepsilon _{it} ^{2}\right)$ is not identified and neither is (16) estimatable. We, therefore, use the following predictor instead:

$$\begin{aligned} E\left( \left. e^{-u_{it}^{j}}\right| \varepsilon _{it}^{j}\right) =\frac{1-{\Phi _{z}}\left( \sigma _{*j}-\mu _{*j}/\sigma _{*j}\right) }{1-{\Phi _{z}}\left( -\mu _{*j}/\sigma _{*j}\right) } \exp \left( -\mu _{*j}+\frac{1}{2}\sigma _{*j}^{2}\right) , \end{aligned}$$

(17)

where $\sigma _{*j}^{2}= \sigma _{vj}^{2}\sigma _{uj}^{2}/\left( \sigma _{vj}^{2}+\sigma _{uj}^{2}\right)$ and $\mu _{*j}=\frac{-\varepsilon _{it}^{j}\sigma _{u j}^{2}}{\sigma _{vj}^{2}+\sigma _{uj}^{2}}$.

5 Empirical Results

This section reports the empirical results based on the setting of the system regression in (1). We summarize the estimated coefficients $\beta _{1}$ and $\beta _{2}$ of the production functions under joint and separate estimation in Table 2(A), the estimates $\delta _{1}$ and $\delta _{2}$ for the parameters contained in the inefficiency terms of Eq. (2) in Table 2(B), and the estimate for the dependence parameter $\gamma$ of Eq. (4) in Table 2(C). Overall, we found that although the estimates obtained from the separate and joint estimation being quite similar, the estimated standard errors under the joint estimation are in relatively smaller magnitudes. We discuss our main findings from Table 2(A)–(C).

Table 2(A) shows that the estimates of hospitals’ production frontiers under separate and joint estimation are quite similar. Among the coefficient estimates, almost all estimates significantly indicate that the number of physician services increased with the inputs invested, except the amount of equipment and the average cost per service. The former negative effect could be a result of hospitals’ expansion of inpatient services with expansive equipments after global budgeting (Chen and Fan 2015), but our data reveal no information on whether the equipments were used by outpatient or inpatient services. The later negative estimate also supports this argument because more expansive examinations could be ordered while the amount of services remained constant.

Fig. 4

Separate and Joint efficiency indices of physician and dentist sectors

Table 2(B) summarizes the coefficient estimates of the determinants $q_{it}^{j}$ on hospital inefficiency through the setting of heteroscedastic variance $\sigma _{uj}^{2}$ given in (2). Despite the test that the estimates from separate and joint estimation are quite similar in signs, these estimates are different in magnitudes and statistical significance. We found that global budgeting has a negative effect on the inefficiency term (or equivalently, positive effect on the efficiency) for both physician and dentist divisions, but only the effect to dentists is statistically significant. However, it is worth emphasizing that the interpretation of global budgeting improving hospital efficiency is conditional on the hospital characteristics, controlled by the cross-product terms of the characteristics and the global budgeting dummy. Evaluation of the overall effect of global budgeting should take into account the effects of the interaction terms together with the global budgeting dummy.

Figure 4 gives the graph of the predicted TE of the physician and dentist divisions over the years 2000–2008 based on Table 2(B) and Eq. (17). The empirical results suggest that the aggregate hospital efficiency was not improved after global budgeting in 2002. In particular, the graph shows that both separate and joint estimation predict similar patterns for hospital efficiency, while the dentists are found to be more efficient than the physicians. The figure also shows that the TE of the physicians was lower after the implementation of global budgeting in 2002 but improved in 2004 and has remained stable around 0.7 since then.¹⁵ For dentists, Fig. 4 shows that the TE from joint estimation indicates a decreasing trend after 2002. This suggests that the TE of the dentist sector was affected by the global budgeting implemented since 2002. This finding, however, is not found by the separate estimation and suggests the importance of controlling the correlations among hospitals’ multi-sectors when estimating hospital efficiency. The results suggest that managers likely reallocated some of their resources from physicians to dentists since 1999, but reallocated again to their physicians in 2002 as they faced the same constraint in that year. Since most Taiwanese used to visit dentists in clinics, we expect hospitals with insufficient resources would focus on the physician market after 2002.

Fig. 5

Efficiency indices of physician and dentist sectors by teaching status

Regarding the effect of hospital teaching status on hospital efficiency, the results show that the teaching hospitals were more efficient than the non-teaching ones for their physician services. However, the dentists in teaching hospitals were found to be less efficient than their counterparts in non-teaching hospitals. The interaction terms of teaching status and global budgeting show the latter efficiency was improved after the 2002 global budgeting, but only the effect on dentists is statistically significant. Because the global budgeting on dentists was implemented in 1999, the hospital dentists in teaching hospitals provided most of their services with high reimbursement from the NHI, such as root canal procedures or ionomer restoration (Lin and Chao 2012). This could contribute to the inefficiency of the dentists in teaching hospital before 2001. The dentists in non-teaching hospitals likely adopted this strategy later as their efficiency dropped after 2001, as shown in Fig. 5. Their efficiency was further dropped after the implementation of global budgeting on physicians in 2002, which is indicated by the estimate of the interaction term of teaching status and global budgeting. This estimate reveals that the dentists in non-teaching hospitals, which are usually smaller than the teaching ones, had to focus on the services with high NHI reimbursement to maintain the profit and stay competitive under the global budgeting on both dentists and physicians. Besides, comparing to teaching hospitals, non-teaching hospitals are often less resourceful and more specialized. Since the dental services accounted much fewer share of the total revenue of hospitals than the physicians, the non-teaching hospitals likely concentrated more on their physician services than the dental services after the global budgeting on hospital physicians. This explains the insignificant estimate of the interaction term for physicians, which reveals the relative efficiency of the physicians between teaching and non-teaching hospitals remains similar after the 2002 global budgeting. Figure 5 also shows that the physicians in the non-teaching hospitals had their efficiency increased after 2003.

Fig. 6

Efficiency indices of physician and dentist sectors by hospital size

Fig. 7

Efficiency indices of physician and dentist sectors by public and private hospitals

Fig. 8

Efficiency indices of physician and dentist sectors by market size

Fig. 9

Correlation estimates between physician and dentist sectors within hospital

Fig. 10

Correlation estimates between physician and dentist sectors within hospital by public and private hospitals

Fig. 11

Correlation estimates between physician and dentist sectors within hospital by hospital size

Fig. 12

Correlation estimates between physician and dentist sectors within hospital by market size

Fig. 13

Correlation estimates between physician and dentist sectors within hospital by teaching status

Table 2(B) also shows that the dentists in public hospitals, small hospitals, and hospitals located in small markets likely suffered efficiency loss after global budgeting. The TE of both physicians and dentists decrease with smaller hospitals, hospitals located in less populated markets, and hospitals with less market share in physician or dental services. To compare the efficiency of physicians and dentists in academic medical centers and the other hospitals, Fig. 6 shows that the efficiency measures for both physicians and dentists in academic medical centers are nearly at the same levels, but the TE is lower for those in small hospitals. The TE of the physicians in small hospitals was particularly low. Figure 6 shows the efficiency trend by hospital locations. While the dentists in hospitals located in large markets were found to be the most efficient among the four groups, physicians of hospitals located in small markets were found to be the least efficient ones. Table 2(B) also reveals that the predicted efficiency indices of physicians increase with private hospitals, while the efficiency indices of dentists are higher in older hospitals. Figure 7 shows the efficiency indices by sector and ownership, where physicians in public hospitals were the least efficient group. Moreover, the efficiency measures of dentists in public hospitals were greatly reduced after 2002. At last, Fig. 8 shows the TE of the dentists in large market is the highest among all dentists and physicians, while the physicians in small market were the least efficiency ones.

Table 2(C) shows the estimates of the determinants of correlation coefficients between physicians and dentists within a hospital. We found that these divisions were less integrated after the implementation of global budgeting. Since the global budgeting limited the profit space of hospitals, they likely responded to this policy by promoting the dental services that are not covered in the health insurance for the patients with high out-of-pocket expenses. For example, the NHI covers the basic teeth scaling but the dentists could recommend the patients to adopt additional procedures such as laser treatments. Because these services are more profitable to the hospitals than the NHI-insured services, the opportunity costs of the hospital dentists for the latter services were increased. As mentioned previously, the hospital dentists would thus prefer to provide the services with high reimbursement from the NHI and refer the patients seeking low reimbursement treatments such as amalgam to clinic dentists. Accordingly, the number of services reimbursed by the NHI was reduced after global budgeting, but the average reimbursement per services were increased as shown in Fig. 3. Patients’ out-of-pocket expenses therefore accounted for more share of the revenue of hospital dental services than the NHI reimbursement. The global budgeting on hospital physicians implemented in 2002 could further strengthen this strategy because the policy limited the profit space from the physician services, where the NHI reimbursed services accounted most of the revenue. The dentists and physicians therefore became less integrated within hospital regarding the NHI reimbursed services after the global budgeting on physicians in 2002.

Table 2(C) also reveals that the physician and dentist divisions became more integrated in the hospitals with a high market share in physician services, or a low market share in dentist services. These two divisions were also more integrated in public hospitals. Figures 9, 10, 11, 12, and 13 show the patterns of correlation coefficient estimates by hospital characteristics. All these graphs show a significant drop in the correlation between the two divisions after global budgeting on hospitals, in terms of the correlation coefficient $\rho$, rank correlation $\rho _{F_{1},F_{2}}$, and the Kendall’s $\tau$. These graphs also indicate that public hospitals, academic medical centers, hospitals located in large markets, and teaching hospitals tend to have a relatively stronger correlation between their physicians and dentists than that of the remaining hospitals.

6 Conclusion

With universal health coverage emerging as a priority goal for many countries, governments pursuing such a goal should be prepared for potential increases in health expenditures. Global budgeting is an effective way to contain healthcare spending, but the fixed budget could result in less efficient medical services. This paper measures hospital efficiency under global budgeting using stochastic frontier analysis, stressing that physicians and dentists within the same hospital were under separate budgets in Taiwan. We found that hospital efficiency was not improved after global budgeting and physicians were found to be less efficient than dentists. Albeit hospital dentists were subject to another budget cap, we found their efficiency was also reduced after global budgeting for hospital physician services. Physicians and dentists in the same hospital were also found to be less integrated after global budgeting.

Our empirical results show that global budgeting in Taiwan did not improve hospital efficiency. Because patients in Taiwan prefer academic medical centers over small hospitals regardless of their severity of illness, small hospitals found it hard to compete with academic medical centers. This likely explains the reason behind our inefficiency measures for the physicians in hospitals that were small, public, non-teaching, located in small markets, and a low market share. Despite their relatively high efficiencies, the academic medical centers in Taiwan face excess demand of their services, which may eventually crowd out their ample resources. Policies aimed at solving the aforementioned problems include a compulsive referral system in which an academic medical center can transfer patients with less severe illnesses to small hospitals. The government can also subsidize small hospitals to hire better physicians and purchase necessary equipments. All these suggestions aim to change patients’ confidence in small hospitals by increasing their efficiencies. However, more evidence is required to show the effectiveness of these policies.

Future research is also required to investigate other reasons behind the hospital efficiency under global budgeting. For example, an investigation of the input allocative efficiency may be plausible to discuss this issue. The primal system approach discussed in Kumbhakar et al. (2015) seems to be a good way to do the prediction or counterfactual analysis. In this primal system approach, the input allocation is endogenously decided under the cost minimization assumption, and we are able to analyze not only the technical but also the allocative inefficiency. Examination of how the input allocation would change after global budgeting seems to be feasible using this approach. However, the primal system approach requires more information about inputs prices, so this approach is not applicable due to our data constraint.