Abstract
We produce predictions of the current state of the Indonesian economy by estimating a dynamic factor model on a dataset of 11 indicators (followed closely by market operators) over the 2002–2014 period. Besides the standard difficulties associated with constructing timely indicators of current economic conditions, Indonesia presents additional challenges typical to emerging market economies where data are often scant and unreliable. By means of a pseudo-real-time forecasting exercise, we show that our model outperforms univariate benchmarks, and it does comparably well with predictions of market operators. Finally, we show that when quality of data is low, a careful selection of indicators is crucial for better forecast performance.

Source: CEIC Data Company (accessed 30 June 2015); Authors’ computation

Source: CEIC Data Company (accessed 30 June 2015); Authors’ computation

Source: CEIC Data Company (accessed 30 June 2015); Authors’ computation

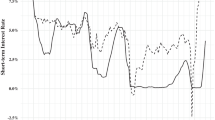
Source: CEIC data company (accessed 30 June 2015)

Sources: Authors’ estimates; Bloomberg and CEIC data company (both accessed 30 June 2015)

Source: Authors’ estimates; Asian Development Bank, Asian Development Outlook database; CEIC Data Company; Concensus Economics, Monthly Concensus Forecasts; and International Monetary Fund, World Economic Outlook database (all accessed 30 June 2015)
Similar content being viewed by others
Notes
GDP for 2013 and 2014 based on the 2000 base year are preliminary figures projected by the statistical office: https://www.bps.go.id/linkTabelStatis/view/id/1217.
A detailed explanation of the System of National Accounts (SNA) can be found at http://unstats.un.org/unsd/nationalaccount/sna.asp.
In fact, even nominal GDP data for the overlapping time periods are not comparable between the different bases for GDP series. Data are available in Table VII.1 at http://www.bi.go.id/en/statistik/seki/terkini/riil/Contents/Default.aspx.
A non-exhaustive list of countries and papers is: the USA (Bańbura et al. 2011, 2013; Giannone et al. 2008), the Euro Area (Angelini et al. 2011; Bańbura and Rünstler 2011), Germany (Marcellino and Schumacher 2010), France (Barhoumi et al. 2010), Ireland (D’Agostino et al. 2012), Norway (Aastveit and Trovik 2012; Luciani and Ricci 2014), China (Giannone et al. 2014), Brazil (Bragoli et al. 2015), New Zealand (Matheson 2010), the Global Economy (Matheson 2013), and Latin America (Liu et al. 2012).
The implicit assumption here is that since based on their expectations on future fundamentals analysts allocate their investments, they know which series to monitor to form appropriate expectations on GDP growth.
As shown by De Mol et al. (2008) since there is a lot of comovement among macroeconomic data, the set of indicators selected with statistical criteria is extremely unstable.
As the index compiled by Danareksa was not available to us, we experimented with the household consumer confidence index compiled by the Bank of Indonesia. The latter, however, displays a trending pattern that appears difficult to reconcile with the state of the economy, and we hence discarded it.
For the policy rate, we adopted the assumption that it is observed the first day of the month following the reference month. For example, the policy rate for January is observed on February 1. Of course this is an approximation because we know what the policy rate is everyday in January. In principle, we could have accounted for daily observations in the interest rate since DFMs allow us to do so (Modugno 2014). However, Bańbura et al. (2013) have shown that including data at the daily frequency is not particularly useful for nowcasting GDP, so we adopted the convention that the interest rate is monthly and is observed on the first day after the reference month.
It is worth noting here that the use of y-o-y transformations likely add persistence also in the idiosyncratic component so that a higher order autoregressive process might be more appropriate. However, increasing the order of the autoregressive process of the idiosyncratic component from an AR(1) to an AR(2) implies adding eleven extra states to the model. In our case, where we have few time series observations, and the quality of the data is doubtfull, adding eleven extra states in the Kalman Filter is feasible, but for sure costly in terms of computation accurancy. In summary, although an AR(1) may be not enough for capturing the whole dynamic in the idiosyncratic process, the cost of adding an extra lag is way higher than the benefits in terms of forecasting accuracy.
As pointed out by Baffigi et al. (2004), differently from DFMs, bridge models are not concerned with particular assumption underlying the DGP of the data, but rather, the inclusion of specific explanatory indicators is based on the simple statistical fact that they embody timely updated information about the target GDP growth series.
Note that the AR(2) and the RW do not update the prediction beyond month 2 of the quarter, but update it between month 1 and month 2 due to the GDP data release. Also, the fact that the RMSE of the AR(2) and the RW in “Backcast” month 1, and “Nowcast” month 2 is different is an artifact due to the fact that when we “Backcast” our target variable is GDP from Q4 2007 to Q3 2014, whereas when we “Nowcast” our target variable is GDP from Q1 2008 to Q4 2014. Of course, had the evaluation period been longer, we would not have this problem.
The average share of exports to GDP in Indonesia in 2010–2014 was about 20% and even slightly lower for imports (at 19%). Trade data, however, provide information about activity across sectors in the economy, and the results in Table 4 show that this is useful information for predicting GDP.
Note that this is all the “real-time” information that we have available since, as mentioned in Sect. 4.1, we do not have any “real-time” information for the other variables in the dataset.
Let \(X^y_q=100\times \log (\hbox {GDP}^y_q)\) be GDP of the q th quarter of year y, and let \(Z^y=100\times \log (\hbox {GDP}^y)\) be GDP of year y. Then, by definition \(x^y_q=X^y_q-X^{y-1}_{q}\) is the y-o-y growth rate, while \(z^y=Z^y-Z^{y-1}\) is the annual growth rate. Following Mariano and Murasawa (2003), we make use of the approximation \(Z^y\approx (X^y_1+X^y_2+X^y_3+X^y_4)/4\), which allow us to write the annual growth rate as a function of y-o-y growth rates: \(z^y=Z^y-Z^{y-1}\approx (X^y_1+X^y_2+X^y_3+X^y_4)/4 - (X^{y-1}_1+X^{y-1}_2+X^{y-1}_3+X^{y-1}_4)/4 = (x^y_4+x^y_3+x^y_2+x^y_1)/4\).
Consensus Economics Inc. forecasts comprise quantitative predictions of private sector forecasters. Each month survey participants are asked for their forecasts of a range of macroeconomic and financial variables for the major economies.
By using the LARS algorithm as in Bai and Ng (2008), we selected 10 out of all available indicators that were retrieved for Indonesia.
With the exception of few technical and minor details, this is essentially the same model used by Giannone et al. (2008). In practice, every time we update the prediction we use a balanced panel to estimate the factor with PCA. Then we fit an AR(2) on the estimated factor and use the Kalman Filter to account for missing values at the end of the sample. Finally we estimate Eq. (4) with OLS. An alternative way to perform this exercise would be to use the collapsed dynamic factor model of Bräuning and Koopman (2014).
References
Aastveit KA, Trovik T (2012) Nowcasting Norwegian GDP: the role of asset prices in a small open economy. Empir Econ 42(1):95–119
Andreou E, Ghysels E, Kourtellos A (2013) Should macroeconomic forecasters use daily financial data and how? J Bus Econ Stat 31(2):240–251
Angelini E, Camba-Mendez G, Giannone D, Reichlin L, Rünstler G (2011) Short-term forecasts of euro area GDP growth. Econom J 14(1):C25–C44
Baffigi A, Golinelli R, Parigi G (2004) Bridge models to forecast the euro area GDP. Int J Forecast 20(3):447–460
Bai J (2003) Inferential theory for factor models of large dimensions. Econometrica 71:135–171
Bai J, Ng S (2008) Forecasting economic time series using targeted predictors. J Econom 146(2):304–317
Bańbura M, Modugno M (2014) Maximum likelihood estimation of factor models on data sets with arbitrary pattern of missing data. J Appl Econom 29(1):133–160
Bańbura M, Rünstler G (2011) A look into the factor model black box: publication lags and the role of hard and soft data in forecasting GDP. Int J Forecast 27(2):333–346
Bańbura M, Giannone D, Reichlin L (2011) Nowcasting. In: Clements MP, Hendry DF (eds) Oxford handbook on economic forecasting. Oxford University Press, New York
Bańbura M, Giannone D, Modugno M, Reichlin L (2013) Now-casting and the real-time data-flow. In: Elliott G, Timmermann A (eds) Handbook of economic forecasting, vol 2. Elsevier-North Holland, Amsterdam, pp 195–237
Barhoumi K, Darné O, Ferrara L (2010) Are disaggregate data useful for factor analysis in forecasting French GDP? J Forecast 29(1–2):132–144
Bragoli D, Metelli L, Modugno M (2015) The importance of updating: evidence from a Brazilian nowcasting model. J Bus Cycle Meas Anal 2015(1):5–22
Bräuning F, Koopman SJ (2014) Forecasting macroeconomic variables using collapsed dynamic factor analysis. Int J Forecast 30(3):572–584
Camacho M, Perez-Quiros G (2010) Introducing the euro-sting: short-term indicator of euro area growth. J Appl Econom 25(4):663–694
D’Agostino A, McQuinn K, O’Brien D (2012) Now-casting Irish GDP. OECD J Bus Cycle Meas Anal 2012(2):21–31
D’Agostino A, Giannone D, Lenza M, Modugno M (2016) Nowcasting business cycles: a Bayesian approach to heterogeneous dynamic factor models. In: Koopman SJ, Hillebrand E (eds) Dynamic factor models, vol 35. Advances in econometrics. Bingley, Emerald
De Mol C, Giannone D, Reichlin L (2008) Forecasting using a large number of predictors: is bayesian shrinkage a valid alternative to principal components? J Econom 146:318–328
Diebold FX, Mariano RS (1995) Comparing predictive accuracy. J Bus Econ Stat 13:253–263
Doz C, Giannone D, Reichlin L (2011) A two-step estimator for large approximate dynamic factor models based on kalman filtering. J Econom 164(1):188–205
Doz C, Giannone D, Reichlin L (2012) A quasi maximum likelihood approach for large approximate dynamic factor models. Rev Econ Stat 94(4):1014–1024
Forni M, Hallin M, Lippi M, Reichlin L (2003) Do financial variables help forecasting inflation and real activity in the Euro Area? J Monet Econ 50(6):1243–1255
Forni M, Giannone D, Lippi M, Reichlin L (2009) Opening the black box: structural factor models versus structural VARs. Econom Theory 25(5):1319–1347
Fulop G, Gyomai G (2012) Transition of the OECD CLI system to a GDP-based business cycle target. OECD composite leading indicators background note
Ghysels E, Sinko A, Valkanov R (2007) Midas regressions: further results and new directions. Econom Rev 26(1):53–90
Giannone D, Reichlin L, Small D (2008) Nowcasting: the real-time informational content of macroeconomic data. J Monet Econ 55(4):665–676
Giannone D, Agrippino SM, Modugno M, Reichlin L (2014) Nowcasting China. Mimeo
Jungbacker B, Koopman SJ, van der Wel M (2011) Maximum likelihood estimation for dynamic factor models with missing data. J Econ Dyn Control 35(8):1358–1368
Kasri R, Kassim SH (2009) Empirical determinants of saving in the Islamic banks: evidence from Indonesia. JKAU Islamic Econ 22(2):181–201
Kubo A (2009) Monetary targeting and inflation: evidence from Indonesia’s post-crisis experience. Econ Bull 29(3):1805–1813
Liu P, Matheson T, Romeu R (2012) Real-time forecasts of economic activity for Latin American economies. Econ Model 29(4):1090–1098
Luciani M (2014a) Forecasting with approximate dynamic factor models: the role of non-pervasive shocks. Int J Forecast 30(1):20–29
Luciani M (2014b) Large-dimensional dynamic factor models in real-time: a survey. Université libre de Bruxelles, Bruxelles
Luciani M, Ricci L (2014) Nowcasting Norway. Int J Cent Bank 10:215–248
Maćkowiak B (2007) External shocks, US monetary policy and macroeconomic fluctuations in emerging markets. J Monet Econ 54(8):2512–2520
Marcellino M, Schumacher C (2010) Factor MIDAS for nowcasting and forecasting with ragged-edge data: a model comparison for German GDP. Oxf Bull Econ Stat 72(4):518–550
Mariano RS, Murasawa Y (2003) A new coincident index of business cycles based on monthly and quarterly series. J Appl Econom 18(4):427–443
Matheson TD (2010) An analysis of the informational content of New Zealand data releases: the importance of business opinion surveys. Econ Model 27(1):304–314
Matheson TD (2013) New indicators for tracking growth in real time. J Bus Cycle Meas Anal 2013(1):51–71
Modugno M (2014) Now-casting inflation using high frequency data. Int J Forecast 29(4):664–675
Parigi G, Schlitzer G (1995) Quarterly forecasts of the italian business cycle by means of monthly economic indicators. J Forecast 14(2):117–141
Raghavan M, Dungey M (2015) Should ASEAN-5 monetary policy-makers act pre-emptively against stock market bubbles? Appl Econ 47(11):1086–1105
Stock JH, Watson MW (2002a) Forecasting using principal components from a large number of predictors. J Am Stat Assoc 97:1167–1179
Stock JH, Watson MW (2002b) Macroeconomic forecasting using diffusion indexes. J Bus Econ Stat 20(2):147–162
Acknowledgements
We would like to thank Dennis Sorino for excellent research assistance. This paper was written while Matteo Luciani was chargé de recherches F.R.S.-F.N.R.S., and he gratefully acknowledges their financial support. The views expressed in this paper are those of the authors and do not necessarily reflect the views and policies of the Asian Development Bank, of the Banca d’Italia or the Eurosystem, and of the Board of Governors or the Federal Reserve System.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Robustness
In this Appendix we show robustness checks with respect to the composition of the dataset.
The first robustrness check aims to answer the question “what if we had selected variables in a different way?”. As discussed in Sect. 3.1, we constructed the database by selecting variables from the set of indicators that market analysts are monitoring, however, a priori there are other equally valid selection criteria. In particular, in performing this robustness check we considered (a) the option of using all the indicators in Table 1 (labeled Bloomberg selection), and (b) the option of selecting indicators automatically by using a statistical technique (labeled as automatic selection).Footnote 18
In Table 6, we show the RMSE for a DFM parameterized as described in Sect. 4.1 but estimated on the two datasets just described. As we can see, our database clearly delivers the best performance, though in forecasting the performance of the DFM estimated over the indicators followed by Bloomberg is comparable. The performance of the DFM is particularly disappointing when the indicators are selected with LARS. We believe that this is a consequence of having too few observations, and some missing values in the time series of our indicators.
The second robustness check aims to answer the question “what if we do not select indicators but include all variables that we are able to retrieve?”. To this end we use a bridge model as in Eq. (4), where the predictor \(x_t^Q\) is a factor extracted from a panel of monthly variables by using principal component.Footnote 19 The last column of Table 6 reports the RMSE for this model and the results confirm that including all variables does not appear to be a good strategy.
1.2 Technical aspects related to y-o-y transformations
In Sect. 3.2 we mention that to estimate the model we use the EM algorithm proposed by Bańbura and Modugno (2014), which can handle both mixed frequencies and missing data. While we refer the reader to Bańbura and Modugno (2014) and Bańbura et al. (2011, 2013) for detailed information on this algorithm and for a formal treatment, in this Appendix we provide basic information related to the use of year over year growth rates.
The first issue is to understand what is the relationship between monthly y-o-y growth rates, and quarterly y-o-y growth rates. Let t denotes months, and let \(Y^Q_t\) be the log-level of a quarterly variable. The y-o-y growth rate is then equal to \(Y^Q_t-Y^Q_{t-12}\) and we will denote it as \(y_t^Q\). Then, let \(Y^M_t\) be the monthly log-level of Y, and let \(y_t^M=Y^M_t-Y^M_{t-12}\) be the monthly y-o-y growth rate. In order to link \(y_t^Q\) and \(y_t^M\) we follow Mariano and Murasawa (2003), and we make use of the approximation \(Y_t^Q \approx Y_t^M + Y_{t-1}^M+Y_{t-2}^M\) which, after some simple algebra, allows us to write:
The second issue is how to write the factor model when we have a vector of monthly and quarterly y-o-y growth rates. Bańbura and Modugno (2014) solved this by treating quarterly series as monthly series with missing observations, and by assigning the quarterly observation to the 3rd month. Suppose for simplicity that we have only one monthly variable \(y_{1t}^M\), one quarterly variable \(y_{2t}^Q\), and one (monthly) factor \(f_t\), then by using (6) we have:
1.3 Why two factors?
The literature on factor models has shown that it suffices to include a small number of factors for forecasting (e.g., Stock and Watson 2002b; Forni et al. 2003). Furthermore, recent literature on small-medium DFMs (Bańbura et al. 2013; Luciani and Ricci 2014; Giannone et al. 2014; Bragoli et al. 2015) often includes one factor only. Therefore, a natural choice would be to follow the literature and to set \(r=1\).
However, these factor models are estimated for q-o-q growth rates, while we are estimating a model for y-o-y growth rates. So if the model for q-o-q growth rates has one factor, then the corresponding model for y-o-y growth rates has four factors: let \(X_t\) be a non-stationary variable in log-levels, and let \(x_t^y=X_t-X_{t-4}\) be the y-o-y growth rates and \(x_t^q=X_t-X_{t-1}\) be the q-o-q growth rates, so that \(x_t^y=x_t^q+x_{t-1}^q+x_{t-2}^q+x_{t-3}^q\). Then, if the true model is \(x_t^q=\lambda f_t+e_t\), we have \(x_t^y=\lambda (1+L+L^2+L^3)f_t+(1+L+L^2+L^3)e_t\), which can be rewritten as \(x_t^y=\lambda {\mathbf {F}}_t+(1+L+L^2+L^3)e_t\) where \({\mathbf {F}}_t\) is a \(4\times 1\) singular vector.
In light of this, we should set \(r=4\), and, indeed, by looking at the eigenvalues of the covariance matrix of the first subsample (July 2002–December 2007), we can see clearly three/four diverging eigenvalues. However, among these three/four eigenvalues, the first two clearly dominate—the first eigenvalue accounts for 70% of the total variance, the second for 20%, the third for 5%, and the fourth for 3%—thus suggesting that the other two mainly carry noise, which is why we choose to set \(r=2\). Furthermore, as a robustness check we estimated the DFM by setting either \(r=1\) or \(r=4\), and found (results not shown here) that including two factors proved optimal.
There are at least three possible alternatives to the strategy of setting \(r=2\). The first would be to estimate a model with four common factors driven by only one common shock, so that the vector \(\mathbf f_t\) in Eq. (2) is \(4\times 1\), while the vector \(\mathbf u_t\) is \(1\times 1\). A second possibility would be to impose the specific lagged structure described above (see, e.g., Camacho and Perez-Quiros 2010), and a third possibility would be to estimate dynamic factor loadings by using the Dynamic Heterogeneous Factor Models of (D’Agostino et al. 2016).
The reason we prefer to use the model with \(r=2\) to all the alternatives is that we want to keep the model as simple as possible, so that it easy to communicate the prediction obtained with our model to policy makers. Furthermore, all three alternatives complicate the state space representation and in our case where we have few time series observations, and the quality of the data is doubtful, while complicating the Kalman Filter is feasible it is costly in terms of computation accuracy.
Rights and permissions
About this article
Cite this article
Luciani, M., Pundit, M., Ramayandi, A. et al. Nowcasting Indonesia. Empir Econ 55, 597–619 (2018). https://doi.org/10.1007/s00181-017-1288-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-017-1288-4