Skip to main content
SpringerLink
Log in

Testing for a housing bubble at the national and regional level: the case of Israel

  • Published:
Empirical Economics Aims and scope Submit manuscript

Abstract

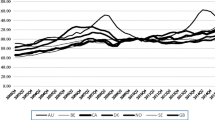
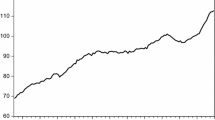
Between 2008 and 2013, home prices in Israel appreciated by roughly 50 % in real terms, with increases in nearly 60 % in some regions. This paper examines whether this phenomenon reflects the presence of a national or regional housing bubble by applying econometric tests for explosive behavior to quality-adjusted national- and regional-level data on the home price to rent ratio, while controlling for various fundamental factors, including interest rates, income and the leverage ratio. Overall, study results indicate that the national- and regional-level data are inconsistent with a housing bubble scenario. Most of the results are robust to a variety of tests and alternate specifications. The framework I provide to study the Israeli case may be applied to study other housing markets facing similar developments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. Diba and Grossman (1988a) were among the first to argue that given a constant discount factor, identifying explosive characteristics in stock prices is equivalent to detecting a bubble.

  2. Regional-level analysis is common in the empirical literature on housing bubbles. For examples see Himmelberg et al. (2005), Case and Shiller (2003), Smith and Smith (2006), Clark and Coggin (2011).

  3. Some other bubble detection strategies, not discussed here, include comparing the annual cost of housing to actual rent (Himmelberg et al. 2005) and a direct derivation of the fundamental price using ex post and projected fundamentals (Smith and Smith 2006).

  4. The “International House Price Database of the Federal Reserve Bank of Dallas” is documented in Mack and Martínez-García (2011).

  5. Case and Shiller (2003), Smith and Smith (2006), Himmelberg et al. (2005) and McCarthy and Peach (2004) are earlier examples of this strand of literature. These papers focus on the US housing market during the pre-subprime crisis.

  6. Housing bubble indices developed in Dovman et al. (2012) are now updated on a regular basis and used for monitoring purposes by the Bank of Israel.

  7. For surveys on other types of bubbles see Brunnermeier (2008), Iraola and Santos (2008) and Scherbina (2013).

  8. Proving the existence of bubbles can also serve as a tool for discriminating between models (Flood and Hodrick 1990).

  9. For a discussion of the approximation’s accuracy, see “Appendix 1”.

  10. For simplicity of exposition, I choose to ignore other variables that might also be included in \( v_t \), such as depreciation, maintenance, property and transaction taxes, the mortgage rate, leverage etc.

  11. The assumption of constant expected risk premiums (or discount factors) is common in the literature on testing for rational bubbles (Gürkaynak 2008). Nonetheless, relaxing this assumption need not change the main conclusions as long as we rule out explosive risk premiums.

  12. Campbell et al. (2009) assume a time-varying risk premium.

  13. Campbell et al. (2009) assume in their model that no bubbles are present.

  14. The explosiveness property of \( b_t \) comes from the fact that \(1+e^{\left( \overline{r-p} \right) }>1\). Hence, when \( b_t\ne 0 \), the log bubble component grows at rate g in expectations, where \( g=e^{\left( \overline{r-p} \right) }>0 \).

  15. Diba and Grossman (1988a) point out another implication of the model, namely, that \( b_t \) can be either zero at all times or positive at all times. To see why, note that a negative value of \( b_t \) today implies that investors expect a future price of zero. Given free disposal, a negative bubble can be ruled out. Yet, a bubble cannot emerge at some point in the future since this necessarily implies that the forecast error of the bubble component is not zero in expectations, thus violating Eq. (9).

  16. See Flood and Hodrick (1990) for an early survey of the literature and Gürkaynak (2008) for an updated survey of econometric tests for bubbles.

  17. Other examples for bubble test methods include the variance bounds test (LeRoy and Porter 1981; Shiller 1981), West’s two-step tests (West 1987) and the intrinsic bubbles test (Froot and Obstfeld 1992).

  18. Phillips et al. (2015b) generalize the PWY procedure such that it is possible to test for multiple bubbles in long time series.

  19. The asymptotic theory of mildly explosive processes is developed in Phillips and Magdalinos (2007).

  20. Large sample properties of the bubble date-stamping procedure are developed in Phillips and Yu (2009).

  21. Hamilton (1986) argues that the interpretation of the results of econometric tests for speculative price bubbles depends on the nature of any nonstationarity in the fundamentals.

  22. Phillips and Magdalinos (2007) define a mildly explosive root using the following data generating process

    $$\begin{aligned} y_t=\delta _n y_{t-1}+\varepsilon _t, \end{aligned}$$

    where \( \delta _n=1+\frac{c}{k_n}\), and where \( (k_n)_{n\in {\mathbb {N}}} \) is a sequence increasing to \( \infty \) such that \( k_n=o(n) \) as \( n\rightarrow \infty \).

  23. We can think of this sample as a standardized version of true sample (i.e., divided by T ).

  24. For a detailed presentation of the date stamping procedure, see Phillips et al. (2011) and Phillips and Yu (2011).

  25. In order to get a consistent test procedure that asymptotically eliminate type I errors there is a need to let \( \beta _{T} \rightarrow 0 \) as \( T\rightarrow 0 \). However in applied work it is convenient to use a constant \( \beta _{T}\) such as 5 % [see Phillips et al. (2015b)].

  26. Phillips and Yu (2011) argue that the date-stamping procedure requires that the duration of the bubble to be non-negligible. In Phillips et al. (2015b) the authors define \( \log (T)/T \) as a minimal lasting time (in fractional terms of the sample) for a bubble period.

  27. The critical values for 90, 95 and 99 % are 6.315, 12.7 and 63.66, correspondingly.

  28. The problem of a biased estimate also holds when the true data are generated with \( \delta \le 1 \).

  29. The latter is included in the CPI, while the former is not.

  30. Expected inflation here is similar to the notion of the ‘TIPS Spread’ in the USA.

  31. Alternatively, I used the yield on 1-year CPI-indexed government bonds (zero coupon bonds). Results are similar (not presented).

  32. For recent surveys on developments in the Israeli housing market see Dovman et al. (2012) and Nagar and Segal (2010).

  33. For further background on the Israeli stabilization program, see Ben Basat (2002) and Liviatan (2003).

  34. For example, testing for a bubble in the stock market during the early 2000s using some general stock price index might miss the presence of a bubble, since the “dot.com” bubble was largely confined to the technology sector. The NASDAQ Composite Index would be more appropriate in this case.

  35. Based on Monte Carlo simulations, Phillips et al. (2015b) argue that the SIC provides satisfactory sizes for the SADF test.

  36. Adding lags is highly relevant when making use of the home prices index since it is constructed as a smoothed index which makes it serially correlated by construction. (The home prices index reported by the CBS is a 2-month moving average.)

  37. In a more recent paper, Phillips et al. (2015a) suggest adding an asymptotically negligible drift to the data generating process of the null as means of increasing the size and power of the test. Adding this drift term does not change my main conclusions. (Not presented, available on demand.)

  38. Though it is possible to apply tests for explosive behavior to any variable, I note that in general, one can rule out explosive behavior in fundamentals (\( \varDelta r_t \) and \( i_t \) in our case) based on theoretical grounds. This stems from the notion that no plausible economic model gives rise to an equilibrium in which fundamental factors exhibit explosive patterns.

  39. Interestingly, the null of no-bubble in the risk-free rate is close to rejection at the 90 % level. However, closer inspection reveals that the probable cause of the rejection is the sudden drop of 200 bp in the Bank of Israel policy rate on January 2002. The SADF test is close to mistakenly identifying this period as bubble.

  40. I estimated the indirect inference estimator using MATLAB, and I have applied the Euclidean distance metric. The m-file is available on demand.

  41. I have also conducted the SADF test on the price to rent ratio (without log), and on the price to income ratio (with and without log) and was unable to reject the null of no-bubble at conventional levels for either of these indicators. (See “Appendix 1”.)

  42. Recall that according to the date-stamping procedure, crossing the threshold from below signals a starting point of a bubble conditioned on the existence of such a bubble, i.e., declaring the starting point of a bubble can only be made in retrospect. However, crossing the threshold from below may be viewed as an early warning sign of a potential bubble.

  43. The zero coupon rate is derived from an estimate of the real yield curve of Israeli government bonds.

  44. \( {V}_t\) is bounded between \( \tilde{V}_t \) (when \( \lambda _t=0 \)) and \( V^m_t \) (when \( \lambda _t=1 \)). Since the natural logarithm function is a monotonic transformation, \( {v}_t\) is also bounded between \( \tilde{v}_t \) and \( i^m_t \) (where \( i^m_t\equiv \log I^m_t \)).

  45. I owe this part to a suggestion from an anonymous referee.

  46. There is another recent study by Nagar and Segal (2010) who estimate a model of the Israeli housing market using cointegration methods and investigates departures from the long-run levels of home prices and rent. I choose not to refer to their analysis in this comparison since despite relating to the possibility of a bubble, the authors do not explicitly model or estimate it. More specifically, in the theoretical section Nagar and Segal (2010) assume that the transversality condition holds, thus they implicitly rule out rational bubbles.

  47. A table with a sensitivity analysis for changing the minimal window size is presented in “Appendix 1”.

  48. In order to make all statistics comparable, I set the first observation of the sample to 1999:M8, namely 1999:M1 plus the maximum number of lags plus one.

  49. The sample issue is irrelevant to the regional analysis since data for mean rent payments only exists since the first quarter of 1998.

  50. Clearly, a rent index based on existing rent does not properly reflect real-time conditions of the housing market but rather the ones at the time they were signed.

  51. The GSADF procedure can be viewed as a mechanism that ’fines’ possible data mining with the SADF procedure. That is, given a specific sample, one can arbitrarily choose any starting point. Experimenting with different samples involves losing degrees of freedom, thus making the SADF critical values invalid. The GSADF procedure takes this into account by computing correct critical values for a procedure that uses the SADF test for every starting point available.

  52. Prior to 1999 the Owner Occupied Dwellings Services Price Index was calculated indirectly using a variation of the home prices index.

  53. In Israel, the kitchen is not counted as a room, and half a room often refers to a small room.

References

  • Arshanapalli B, Nelson W (2008) A cointegration test to verify the housing bubble. Int J Bus Finance Res 2(2):35–43

    Google Scholar 

  • Ben Basat A (2002) The Israeli economy, 1985–1998: from government intervention to market economics. MIT Press, Cambridge

    Google Scholar 

  • Brunnermeier MK (2008) Bubbles. In: Durlauf SN, Blume LE (eds) The new Palgrave dictionary of economics. Palgrave Macmillan, Basingstoke

    Google Scholar 

  • Campbell JY, Shiller RJ (1988) The dividend-price ratio and expectations of future dividends and discount factors. Rev Financ Stud 1(3):195–228

    Article  Google Scholar 

  • Campbell SD, Davis MA, Gallin J, Martin RF (2009) What moves housing markets: a variance decomposition of the rent-price ratio. J Urban Econ 66(2):90–102

    Article  Google Scholar 

  • Case KE, Shiller RJ (2003) Is there a bubble in the housing market? Brook Pap Econ Activity 2003(2):299–362

    Article  Google Scholar 

  • Caspi I (2013) Rtadf: testing for bubbles with EViews

  • Clark SP, Coggin TD (2011) Was there a us house price bubble? An econometric analysis using national and regional panel data. Q Rev Econ Finance 51(2):189–200

    Article  Google Scholar 

  • Diba BT, Grossman HI (1988a) Explosive rational bubbles in stock prices? Am Econ Rev 78(3):520–530

    Google Scholar 

  • Diba BT, Grossman HI (1988b) The theory of rational bubbles in stock prices. Econ J 98(392):746–754

    Article  Google Scholar 

  • Dickey DA, Fuller WA (1979) Distribution of the estimators for autoregressive time series with a unit root. J Am Stat Assoc 74(366a):427–431

    Article  Google Scholar 

  • Dovman P, Ribon S, Yakhin Y (2012) The housing market in Israel 2008–2010: are house prices a ’bubble’? Israel Econ Rev 10(1):1–30

    Google Scholar 

  • Engsted T, Pedersen TQ, Tanggaard C (2012) The log-linear return approximation, bubbles, and predictability. J Financ Quant Anal 47(3):643

    Article  Google Scholar 

  • Engsted T, Hviid SJ, Pedersen TQ (2014) Explosive bubbles in house prices? Evidence from the OECD countries

  • Evans GW (1991) Pitfalls in testing for explosive bubbles in asset prices. Am Econ Rev 81(4):922–930

    Google Scholar 

  • Flood RP, Hodrick RJ (1990) On testing for speculative bubbles. J Econ Perspect 4(2):85–101

    Article  Google Scholar 

  • Froot KA, Obstfeld M (1992) Intrinsic bubbles: the case of stock prices. In: Technical report, National Bureau of Economic Research

  • Galí J (2014) Monetary policy and rational asset price bubbles. Am Econ Rev 104(3):721–752

    Article  Google Scholar 

  • Glaeser EL, Gyourko J, Saiz A (2008) Housing supply and housing bubbles. J Urban Econ 64(2):198–217

    Article  Google Scholar 

  • Gürkaynak R (2008) Econometric tests of asset price bubbles: taking stock. J Econ Surv 22(1):166–186

    Article  Google Scholar 

  • Hamilton JD (1986) On testing for self-fulfilling speculative price bubbles. Int Econ Rev 27(3):545–552

    Article  Google Scholar 

  • Himmelberg C, Mayer C, Sinai T (2005) Assessing high house prices: bubbles, fundamentals and misperceptions. J Econ Perspect 19(4):67–92

    Article  Google Scholar 

  • Homm U, Breitung J (2012) Testing for speculative bubbles in stock markets: a comparison of alternative methods. J Financ Econom 10(1):198–231

    Article  Google Scholar 

  • Iraola MA, Santos MS (2008) Speculative bubbles. In: Durlauf SN, Blume LE (eds) The new Palgrave dictionary of economics. Palgrave Macmillan, Basingstoke

    Google Scholar 

  • LeRoy SF, Porter RD (1981) The present-value relation: tests based on implied variance bounds. Econ J Econ Soc 49(3):555–574

    Google Scholar 

  • Liviatan N (2003) Fiscal dominance and monetary dominance in the Israeli monetary experience, bank of Israel. Discussion paper no. 2003:17

  • Mack A, Martínez-García E (2011) A cross-country quarterly database of real house prices: a methodological note. In: Federal Reserve Bank of Dallas Globalization and Monetary Policy Institute working paper, no. 99

  • McCarthy J, Peach RW (2004) Are home prices the next ’bubble’? FRBNY Econ Policy Rev 10(3):1–17

    Google Scholar 

  • Nagar W, Segal G (2010) What explains the movements in home prices and rent in Israel during 1999–2010? (in Hebrew). In: Bank of Israel Survey, vol 85, pp 7–59

  • Pavlidis E, Yusupova A, Paya I, Peel D, Martinez-Garcia E, Mack A, Grossman V (2013) Monitoring housing markets for episodes of exuberance: an application of the phillips et al. (2012, 2013) GSADF test on the dallas fed international house price database. In: Federal Reserve Bank of Dallas Globalization and Monetary Policy Institute Working Paper (165)

  • Phillips PCB, Magdalinos T (2007) Limit theory for moderate deviations from a unit root. J Econom 136(1):115–130

    Article  Google Scholar 

  • Phillips PCB, Yu J (2009) Limit theory for dating the origination and collapse of mildly explosive periods in time series data, Sim Kee Boon Institute for Financial Economics, Singapore Management University, Unpublished manuscript

  • Phillips PCB, Yu J (2011) Dating the timeline of financial bubbles during the subprime crisis. Quant Econ 2(3):455–491

    Article  Google Scholar 

  • Phillips PCB, Wu Y, Yu J (2011) Explosive behavior in the 1990s NASDAQ: when did exuberance escalate asset values? Int Econ Rev 52(1):201–226

    Article  Google Scholar 

  • Phillips PCB, Shi S, Yu J (2015a) Testing for multiple bubbles: limit theory of dating algorithms. Int Econ Rev (forthcoming)

  • Phillips PCB, Shi S, Yu J (2015b) Testing for multiple bubbles: historical episodes of exuberance and collapse in the S&P 500. Int Econ Rev (forthcoming)

  • Poterba J (1984) Tax subsidies to owner-occupied housing: an asset-market approach. Q J Econ 99(4):729--752. http://qje.oxfordjournals.org/content/99/4/729.short

  • Santos MS, Woodford M (1997) Rational asset pricing bubbles. Econom J Econom Soc 65(1):19–57

    Google Scholar 

  • Scherbina A (2013) Asset price bubbles: a selective survey. In: International monetary fund

  • Shiller RJ (1981) Do stock prices move too much to be justified by subsequent changes in dividends? Am Econ Rev 71(3):421–436

    Google Scholar 

  • Smith MH, Smith G (2006) Bubble, bubble, where’s the housing bubble? Brook Pap Econ Activity 2006(1):1–67

    Article  Google Scholar 

  • Taipalus K (2006) A global house price bubble? Evaluation based on a new rent-price approach Bank of Finland Research Discussion Papers, 29

  • Taylor JB (2007) Housing and monetary policy. In: Working paper 13682, National Bureau of Economic Research. doi:10.3386/w13682, http://www.nber.org/papers/w13682

  • West KD (1987) A specification test for speculative bubbles. Q J Econ 102(3):553–580

    Article  Google Scholar 

  • Wu Y (1995) Are there rational bubbles in foreign exchange markets? Evidence from an alternative test. J Int Money Finance 14(1):27–46

    Article  Google Scholar 

  • Yiu MS, Yu J, Jin L (2013) Detecting bubbles in Hong Kong residential property market. J Asian Econ 28(2013):115–124

    Article  Google Scholar 

Download references

Acknowledgments

I thank Yossi Yakhin, Nathan Sussman, Akiva Offenbacher, Sigal Ribon, Offer Lieberman, Jonathan Benchimol, Dana Orfaig, Nadav Steinberg, Lior Gallo, two anonymous referees, as well as the participants at the Bank of Israel’s Research Department seminar and the DIW Macroeconometric Workshop for helpful comments and discussions.

Author information

Authors and Affiliations

  1. Research Department, Bank of Israel, P.O. Box 780, Jerusalem, Israel

    Itamar Caspi

Authors
  1. Itamar Caspi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Itamar Caspi.

Additional information

Grants or other notes about the article that should go on the front page should be placed here. General acknowledgments should be placed at the end of the article.

Appendices

Appendix 1: Approximation accuracy analysis

The validity of the conclusions rising from the theoretical and empirical section rely heavily on the accuracy of the Campbell–Shiller log-linear approximation procedure. The approximation, stated in price to rent ratio terms, is given as

$$\begin{aligned} p_t-r_t\approx \kappa -v_{t+1}+\varDelta {r_{t+1}} +\rho \left( p_{t+1}-r_{t+1}\right) \end{aligned}$$
(24)

where \(\kappa \) and \(\rho \) are both functions of the linearization point, which in our case is the sample mean log rent to price ratio, denoted as \( \overline{r-p} \). Clearly, as in any other Taylor expansion, large deviations of the true relation from the approximated one will result in little reliance on the interpretation of the model. Thus, the approximation error between the left-hand side and the right-hand side of (24) must be investigated.

Formally, the approximation error can be defined by writing the exact form of (24) as

$$\begin{aligned} p_t-r_t=\kappa -v_{t+1}+\varDelta {r_{t+1}}+\rho \left( p_{t+1} -r_{t+1}\right) +e_t, \end{aligned}$$
(25)

where \( e_t \) is the approximation error. Summarizing several statistical properties of \( e_t \) such as the mean, and the percent deviation from the non-approximated value, along with a comparison of the approximated log ratio with the actual log ratio, can thus shed light on the validity of the approximation and the results that follow. The literature contains several studies aimed at examining the accuracy of the Campbell–Shiller approximation. One recent example, in the context of rational bubbles is Engsted et al. (2012), where the authors apply Monte Carlo methods to investigate the error of the log-linear approximation, both under stationarity and under explosiveness of the log price to dividend ratio. The authors find that under constant returns, the error is quite small, even in the presence of relatively large bubbles.

Despite the general results obtained in Engsted et al. (2012), an examination of my specific case is still necessary because each case may have its own special properties. Before proceeding to an analysis of the approximation error, a few preliminary steps need to be taken. First, in order to calculate the approximated ratio, we need to use log returns \( v_t \). However, when compiling the log price to rent ratio at the national level, I used the home price and rent indices. Though using indices enables us to construct an index of the log price to rent ratio that reliably describes developments in the ratio, it does not enable us to calculate returns. Calculating returns can only be done if we have measures of the levels of home prices and rent. To overcome this obstacle, I proceed with a few simplifying assumptions. First, I turn to the data on the aggregate average price and rent for 3.5–4 room apartments, used in the regional-level analysis, and assume that the average home price and rent observed in the first quarter of 2000 are the true values that hold at the national level in January 2000. Next, I assume that the development (i.e., growth rates) of prices and rent follow what is implied by the home price and rent indices throughout the rest of the period 1999:M1–2013:M7. Using these artificial series enables us to calculate all that is needed for the log-linear approximation, including home prices, rent and returns.

Fig. 9
figure 9

Actual, approximated and the error of approximation of the log price to rent ratio at the national level (1999:M1–2013:M7). Notes: The solid black line presents the sample mean of the approximation error (dashed, green). Positive values of the error term mean that the log ratio is underestimated by the approximated log ratio. (Color figure online)

Full size image

Deriving the approximated ratio depends on the constants of linearization \( \kappa \) and \( \rho \), which are functions of the linearization point—the mean log rent to price ratio \(\overline{r-p}\). In the specific sample I use, these parameters equal

$$\begin{aligned}&\overline{r-p}=-3.046\\&\rho =1\big /\left[ 1+e^{\left( \overline{r-p} \right) }\right] =0.956\\&\kappa =-\log (\rho )-(1-\rho )\log \left( \frac{1}{\rho }-1\right) =0.185. \end{aligned}$$

Using these parameters along with prices, rent and returns series, I calculate the approximated price to rent ratio defined by Eq. (24). The results of this exercise are presented in Fig. 9. The figure shows the actual log price to rent ratio, the approximated ratio and the approximation error (in percent). The log ratio (solid, blue) and its corresponding approximation (dotted, red) are quite indistinguishable during the sample period. Moreover, the sample correlation between the two series is close to 1, and the correlograms of both series (not presented) are nearly identical. Hence, both series exhibit very similar dynamics. Since the test for explosiveness relies on these dynamics for inference, this finding is important. A closer inspection of the differences between the log ratio and the approximation is made using the percent error of approximation (dashed, green). As the figure shows, the maximal value of percent error is valued at around 0.02 %, while its sample mean stands below 0.005 %. These results indicate a negligible error of approximation, thus further validating the use I made of the Campbell–Shiller linearization method.

The same analysis is performed on the regional-level data. In this case, since prices and rent are already given in their nominal values, the calculation is straightforward. For example, for the Tel Aviv region, the parameters of the approximation are given by

$$\begin{aligned}&\overline{r-p}=-3.333\\&\rho =1\big /\left[ 1+e^{\left( \overline{r-p} \right) }\right] =0.966\\&\kappa =-\log (\rho )-(1-\rho )\log \left( \frac{1}{\rho }-1\right) =0.150. \end{aligned}$$

The picture that emerges from the approximation for the Tel Aviv region ratio, presented in Fig. 10, is very similar to the one presented for the national-level region data. The approximation percent error (dashed, green) is maxed at 0.05 %, while its sample mean stands at around 0.01 %. Here also I can reasonably conclude that the error is negligible and that the approximated ratio retains the dynamic properties of the actual ratio. Similar findings hold for all other eight regions analyzed in Sect. 5.5 (not presented).

Fig. 10
figure 10

Actual, approximated and the error of approximation of the log price to rent ratio for the Tel Aviv area (1998:Q1–2013:Q2). Notes: The solid black line presents the sample mean of the approximation error (dashed, green). Positive values of the error term mean that the log ratio is underestimated by the approximated log ratio. (Color figure online)

Full size image

Appendix 2: Further sensitivity analysis

See Tables 8, 9, 10.

Table 8 Sensitivity of the SADF test for the local price to rent ratios to the choice of minimal window size
Full size table
Table 9 Results of the ADF and SADF tests
Full size table
Table 10 Sensitivity of the ADF and SADF test statistics to specifications of lag lengths
Full size table

Appendix 3: Data

The following section further elaborates on the data used in the empirical analysis.

1.1 National level

  • Home prices Home prices are proxied by the hedonic (quality adjusted) Prices of Dwellings Index that is published on a monthly basis by the Israeli Central Bureau of Statistics. The index is based on the survey of prices of owner occupied homes. The index, in its current form, exists since January 1994.

  • Rent Rent prices are proxied by the Owner Occupied Dwellings Services Price Index, included in the CPI and published by the Israeli Central Bureau of Statistics on a monthly basis. Since January 1999 the index is based on new renewed rent contracts.Footnote 52

  • Inflation The change in the Consumer Price Index, published on a monthly basis by the Israeli CBS. The index is calculated as changes in the price of a fixed basket of consumer goods.

  • Short-term risk-free real interest rate This interest rate is calculated as the difference between the Bank of Israel’s official benchmark rate on monetary loans and expected inflation derived from the spread between CPI-indexed and unindexed government bonds. Both the monetary rate and expected inflation are obtained from the Bank of Israel.

1.2 Regional level

  • Home prices and rent average prices of owner occupied dwellings (purchase price) and rent for 3.5–4 room apartments, in nominal terms (current shekels), classified for nine geographic regions (see Table 11).Footnote 53 The data are published on a quarterly basis by the Israeli CBS. The aggregate average level of home prices and rent are calculated as a weighted sum of the different regions, where the weights for each region are determined by the proportion of the region’s value of homes out of the total (Table 11).

Table 11 Geographic areas included in the average quarterly dwelling prices and rent
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Caspi, I. Testing for a housing bubble at the national and regional level: the case of Israel. Empir Econ 51, 483–516 (2016). https://doi.org/10.1007/s00181-015-1007-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00181-015-1007-y

Keywords

JEL Classification

Search

Navigation