Latent variables and propensity score matching: a simulation study with application to data from the Programme for International Student Assessment in Poland

Abstract

This paper examines how including latent variables can benefit propensity score matching. Latent variables can be estimated from the observed manifest variables and used in matching. This paper demonstrates the benefits of such an approach by comparing it with a method where the manifest variables are directly used in matching. Estimating the propensity score on the manifest variables introduces a measurement error that can be limited with estimating the propensity score on the estimated latent variable. We use Monte Carlo simulations to test how the proposed approach behaves under distinct circumstances found in practice, and then apply it to real data. Using the estimated latent variable in the propensity score matching limits the measurement error bias of the treatment effects’ estimates and increases their precision. The benefits are larger for small samples and with better information about the latent variable available.

1 Introduction

This paper demonstrates how incorporating latent variable modeling into propensity score matching can limit measurement error in the propensity score and, in effect, increase precision of the estimates of treatment effects. This is not the first paper to introduce latent variable modeling into propensity score matching. The seminal work of James Heckman and others was helpful when developing the framework we present (see Abbring and Heckman 2007, Sect. 2.7 for discussion and further references). However, our approach differs in one important aspect. Heckman and others modeled residuals from outcome equations across quasi-experimental groups assuming that there are latent traits behind them. We assume, instead, that values of the latent variable are associated with values of the manifest variables that are observable and can be used to estimate the latent variable. We present the benefits of using the estimated latent variable in the propensity score matching, showing that it can notably limit the measurement error bias and lower the variance of treatment estimators. We demonstrate this with Monte Carlo simulations and real data examples.

The paper is organized as follows. Section 2 shows how latent variables modeling can be introduced into propensity score matching using the measurement error model of the relation between the latent trait and the manifest variables. Section 3 provides evidence from a Monte Carlo study on how the proposed approach increases efficiency of the matching estimators of the treatment effects. Section 4 empirically applies this approach to data. Section 5 concludes.

2 Modeling latent variables in propensity score matching

2.1 Modeling latent variables

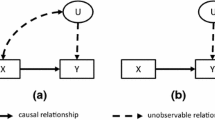
Latent variables can reflect either hypothetical constructs or existing phenomena which cannot be directly measured but are often reflected in observed variables that are proxies of measured phenomena. These observable manifestations are correlated with latent variables but also contain an independent component, or, in other words, manifest variables contain a signal about the latent variable and the random component (often called the “measurement error”) that is uncorrelated with this variable.

A relation between the latent variable and the manifest variables can be presented using the one-factor model or the congeneric measurement error model (Joreskog 1971; Skrondal and Rabe-Hesketh 2004). We assume that the observed $j$-th variable is measured with error and on a scale specific to that variable. Values for a set of such manifest variables are observed for each $i$-th individual. This is modeled through the following equation:

$$\begin{aligned} M_{ij} =\delta _j +\lambda _j \eta _i +E_{ij}, \end{aligned}$$

(1)

where $\eta$ is the latent variable or common factor and $M_{ij}$ are observed realizations of manifest variables. We assume independent error terms $E_{ij}$ and $N(0,\sigma _j )$. This model can also be interpreted as a measurement error model where true scores $\eta$ are reflected in each $j$-th variable with random error on the scale defined by $\delta _j$ and $\lambda _j$. In factor analysis $\lambda _j$ are called factor loadings and $\delta _j$ are called intercepts. To identify this model some restrictions are needed, for example, that $\lambda _1 =1$ or that the Var($\eta )=1$. This model assumes that there is only one latent variable behind the manifest variables; however, dealing with several latent variables is quite straightforward within this framework.

If the model we present above is true, the latent variable can be estimated from the manifest variables using the factor analysis approach. Specification of a latent variable factor model has to be driven by theoretical considerations and carefully tested empirically. Usually, models assuming different numbers of common factors are estimated and compared on how they fit the data. A problem arises when such models all seem to be plausible, in which case theoretical considerations can play an important role. In this paper, we abstract from these issues, assuming that a latent variable model properly reflects the latent structure behind the data. Moreover, we assume there is only one latent variable behind each set of manifest variables. Our approach can be easily extended to more complex situations, for example, involving more latent variables and allowing for correlations with other variables in a model. However, simple models considered in this paper illustrate the main benefits of incorporating latent variables in matching. Our general findings should also hold under more complex circumstances.

We are not aware of any other study, other than the efforts of James Heckman and his colleagues described in the introduction, which attempts to model latent traits in the propensity score matching. The usefulness of latent variable modeling in economic research can be reconsidered when taking into account modern developments in statistics. Recent work demonstrates that current approaches are much more reliable, theory driven and more adverse to ad hoc interpretations (see Skrondal and Rabe-Hesketh 2004, for an extensive discussion and a unifying framework; for discussion and examples of latent variable modeling in econometrics see Kmenta 1991; Wansbeek and Meijer 2000; Aigner et al. 1984). In addition to this, there are circumstances, such as evaluating labor market training or school programs, where latent traits like attitudes play an important role in the choices of participants and non-participants. In labor market studies, it was shown that job satisfaction, even if measured through a single simple question, significantly changes quasi-experimental estimates (White and Killeen 2002). Large economic literature discusses how personality traits affect labor market outcomes. For example, Girtz (2012) shows how self-esteem and locus of control, two personality traits modeled as latent variables, affect wages of adults.

In evaluation studies, attitudes toward work or other personal traits are used to control for selection and factors driving the outcomes. For example, in evaluation studies in Germany researchers very often use data from the German Socio-Economic Panel (GSOEP) which contain information on attitudes or personality traits which can be used by researchers in propensity score matching (for examples see Lechner 2000; Barg and Beblo 2009; Heineck and Anger 2010). In educational studies, a number of works demonstrate the importance of student attitudes or latent family characteristics (OECD 2009; Jakubowski and Pokropek 2009). Behavioral economics often looks into the ways personality traits or attitudes affect people’s behavior, for example, in experiments analyzing risk aversion or economic preferences (see Fairlie and Holleran 2012; Grabner et al. 2009; Ovchinnikova et al. 2009; Ben-Ner et al. 2008).

Survey responses are often used to reflect latent traits instead of modeling these traits directly. In studies of anti-poverty programs direct responses about household possessions are typically used (see Jalan and Ravallion 2003), although they could be modeled as latent traits reflecting household wealth and socio-economic position (we use a similar example in this paper).¹ In a well-known paper by Agodini and Dynarski (2004) on propensity score matching, student responses to questions about time use and attitudes toward learning were added to the list of matching covariates instead of being used to model the latent characteristics behind them. In evaluation studies mentioned above, researchers prefer to use single questions rather than scales summarizing responses to questionnaire items which are reflecting some latent traits. For example, Lechner (2000) uses single responses to chosen questions about people’s optimism, although they are part of a set of questions which could be used to build a scale reflecting overall optimism of a person.

We propose an approach where the latent variable is estimated from the manifest variables and directly used in the propensity score matching. Our simulation results and empirical examples demonstrate that modeling the latent variable might decrease bias and increase precision of propensity score matching estimates of treatment effects.

2.2 Propensity score matching with latent variables

Consider a situation where we want to compare outcomes between two groups in which the latent variable is unbalanced. One of these quasi-experimental groups is affected by a treatment, while the other remains unaffected and serves as a baseline reference group. We call subjects in the first group the “treated” and subjects in the latter group the “controls.” We assume that the latent variable affects outcomes in both groups, and that the imbalance in the latent variable creates bias when comparing group outcomes.

For observational studies, a matching approach was proposed to balance covariates among groups of treated and controls (Rubin 1973). Propensity score matching is currently the most popular version of this approach and is based on balancing covariates through matching conducted on a propensity score (Rosenbaum and Rubin 1983). The propensity score is usually estimated by logit or probit and reflects the probability of being selected to the group of treated. Matching based on the propensity score instead of matching on all covariates solves the so-called curse of dimensionality that makes normal matching inadvisable or even impossible in smaller samples. After balancing covariates by using matching, simple outcome comparisons provide unbiased estimates of treatment effects, assuming that all differences between the two groups are observed and taken into account when estimating the propensity score (see Heckman et al. 1998, for detailed assumptions).

Consider that not only the imbalance of the observed covariates, but also the imbalance of the latent variable, poses a potential barrier to estimating the treatment effects. In this case, a researcher would like to include the latent variable in matching; however, it is not observed. Instead, matching has to be conducted on the observed variables, including the manifest variables that are only proxies of the latent trait and, by assumption, reflect it with a random error. Estimating the propensity score on the manifest variables thus introduces additional noise into matching. Intuitively, the greater the error, more often are subjects mismatched, which affects the quality of matching estimators. The smaller the error is or the stronger a signal from the latent variable reflected in the manifest variables is, more negligible is the fact that matching is not conducted directly on the latent variable.

This paper discusses how estimating the latent variable, and conducting matching on this estimate rather than on a set of manifest variables, can increase the quality of matching in some situations, particularly in smaller samples or when a relatively weak signal about the latent variable is available in the manifest variables. If the latent variable model is correct, the estimated latent variable should reflect the latent variable with more precision than observable proxies. This will benefit matching, as less error is introduced.

More formally, consider first a hypothetical situation where the latent variable is directly observed and can be used for matching. In this case, a propensity score is given by:

$$\begin{aligned} p(\mathbf{X},\eta )\equiv \Pr \{D=1|\mathbf{X},\eta \}=E\{D|\mathbf{X},\eta \}, \end{aligned}$$

(2)

where $D=\{0,1\}$ is the indicator of treatment exposure, $\eta$ is the latent variable that has to be balanced together with other covariates contained in the vector X. Rosenbaum and Rubin (1983) show that if the treatment assignment is random conditionally on multidimensional vector $(\mathbf{X}, \eta )$, it is also random when conditioning on the $p(\mathbf{X}, \eta )$. In this case, after successful matching which balances the latent variable and other covariates among quasi-experimental groups, the average treatment effect on the treated (ATT) can be estimated through comparisons of expected outcomes in a group of treated and matched controls (Becker and Ichino 2002):

$$\begin{aligned} \hbox {ATT}=E\left\{ {E\left\{ {Y_1 |D=1,p(\mathbf{X},\eta )} \right\} -E\left\{ {Y_0 |D=0,p(\mathbf{X},\eta )} \right\} |D=1} \right\} , \end{aligned}$$

(3)

where the outer expectation is over the distribution of $p(\mathbf{X},\eta )|D=1$, while $Y_{1}$ and $Y_{0}$ are potential outcomes in case of treatment and no treatment, respectively.

Assumptions needed to identify treatment effects using propensity score matching require that the propensity score is defined for all treated (common support) and that a researcher observes a set of covariates such that after controlling for these covariates the potential outcomes are independent of the treatment. Formally, for the average treatment effect on the treated, these two assumptions can be written as:

$$\begin{aligned}&Y_0 \,\bot \, D|\left( {\mathbf{X},\eta } \right) \end{aligned}$$

(4)

$$\begin{aligned}&p(\mathbf{X},\eta )<1. \end{aligned}$$

(5)

If these two assumptions are satisfied, we call the treatment assignment strongly ignorable and the formula (3) provides an unbiased ATT estimate.

Battistin and Chesher (2009), extending the seminal work by Cochran and Rubin (1973), show that even if strong ignorability holds when covariates are measured without error, it does not mean that this assumption will hold if some covariates are measured with error. Cochran and Rubin analyze a relatively simple situation where outcome equations are linear in X and matching is conducted on only one covariate. Battistin and Chesher analyze a more general setting, but in both cases it is shown that measurement error in covariates can have substantial bias on the ATT estimate, with the sign of bias hard to predict under more complex circumstances. In general, both papers show that the bias increases with larger measurement error variance and with stronger effect of the error-prone covariate on the outcome. Battistin and Chesher propose a method to approximate this bias, which can be applied for cases with relatively small measurement error variance and typical distribution of X.

According to both papers, the measurement error bias in matching is difficult to assess analytically. Even the sign of the bias might be impossible to evaluate under more complex circumstances or with large measurement error variance. In our application, we focus on a specific case where observed manifest variables are error-prone reflections of the latent variable. In this case, measurement error can be limited by attempts to estimate the latent trait and use it directly in matching. We provide insights based on Monte Carlo simulations and present empirical application, as general analytical solutions are too difficult to derive in this case. If we estimate the propensity score using information on the latent variable reflected in a set of manifest variables, the propensity score is given by:

$$\begin{aligned} p(\mathbf{X},\mathbf{M})\equiv \Pr \{D=1\,|\,\mathbf{X},\mathbf{M}\}=E\{D|\mathbf{X},\mathbf{M}\}. \end{aligned}$$

(6)

As $p$(X,M) is an error-prone reflection of $p(\mathbf{X}{,\eta })$, matching does not necessarily have the balancing property that is needed to obtain unbiased ATT. In other words, matching on $p(\mathbf{X},\mathbf{M})$ will not necessarily eliminate all the differences between the treated and controls in terms of the latent variable $\eta$.

Instead of matching on the manifest variables, we propose estimating the latent variable from the manifest variables in the first step. We assume that the latent structure and the model to estimate it follow the one described by the set of equations (1), in which one latent factor is reflected in the observed manifest variables. Here, the latent variable can be estimated by the factor analysis model, and the latent variable estimate $\hat{{\eta }}$ can be used to obtain the propensity score:

$$\begin{aligned} p(\mathbf{X},\hat{{\eta }})\equiv \Pr \{D=1\,|\,\mathbf{X},\hat{{\eta }}\}=E\{D|\mathbf{X},\hat{{\eta }}\}. \end{aligned}$$

(7)

As $\hat{{\eta }}$ is a less noisy measure of the latent variable $\eta$ than the set of manifest variables M, it follows that matching on $p(\mathbf{X},\hat{{\eta }})$ should give results closer to matching on $P(\mathbf{X},\eta )$ than the matching on $p(\mathbf{X},\mathbf{M})$.

Obtaining exact formulas for the bias in the ATT or for the variance of the matching estimators is difficult or even impossible for matching methods (see Abadie and Imbens 2009, for attempts to derive analytical formulas). As noted, Battistin and Chesher (2009) and Cochran and Rubin (1973) show that measurement error in matching covariates will cause bias in the ATT matching estimate. We are not able to provide analytical formulas for the biased matching estimator variance. Instead, we use simulation to provide evidence that the measurement error increases it. We then propose a method which might decrease matching estimator variance by limiting measurement error in matching covariates.

We described above three propensity scores that can be used for balancing the latent variable and covariates through propensity score matching: a hypothetical propensity score $P(\mathbf{X},\eta )$ estimated on an unobservable latent variable, a propensity score $p(\mathbf{X},\mathbf{M})$ estimated from the observed manifest variables, and finally a propensity score $p(\mathbf{X},\hat{{\eta }})$ obtained through an estimate of the latent variable from the manifest variables. Through a simulation study in which matching is conducted under various circumstances commonly found in the practice of empirical research, we try to establish how bias in the matching estimate of treatment effects differs when using these three different propensity scores. In the simulation, we compare the results obtained with the hypothetical propensity score estimated using the unobserved latent variable with results obtained with error-prone propensity scores used in practice. In Sect. 3, we also apply the strategy suggested by the simulation results to data from an educational study.

3 Simulation study

In the simulation study, we analyze two outcome equations and two different selection to treatment mechanisms. The data were simulated for four variables with ${X}_{1}, \eta$ and ${X}_{2}$ having a normal distribution with mean zero and covariance matrix given below by vector M and matrix V:

$$\begin{aligned} \left( {\begin{array}{l} {X}_1 \\ \eta \\ {X}_2 \\ \end{array}} \right) =N(\mathbf{M},\mathbf{V}),\quad \hbox { where }\mathbf{M}=\left( {\begin{array}{l} 0 \\ 0 \\ 0 \\ \end{array}} \right) ,\quad \mathbf{V}=\left( {{\begin{array}{ccc} 2 &{}\quad 1&{}\quad {-1} \\ 1&{}\quad 1&{} \quad {0.5} \\ {-1}&{}\quad {-0.5}&{}\quad 1 \\ \end{array} }} \right) \end{aligned}$$

(8)

and ${X}_{3}$ distributed N(0,1) and uncorrelated with other variables.

Four selection equations were studied. In each case, different error term was simulated. In the first model selection to treatment is random:

$$\begin{aligned} \hbox {Model A: }\quad {D}_\mathrm{A} =1\left( {{U}>0.\hbox {5}} \right) \quad {U }\sim N\left( {0,1} \right) . \end{aligned}$$

In the following three models treatment selection depends on a set of covariates which include the latent variable. The distribution of covariates among the treated and control groups depends on the distribution of the error term. Three different models specified below assume different distributions of the error term U providing different matching scenarios:

$$\begin{aligned}&\hbox {Model B:}\quad {D}_\mathrm{B} =1(\eta +{ X}_\mathrm{1} -{ X}_\mathrm{2} -{X}_{3} +{ U }> 1 ), \quad {U}=\sqrt{30}{Z},\quad { Z}\sim {N}\left( {0,{1}} \right) \\&\hbox {Model C:}\quad {D}_\mathrm{C} =1(\eta +{ X}_\mathrm{1} -{ X}_{2} -{X}_{3} +{ U }>1 ),\quad {U}=\sqrt{5}{Z},\quad {Z}\sim {N}\left( {0,1} \right) \\&\hbox {Model D:}\quad {D}_\mathrm{D} ={ 1}(\eta +{ X}_{1} -{ X}_{2} -{X}_{3} +{ U }>3 ),\quad {U}=\hbox {3}Z,\quad { Z}\sim \chi ^{2}\left( 1 \right) . \end{aligned}$$

These selection equations give different distributions of covariates among the treated and controls and different proportion of the treated in a sample. This is reflected in the varying distribution of the propensity score among models depicted on Fig. 1 for an exemplary sample.

Fig. 1

Propensity score distributions for different models

In Model A, all the treated and controls are on the same support. In Model B around 1 % of the treated might not be on the same support, as well as around 5 % of the treated in Model C and around 1/3 in Model D. Thus, Models C and D are much more demanding matching scenarios with many treated without good matches. The proportion of treated also differs between models, with around 30 % assigned to treatment in Model A and around 40 % assigned to treatment in Models B, C and D.

We study three outcome equations. In all equations the outcome differs among the treated $(D=1)$ and controls $(D=0)$ by a known constant equal 3. Equation 1 represents a simple situation where all covariates are linearly related to the outcome, while in Eq. 2 the relationship between the outcome and covariates, including the latent variable, is more complex and non-linear.

$$\begin{aligned}&\hbox {Outcome 1:}\quad y=-10+\eta +3D+X_1 -X_2 -X_3 +\varepsilon \\&\hbox {Outcome 2:} \quad y=-10+\eta ^{3}+3D+X_1 ^{2}-2X_2 -X_3 ^{3}+\varepsilon . \end{aligned}$$

The third equation adds an interaction between the latent variable and treatment to the Eq. 1, so the effect of the latent variable on the outcome is doubled for the treated:

$$\begin{aligned} \hbox {Outcome 3:} \quad y=-10+\eta +3D+\eta D+X_1 -X_2 -X_3 +\varepsilon . \end{aligned}$$

In all cases $\varepsilon$ is independently and normally distributed N(0,1). In all simulations, 10,000 random draws were studied.

Although values of the latent variable are observed in our simulation, we assume that a researcher observes only manifest variables that are generated by a set of equations:

$$\begin{aligned} M_j =\eta +kZ_j , \end{aligned}$$

(9)

where $M_{j}$ denotes the $j$-th manifest variable constructed from the latent variable $\eta$ by adding a random noise $Z_{j}$ specific to each manifest variable. Correlation between the latent variable and the manifest variables depends on a signal-to-noise ratio captured in the parameter $k$ that is studied in the simulation. For example, with $k=2$ the signal-to-noise ratio equals 1:2, which means that correlation between the latent variable and a manifest variable is close to 0.45. We studied also the results for value of k equal to 1 where correlation between the latent variable and a manifest variable is close to 0.7. This gives a typical range found in empirical research. In practice, when correlation of manifest variables (commonly called “items”) is weaker than 0.4, that is usually taken as a sign that this variable has no relation to the latent construct. In such a case, the variable is usually dropped and other manifest variables are used.

We also varied the number of manifest variables from which a researcher can estimate the latent variable. Usually, the higher the number of manifest variables is, the better an estimate of the latent variable. We simulated data with 5 and 10 manifest variables, a range that covers typical situations. The quality of the estimated latent variable depends also on the sample size. We studied sample sizes with 500 and 5,000 observations, which provides evidence on the impact of measurement error in small samples and samples typically found in surveys.

For each simulated sample propensity score matching was conducted three times. First, matching was conducted on the latent variable that is normally unobserved, which provides a proper baseline for further comparisons. Second, matching was conducted on a set of manifest variables. Finally, matching was conducted on the estimated latent variable using information reflected in the manifest variables. We estimated the latent variable through a basic one-dimensional factor model using a standard procedure in Stata software (see Stata documentation on the -factor- command).² This model reflects the process in which manifest variables were generated, assuming that the model used for the latent variable estimation was correctly specified. Obviously, that is not always the case in empirical research. However, we do not study how mistakes in estimation of the latent variable can affect the quality of matching, but simply assume this step was conducted properly.

Main results are presented in Tables 1 and 2. They demonstrate how using the manifest variables instead of the latent one lowers the quality of matching estimates and how matching based on the estimated latent variable can help. The first part of the table presents results from 1-to-1 nearest neighbor propensity score matching without any additional restrictions, while the second part present results with the common support restriction imposed and caliper matching (with caliper 0.05).³ The latter are more suited for comparisons in models with strong selection and unequal distribution of covariates among treated and controls. In fact, for models C and D only results with these additional restrictions should be considered. For these models, due to strong selection to treatment, distribution of covariates do not fully overlap and unrestricted matching estimates can be seriously biased.

Generally, results presented in Tables 1 and 2 suggest that measurement error can introduce serious bias in the estimate of treatment effect. Mean estimates of the simulated ATT effects are close to the true value of 3.0 mainly for matching on the latent variable and for large samples. Mean ATT estimates are seriously biased when matching is not conducted on the latent variable, especially in smaller samples and for models with strong selection. Under more demanding circumstances even the estimates from matching on the latent variable are biased, although this bias is always smaller than the bias for matching on the manifest variables or matching on the estimated latent variable. Thus, measurement error bias is present under almost all circumstances and adds to other sources of bias in matching.

Importantly, in smaller samples estimates obtained from matching on the estimated latent variable are marginally less biased, have slightly smaller variance and have smaller root mean squared error. Matching on the estimated latent variable outperforms matching on the set of manifest variables in smaller samples, while in large samples these differences partly disappear. It is worth noting that even unbiased estimates of the ATT, which can be obtained for simpler models from both matching on the manifest variables and on the estimated latent variable, have slightly larger variance for matching on the manifest variables. The benefits are thus twofold: first, matching on the estimated latent variables increases precision of the estimate. Second, it gives marginally less biased estimate of the ATT comparing to matching on observed manifest variables. Therefore, it is possible to say that matching on the estimated latent variable decreases bias and increases precision of the ATT estimates under all models. On the other hand, however, these gains are modest in the smaller sample and very small in the large sample. Both methods still introduce bias in the estimation, while in larger samples the difference in performance of both methods is rather small.

Tables 1 and 2 results confirm findings by Battistin and Chesher (2009) and Cochran and Rubin (1973) that ATT estimates from matching on error-prone covariates can be seriously biased. Additional evidence here is that measurement error in observed manifestations of the latent variable not only introduces bias but also decreases precision of the matching estimator. These results suggest that estimating latent variable and using it directly in matching helps to mitigate the impact of measurement error to some extent, providing less biased and more precise results, especially in smaller samples. Under the most demanding circumstances in the model with strong selection and no overlapping support, matching on the manifest variables without common support restriction and caliper might even result in smaller standard errors although with larger bias and overall larger RMSE. In fact, in both methods the measurement error bias remains large, particularly for models with strong selection and non-linear relationship between outcome and latent variable.

These results are due to smaller measurement error in the propensity score obtained using the estimated latent variable. Measurement errors in binary choice models like logit or probit, which are usually applied to estimate propensity score, can bias estimates in a complex way (see Carroll et al. 1995). The exact bias is hard to assess without additional information on measurement errors. The propensity score obtained from the probit or logit model with error-prone covariates will therefore usually be biased. As already mentioned, bias in the propensity score affects its balancing property which in turn biases the final treatment effect estimates from matching.

Table 3 below demonstrates results from the simulation study in which the bias in the propensity score and balancing tests were analyzed for Models B, C and D. In these models, selection to treatment is not random and results in imbalance in the distribution of covariates among treated and controls. Our balancing test is based on comparisons of the standardized percentage bias, that is the percentage difference of the sample means in the treated and controls group before and after matching as a percentage of the square root of the average of the sample variances in the treated and control groups (see Rosenbaum and Rubin 1985). Table 3 reports the absolute standardized bias for the unobserved latent variable before and after matching, but also the mean absolute standardized bias for all matching covariates.⁴

Table 3 Standardized percentage bias before and after matching

Average correlation across 10,000 random draws between the propensity score obtained using the latent variable and the propensity score obtained using the estimated latent variable was around 0.99, while correlation between the propensity score obtained using the latent variable and the propensity score obtained using the manifest variables was slightly lower around 0.97–0.98. As Table 3 shows, this results in slightly better balancing property of matching on the estimated latent variable rather than on the manifest variables (after imposing common support for the most demanding model D). It is also clear from the results in Table 3 that while matching on the estimated latent variable is superior to matching on the manifest variables, it also introduces bias due to measurement error, although somewhat smaller in the magnitude.

Below we provide additional simulation results for different numbers of manifest variables and for different signal-to-noise ratios. For brevity, below we provide results for Model C and outcome Eq. 1 only. Results for other models and outcome equations provide similar conclusions and are presented in the Appendix (Tables 9, 10, 11). Table 4 provides results for different signal-to-noise ratios defined by the value of parameter $k$ in Eq. (9), and compares results obtained with 5 manifest variables to those obtained with 10 manifest variables. As previously, estimates are given for sample size of 500 and 5,000.⁵

Results in Table 4 show that precision always increases with the number of manifest variables available, but the benefits from having more manifest variables are augmented by using the estimated latent variable instead of matching directly on the manifest variables. For example, with $k=1$ and sample size of 500, root mean squared error is 0.490 for matching on five manifest variables and 0.479 when matching on the latent variable estimated from those five variables. With 10 manifest variables available, root mean squared error goes down to 0.475 for matching on the manifest variables and to 0.445 for matching on the estimated latent variables. Thus, at least for smaller samples, the benefits of matching on the estimated latent variable increase with the number of manifest variables available. For larger samples these differences are relatively small.

Table 4 Simulation results for larger number of manifest variables and different signal-to-noise ratios (Model C and outcome Eq. 1)

Modest benefits of observing less noisy manifestations for all the models, but here again matching on the estimated latent variable proves superior to matching on the manifest variables mainly for smaller samples. For large samples, the benefits of matching on the estimated latent variable are again marginal for both more and less noisy manifestations.

Results of propensity score matching differ according to the specific matching method applied. The results presented above are based on the 1-to-1 nearest neighbor method, while results for other matching methods could not only provide different point estimates but also vary in terms of estimators’ variance (see Abadie and Imbens 2009). In the appendix, we present additional results calculated for other popular propensity score matching methods: the nearest neighbor 1-to-5 matching (where 5 best matches are used instead of 1 to construct the counterfactual outcome), local linear matching (where counterfactual outcome is constructed using local linear regression with tricube kernel function and 0.8 bandwidth) and kernel matching (with epanechnikov kernel and 0.6 bandwidth). Appendix Tables 12 and 13 present comparisons of simulation results for the four different methods and sample size 500, five manifest variables and signal-to-noise ratio 1:1.

For the least demanding model A the nearest neighbor 1-to-1 method performs well, while for more difficult models with strong selection and complex relationship between covariates and outcome kernel matching outperforms other methods. This reflects the well-known choice between bias and efficiency in matching with 1-to-1 method: providing results with the smallest bias if the pool of good matches is easily available and kernel or local linear regression matching increasing efficiency in case when interpolation from several possible matches is necessary (Caliendo and Kopeinig 2008).

Matching based on the estimated latent variable outperforms matching based on the manifest variables in all cases except the simplest model A and gives similar results for Model B. In these models, matching on manifest variables with the kernel method provides the most precise results, as in this case all matches provide good basis for interpolation. In cases where there is strong selection between treated and controls, matching on the estimated latent variable usually performs better. These findings suggest that, while matching methods in fact provide different results, the conclusion that in smaller samples under most circumstances matching on the estimated latent variable is better than matching on the manifest variables holds despite the choice of the matching method.

4 Empirical application to human capital research

The simulation results suggest that estimating the latent variable from the manifest variables instead of using these variables directly in matching can limit the measurement error bias and increase the precision of the treatment estimates, especially with moderate sample sizes and several manifest variables available in a dataset. The suggested procedure has three steps. In the first step, the researcher has to estimate the latent variable from the observed manifest variables. This step is crucial and has to be based on a theoretically and empirically sound theory that relates observed manifest variables to the latent variable. In the remaining steps, the usual propensity score matching approach is applied. The propensity score is estimated on a set of matching covariates that includes the estimated latent variable. Matching is conducted on this propensity score, and the average treatment effect on the treated is calculated.

In this section, we apply this approach to see how selecting students into different school programs or tracks affects their achievement. This is the topic extensively analyzed in economics of education literature (see Hanushek and Woessmann 2006; Brunello and Checchi 2007; Duflo et al. 2011; Pekkarinen 2008; and for reviews Meier and Schütz 2007; Woessmann 2009). In this research, outcomes of students or adults who attended different school tracks are compared. For example, students of general-comprehensive schools are compared in outcomes with students of vocational schools. Obviously, students who go to comprehensive and vocational schools differ in many aspects, mainly in their academic achievement, as students usually are selected to different schools based on their school grades or exams. Thus, observing students’ pre-selection school outcomes is crucial when assessing the impact of tracking. We use a unique dataset collected in Poland which used internationally developed tests to measure achievement of upper-secondary school students but was also linked to these students’ outcomes in comprehensive lower secondary schools. In addition, the survey collected extensive information on socio-economic background of families which can be used to additionally control for selection of students into different school types.

In our application, we use a subset of data collected in the Programme for International Student Assessment (PISA). The PISA study is conducted by the OECD every three years and measures the achievement of 15-year-olds across all OECD countries and other countries that join the project (see OECD 2007, 2009, for a detailed description of the PISA 2006 study). We use data for Poland from the PISA 2006 national study that extended the sample to cover 16- and 17-year-olds (10th and 11th grade in the Polish school system). Another, already mentioned, unique feature of the Polish dataset is supplementary information on student scores in national exams, which extends significantly the possibilities of evaluating school policies, as prior scores can be used to control for student ability or for intake levels of skills and knowledge.

We apply the approach proposed in this paper to evaluate differences in the magnitude of student progress across two types of upper secondary education: general–vocational and vocational. We use data for 16- and 17-year-olds only, as 15-year-olds are in comprehensive lower secondary schools. In 2006, there were four types of upper secondary educational programs: general, technical, general–vocational and vocational. The general–vocational schools were introduced by the reform of 2000, to replace some vocational schools with more comprehensive education but existing evidence suggests that they might not be effective in helping students develop more comprehensive skills (Jakubowski et al. 2010). The following empirical example seeks to establish whether, in fact, these schools equip students with a set of comprehensive skills not taught in purely vocational schools. In the PISA sample, we have slightly more than 1,000 observations of 16- and 17-year-olds attending these two types of upper secondary schools.

The PISA tests are suitable instruments to capture the extent to which different schools teach comprehensive skills, as they aim at testing general student literacy in mathematics, reading and science, using a general framework that defines internationally comparable measures of literacy. PISA tries to capture skills and knowledge needed in adult life, rather than those simply reflecting schools’ curricula. This makes comparisons between schools more objective, and internationally developed instruments assure that they are not biased toward curriculum used in one type of Polish school.

To compare the impact of distinct types of schools on student outcomes it is necessary to control for student selection into these schools. This selection is probably based on previous student skills and knowledge, but also on other important student and family characteristics. The unique feature of the Polish PISA dataset is that students’ prior scores on national exams are linked to data obtained through internationally comparable instruments. These are scores from the obligatory national exam conducted at the end of lower secondary school (at age 15) that contains two parts, one for mathematics and science, and one for humanities. We combine both scores in one measure reflecting the level of student intake knowledge and skills across disciplines.

We also use detailed data on student and family characteristics. In PISA, student background information is available in two types of indicators. In the first type, variables directly reflect student responses about their observable and easy-to-define characteristics. Among those, we use dummies denoting student gender and school grade level, parents’ highest level of education measured on the ISCED scale and parents’ highest occupation status measured on the ISEI scale (the International Socio-Economic Index of occupational status, see Ganzeboom et al. 1992). The second type of variables summarizes responses to several questions (so-called items) that reflect a common latent characteristic (OECD 2009, pp. 303–349). Here, we use student responses about more than 20 types of home possessions, including consumption, educational, and cultural goods. The original PISA dataset contains four indices that summarize information on household goods: homepos for all home possessions, wealth for consumption goods (e.g., TV, DVD player, number of cars), cultpos for cultural possessions (e.g., poetry books), and hedres for educational resources (e.g., study desk). We re-estimated these indices to include additional available information. Therefore, we took one item from the wealth index (“having a microscope”) and added it to educational resources under hedres. We also estimated the cultpos index including a question about the number of books at home that was originally not considered.

The latent constructs were estimated using the principal component analysis models based on polychoric and polyserial correlations matrix as student responses were measured on ordinal scale (see Kolenikov and Angeles 2009). The estimated indices have relatively high reliabilities in a range from 0.6 to 0.8 that are higher for Poland than most OECD countries (OECD 2009, p. 317). Correlations between items used in the same index were from 0.3 to 0.5, which is the range modeled in our simulation study. Correlations between cultpos, wealth, and hedres indices were relatively low, between 0.37 and 0.56. Responses within each index were also more strongly correlated with each other than with responses from other indices. This suggests that they might represent different constructs (see Jakubowski and Pokropek 2009, for additional information on these indices).

We conducted the propensity score matching three times, to see how results are affected by including the estimated latent variable instead of a set of manifest variables. First, we included all the manifest variables in the list of matching covariates, or, more precisely, we included all dummy variables denoting household items. Second, we included three indices estimated from the manifest variables and reflecting three latent variables: household wealth, household cultural possessions and household educational resources. Finally, we estimated only one latent variable using all manifest variables and reflecting all possible home possessions. We expected that the first approach would differ from the second in terms of bias and the precision of the estimates of the average treatment effect. More precisely, we expected that the second approach would provide estimates that are different and have smaller standard errors, in line with the theory and simulation results presented above. Furthermore, we expected that the third approach, based on only one latent variable instead of three, could be less efficient, as restricting a latent dimension to one limits the amount of relevant information provided in matching if there are, in fact, three distinct latent variables behind the values of the manifest variables. This example demonstrates typical problems that arise in empirical research: first, whether to estimate the latent trait instead of using manifest variables directly in matching; and second, how many latent variables should be estimated.

Tables 5 and 6 presents results for this empirical exercise with additional results presented in the appendix. Table 5 shows imbalance between students who go to vocational (control group) and general–vocational (treated group) schools in terms of the estimated indices and other matching covariates: gender, grade, HISEI (the highest occupational status of parents as measured by the International Socio-Economic Index of occupational status, see Ganzeboom et al. 1992; OECD 2009, p. 305), and lower secondary national exam scores. The table also shows how propensity score matching helps to balance these variables. Summary statistics for all matching covariates and propensity score equations (probit regression) are presented in the appendix. Table 5 compares variable means between these two groups of students and percentage bias before and after matching. It also shows reduction in absolute percentage bias and t-test results for the nearest neighbor 1-to-1 propensity score matching with replacement, for the same 1-to-1 matching but with the common support restriction and caliper (0.05) and for kernel matching (with epanechnikov kernel and 0.6 bandwidth).

Table 5 Balance of matching covariates

The results show important differences between students who went to general–vocational and vocational schools in terms of matching covariates. Propensity score matching is, however, able to reduce these differences to construct comparable groups of control and treated students. The mean absolute percentage bias across all covariates goes down from 49.8 to 5.7 % with 1-to-1 matching. Imposing common support for 1-to-1 matching reduces mean absolute percentage bias to 4.8 %, while with kernel matching mean absolute percentage is further reduced to 4.5 %

Table 6 shows outcome differences before and after matching. The results are presented for all three methods: the nearest neighbor 1-to-1 matching with and without common support and caliper and for kernel matching. For matching on the manifest variables only one set of results is presented per matching method, while for matching on the estimated latent variables (one overall index of home possessions or three separate indices) two sets of results are presented. The first set of results presented in columns (2), (4) and (6) was obtained by estimating the latent variable before matching, so the same index was used for all bootstrapped samples. These results reflect common practice of not re-estimating indices available in the original dataset and using the same index across all resampled samples. Clearly, this might result in biased variance estimates as calculations omit the first step of estimating latent variable. In columns (3), (5), and (7) results are presented with the latent variables re-estimated in each bootstrap sample. These results include all sources of variance in our three-step estimation method.

First, note that the differences in outcomes go down after matching. This was expected, as differences in outcomes between different types of schools are driven mainly by differences in student characteristics. However, the outcome differences remain quite large and in favor of general–vocational schools, even after adjusting for intake scores, gender, parents’ education and occupation, and family resources. The average treatment effects vary across the sets of results, with the biggest gap being found in reading. Results with common support imposed and caliper matching (last column) are similar to those obtained with unrestricted 1-to-1 matching. Differences are visible only for matching on manifest variables, which is due to larger amount of observations excluded from the analysis in this case. Common support restriction was not satisfied for only 6 and 11 observations when matching on the one estimated index and matching on the three estimated indices, respectively, but for matching on the manifest variables 25 treated observations had to be excluded. Kernel matching generally provides results similar to 1-to-1 matching without restrictions, although with marginally smaller standard errors.

Table 6 Empirical example: achievement difference between general–vocational and vocational schools

The results mainly demonstrate the benefits of using the estimated latent variables in matching that are related to the precision of estimates. While the average treatment effects are reasonably similar across matching methods, the standard errors are 20–40 % higher for matching conducted on the manifest variables. This is also true for standard errors that include error for the estimation of the latent variable as they differ only slightly from the errors calculated without this step. This suggests that in this case adding errors related to the estimation of the latent variable was not crucial for the results.

The results are quite similar for matching on the three estimated latent variables and for matching on the one estimated variable. Standard errors are slightly higher when matching on only one instead of three latent variables, which suggests that our data have three-dimensional latent structure. However, standard errors are also much lower in this case, compared to matching directly on all manifest variables.

This example confirms our main findings from the simulation study: benefits are gained from matching on estimated latent variables rather than on a set of manifest variables, at least with moderate sample sizes and a well-developed latent variables framework. Matching on three estimated latent variables lowered standard errors of the treatment effects. Matching on one latent variable gave similar results, which were still better than those obtained with matching directly on manifest variables.

5 Summary

This paper demonstrates how modeling and including the latent variable in the propensity score matching might limit the bias and increase precision of the treatment estimates in comparison to a more standard approach when matching is conducted directly on the set of manifest variables, even if they reflect the same latent trait. Including the estimated latent variable can limit the measurement error bias in the propensity score matching estimates introduced by a noisy signal contained in the manifest variables. We present simulation studies demonstrating how our approach helps limit the bias in average treatment effect estimates, and the range of efficiency gains provided by incorporating the latent variable in matching. Finally, we apply these to real educational data, showing the importance of our findings on an empirical example.

We find that in various models studied estimating the latent variable and using this estimate for propensity score matching decreases the measurement error bias in the average treatment effects and lowers the variance of the average treatment estimators in smaller samples. While in some cases the bias and the variance are smaller even for large samples, in general, matching on the estimated latent variable provides similar results or only modest gains compared to matching on manifest variables with large sample sizes. Thus, while in larger samples the choice might be less important, in smaller samples we suggest following our three-step strategy: estimate the latent variable using observed manifest variables; use this estimate to estimate the propensity score; and match on this propensity score to estimate the average treatment effects.

Appendix

See Tables 7, 8, 9, 10, 11, 12, 13 and 14.

Table 7 Summary statistics of matching covariates for the empirical application

Table 8 Probit regression for the propensity score

Table 9 Additional simulation results for models A, B and D and outcome Eq. 1

Table 10 Simulation results for four models and outcome Eq. 2

Table 11 Simulation results for four models and outcome Eq. 3

Table 12 Simulation results for four models, outcome Eq. 1 and different propensity score matching methods: nearest neighbor 1-to-1 matching (1-to-1), nearest neighbor 1-to-5 matching (1-to-5), local linear matching (llr) and kernel matching (kernel)

Table 13 Simulation results for four models, outcome Eq. 2 and different propensity score matching methods: nearest neighbor 1-to-1 matching (1-to-1), nearest neighbor 1-to-5 matching (1-to-5), local linear matching (llr) and kernel matching (kernel)

Table 14 Simulation results for four models, outcome Eq. 3 and different propensity score matching methods: nearest neighbor 1-to-1 matching (1-to-1), nearest neighbor 1-to-5 matching (1-to-5), local linear matching (llr) and kernel matching (kernel)