1 Introduction

In a cluster analysis context, a finite mixture of Gaussians is frequently used to classify a sample of observations (see McLachlan and Peel 2000). However, the application of this model in practice presents two major problems. First, a large number of parameters needs to be estimated when many variables are involved. Second, it is difficult to identify the roles that the different variables play in the classification, i.e. to understand if and how the variables discriminate among groups. A simple solution to those problems could be the use of the so called “tandem analysis”, where a preliminary principal component analysis (PCA) to reduce the dimension of the data (in terms of the number of variables) is followed by a cluster analysis performed on the main component scores. Although this procedure is very common in practice, it has been criticized by several authors (e.g., Chang 1983; De Soete and Carroll 1994). The reason is that principal components account for the maximal amount of the total variance of the data but do not necessarily contain information about the classification, even when many components are retained. To avoid this, PCA could be used after the estimation of the cluster structure, to analyse the between covariance matrix. In this case, the principal components are identified to explain the maximum between variability instead of the total one. Nevertheless, even in this case some problems arise. First, it is not known how the number of components to be retained has to be chosen. Second, the discriminating power of any component depends on its both between and within variability. The first should be as high as possible while the latter should be low. The components identified by a PCA of the between covariance matrix do not necessarily satisfy such property because they guarantee only a high level of between variability. Third, the reduction step should help the estimation of the clustering structure by removing noise dimensions from the data and reducing the number of parameters. This is not possible if PCA is done as final step.

In the literature, there is a large consensus in identifying as a solution to the aforementioned problems to perform clustering and dimensionality reduction simultaneously. Indeed, several authors have already proposed such methods (see for example: De Soete and Carroll 1994; Vichi and Kiers 2001) but only in an optimization approach. Others formulated some models following a model based approach (see for example: Kumar and Andreou 1998; Bouveyron and Brunet 2012b; Ranalli and Rocci 2017). Quite frequently information has a complex structure like three-way data, where the same variables are observed on the same units over different occasions. Some typical examples are represented by longitudinal data on multiple response variables or spatial multivariate data. Other examples arise when some objects are rated on multiple attributes by multiple experts or from experiments in which individuals provide multiple ratings for multiple objects (Vermunt 2007). Furthermore, we find some other examples among symbolic data provided that the complex information can be structured as multiple values for each variable (Billard and Diday 2003). In this context, clustering is performed in several ways. We find proposals where three-way data is transformed into two-way data by using some dimension reduction techniques to one of the ways, such as PCA. This allows us to apply conventional clustering techniques. Other proposals take into account the "real" three-way data structure in a least-square approach (see for example: Gordon and Vichi 1998; Vichi 1999; Rocci and Vichi 2005). On the other hand, we find model-based clustering for three-way data. Basford and McLachlan (1985) adapted the Gaussian mixture model to the three-way data, followed by the extensions proposed by Hunt and Basford (1999) for dealing with mixed observed variables. Vermunt (2007) used a hierarchical approach, similar to the one proposed for the multilevel latent class model (Vermunt 2003), to allow units to belong to different classes in different occasions. However, all of them are based on the conditional independence assumption. In other words, the aforementioned proposals do not explicitly estimate the correlations between occasions (they are implicitly taken to be zero). Moreover, correlations between variables are assumed to be constant across the third mode. It is interesting to interpret three-way data as matrix variate rather than multivariate. From this point of view, the Gaussian mixture model has been generalized to the mixtures of matrix Normal distributions within a frequentist (Viroli 2011a) and a Bayesian (Viroli 2011b) framework. Both contributions take into account the full information on the two ways, not separately but simultaneously. At this aim, the model is based on the matrix-variate normal distribution (Nel 1977; Dutilleul 1999). Based on this framework, more recently, further extensions have been proposed by: Melnykov and Zhu (2018) to model skewed three-way data for unsupervised and semi-supervised classification; Sarkar et al. (2020) to reduce the number the number of parameters introducing more parsimonious matrix-variate normal distributions based on the spectral decomposition of covariance matrices; Tomarchio et al. (2020) to handle data with atypical observations introducing two matrix-variate distributions, both elliptical heavy-tailed generalization of the matrix-variate normal distribution; Tomarchio et al. (2021) to extend to the three-way data the cluster-weighted models, i.e. finite mixtures of regressions with random covariates; Ferraccioli and Menardi (2023) where the nonparametric formulation of density-based clustering, also known as modal clustering, is extended to the framework of matrix-variate data.

However, even in the three-way case the problems (large number of parameters when many variables are involved and understanding if and how the variables discriminate among groups) arise and, tentatively, solved by a tandem analysis where dimensionality reduction and clustering are sequentially combined. The components can be extracted by using a three-mode principal component analysis (Kroonenberg and De Leeuw 1980) while the clustering can be done adopting a suitable mixture model (Basford and McLachlan 1985). However, all the issues described above for the two-way data remain unsolved even for the three-way case unless the two steps are performed simultaneously. Several authors have already proposed such methods in the three-way case (see for example: Rocci and Vichi 2005; Vichi et al. 2007; Tortora et al. 2016) but only in an optimization approach.

In this paper a model is proposed in the context of three-way data by using a finite mixture as a form to describe data suspected to consist of relatively distinct groups. In particular, it is assumed that the observed data are sampled from a finite mixture of Gaussians, where each component corresponds to an underlying group. The group-conditional mean vectors and the common covariance matrix are reparametrized according to parsimonious models able to highlight the discriminating power of both variables and occasions while taking into account the three-way structure of the data.

The plan of the paper is the following: in the second section, we present the Simultaneous Clustering and Reduction (SCR) model for two-way data; in Sect. 3, it is extended to the three-way case. The EM algorithm used to estimate the model parameters is presented in Sect. 4. Sections 5 and 6 deal with model interpretation and comparison with related models, respectively. In Sect. 7, the results of a simulation study conducted to investigate the behaviour of the proposed methodology are reported. In Sect. 8, an application to real data is illustrated. Some remarks are pointed out in the last section.

2 The SCR model for two-way data

Let x = [x1, x2, …, xJ]′ be a random vector of J variables. We assume that x is sampled from a population which consists of G groups, in proportions p1, p2, …, pG. The density of x in the gth group is multivariate normal with mean μg and covariance \({\varvec{\varSigma}}_V\). As a result, the unconditional, or marginal, density of x is the homoscedastic finite mixture

$${\text{f}}({\bf{x}}) = \sum_{{\text{g}} = 1}^{\text{G}} {{\text{p}}_{\text{g}} {{\varphi }}({\bf{x}};{\varvec{\mu }}_{\text{g}} ,{\varvec{\Sigma }})}$$
(1)

The Simultaneous Clustering and Reduction (SCR) model leaves unstructured the covariance matrix as \({\varvec{\varSigma}} = {\varvec{\varSigma}}_V\) and performs a dimensionality reduction on the mean vectors of the groups by a Principal Component Analysis (PCA). In particular, the mean μgj of the jth variable in the gth group is related to a reduced set of Q (< J) latent variables following the linear model below

$${\upmu }_{{\rm {gj}}} = {\upmu }_{\text{j}} + \mathop \sum \limits_{{\rm {q}} = 1}^{\rm {Q}} {{\rm {b}}_{{\text{jq}}} {\upeta }_{{\text{gq}}}} ,$$
(2)

where ηgq represents the score of the qth latent variable in the gth group, bjq is the loading of variable j on the qth latent variable. In, obvious, compact matrix notation, Eq. (2) is

$$ {\varvec{\mu}}_{\text{g}} = {\varvec{\mu}} + {B\varvec{\eta }}_{\text{g}} ,$$
(3)

where for identification purposes, \(\sum^p_g {\varvec{\eta}}_g = 0.\) Therefore, the mean vector of each group, which lies into a J dimensional space, is reproduced into a subspace of (reduced) dimension Q according to the linear model (3). It has to be noted that, as in factor analysis, parameters involved in (3) are not uniquely determined. The loading matrix can be rotated without affecting the model fit, provided that the latent vectors ηg are counter-rotated by the inverse transformation. This can be easily shown by noting that, for any non-singular matrix D, we can write

$$ {B\varvec{\eta }}_{\text{g}} = {\bf{BD}}^{ - 1} {\varvec{D\eta }}_{\text{g}} = {\varvec{BD}}^{ - 1} {\tilde{\varvec{\eta }}}_{\text{g}} = {\varvec{\tilde{B}\tilde{\eta }}}_{\text{g}}$$
(4)

In words, only the subspace spanned by the columns of B is identified. To make easier the computation and improve the interpretation, we exploit such rotational freedom by requiring that

$${\bf{B}}^{\prime} {\varvec{\varSigma}}_{\text{V}}^{ - 1} {\bf{B}} = {\bf{I}}_{\text{Q}} .$$
(5)

It is important to note that (5) does not identify a unique solution. This implies that, as in the ordinary factor analysis model, the loading matrix B can be furtherly rotated to enhance model interpretation.

3 The extension of the SCR model to three-way data

In this section, we extend the previous framework to the case of three-way data. Let x = [x11, x21, …, xJ1, …, x1K, x2K, …, xJK]′ be a random vector of J variables observed at K different occasions. We assume that x follows the Gaussian homoscedastic finite mixture model, specified in (1).

To reduce the number of parameters, the within covariance matrix is modelled as a direct product model (Browne 1984)

$${\varvec{\varSigma}} = {\varvec{\varSigma}}_{\text{O}} \otimes {\varvec{\varSigma}}_{\text{V}} ,$$
(6)

Where \(\otimes\) is the Kronecker product of matrices and \({\varvec{\varSigma}}_O\) and \({\varvec{\varSigma}}_V\) represent the covariance matrices of occasions and variables, respectively. The dimensionality reduction is performed on the mean vectors of the groups following a Tucker2 (Tucker 1966) model. In particular, the mean μgjk of the jth variable observed at the kth occasion in the gth group is related to a reduced set of Q (< J) latent variables measured in R (< K) latent occasions according to the following bilinear model

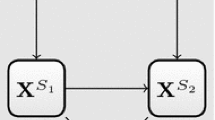
$${\upmu }_{gjk} = {\upmu }_{jk} + \mathop \sum \limits_{q = 1}^Q \mathop \sum \limits_{r = 1}^R {\text{b}}_{jq} {\text{c}}_{k{\text{r}}} {\upeta }_{gqr} ,$$
(7)

where ηqrg represents the score of the qth latent variable at the rth latent occasion in the gth group, bjq is the loading of variable j on the qth latent variable while ckr is the loading of occasion k at the rth latent occasion. The model can be graphically represented as in Fig. 1.

Fig. 1
figure 1

Graphical representation of Tucker 2 model

Full size image

In matrix notation, Eq. (7) is

$${\varvec{\mu}}_g = {\varvec{\mu}} + ({\bf{C}} \otimes {\bf{B}}){\varvec{\eta}}_g ,$$
(8)

where, for identification purposes, \(\sum^{\text{p}}_g {\varvec{\eta}}_g = 0\). The bilinear model (7, 8) allows us to project the within-group means, lying into a JK dimensional space, onto a subspace of (reduced) dimension QR. The Tucker2 model can be seen as a PCA where the matrix of loadings is constrained to be the Kronecker product of two loading matrices, one for the variables and the other for the occasions, to take into account the three-way structure of the data.

For the same reasons explained at the end of Sect. 2, only the subspaces spanned by the columns of B and C are identified. To make easier the computation and improve the interpretation, we require that

$${\bf{B}}^{\prime} {\varvec{\varSigma}}_{\text{V}}^{ - 1} {\bf{B}} = {\bf{I}}_{\text{Q}} ,\;{\bf{C}}^{\prime} {\varvec{\varSigma}}_O^{ - 1} {\bf{C}} = {\bf{I}}_R .$$
(9)

Even in this case, constraints (9) do not identify a unique solution and matrices B and C can be rotated to enhance model interpretation.

4 The EM algorithm

In this section, we describe the EM algorithm needed to carry out the maximum likelihood parameter estimates. We refer to the general three-way data case, but it can be easily adjusted to K = 1, i.e. the two-way data case. Algorithms presented here have been implemented in MatLab. Codes can be found online at https://github.com/moniar412/SCR3waydata.

On the basis of a sample of N independent and identically distributed observations, the log-likelihood of the mixture model in (1), reparameterized according to (6) and (8), is

$${\text{L}}(\varvec{\theta} ) = \mathop \sum \limits_{n = 1}^N \log \left( {\mathop \sum \limits_{g = 1}^G p_g {{\varphi }}_{ng} } \right)$$
(10)

where \( \varphi_{ng} = \varphi ({x}_n ;{\varvec{\mu}}_g ,{\varvec{\varSigma}})\) and ϑ is the set containing all model parameters. It can be shown (Hathaway 1986) that to maximize (10) is equivalent to maximize

$$\ell (\varvec{\theta} ) = \sum \limits_{ng} {\text{u}}_{ng} \log \left( {p_g {{\varphi }}_{ng} } \right) - \sum \limits_{ng} {\text{u}}_{ng} \log \left( {{\text{u}}_{ng} } \right)$$
(11)

subject to the constraints ung ≥ 0 and \(\sum\nolimits_g {u_{ng} = 1}\) (n = 1, 2,…, N; g = 1, 2, …, G). An algorithm to maximize (11) can be formulated as a grouped version of the coordinate ascent method where the function is iteratively maximized with respect to a group of parameters conditionally upon the others. The basic steps of the algorithm can be described as follows.

First of all, it has to be noted that the ML estimate of μ in (8) is the sample mean \({\overline{\user2{x}}}.\). For sake of brevity, in the following we assume the data as centred and set μ = 0.

a) Update ung. Function (11) attains a maximum when \({\text{u}}_{ng} = {\text{p}}_g {{\varphi }}_{ng} \left( {\sum\nolimits_h {p_h {{\varphi }}_{nh} } } \right)^{ - 1}\), which is the posterior probability that observation n belongs to group g given the data xn.

b) Update pg. As in the ordinary EM algorithm, the update is \({\text{p}}_g = N^{ - 1} \sum\nolimits_n {u_{ng} }\).

c) Update \({\varvec{\varSigma}}_O\). Let Xn and Mg be J × K matrices such that vec(Xn) = xn and vec(Mg) = μg, function (11) can be rewritten as

$$\begin{aligned} \ell \left( \varvec{\theta} \right) & = \sum \limits_{ng} u_{ng} \left\{ { - \frac{1}{2}{\text{log}}\left| {{\varvec{\varSigma}}_O \otimes {\varvec{\varSigma}}_V } \right| - \frac{1}{2}\left( {{\bf{x}}_n - {\varvec{\mu}}_g } \right)^T \left( {{\varvec{\varSigma}}_O^{ - 1} \otimes {\varvec{\varSigma}}_V^{ - 1} } \right)\left( {{\bf{x}}_n - {\varvec{\mu}}_g } \right)} \right\} + c \\ & = \sum \limits_{ng} u_{ng} \left\{ { - \frac{J}{2}{\text{log}}\left| {{\varvec{\varSigma}}_O } \right| - \frac{K}{2}{\text{log}}\left| {{\varvec{\varSigma}}_V } \right| - \frac{1}{2}\left( {{\bf{x}}_n - {\varvec{\mu}}_g } \right)^T \left( {{\varvec{\varSigma}}_V^{ - 1} \left( {{\bf{X}}_n - {\bf{M}}_g } \right){\varvec{\varSigma}}_O^{ - 1} } \right)} \right\} + c \\ & = \sum \limits_{ng} u_{ng} \left\{ { - \frac{J}{2}{\text{log}}\left| {{\varvec{\varSigma}}_O } \right| - \frac{K}{2}{\text{log}}\left| {{\varvec{\varSigma}}_V } \right| - \frac{1}{2}tr\left[ {\left( {{\bf{X}}_n - {\bf{M}}_g } \right)^T {\varvec{\varSigma}}_V^{ - 1} \left( {{\bf{X}}_n - {\bf{M}}_g } \right){\varvec{\varSigma}}_O^{ - 1} } \right]} \right\} + c \\ \end{aligned}$$
(12)

where c is a constant term and \(\left| {{\varvec{\varSigma}}_O \otimes {\varvec{\varSigma}}_V } \right| = \left| {{\varvec{\varSigma}}_O } \right|^J \left| {{\varvec{\varSigma}}_V } \right|^K\). As a result, the maximizer of (12) is the minimizer of

$$\frac{NJ}{2}\log \left( {\left| {{\varvec{\varSigma}}_O } \right|} \right) + \frac{NJ}{2}{\text{tr}}\left( {{\bf{S}}_O {\varvec{\varSigma}}_O^{ - 1} } \right),$$
(13)

where \({\bf{S}}_O = \left( {NJ} \right)^{ - 1} \sum\nolimits_{ng} {u_{ng} ({\bf{X}}_n - {\bf{M}}_g )^{\prime}{\varvec{\varSigma}}_V^{ - 1} ({\bf{X}}_n - {\bf{M}}_g )}\). This minimizer is \({\varvec{\varSigma}}_O\) = SO.

d) Update \({\varvec{\varSigma}}_V\). As in previous step, it can be shown that the update is \({\varvec{\varSigma}}_V = {\bf{S}}_V\), where \({\bf{S}}_V = \left( {NK} \right)^{ - 1} \sum\nolimits_{ng} {{\text{u}}_{ng} ({\bf{X}}_n - {\bf{M}}_g ){\varvec{\varSigma}}_O^{ - 1} ({\bf{X}}_n - {\bf{M}}_g )^{\prime}.}\)

e) Update ηg and B. By exploiting the equality \({\varvec{\mu}}_g = ({\bf{C}} \otimes {\bf{B}}){\varvec{\eta}}_g ,\) function (11) can be rewritten as

$$\begin{aligned} \ell \left( \varvec{\theta} \right) & = \sum \limits_{ng} u_{ng} \left\{ { - \frac{1}{2}\left[ {{\bf{x}}_n - \left( {{\bf{C}} \otimes {\bf{B}}} \right){\varvec{\eta}}_g } \right]^T \left( {{\varvec{\varSigma}}_O^{ - 1} \otimes {\varvec{\varSigma}}_V^{ - 1} } \right)\left[ {{\bf{x}}_n - \left( {{\bf{C}} \otimes {\bf{B}}} \right){\varvec{\eta}}_g } \right]} \right\} + c^{\prime} \\ & = \sum \limits_{ng} u_{ng} \left\{ { - \frac{1}{2}\left[ {{\bf{x}}_n^T \left( {{\varvec{\varSigma}}_O^{ - 1} \otimes {\varvec{\varSigma}}_V^{ - 1} } \right){\bf{x}}_n - 2{\varvec{\eta}}_g^T \left( {{\bf{C}} \otimes {\bf{B}}} \right)^T \left( {{\varvec{\varSigma}}_O^{ - 1} \otimes {\varvec{\varSigma}}_V^{ - 1} } \right){\bf{x}}_n + {\varvec{\eta}}_g^T {\varvec{\eta}}_g } \right]} \right\} + c^{\prime} \\ & = \sum \limits_g \left[ {u_{ + g} {\varvec{\eta}}_g^T \left( {{\bf{C}} \otimes {\bf{B}}} \right)^T \left( {{\varvec{\varSigma}}_O^{ - 1} \otimes {\varvec{\varSigma}}_V^{ - 1} } \right)\overline{\user2{\bf{x}}}_g - \frac{1}{2}u_{ + g} {\varvec{\eta}}_g^T {\varvec{\eta}}_g } \right] + c^{\prime \prime} \\ \end{aligned}$$
(14)

where \(c^{\prime}\) and \(c^{\prime \prime}\) are constant terms, \({\text{u}}_{ + g} = \sum_n {u_{ng} }\) and \({\overline{\user2{\bf{x}}}}_g = {\text{u}}_{ + g}^{ - 1} \sum\nolimits_n {u_{ng} {\bf{x}}_n }\). It follows that the updating of ηg is simply a weighted regression problem

$${\varvec{\eta}}_g = ({\bf{C}} \otimes {\bf{B}})^{\prime}\left( {{\varvec{\varSigma}}_O^{ - 1} \otimes {\varvec{\varSigma}}_V^{ - 1} } \right){\overline{2{\bf{x}}}}_g = \left( {{\varvec{\varSigma}}_O^{ - \frac{1}{2}} {\bf{C}} \otimes {\varvec{\varSigma}}_V^{ - \frac{1}{2}} {\bf{B}}} \right)^{\prime} \left( {{\varvec{\varSigma}}_O^{ - \frac{1}{2}} \otimes {\varvec{\varSigma}}_V^{ - \frac{1}{2}} } \right){\overline{2{\bf{x}}}}_g = ({{{\mathop{\bf C}\limits^{\frown}} }} \otimes {{{\mathop{\bf B}\limits^{\frown}} }})^{\prime}{\overline{2{\bf{z}}}}_g$$
(15)

where \({\overline{2{\bf{z}}}}_g = ({\varvec{\varSigma}}_O^{ - \frac{1}{2}} \otimes {\varvec{\varSigma}}_V^{ - \frac{1}{2}} ){\overline{\user2{\bf{x}}}}_g\) is the so-called within-standardized centroid and \({{{\mathop{ \bf C}\limits^{\frown}} }} = {\varvec{\varSigma}}_O^{ - \frac{1}{2}} {\bf{C}}\) and \({{{\mathop{ \bf B}\limits^{\frown}} }} = {\varvec{\varSigma}}_V^{ - \frac{1}{2}} {\bf{B}}\) are the so-called within-standardized loadings matrices. The update of B can be obtained by noting that (11) can be equivalently maximized with respect to \({{{\mathop{ \bf B}\limits^{\frown}} }}\) under the constraint \({{{\mathop{ \bf B}\limits^{\frown}}^{\prime}{\mathop{B}\limits^{\frown}} }} = {{ {\bf B}^{\prime}\Sigma }}_V^{ - 1} {\bf{B}} = {\bf{I}}.\) Substituting (15) into (14) and indicating with \({\overline{\user2{\bf{Z}}}}_g\) the J × K matrix such that \(vec({\overline{\user2{\bf{Z}}}}_g ) = {\overline{\user2{\bf{z}}}}_g\), we obtain

$$\begin{aligned} 2\ell \left( \varvec{\theta} \right) - 2c^{\prime \prime} & = \sum \limits_g \left[ {2u_{ + g} {\overline{\user2{\bf{z}}}}_g^T \left( {{{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}} \otimes {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}} \right){\overline{\user2{z}}}_g - u_{ + g} {\overline{\user2{\bf{z}}}}_g^T \left( {{{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}} \otimes {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}} \right){\overline{\user2{\bf{z}}}}_g } \right] \\ & = \sum \limits_g u_{ + g} {\overline{\user2{\bf{z}}}}_g^T \left( {{{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}} \otimes {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}} \right){\overline{\user2{\bf{z}}}}_g \\ & = \sum \limits_g u_{ + g } tr \left[ {{\overline{\user2{\bf{Z}}}}_g^T {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}{\overline{\user2{\bf{Z}}}}_g {{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}}} \right] \\ & = {\text{tr}}\left[ {{{{\mathop{ \bf B}\limits^{\frown}}^{\prime}}}\left( { \sum \limits_g u_{ + g } {\overline{\user2{\bf{Z}}}}_g {{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}}{\overline{\user2{\bf{Z}}}}_g^T } \right){{{\mathop{ \bf B}\limits^{\frown}} }}} \right] \\ \end{aligned}$$
(16)

From (16) it is clear that the update of \({\bf{B}} = {\varvec{\varSigma}}_V^\frac{1}{2} {{{\mathop{ \bf B}\limits^{\frown}} }}\) is obtained by setting \({{{\mathop{ \bf B}\limits^{\frown}} }}\) equal to the first Q eigenvectors of \(\sum\nolimits^u_{ + g} {{\overline{\bf{Z}}}}_g {{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}}{{\overline{\bf{Z}}^{\prime}}}_g .\)

f) Update ηg and C. Formula (16) can also be written as

$$\ell (\varvec{\theta} ) = \frac{1}{2} \sum \limits_g u_{ + g} tr\left[ {{{\overline{\bf Z}^{\prime}}}_g {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}{\overline{\bf{Z}}}_g {{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}}} \right] + c^{\prime\prime\prime} = \frac{1}{2}tr\left[ {{{{\mathop{ \bf C}\limits^{\frown}}^{\prime}}}\left( { \sum \limits_g u_{ + g} {{\overline{\bf Z}^{\prime}}}_g {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}{\overline{\bf{Z}}}_g } \right){{{\mathop{ \bf C}\limits^{\frown}} }}} \right] + c^{\prime\prime\prime},$$
(17)

The update of C is then obtained by setting \({{{\mathop{ \bf C}\limits^{\frown}} }}\) equal to the first R eigenvectors of \(\sum\nolimits^u_{ + g} {{\overline{\bf Z}^{\prime}}}_g {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}{\overline{\bf{Z}}}_g .\)

5 Interpretation of components and connection with the Linear Discriminant Analysis (LDA)

On the basis of the results shown in the previous section, we will illustrate some interesting properties of the components generated by the model. For simplicity of exposition, we first discuss the two-way case, i.e. K = 1. Linear discriminant analysis (LDA) is a well-known supervised classification procedure that can also be seen as a data reduction tool. According to this, it can be used to represent multiclass data in a low dimensional subspace highlighting class differences.

First of all, we show how the within-standardized loadings matrix \({{{\mathop{ \bf B}\limits^{\frown}} }} = {\varvec{\varSigma}}_V^{ - \frac{1}{2}} {\bf{B}}\) derives from a PCA of the matrix of within-standardized centroids. This follows if we note that to maximize (11) with respect to B and ηg (g = 1,2, …,G) is equivalent to

$$\begin{aligned} \ell \left( \varvec{\theta} \right) & = \sum \limits_{ng} u_{ng} \left\{ { - \frac{1}{2}\left[ {\left( {{\bf{x}}_{n} - {\bf{B}\varvec{\eta }}_g } \right)^T {\varvec{\varSigma}}_V^{ - 1} \left( {{\bf{x}}_{n} - {\bf{B}\varvec{\eta }}_g } \right)} \right]} \right\} + c^{\prime} \\ & = \sum \limits_{ng} u_{ng} \left\{ { - \frac{1}{2}\left[ { {\bf{x}}_n^T {\varvec{\varSigma}}_V^{ - 1} {\bf{x}}_n - 2{\varvec{\eta}}_g^T {\bf{B}}^T {\varvec{\varSigma}}_V^{ - 1} {\bf{x}}_n + {\varvec{\eta}}_g^T {\varvec{\eta}}_g } \right]} \right\} + c^{\prime} \\ & = \sum \limits_g \left[ {u_{ + g} {\varvec{\eta}}_g^T {\bf{B}}^T {\varvec{\varSigma}}_V^{ - 1} {\overline{\bf{x}}}_g - \frac{1}{2}u_{ + g} {\varvec{\eta}}_g^T {\varvec{\eta}}_g } \right] + c^{\prime \prime} \\ \end{aligned}$$
(18)

where \(c^{\prime}\) and \(c^{\prime \prime}\) are constant terms, \(u_{ + g} = \sum_n {{\text{u}}_{ng} }\) and \({\overline{\bf{x}}}_g = {\text{u}}_{ + g}^{ - 1} \sum_n {{\text{u}}_{ng} {\bf{x}}_n }\). If we multiply (18) by − 2, add the constant term \(\sum\nolimits_g {{\text{u}}_{ + g} {{\overline{}^{\prime}}}_g {\varvec{\varSigma}}_V^{ - 1} {{\overline{\bf{x}}}}_g }\) and ignore c′ and c′′, we can transform the maximization of (18) into the minimization of

$$\begin{aligned} & \sum_g {u_{ + g} \left( {{{{\bar{\bf X}}^{\prime}}}_g {{\varvec{\Sigma}}}_V^{- 1} {{{\bar{\bf X}}}}_g - 2{{\varvec{\eta}^{\prime}}}_g {{\bf{B}^{\prime}\Sigma }}_V^{ - 1} {{\bar{\bf X}}}_g + {{\varvec{\eta}^{\prime}}}_g {\varvec{\eta }}_g } \right)}\\ &\quad = \sum \limits_g {\text{u}}_{ + g} ({{\bar{\bf X}}}_g - {\bf{B}\varvec{\eta }}_g )^{\prime}{\varvec{\Sigma }}_V^{ - 1} ({{\bar{\bf X}}}_g - {\bf{B}}{\varvec{\eta }}_g )\\ &\quad = {\bf{D}}^{\frac{1}{2}} {{\bar{\bf X}}\varvec{\Sigma }}_V^{ - \frac{1}{2}} - {\bf{D}}^{\frac{1}{2}} {\bf{N}}{{ {\bf B}^{\prime}}}{{\varvec{\Sigma }}_V^{ - \frac{1}{2}}}^2 \\ &\quad = {\bf{D}}^{\frac{1}{2}} {{\bar{\bf Z}}} - {\bf{D}}^{\frac{1}{2}} {{N{\mathop{\bf B}\limits^{\frown}}^{\prime}}}^2 \end{aligned}$$
(19)

where \({\overline{\bf{X}}}\) is the matrix having the centroids \({\overline{\bf{x}}}_g\) as rows, \({\overline{\bf{Z}}} = {{\overline{\bf x}\Sigma }}_V^{ - \frac{1}{2}}\) being its within-standardized version, N is the matrix having the reduced centroids ηg as rows and D is the diagonal matrix with weights u+g on the main diagonal. The within-standardized data projected on the subspace identified by PCA, are the component scores

$${\bf{Y}} = {{{\bf Z}{\mathop{\bf B}\limits^{\frown}} }} = {\bf{X}\varvec{\varSigma}}_{\text{V}}^{ - \frac{1}{2}} {\varvec{\varSigma}}_{\text{V}}^{ - \frac{1}{2}} {\bf{B}} = {\bf{X}\varvec{\varSigma}}_{\text{V}}^{ - 1} {\bf{B}} = {{{\bf X}{\mathop{\bf B}\limits^{\smile}} }}$$
(20)

that are linear combinations of the original variables having the elements of the weight matrix \({{{\mathop{ \bf B}\limits^{\smile}} }}\) as coefficients. It is possible to show that they maximize the between variance subject to the constraint of unit within variance. In fact, the between and within variances for a linear combination v = Xb are \({{{\bf v}^{\prime}}}\left( {\sum\nolimits_g {{\text{u}}_{ + g} {\overline{\bf{x}}}_g {{\overline{\bf{x}}^{\prime}}}_g } } \right){\bf{v}}\) and \({{{\bf v}^{\prime}\Sigma }}_V {\bf{v}}\). Now, setting K = 1, (116 can be rewritten as

$$2\ell (\varvec{\theta} ) - 2c^{\prime \prime} = \sum \limits_g {\text{u}}_{ + g} {{\overline{\bf Z}^{\prime}}}_g {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}{\overline{\bf Z}}}}_g = {\text{tr}}\left[ {{{{\mathop{ \bf B}\limits^{\frown}}^{\prime}}}\left( { \sum \limits_g {\text{u}}_{ + g} {\overline{\bf{z}}}_g {{\overline{\bf{z}}^{\prime}}}_g } \right){{{\mathop{ \bf B}\limits^{\frown}} }}} \right] = {\text{tr}}\left[ {{{{\mathop{ \bf B}\limits^{\smile}}^{\prime}}}\left( { \sum \limits_g {\text{u}}_{ + g} {\overline{\bf{x}}}_g {{\overline{\bf{x}}^{\prime}}}_g } \right){{{\mathop{ \bf B}\limits^{\smile}} }}} \right],$$
(21)

we note that the component weights maximize the sum of the between variances of the component scores subject to the constraints \({{{\mathop{ \bf B}\limits^{\smile}} }}^T {\varvec{\varSigma}}_V^{ - 1} {{{\mathop{ \bf B}\limits^{\smile}} }}\) = \({\bf{B}}^T {\varvec{\varSigma}}_V^{ - 1} {\varvec{\varSigma}}_{{V}} {\varvec{\varSigma}}_V^{ - 1} {\bf{B}} = {\bf{B}}^T {\varvec{\varSigma}}_V^{ - 1} {\bf{B}} = {\bf{I}}_Q .\) In other words, the components are chosen in order to maximize the between to within variances ratio as in multiple linear discriminant analysis. The results above can be extended to the general three-way case as follows. First, we note that (19) extend to

$${\bf{D}}^\frac{1}{2} {\overline{\bf{X}}}\left( {{\varvec{\varSigma}}_O^{ - \frac{1}{2}} \otimes {\varvec{\varSigma}}_V^{ - \frac{1}{2}} } \right) - {\bf{D}}^\frac{1}{2} {\bf{N}}\left( {{{{\bf C}^{\prime}}} \otimes {{ {\bf B}^{\prime}}}} \right)\left( {{\varvec{\varSigma}}_O^{ - \frac{1}{2}} \otimes {\varvec{\varSigma}}_{\text{V}}^{ - \frac{1}{2}} } \right)^2 = {\bf{D}}^\frac{1}{2} {\overline{\bf{Z}}} - {\bf{D}}^\frac{1}{2} {\bf{N}}\left( {{{{\mathop{ \bf C}\limits^{\frown}}^{\prime}}} \otimes {{ {\bf B}^{\prime}}}} \right)^2$$
(22)

thus, the within-standardized component weights matrices can be seen as obtained from a Tucker2 analysis of the matrix of within-standardized centroids. Second, the component scores

$${\bf{Y}} = {\bf{Z}}({{{\mathop{ \bf C}\limits^{\frown}} }} \otimes {{{\mathop{ \bf B}\limits^{\frown}} }}) = {\bf{X}}({\varvec{\varSigma}}_O^{ - 1} \otimes {\varvec{\varSigma}}_V^{ - 1} )({\bf{C}} \otimes {\bf{B}}) = {\bf{X}}({{{\mathop{ \bf C}\limits^{\smile}} }} \otimes {{{\mathop{ \bf B}\limits^{\smile}} }})$$
(23)

are bilinear combinations of the original variables and occasions, and of maximum between variance among those of within variance equal to 1. In fact, the component weights maximize

$$\begin{aligned} 2\ell \left( \varvec{\theta} \right) - 2c^{\prime \prime} & = \sum \limits_g u_{ + g} {\overline{\bf{z}}}_g^T \left( {{{{\mathop{ \bf C}\limits^{\frown}} {\mathop{C}\limits^{\frown}}^{\prime}}} \otimes {{{\mathop{ \bf B}\limits^{\frown}} {\mathop{B}\limits^{\frown}}^{\prime}}}} \right){\overline{\bf{z}}}_g \\ & = \sum \limits_g u_{ + g} tr\left[ {\left( {{{{\mathop{ \bf C}\limits^{\frown}}^{\prime}}} \otimes {{{\mathop{ \bf B}\limits^{\frown}}^{\prime}}}} \right){\overline{\bf{z}}}_g {\overline{\bf{z}}}_g^T \left( {{{{\mathop{ \bf C}\limits^{\frown}} }} \otimes {{{\mathop{ \bf B}\limits^{\frown}} }}} \right)} \right] \\ & = tr\left[ {\left( {{{{\mathop{ \bf C}\limits^{\smile}} }} \otimes {{{\mathop{ \bf B}\limits^{\smile}} }}} \right)^T \left( { \sum \limits_g u_{ + g} {\overline{\bf{x}}}_g {\overline{\bf{x}}}_g^T } \right)\left( {{{{\mathop{ \bf C}\limits^{\smile}} }} \otimes {{{\mathop{ \bf B}\limits^{\smile}} }}} \right)} \right] \\ \end{aligned}$$
(24)

subject to the constraints \({{{\mathop{C}\limits^{\smile^{\prime}}}\Sigma }}_O {{{\mathop{C}\limits^{\smile}} }} = {\bf{I}}_R\) and \({{{\mathop{B}\limits^{\smile}}^{\prime}\Sigma }}_V {{{\mathop{B}\limits^{\smile}} }} = {\bf{I}}_Q\). In other words, given the classification, the proposal can be seen as a bilinear discriminant analysis, that is the components are chosen in order to maximize the between to within variances ratio for variables and occasions.

6 Related models

In this paper, we propose a way to simultaneously cluster and reduce three-way data by identifying the informative clustering subspace. Such construction mainly allows us to identify the factors that explain the between variability in terms of different class-conditional means. Beside the linear discriminant analysis, seen in the previous section, the model can also be used for variable selection and/or parsimonious modelling purposes. It follows that our model can also be compared to models/methods following one of the two aforementioned purposes. In particular, within the first purpose, Raftery et al. (2006) formulate the problem of variable selection, for two-way data, as a model comparison problem using the BIC. Here the variables are projected into an informative subspace. This allows to identify the relevant variables. Different extensions have been proposed, such as in Maugis et al. (2009) and Witten and Tibshirani (2010). Within the second purpose, parsimonious modelling, the idea is to define model-based clustering by using a reduced set of parameters. One of the earliest parsimonious proposal is given in Celeux and Govaert (1995), where a mixture of Gaussians for two-way data is made parsimonious by imposing some equality constraints on some elements of the spectral decompositions of the class-conditional covariance matrices. Another parsimonious proposal is given by the mixture of factor analyzers (MFA) (see Ghahramani and Hinton 1997; Hinton et al. 1997; Ranalli and Rocci 2023, and references therein). Later, a general framework for the MFA model was proposed by McNicholas and Murphy (2008). Furthermore, we point the reader to see also Tipping and Bishop (1999) and Bishop (1998) who considered the related model of mixtures of principal component analyzers for the same purpose. Further references may be found in chapter 8 of Mclachlan and Peel (2000) and in a review on model-based clustering of high dimensional data (Bouveyron and Brunet 2012a, 2012b).

7 Model assessment

The effectiveness of our proposal has been tested trough a large simulation study where the SCR model (S3) with Q and R components has been compared with: the “ordinary” homoscedastic finite mixture of Gaussians (H); the SCR model applied ignoring the three-way data structure (S2) with Q × R components. Data is sampled from a homoscedastic finite mixture of multivariate J × K Gaussians with parameters randomly generated in a such a way that only Q variables in R occasions are informative for the clustering structure, i.e. have different class-conditional means. Two main scenarios are defined: few (J = 5, Q = 2, K = 5, R = 2—scenario (i) and many variables (J = 20, Q = 5, K = 5, R = 2—scenario (ii). Under each scenario we consider four different data generation processes (dgp) obtained by combining the situations where the S3 model is true or not for the means, with the situations where the S3 model is true or not for the covariance matrix. The levels of the experimental factor dgp are then 4: (1) true model; (2) false means—true covariance; (3) true means—false covariance; (4) false model. In particular, the true means are generated according to (8) with B and C being the first Q and R columns of an identity matrix; while the true covariance is generated according to (6). Additionally, other three different experimental factors are considered: sample size (small: N = 300 for scenario i and N = 500 for scenario ii; large: N = 500 for scenario i and N = 1000 for scenario ii), number of mixture components (G = 3, 5, 7), number of starting points (rep = 1, 3). It is important to note that our proposal is definitely less favored. Indeed, S3 is true only when dgp = 1 while H is always true and S2 is false only when the group means lie on a space of dimension greater than Q × R, i.e. (dgp = 2, G = 7, scenario = i) or (dgp = 4, G = 7, scenario = i). Within each scenario, 250 samples were generated for every combination of factor levels. The performances were evaluated in terms of recovering the true cluster structure calculating the Adjusted Rand Index (ARI) (Hubert and Arabie 1985) between the true hard partition matrix and that estimated. Simple descriptive statistics about the distributions of the ARIs in each setting are reported in the appendix as well as their boxplots. In the following two subsections we report some comprehensive boxplots along with some comments to see the performances in terms of ARI of the models in combination with different number of groups and the level of an experimental factor among sample size, number of repetitions or data generation process.

7.1 Scenario i

Under the first scenario, we explore the clustering performances through some boxplots depending on the sample size, the number of groups and the generation data process (boxplots of ARI distributions aggregated over the remaining experimental factors in Figs. 2, 3, 4).

Fig. 2
figure 2

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture aggregated by number of repetitions (1, 3) and data generation process (1, 2, 3, 4). G = 3, 5, 7, N = 300, 500, J = 5, Q = 2, K = 5 and R = 2

Full size image
Fig. 3
figure 3

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture aggregated by sample sizes (300, 500) and data generation process (1, 2, 3, 4). G = 3, 5, 7, nrep = 1, 3, J = 5, Q = 2, K = 5 and R = 2

Full size image
Fig. 4
figure 4

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture aggregated by sample sizes (300, 500) and number of repetitions (1, 3). G = 3, 5, 7, dgp = 1, 2, 3, 4, J = 5, Q = 2, K = 5 and R = 2

Full size image

As the sample size increases (Fig. 2), the performances improve for all models. When.

N = 300 and G = 3, the means of ARI are equal to 0.85, 0.81 and 0.82 for S3, S2 and H, respectively; when N = 300 and G = 5, the means of ARI are equal to 0.84 for S3 and 0.90 for S2 and H; when N = 300 and G = 7, the means of ARI are equal to 0.85 for S3 and 0.83 for S2 and H, respectively. By increasing the sample sizes to N = 500, the means ARI increase mainly for S2 and H, giving better performances: S3 equals to around 0.85 for all G; S2 and H equal to 0.87, 0.92 and 0.88 when G = 3, 5, 7, respectively.

Considering the number of starting points (Fig. 3), when they increases the performances improve for all models. This confirms the fact that the EM algorithm could reach local maxima. With only one starting point and when G = 3, the means of ARI are equal to 0.80 for S3 and 0.78 for S2 and H; when G = 5, the means of ARI are equal to 0.77 for S3 and 0.86 for S2 and H; when G = 7, the means of ARI are equal to 0.69, 0.90 and 0.87 for S3, S2 and H, respectively. We note that the clustering performances of S3 worsen with higher G, i.e. when the model involves a larger number of parameters. The situation improves by increasing the number of starting points to 3: when G = 3, the means ARI increase to 0.90 for all models; when G = 5, the means ARI increase to 0.91 for S3 and 0.95 for S2 and H; while when G = 7, they increases to 0.86, showing a very large improvement, for S3, 0.94 and 0.92 for S2 and H. S3 seems to be the most affected by the number of repetitions among the models analysed. This is due to the fact that it involves more parameter constraints; this means that it is less flexible from a computational point of view; indeed S3 is more parsimonious, but also more computationally complex.

Overall, as regards the data generation process (Fig. 4), it is important to remember that S3 is true only when dgp = 1 while H is always true and S2 is false only when the group means lie on a space of dimension greater than Q × R, i.e. dgp = 2, 4 and G = 7. For G = 3, S3 performs equal or better than S2 and H for all dgp. Indeed, when dgp = 1 the ARI means are equal to 0.84 for S3 and 0.82 for S2 and H; when dgp = 2, the mean are equal to 0.85, 0.81 and 0.82 for S3, S2 and H, respectively; when dgp = 3, they are equal to 0.87 for all models, while when dgp = 4 they are equal to 0.86 for all models.

For G = 5, S3 performs slightly worse than S2 and H for all dgp. Indeed, when dgp = 1 or dgp = 2, the ARI means are equal to 0.85 for S3 and 0.90 for S2 and H; when dgp = 3, the mean are equal to 0.83 for S3 and 0.91 for S2 and H; when dgp = 4, the mean are equal to 0.84 for S3 and 0.91 for S2 and H.

For G = 7 S3 seems to show lower performances than S2 and H. Indeed, when dgp = 1, the ARI means are equal to 0.78, 0.92 and 0.89 for S3, S2 and H, respectively; when dgp = 2, the ARI means are equal to 0.80, 0.91 and 0.89 for S3, S2 and H, respectively; when dgp = 3, the mean are equal to 0.75, 0.92 and 0.90 for S3, S2 and H, respectively; when dgp = 4, the mean are equal to 0.75, 0.93 and 0..90 for S3, S2 and H, respectively.

Finally, as it is possible to see from the appendix, under this scenario, i.e. few variables (J = 5) and low proportion of noise variables/occasions, the computational complexity plays a main role. When G = 3, regardless the specific experimental factor, S3 often results to be the best model in terms of median (varying from 0.96 to 1.00 over different combinations of experimental factors) from a fitting clustering point of view. However, in terms of means, when the model is false (dgp = 4) for S3, then S2 is the best model compared to S3 when the number of repetitions is only one (0.79 compared to 0.77, and 0.85 compared to 0.80 for N = 300 and N = 500, respectively). However, when the number of repetitions is equal to 3, S3 improves and results to be even the best one when N = 300 (0.87 compared to 0.85). As G increases (G = 5, 7), S3 is not anymore the best model, even when the model is well specified and the number of repetitions is equal to 3. Finally, comparing S2 with H, they show similar behavior, since the data structure is not complex at all and the cluster structure can be easily recovered.

7.2 Scenario ii

Differently from the first scenario, under the second one, N is relatively large, many variables (J = 20) and high proportion of noise variables/occasions, the model parsimony plays a main role (rather than computational complexity). Also under this scenario, we consider the clustering performances depending on the sample size, the number of repetitions and the generation data process (see the boxplots of ARI distributions aggregated by the remaining experimental factors in Figs. 5, 6, 7), but in this case the main considerations point against the model competitors, S2 and H (although they are never false under this scenario).

Fig. 5
figure 5

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture aggregated by number of repetitions (1, 3) and data generation process (1, 2, 3, 4). G = 3, 5, 7, N = 500, 1000, J = 20, Q = 5, K = 5 and R = 2

Full size image
Fig. 6
figure 6

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture aggregated by sample sizes (500, 1000) and data generation process (1, 2, 3, 4). G = 3, 5, 7, nrep = 1, 3, J = 20, Q = 5, K = 5 and R = 2

Full size image
Fig. 7
figure 7

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture aggregated by sample sizes (500, 1000) and number of repetitions (1, 3). G = 3, 5, 7, dgp = 1, 2, 3, 4, J = 20, Q = 5, K = 5 and R = 2

Full size image

The performances improve for all models when the sample size increases (Fig. 5). When N = 500 and G = 3, the means of ARI are equal to 0.89 for S3 and 0.59 for S2 and H; when N = 500 and G = 5, the means of ARI are equal to 0.90, 0.51 and 0.50 for S3, S2 and H, respectively; when N = 500 and G = 7, the means of ARI are equal to 0.90 for S3 and 0.60 for S2 and H, respectively. By increasing the sample sizes to N = 1000, the means ARI of S2 and H are more affected, even if they are still performing worse than S3. Indeed, for G = 3 the means are equal to 0.89 for S3 and 0.68 for S2 and H; when G = 5, they are equal to 0.92 for S3 and 0.74 for S2 and H; while when G = 7, they are equal to 0.90 for S3 and 0.70 for S2 and H.

As the number of starting points increases, the performances of S3 always improves substantially (Fig. 6). With only one staring point and when G = 3, the means of ARI are equal to 0.86 for S3 and 0.64 for S2 and H; when G = 5, the means of ARI are equal to 0.88 for S3 and 0.61 for S2 and H; when G = 7, the means of ARI are equal to 0.91 for S3 and 0.59 for S2 and H. The situation improves by increasing the number of starting points to 3: when G = 3 or G = 5, the means ARI increase to 0.93 for S3 and 0.30 for S2 and H; while when G = 7, they increases to 0.96, showing a very large improvement, for S3 and 0.40 for S2 and H. We note that, differently from the previous scenario, the clustering performances of S3 improve with higher G, i.e. when the model involves a larger number of parameters. We recall that here we are considering a higher proportion of noise, so S3 works better in capturing the clustering structure in a parsimonious way.

Regarding the data generation process (Fig. 7), it is important to remember that S3 is true only when dgp = 1 while H and S2 are always true. For all G, S3 performs always better than S2 and H. Indeed, when dgp = 1 the ARI means are equal to 0.91, 0.44 and 0.45 for S3, S2 and H, respectively; when dgp = 2, the mean are equal to 0.91 for S3 and 0.48 for S2 and H; when dgp = 3, they are equal to 0.88 for S3 and 0.81 for S2 and H, while when dgp = 4 they are equal to 0.87 for S3 and 0.80 for S2 and H. For G = 5, when dgp = 1 or dgp = 2, the ARI means are equal to 0.91 for S3 and 0.43 for S2 and H; when dgp = 3, the means are equal to 0.91 for S3 and 0.83 for S2 and H; when dgp = 4, the means are equal to 0.91 for S3 and 0.81 for S2 and H. For G = 7 when dgp = 1, the ARI means are equal to 0.92, 0.43 and 0.42 for S3, S2 and H, respectively; when dgp = 2, the ARI means are equal to 0.92 for S3 and 0.42 for S2 and H; when dgp = 3, the means are equal to 0.95, 0.81 and 0.80 for S3, S2 and H, respectively; when dgp = 4, the means are equal to 0.95 for S3 and 0.80 for S2 and H.

Some further details can be drawn from the results in the appendix. Differently from scenario i, under this scenario, S3 wins over the two competitors in all experimental factors, thanks to its ability to take into account the presence of noise variables/occasions. It parsimoniously discards all the uninformative variables/occasions. S3 is not only the best model from a fitting clustering point of view, it also shows robustness. Indeed, although the data generation is different from the structure of data assumed by the model (dgp = 2, 3 and 4), S3 is able to capture the true cluster structure, discarding all the irrelevant information. It shows similar behaviors as the case dgp = 1.

8 An application on real data

The new mixture model for three-way data is illustrated by reanalyzing the classical soybean data set used by Basford and McLachlan (1985). The data originated from an experiment in which 58 soybean genotypes were evaluated at four locations (Lawes, Brookstead, Nambour, Redland Bay) in Queensland, Australia, at two time points (1970, 1971). The eight location × time combinations are referred as environments. Various chemical and agronomic attributes were measured on the genotypes. Following Basford and McLachlan (BandM, Basford and McLachlan 1985) only seed yield (kg/ha) and seed protein percentage are considered. On this data set BandM have found 7 groups forming two clearly distinct subsets (the first three vs. the last four). Reduced mixture models have been estimated for G, Q, and R values ranging in 2:7, 1:2 and 1:8. For the covariance matrix \({\varvec{\varSigma}}_O\) two different forms have been assumed: either diagonal or with non null covariances only between the same locations. The best model selected by the BIC criterion has been: G = 7, Q = 2, R = 2 and \({\varvec{\varSigma}}_O\) diagonal. Table 1 displays the percentage of variation accounted for by the components (two latent variables at two latent occasions), calculated on the within-standardized data.

Table 1 Percentage of variation accounted for by the components
Full size table

In Table 2, the classification into 7 groups has been compared with that obtained by BandM. They are quite different but display the same two distinct subsets even if in our analysis group 3 from BandM is split into two groups.

Table 2 Basford and McLachlan (B and M) and our classifications (RVR)
Full size table

The aforementioned distinction is clear when we look at Fig. 8, where the scores of the genotypes on the first latent variable are displayed at the two latent occasions (the coordinates are the first and third columns of Y, see (23)). The biplot represents both cluster centroids [the coordinates are given by the first and third columns of N, see (15) and (22)] and occasions [the coordinates are given by the columns of \({{{\mathop{ \bf C}\limits^{\frown}} }}\), see (22)]. The scalar products between occasions and centroids represent the deviations from the grand mean of the group-conditional means of the first latent variable at the different occasions (the odd columns of \({\overline{\bf{Z}}}({\bf{I}}_8 \otimes {{{\mathop{ \bf B}\limits^{\frown}} }})\)). This graphical representation helps in identifying the discriminating power of the occasions. For example, we can see that the Redland Bay in 1970 (R0) is the environment better clarifying the separation between the two subsets.

Fig. 8
figure 8

Biplot on the first latent variable at the two latent occasions

Full size image

9 Concluding remarks

In this paper, we proposed a model that reduces the data dimensionality by identifying latent components that are (informative) able to explain the clustering structure underlying the three or two-way data structure. This allows to overcome the issues arising in applying reduction techniques and clustering methods separately (i.e. sequentially). The proposal involves a finite mixture of Gaussians whose mean vectors present a Tucker2 structure, while the covariance matrix can be decomposed as \({\varvec{\varSigma}} = {\varvec{\varSigma}}_O \otimes {\varvec{\varSigma}}_V\) (commonly used in the multitrait-multimethod literature).

As noted by a referee, on the mean vectors we could impose a Tucker3 model rather than a Tucker2. The difference between the two is that the former would provide also a reduction for the centroids. In formulas we would have

$$\mu_{gjk} = \mu_{jk} + \mathop \sum \limits_{p = 1}^P \mathop \sum \limits_{q = 1}^Q \mathop \sum \limits_{r = 1}^R a_{gp} b_{jq} c_{kr} \eta_{pqr} ,$$
(25)

where A = [agp] is a G × P matrix of component loadings for the centroids. The model can be graphically represented as in Fig. 9.

Fig. 9
figure 9

Graphical representation of Tucker 3 model

Full size image

In this paper, we preferred the Tucker2 model because the centroids can be already considered as a reduced mode derived from the units mode. However, we do not exclude that the Tucker3 model could be useful when the number of centroids is very large.

Fig. 10
figure 10

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture models over 16 settings by varying the number of starting points (1, 3), the data generation process (1, 2, 3, 4) and the sample size (300, 500). G = 3, J = 5, Q = 2, K = 5 and R = 2

Full size image
Fig. 11
figure 11

Box-plots of ARI distributions for SCR three-way, SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture models over 16 scenarios by varying the number of starting points (1, 3), the data generation process (1, 2, 3, 4) and the sample size (300, 500). G = 5, J = 5, Q = 2, K = 5 and R = 2

Full size image
Fig. 12
figure 12

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture models over 16 scenarios by varying the number of starting points (1, 3), the data generation process (1, 2, 3, 4) and the sample size (300, 500). G = 7, J = 5, Q = 2, K = 5 and R = 2

Full size image
Fig. 13
figure 13

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture models over 16 scenarios by varying the number of starting points (1, 3), the data generation process (1, 2, 3, 4) and the sample size (500, 1000). G = 3, J = 20, Q = 5, K = 5 and R = 2

Full size image
Fig. 14
figure 14

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture models over 16 scenarios by varying the number of starting points (1, 3), the data generation process (1, 2, 3, 4) and the sample size (500, 1000). G = 5, J = 20, Q = 5, K = 5 and R = 2

Full size image
Fig. 15
figure 15

Box-plots of ARI distributions for SCR three-way (S3), SCR two-way (S2), and homoscedastic (H) mixture models over 16 scenarios by varying the number of starting points (1, 3), the data generation process (1, 2, 3, 4) and the sample size (500, 1000). G = 7, J = 20, Q = 5, K = 5 and R = 2

Full size image

Although the effectiveness of the model has been assessed empirically through a large simulation study and a real data application, we did not discuss a desirable property of the model, i.e. the scale invariance. Given the structure of the covariance and component loading matrices, the model is scale invariant under bilinear transformations. In other terms, if a variable is scaled, it should be scaled in the same way over all occasions. Formally, if data are scaled by a matrix D, scale invariance holds only if D can be decomposed into \({\bf{D}} = {\bf{D}}_O \otimes {\bf{D}}_V\).

The model here presented can be extended in several ways in different directions. For example, it would be interesting to explore the extensions to the case of particular data types such as compositional, functional or mixed.