Depth-based reconstruction method for incomplete functional data

Abstract

The problem of estimating missing fragments of curves from a functional sample has been widely considered in the literature. However, most reconstruction methods rely on estimating the covariance matrix or the components of its eigendecomposition, which may be difficult. In particular, the estimation accuracy might be affected by the complexity of the covariance function, the noise of the discrete observations, and the poor availability of complete discrete functional data. We introduce a non-parametric alternative based on depth measures for partially observed functional data. Our simulations point out that the benchmark methods perform better when the data come from one population, curves are smooth, and there is a large proportion of complete data. However, our approach is superior when considering more complex covariance structures, non-smooth curves, and when the proportion of complete functions is scarce. Moreover, even in the most severe case of having all the functions incomplete, our method provides good estimates; meanwhile, the competitors are unable. The methodology is illustrated with two real data sets: the Spanish daily temperatures observed in different weather stations and the age-specific mortality by prefectures in Japan. They highlight the interpretability potential of the depth-based method.

1 Introduction

Partially observed functional data (POFD) are becoming more recurrent, invalidating many existing methodologies of Functional Data Analysis (FDA) (Ramsay and Silverman 2005; Ferraty and Vieu 2006). Diverse case studies motivate the development of statistical tools for these data types. For example, many data sets are recorded in medical studies through periodical check-ups. Patients who miss appointments or devices that fail to register may be typical sources of censoring. These situations may present in different types of monitoring, such as ambulatory blood pressure, the health status of human immunodeficiency virus tests, growth curves, and the evolution of lung function (James et al. 2000; James and Hastie 2001; Delaigle and Hall 2013; Kraus 2015; Delaigle and Hall 2016). Sangalli et al. (2009, 2014) also consider POFD from aneurysm studies where the source of censoring comes from a prior reconstruction of the sample and posterior processing to make the data comparable across subjects. In demography, it is common that age-specific mortality rates for older ages are not completely observed due to the decreasing number of survivors (Human Mortality Database 2022) and this cohort is the focus of actuarial science studies (see, e.g., D’Amato et al. 2011). Other examples involve electricity supply functions that may not be completely observed because suppliers and buyers typically agree on prices and quantities depending on the market conditions (Kneip and Liebl 2020; Liebl and Rameseder 2019).

Prominent literature has tackled estimating missing parts of POFD, providing several benchmark methods. Among them, the methods of (Yao et al. 2005; Goldberg et al. 2014; Kraus 2015; Delaigle and Hall 2016; Kneip and Liebl 2020). This article proposes a new method and compares it with two of the above benchmark methods. We selected those that provided the best performance to minimize the mean squared prediction error (MSPE) on our simulations and considered case studies. The chosen benchmark methods are the method of Kraus (2015) and the method of Kneip and Liebl (2020). Notably, Kraus (2015) develops a procedure based on functional ridge regression with automatic parameters to predict the principal component scores and the unobserved part of a function when only a fragment of the curve is available. In Kraus and Stefanucci (2020), the authors prove that this ridge reconstruction method is asymptotically optimal. On the other hand, Kneip and Liebl (2020) approaches the problem by introducing a new optimal operator based on a local linear kernel to produce smooth results and avoid artificial jumps between observed and reconstructed parts. The best-performing reconstruction methods that outperform Yao et al. (2005) and Kraus (2015) involve an alignment step to link the predicted fragments with the partially observed curve. In this article, we focus on a comparison between methods without any post-processing step.

Our approach combines two novel functional tools: (1) the concept of functional envelope and projection methods proposed in Elías et al. (2022b); and (2) a functional depth for POFD (Elías et al. 2022a). The literature on depth-based reconstruction methods for functional data is scarce. Remarkably, Mozharovskyi et al. (2020) proposed an iterative imputation method for multivariate data by data depth motivated by iterative regression imputation methods. The authors propose to replace the missing values on some of the dimensions with the corresponding value that maximizes the depth on the remaining completely observed dimensions. Differently, we select a subset of sample trajectories representative of the curve to reconstruct in terms of shape and magnitude, called envelope (Elías et al. 2022b), that maximizes the functional depth of the curve to reconstruct. Then, we “project” the envelope to the missing regions and use all the projected curves to provide a reconstruction. We do not restrict our search to a completely observed part of the domain nor to completely observed functions, thanks to a suitable functional depth for partially observed data (Elías et al. 2022a) and a measure of similarity between POFD. In our context, every single datum might contain missing parts, and we do not require to have complete observability at any region of the curves’ domain. This fact also makes our problem different from the imputation problem of Liebl and Rameseder (2019) where the missing parts are not systematic.

The new method is designed for: (1) Scenarios where the estimation of the covariance function is complex or impossible: The existing reconstruction methods depend on a proper covariance estimation. Its estimators might be very sensitive and become unreliable for many analyses, particularly for principal component analysis (Hubert et al. 2005). In addition, data coming from multiple populations and low number of complete functions in the sample also hampers the estimation procedures and makes it impossible if all the sample functions are partially observed (Kneip and Liebl 2020). (2) Reconstructing non-smooth functions: Some methods are designed to deal with smooth functions; consequently, their results are smooth and aligned functions (Kneip and Liebl 2020). Our goal is to provide a method that produces reconstructed functions while remaining as accurate as possible in roughness and variability. (3) Adding interpretability: It might be useful to get a precise estimation and insights into the final reconstruction drivers. We consider simulated and empirical data for illustrating the issues listed above. On the one hand, we consider yearly curves of Spanish daily temperatures. This data set is gathered by the Spanish Agency of Meteorology (AEMET) at different weather stations spread along with the Spanish territory. On the other hand, we consider age-specific yearly mortality rates recorded at each Japanese prefecture (political territory division).

The structure of this paper is as follows: Sect. 2 introduces notation and the method. Section 3 shows various simulated results based on Gaussian Processes under different simulated regimes of partial observability. In addition, we illustrate the method’s performance with the Spanish daily temperatures data set and the Japanese age-specific mortality rates by prefecture. In Sect. 4, we make some conclusions, along with some ideas on how the methodology can be further extended.

2 Depth-based reconstruction method

2.1 Definition and notation

Let $X = \{X(t): t\in [a,b]\}$ be a stochastic process of continuous trajectories and $(X_1, \dots , X_n)$ independent copies of X. To simplify the notation, we assume without loss of generality $[a, b] = [0,1]$. We consider the case $X_1, \dots , X_n$ are partially observed. Following Delaigle and Hall (2013), we model the partially observed setting by considering a random mechanism Q that generates compact subsets of [0, 1] where the functional data are observed. Specifically, let O be a random compact set generated by Q,  and let $(O_1, \dots , O_n)$ be independent copies of O. Therefore, for $1\le i \le n,$ the functional datum $X_i$ is only observed on $O_i$. Let $(X_i, O_i) = \{X_i(u): u \in O_i\}$ and $M_i = [0,1]\setminus O_i$. Then, the observed and missing parts of $X_i$ are $(X_i, {O_i})$ and $(X_i, {M_i})$. As it is standard in the literature of POFD, we assume that $(X_1,O_1), \dots , (X_n,O_n)$ are i.i.d. realizations from $P \times Q$. This is, $\{X_1, \dots , X_n\}$ and $\{O_1, \dots , O_n\}$ are independent samples. This assumption has been termed Missing-Completely-at-Random and, notedly, only Liebl and Rameseder (2019) has considered a specific violation of this assumption. As illustration, the top panel of Fig. 1 presents two examples of incomplete functional data under two different missing scenarios (left and right panels). The observed fragments of two incomplete curves $(X_i, {O_i})$ are in red.

Fig. 1

In the top panels, an illustration of how Algorithm 1 works. The sample curves correspond to 1000 i.i.d. trajectories of a Gaussian process. We considered partially observed curves for the left panels by removing six random intervals from [0, 1]. For the right panels, we considered missing data uniformly. On average, only 50% of each curve was observed for both runs. The partially observed function that we reconstructed is colored in red and plotted entirely in the bottom panels jointly with its estimation (in blue)

The core idea of our method is based on the depth-based method for dynamic updating on functional time series Elías et al. (2022b). In this context, by using the notation introduced here, the functional sample, ($X_1, \dots , X_n$), was ordered in time, n being the most recent time period. $X_n$ was only observed on $O_n = [0,q]$, with $0\ll q< 1$, and the rest of sample curves $\{X_j:j< n\}$ were fully observed on [0, 1]. This is, for all $j<n$, $O_j = [0,1]$. We may summarize the depth-based approach for dynamic updating as follows: if $(X_n,O_n)$ is depth in $\{(X_j,O_n) : j \in \mathcal{J}_n\}$, for some set of curves $\mathcal{J}_n\subset \{1,\ldots ,n-1\}$, and the band delimited by the curve segments $\{(X_j,O_n) : j \in \mathcal{J}_n\}$ captures both the shape and magnitude of $(X_n,{O_n})$, we may estimate $(X_n,M_n)$ from $\{(X_j,M_n): j\in \mathcal{J}_n\}$. In particular, point estimators of $(X_n,M_n)$ were obtained by computing weighted averages on the curve segments of $\{(X_j,M_n): j\in \mathcal{J}_n\}$. In our jargon, $\{(X_j,O_n): j\in \mathcal{J}_n\}$ is called the envelope of $(X_n,{O_n})$.

In contrast to the dynamic updating framework of Elías et al. (2022b), this article deals with sample curves that might not be temporarily ordered in the partially observed scenario. What is more important, every single curve may be partially observed. So, for enveloping the observed part of a curve, say us $(X_i, {O_i})$, we could only have curve segments, namely $\{(X_j,O_i\cap O_j) : j \ne i\}$, with $| O_i\cap O_j | \ne \emptyset$. Moreover, without loss of generality, we assume that $O_i\cap O_j$ has a non-zero Lebesgue measure. Similarly, we may only have curve segments, specifically $\{(X_j,M_i\cap O_j) : j \ne i\}$, for estimating the missing part of $X_i$, that is $(X_i,M_i)$. Applying the depth-based approach to these cases is a challenging and open problem we address in this article. The method can be explained in two steps: one concerned about how to obtain an envelope of each $(X_i,O_i)$, described in Sect. 2.2 and one on how to estimate or reconstruct $(X_i,M_i)$ from the observed parts of the curves used for enveloping $(X_i,O_i)$, described in Sect. 2.3.

2.2 A depth-based algorithm for focal-curve enveloping

The concept of depth arises for ordering multivariate data from the center to outward (Liu 1990; Liu et al. 1999; Rousseeuw et al. 1999; Zuo and Serfling 2000; Serfling 2006; Li et al. 2012). Let ${\mathcal {F}}$ be the collection of all probability distribution functions on ${\mathbb {R}}$, $F\in {\mathcal {F}}$ and $x\in {\mathbb {R}}$. In the univariate context, a depth measure is a function $D:{\mathbb {R}} \times {\mathcal {F}}\rightarrow [0,1]$ such that, for any fixed F, D(x, F) reaches their maximum value at the median of F, this is at x such that $F(x)=1/2$, and decreases to the extent that x is farthest from the median. Examples of such univariate depth measures are

$$\begin{aligned} D(x,F) = 1- \Big | \frac{1}{2} - F(x)\Big | \end{aligned}$$

(1)

and

$$\begin{aligned} D(x,F) = 2 \{F(x) \big [1-F(x)\big ] \}. \end{aligned}$$

(2)

Denote by P to the generating law of the process X and by $P_t$ to the marginal distribution of X(t), this is $P_t(x) = {\mathbb {P}} [X(t)\le x]$. Given a univariate depth measure D, the Integrated Functional Depth of X with respect to P is defined as

$$\begin{aligned} \text{ IFD }(X,P) = \int _0^1 D\big (X(t), P_t \big ) w(t)dt, \end{aligned}$$

(3)

where w is a weight function that integrates to one (Claeskens et al. 2014; Nagy et al. 2016). It is worth mentioning that when $w(t) = 1, \forall t$, and D is defined by (1), the integrated functional depth corresponds to the seminal Fraiman and Muniz ’s (2001) functional depth. When D is defined by (2), the corresponding IFD is the celebrated Modified Band Depth with bands formed by two curves (López-Pintado and Romo 2009).

Define $\mathcal{J}(t) = \{1\le j \le n: t\in O_j \}$. Suppose $\mathcal{J}(t) \ne \emptyset$ and let q(t) be the cardinality of $\mathcal{J}(t)$. Denote by $F_{\mathcal{J}(t)}$ to the empirical distribution function of the univariate sample $\{X_j(t): j\in \mathcal{J}(t)\}$. This is the probability distribution that assigns constant mass equals to 1/q(t) to each available observation at time t. Then, for any pair $(X_i,O_i)$ and a given univariate depth D, we consider the Partially Observed Integrated Functional Depth (Elías et al. 2022a) restricted to $O_i$ defined by

$$\begin{aligned} \text{ POIFD }\Big ((X_i,O_i), P \times Q \Big ) = \frac{\int _{O_i} D\big (X(t), F_{\mathcal{J}(t)}\big ) q(t)dt}{\int _{O_i} q(t) dt}. \end{aligned}$$

(4)

This definition of depth considers that the sample of curves is incomplete and weights the parts of the domain proportionally to the number of observed curves. The larger $\text{ POIFD }((X_i,O_i), P \times Q)$, the deeper will be $(X_i, O_i)$ in the partially observed sample.

In line with the approach for dynamic updating introduced by Elías et al. (2022b), we search for an envelope $\mathcal{J}$ that is a subset of incomplete curves, as big as possible, that captures the shape and magnitude of $(X_i, O_i)$ such that $i\notin \mathcal{J}$ and with the following desirable properties:

• P1) $(X_i,O_i)$ is deep in $\{(X_j, O_j): j\in \mathcal{J} \cup \{i\}\}$, the deepest if possible. For measuring depth here we use the Partially Observed Integrated Functional Depth restricted to $O_i$ defined in (4).

• P2) $(X_i,O_i)$ is enveloped by $\{(X_j,O_j): j\in \mathcal{J}\}$ as much as possible. Here, we say $(X_i,O_i)$ is more enveloped by $\{(X_j,O_j): j\in \mathcal{J}\}$ than by $\{(X_j,O_j): j\in \mathcal{J}'\}$ if and only if

  $$\begin{aligned}&\lambda \left( \left\{ t\in O_i: \min _{j\in \mathcal{J}(t)} X_j(t) \le X_i(t) \le \max _{j\in \mathcal{J}(t)} X_j(t) \right\} \right) \\&\quad > \lambda \left( \left\{ t\in O_i: \min _{j\in \mathcal{J}'(t)} X_j(t) \le X_i(t) \le \max _{j\in \mathcal{J}'(t)} X_j(t) \right\} \right) , \end{aligned}$$

  with $\lambda$ being the Lebesgue measure on ${\mathbb {R}}$.

• P3) $\{(X_j,O_j): j\in \mathcal{J}\}$ contains near curves to $(X_i,O_i)$, as many as possible. For measuring nearness, we use mean $L_2$ distance between couples of POFD that overlap i.e. $\lambda (O_i\cap O_j)>0$. This is,

  $$\begin{aligned} \Vert (X_i,O_i)-(X_j,O_j)\Vert = \frac{\sqrt{\int _{O_i\cap O_j} |X_i(t)-X_j(t)|^2 dt}}{\lambda (O_i\cap O_j)}. \end{aligned}$$

  (5)

Algorithm 1 provides a set of curves with the three features above that we call the i-curve envelope and denote by $\mathcal{J}_i$ hereafter. The algorithm is a variation of Algorithm 1 of Elías et al. (2022b), adapted to POFD. It iteratively selects as many sample curves as possible, from the nearest to the farthest to $(X_i, O_i)$, for enveloping $(X_i, O_i)$ (algorithm lines from 3 to 10) and increasing its depth at each iteration (algorithm lines from 11 to 13). The second row of Fig. 1 presents the first iteration where the black curves are not only the closest ones to their corresponding red curve (P3) but also they surround and cover the curve to reconstruct $(X_i, O_i)$ on $O_i$ (P2). The third row is the last iteration of the algorithm that contributes with an additional set of curves that makes $(X_i, O_i)$ deeper (P1).

Figure 1 illustrates how Algorithm 1 works. We consider the first, second, and final iteration of two runs from the algorithm based on 1000 i.i.d. trajectories of a Gaussian process. We considered partially observed curves for the run shown in the left panels by removing six random intervals of the observation domain for every single functional datum. We considered missing data uniformly on the observation domain for the run shown in the right panels. On average, only 50% of each curve was observed for both runs. The partially observed function we intend to reconstruct is colored in red and plotted entirely in the bottom panels jointly with its estimation that we describe below.

2.3 Reconstruction of missing parts

For estimating the unobserved part of $X_i$, this is $(X_i, M_i)$, we use a weighted functional mean from data of the curve envelope $\mathcal{J}_i$. Only here, these functional data may be partially observed. Specifically, these data are $\{(X_j,M_i\cap O_j) : j \in \mathcal{J}_i\}$. Consider $\mathcal{J}_i(t) = \{j\in \mathcal{J}_i: t\in O_j\}$, assume $\mathcal{J}_i(t)\ne \emptyset$ for all $t\in O_i$, and let $\delta = \min _{j\in \mathcal{J}_i} \Vert (X_i,O_i)-(X_j,O_j)\Vert$. Then, we estimate $X_i$ on $M_i$ by

$$\begin{aligned} {\widehat{X}}_i^\theta (t)= \frac{\sum _{j\in \mathcal{J}_i(t)} w_j X_j(t)}{\sum _{j\in \mathcal{J}_i(t)} w_j },\ \ \text{ with } \ \ w_j = \exp \left( \frac{-\theta \Vert (X_i,O_i)-(X_j,O_j)\Vert }{\delta }\right) . \end{aligned}$$

(6)

This estimator is a version of the envelope projection with exponential weights (see Elías et al. 2022b, Equation (2)), adapted to the partially observed data context. Notice that the exponential weights increase the influence of the closest curves in the estimation and give little importance to the farthest trajectories of the envelope. The parameter $\theta$ is automatically chosen by minimizing the mean squared error (MSE) on $(X_i, O_i)$, and it tunes the importance of each curve of the envelope in the reconstruction. In practice, if ${\widehat{O}}_i$ is the observational set where ${\widehat{X}}_i$ can be computable, this is $\cup _{j\in \mathcal{J}_i} (O_i\cap O_j)$, then

$$\theta = \arg \min _{\nu }\sum _{i=1}^n\Vert (X_i, O_i)-({\widehat{X}}^{\nu }_i,{\widehat{O}}_i)\Vert ^2.$$

As an illustration, the bottom panels of Fig. 1 show reconstructions of missing parts of the two simulated cases discussed above.

3 Results

We compare results obtained using the depth-based method with those obtained from studies by Kraus (2015) and Kneip and Liebl (2020). Kraus (2015) propose a regularized regression model to predict the principal component scores (Reg. Regression), whereas Kneip and Liebl (2020) introduces a new class of reconstruction operators that are optimal (Opt. Operator). The two methods were implemented by using the R-codes available at https://is.muni.cz/www/david.kraus/web_files/papers/partial_fda_code.zip and https://github.com/lidom/ReconstPoFD. The depth for partially observed curves and the data generation settings are implemented using the R-package fdaPOIFD of Elías et al. (2021).

Section 3.1 introduces the simulation setting and the data generation process for POFD and shows results with synthetic data. Section 3.2 uses the same simulation settings but applied to AEMET temperature data. Additionally, it illustrates the reconstruction of some yearly temperature curves that are partially observed in reality. Finally, Sect. 3.3 presents another real case study where Japanese age-specific mortality functions are reconstructed.

3.1 Simulation study

Let us denote by $c\%$ the percentage of sample curves that are partially observed. Benchmark methods perform better as the parameter c is larger. This finding is because these reconstruction methods strongly depend on the information of the completely observed curves to estimate the covariance or the components of its eigendecomposition. However, the depth-based method can handle the case $c=0$, i.e., there are no complete functions in the sample. Therefore, results for this case are reported without comparison.

We considered two Missing-Completely-at-Random procedures for generating partially observed data for our simulation study. These procedures have previously been used in the literature (Elías et al. 2022a) and are in line with the partial observability of the real case studies. They are:

Random Intervals,:

with which c% of the sample curves is observed on a number m of random disjointed intervals of [0, 1].

Random points,:

with which c% of the functions is observed on a very sparse random grid.

First, we apply these observability patterns to simulated trajectories. Concretely, we consider a Gaussian process $X(t) = \mu (t) + \epsilon (t)$ where $\epsilon (t)$ is a centered Gaussian process with covariance kernel $\rho _{\epsilon }(s, t) = \alpha e^{-\beta | s - t |}$ for $s,t \in [0,1]$. The functional mean $\mu (t)$ is a periodic function randomly generated by a centered Gaussian process with covariance $\rho _{\mu }(s,t) = \sigma e^{-(2\sin (\pi |s - t|)^2/l^2)}$. Thus, each sample will present different functional means. The set of parameters used for our study were $\beta = 2$, $\alpha = 1$, $\sigma = 3$ and $l=0.5$. Examples of the generated trajectories by this model are those shown in Fig. 1.

We considered small and large sample sizes for the study by making $n= 200$ and 1000. Also, we considered different percentages of observed curves that were partially observed. Specifically, we tested with $c = 0, 25, 50$ and 75. In addition, we considered different percentages of time on which the incomplete curves of a sample were observed. Henceforth, we term this percentage by $p\%$. We considered $p = 25, 50$ and 75 for small samples but only $p = 25$ and 50 for large samples. This is due to the computational cost of the benchmark methods when $n=1000$ and $p=75$. Note that this parameter setting implies the highest computational cost for estimating covariance functions. Finally, we replicate 100 samples of each data set to estimate median values of MSPE.

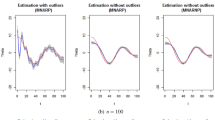
Table 1 presents results for $n=200$. It shows MSPE from the Gaussian data and points out the superiority of the Reg. Regression method (Kraus 2015) when covariance function is simple to estimate, as is the case of the exponential decay covariance function involved in these data (see left panel of Fig. 2). Even in this case, we remark that the depth-based method is slightly better than the Opt. Operator method (Kneip and Liebl 2020). When all the functions of the sample are partially observed ($c=0\%$), only the depth-based method can provide a reconstruction, and, surprisingly, the MSPE remains reasonably similar to those cases with a proportion of complete functions significantly large ($c = 25, 50, 75 \%$). With regards to estimation uncertainty, the depth-based method is superior to Opt. Operator and comparable with Reg. Regression, observed from the top panel of Fig. 3. Similar results are obtained with other sample sizes and the Random Interval setting (see the detailed results in Appendix 1.1).

Table 1 Median values of MSPE over 100 pseudo-random replicates

Appendix 1.2 includes results with functional data generated from truncated Karhunen-Loève expansions following the simulations in Liebl and Rameseder (2019) for sample sizes of 100 and 500. First, we consider one population data and, in this setting, Opt. performs better than the Gaussian processes making Opt. Operator method and Reg. Regression comparable. This finding is in line with the results reported in Liebl and Rameseder (2019). Additionally, motivated by our empirical case studies, we consider a setting with smooth functions generated with truncated Karhunen-Loève expansions for generating multiple populations. In this context, our depth-based proposal starts being competitive, achieving better results than Opt. Operator and sometimes even better than Reg. Regression. The detailed explanation of the data generation and the results are reported in Sect. A.3.

Fig. 2

Covariance estimations based on the available functions are completely observed. Left panel, Gaussian processes with an exponential decay covariance. Central panel: Spanish daily temperatures with lower covariance values in Spring and Autumn periods and higher covariance in Summer and Winter. Right panel: Japanese age-specific mortality rates with higher correlations at the oldest ages

3.2 Case study: reconstructing AEMET temperatures

Spanish Agency of Meteorology (AEMET) provides meteorological variables recorded from different stations in the whole Spanish territory (see http://www.aemet.es/es/portada). This analysis focus on maximum daily temperatures of 73 stations located in the capital of provinces. Following the literature of FDA, we consider this data as a functional data set where each function is the temperatures of each complete year (see also Febrero-Bande and Oviedo de la Fuente 2012; García-Portugués et al. 2014). Some of the curves are partially observed in the historical data, and our goal is to reconstruct the data set.

Temporal data availability depends from one station to the other. For example, Madrid-Retiro station is the oldest, being monitored from 1893, and Ceuta from 2003. We consider a set of 2786 entirely observed curves of different years and weather stations. This large sample of complete functions allows reproducing the simulation in Sect. 3.1 by randomly generating random functional samples. To do that, we randomly generate 100 samples of curves without replacement. The results for sample sizes of $n=200$ and $n=1000$ are given in Table 2. Unlike Gaussian data, the depth-based method is superior to the competitors in the simulation with AEMET data, showing small MSPE and comparable variances (see bottom panel of Fig. 3 for an insight into the uncertainty of the estimation for each method). Only for high proportions of complete functions $c=75$ and small sample size $n = 200$, Kraus ’s (2015) method was superior. The depth-based method is superior for smaller values of c or larger sample sizes $n = 1000$. These results can be explained by the complex structure of AEMET data and the availability of multiple stations with different weather conditions, as shown in the center panel of Fig. 2.

Fig. 3

Boxplots of the MSPE for 100 replicates, $p=50$ and $n=200$. Top (Gaussian data) and bottom (AEMET data) panels were obtained with the same data as Tables 1 and 2, respectively

Table 3 shows the same simulation setup with AEMET data but under the Random Interval setting and small sample size. In this setting, we generate partially observed data for a different number of observed intervals (m), percentages of completely observed curves (p), and the mean observability percentage of each partially observed curve (c). The result shows that when $p=25$, the regression method performs better than the competitors. This finding is because our implementation of the partially observed mechanism produces a sample of POFD with more proportion of observed curves in the center of the domain than in the extreme. Then, for small p the reconstruction of POFD observed in the middle of the domain worsens the results of the depth-based method. However, when p increases, our implementation of the random censoring mechanism produces a sample of POFD that uniformly covers the complete domain.

Table 2 Median values of MSPE over 100 pseudo-random replicates

Table 3 Median values of the MSPE after 100 pseudo-random replicates

In Fig. 4, we plot the reconstructions obtained by the three methods under consideration from one random sample. This was obtained by randomly taking 1000 curves from the total observed curves of the AEMET data. Then, we generated partially observed data by applying the Missing-Completely-at-Random procedure based on random intervals described above, with $m = 4$, $p=50$, and $c=50$. Finally, we randomly selected one function to reconstruct, namely, VALLADOLID/VILLANUBLA-1956, where VALLADOLID/VILLANUBLA refers to the location of the station and 1956 is the observation year. VALLADOLID/VILLANUBLA-1956 is plotted in red according to a general view of its shape. In contrast, the reconstructions are only plotted on the four intervals where the curve was observed in our simulation. The top panels of the figure show output produced by the depth-based method (Depth-based in blue), Kneip and Liebl (2020) (Opt. Operator in green), by Kraus (2015) (Reg. Regression in black). The depth-based method is superior to the benchmark methods. The bottom panel of the figure shows some descriptive statistics related to the depth-based method. We show the years used for reconstructing (the years of the curves in the envelope). The frequency of each year (number of curves into the envelope with the same year) is represented by a proportional blue bubble. Similarly, we show the locations of the curves on the right side of the envelope. From our understanding, all of them have similar geographical features.

Fig. 4

Simulated exercise reconstruction of “VALLADOLID/VILLANUBLA-1956”. Top three panels present the reconstruction by the depth-based method, Kraus (2015) and Kneip and Liebl (2020). Bottom panel, the spatial (Spanish map), and temporal (bubble plot) descriptive analyses are shown by the depth-based methodology and the envelope

Finally, Fig. 5 illustrates the actual case of “BURGOS/VILLAFRÍA-1943” a station that probably started operating in the middle of the year 1943. Consequently, only the year’s second half is recorded (red curve at the top panel). We apply the three reconstructing methods to complete the first half of the curve (Reg. Regression (Kraus 2015) in black, Opt. Operator (Kneip and Liebl 2020) in green, and the depth-based method in blue). The depth-based methodology supports the reconstruction with the additional information provided by the most important curves of the envelope. In this case, the envelope of “BURGOS/VILLAFRÍA-1943” contains distant-past functions from 1905 from the MADRID-RETIRO station and also more recent functions from the 90s from the same station. Additionally, the largest proportion of functions belongs to 1943 (biggest blue bubble), the same year of the curve to reconstruct.

Fig. 5

Holdout partially observed function, “BURGOS/VILLAFRÍA-1943”. Top panel: reconstructions by Kraus (2015) (in black) Kneip and Liebl (2020) (in green) and the depth-based method (in blue). The bottom panel shows the descriptive analysis of the most relevant curves in reconstructing “BURGOS/VILLAFRÍA-1943”. The left part is time analysis (bubble plot of the involved years); the right is spatial analysis (map with the most relevant and involved stations)

3.3 Case study: reconstructing Japanese mortality

The Human Mortality Data Set (https://www.mortality.org) provides detailed mortality and population data of 41, mainly in developed countries. Some countries also offer micro-information by subdividing territory, providing challenging spatial and temporal information. In particular, the Japanese mortality data set is available at http://www.ipss.go.jp/p-toukei/JMD/index-en.asp for its 47 prefectures for males, females, and the total population.

A common FDA approach to analyzing mortality data is to consider that each function is the yearly mortality for each age cohort (see, e.g. Shang and Hyndman 2017; Shang and Haberman 2018; Gao et al. 2019; Shang 2019). With this configuration and arranging the 47 prefectures together, we deal with a male, female, or total Japanese mortality data set of size 2007. Each prefecture does not have the same number of functions, and the range of observed years is also different. However, roughly, we have yearly mortality functions between 1975 and 2016.

Fig. 6

Reconstruction of the most poorly observed function of the sample, “Saitama-2007”. The top panel presents the reconstruction given by Reg. Regression method by Kraus (2015) (black), Opt. Operator method by Kneip and Liebl (2020) (green) and the depth-based method (blue). The bottom panel shows the year of the most important functions of the envelope, and the maps show the corresponding prefectures, in red the one to be reconstructed

In this case study, the poor availability of complete functions invalidates the possibility of resampling as done for the AEMET data set. Thus, we are only able to illustrate some empirical situations. Figures 6 and 7 present two reconstruction problems and the results obtained from the three methods. In Fig. 6, we reconstruct the shortest available curve, “Saitama-2007”, that was only available in a very short interval of mortality rates for the youngest cohorts. Reg. Regression (Kraus 2015) and Opt. Operator (Kneip and Liebl 2020) methods produce smooth results (black and green, respectively). The depth-based method produces more spiky results in concordance with other available curves. The bottom panel presents the bubble plot illustrating the period of the envelope functions and the prefectures on the map. Figure 7 presents a case with the function “Tottori-2015” that is not observed in six intervals fragments (domain where only the red curve is visible).

Fig. 7

Holdout partially observed sample function observed in six fragments, Tottori-2015. The top panel presents the reconstruction given by Reg. Regression method by Kraus (2015) (black), Opt. Operator method by Kneip and Liebl (2020) (green) and the depth-based method (blue). The bottom panel shows the year of the most important functions of the envelope, and the right map shows its prefectures

4 Conclusion

This article introduces a non-parametric method to reconstruct samples of incomplete functional data. Our proposal relies on the concept of depth for POFD to select a subset of sample curves defined to share shape and magnitude with the observed part of the curve to predict. This subset of sample curves is termed envelope, and we use it to propose a point reconstruction method based on a weighted average. These weights only depend on a parameter we set by minimizing the MSPE where the curve to predict is observed.

We compare the new method’s performance with other alternatives in the literature. Our simulation exercises consider simulated and empirical data as well as various random procedures to generate incomplete data scenarios. The available reconstruction methods seem unbeatable when covariance can be efficiently estimated in our settings. Gaussian processes exemplify these favorable circumstances with stationary covariance functions and other more complex covariance regimes, including a considerable proportion of completely observed curves. In contrast, our method outperforms when the covariance can not be properly estimated due to a richer covariance structure and highly scarce data settings. To show that, we test the methods under severe incomplete data settings and introduce more complex covariance structures. We decrease the number of completely observed functions up to zero and consider empirical data with complex covariance structures, such as yearly age-specific mortality and temperature data. Finally, our simulation exercises show that our proposal can provide a reasonable reconstruction output when every function is partially observed or, in other words, when there are no complete functions in the sample.

The depth-based method requires the Missing-Completely-at-Random assumption, which is standard in the literature. This assumption implies that the partially observed functions cover densely the reconstruction domain and that the observability process is not conditional to external information. Future research could allow for specific relationships between the functional process and generate partial observability. In addition, the depth-based algorithm requires a notion of proximity between POFD that we fill with a $L_2$ distance between the observed segments. Developments along this line would also be valuable for our proposal.

In summary, this article provides an alternative data-driven and model-free method to reconstruct POFD preferable under challenging scenarios. Last but not least, we believe that the interpretability of the results might help provide different insides into the data under analysis.

Appendix 1: Additional simulation results

1.1 Appendix 1.1: Gaussian processes

The random functions are generated as explained in Sect. 3.1. Then, the Missing-Completely-at-Random procedures are applied to generate partially observed functional data $(X_i, O_i)$. The simulation results are collated in Table 4, for Random Intervals, and in Table 5, for Random Points.

Table 4 Median values of the MSPE after 100 pseudo-random replicates

Table 5 Median values of MSPE over 100 pseudo-random replicates

1.2 Appendix 1.2: Karhunen-Loève processes

The random functions are generated by Karunhen-Loève expansions following the data generation processes in Kneip and Liebl (2020). Each function is generated as: $X_i(t) = \mu (t) + \sum _{k=1}^{50} \xi _{ik,1} cos(k \pi t) + \xi _{ik,1} sin(k \pi t)$ where $\mu (t) = t + \sin (2 \pi t)$, $\xi _{ik,1} = 50 \sqrt{\exp (-(k-1)^2)} Z_{i,1}$ and $\xi _{ik,2} = 50 \sqrt{\exp (-k^2)} Z_{i,2}$ with $Z_{i,1}, Z_{i,2} \sim N(0,1)$. Then, the Missing-Completely-at-Random procedures are applied to generate POFD $(X_i, O_i)$. The simulation results are collated in Table 6, for Random Intervals, and in Table 7, for Random Points.

Table 6 Median values of the MSPE after 100 pseudo-random replicates

Table 7 Median values of MSPE over 100 pseudo-random replicates

1.3 Appendix 1.3: Karhunen-Loève processes with multiple populations

We follow the data generation procedure of Sect. A.2 but we create ten different populations by modifying the mean function $\mu (t)$ as follows: $\mu _1(t) = \sin (10 \pi t)$, $\mu _2(t) = -\sin (10 \pi t)$, $\mu _3(t) = \cos (10 \pi t)$, $\mu _4(t) = -\cos (10 \pi t)$, $\mu _5(t) = 5t + \sin (10 \pi t + 0.5)$, $\mu _6(t) = 5t - \sin (10 \pi t + 0.5)$, $\mu _7(t) = 5t + \cos (10 \pi t + 0.5)$, $\mu _8(t) = 5t - \cos (10 \pi t + 0.5)$, $\mu _9(t) = 2t + \cos (3 \pi t - 0.5)$ and $\mu _10(t) = -5t - \cos (4 \pi t \sin (4 \pi t)$. These populations are equally probable. The Missing-Completely-at-Random procedures are applied to generate partially observed functional data $(X_i, O_i)$. The simulation results are collated in Table 8, for Random Intervals, and in Table 9, for Random Points.

Table 8 Median values of the MSPE after 100 pseudo-random replicates

Table 9 Median values of MSPE over 100 pseudo-random replicates

1.4 Appendix 1.4: Computational time performance

See Table 10.

Table 10 Computational time performance