Abstract
One-parameter link functions play a fundamental role in regression via generalized linear modelling. This paper develops the general theory for two-parameter links in the very large class of vector generalized linear models by using total derivatives applied to a composite log-likelihood within the Fisher scoring/iteratively reweighted least squares algorithm. We solve a four-decade old problem with an interesting history as our first example: the canonical link for negative binomial regression. The remaining examples are fitting Weibull regression using both the mean and quantile directly compared to GAMLSS, and performing quantile regression based on the Gaussian distribution. Numerical examples based on real and simulated data are given. The methods described here are implemented by the VGAM and VGAMextra R packages, available on CRAN. Supplementary materials for this article are available online.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For 50 years now generalized linear models (GLMs; Nelder and Wedderburn 1972) have been the foundational building block of generalized regression. Its central formula is
with \(\mu ={\mathbb {E}}(Y)\) as the mean response and link function \({\mathcal {G}}\) having strict monotonicity and being twice-differentiable in the range of \(\mu \). In its original formulation (1.1) was restricted to Y belonging to the one-parameter exponential family (see, e.g., Efron 1978), and Fisher scoring/iteratively reweighted least squares (IRLS; see, e.g., Green 1984) has become the standard GLM algorithm. The purpose of this paper is to develop its natural extension to two parameters \(\theta _1\) and \(\theta _2\), written as
to also be solved by IRLS. Here, \(\theta _j\) are general parameters and not necessarily a mean. The core problem is to derive the working weight matrices associated with this. It will be seen that total derivatives with chain rule expressions hold the key to handling multi-parameters. In (1.2) we say the parameters are intertwined in a composite linear predictor.
The most celebrated example of (1.2) is the canonical link of the negative binomial distribution (NBD),
where \(Y \sim \mathrm {NB}(\mu , k)\) with variance \(\mu (1+\mu /k)\), and \({\mathcal {G}}_2(\mu , k; {{\varvec{x}}}) = \log k\). This model is often abbreviated NB-C by some authors, e.g., Hilbe (2011), and it can be treated as an ordinary GLM if k is known. Prior to this work, estimation of (1.3) was deemed too difficult by some or it was ‘solved’ defectively by others; we recount some of its history in Sect. 4.1 and solve this four-decade old problem as our first application.
Given a suitable computational framework, (1.1)–(1.3) can also be used for GLM-like extensions such as the class of generalized additive models (GAMs; Hastie and Tibshirani 1986, 1990; Wood 2017) and Bayesian additive models for location scale and shape (Umlauf et al. 2018). This paper is motivated by the work of Miranda-Soberanis and Yee (2019) on one-parameter quantile link functions and uses the vector generalized linear and additive model classes (VGLMS/VGAMs; Yee 2015) as the computational and statistical framework. VGLMs can be loosely thought of as multivariate GLMs beyond the exponential family and this allows diversification to different data types such as categorical data (Yee 2010), extremes (Yee and Stephenson 2007), quantile regression (Yee 2004) and time series analysis (Miranda-Soberanis 2018). VGLMs/VGAMs handle M linear predictors \(\eta _j\) so that the present work is focussed on \(M=2\). Our work should not be confused with the composite link functions of Thompson and Baker (1981) who extended GLMs by associating more than one \(\eta _j\) to each mean value \(\mu _i\) (\(i=1,\ldots ,n\)). Our approach works in the opposite direction by associating \(M = 2\) parameters to each \(\eta _j\) with both sides being i-specific. The linear/additive predictors thus involve two interlaced parameters so that the likelihood that now can be handled is what might be described as a composite likelihood.
This work confers several immediate benefits. First, as (1.2) allows \({{\varvec{x}}}\) to affect both parameters directly, it is much more flexible than (1.1) operating twice separately. Consequently, a second benefit is that we can now fit models previously unimplemented such as the NBD with its canonical link. Indeed, the methodology can be applied to any function of \(\varvec{\theta } = \left( \theta _1, \theta _2 \right) ^T\) with a tractable inverse, as defined in Sect. 3.1. In this paper we present three diverse applications, e.g., the mean \(\left( \mu _{W}\right) \) and the quantile functions of the two-parameter Weibull distribution, and the normal distribution’s quantile function. The new link functions have the form \(\eta = {\mathcal {G}}\left( \mu _{W}(\theta _1, \theta _2) \right) \) or \(\eta = {\mathcal {G}}\left( \tau ^{\text {th}}(\theta _1, \theta _2) ~quantile \right) \). However, our approach is broader still. In theory, one can directly model, say, the variance as an alternative to study a model’s underlying homoscedasticity assumptions. A third benefit is that the methodology can be readily extended to three-parameter VGLMs, and theoretically to M-parameter link functions, and so introducing more flexibility by handling statistical measures of distributions having location, scale and shape parameters (or LSS–links). The basic motivation for using LSS–links rather than simple one–parameter links is that the stochastic relationship between predictors and response can be modelled much better and with greater accuracy. Thus this work points towards \(\eta _j={\mathcal {G}}_j({\varvec{\theta }};\, {{\varvec{x}}}),\ j=1,\ldots ,M\), with \({\varvec{\theta }}= \left( \theta _1, \ldots , \theta _M \right) ^T\), as being the ultimate set of link functions.
An outline of this paper is as follows. Sect. 2 summarizes skeletal details of VGLMs needed here. Sect. 3 gives the general theory for two-parameter links. Sect. 4 solves the NBD canonical link problem and proposes two-parameter Weibull mean and quantile regression as well as Gaussian quantile regression. Numerical examples involving real and simulated data including a comparison to generalized additive models for location, scale and shape (GAMLSS) appear in Sect. 5. The paper ends with a discussion. An R script file and online appendices are available as supplementary material.
Notationally, we use ‘\(\partial \)’ for partial derivatives and ‘d’ for total derivatives (see, e.g., Loomis and Sternberg 1990). The digamma and trigamma functions are denoted by \(\psi \) and \(\psi '\). The Hadamard (element-by-element) and Kronecker products of two matrices \({{\varvec{A}}}\) and \({{\varvec{B}}}\) are \({{\varvec{A}}}\circ {{\varvec{B}}}= [(a_{js} \cdot b_{js})]\) and \({{\varvec{A}}}\otimes {{\varvec{B}}}= [(a_{js} \cdot {{\varvec{B}}})]\) respectively.
2 VGLM review
VGLMs operate on data \(({{\varvec{x}}}_i, {{\varvec{y}}}_i)\), \(i = 1, \ldots , n\), independently with \({{\varvec{y}}}_i\) a Q-dimensional response and covariates \({{\varvec{x}}}_i = \left( x_{i1}, x_{i2}, \ldots , x_{id} \right) ^T\) with \(x_{i1} = 1\) if there is an intercept. A VGLM is defined in terms of M linear predictors as a model where the conditional distribution of \({{\varvec{y}}}\) given \({{\varvec{x}}}\) has the form (dropping the subscript i for simplicity)
for some function \({\mathcal {F}}(\cdot )\), where \({{\varvec{B}}}\) is \(d \times M\) with \({\varvec{\eta }}= {\varvec{\eta }}({{\varvec{x}}}) = \)
In the usual case the jth linear predictor is \(\eta _j({{\varvec{x}}}) = {\varvec{\beta }}^T_j {{\varvec{x}}}\) and can be tied in to the parameters \(\theta _j\) of any distribution as \( {\mathcal {G}}_j (\theta _j) = \eta _j = {\varvec{\beta }}_j^T {{\varvec{x}}}\), \(j = 1, \ldots , M \).
Fitting VGLMs produce full maximum likelihood estimates (MLEs). The ‘general’ VGLM log-likelihood is
for known fixed positive prior weights \(w_i\). A Newton-like algorithm for maximizing (2.2) has the form \( {\varvec{\beta }}^{(a)} = {\varvec{\beta }}^{(a - 1)} + {\varvec{\mathcal{I}}}\left( {\varvec{\beta }}^{(a - 1)}\right) ^{-1} \varvec{U}\left( {\varvec{\beta }}^{(a - 1)}\right) \) at iteration a . For VGLMs, the vector of coefficients \({\varvec{\beta }}^{(a)}\) is obtained by iteratively regressing the working responses \({{\varvec{z}}}^{(a - 1)}\) on the ‘big’ model matrix \( {{{\varvec{X}}}}_{\scriptstyle {\text {{VLM}}}} = \left( {{{\varvec{X}}}}_1^T, \ldots , {{{\varvec{X}}}}_n^T\right) ^T, \) which has the form
where \({{{\varvec{X}}}}_{\scriptstyle {\text {{VLM} }}} = {{\varvec{X}}}_{{\mathrm{LM}}} \otimes {{\varvec{I}}}_M\), known as the ‘large’ model matrix, has dimension \(nM \times Md\), and \({{{\varvec{X}}}}_i\) is the \(M \times (Md)\) block-matrix \({{{\varvec{X}}}}_i = {{\varvec{x}}}_i \otimes {{{\varvec{I}}}}_M\).
In (2.3), \({{{\varvec{U}}}} = \left( \varvec{u}_1, \ldots , \varvec{u}_n \right) ^T\) comprises the individual score vector \({{\varvec{u}}}_i\) whose jth element is \(\displaystyle { \left( {{\varvec{u}}}_i \right) _j = \frac{\partial \ell _i}{ \partial \eta _j} } \) and \({{\varvec{W}}}\) is the matrix \({{\varvec{W}}}= \text {diag}\left( w_1 {{\varvec{W}}}_1^{-1}, \ldots , w_n {{\varvec{W}}}_n^{-1}\right) \). The \({{{\varvec{W}}}}_i\)s are the ‘general’ \(M \times M\) working weight matrices, with (j, k)th element \( \displaystyle {\left[ {{{\varvec{W}}}}_i\right] _{j, k} = - w_i~{\mathbb {E}} \left( \frac{\partial ^2 \ell _i}{ \partial \eta _j \partial \eta _k} \right) }. \)
At convergence, the estimated variance-covariance matrix is \( \widehat{\text {Var}} \left( \widehat{{\varvec{\beta }}^{*}}\right) = {\widehat{\phi }} \left( {{\varvec{X}}}^T_{\text {VLM}} {{\varvec{W}}}^{(a)} {{\varvec{X}}}_{\text {VLM}} \right) ^{-1} \). Using the observed information matrix (OIM) corresponds to the Newton-Raphson algorithm. Fisher scoring is primarily used within the VGLM framework over Newton-Raphson because the expected information matrices (EIMs) are positive-definite over a larger portion of the parameter space.
With multiple \(\eta _j\) one can enforce linear relationships between them via
for known constraint matrices \({{\varvec{H}}}_k\) of full column-rank (i.e., rank \({{\varvec{H}}}_k = {\mathcal {R}}_k = {\texttt {ncol}}({{\varvec{H}}}_k)\)), and \({\varvec{\beta }}^{*}_{(k)}\) is a possibly reduced set of regression coefficients to be estimated. The matrices \({{\varvec{H}}}_k\) can constrain the effect of a covariate over some \(\eta _j\) and to have no effect for others. Trivial constraints are attained with \({{\varvec{H}}}_k={{\varvec{I}}}_M\) for all k, where \({{\varvec{X}}}_{{\mathrm{VLM}}} = {{\varvec{X}}}_{{\mathrm{LM}}} \otimes {{\varvec{I}}}_M\) is preserved. Other common examples include parallelism (\({{\varvec{H}}}_k=\mathbf{1}_M\)), exchangeability, and intercept-only parameters \(\eta _j=\beta _{(j)1}^*\). For a general review on VGAMs see Yee (2015, Sec. 1.3.2).
3 General theory for two-parameter links
3.1 Problem formulation
Given the preceding background, our attention focusses on \(M = \text {dim}({\varvec{\varTheta }})= 2\) transformations of \({\varvec{\varTheta }}= \{ \left( \theta _1, \theta _2 \right) ^T; \theta _j \in A_j \subset {\mathbb {R}} \}\) of the form
for known bivariate functions \({\mathcal {G}}_k: {\varvec{\varTheta }}\rightarrow B \subseteq {\mathbb {R}}\), \(k = 1, \dots M\). Here, B, and \(A_j, j = 1, 2\) are open intervals. Consequently, the VGLM log-likelihood (2.2) reduces to
where \({\varvec{\eta }}= \left( \eta _{{\mathcal {G}}_1}, \eta _{{\mathcal {G}}_2} \right) ^T\).
Equation (3.1) is central to this article and gives rise to the three cases
We assume that \(\eta _{{\mathcal {G}}_j}\) can be solved at least iteratively for \(\theta _j\) (cf. (3.9)), allowing (3.2)–(3.4) to be expressed as
The interdependency between the \(\theta _j\) enforces a reparametrized log-likelihood. For example, for the general case (3.7) above we have
We call (3.8) the modified VGLM log-likelihood as it reflects the composite structure of two-parameter linear predictors. Fisher scoring must be consequently adjusted.
Before detailing its solution, we list the assumptions made over \({\mathcal {G}}_k\) in (3.1) required.
Assumptions
-
(i)
For each \({\mathcal {G}}_j\) in (3.1) the derivatives \(\partial {\mathcal {G}}_j / \partial \theta _k\), \(\partial ^2 {\mathcal {G}}_j / \partial \theta _k^2\) and \(\partial ^2 {\mathcal {G}}_j / \partial \theta _l \partial \theta _k\) exist over either \(A_j\) or \({\varvec{\varTheta }}\) accordingly.
-
(ii)
For each equation in (3.1), \(\eta _{{\mathcal {G}}_j}\) can be solved for \(\theta _j\), in the form
$$\begin{aligned} \theta _1 = \theta _1\left( \eta _{{\mathcal {G}}_1}, \theta _2 \right) = {\mathcal {G}}_1^{*}( \eta _{{\mathcal {G}}_1}, \theta _2) ~~\text {and}~~ \theta _2= \theta _2\left( \theta _1, \eta _{{\mathcal {G}}_2} \right) = {\mathcal {G}}_2^{*}\left( \theta _1, \eta _{{\mathcal {G}}_2} \right) , \end{aligned}$$(3.9)for known functions \({\mathcal {G}}_j^{*}\), \(j = 1, 2\).
-
(iii)
For every \({\varvec{\eta }}^{0} = \left( \eta _{{\mathcal {G}}_1}^{0}, \eta _{{\mathcal {G}}_2}^{0}\right) ^T \in B \times B\), the system (3.1) has unique solution, denoted \( {\varvec{\theta }}_{{\mathcal {G}}} = \left( \theta ^1_{{\mathcal {G}}}, \theta ^2_{{\mathcal {G}}}\right) ^T\), given by
$$\begin{aligned} \theta ^1_{{\mathcal {G}}} = \theta _1\left( \eta _{{\mathcal {G}}_1}^0, \theta _2 \right) = {\mathcal {G}}_1^{*}( \eta _{{\mathcal {G}}_1}^0, \theta _2) ~~\text {and}~~ \theta ^2_{{\mathcal {G}}} = \theta _2\left( \theta _1, \eta _{{\mathcal {G}}_2}^0 \right) = {\mathcal {G}}_2^{*}\left( \theta _1, \eta _{{\mathcal {G}}_2}^0 \right) . \end{aligned}$$(3.10) -
(iv)
From (3.9),
-
(a)
the derivatives
$$\begin{aligned} \frac{\partial \theta _j}{\partial \eta _{{\mathcal {G}}_j}} ~~\text {and}~~~ \frac{\partial ^2 \theta _j}{\partial \eta _{{\mathcal {G}}_j}^2}, \quad j = 1, 2, \end{aligned}$$(3.11)exist on B, and
-
(b)
the derivatives
$$\begin{aligned} \displaystyle { \frac{\partial \theta _j}{\partial \theta _k}, \qquad j, k = 1, 2,~~j \ne k, } \end{aligned}$$(3.12)exist over \(A_k\).
-
(a)
When \({\mathcal {G}}_j^{*}, j = 1, 2,\) in (3.1) are not tractable then \({\mathcal {G}}_j^{*}\) and \({\varvec{\theta }}_{{\mathcal {G}}}\) in (3.10) can be computed via iterative methods. Optionally, implicit differentiation applied to (3.1) can be used to obtain (3.11) and (3.12) if (3.1) cannot be explicitly solved for \(\theta _j\). In particular, \( {\partial ^2 \theta _j} / ({\partial \eta _{{\mathcal {G}}_1} \partial \eta _{{\mathcal {G}}_2}}) = 0. \)
3.2 Solution
Expressions (3.5)–(3.7). shed light on the interdependence between \(\theta _j\) and \(\theta _k\) and its pivotal role when computing
from the modified log-likelihood (3.8). Note that
The solution to incorporating two-parameter linear predictors to the VGLM framework relies on computing (3.13) by appropriately embedding (3.8) and (3.14). Total derivatives are necessary since \(\theta _1\) and \(\theta _2\) now vary simultaneously, and the solution produces a new set of expressions for the score vector and working weight matrices.
For the score vector, each component is a total derivative \({{\text {d} \ell } / {\text {d} \theta _j}}\) given by
which apply to VGLMs with the two linear predictors as in case (3.4). For the special cases (3.2) and (3.3), at least one linear predictor is univariate, that is, a function of either \(\theta _1\) or \(\theta _2\) (but not both), hence \({\partial \theta _2} / {\partial \theta _1} = 0\) or \({\partial \theta _1} / {\partial \theta _2} = 0\). Table 9 in Appendix A shows the expressions for the three cases (3.2)–(3.4).
Likewise, the EIMs for VGLMs with \(M = 2\) linear predictors \({\varvec{\eta }}\) is given by \(\mathcal {{\mathcal {I}}}_{E}({\varvec{\eta }}) = - {\mathbb {E}} \left[ {\partial ^2 \ell } / ({ \partial {\varvec{\eta }}\; \partial {\varvec{\eta }}^T }) \right] \) where
Applying the chain rule with the inclusion of total derivatives,
Under regularity conditions, the terms in braces vanish after taking the expectation, giving place to the new expressions for the EIMs:
Again, new complementary expressions for \({\text {d}^2 \ell } / {\text {d} \theta _j^2}\) and \({\text {d}^2 \ell } / {\text {d} \theta _j \, \text {d} \theta _k}\), \(j, k = 1, 2\), are required. For the the general case (3.4), where each linear predictor depends on \(\theta _1\) and \(\theta _2\), these are
respectively. Tables 10 and 11 outline the expressions for the three cases (3.2)–(3.4).
4 Some applications
We present direct applications of the previous section, tying it in with software implementations both new and old. The first shows that the NB-C can be straightforwardly estimated as a VGLM by adjusting the score vector and working weight matrices of the composite log-likelihood. The second considers two variants of Weibull regression: the mean parameterization coincides with WEI3() in gamlss.dist whereas the quantile parameterization is novel. The third sketches the details for directly fitting the two-parameter quantile function of the normal distribution, as implemented by a new link function normalQlink() from VGAMextra 0.0-5.
4.1 Negative binomial canonical link
The estimation of the NB-C has a somewhat interesting history. If we take the problem as beginning with the admission of McCullagh and Nelder (1983, p.195) [see also McCullagh and Nelder (1989, p.374)] that the NB is little used in applications and has a “problematical” canonical link then to our knowledge only one other publicized attempt has been made since to solve the problem seriously. It eluded McCullagh and Nelder because the model makes \(\eta \) a function of a parameter of the variance. Hilbe (2011, pp. 210,309,315–6) sheds more light on the problem as well as proposing an adhoc method that tends to work in most cases. He writes “In discussing this statement with Nelder, I found that the foremost problem they had in mind was the difficulty they experienced in attempting to estimate the model. They do not state it in their text, but the problem largely disappears when k is entered into the GLM estimating algorithm as a constant” [italics added]. He notes that having k in the link and variance can result in estimation difficulties in a full MLE algorithm, with it being sensitive to initial values and having tedious convergence with Newton-Raphson-type algorithms. To our knowledge his R package COUNT function ml.nbc() is the only other NB-C MLE-implementation. It treats k as constant at each iteration but it is iteratively estimated in the process. It also treats k as an additional scalar parameter to be estimated, hence is constrained to be intercept-only. A general optimizer stats::optim() is invoked and it has by default some prechosen constants for initial values (\(k^{(0)}=2\) and \(\mu ^{(0)}=e^{-1} \approx 0.368\)) so that it will be unreliable for large \(\mu \) and k. In contrast, we believe our solution to be nondefective. Prior to this work, the NB-C had also been unsatisfactorily implemented in VGAM 1.0-3 or earlier (see, e.g., Yee 2015, Sec.11.3.4) but has since been corrected in functions negbinomial() and nbcanlink()—more details are given in Miranda-Soberanis (2018).
Ordinarily, NB regression operates with
and adopting the R parametrization
with \(0 < \mu \) and \(0<k\), if the ancillary parameter k is intercept-only then this is referred to as the NB-2 model. The NB-C is of the first case of Table 9, and is
The ith contribution to the log-likelihood is given by
With the ordinary \(\eta _j\) of (4.1), one has
However, with the \(\eta _j\) as in (4.3), the relationship \(\mu = {k}/{[e^{-\eta _1} - 1]}\) implies (the subscript i is dropped for simplicity)
The partial derivatives here are directly computed from (4.4), resulting in
and \(\partial \ell / \partial k\) as in (4.5). Substituting these into (4.6) gives
which is (4.5) without its last term. Also, \({\text {d} \ell } / {\text {d} \mu } = {\partial \ell } / {\partial \mu }\) is given in (4.7), completing the score vector.
The new EIMs are fully specified by (3.17) (see Table 11). Unlike other NB variants the NB-C EIM is nondiagonal. The adjusted nondiagonal component is given by
Moreover, while \( {\mathbb {E}}\left[ {\text {d}^2 \ell } / {\text {d} \mu ^2} \right] \) remains as usual, the other diagonal element needs adjustment:
where \(\mathcal{W}_{kk}\) is the usual 2–2 element. Combining everything, the working weight matrix is
when \(\eta _{{\mathcal {G}}_2} = \log k\). Because the EIM of all NB variants except for the NB-C is diagonal the alternating algorithm adopted by Hilbe and MASS::glm.nb() is less prone to failure. But with NB-C, \(\mu \) and k are asymptotically dependent therefore the alternating algorithm is more likely to fail.
4.2 Weibull regression
The VGAM family function weibullR() follows from base R’s [dpqr]weibull() parameterization \(f(y) = (s/b) (y/b)^{s-1}\) \(\exp (- (y/b)^s)\) for shape parameter \(s>0\) and scale parameter \(b>0\) on \(y \in (0, \infty )\). Its mean is \(b \; \varGamma (1+ s^{-1})\). For \({\varvec{\theta }}=(b, s)^T\), weibullR(lss = TRUE) has EIM
where \(\gamma = -\psi (1)\) is the Euler–Mascheroni constant (Yee 2015, Table 12.3). For this, \(\eta _1 = \log b\) and \(\eta _2 = \log s\).
Adapted for the Weibull, the methodology of this paper results in the addition of two new 2–parameter links for mean and quantile modelling, called weibullMlink() and weibullQlink(). To our knowledge the latter is first implementation to exist in such general form. They are used in conjunction with the newly written weibullRff() in VGAMextra 0.0-5. These links apply only to \(\eta _1\). Table 1 gives the Weibull distribution’s new links and their inverses \(\eta _1^{-1} = b(s) = b_s\) as a function of s, hence the composite \(\ell (b(s), s; y) = \log s + (s - 1) \log y - \left( {y} / {b_s} \right) ^{s} - s \log b_s\). The new EIMs have form
It is noted that Noufaily and Jones (2013) concerns parametric quantile regression like ours but based on a generalized gamma distribution.
4.3 Distribution–specific quantile regression: the normal distribution
Another example is a two-parameter link for the quantiles of the normal distribution defined as
where \(\varPhi \) is the standard normal CDF and pre-specified quantiles of interest \({\varvec{\tau }}= \left( \tau _1, \ldots , \tau _s\right) ^T\). Its implementation is uninormalQlink(), available in VGAMextra 0.0-5.
Ordinarily, \({\varvec{\theta }}= \left( \mu ,\ \sigma \right) ^T\) can be estimated with VGAM::uninormal() whose default linear predictors are \(\eta _{1}(\mu ; {{\varvec{x}}}) = \mu \) and \(\eta _{2}(\sigma ; {{\varvec{x}}}) = \log \sigma .\) For uninormal(var.arg = FALSE) the EIMs are
With uninormalQlink() we allow \(\eta _1\) of uninormal() to handle (4.10):
implemented in the brand–new VGAMextra::uninormalff(). Using \(\displaystyle {\frac{\partial \mu }{\partial \sigma } = - \varPhi ^{-1}(\varvec{\tau })}\), the new EIMs are
Our work on quantile regression have the following advantages over Koenker and Bassett (1978):
-
(i)
Parametric quantile regression provides more accurate inference when the data comes from the stipulated distribution. In contrast, theirs is a nonparametric \(L_1\)–norm method based on linear programming which is less familiar to statisticians than \(L_2\) methods like IRLS. Moreover, VGAM computes confidence intervals based on the well–known Wald and score tests. In theirs the confidence intervals are based on piecewise linear approximations and when using large number of predictors the algorithm may become unstable, see, e.g., Kneib (2013).
-
(ii)
The VGLM/VGAM framework can circumvent the quantile crossing problem by choosing appropriate constraint matrices \({{\varvec{H}}}_k\) (Eq. (2.4); see also Yee (2015, Sec. 3.3)). Indeed, for some VGLMs such as the exponential and Maxwell the \(\eta _j\) are naturally parallel and so constraints need not to be enforced specifically (Miranda-Soberanis and Yee 2019).
-
(iii)
While their methodology is less sensitive to extreme values than least squares, ours is more amenable to skewed distributions such as the lognormal (theoretically, we can now implement quantile link functions for as often as needed), thus providing a more suitable framework to handle various asymmetric data such as income or wealth.
-
(iv)
VGAM has infrastructure to accommodate spline modelling, so matching Koenker and et al. (2020) which includes linear as well as nonlinear effects.
5 Examples
5.1 NB canonical link
In this section we present two numerical examples of NB-C regression. The first aims to demonstrate the instability of Fisher scoring without total derivative adjustment. We also compare our results to quantile regression using quantreg (Koenker and et al. 2020). The second uses the data set medpar from COUNT to compare the Hilbe’s and our software. We aim to demonstrate the advantages conferred by negbinomial() and its ability to handle the size parameter as a covariate-specific linear predictor. All the R code is available as a supplement.
5.1.1 Simulated data
To illustrate the unreliability of ml.nbc() we adapted code from the COUNT online help and generated \(n=1000\) random variates for \({\varvec{\beta }}_1 = (-3, 1.25, 0.1)^T\), \(k=e^{7} \approx 1100\), and \(x_2\) and \(x_3 \sim \mathrm {Unif}(0, 1)\) independently. Upon fitting the model, several warnings were issued by ml.nbc() from attempts to evaluate (4.2) outside the parameter space. When \(k = e^{8} \approx 2980\) was attempted ml.nbc() issued an error message. A brief comparison of the fits is as follows. The log-likelihood of the ml.nbc() fit, \(-3917.8\), is grossly suboptimal compared to VGAM (\(-3880.2\)). Also, its estimated regression coefficients differ much from the true values (Table 2). In comparison, the results of VGAM fare well in Table 2 as well as the Wald 95% confidence intervals (Table 3) which cover the true values. For the latter, ml.nbc() fails on all counts. From experience, about 5–8 iterations is typical for well-fitting VGLMs and the VGAM fit took 5 iterations to converge, and \(\log {\widehat{k}}\approx 6.66082\) with SE 0.22791. In VGAM 1.0-6 or earlier, ‘convergence’ was not achieved within 30 iterations.
5.1.2 Lake Otamangakau trout data
Dedual et al. (2000) describe a quantitative study of the ecology of brown (Salmo trutta) and rainbow trout (Oncorhynchus mykiss) in the central North Island of New Zealand. We fit four NB-variants to closely related data, which may be found in the trapO data frame in VGAMdata. Comprising 1226 rows of daily captures of the two species by gender at the Te Whaiau Trap at Lake Otamangakau, the data were collected during the main spawning period over 8 consecutive years by the Department of Conservation. The primary aim of this analysis is to model \(Y=\) the number of male brown trout captured as a function of the day of the year (e.g., 1 = Jan 1, 244 = Sep 1), i.e., doy is the sole (primary) explanatory variable. It is well known that spawning peaks around the second half of May.
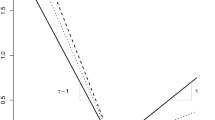
The variance-to-mean ratio of 12.12 indicates overdispersion relative to the Poisson. Following the same nomenclature as Hilbe (2007), the four NB-variants fitted here are abbreviated NB-1, NB-2, NB-H and NB-C. The former has \({\mathrm{var}}(Y) \propto \mu \), and the NB-H has \(\eta _2=\log k={\varvec{\beta }}_2^T {{\varvec{x}}}\) while NB-2 has an intercept-only \(\eta _2\). All four models have \(\eta _1 = {\varvec{\beta }}_1^T {{\varvec{x}}}\). Because \(\mu \) is clearly unimodal, we fit a NB-H VGAM to explore the data; the component functions are overlaid in Fig. 1a. Interestingly, both have an approximate quadratic shape with different peaks and curvature. It was considered safest to model the nonlinearity in both \(\eta _j\) nonparametrically.
To compare the variants more rigourously we replace the cubic (vector) smoothing splines (Yee and Wild 1996) by regression splines because inference is more standard (Figure 1). In R this was the term bs(doy) used by vglm() rather than s(doy) within vgam(). The term offers 3 degrees of freedom excluding an intercept.
Table 4 summarizes the results ranked by AIC. The NB-C was superior followed by the NB-H, and this suggests that the day of the year strongly affects both \(\mu \) and k—the other models are too simple. That the NB-C performed best suggests that the relationship between the mean and variance is not as simple as what a basic loglinear relationship can allow. Indeed, \(\mu \) appears to be coupled with k in the more complex nonlinear manner provided by the canonical link. Other NB analyses, including the NB-C, on real data are presented in Yee (2020).
a Centred component functions (overlaid) with pointwise \(\pm 2\)SE bands of a fitted NB-H VGAM: \({\widehat{\eta }}_1\) is blue, \({\widehat{\eta }}_2\) is orange; b Fitted values \({\widehat{\mu }}_i\) of the NB-C using regression splines. The vertical lines denote the first day of the months April to September (color figure online)
5.2 Distribution-specific quantile regression: the Weibull distribution
We use the Munich rental guide data (Fahrmeir et al. 2013, Page 5) available in the gamlss R package (data set rent99) which has been analysed using a Box-Cox Cole and Green (BCCG) regression with GAMLSS by Rigby et al. (2013) (Table 5).
As an alternative, we re-analyse this data using Weibull quantile regression with weibullQlink() for two reasons: as a demonstration of the new link function, and to show that the Weibull distribution appears to work well for the target variable rent, even though it is traditionally used more in survival analysis. The proposed GAMLSS model is
where \({\mathcal {G}}\) is either the BCCG or the Weibull distribution. Intercept–only models for \(\sigma \) and \(\nu \) are set for comparison purposes.
To check on the distributional assumptions we fit BCCG and Weibull regressions to the data as in (5.1). The estimated BCCG and Weibull QQ-plots shown in Figure 2, and AICs and BICs from both models in Table 6 show the Weibull distribution performs as well as or better than the BCCG method.
We now compare Weibull quantile regression with \(\varvec{\tau } = c(0.5, 0.25, 0.50, 0.75, 0.95)^T \) and weibullQlink() from VGAMextra to the \(\tau \) quantile of rent under GAMLSS given by \(y_{\tau } = \mu ~\cdot ~\)qBCCG(\(\tau , 1, \sigma , \nu \texttt {)}\), where qBCCG(\(\tau , 1, \sigma , \nu \texttt {)}\) is the \(\tau \) quantile of the BCCG distribution. Figure 3 shows the estimated quantile curves and Table 7 gives the empirical quantiles. Both methods are effectively comparable and perform equally well.
5.3 Quantile modelling with the normal distribution
This example is based on Koenker and Hallock (2001) who performed conditional quantile regression of covariates associated to birth weight of live babies to demonstrate its better performance over ordinary least squares (OLS) when estimating the effects on the lower tail of the skewed birthweight distribution. This relationship was initially explored by Abreveya (2001). Koenker and Hallock (2001) used a sample (\(n = 198,377\)) of the June 1997 Detailed Natality Data published by the National Centre for Health Statistics (NCHS) that contains information from live, singleton births, mothers aged 18–45 and residing in USA.
5.3.1 An example using uninormalQlink()
To test the quantile regression framework introduced in Sect. 4.3 we carry out VGLM quantile modelling with uninormaQlink() and uninormalff(), and compare our results to Koenker and Hallock (2001) via rq() from quantreg. Due to availability constraints, we restrict ourselves to a \(n = 50,000\) subsample of the the 1997 NCHS data (Koenker and Hallock 2001) stored in the file BWeights.csv and incidentally obtained from the SAS® file Sashelp.BWeights. Section D of the Online Supplements gives a short description of BWeights.csv and SAS® code used to generate it, as well as supplementary code pertaining this section. BWeights.csv is available in the Supplementary Materials.
Following Koenker and Hallock (2001) and Abreveya (2001), the response is birthweight (recorded in grames) and the remaining factors are added into the model as covariates including a quadratic term for the mother’s age and the mother’s reported weight gain during pregnancy:
We set \({\varvec{\tau }}= \left( 0.05, 0.25, 0.50, 0.75, 0.95 \right) \).
Regression estimates by quantile level for the birthweight model using uninormalQlink() (orange) and quantreg (black), c.f. Koenker and Hallock (2001, p. 150) (color figure online)
The trace output from vglm() looks natural and correct. We have set zero = NULL to allow both linear predictors to be regressed on all the covariates. Note, \(\eta _{{\mathcal {G}}_1}\) in (4.11) is managed by the new link function uninormalQlink(). The function Q.reg() is required to create a multiple responses matrix spanning r = length(mytau) columns.
Figure 4 shows the estimated parameters by quantile level from VGAMextra and quantreg for a few relevant covariates. Results conform with Koenker and Hallock (2001, p.150) to a great extent showing similar trends, except by Mom weight gain perhaps due the large range covered by this covariate (largest range among all covariates), as shown in Table 8.
Infants born to black mothers appear to weigh less, by between 100 and 300 grams, than newborns from white mothers across 5% to 95% quantiles. Likewise, although to a smaller extent, ‘smoking’ (this is Cigarettes per day (CigsPerDay) coded as ‘1’ if the mother smokes more than five cigarettes p/day and ‘0’ otherwise) is associated with newborns’ weight loss. With smaller effects, maternal age appears to top birth weight up incrementally, by 4–6 grams, from the 5% quantile to the 95% quantile, while every kilogram gained during pregnancy is associated with gradual reductions in the infant’s weight (4–5 grams). The model summary is in Section D of the Online Supplements.
6 Discussion
This paper has developed the general methodology for two-parameter link functions and used the NB-C and quantile modelling as the primary examples. The approach taken here is the first of two general options: (i) offer one family function that handles several different link parameterizations; (ii) offer several family functions corresponding to several different parameterizations of the same distribution. Each option has its advantages and disadvantages. Writing a new link function arguably involves less work and also the EIM may be too difficult to derive directly. However, given a choice, it is likely that many practitioners would choose a particular family function and use that solely.
Over many years the NB-C has been widely referred to in mathematical statistics because of its connections with core concepts such as sufficient statistics,GLMs and variance functions. Despite this, Hilbe (p. 315, 2011) writes concerning its practical use: “Little work as been done with NB-C models. No research has been published using an NB-C model on data.” This might be partially explained by the observation that almost all practitioners use existing implementations written by others and that the NB-C is a model with practical shortcomings such as \(\eta _{{\mathcal {G}}_1} < 0\) in (4.3) rather than being unbounded. It is disappointing that, after several decades, our implementation is the first to fit the NB-C by a ‘proper’ algorithm because some packages simply call a general optimizer such as optim(). Our solution is naturally flexible too, as seen by the NB-C-H VGAM fitted in Sect. 5.1.2.
Our results on quantile regression showing that it is loosely ‘regression estimated on multiple quantiles’ are obviously dependent on a strong distributional assumption, however there are real practical benefits and realistic applications, as discussed in Sects. 4.3 and 5. The Weibull distribution is used invariably to model observed failures in survival analysis and reliability, and the normal distribution is almost foundational for many natural phenomena. Covariates can also be included and their effects on the distributions examined. We believe that drawbacks from a distribution-specific framework are ameliorated by smoothing-based infrastructure capable of identifying nonlinearity automatically and graphically, as well as the handling of a very broad range of response types such as categorical and survival data.
It is not surprising that this work is seemingly related to that of others. For example, Efron (1986) and Smyth and Verbyla (1999) model the mean and dispersion simultaneously in what are called ‘double exponential families’ and ‘double GLMs’ respectively. However, both apply separate ordinary links to each of the first two moments rather than including a single link function of both parameters. Likewise, Cepeda-Cuervo et al. (2014) develop ‘double GLMs’ with random-effects utilizing the same type of ordinary link functions.
There is scope for future work. Slightly more interpretable than the NB-C link might be \( \eta _{{\mathcal {G}}} = \log \left[ - \log \{ {\mu } / {(\mu + k)} \} \right] \), and practically, other alternatives include \(\mathrm {logit}\{ {\mu } / {(\mu + k)} \} = \log \{ \mu / k \}\) and \(\varPhi ^{-1}( {\mu } / {(\mu + k)}\); they could easily be estimated with the present methodology. More generally, NB regression has the limitation that it does not handle underdispersion relative to the Poisson, hence other alternatives such as the Conway-Maxwell-Poisson distribution have gained popularity (see, e.g., Sellers and Shmueli 2010). Of course, the methodology could be generalized to \(M > 2\) parameters and in particular, the \(M=3\) case would match distributions having a location, scale and shape parameter.
Quantile and mean modelling is another area to be further exploited in the short-term. We are applying this methodology to several two–parameter distributions which will soon have, as the Weibull example, links of the form distribution Qlink() or distribution Mlink() alluding the ‘quantile’ and ‘mean’ link respectively. We have already commenced work in this direction, e.g., with the ‘mean link’ for the 2–parameter gamma distribution, viz. VGAMextra::gammaRMlink(). However, the VGLM framework is broader, with further options such as additive models (Yee and Wild 1996) and reduced–rank regression (Yee and Hastie 2003) over the same \({\varvec{\eta }}\). We hope to investigate these options too, including nlrq() from quantreg for nonlinear quantile regression.
References
Abreveya J (2001) The effects of demographics and maternal behaviour on the distribution of birth outcomes. J Econ 26(1):247–257
Cepeda-Cuervo E, Migon HS, Garrido L, Achcar JA (2014) Generalized linear models with random effects in the two-parameter exponential family. J Stat Comput Simul 84(3):513–525
Dedual M, Maxwell ID, Hayes JW, Strickland RR (2000) Distribution and movements of brown (Salmo trutta) and rainbow trout (Oncorhynchus mykiss) in Lake Otamangakau, central North Island, New Zealand. New Zealand J Marine Freshwater Res 34(4):615–627
Efron B (1978) Geometry of exponential families. Ann Statist 6(2):362–376
Efron B (1986) Double exponential families and their use in generalized linear regression. J Amer Statist Assoc 81(395):709–721
Fahrmeir L, Kneib T, Lang S, Marx B (2013) Regression: models. Springer, Methods and Applications
Green PJ (1984) Iteratively reweighted least squares for maximum likelihood estimation, and some robust and resistant alternatives. J Roy Statist Soc Ser B 46(2):149–192
Hastie T, Tibshirani R (1986) Generalized additive models. Stat Sci 1(3):297–318
Hastie T, Tibshirani R (1990) Generalized additive models. Chapman & Hall, London, UK
Hilbe JM (2007) Negative binomial regression. Cambridge University Press, Cambridge
Hilbe JM (2011) Negative binomial regression, 2nd edn. Cambridge University Press, Cambridge, UK
Kneib T (2013) Beyond mean regression. Stat Model 13(2):275–303
Koenker R, Bassett JG (1978) Regression Quantiles. Econom J Econom Soc 46(1):33–50
Koenker R, et al (2020) quantreg: Quantile Regression. URL https://CRAN.R-project.org/package=quantreg. R package version 5.67
Koenker R, Hallock K (2001) Quantile regression. J Econ Perspect 15(4):143–156
Loomis LH, Sternberg S (1990) Advanced calculus. Jones and Bartlett Publishers, Boston, USA, revised edition edition
McCullagh P, Nelder JA (1983) Generalized linear models, 1st edn. Chapman & Hall, London, UK
McCullagh P, Nelder JA (1989) Generalized linear models, 2nd edn. Chapman & Hall, London, UK
Miranda-Soberanis, V (2018) Vector generalized linear time series models with an implementation in R. PhD thesis, Department of Statistics, University of Auckland, New Zealand
Miranda-Soberanis VF, Yee TW (2019) New link functions for distribution-specific quantile regression based on vector generalized linear and additive models. J Probab Stat 5:1–11
Nelder JA, Wedderburn RWM (1972) Generalized linear models. J Royal Stat Soc Series B 135(3):370–384
Noufaily A, Jones MC (2013) Parametric quantile regression based on the generalized gamma distribution. J Royal Stat Soc Series C 62(5):723–740
Rigby RA, Stasinopoulos DM, Voudouris V (2013) Discussion: a comparison of GAMLSS with quantile regression. Stat Model 13(4):335–348
Sellers KF, Shmueli G (2010) A flexible regression model for count data. Annals Appl Stat 4(2):943–961
Smyth GK, Verbyla AP (1999) Double generalized linear models: approximate REML and diagnostics. In: H. Friedl, A. Berghold, and G. Kauermann (eds) Statistical modelling: proceedings of the 14th international workshop on statistical modelling, Graz, Austria, July 19–23, pages 66–80, Technical University, Graz, Austria
Thompson R, Baker RJ (1981) Composite link functions in generalized linear models. J Roy Statist Soc Ser C 30(2):125–131
Umlauf N, Klein N, Zeileis A (2018) BAMLSS: Bayesian additive models for location, scale, and shape (and beyond). J Comput Graph Stat 27(3):612–627
Wood SN (2017) Generalized additive models: an introduction with R, 2nd edn. Chapman & Hall, New York, USA
Yee TW (2004) Quantile regression via vector generalized additive models. Stat Med 23(14):2295–2315
Yee TW (2010) The VGAM package for categorical data analysis. J Stat Softw 32(10):1–34
Yee TW (2015) Vector generalized linear and additive models with an implementation in R. Springer, New York, USA
Yee TW (2020) The VGAM package for negative binomial regression. Aust N. Z. J Stat 62(1):116–131
Yee TW, Hastie TJ (2003) Reduced-rank vector generalized linear models. Stat Model 3(1):15–41
Yee TW, Stephenson AG (2007) Vector generalized linear and additive extreme value models. Extremes 10(1):1–19
Yee TW, Wild CJ (1996) Vector generalized additive models. J Royal Soc Series B 58(3):481–493
Acknowledgements
The first author’s work was partially supported by a University of Auckland Doctoral Scholarship.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix: Expressions for complementary derivatives
Appendix: Expressions for complementary derivatives
This appendix summarizes the new complementary expressions for \(\text {d} \ell / \text {d} \theta _j\), \(\text {d}^2 \ell / \text {d} \theta _j^2\) and \(\text {d}^2 \ell / \text {d} \theta _j \text {d} \theta _k\), in Table 9, Table 10 and Table 11 respectively, for the three cases (3.2)-(3.4).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miranda-Soberanis, V.F., Yee, T.W. Two-parameter link functions, with applications to negative binomial, Weibull and quantile regression. Comput Stat 38, 1463–1485 (2023). https://doi.org/10.1007/s00180-022-01279-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-022-01279-4