1 Introduction

Countries’ performances are often measured by elementary or composite indicators, whose values are used for ranking purposes. Indicators and rankings are simplified and widely used representations of complex phenomena, and are increasingly employed by international agencies and governments to assess a country’s achievements (Bellantuono et al. 2020; Kelley and Simmons 2019). In particular, the analysis of ranks provides useful information in a comparative perspective, returning the relative position of each country with respect to the others. Ranking problems can arise in many fields, such as wealth (Malul et al. 2009), human development (Zheng and Zheng 2015; Wu et al. 2014; Cherchye et al. 2008), well-being (Peiro-Palomino and Picazo-Tadeo 2018; Phillis et al. 2011), energy (Lee and Chang 2018), biology (Shah and Wainwright 2017; Di Battista et al. 2016, 2017), growth studies (Ramsay and Silverman 2002), analysis of choices behaviour (Yu et al. 2013), and performance evaluation (Zhang et al. 2021). Although there is a growing agreement on the use of ranks to compare performance, they are generally evaluated from a static point of view. However, the analysis of rank evolution over time is crucial to evaluate whether, comparatively, a country is experiencing an improvement, worsening or stability in its performance and, consequently, to evaluate the effect of adopted policies. The analysis of ranks over time has been restricted to specific applications, such as sports tournaments (Cattelan et al. 2013; Jabin and Junca 2015; Motegi and Masuda 2012). Moreover, dynamic approaches for the analysis of rankings have been largely limited to some syntectic measures, such as average annual ranks, absolute differences among ranking positions at consecutive times, and percentage changes (Tsui 1996; Chakraborty 2011).

Given that the observations of performance over time are constantly evolving and could also be high-dimensional, the functional data analysis (FDA) approach is the most natural tool to analyse these data (Ramsay and Silverman 2005; Ferraty and Vieu 2006). The usefulness of this approach lies in two reasons: the first is the reduction of dimensionality and the second is the possibility to take advantage of additional tools to capture the characteristics of the trends. In the FDA framework, ranks obtained for each country at different times can be considered as discrete observations of smooth rank trajectories. Once the ranking series of each country is approximated by a function, the focus is on modeling the ranks of individuals and their patterns over time. The FDA approach is very useful in this context because it allows us to visualise the rank’s behaviour over time, to introduce functional tools and to tackle cases where data have missing values or are measured at unmatched time points. The FDA approach is widely used in many areas, such as ecology (Lin and Zhou 2017; Febrero et al. 2007; Fortuna et al. 2020), electricity demand (Jan et al. 2022; Shah et al. 2020, 2022; Bibi et al. 2021), economics (Gattone et al. 2021; Bongiorno and Goia 2019), medical research (Cao and Ramsay 2007; Maturo and Verde 2022), behavioural sciences (Aguilera et al. 2021), spectrometric (Reiss and Ogden 2007), and education (Maturo et al. 2019; Ramsay 1991), among the others. However, the analysis of rank dynamics by means of the FDA approach is a rather recent topic. The pioneering work in this field was published by Chen et al. (2020), who suggested a decomposition of rank derivatives into a population and an individual contribution to the rank evolution. The need for this decomposition is due to the dependence of rank dynamics on the interplay between individual and population changes.

Starting from the work of Chen et al. (2020), this paper aims to evaluate countries’ performances by taking into account both their ranking position and their evolutionary behaviour; that is, by jointly considering the magnitude and the evolution of performances in the entire temporal domain. Indeed, it is convenient to complement information concerning the level attained by a country with the dynamic behaviour of its trajectory. Consequently, two functional measures are introduced. The first returns an overall ranking, which reflects the magnitude of ranks and is based on the modified hypograph index (MHI) that was initially suggested by Lopez-Pintado and Romo (2011). MHI represents the proportion of the time span that the graphs of the functions in the sample are in the hypograph of a specific curve; that is, the proportion of time that the curves of the sample are below a specific trajectory. Of course, a high value of MHI corresponds to a high rank position over the whole domain, and vice versa. However, in many cases MHI is not sufficient to distinguish the behaviours of different curves—equal values of MHI could correspond to different shapes. Therefore, a limitation of this measure is that it neglects the way in which a country reaches a specific position. This drawback may be overcome by considering the derivatives of the curves, which emphasise the first signs of growth or decrease of the original function (Ramsay and Silverman 2005). To this end, Chen et al. (2020) proposed the integrated first derivative to quantify how variable the rank of a unit is over time. The disadvantage of this measure is that it reflects the total behaviour of the first derivative without distinguishing how long the original function shows a certain trend. Moreover, the first derivative of the rank trajectory does not represent the single country’s evolution. In fact, a county’s rank is affected by the entire population’s dynamic: a country could change rank while maintaining its trend.

To overcome these limitations, this research suggests the use of the first derivatives computed on the original trajectories as an additional tool to assess a country’s performance over time. Specifically, the weighted integrated first derivative (DW) is proposed as a second functional measure. In addition, a visualisation tool, named \(MHI-DW\) plot, is suggested to jointly interpret magnitude and dynamic variations of a rank’s trajectory. Countries are represented in the Cartesian plane defined by MHI and DW. Consequently, the proposed graph helps to interpret the behaviour of trends and identify countries with similar or dissimilar behaviours based on their positioning in the generated space. To assess the reliability of the two functional measures, a simulation study is carried out, by evaluating MHI in combination with different evolutionary measures. The results indicate that the combined use of MHI and DW is an efficient tool for distinguishing functions with similar magnitude and evolution. Moreover, the suggested methodology is applied to study the rankings’ evolution of an institutional quality services indicator, namely the Government Effectiveness (GE) index (Kaufmann et al. 2010; Gisselquist 2014), using the ranking series of 27 European countries over the period 1996 to 2020.

This paper is organised as follows. In Sect. 2, the ranks functional approximation is presented. In Sect. 3, the two functional measures and the \(MHI-DW\) plot are defined. A simulation study is conducted in Sect. 4. In Sect. 5, the \(MHI-DW\) plot is applied to a real dataset concerning the GE index of 27 European countries. Finally, Sect. 6 concludes the paper.

2 Ranking functions through functional data analysis

Let \(y_i(t)\), \(i=1,2,\ldots ,n\), be a sample of n curves, with \(t \in T\), representing n i.i.d. realisations of a functional stochastic process, Y(t), taking its values in the Hilbert space of square integrable functions, \(L^2(T)\), with inner product \(<\cdot , \cdot>\) and inner norm \(||\cdot ||\). The functional rank process associated with Y(t) is defined through a probability transform for each \(t \in T\) as follows (Chen et al. 2020):

$$\begin{aligned} R(t)=F_t\Bigl (Y(t)\Bigr ), \;\; \forall t \in T, \end{aligned}$$
(1)

where \(F_t\Bigl (Y(t)\Bigr )=P\Bigl (Y(t)\le y\Bigr )\) is the cross-sectional distribution of Y at time t. In practice, any realisation of the functional process is observed with noise on a discrete set of points, \(t_l\), \(l=1,2,\ldots ,L\), with \(t_l \in T\). Thus, starting from the n pairs \(\{t_{il}, y_{il}\}_{i=1}^n\), functional rank trajectories, \(R_i(t)=F_t\Bigl (Y_i(t)\Bigr )\), are obtained by applying the probability transform at each time point, that is:

$$\begin{aligned} R_i(t)=F_{n,t}\Bigl (y_i(t)\Bigr )=\frac{1}{n}\sum _{k=1}^{n}I\Bigl (y_k(t) \le y_i(t)\Bigr ), \;\;\; \forall t \in T; \end{aligned}$$
(2)

where \(F_{n,t}\Bigl (y_i(t)\Bigr )\) is the ranking of the i-th curve relative to the other curves in the dataset, which (in practice) is based on the empirical cumulative distribution function (ECDF) of \(y_i(t)\) at a given time point \(t \in T\); and \(I(\cdot )\) denotes the indicator function. Clearly, the range of \(R_i(t)\) is always the interval [0, 1] and Eq. (2) represents the non-smoothed version of the cross-sectional empirical distribution of the i-th function.

The rank trajectory can easily be obtained by sorting, at each time point, the observed data in ascending order, \(y_{(1)},\ldots ,y_{(n)}\), and (from a practical point of view) it is obtained by computing the ECDF. Given that the ECDF is discontinuous, one might prefer to consider a smoothed version, which leads to approximate ranks. This second choice requires a two-step procedure where in the first step the unsmoothed raw estimates of the ECDF are obtained at a set of distinct time points and in the second step, smoothing methods are applied to the raw estimates. Several smoothed versions can be considered. For ECDFs, the use of Bernstein Polynomials is well-documented in the literature (Vitale 1975; Leblanc 2010) and is particularly suited for ECDFs with compact support (Babu et al. 2002; Menafoglio et al. 2014). A further choice is to consider the kernel estimator of ECDFs (Roussas 1969; Samanta 1989; Ferraty and Vieu 2006; Veraverbeke et al. 2014). In this paper, smooth estimates of the rank trajectories are obtained by considering a kernel estimate of ECDF, as in Chen et al. (2020):

$$\begin{aligned} \widetilde{F}_t(t)=\frac{n^{-1}\sum _{i=1}^n \widetilde{Q}_{1i}(y,t)}{n^{-1}\sum _{i=1}^n \widetilde{Q}_{2i}(y,t)}, \end{aligned}$$
(3)

where:

$$\begin{aligned}&\widetilde{Q}_{1i}(y,t)=\frac{1}{L}\sum _{l=1}^L h_T^{-1}H\Bigl (\frac{y-Y_{il}}{h_Y}\Bigr )K\Bigl (\frac{t-t_{il}}{h_T}\Bigr ); \end{aligned}$$
(4)
$$\begin{aligned}&\widetilde{Q}_{2i}(y,t)=\frac{1}{L}\sum _{l=1}^L h_T^{-1}K\Bigl (\frac{t-t_{il}}{h_T}\Bigr ); \end{aligned}$$
(5)

with K and H being a kernel function and an integrated kernel, respectively; and \(h_Y\) and \(h_T\) being the bandwidths controlling the kernel widths, chosen by cross-validation.

3 Functional measures of magnitude and evolution

In the assessment of social phenomena, such as in the case of countries’ performances, it is difficult to provide an overall ranking of units across time. Indeed, in the evaluation process, both the magnitude and evolutionary behaviour of each unit should be taken into account. To this end, two functional measures are considered: the first is the modified hypograph index (MHI), which is computed with respect to the rank trajectories; and the second is the weighted integrated first derivative (DW), which is computed on the original functions. The two distinct orderings induced by these measures reflect the magnitude and the evolutionary behaviour of each country, respectively.

The MHI of a given rank trajectory, R(t), with respect to a sample of functions, \(R_i(t)\), \(i=1,2,\ldots ,n\), is defined as follows (Lopez-Pintado and Romo 2011):

$$\begin{aligned} MHI\Bigl (R(t)\Bigr )=\sum _{i=1}^n \frac{\lambda (\{G(R) \subseteq hyp(R)\})}{n\lambda (T)}; \end{aligned}$$
(6)

where \(G(R)=\{(t, R(t)), t \in T\}\) is the graph of the rank function R(t); \(hyp(R)=\{(t,y) \in T \times \mathbb {R}: y \le R(t)\}\) is the hypograph of R(t), and \(\lambda (\cdot )\) stands for the Lebesgue measure on \(\mathbb {R}\). Clearly, the graph of any curve R(t) is contained in its hypograph. MHI represents the proportion of T that the graphs of the functions in the sample are in the hypograph of R(t); that is, the proportion of T in which the curves of the sample are below R(t). Roughly speaking, the hypograph of a function is the area under its graph and MHI also considers how long the curves are in the hypograph of a given function. Thus, a high value of MHI indicates that many functions are contained in the hypograph of a given curve. An overall magnitude-based ranking of the curves can be obtained by sorting in descending order the MHI values. Because the functions represent rankings over time, a MHI value equal to 0.5 indicates that the curve is located at the center of the sample. In other words, the curve assumes a central rank position. Meanwhile, MHI values close to 0 and 1 reflect the worst and best rank positions in the whole time span, respectively.

The main disadvantage of MHI is that it does not account for the path taken by each country to reach a given position so that different shapes of the curves can yield equal values of MHI. The analysis of the first derivatives provides a suitable solution to this aspect because it offers a valuable insight into the time dynamics of functional data. For instance, a first derivative that is different from zero indicates that the curve changes over time. Thus, the integrated first derivative can be computed to quantify how variable a rank trajectory is in the time span (Chen et al. 2020). However, the integrated first derivative of the rank trajectories presents two limitations. The first limitation is that it does not represent a single country’s evolution. Indeed, each rank trajectory strongly depends on the entire population’s dynamic—a country could change rank while maintaining its performance. The second limitation is that the integrated first derivative of the rank trajectory reflects the total behaviour of the first derivative without distinguishing how long the function shows a certain trend. To solve the first issue, and hence to better evaluate the dynamics of each country, we suggest to compute the integrated first derivative on the original functions rather than on ranks as Chen et al. (2020) suggests, that is:

$$\begin{aligned} D_i=\int _T y_i'(t)\, dt. \end{aligned}$$
(7)

To address the second limitation, and hence to take into account how long a curve maintains a specific behaviour, a weighted local integrated first derivative, DW, is proposed. Considering sub-intervals of the domain, determined by the changes of the first derivative sign, DW is obtained as a linear combination of the integrated first derivatives in each sub-interval, with coefficients equal to the proportion of the width of each sub-interval. Specifically, each function is divided into \(M + 1\) segments according to a set of points, \(m=1,2,\ldots ,M\), which are defined by the changes in the first derivative sign. At each sub-interval, \(k_1, k_2,\ldots , k_{M+1}\), the integrated first derivative is computed on the original functions, leading to a series of local values, which are denoted as \(D_{ij}\), \(i = 1, 2,\ldots , n\), \(j = 1, 2,\ldots , M+ 1\). Then, \(D_{ij}\) is locally weighted with the proportion of the width of the segment over the total width. Finally, an overall measure is obtained for each function, as follows:

$$\begin{aligned} DW_i = \sum _{j=1}^{M+1}D_{ij}w_{ij}, \end{aligned}$$
(8)

where:

$$\begin{aligned} w_{ij}=\frac{(t_m-t_{m-1})}{(t_L-t_0)}, \end{aligned}$$
(9)

where \(t_0\) and \(t_L\) are the start and end points of the domain of the curves.

MHI and DW reflect two distinct aspects that should be jointly considered to evaluate countries’ performances. To this end, a visualisation tool is suggested. Countries are represented in the Cartesian plane defined by MHI and DW, which allows us to distinguish countries according to their magnitude and more or less deserving behaviour. The values of MHI are included in the interval [0, 1], while DW assumes values in (\(-\infty ,+ \infty \)). The \(MHI-DW\) plot can be divided into four quadrants by drawing a horizontal and a vertical line at \(DW=0\) and \(MHI=0.5\), respectively. The value \(MHI = 0.5\) discriminates among countries that belong to the top half of the hypograph ranking and those in the lower half; whereas the value \(DW=0\) distinguishes between countries that experience an improvement (\(DW>0\)) or a worsening (\(DW<0\)) of their performance. The first quadrant (top right-hand panel of the plot) includes the most virtuous countries because they present higher magnitude values (\(MHI > 0.5\)) that are obtained by improving their performance over time (\(DW > 0\)). It is worth noting that when DW is close to zero and MHI is close to one, countries start from very high ranking levels and maintain them throughout the period considered. In this case, the stability of the function is to be rewarded. The second quadrant (bottom right-hand panel of the plot) is defined by countries that have a magnitude above the median value (\(MHI> 0.5\)) but whose performance has worsened in the time interval considered (\(DW < 0\)). The third quadrant (bottom left-hand panel of the plot) is defined by countries with \(MHI <0.5\) and \(DW < 0\). Clearly, the countries in this quadrant are in the worst position and policy interventions will have to be stronger than in other cases. Finally, the fourth quadrant (top left-hand panel of the plot) includes countries with a magnitude below the median (\(MHI <0.5\)) but with a predominant improvement of their performance (\(DW> 0\)). Obviously this graphical tool allows us to distinguish countries with different magnitude and evolution trends at a glance. Table 1 provides a summary description of the four quadrants resulting from the \(MHI-DW\) plot.

Table 1 Description of the four quadrants resulting from the \(MHI-DW\) plot
Full size table

4 Simulation study

A simulation study is performed to investigate the ability of the proposed functional measures to distinguish countries according to both their magnitude and evolution in the entire domain. To reflect specific magnitude and evolutionary behaviour of the trajectories, a population of n functions is divided into \(G=4\) groups, each with sample size \(n_g=30\) with \(g=1,2,\ldots ,G\) and \(n=\sum _{g=1}^Gn_g=120\). The curves are observed in the interval [0, 1] with a grid of \(L=30\) equally spaced points. For each g-th group, functional data, \(y_1(t), \ldots , y_{n_g}(t)\), are obtained as realisations of a Gaussian process, \(Y_g(t)\in L^2(T)\), of the following form:

$$\begin{aligned} Y_g(t) = \mu _g(t) + e(t), \,\,\, g=1,2,\ldots ,G, \end{aligned}$$
(10)

where \(\mu _g(t)\) accounts for the specific performance of the g-th group, and e(t) is a Gaussian process, which is common for all the G groups, with mean 0 and covariance function \(\gamma (s,t)=\exp (-|t-s|)\). The functional means of the G groups are defined as follows:

$$\begin{aligned} \mu _1(t)= & {} 2\exp (t); \;\;\; \;\; \; \mu _2(t)=30t(1-t)^{3/2}; \nonumber \\ \mu _3(t)= & {} 2\exp (-t); \;\;\; \; \mu _4(t)=3-\mu _2(t). \end{aligned}$$
(11)
Fig. 1
figure 1

Simulated functions of each g-th group in the s-th simulation, with \(s=1\)

Full size image

This procedure is replicated \(S=3000\) times. Figure 1 shows the simulated functions for each g-th group in a single simulation, \(s=1\), \(s=1,2,\ldots ,S\). The first group of functions (solid lines in Figs. 1 and 2) is characterised by a rather high magnitude and a predominantly increasing trend. The second group of functions (dotted lines in Figs. 1 and 2) is characterised by a rather high magnitude and a predominantly decreasing trend. The third group of functions (dashed lines in Figs. 1 and 2) is characterised by medium magnitude and a predominantly decreasing trend. Finally, the fourth group of functions (dot-dash lines in Figs. 1 and 2) is characterised by rather low magnitude and a predominantly increasing trend. In Fig. 2 the functional means of the G groups for \(s=1\) are plotted in the same graph. The average function of \(g_1\) shows an increasing trend with high levels of magnitude throughout the domain. The mean function of \(g_2\) shows high levels of magnitude, especially in the middle part of the domain with an initially increasing and then decreasing trend that persists for more than half of the domain. The average function of \(g_3\) has an almost always decreasing trend (even if slightly) and shows an intermediate level of magnitude compared to the other groups, but with some exceptions. Indeed, the magnitude of \(g_3\) is almost always below that of \(g_1\) and \(g_2\), whereas it is above the magnitude of \(g_4\), except for the first and last part of the domain. Throughout most of the domain, the mean function of \(g_4\) shows the lowest magnitude with an initially decreasing and then increasing trend for most of the domain.

Fig. 2
figure 2

Functional means of the G groups in the s-th simulation, with \(s=1\)

Full size image

Starting from the n functions, \(y_i(t)\), and for each s-th replication, functional rank trajectories, \(R_i(t)\), are obtained by applying the probability transform at each time point as in Eq. (2). Their smooth versions are then obtained using the Kernel estimator in Eq. (3). Each function is placed in a specific group according to its MHI and DW values, which are computed as in Eqs. (6) and (8), respectively. Each group corresponds to one of the four quadrants defined by the \(MHI-DW\) plot. The representation of each curve in the \(MHI-DW\) plot allows us to understand the behaviour of each country with respect to the considered characteristics and to check the consistency with the simulated data. Figure 3 shows the functional observations for \(s=1\) in the \(MHI-DW\) plot. The curves of the first group (black dots in Fig. 3) are prevalently located in the first quadrant, which indicates high MHI values and positive DW values. The curves of the second group (black triangles in Fig. 3) are mainly placed in the second quadrant, which is the one with \(MHI > 0.5\) and \(DW < 0\). The curves of the third (white dots in Fig. 3) and of the fourth (black squares in Fig. 3) group are, respectively, concentrated in the third and fourth quadrants of the plot because both groups present low MHI values with negative and positive DW values, respectively.

To examine the performance of the proposed method, the proportion of correct assignment is recorded for each i-th observation among the S replications, as follows:

$$\begin{aligned} P_c=\frac{1}{S} \sum _{s=1}^S p_s, \end{aligned}$$
(12)

with \(p_s\) representing the proportion of correct assignments of the functions in the quadrant divided by the total number of curves, for the s-th replication. \(P_c\) is computed with respect to four evolutionary measures combined with MHI: the weighted local integrated first derivative computed on both the original functions (DW) and the rank trajectories (\(DW_{R}\)); and the integrated first derivative computed on both the original functions (D) and the rank trajectories (\(D_R\)). Table 2 shows the \(P_c\) values and the respective standard deviations for the four different cases. The results show that the weighted local integrated first derivative of the original functions (DW) is the best evolutionary measure to complement the information provided by MHI because it leads to the highest level of correct assignment of the functional observations in the four groups. Meanwhile, the combination of MHI with the integrated (non-weighted) first derivative of the original functions (D) leads to lower performance than using DW. Moreover, when the evolutionary behaviour is evaluated on the rank trajectories, the weighted local integrated first derivative yields the best results compared to its unweighted counterpart.

Table 2 Proportion of correct assignment (\(P_c\)) values and their standard deviations resulting from the combination of MHI with different evolutionary measures
Full size table

To quantify the between simulation variability, the following squared error measure is provided:

$$\begin{aligned} EE(f)=\frac{1}{S}\sum _{i=1}^n\sum _{s=1}^S\left( f_{is}-\overline{f}\right) ^2, \end{aligned}$$
(13)

where \(f_{is}\) is a generic measure, which can be one of the following: \(MHI_{is}\), \(DW_{is}\), \(DW_{R_{is}}\), \(D_{is}\) or \(D_{R_{is}}\), respectively; and \(\overline{f}\) is the mean of each functional measure across the S replications. Table 3 reports the squared error values for the MHI and the four evolutionary measures. In all cases, the variability is extremely low.

Table 3 Squared error measure (EE(f)) for MHI and the four evolutionary measures across the S replications
Full size table
Fig. 3
figure 3

Functional observations in the \(MHI-DW\) plot for the s-th simulation, with \(s=1\)

Full size image

5 Application

The proposed method is applied to the Government Effectiveness (GE) index of 27 European countries in the period from 1996 to 2020. The GE index captures perceptions of the quality of public services, the quality of public administration and the degree of its independence from political pressures, the quality of policy formulation and implementation, and the credibility of the government’s commitment to these policies (Kaufmann et al. 2010). The GE index is part of the Worldwide Governance Indicators (WGI) project, which reports aggregate and individual governance indicators for over 200 countries and territories based on six dimensions of governance, including political stability, government effectiveness, and control of corruption. Data are available at https://databank.worldbank.org/reports.aspx?source=1181 &series=GE.EST and in the supplementary material. The analysis is performed in the R environment (R Core Team 2020) and the R script is available in the supplementary material.

The GE index is obtained by aggregating 45 basic variables by means of the Unobserved Component Model (UCM) (Goldberger 1972). The main variables that are considered refer to quality of bureaucracy, quality of road infrastructure, quality of primary education, satisfaction of the public transportation system, quality of the health care system, allocation and management of public resources for rural development, infrastructure disruption, state failure, and policy instability. The resulting composite measures are in units of a standard normal distribution, with mean zero, standard deviation one, and range approximately between – 2.5 and 2.5, with higher values corresponding to best governance effectiveness.

Fig. 4
figure 4

Functional GE index and smooth rank trajectories of the European countries

Full size image

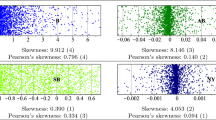
The GE time series of each country are considered as continuous functions observed at \(L = 22\) discrete points. Therefore, raw temporal sequences of GE index are converted into a sample of functions, \(y_i(t)\), by adopting a kernel smoothing method. The upper panel of Fig. 4 shows the reconstructed functional GE index for each country; that is, the smooth version of the original functions, \(y_i(t)\). A list of countries in the sample is provided in Table 4. Starting from the GE functions, smooth rank trajectories, \(R_i(t)\), are obtained as in Eq. (3). The functional rank trajectories are plotted in the bottom panel of Fig. 4. Figure 5 shows the first derivatives of both the functional GE index (upper panel of Fig. 5) and the functional rank trajectories (bottom panel of Fig. 5). The range of the first derivatives is rather limited because their values vary between − 0.126 and 0.105 for the original functions, and between − 0.205 and 0.163 for the rank trajectories. To provide information regarding the temporal evolution of the indicator itself, we compute DW on the functional GE index for each country as in Eq. (8). Figure 6 displays the 27 European counties on the \(MHI-DW\) plot. In total, 41% of the counties are located in the second quadrant. This result raises some concern because a high number of countries, although highly ranked on GE index, are experiencing a decrease over time. Furthermore, within this quadrant, Belgium occupies the worst position, presenting the lowest value of DW. Meanwhile, 33% of countries are located in the fourth quadrant: these are countries with a low rank position but which are experiencing a growth in their GE over time. In particular, the performances of Latvia and Lithuania are highlighted due to their best position within this quadrant with reference to the evolutionary behaviour. The third quadrant contains 19% of countries. These countries are struggling to increase their GE level, which makes policy intervention necessary. The first quadrant is occupied only by Finland and Portugal. Specifically, Finland is in a better position than Portugal because it has a significantly higher level of GE. It is certainly important to note that countries with low GE index values tend to experience the highest increase. In contrast, when GE index becomes high, it is difficult to increase it further (Sen 1981; Chakraborty 2011). On the basis of these considerations, the countries in the second and third quadrants are those with the greatest degree of criticality. For each country, Table 4 reports the orderings induced by the MHI and DW values, which are considered both individually and jointly. The joint ordering is obtained from the \(MHI-DW\) plot and consists of identifying the quadrant of the plot occupied by each country.

Fig. 5
figure 5

Functional GE first derivatives (\(y_i^{\prime }(t)\)) and rank trajectories first derivatives (\(R_i^{\prime }(t)\)) of the European countries

Full size image
Fig. 6
figure 6

\(MHI-DW\) plot for the European countries

Full size image
Table 4 Overall rank position of the European countries according to MHI, DW and the \(MHI-DW\) plot (Quadrant)
Full size table

6 Conclusions

Countries’ performances are usually evaluated through rankings that arise from single or, more often, composite indicators. Rankings are often analysed from a static point of view, which makes it impossible to determine whether a country is undergoing an increase, a decline or a stability in its performance. In this context, the functional data analysis (FDA) approach represents a useful method for the analysis of rank dynamics. Specifically, by approximating the time series of both the original data and the resulting ranks with smooth functions, functional tools can be exploited to provide additional information. This paper proposes to use two overall functional measures to evaluate countries’ performances, while taking into account both their ranking position and their evolutionary behaviour: the modified hypograph index (MHI) and the weighted integrated first derivative (DW). The first measure refers to the magnitude of the rank position over the entire domain, whereas the second measure relates to the increasing or decreasing behaviour of the smoothed time series. One of the main advantages provided by DW is that it reflects how long the original function shows a certain trend. Moreover, we suggest to evaluate the evolutionary aspect on the original trajectories rather than on the rank functions to focus on the country’s evolution. Simulation results reveal that DW is more successful in identifying the predominant trend of countries than other evolutionary measures. Finally, a visualisation tool that combines information resulting from MHI and DW is suggested. A scatterplot of these measures allows an immediate understanding and perception of countries according to their magnitude and evolution trends.

A further research project could be to extend DW to the second functional derivatives, highlighting the acceleration with which countries show a certain trend. However, indicators are used for assessing complex phenomena that change slowly over time, thus, DW computed on the second derivative should be used in conjunction with the two introduced measures, to cluster countries according to their functional characteristics. Moreover, since many indicators are the result of the aggregation of multiple elementary indicators, a possible development of this work could be to generalize DW to the more complex multivariate functional case, to take into account the behaviour of each component of the indicator. In conclusion, FDA appears to be a useful approach to analyze rank dynamics. However, a possible limitation of this approach is that it is necessary to have a sufficient number of temporal observations of the phenomenon under study and, in the case of complex social phenomena, this condition is not always met.