Computational advances for spatio-temporal multivariate environmental models

Abstract

In multivariate Geostatistics, the linear coregionalization model (LCM) has been widely used over the last decades, in order to describe the spatial dependence which characterizes two or more variables of interest. However, in spatio-temporal multiple modeling, the identification of the main elements of a space–time linear coregionalization model (ST-LCM), as well as of the latent structures underlying the analyzed phenomenon, represents a tough task. In this paper, some computational advances which support the selection of an ST-LCM are described, gathering all the necessary steps which allow the analyst to easily and properly detect the basic space–time components for the phenomenon under study. The implemented algorithm is applied on space–time air quality data measured in Scotland in 2017.

1 Introduction

In environmental studies, the analysis of the relationships among two or more variables, measured in space and time, is of wide interest. For prediction purposes, the first stage to be tackled in Geostatistics concerns the identification of a suitable multivariate model which describes the spatio-temporal covariance matrix computed for the observed variables. As thoroughly reviewed by Genton and Kleiber (2015), one can choose among various models of spatial multiple correlation; however, the LCM is still very common in practice, since it is computationally flexible and convenient (Babak and Deutsch 2009; Emery 2010; Gneiting et al. 2010; Bevilacqua et al. 2015). Its adequacy can be also tested by applying the statistics proposed by Li et al. (2008). Nevertheless, in the space–time context the definition of the main elements of the ST-LCM, namely the basic structures characterizing the variables of interest, represents yet a tough task, due to the lack of software to analyze multivariate spatio-temporal data. A first attempt to propose a procedure to support the identification of an ST-LCM for a multivariate data set was given in De Iaco et al. (2012), where the authors assumed to model the basic components through the product–sum class. Although the restriction on this specific class of covariance models to be used for describing the basic components was abandoned in some further applications, only the contribution in De Iaco et al. (2019) pointed out that the basic components can be modelled by using different families of covariance models and the choice of the family for one basic component does not influence the choice for the other components, since the selection of each class can be reasonably relied on the main features of the sample basic covariance surfaces. However, the procedure of choosing suitable LCMs for spatio-temporal data was presented without discussing the related computational issues, as also clarified by the same authors. Thus, in this paper, the proposed algorithm focuses, in a very compact and analytic way, on the implementation of the multivariate modeling procedure of an ST-LCM, where no specific class of covariance models is assumed a priori for the basic components. Moreover, differently from the common approach which consists in using the same class of models for all the components of the ST-LCM as in De Iaco et al. (2003), the new algorithm allows the users to obtain a flexible ST-LCM, whose components can have different properties in terms of symmetry/asymmetry, separability/non-separability and, in case of non-separability, positive/negative non-separability (De Iaco et al. 2019). To our knowledge, these advances have not been tackled in previous works and represent a remarkable step forward of the current state of computational progress in spatio-temporal multivariate analysis. The steps of the presented algorithm can be easily carried out by implementing some ad-hoc R functions (R Core Team 2015), as done by the authors.

The computational advances are applied to model the spatio-temporal multivariate covariance function of three different pollutants, which are still critical in Scotland, i.e. nitrogen dioxide (NO$_2$), nitric oxide (NO) and fine particles (PM$_{10}$). The data consist of hourly measurements recorded in 2017 at 18 monitoring stations around Glasgow. However, the same algorithm can be useful even for other environmental applications when the identification of a spatio-temporal multivariate model, able to capture the common latent structures underling the analyzed variables, is required.

The paper outline is as follows. Section 2 provides some basic notions on multivariate spatio-temporal Geostatistics; Sect. 3 offers a detailed description of the algorithm for the ST-LCM selection, then, the application on the data set concerning the above-mentioned air pollutants is presented through the various steps of the proposed algorithm and some interesting practical aspects are highlighted (Sect. 4). Then, the adequacy of the chosen ST-LCM for the studied data set is evaluated and successively the model is used for prediction purposes. Finally, in Sect. 5, the proposed procedure is compared with respect to the exiting fitting method based on the use of the same class of covariance models for all the basic components.

2 A synthetic multivariate framework

Let $\mathbf{X}$ be a multiple second-order stationary random function (MSRF), defined on a spatio-temporal domain $D \times T \subseteq \mathbb {R}^{d}\times \mathbb {R}$, which consists of m components $X_1(\mathbf{s}, t), \ldots , X_m(\mathbf{s}, t)$, with $(\mathbf{s}, t) \in D \times T$ and $m \ge 2$. Its first and second order moments are respectively:

$$\begin{aligned} {\varvec{\mu }}=[\mu _1, \ldots , \mu _m]^T \quad \text {and} \quad \mathbf{C}({\varvec{\delta }}_s,\delta _t) = [C_{ij} ({\varvec{\delta }}_s, \delta _t)], \end{aligned}$$

(1)

where $\mu _i$ is the expected value of $X_{i}, i=1, \ldots ,m$; $({\varvec{\delta }}_s,\delta _t)\in \mathbb {R}^{d}\times \mathbb {R}$ is the spatio-temporal separation lag, with ${\varvec{\delta }}_s=(\mathbf{s}-\mathbf{s}')$ and $\delta _t=(t-t')$, given any two points $(\mathbf{s}, t)$ and $(\mathbf{s}', t')$ in the domain $D\times T$; $C_{ij}({\varvec{\delta }}_s, \delta _t)= E[(X_{i}(\mathbf{s}+{\varvec{\delta }}_s, t+\delta _t) \cdot X_{j}(\mathbf{s}, t))] - \mu _{i} \, \mu _{j}$ corresponds to the direct and cross-covariance functions of the MSRF $\mathbf{X}$. In particular, for $i = j$, $C_{ii}$ is the direct covariance function of the $X_{i}$, while for $i \ne j$, $C_{ij}$ is the cross-covariance function between $X_{i}$ and $X_{j}$.

As already clarified in the introduction, the ST-LCM is still extensively used to model the matrix $\mathbf{C}$ in various scientific fields. This is done through the following linear combination of basic covariance functions:

$$\begin{aligned} \mathbf{C}({\varvec{\delta }}_s, \delta _t)= \displaystyle \sum _{l=1}^L \; \mathbf{B}_l \; c_l({\varvec{\delta }}_s, \delta _t), \end{aligned}$$

(2)

where $c_l({\varvec{\delta }}_s, \delta _t)$ are covariance functions and $\mathbf{B}_l = [b_{ij}^l], l=1,\ldots ,L,$ with $L \le m,$ are $(m \times m)$ positive definite matrices and are called coregionalization matrices. Note that $c_l$ can be interpreted as the covariance functions of the latent variables which characterize the random field $\mathbf{X}$.

3 Algorithms for an ST-LCM selection

The main algorithm, shown below, recalls the following steps:

• I. detection of the basic components determined through simultaneous diagonalization of the covariance matrices;

• II. identification of suitable models for the basic components, by taking into account the results concerning hypothesis testing of their main features;

• III. computation of coregionalization matrices and check of their admissibility through the singular value decomposition.

Main algorithm
1: Load the multivariate data set of $m\ge 2$ spatio-temporal variables
2: Recall the Algorithm 1: “Identify basic components”
3: For each basic component l ($l\le L$), test the empirical characteristics of the sample basic covariance surface and define the appropriate model by recalling the Algorithm 2: “Test main features and select basic models”
4: Recall the Algorithm 3: “Compute coregionalization matrices”
5: Define the ST-LCM by using equation (2)

The above-mentioned steps can be executed in the R environment.

3.1 Algorithm 1: Identify basic components

The first algorithm has the objective to determine the basic components of the MSRF $\mathbf{X}$ and to identify the corresponding covariance functions and their scales of variability.

Given the spatio-temporal data set $\mathbf{x}$ of size $(N \times m)$ related to the N observations of m variables over the spatio-temporal domain, let $\widehat{\mathbf{C}}({\varvec{\delta }}_s,\delta _t)_k = [\widehat{C}_{ij}({\varvec{\delta }}_s,\delta _t)_k]$ be the symmetric $(m\times m)$ matrix of direct and cross-covariance functions estimated at each lag k, with $k=1,\ldots ,K$. Then, the matrices $\widehat{\mathbf{C}}({\varvec{\delta }}_s,\delta _t)_k$ are simultaneously diagonalized through a $(m\times m)$ orthonormal matrix ${\varvec{\Psi }}$, i.e.

$$\begin{aligned} {\varvec{\Psi }}\,\widehat{\mathbf{C}}({\varvec{\delta }}_s,\delta _t)_k \,{\varvec{\Psi }}^T = \mathbf{D}({\varvec{\delta }}_s,\delta _t)_k, \quad k=1,\ldots , K, \end{aligned}$$

(3)

where $\mathbf{D}({\varvec{\delta }}_s,\delta _t)_k$ are diagonal, or nearly diagonal, $(m\times m)$ matrices.

Among the different methods proposed in the literature to perform simultaneous diagonalization of several symmetric matrices, the one used in the present work is based on an extension of the Jacobi technique where the criterion of simultaneous diagonalization is iteratively minimized under plane rotations applied to the matrices to be diagonalized (Cardoso and Souloumiac 1996).

Given the elements $d_{ij,k}$ of the matrices $\mathbf{D}({\varvec{\delta }}_s,\delta _t)_k$, with $i,j=1,\ldots ,m, \, k=1,\ldots ,K$, for the K spatio-temporal lags, the goodness of the diagonalization procedure is assessed by evaluating the following index:

$$\begin{aligned} \phi _k = \frac{\sum _{i=1}^{m}\sum _{j=1;j\ne i}^{m} d^2_{ij,k}}{\sum _{i=1}^{m} d^2_{ii,k}}, \quad k=1,\ldots ,K. \end{aligned}$$

(4)

Then, the matrix ${\varvec{\Psi }}$ is used to compute the empirical independent components $\mathbf{y}_l$, characterizing the data matrix $\mathbf{x}$ as follows:

$$\begin{aligned} \mathbf{y}=\mathbf{x}{\varvec{\Psi }}, \end{aligned}$$

(5)

so that the m basic covariance functions $c_l$ are estimated, at K user-chosen space–time lags, from the m latent components $\mathbf{y}_l$ and denoted with $\hat{c}_l, \, l=1,\ldots ,m$. Note that $\mathbf{y}_l$ indicates the column vector, of size N, of the $(N \times m)$ matrix $\mathbf{y}$.

A joint visual inspection of the plots of the covariance surfaces $\hat{c}_l$ and their spatial and temporal marginals, is useful to detect the different scales of variability, which correspond to the different lags where the surfaces of the basic covariances decay. Thus, the analyst is able to define the $L \le m$ distinct scales of spatio-temporal variability and to select the $L \le m$ basic components of the ST-LCM.

The instructions of Algorithm 1 can be specified as follows.

Algorithm 1: Identify basic components
1: Load the multivariate data set of $m\ge 2$ spatio-temporal variables and the coordinates of the spatial locations
2: Load the set of K spatio-temporal lags
3: Load the matrix $(K\times m^2)$ of the spatio-temporal direct and cross-covariance estimates
4: Perform the simultaneous diagonalization of the real-valued $(m \times m)$ matrices of the sample direct and cross-covariances estimated at the K user-defined spatio-temporal lags
5: Determine the diagonality index as in (4)
6: Obtain a realization of the m independent components $\mathbf{y}_l$ from equation (5)
7: Determine the space–time covariance surfaces of the m independent components
8: Plot the space–time covariance surfaces and determine (even graphically) the corresponding scales of variability. Then compare the scales of variability and define the $L \le m$ basic components with distinct scales of variability

3.2 Algorithm 2: Test main features and select basic models

The second algorithm supports the steps for assessing the main features of the basic components; it ends with the selection of the appropriate classes of covariance models as well as with their fitting.

First of all the full symmetry hypothesis is tested. In particular, the null hypothesis is formulated as

$$\begin{aligned} H_0: c_{l}({\varvec{\delta }}_s,\delta _t)-c_{l}({\varvec{\delta }}_s,-\delta _t)= 0, \end{aligned}$$

(6)

with $({\varvec{\delta }}_s,\delta _t)\in Q_l, ({\varvec{\delta }}_s,-\delta _t)\in Q_l,\, l=1,\ldots ,L$, where $Q_l$ denotes the set of the space–time lags fixed by the analyst at each scale l, where its cardinality is $p_l$ $(p_l \ge 2)$. Alternatively, the hypothesis in (6) is also expressed as $H_0:\mathbf{A} _l \mathbf{G} _l = \mathbf{0}$, where $\mathbf{A} _l$ is usually called contrast matrix (with $rank(\mathbf{A} _l)=r_l$) and $\mathbf{G} _l$ is the vector of the covariances $c_l$ at the lags $({\varvec{\delta }}_s,\delta _t)\in Q_l$.

By recalling the assumptions in Li et al. (2007), the hypothesis (6) can be tested by applying the following statistic

$$\begin{aligned} TS_{1l} = \left| T_n\right| \left[ \mathbf {A}_l \widehat{\mathbf {G}}_{ln}\right] ^T (\mathbf {A}_l \varvec{\Sigma }_l \mathbf {A}_l^T)^{-1}\left[ \mathbf {A}_l \widehat{\mathbf {G}}_{ln} \right] {\mathop {\rightarrow }\limits ^{d}} \chi ^2(r_l), \quad l=1, \ldots , L, \end{aligned}$$

(7)

where $\widehat{\mathbf {G}}_{ln}$ is the vector of the covariance estimators based on a sample extracted from the domain $D\times T_n$, with $D \subseteq \mathbb {R}^{d}$ and $T_n=\{1,\ldots , n\}$, $\left| T_n\right|$ is the cardinality of the set $T_n$ and $\varvec{\Sigma }_l = \lim _{n\rightarrow \infty }|T_n|Cov(\widehat{\mathbf{G }}_{ln},\widehat{\mathbf{G }}_{ln})$ and $\chi ^2$ denotes the chi square distribution.

If the full symmetry test does not end with the rejection of $H_0$, then the separability condition can be tested.

Analogously to the previous test, it is necessary to specify the null hypothesis of separability, i.e.

$$\begin{aligned} H_0: c_l({\varvec{\delta }}_s,\delta _t)-c_l({\varvec{\delta }}_s,0)c_l(\mathbf{0},\delta _t)= 0, \end{aligned}$$

(8)

with $({\varvec{\delta }}_s,\delta _t)\in Q_l, l=1,\ldots ,L,$ and the test statistic is

$$\begin{aligned} TS_{2l} = \left| T_n\right| \left[ \mathbf {A}_l \mathbf {f}(\widehat{\mathbf {G}}_{ln})\right] ^T (\mathbf {A}_l \mathbf {B}_l^T \varvec{\Sigma }_l \mathbf {B}_l \mathbf {A}_l^T)^{-1}\left[ \mathbf {A}_l \mathbf {f}(\widehat{\mathbf {G}}_{ln}) \right] {\mathop {\rightarrow }\limits ^{d}} \chi ^2(r_l), \end{aligned}$$

(9)

where $r_l=rank(\mathbf{A} _l)$, $\mathbf {B}_l$ is a matrix whose elements are ${B}_{vw,l} =\displaystyle {\partial f_{w}\over \partial G_{v}}, \, v=1,\ldots ,p_l, w=1,\ldots ,r_l,$ with $G_{v}$ the $v-$th element of $\mathbf {G}_l$ and $f_{w}$ the $w-$th element of the vector $\mathbf {f}$ of real-valued functions $(f_1,\ldots , f_{r_l})$ which are differentiable at $\mathbf {G}_l, l=1,\ldots ,L$ (Harville 2001).

Subsequently, if separability is rejected, it is convenient to investigate on the type of non-separability. To begin with, the empirical non-separability ratios are computed, i.e.

$$\begin{aligned} \widehat{r}_l({\varvec{\delta }}_s, \delta _t)=\frac{\widehat{\rho }_l({\varvec{\delta }}_s, \delta _t)}{\widehat{\rho }_l({\varvec{\delta }}_s, 0)\widehat{\rho }_l(\mathbf{0} , \delta _t)}, \quad l=1,\ldots ,L. \end{aligned}$$

(10)

Depending on the values that this index takes on, the analyst can draw some tips regarding the type of non-separability. Indeed,

• if the index $\widehat{r}_l({\varvec{\delta }}_s, \delta _t)$ is greater (smaller) than 1 for all the given lags, the uniform positive (negative) non-separability is reasonably suggested;

• otherwise non uniform non-separability can be supposed.

During this step, the box diagrams of the indexes in (10) can support the formalization of the hypotheses to be tested, i.e.

$$\begin{aligned} H^{\text {(-)}}_0: \mathbf {1}\mathbf {A}_l\mathbf {f}(\mathbf {G}_l)\le 0, \quad \text {against} \quad H^{\text {(+)}}_1: \mathbf {1}\mathbf {A}_l\mathbf {f}(\mathbf {G}_l)>0, \end{aligned}$$

(11)

or alternatively

$$\begin{aligned} H^{\text {(+)}}_0: \mathbf {1}\mathbf {A}_l\mathbf {f}(\mathbf {G}_l)\ge 0, \quad \text {against} \quad H^{\text {(-)}}_1: \mathbf {1}\mathbf {A}_l\mathbf {f}(\mathbf {G}_l)<0, \end{aligned}$$

(12)

where $\mathbf {1}=[1]_r$ and $\mathbf {A}_l$ is the associated contrast matrix (with $rank(\mathbf{A} _l)=r_l$), $l=1, \ldots , L$. These hypotheses can be tested by using the test statistic $TS_{3l}, l=1,\ldots , L$, which is obtained through the standardization of the following statistic (Cappello et al. 2018)

$$\begin{aligned} \sqrt{|T_n|}[\mathbf {1}\mathbf {A}_l\mathbf {f}(\widehat{\mathbf {G}}_{ln})]{\mathop {\rightarrow }\limits ^{d}} N({0},\mathbf {1}\mathbf {A}_l\mathbf {B}_l^T \varvec{\Sigma }_l\mathbf {B}_l\mathbf {A}_l^T\mathbf {1}^T). \end{aligned}$$

(13)

The instructions of Algorithm 2 are listed in the proper frame.

Algorithm 2: Test main features and select basic models
1: Load the l-th basic component
2: Test the validity of full symmetry of the l-th component
3: If the hypothesis of full symmetry is not rejected, the separability assumption must be verified
4: If the hypothesis of separability is unlikely from the empirical evidence and it is rejected, compute the sample non-separability ratios, plot the values classified by spatial and temporal lags, then test the type of non-separability
5: Choose the class of covariance models according to the tested features and fit the selected model
6: Compute indexes of fitting goodness

3.3 Algorithm 3: Compute coregionalization matrices

The third algorithm concerns the computation of the elements of the $(m\times m)$ coregionalization matrices $\mathbf{B} _l, l=1,\ldots , L.$

The entries of $\mathbf{B} _l$ represent the contribution to be associated to each basic component at the distinct scales of variability. To this aim, it is important to fix the value reached by $\widehat{C}_{ij}$ (for each $i,j=1,\ldots ,m$) at each selected scale of variability. This can be determined, for each $i,j=1,\ldots ,m,$ by averaging the sample covariances $\widehat{C}_{ij}$ that fall in a neighborhood of the l-th scale of variability.

Then, the elements ${b}^l_{ij}$ of matrices $\mathbf{B}_l, l=1,\ldots ,L,$ $i,j=1,\ldots , m, \, i\le j,$ are computed as follows

$$\begin{aligned} {b}^l_{ij} = \frac{[\widehat{C}_{ij}({\varvec{\delta }}_s, \delta _t)_{l-1}]-[\widehat{C}_{ij}({\varvec{\delta }}_s, \delta _t)_{l}]}{[c_l(\mathbf{0}, 0)]}, \end{aligned}$$

(14)

where $\widehat{C}_{ij}({\varvec{\delta }}_s, \delta _t)_0=\widehat{C}_{ij}(\mathbf{0}, 0).$ Note that the difference at the numerator corresponds to the net contribution of $\widehat{C}_{ij}$ at each scale of variability.

However, the matrices $\mathbf{B}_l$ are admissible if they are positive definite. Consequently, it is necessary to check their validity or equivalently, to verify if their eigenvalues are non negative. This can be carried out through the spectral decomposition of the matrices $\mathbf{B}_l$, i.e.

$$\begin{aligned} \mathbf{B}_l=\mathbf{V}_l {\varvec{\Lambda }}_l \mathbf{V}^T_l, \quad l=1, \ldots , L, \end{aligned}$$

where $\mathbf{V}_l$ is the eigenvectors matrix and ${{\varvec{\Lambda }}}_l$ is the diagonal matrix of the eigenvalues. In case of negative eigenvalues, it is suggested to modify them by forcing the negative eigenvalues to be equal to zeros and to produce the following admissible matrix $\mathbf{B} '_l$:

$$\begin{aligned} \mathbf{B}_l'=\mathbf{V}_l {{\varvec{\Lambda }}}'_l \mathbf{V}^T_l, \quad l=1, \ldots , L, \end{aligned}$$

(15)

where the new diagonal matrix of the eigenvalues ${{\varvec{\Lambda }}}'_l$ is obtained from ${{\varvec{\Lambda }}}_l$ by substituting the negative eigenvalues with zeros.

The instructions of Algorithm 3 are specified in the proper frame.

Algorithm 3: Compute coregionalization matrices
1: Load the $(K\times m^2)$ matrix of sample direct and cross-covariances
2: Load the L sample covariances of the basic components and the spatio-temporal lags associated with the scales of variability
3: For each scale of variability, compute the coregionalization matrix by using equation (14)
4: Check for admissibility of the coregionalization matrix through spectral decomposition and modify it, according to (15), if needed

Note that there is not a specific order in executing the last two algorithms (2 and 3), since the corresponding results do not depend from each other.

4 An application on air pollutants

The present case study aims to describe the various steps of the algorithm previously proposed, in order to identify an apt ST-LCM for the data of interest. The analyzed variables concern air pollution which still represents one of the major health risks, notwithstanding the introduction of national and supranational regulations for the environmental protection and control.

Moreover, as air pollution is the result of the interaction of various contaminants, which change in space and in time, a proper and punctual air quality assessment requires a deep multivariate analysis of the joint spatio-temporal behavior of the variables of interest.

In the proposed case study, the evolution in space and time of NO$_2$, NO and PM$_{10}$ hourly concentrations measured in 2017 at 18 environmental monitoring stations in Scotland is analyzed in order to detect possible latent independent components which are common to the variables and describe their direct and cross-correlation in space–time.

4.1 The sampling data: main features

In Scotland, the concentration levels of the most hazardous air pollutants, such as particulate matter (i.e. PM$_{10}$, PM$_{2.5}$) and nitrogen oxides (i.e. NOx, NO$_2$) have gradually reduced over the past decades, nevertheless the limit values fixed by the European Union for these pollutants are often exceeded at some Scottish locations. In 2017, the Lancet Commission on pollution and health, declared “Glasgow as one of the most polluted parts of the UK”.

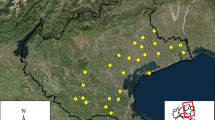
The analyzed data, which are openly available at the following web site http://www.scottishairquality.scot/data/, come from the air quality monitoring sites operated by Defra, the Scottish Government and Local Authorities (Defra 2020). They refer to hourly measurements of NO$_2$, NO and PM$_{10}$, expressed in $\upmu \mathrm{g}/\mathrm{m}^3$. The data have been collected in 2017 in Scotland, at 18 monitoring stations close to Glasgow (Fig. 1), most of which are named “urban traffic stations” due to their location at city centers and close to roadways where the main emission sources are vehicles and home heating. On the other hand, the “urban background station” is located in an urban residential area and reflects mainly the city-wide background conditions; while the “rural background station” is situated in countryside where the principal emission source consists of the regional long-range transport.

Fig. 1

Posting map of the sampling stations for NO$_2$, NO and PM$_{10}$, with the locations’ coding

As known, several studies have shown that long-term exposures of these air pollutants caused negative effects on human health, such as respiratory as well as acute and chronic cardiovascular outcomes (Ayyagari et al. 2007; Hoek et al. 2002). For these reasons the interest of the scientific community is mainly in studying and modeling the joint behaviour of these hazardous pollutants, which exhibit the same evolution in time, with a daily periodicity characterized by very low values early in the morning and high values during the work hours (from 6 a.m. till 6 p.m.), as shown in Fig. 2. Moreover, it is evident that the lowest mean values for the three pollutants occurred at the rural and urban background stations (coded as GLA7 and GLKP, respectively), which presented the same daily periodic component as the other urban-traffic stations.

Fig. 2

Chart of the NO$_2$, NO and PM$_{10}$ concentrations averaged per hour, for each survey station

The 24-h periodicity, which immediately appears in Fig. 2 for the variables under study, has been removed, station by station, by using the moving average technique applied to homogeneous subsets of the temporal span. Note that the program REMOVEMULT (Brockwell and Davis 1987; De Iaco et al. 2010), utilized to treat the systematic component in time, performs also a linear time interpolation in the presence of a maximum of 5 consecutive missing values. However, it is worth pointing out that, in the analyzed data set, the number of missing values is very low, indeed for all the stations the percentage of missing values is on average at most 4.3%, with a maximum of 14.2% for one of the stations. Moreover, there are few sequences of 5 or more consecutive missing values (on average, 5 sequences for all the stations).

The effects of various factors (such as traffic volumes, seasonality, working/non-working days) which may affect the air pollution magnitude and cycle have been essentially removed by filtering out, station by station, the systematic component. In addition, it is worth pointing out that, on the basis of a descriptive analysis of the data, the altitude of the locations has no significant effects on the daily behavior of the pollutants, this is mainly due to the orography of the area under study which is also not very extended. Thus the NO$_2$, NO and PM$_{10}$ residuals have been examined in order to detect the most appropriate ST-LCM, by following the procedure previously described.

4.2 Basic components’ identification

As described in Sect. 3, the first step towards the identification of the most suitable ST-LCM, concerns the computation of the sample covariances, both direct and cross, for a proper selection of lags fixed by the researcher on the basis of the spatio-temporal sampling.

For the present case study, 8 lags in space and 37 lags in time, in total 296 lags in space–time, have been chosen, thus the spatio-temporal direct and cross-covariance surfaces have been computed at the selected lags for NO$_2$, NO and PM$_{10}$ residuals (Fig. 3).

Fig. 3

Empirical surfaces of a NO$_2$, b NO$_2$ versus NO, c NO$_2$ versus PM$_{10}$, d NO, e NO versus PM$_{10}$ and f PM$_{10}$ residuals

Successively, the 296 symmetric $(3\times 3)$ matrices of the estimated covariance functions have been nearly diagonalized through the package Jade (Miettinen et al. 2017) developed in the R environment (R Core Team 2015). The diagonalization accuracy has been quantified by the relative index (4) determined to measure the closeness of the nearly diagonalized matrices to diagonal matrices. In this case, index (4) has shown very low values (approximately 8 out of 10 values are less than 0.01) confirming thus the diagonalization’s goodness.

Then, by the product between the matrix of the NO$_2$, NO and PM$_{10}$ residuals and the following orthonormal matrix

$$\begin{aligned} {{\varvec{\Psi }}} = \left[ \begin{array} {lll} 0.8597 &{} \quad 0.4985 &{} \quad -0.1116 \\ -0.5033 &{} \quad 0.8639 &{} \quad -0.0184 \\ 0.0872 &{} \quad 0.0720 &{} \quad 0.9936 \\ \end{array} \right] , \end{aligned}$$

which has nearly diagonalized the 296 sample covariance matrices, three sample independent latent components have been computed, as indicated in (5).

Afterwards, the spatio-temporal covariance functions have been estimated for the obtained independent components and, through the visual exploration of their surfaces, two basic components ($L=2$) have been retained since they have exhibited different scales of variability in space–time: (a) a short distance variability scale around 10 km and 12 h, which represents the short distance component (SDC), and (b) a long distance variability scale around 13 km and 24 h which represents the long distance component (LDC). The remaining component has been discarded considering that its spatio-temporal variability is quite similar to one of the chosen components.

The covariance surfaces corresponding to the two basic components are shown in Fig. 4 together with the respective marginals in space and time, whose behavior is linear at the origin and concave for small spatial and temporal lags.

Fig. 4

Surfaces of a the SDC, b the LDC, with their corresponding spatial and temporal marginals

4.3 Basic components’ modeling

As second step of the proposed selection procedure, the main features (full symmetry, non-separability and type of non-separability) of the chosen basic components, need to be tested. In particular, the aforementioned tests have been performed through the covatest package (Cappello et al. 2020). The results of these tests immediately indicate the most apt classes of covariance models for the retained components.

4.3.1 Main characteristics of the selected basic components: tests’ results

The full symmetry test (7) has been carried out for each basic component on the set of lags where the correlation in space and time was significant; in particular spatial lags equal to 2.2 and 4.5 km, and temporal lags equal to 1 and $-1$ h, have been fixed.

At 5% significance level, it results that the null hypothesis of full symmetry cannot be rejected for both components, since $TS_{11}=3.561$ (p value $= 0.169$), for the SDC and $TS_{12}=1.113$ (p value $= 0.573$), for the LDC.

Then the separability condition has been checked after selecting the following spatio-temporal lags:

• $||{\varvec{\delta }}_{s_1}||=2.2$ km and $\delta _{t_1}=1$ h,

  $||{\varvec{\delta }}_{s_2}||=4.5$ km and $\delta _{t_2}=2$ h,

for the SDC and

• $||{\varvec{\delta }}_{s_1}||=6.5$ km and $\delta _{t_1}=5$ h,

  $||{\varvec{\delta }}_{s_2}||=8.9$ km and $\delta _{t_2}=6$ h,

for the LDC.

The null hypothesis in (8) can be rejected, at 5% significance level, since

• $TS_{21}=18.864, r=2$ (p value $=0.000$) for the SDC,

• $TS_{22}=22.141, r=2$ (p value $=0.000$) for the LDC.

On the basis of the above results it is reasonable to assume that the two selected components are fully symmetric and non-separable; hence the type of non-separability has been checked. For this purpose, the non-separability ratios (10) have been computed and classified per spatial and temporal lags (Fig. 5).

Fig. 5

Non-separability ratios grouped for spatial and temporal lags, computed for a the SDC and b the LDC

This graphical tool represents a very simple way to have information on the type of non-separability which will be successively tested. In this case, the non-separability ratios (10) computed for the SDC are uniformly smaller than 1, thus a uniform negative non-separability can be reasonably assumed; while for the LDC, the sample ratios (10) are greater than 1 for all spatio-temporal lags, hence a positive non-separability can be assumed.

At the significance level $\alpha =0.05$, the test in (13) is conducted, for the hypotheses (11), on the right tail of the standard normal distribution for the SDC, while the test in (13) is applied, for the hypotheses in (12), on the left tail of the standard normal distribution for the LDC.

In particular, after choosing different spatial lags (namely, lags equal to 2.2 km, 4.5 km, 6.5 km and 8.9 km) and temporal lags (namely, from 1 to 6 h), the null hypotheses previously fixed are not rejected at $5\%$ significance level.

4.3.2 Modeling the selected basic components

The results concerning the test on the main characteristics of the two basic components drive the analyst towards the identification of the most appropriate covariance models (De Iaco et al. 2013). In this case study, there is a statistical evidence to model the surface of the SDC with a fully symmetric, negative non-separable space–time covariance function, while the LDC’s surface can be described by a fully symmetric, positive non-separable space–time covariance function. In particular, the product–sum covariance function, which is a fully symmetric and negative non-separable space–time covariance model (De Iaco et al. 2001; De Iaco and Posa 2013), can be reasonably used for SDC ($l=1$)

$$\begin{aligned} {}_{_{PS}}c_{1}({\varvec{\delta }}_s,\delta _t) = k_{11} C_{s_1}({\varvec{\delta }}_s)C_{t_1}(\delta _t) + k_{21} C_{s_1}({\varvec{\delta }}_s) + k_{31} C_{t_1}(\delta _t), \end{aligned}$$

(16)

with $k_{11}>0, k_{21}\ge 0, k_{31}\ge 0,$ $C_{s_1}$ the spatial exponential covariance model in $\mathbb {R}^d, (d=2)$ and $C_{t_1}$ the temporal exponential covariance model in $\mathbb {R}$, with practical ranges $a_{s_1}$ and $a_{t_1}$, respectively.

On the other hand, the Gneiting class of model (Gneiting 2002), which is characterized by full symmetry and positive non-separability (De Iaco and Posa 2013), has been considered for the LDC ($l=2$)

$$\begin{aligned} {}_{_{G}}c_2({\varvec{\delta }}_s,\delta _t) = N + C\displaystyle {1 \over {\displaystyle {\left( 1+{\delta _t / a_{t_2}}\right) }}} \mathrm{exp}\left\{ - \displaystyle {{\varvec{\delta }}_s}/{a_{s_2}} \over {{\displaystyle {\left( 1+{\delta _t / a_{t_2}}\right) }^{0.5\beta }}}\right\} \end{aligned}$$

(17)

where $a_{s_2}$ and $a_{t_2}$ are the practical ranges in space and time, respectively, while N and C are positive values representing the contributions to the variance and $\beta \in [0, \, 1].$

The parameters’ estimates of the above mentioned covariance models are shown in Table 1: they have been obtained by carrying out the non-linear regression method developed in SPSS on the basis of the Newton–Lagrange approach (Alt and Malanowski 1993).

Table 1 Estimates of the covariance models’ parameters

Hence, the fitted ST-LCM is the following:

$$\begin{aligned} \mathbf{C}({\varvec{\delta }}_s, \delta _t)= \mathbf{B}_1 \; _{_{PS}}c_1({\varvec{\delta }}_s, \delta _t)+\mathbf{B}_2 \; _{_{G}}c_2({\varvec{\delta }}_s, \delta _t), \end{aligned}$$

(18)

where the coregionalization matrices $\mathbf{B}_1$ and $\mathbf{B}_2$ are estimated as described hereafter.

4.4 Estimation of the coregionalization matrices

As clarified in Sect. 3.3, the estimation of the coregionalization matrices is the object of the third algorithm.

In this case, the computation of the entries of $\mathbf{B}_l, \, l=1,2,$ as indicated in (14), requires the values $c_1(\mathbf{0}, 0)$ and $c_2(\mathbf{0}, 0)$ of the two basic components, as well as the information coming from the sample covariance of the variables under study, i.e.

• $\widehat{c}_{ij}(\mathbf{0}, 0), i,j=1,2,3,$

• $\widehat{c}_{ij}({\varvec{\delta }}_s, \delta _t)_1$ and $\widehat{c}_{ij}({\varvec{\delta }}_s, \delta _t)_2$, detected at the first and the second scales of spatio-temporal variability, i.e. at 10 km and 12 h, and at 13 km and 24 h, respectively,

where $i=1$ refers to NO$_2$ residuals, $i=2$ to NO residuals and $i=3$ to PM$_{10}$ residuals.

By looking at Figs. 3 and 4, the above-mentioned values are easily identified and consequently the elements of the coregionalization matrices are immediately determined. In particular, for the elements of $\mathbf{B}_1$ it results:

$$\begin{aligned} \begin{array} {lllll} b_{11}^1= \displaystyle \frac{449.869-142.914}{144.800} &{} &{} b_{12}^1= \displaystyle \frac{617.259-243.636}{144.800} &{} &{} b_{13}^1= \displaystyle \frac{61.775-19.758}{144.800} \\ b_{21}^1= b_{12}^1 &{} &{} b_{22}^1= \displaystyle \frac{1423.198-400.513}{144.800} &{} &{} b_{23}^1= \displaystyle \frac{101.030-37.763}{144.800} \\ b_{31}^1= b_{13}^1 &{} &{} b_{32}^1= b_{23}^1 &{} &{} b_{33}^1= \displaystyle \frac{85.298-26.300}{144.800} \\ \end{array} \end{aligned}$$

and for the elements of $\mathbf{B}_2$ it results:

$$\begin{aligned} \begin{array} {lllll} b_{11}^2= \displaystyle \frac{142.914-100.912}{75.587} &{} &{} b_{12}^2= \displaystyle \frac{243.636-153.660}{75.587} &{} &{} b_{13}^2= \displaystyle \frac{19.758-11.462}{75.587} \\ b_{21}^2= b_{12}^2 &{} &{} b_{22}^2= \displaystyle \frac{400.513-193.999}{75.587} &{} &{} b_{23}^2= \displaystyle \frac{37.763-11.061}{75.587} \\ b_{31}^2= b_{13}^2 &{} &{} b_{32}^2= b_{23}^2 &{} &{} b_{33}^2= \displaystyle \frac{26.300-18.847}{75.587} \\ \end{array} \end{aligned}$$

Finally, the matrices $\mathbf{B}_l, l=1,2,$ are as follows:

$$\begin{aligned} \mathbf{B}_1 = \left[ \begin{array} {lll} 2.120 &{} \quad 2.580 &{} \quad 0.290 \\ 2.580 &{} \quad 7.063 &{} \quad 0.437 \\ 0.290 &{} \quad 0.437 &{} \quad 0.407 \\ \end{array} \right] , \quad \mathbf{B}_2 = \left[ \begin{array} {lll} 0.556 &{} \quad 1.190 &{} \quad 0.110 \\ 1.190 &{} \quad 2.732 &{} \quad 0.353 \\ 0.110 &{} \quad 0.353 &{} \quad 0.099 \\ \end{array} \right] , \end{aligned}$$

(19)

whose eigenvalues are non negative ensuring, in this way, the positive definiteness of the $\mathbf{B}_l, l=1,2,$ and consequentially the admissibility of the fitted ST-LCM, which is now completely specified:

$$\begin{aligned} \mathbf{C}({\varvec{\delta }}_s, \delta _t)= \left[ \begin{array} {lll} 2.120 &{} \quad 2.580 &{} \quad 0.290 \\ 2.580 &{} \quad 7.063 &{} \quad 0.437 \\ 0.290 &{} \quad 0.437 &{} \quad 0.407 \\ \end{array} \right] \, _{_{PS}}c_1({\varvec{\delta }}_s,\delta _t) + \left[ \begin{array} {lll} 0.556 &{} \quad 1.190 &{} \quad 0.110 \\ 1.190 &{} \quad 2.732 &{} \quad 0.353 \\ 0.110 &{} \quad 0.353 &{} \quad 0.099 \\ \end{array} \right] \, _{_{G}}c_2({\varvec{\delta }}_s,\delta _t). \end{aligned}$$

(20)

4.5 Adequacy of the fitted ST-LCM

A way to evaluate the adequacy of the fitted ST-LCM consists in exploring the results of the cross-validation procedure which produces leave-one-out predictions on the basis of the fitted model and the data set under study. At each point of the domain, the observed value is temporarily eliminated and estimated by using the fitted ST-LCM and the measurements available in a neighborhood properly defined. In the spatio-temporal multivariate case, cokriging estimations can be computed for cross-validation purposes through the routine “COK2ST” implemented in the GSLib package (De Iaco et al. 2010).

In this case study, the previously mentioned program has been executed in order to obtain leave-one-out predictions of the residuals for each variable in turn (NO$_2$, NO and PM$_{10}$), by using the model in (20). Moreover, the suitability of the selected ST-LCM has been evaluated even for a decreasing number of observations; in other terms, the cross-validation procedure has been performed by considering, alternatively, three different input databases, composed of 100%, 80% or 60% of the data (residuals). Note that the cut data sets have been obtained from the original data set through a random selection.

The Spearman correlation coefficients calculated between the residuals of the analyzed variables and the cross-validation estimates have been reported in Table 2, together with the relative mean absolute estimation errors (RMAE).

Table 2 Cross-validation results for the ST-LCM (20)

Note that the linear correlation coefficients are very high for all the analyzed variables (at 1% significance level), even when the reduced data sets are used. Indeed, the reduction of Spearman coefficients is at most of 3.4% for the cut data sets. The RMAEs are approximately constant for all the alternative databases and show that the relative discrepancies (between the observed and the estimated values) are on average less than 20%. Thus, these results can be used to confirm the adequacy of the fitted ST-LCM.

5 A comparative analysis

In this section, the proposed procedure has been compared with respect to the exiting fitting method, which consists in using the same class of covariance models for all the basic components, without considering the main features of the basic components that the statistical tests can reveal. To this aim, two other alternative ST-LCMs have been fitted, as specified below:

• the ST-LCM based on the product–sum covariance model, which has been fitted either for the SDC and the LDC, i.e.

  $$\begin{aligned} \mathbf{C}'({\varvec{\delta }}_s, \delta _t)= \mathbf{B}_1 \; _{_{PS}}c_1({\varvec{\delta }}_s, \delta _t)+\mathbf{B}_2 \; _{_{PS}}c_2({\varvec{\delta }}_s, \delta _t), \end{aligned}$$

  (21)

  where $_{_{PS}}c_1({\varvec{\delta }}_s, \delta _t)$ is as in (16) and

  $$\begin{aligned} {}_{_{PS}}c_{2}({\varvec{\delta }}_s,\delta _t) = k_{12} C_{s_2}({\varvec{\delta }}_s)C_{t_2}(\delta _t) + k_{22} C_{s_2}({\varvec{\delta }}_s) + k_{32} C_{t_2}(\delta _t), \end{aligned}$$

  with $k_{12}= 17.015, \, k_{22}= 18.572, \, k_{32}=40,$ $C_{s_2}$ is the spatial exponential covariance model in $\mathbb {R}^d$ and $C_{t_2}$ the temporal exponential covariance model in $\mathbb {R}$, with practical ranges $a_{s_2}=13$ km and $a_{t_2}=24$ h, respectively;

• the ST-LCM, obtained by using the Gneiting class of model for both the SDC and the LDC, i.e.

  $$\begin{aligned} \mathbf{C}''({\varvec{\delta }}_s, \delta _t)= \mathbf{B}_1 \; _{_{G}}c_1({\varvec{\delta }}_s, \delta _t)+\mathbf{B}_2 \; _{_{G}}c_2({\varvec{\delta }}_s, \delta _t), \end{aligned}$$

  (22)

  where

  $$\begin{aligned} {}_{_{G}}c_1({\varvec{\delta }}_s,\delta _t) = N + C\displaystyle {1 \over {\displaystyle {\left( 1+{\delta _t / a_{t_1}}\right) }}} exp\left\{ - \displaystyle {{\varvec{\delta }}_s}/{a_{s_1}} \over {{\displaystyle {\left( 1+{\delta _t / a_{t_1}}\right) }^{0.5\beta }}}\right\} \end{aligned}$$

  with $a_{s_1}=9.5$ km, $a_{t_1}=12$ h, $N=79.8$, $C=65$ and $\beta =0.01$, while $_{_{G}}c_2({\varvec{\delta }}_s, \delta _t)$ is as indicated in (17).

Then the adequacy of the ST-LCM in (20), defined by using the proposed algorithm, has been compared to the one of the models (21) and (22), developed through the usual fitting procedure.

First of all, the comparative analysis has been conducted by computing the discrepancies between the empirical and the theoretical surfaces associated to the direct and cross-covariance functions. To this aim, the relative mean difference ($\Delta$) has been determined and analyzed as the number of lags increases, starting from small spatial and temporal distances and including step by step larger distances. This index represents an adequate synthesis of the errors between the fitted model and empirical covariance surface and is defined as follows:

$$\begin{aligned} \Delta _{ij}=\frac{1}{{\sum _{k=1}^{K}\widehat{c}_{ij}({\varvec{\delta }}_s,\delta _t)_k}} {\displaystyle \sum _{k=1}^{K}[\widehat{c}_{ij}({\varvec{\delta }}_s,\delta _t)_k-{c}_{ij}({\varvec{\delta }}_s,\delta _t)_k]}, \quad i,j=1,\ldots , m, \end{aligned}$$

(23)

where $\widehat{c}_{ij}({\varvec{\delta }}_s,\delta _t)_k$ are the values of the direct ($i=j$) and cross ($i\ne j$) sample covariance, while ${c}_{ij}({\varvec{\delta }}_s,\delta _t)_k$ are the values of the fitted covariance model at the K fixed lags.

Table 3 shows the values of index (23) for each fitted ST-LCM, computed for an increasing number K of lags, as specified below:

• $K=52,$ when the first 4 and 13 lags in space and time are analyzed;

• $K=150,$ when the first 6 and 25 lags in space and time are considered;

• $K=296,$ when all lags fixed in space and time for the structural analysis are examined.

Table 3 Results of the adequacy assessment for ST-LCMs (20), (21) and (22)

Table 4 RMAEs from cross-validation based on models (20), (21), (22), classified with respect to the variables under study

Thus, from the comparison between the empirical and the theoretical covariance surfaces, the ST-LCM in (20), obtained on the basis of the proposed algorithm, has performed better than the other two models, with an improvement (in terms of reduction of the index $\Delta$) of 8% on average. It is worth pointing out that:

• the improvement, with respect to the model (21), rises up to 13.3% for $\mathrm{K} = 296$; thus the discrepancy increases when large spatial and temporal distances are included in the computation of the index $\Delta$, since in model (21), the LDC was forced to be modelled by using the product–sum class;

• the improvement, with respect to the model (22), rises up to 14.1% for K = 52; thus the discrepancy increases mainly for small spatial and temporal distances, since in the model (22), the SDC was forced to be modelled by using the Gneiting class.

In addition, the superiority of the ST-LCM in (20), coming out from the proposed algorithm, has been also evaluated on the basis of the cross-validation results. In particular, the leave-one-out estimates of each variable under study (NO$_2$, NO and PM$_{10}$) have been also computed through cokriging, by using the models in (21) and (22). As done in Sect. 4.5, the cross-validation technique has been performed by considering, alternatively, three different input databases, composed of 100%, 80% or 60% of the original residual data. Then the RMAEs have been determined and compared with respect to the ones of the ST-LCM in (20). From the results given in Table 4, it is worth pointing out that the RMAEs associated to the ST-LCM in (20) are significantly lower than the ones of the other models. Indeed, the percentage decrease varies from 16 to 28%: in detail, it is in the range 15.56–16.20% when the complete data set is used, or in the range 20.42–21.07% when the 80% of the data are considered, or in the range 25.39–27.65% for the smaller data set.

6 Summary

This paper aimed to present some computational advances regarding the selection of an ST-LCM to be used for modeling the joint spatio-temporal evolution of environmental variables. It is also worth pointing out that the flexibility and good reliability of the developed procedure support an easy reproduction of all stages for data sets concerning either the same information but updated in space and time, or different variables. Moreover, the algorithms can be performed with the support of ad-hoc R functions (R Core Team 2015), thus practitioners can use this procedure for other applications. For this reason, as a future development, the effort should be concentrated on the construction of an R package.