Bayesian analysis of restricted penalized empirical likelihood

Abstract

In this paper, we introduce restricted empirical likelihood and restricted penalized empirical likelihood estimators. These estimators are obtained under both unbiasedness and minimum variance criteria for estimating equations. These scopes produce estimators which have appealing properties and particularly are more robust against outliers than some currently existing estimators. Assuming some prior densities, we develop the Bayesian analysis of the restricted empirical likelihood and the restricted penalized empirical likelihood. Moreover, we provide an EM algorithm to approximate hyper-parameters. Finally, we carry out a simulation study and illustrate the theoretical results for a real data set.

1 Introduction

Empirical likelihood (EL) is a statistical tool that provides robust inferences for given data under some general conditions. The EL approach was initially used by Thomas et al. (1957) and then further developed by Owen (1990). Nowadays, many statisticians use this method to analyze various real-world data.

Owen (1988 and 1990) developed and applied the EL ratio statistics to some non-parametric problems. The author proved that these statistics have asymptotically a chi-squared distribution. Furthermore, the author developed confidence intervals and hypothesis tests for model parameters based on likelihood ratio statistics under a parametric model. The asymptotic properties and some essential corrections of these statistics were presented in DiCiccio and Romano (1989) and Hall and La Scala (1990). Qin and Lawless (1994) showed that EL, along with some appropriate estimating equations, provides an acceptable non-parametric fit to data.

Practically, in the EL approach, estimates are obtained by maximizing the EL function based on estimating equations along with some additional restrictions. Of these constraints, we would point out the zero expectation value of estimating equations under the probability model $\{p_1,p_2, \dots ,p_n\}$ of observations. Newey and Smith (2004) and Chen and Cui (2006 and 2007) showed that the obtained estimators have some appealing statistical properties; for more details, see Owen (2001) and Qin and Lawless (1994). In addition to the studies by Chen et al. (2009), Hjort et al. (2009), Tang and Leng (2010), Leng and Tang (2012), Chang et al. (2015) revealed that the conventional asymptotic results of EL estimators are expected to hold only when the dimension p of parameters and the number r of estimating equations both grow at some rate slower than the sample size n. On the other hand, challenges due to high-dimensionality require approaches to deal with cases in which both p and r grow with sample size. Along this line, Tang and Leng (2010), Leng and Tang (2012), and Chang et al. (2015) utilized sparsity assumption of model parameters and applied penalty functions to achieve parameter sparsity. Their results revealed that sparse parameter estimators with reasonable properties are achievable at all. However, there are still several challenges for high dimensional data analysis using EL.

Tsao (2004) found out that for fixed n with relatively large p, the coverage rate that the true parameter values are contained in an EL-based confidence region can be substantially smaller than the nominal level, which is called under-coverage problem. Tsao and Wu (2013 and 2014) proposed an extended EL approach to address the under-coverage issue due to some more constraints on the parameter space. To avoid extra constraints, Bartolucci (2007) proposed a penalized EL method which optimizes the product of probabilities that is penalized by a loss function depending on model parameters. Lahiri and Mukhopadhyay (2012) did a similar work to Bartolucci (2007) but with a different type of loss function. They studied the properties of penalized EL ratio statistic in a high-dimensional framework. Moreover, Chang et al. (2017) studied, from a new scope, the penalized EL estimator under the setting of high-dimensional sparse model parameters.

As we understand, the EL approach essentially is based on the unbiasedness property of estimating equations. It seems that using only the unbiasedness condition for estimating equations leads to estimates of corresponding probabilities, $p_1,p_2,\dots ,p_n$, such that they almost assume the same value for all observations. In contrast, in real datasets there are frequently some outliers and we hope to minimize their impact on EL estimators. In this work, we try to reduce the impact of outliers by controlling the variance of estimating equations, because the impact of outliers is directly reflected in estimating equations. Specifically, a summary of findings and contributions of this work is listed below.

• 1. While the traditional EL method is solely based on the unbiasedness of estimating equations, here we try to find the maximum EL estimator under both unbiasedness and minimum variance criteria on estimating equations. This new scopes produces a new estimation which has appealing properties and is more robust against outliers than the traditional EL method. We call this methodology the restricted empirical likelihood (REL).

• 2. When estimating equations are linear functions of model parameters or satisfy certain mild conditions, $-\log (REL)$ is a convex function, an appealing property in statistical inference. Moreover, positive coefficients of estimating equations play an important role (act as weights) in removing equations with ignorable effects, a big challenge in problems with many estimating equations.

• 3. Assuming a prior density for the parameters and that the REL acts as a usual likelihood function, we develop a Bayesian analysis for REL estimator. In this aspect, we obtain all conditional posterior distributions that have closed-form and facilitate sampling for a large class of estimating equations.

• 4. One of the most critical challenges in the REL approach is the choice of valid estimating equations among many candidates. We deal with this problem by assuming some penalized functions. We call the resulted estimator the restricted penalized empirical likelihood (RPEL) estimator.

• 5. Another task of Bayesian analysis method is to estimate prior density parameters (or hyper-parameters). Although this is of secondary importance, we provide an EM algorithm to estimate hyper-parameters.

The paper is organized as follows. In Sect. 2, we review some basic concepts and then introduce the REL estimation and the RPEL estimation. The Bayesian analysis of RPEL and model selection criterion for RPEL are presented in Sects. 3 and 4 respectively. As an example of penalized functions, in Sect. 5, we discuss the conditional posterior and Gibbs sampling scheme for a multiple linear regression model. In Sect. 6, we carry out both a simulation study and a real data application to evidence and illustrate our theoretical results. Finally, a conclusive summary is presented in Sect. 7.

2 Restricted penalized empirical likelihood

In this section, we first review some basic concepts in EL and then introduce the REL and RPEL estimators. All necessary notations and definitions used throughout the paper will be presented.

2.1 Empirical likelihood estimation

Let ${\mathbf {x}}_1, {\mathbf {x}}_2,\ldots , {\mathbf {x}}_n\in {\mathcal {R}}^d$ be i.i.d. observations and $\varvec{\theta }=(\theta _1,\dots ,\theta _p)^T$ be a p-dimensional parameter in parameter space $\varvec{\Theta }$. Moreover, we assume that ${\mathbf {g}}({\mathbf {X}}; \varvec{\theta }) = \big (g_1({\mathbf {X}}; \varvec{\theta }), \dots , g_r({\mathbf {X}}; \varvec{\theta })\big )^T$ is a r-dimensional vector of estimating equations which satisfies the unbiased conditions

$$\begin{aligned} E\{g_j({\mathbf {X}};\varvec{\theta }_{0})\}=\sum _{i=1}^np_ig_j(\mathbf{x}_i;\varvec{\theta }_{0})=0,\qquad j=1,\ldots , r. \end{aligned}$$

(1)

Here, we assume that $\varvec{\theta }_0\in \varvec{\Theta }$ is the true vector of parameters and $p_1,p_2,\ldots ,p_n$ are the corresponding probabilities; for more details see Hjort et al. (2009) and Chang et al. (2015).

In the usual EL approach, the probabilities $p_i$’s are estimated by maximizing the EL function

$$\begin{aligned} L(\varvec{\theta })\propto \prod _{i=1}^{n}p_{i} \end{aligned}$$

(2)

under constraints $\sum _{i=1}^{n}p_i=1,$ $p_i>0$ and (1). That is,

$$\begin{aligned} \sup _{p_1,\ldots ,p_n}\; \bigg \{\; \prod _{i=1}^{n}p_{i}:\; p_{i}>0, \; \sum _{i=1}^{n}p_i=1,\ \sum \limits _{i=1}^{n}p_{i}g_j(\mathbf{x}_{i};\varvec{\theta })=0\bigg \}. \end{aligned}$$

(3)

According to Qin and Lawless (1994) and Owen (1988), (3) gives

$$\begin{aligned} p_{i}\propto \frac{1}{1+\varvec{\lambda }^T {\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })}, \end{aligned}$$

(4)

where $\varvec{\lambda }=(\lambda _1,\lambda _2,\ldots ,\lambda _r)^T$ are some Lagrange multiplier constants. Given these $p_i$’s along with (2), the logarithm of the EL function is given as

$$\begin{aligned} \ell (\varvec{\theta })=-\sum \limits _{i=1}^n \log \left[ 1+\varvec{\lambda }^T {\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })\right] +\mathrm{constant}. \end{aligned}$$

(5)

So, the maximum EL estimator $\hat{\varvec{\theta }} ^ {EL}$ of $\theta$ is obtained as

$$\begin{aligned} (\hat{\varvec{\theta }}^{EL},\hat{\varvec{\lambda }}) =\arg \min _{\varvec{\theta }}\max _{\varvec{\lambda }} \left\{ \sum \limits _{i=1}^n \log \left[ 1+\varvec{\lambda }^T \mathbf{g}({\mathbf {x}}_{i};\varvec{\theta })\right] \right\} . \end{aligned}$$

(6)

To compute $\hat{\varvec{\theta }}^{EL},$ a two-layer algorithm was proposed by Tang and Wu (2014). The inner layer of this algorithm produces $\hat{\varvec{\lambda }}$ by maximizing (6) for a given $\varvec{\theta }.$ Then the outer layer of the algorithm computes the optimal value of $\varvec{\theta }$ as a function of $\hat{\varvec{\lambda }}.$ Both layers can be performed using the coordinate descent algorithm by updating one component at each time. For more details, see Tang and Wu (2014).

2.2 Restricted empirical likelihood estimation

So far, all we have illustrated on EL estimation are based on the unbiasedness condition (1) of estimating equations. However, there is a fundamental question that deserves more attention: how can one control the estimating equations’ variation in order to reduce the effect of outliers on maximum EL estimator via allocating smaller probabilities to outliers? Naturally, this question induces us to maximize the EL function under both unbiasedness and minimum variance criteria on estimating equations at the same time. For this purpose, the estimators of $p_1,\dots ,p_n$ should minimize equations

$$\begin{aligned} {\left\{ \begin{array}{ll} Q_{1}(p_1,\ldots ,p_n) \ = \ \sum \limits _{i=1}^{n} p_{i} {\mathbf {g}} ({\mathbf {x}}_{i};\varvec{\theta })^T {\mathbf {g}} ({\mathbf {x}}_{i};\varvec{\theta }) -\varvec{\gamma }^T \sum \limits _{i=1}^{n} p_{i} {\mathbf {g}}({\mathbf {x}}_{i};\varvec{\theta }),\\ \\ Q_{2}(p_1,\ldots ,p_n) \ = \ -\sum \limits _{i=1}^{n} \log p_{i}+\nu \left( 1-\sum \limits _{i=1}^{n} p_{i}\right) -n\varvec{\lambda }^T \sum \limits _{i=1}^{n} p_{i} {\mathbf {g}}({\mathbf {x}}_{i};\varvec{\theta }), \end{array}\right. }\nonumber \\ \end{aligned}$$

(7)

where scaler $\nu$ and vectors $\varvec{\gamma }$ and $\varvec{\lambda }$ are Lagrange multipliers. In (7), $Q_{2}(p_1,\ldots ,p_n)$ is exactly the usual EL method in which $-\sum \nolimits _{i=1}^{n}\log p_{i}$ is minimized under the two constraints $\sum \nolimits _{i=1}^{n} p_{i}=1$ and $\sum \nolimits _{i=1}^{n} p_{i}{\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })=0$. The main contribution of this paper is the addition of objective function $Q_{1}(p_1,\ldots ,p_n)$ in (7), in which we minimize the total variation $\sum \nolimits _{i=1}^{n} p_{i} {\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })^T{\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })$ under the constraint $\sum \nolimits _{i=1}^{n} p_{i} {\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })=0$ in order to control the effect of outliers in model fitting. The minimizer $p_i$’s of $Q_{2}(p_1,\ldots ,p_n)$ is given by $p_{i}\propto \frac{1}{1+\varvec{\lambda }^T {\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })}$. With these quantities, the second term in $Q_{1}(p_1,\ldots ,p_n)$ is equal to 0. Therefore, using inequality ${\mathbf {a}}^T{\mathbf {b}}\le \frac{\Vert \mathbf{a}\Vert ^2+\Vert {\mathbf {b}}\Vert ^2}{2}$ for arbitrary vectors ${\mathbf {a}}$ and ${\mathbf {b}}$, where $\Vert \cdot \Vert$ denotes the $l^2$-norm, we have the total variation (TV)

$$\begin{aligned} Q_{1}(p_1,\ldots ,p_n)&=\sum \limits _{i=1}^{n} p_{i} {\mathbf {g}} ({\mathbf {x}}_{i};\varvec{\theta })^T{\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta }) \\&=\sum \limits _{i=1}^{n} \frac{1}{1+\varvec{\lambda }^T \mathbf{g}({\mathbf {x}}_{i};\varvec{\theta })} {\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })^T{\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta }) \\&\quad \ge \sum \limits _{i=1}^{n} \frac{1}{1+\frac{\Vert \varvec{\lambda }\Vert ^2+ \Vert {\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })\Vert ^2}{2}} {\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })^T{\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })\\&=w\sum \limits _{i=1}^{n} \frac{1}{1+w \Vert {\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })\Vert ^2} {\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })^T{\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })\\&=w\sum \limits _{i=1}^{n} p^*_{i} {\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta })^T{\mathbf {g}} (\mathbf{x}_{i};\varvec{\theta }), \end{aligned}$$

where $w=\frac{2}{2+\Vert \varvec{\lambda }\Vert ^2}$ and $p^*_i=\frac{1}{1+w \Vert {\mathbf {g}}(\mathbf{x}_{i};\varvec{\theta })\Vert ^2}$. This introduction of probabilities $p^*_i$’s has the following four desirable features.

• i) For all ${\mathbf {x}}$ and $\varvec{\theta },$ the probabilities $p^*_{i}$’s are always positive and thus there is no need to impose additional constraints on $\varvec{\lambda }$ as for $p_i$’s.

• ii) These probabilities $p^*_{i}$’s practically produce the minimum TV.

• iii) Outliers that make $\Vert g({\mathbf {x}}_{i};\varvec{\theta })\Vert ^2$ larger will receive smaller weight $p^*_{i}$. This indicates that statistical inferences via probability model $(p^*_1, \dots , p^*_n)$ are robust against outliers.

• iv) For a large class of estimating equations (including usual linear estimating equations of $\varvec{\theta }$), $-\log p_i^*$ is a convex function of $\varvec{\theta }$, which is an important property in statistical inference.

According to above derivations, we define our REL under the more general probability model

$$\begin{aligned} p_{i}^*\propto \frac{1}{1+{\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })} \end{aligned}$$

(8)

as

$$\begin{aligned} L_R(\varvec{\theta }, \mathbf{w})\propto \prod _{i=1}^{n}p^*_{i}=\prod _{i=1}^{n}\frac{1}{1+\mathbf{w}^T {\mathbf {g}}^{*}({\mathbf {x}}_{i};\varvec{\theta })}, \end{aligned}$$

where ${\mathbf {g}}^*({\mathbf {x}};\varvec{\theta })=\big (g_1^2(\mathbf{x};\varvec{\theta }),\dots ,g^2_r(\mathbf{x};\varvec{\theta })\big )^T$ and ${\mathbf {w}}=(w_1,\ldots ,w_r)^T\in {{\mathcal {R}}^+}^r.$

Practically, the REL $L_R(\varvec{\theta }, {\mathbf {w}})$ has two appealing properties in contrast to $L(\varvec{\theta })$ given in (2). First, we can assume in $L_R(\varvec{\theta }, {\mathbf {w}})$ that the elements of vector ${\mathbf {w}}$ are independent of $\varvec{\theta }$, while in $L(\varvec{\theta })$ dependency of $\varvec{\lambda }$ on $\varvec{\theta }$ is a basic assumption. This means that $L_R(\varvec{\theta }, {\mathbf {w}})$ can be considered as a semi-parametric version of the usual EL function. Second, by assuming sparsity of vectors $\varvec{\theta }$ and ${\mathbf {w}}$ (to reduce the number of parameters and the number of the estimating equations respectively) and $-\log REL$ being convex, we can use the REL method for high-dimensional data.

With the REL given above, the corresponding logarithm of REL is

$$\begin{aligned} \ell _R(\varvec{\theta }, {\mathbf {w}})= -\sum \limits _{i=1}^{n}\log \left[ 1+{\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })\right] +\text {constant}. \end{aligned}$$

Based on $\ell _R(\varvec{\theta }, {\mathbf {w}}),$ the maximum estimators of $(\varvec{\theta }, {\mathbf {w}})$, namely $(\hat{\varvec{\theta }}^{REL}, \hat{{\mathbf {w}}}^{ REL}),$ are given as

$$\begin{aligned} (\hat{\varvec{\theta }}^{REL}, \hat{{\mathbf {w}}}^{ REL}) \ = \ \arg \;\min _{\varvec{\theta }\in \varvec{\Theta }}\;\max _{{\mathbf {w}}\in {\mathbf {W}}_{n}(\varvec{\theta })}\;\left\{ \sum \limits _{i=1}^{n}\log \left[ 1+{\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })\right] \right\} , \end{aligned}$$

(9)

where ${\mathbf {W}}_{n}(\varvec{\theta })=\{\mathbf{w}\in {{\mathbb {R}}^{+}}^r:\ {\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })<\gamma \}$ for the tuning parameter $\gamma$.

2.3 Restricted penalized empirical likelihood

Although the REL estimator ${\hat{\theta }}^{REL}$ performs well in practice, still for high-dimensional settings with many parameters, the estimator is not efficient at all. On the other hand, it happens sometimes that a model has sparsity in its parameters. This situation often occurs in high-dimensional regression models where many independent variables are irrelevant to the response. In order to degenerate those irrelevant parameters in (9) to zero, one way is to use an appropriate penalty function to reduce the number of parameters in the model. In general, the following three scenarios can be considered in the RPEL approach.

• 1. We may add a penalty function $P_ {1} (\varvec{\theta })$ to (9) in order to control the number of model parameters. In another word, with a tuning parameter $u_1$, the corresponding estimators are given by

  $$\begin{aligned} (\hat{\varvec{\theta }},\hat{{\mathbf {w}}}) \ = \ \arg \;\min _{\varvec{\theta }}\; \max _{{\mathbf {w}}\in \mathbf{W}_{n}(\varvec{\theta })}\;\left\{ \sum \limits _{i=1}^{n}\log \left[ 1+\mathbf{w}^T {\mathbf {g}}^{*}({\mathbf {x}}_{i};\varvec{\theta })\right] + u_1P_{1}(\varvec{\theta })\right\} . \end{aligned}$$

  (10)

• 2. We may add a penalty function $P_ {2} (\varvec{\theta })$ to (9) in order to control the number of estimating equations via their weights. In another word, with a tuning parameter $u_2$, the corresponding estimators are given by

  $$\begin{aligned} (\hat{\varvec{\theta }},\hat{{\mathbf {w}}}) \ = \ \arg \min _{\varvec{\theta }}\min _{\mathbf{w}}\;\left\{ \sum \limits _{i=1}^{n}\log \left[ 1+{\mathbf {w}}^T \mathbf{g}^{*}({\mathbf {x}}_{i};\varvec{\theta })\right] + u_2P_{2}({\mathbf {w}}) \right\} . \end{aligned}$$

  (11)

• 3. Both penalty functions $P_ {1} (\varvec{\theta })$ and $P_ {2} ({\mathbf {w}})$ are utilized to control both the number of parameters and the number of estimating equations simultaneously. In this case, with tuning parameters $u_1$ and $u_2$, the estimators are given by

  $$\begin{aligned} (\hat{\varvec{\theta }},\hat{{\mathbf {w}}}) = \arg \min _{\varvec{\theta }}\min _{\mathbf{w}}\;\left\{ \sum \limits _{i=1}^{n}\log \left[ 1+{\mathbf {w}}^T \mathbf{g}^{*}({\mathbf {x}}_{i};\varvec{\theta })\right] +u_1P_{1}(\varvec{\theta })+ u_2P_{2}({\mathbf {w}})\right\} . \end{aligned}$$

  (12)

3 Bayesian analysis of RPEL

Practically, computing the RPEL estimates is a big challenge, especially when the penalty functions have complex structures. Therefore, in this paper we focus on the Bayesian analysis of the parameters. Our Bayesian approach for RPEL is different from the Bayesian approach for EL investigated by Lazar (2003), for the reason that our approach considers different priors for $\varvec{\theta }$ and ${\mathbf {w}}$ and provides conditional posteriors with closed-form for a variety of estimating equations; see Sect. 5 for details in an example.

It is evident that the three estimators in (10)-(12) are indeed the modes of posterior density under some appropriate priors. Taking scenario 3 in Sect. 2.3 as an example, the estimators (12) are the mode of the posterior density with likelihood function

$$\begin{aligned} L(\varvec{\theta },{\mathbf {w}})\propto \prod _{i=1}^{n}\frac{1}{1+{\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })} \end{aligned}$$

(13)

under the priors

$$\begin{aligned} \pi _1(\varvec{\theta })\propto e^{-u_1P_{1}(\varvec{\theta })} ,\qquad \pi _2({\mathbf {w}}) \propto e^{-u_2P_{2}({\mathbf {w}})}. \end{aligned}$$

(14)

Given the dataset D, this posterior is

$$\begin{aligned} \pi (\varvec{\theta },{\mathbf {w}}|D)\propto \prod _{i=1}^{n}\frac{1}{1+{\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })}\times e^{-u_1P_{1}(\varvec{\theta })}\times e^{-u_2P_{2}({\mathbf {w}})}. \end{aligned}$$

(15)

Practically, the posterior distribution (15) can be used for Bayesian analysis of the parameters of interest. One of the issues for this density is on the sample selection from marginal densities of $\varvec{\theta }$ and ${\mathbf {w}}$. To solve this problem, note that

$$\begin{aligned} \frac{1}{1+{\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })}=\int _{0}^{\infty }e^{-s(1+{\mathbf {w}}^T {\mathbf {g}}^{*}({\mathbf {x}}_{i};\varvec{\theta }))}ds. \end{aligned}$$

Thus (13) can be rewritten as

$$\begin{aligned} L(\varvec{\theta },{\mathbf {w}})&=\prod _{i=1}^{n}\frac{1}{1+\mathbf{w}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })}=\int _{0}^{\infty }\cdots \int _{0}^{\infty }e^{-\sum _{i=1}^{n}s_{i}(1+\mathbf{w}^T {\mathbf {g}}^{*}({\mathbf {x}}_{i};\varvec{\theta }))}ds_{1}\cdots ds_{n}. \end{aligned}$$

As a result, the posterior distribution of $\varvec{\theta }$ is its marginal distribution of the joint posterior distribution

$$\begin{aligned} \pi (\varvec{\theta },{\mathbf {w}},s_1,\ldots ,s_n|D)\propto e^{-\sum _{i=1}^{n}s_{i}\big (1+{\mathbf {w}}^T {\mathbf {g}}^{*}(\mathbf{x}_{i};\varvec{\theta })\big )-u_1P_{1}(\varvec{\theta })-u_2P_{2}(\mathbf{w})}. \end{aligned}$$

(16)

For statistical inference, one can derive random samples from the marginal densities by using MCMC methods.

4 Empirical BIC for RPEL

In this part, we introduce the empirical Bayesian information criterion (EBIC) for RPEL. For this purpose, we let $(\hat{\varvec{\theta }},\hat{{\mathbf {w}}})$ denote the RPEL estimators. Similar to BIC, in the RPEL approach with weights given in (8), the EBIC for a model $M_0$ is defined as

$$\begin{aligned} EBIC&:=\frac{p(M_0)+r(M_0)}{2}\log n+\sum _{i=1}^{n}\frac{1}{1+\Vert {\mathbf {w}}\Vert _1}\log \left[ 1+\hat{\mathbf{w}}^T {\mathbf {g}}^{*}({\mathbf {x}}_{i};\hat{\varvec{\theta }})\right] , \end{aligned}$$

(17)

where $p(M_0)$ is the number of parameters and $r(M_0)$ is the number of estimating equations in model $M_0$. It is straightforward to see that

$$\begin{aligned} 0<EBIC< \frac{p(M_0)+r(M_0)}{2}\log n+ \frac{\Vert \hat{\mathbf{w}}\Vert _\infty }{1+\Vert {\mathbf {w}}\Vert _1}\sum _{i=1}^{n}\Vert {\mathbf {g}}^{*}(\mathbf{x}_{i};\hat{\varvec{\theta }})\big \Vert _1, \end{aligned}$$

where $\Vert \cdot \Vert _\infty$ and $\Vert \cdot \Vert _1$ stand for the sup-norm and $l_1$-norm respectively.

Practically, small EBIC values confirm the adequacy of the considered model whereas large EBIC values indicate the inadequacy of the model.

5 Bayesian analysis of RPEL in a multiple linear regression model

From Sects. 3 and 2.3 we see that although we can use in practice any type of penalty functions for $\varvec{\theta }$ and ${\mathbf {w}}$, in this work we particularly develop our derivations and discussions with use of the quadratic penalty function $P_{1}(\varvec{\theta })=\sum _{k=1}^{p}\theta _{k}^2$ for $\varvec{\theta }$ and the penalty function for ${\mathbf {w}}$ given by

$$\begin{aligned} P_{2}(\mathbf{w})=\sum _{j=1}^r\bigg \{\frac{(w_j-a)^2}{2w_j}+\frac{3}{2}\log w_j-\log a\bigg \}, \qquad w_j>0 \end{aligned}$$

(18)

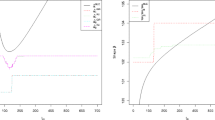
for some fixed $a>0.$ It is easy to verify that the penalty function (18) is sensitive to both small and large values of ${\mathbf {w}}$, a desired property that controls the number of effective estimating equations by eliminating those of less importance. Figure 1 depicts the shape of the penalty function (18) for $r = 1$ and different values of a. To the best of our knowledge, this is the first time that (18) is used as a penalty function to control the number of positive elements in a vector with non-negative entries.

Fig. 1

Shape of the penalty function (18) for $r = 1$ and varying values of a

5.1 Regression model analysis using REL

To demonstrate the application of REL in the analysis of multiple linear regression models, consider the regression model

$$\begin{aligned} y_i=\theta _1x_{i1}+\theta _2x_{i2}+\theta _3x_{i3}+\cdots +\theta _{p}x_{ip}+\epsilon _i, \end{aligned}$$

(19)

where $(x_{i1},\dots , x_{ip})^T$, $i=1,\dots ,n$, are independent covariate vectors with $x_{i1}=1$, and $\epsilon _i$, $i=1,\dots , n$, are independent random errors. We assume that there are M different candidate structures to describe the variance of $\epsilon _i$’s, given by

$$\begin{aligned} Var(\epsilon _i)=\sigma ^2U_{\nu ,i}^{-1},\quad U_{\nu ,i}>0,\quad \nu =1,\ldots , M, \end{aligned}$$

where $U_{\nu ,i}$ is an appropriate weight associated with individual i under the $\nu ^{th}$ variance structure. Therefore, essentially there are pM estimating equations

$$\begin{aligned} g_{\nu }(x_{ij};\varvec{\theta }):=U_{\nu i}&\;x_{ij} \big (y_i-\theta _1x_{i1}-\theta _2x_{i2}-\cdots -\theta _px_{ip}\big ),\\&i=1,\ldots , n,\quad j=1,\ldots ,p,\quad \nu =1,2,\ldots ,M \end{aligned}$$

that are used to estimate the regression coefficients $(\theta _1, \dots , \theta _p)^T$.

For notation simplicity, we define

$$\begin{aligned} g_{i\nu j}^{*}(\varvec{\theta }):=g_{\nu }^{*}(x_{ij};\varvec{\theta })&=U_{\nu i}^2 \;x_{ij}^2 (y_i-\theta _1x_{i1}-\theta _2x_{i2}-\cdots -\theta _px_{ip})^2,\\&i=1,\ldots , n, \quad j=1,\ldots ,p, \quad \nu =1,2,\ldots ,M. \end{aligned}$$

Then the corresponding REL function for the regression model (19) is given by

$$\begin{aligned} L_R(\varvec{\theta },{\mathbf {w}})=\int _{0}^{\infty }\cdots \int _{0}^{\infty }&e^{-\sum \limits _{i=1}^{n}s_{i}\bigg (1+\sum \limits _{\nu =1}^{M}\sum \limits _{j=1}^{p}w_{\nu j}g_{i\nu j}^{*}(\varvec{\theta })\bigg )}ds_{1}\cdots ds_{n}. \end{aligned}$$

With the penalty functions $P_{1}(\varvec{\theta })=\sum _{k=1}^{p}\theta _{k}^2$ and $P_2({\mathbf {w}})$ given in (18), the prior distribution (14) is reduced to

$$\begin{aligned} \pi _1(\varvec{\theta })&= e^{-u_1P_{1}(\varvec{\theta })}= \frac{1}{B^\frac{p}{2}}e^{-\frac{1}{2B}\sum _{j=1}^p\theta _j^2}, \\ \pi _2({\mathbf {w}})&= e^{- u_2P_{2}({\mathbf {w}})}= \prod _{j=1}^{p}\prod _{\nu =1}^{M}\frac{A}{w_{\nu j}^{3/2}}e^{-\frac{(w_{\nu j}-A)^2}{2w_{\nu j}}}. \end{aligned}$$

Therefore, the posterior density of $(\varvec{\theta }, \mathbf{w}, s_1, \ldots , s_n)$ is given by

$$\begin{aligned} \pi (\varvec{\theta }, {\mathbf {w}},s_1,\ldots ,s_n|D)\propto&\ e^{-\sum _{i=1}^{n}s_{i}\bigg (1+\sum _{\nu =1}^{M}\sum _{j=1}^{p}w_{\nu j}g_{i\nu j}^{*}(\varvec{\theta })\bigg )}\nonumber \\&\ \ \times \frac{1}{B^\frac{p}{2}}e^{-\frac{1}{2B}\sum _{j=1}^p\theta _j^2}\times \prod _{j=1}^{p}\prod _{\nu =1}^{M}\frac{A}{w_{\nu j}^{3/2}}e^{-\frac{(w_{\nu j}-A)^2}{2w_{\nu j}}}, \end{aligned}$$

(20)

where A and B are some positive constants called the hyper-parameters. Given the joint posterior density (20), the conditional posterior densities are obtained as

$$\begin{aligned} \left\{ \begin{array}{lll} s_i&{} \sim &{}\exp \left[ 1+\sum \limits _{\nu =1}^M\sum \limits _{j=1}^pw_{\nu j} \; g^*_{i\nu j}(\varvec{\theta })\right] ,\quad \quad \quad i=1,\dots ,n, \\ \\ w_{\nu j} &{}\sim &{} {giG}\left( 2\sum \limits _{i=1}^n s_ig^*_{i\nu j}(\varvec{\theta })+1, \ A^2, \ -\frac{1}{2}\right) ,\quad \quad \nu =1,\ldots ,M, \quad j=1,\dots ,p,\\ \\ \theta _{\ell } &{} \sim &{} {N}\left( \mu _{\ell },\sigma ^2_{\ell }\right) ,\quad \quad l=1,\ldots p, \end{array} \right. \end{aligned}$$

(21)

where

$$\begin{aligned} \mu _{\ell }=\frac{\sum \nolimits _{i=1}^n\sum \nolimits _{\nu =1}^M\sum \nolimits _{j=1}^ps_iw_{\nu j}U_{\nu i}^2 x_{ij}^2x_{i\ell }\Big (y_i-\sum \nolimits _{k \ne \ell }x_{ik}\theta _k\Big )}{\sum \nolimits _{i=1}^n\sum \nolimits _{\nu =1}^M\sum _{j=1}^ps_iw_{\nu j}U_{\nu i}^2x_{ij}^2x_{il}^2+\frac{1}{2B}},\quad \\ \sigma _{\ell }=\left[ 2\sum \limits _{i=1}^n\sum \limits _{\nu =1}^M\sum \limits _{j=1}^ps_iw_{\nu j}U_{\nu i}^2x_{ij}^2x_{il}^2+\frac{1}{B}\right] ^{-1/2}, \end{aligned}$$

and giG stands for the generalized inverse Gaussian distribution with probability density function $f(x; a, b, p)= \frac{(a/b)^{p/2}}{2K_p(\sqrt{ab})}x^{p-1}e^{-\frac{ax+b/x}{2}}$, where $a>0,b>0,$ $p\in {\mathcal {R}}$ and $K_p$ is a modified Bessel function of second kind.

Given the conditional densities (21), it is straightforward to use Gibbs sampling method to generate random samples from marginal distribution of $\varvec{\theta }$ for the purpose of any statistical inferences.

5.2 EM algorithm for estimating hyper-parameters

One of the major challenges in sampling from conditional densities (21) is that the two quantities A and B are generally unknown. Practically, there are several methods to estimate these quantities. Nevertheless, for a separate interest, we introduce in this paper an EM algorithm to estimate them.

From (20), the marginal density of the observations is obtained as

$$\begin{aligned} f(D|A,B)=&\int \cdots \int e^{-\sum \limits _{i=1}^{n}s_{i}\bigg (1+\sum \limits _{\nu =1}^{M}\sum \limits _{j=1}^{p}w_{\nu j}g_{i\nu j}^{*}(\varvec{\theta })\bigg )} \times \frac{1}{B^\frac{p}{2}}e^{-\frac{1}{2B}\sum \limits _{j=1}^p\theta _j^2}\nonumber \\&\times \prod _{j=1}^{p}\prod _{\nu =1}^{M}\frac{A}{w_{\nu j}^{3/2}}e^{-\frac{(w_{\nu j}-A)^2}{2w_{\nu j}}}ds_1\cdots ds_n\;dw_{11}\cdots dw_{Mp}\;d\theta _1,\cdots d\theta _p. \end{aligned}$$

(22)

Now consider the logarithm of the integrand in (22) as a function of the A and B. Specifically, define

$$\begin{aligned} {I}(A,B)&= -\sum \limits _{i=1}^{n}s_{i}\bigg (1+\sum \limits _{\nu =1}^{M}\sum \limits _{j=1}^{p}w_{\nu j}g_{i\nu j}^{*}(\varvec{\theta })\bigg ) -\frac{p}{2}\log B-\frac{1}{2B}\sum \limits _{j=1}^p\theta _j^2\nonumber \\&\quad + pM\log A-\frac{3}{2} \sum \limits _{j=1}^{p}\sum \limits _{\nu =1}^{M}{w_{\nu j}}- \sum \limits _{j=1}^{p}\sum \limits _{\nu =1}^{M}\frac{(w_{\nu j}-A)^2}{2w_{\nu j}}. \end{aligned}$$

(23)

The EM steps of our proposed algorithm are give bellow.

Step 1.:

Select the initial values $B^{(0)} (> 0)$ and $A ^ {(0)} (> 0)$ and start with $k = 1$.

Step 2.:

Given $B^{(k)}$ and $A ^ {(k)},$ produce a sample from the conditional distributions (21).

Step 3.:

E-step: Calculate the average I (A, B) using the generated samples in Step 2. Here, it is worthy to note that one only needs to calculate the means of those terms in I (A, B) that depend on A and B only.

Step 4.:

M-step: Update A and B by maximizing

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Q_3(B)= \frac{p}{2}\log B+\frac{1}{2B^{(k)}}\sum \limits _{j=1}^pE_{B^{(k)}, A^{(k)}}\big [\theta _j^2\big ], \\ \\ \displaystyle Q_4(A)= pM\log A- \sum \limits _{j=1}^{p}\sum \limits _{\nu =1}^{M}E_{B^{(k)}, A^{(k)}}\bigg [ \frac{(w_{\nu j}-A^{(k)})^2}{2w_{\nu j}}\bigg ] \end{array} \right. \end{aligned}$$

with respect to A and B, which leads to the the updated values

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle B^{(k+1)}=\frac{1}{p}\sum \limits _{j=1}^p E_{B^{(k)}, A^{(k)}}\big [\theta _j^2\big ] \\ \\ \displaystyle A^{(k+1)}=\frac{pM+\sqrt{(Mp)^2+4Mp \sum \nolimits _{j=1}^{p}\sum \nolimits _{\nu =1}^{M}E_{B^{(k)}, A^{(k)}} \big [\frac{1}{w_{\nu j}}\big ]}}{2\sum \nolimits _{j=1}^{p}\sum \nolimits _{\nu =1}^{M}E_{B^{(k)}, A^{(k)}} \big [\frac{1}{w_{\nu j}}\big ]}. \end{array} \right. \end{aligned}$$

(24)

6 Simulation study and application

In this section, we first carry out a simulation study to evaluate our proposed methods. Then we apply them to a real data analysis to demonstrate the applications of our proposed methods.

6.1 Simulation study

In this subsection, we evaluate the performance of the RPEL estimators for regression models using a simulation study. To measure the performance of the estimators, we estimate the parameters, their variances and the corresponding EBIC and weighted MSE. We run the corresponding Gibbs sampling scheme (21) to generate $N=5000$ samples from the marginal distributions of the parameters.

Consider the regression model

$$\begin{aligned} y_i=\theta _1 +\theta _2 x_{i2}+\epsilon _i, \quad i=1,2,\dots , n, \end{aligned}$$

(25)

where $\varvec{\theta }=(\theta _1,\theta _2)^T$ is the parameter vector of our interest, $x_ {i2}$’s are independent samples from the exponential distribution Exp(1), and given $x_{i2}$’s the multiplied errors $x_{i2} \epsilon _i$’s are independent samples from the mixture distribution

$$\begin{aligned} x_{i2} \epsilon _i \ \sim \ 0.5\; N(0,0.5)+0.5\; Unif(-1,1), \end{aligned}$$

(26)

or equivalently

$$\begin{aligned} \epsilon _i \ \sim \ 0.5\; N\left( 0,\ 0.5/x_{i2}^2\right) +0.5\; Unif\left( -1/x_{i2},\ 1/x_{i2}\right) . \end{aligned}$$

We assume the true parameter values $\varvec{\theta }= (1,2)^T,$ and the data is generated for various sample sizes $n = 20,$ 50 and 500. For various sample size, we evaluate how well the true model and some candidate models fit to the generated data. For this purpose, we consider three regression models

• Model I: $y_i = \theta _1+\theta _2x_{i2}+\epsilon _i$,

• Model II: $y_i=\theta _1+\theta _2e^{x_{i2}}+\epsilon _i$,

• Model III: $y_i=\theta _1+\theta _2\ln (x_{i2})+\epsilon _i$,

where Model I is the true model and Models II and III are two candidate models.

Note that the variances of the errors $\epsilon _i$’s in (26) are proportion to $1/x_{i2}^2$, to investigate the goodness-of-fit of Models I, II, and III, we consider two related weight structures $U _ {1 i} =x_ {i2}^2$ and $U _ {2 i} = x_ {i2} ^ {- 1}.$ The corresponding estimating equations are given by

$$\begin{aligned}&\sum _{i=1}^n U_{\nu i}(y_i-\theta _1-\theta _2x_{i2})=0,\\&\sum _{i=1}^n U_{\nu i}x_{i2} (y_i-\theta _1-\theta _2x_{i2})=0, \end{aligned}$$

where $\nu =1,2$ correspond to the two weight structures. In the sequel, we divide our simulation study into three parts to evaluate model fit using RPEL method. Part A includes the results of simulation for the regression model (25) with error structure (26). Part B evaluates the effect of outliers in model (25). In Part C we study the fitness of a sparse regression model by adding some zero coefficient covariates to model (25).

Part A: Table 1 contains all estimates of parameters, their standard errors and the corresponding EBIC criterion under different sample sizes for various Models I, II and III. Results obviously shows that the Bayesian estimates of $\varvec{\theta }$ are getting closer to the true value $\varvec{\theta }=(1,2)^T$ when the sample size increases. Furthermore, the corresponding EBIC and weighted MSE show that the Model I fit the data much better than the other competitors.

Table 1 Estimates (variances) under various models

Part B: To evaluate the effect of outliers on estimates of parameters, we replace 5% of the response variable y with random values from N(10, 1) distribution. The results are given in Table 2. This table clearly shows that using the RPEL leads us to estimates of parameters that are very close to the true values, so, we conclude the RPEL estimates are very robust against outliers under different sample sizes.

Table 2 Estimates (variances) under various models with outliers

Part C: To evaluate the efficiency of RPEL in analyzing a regression model with high sparsity, we add to model (25) eighteen irrelevant independent variables whose values are generated from N(0, 0.25) distribution. Indeed, in this case, our regression model is

$$\begin{aligned} y_i=\theta _1 +\theta _2 x_{i2}+\theta _3 x_{i3}+\cdots +\theta _{20} x_{i,20}+\epsilon _i, \end{aligned}$$

where $\theta _3=\cdots =\theta _{20}=0.$ We also replace 5% of the response variable y with random values from N(10, 1). With both of above interferences, and assuming that $w_{ij}$s are equal, the estimates of parameter $\varvec{\theta }$ are given in Table 3. This table shows that using RPEL provides good fit to the data.

Table 3 Estimates (variances) under various models with irrelevant covariates

6.2 Application to a real data

In this section, we demonstrate the implementation of our proposed methods to a real data analysis. Table 4 presents the information of the recent 12 auctions of a big company. It contains explanatory variables

$$\begin{aligned} x_1:&\ \ \text {Bid at auction (in million dollar)}; \\ x_2:&\ \ \text {How big the size is; } 0=\text {Small}, 1=\text {Big } \end{aligned}$$

and response variable

$$\begin{aligned} y:&\ \ \text {Cost of auction (in million dollar)}. \end{aligned}$$

This data was also analyzed in Ghoreishi and Meshkani (2014) from a different aspect. The least squares regression, to fit the regression model

$$\begin{aligned} y_i = \beta _0+\beta _1x_{i1}+\beta _2x_{i2}+\epsilon _i, \end{aligned}$$

shows $R^2=0.800$ and the $MSE=28.284$, while a weighted least squares fit, with weights $x_{i1},$ gives $R^2=0.937$ and weighted MSE 0.633. This shows that weighted regression fits much better than the unweighted version. However, two points have been overlooked in fitting this weighted regression model: (i) variable selection and (ii) which weight function can lead to a better fit. Regarding (ii), more specifically, are the weights $x_{i1}$ sufficient to produce a good fitted model or should we use some other functions in our analysis to get a better fit? Among the different weights, we restrict ourselves to only two functions $U _ {1 i}= x_1 ^ 2$ and $U _ {2 i} =x_1 ,$ to survey our methodology. After applying RPEL method, we obtain $MSE = 0.461$ and $EBIC = 198.96$ for the regression model. The estimates of all parameters are given in Table 5. Here, we see that using different weights ($U _ {1 i}= x_1 ^ 2$ and $U _ {2 i} =x_1$) leads to a better fit, in addition to detecting the best and most effective functions of weights in practice.

Table 4 Auction data

Table 5 Model fit from different methods

7 Conclusive summary

In this paper, we introduced the REL as an alternative approach to the traditional EL and we showed that the REL method has desirable properties such as robustness against outliers. We focused on the REL estimator which is obtained under both the unbiasedness and minimum variance criteria on estimating equations. We developed a Bayesian analysis for REL in which we obtained all conditional posterior distributions with closed-form that can facilitate the sampling for a large class of estimating equations. In addition, by adding penalty functions of parameters, we made the REL method applicable in high-dimensional setting; we call the resulting method the RPEL. Moreover, we provided an EM algorithm to determine hyper-parameters.

Robust estimating equation method is another one that achieves robustness against outliers, but it usually involves the introduction of a ‘link’ function or a class of functions with an extra parameter and often produces biased estimator. Even though our Bayesian REL estimates are also often biased, the introduced minimum variance constraint ensures that they concentrate highly around the true value, as indicated by standard errors in our simulation study. In addition, our REL method avoids the arbitrariness in the function employed in robust estimating equation method and thus provides a more generic method to handle outliers. From this sense, the REL method is more flexible and straightforward and can be applied to classical, Bayesian and high-dimensional analyses.