Abstract
We consider the problem of predicting a categorical variable based on groups of inputs. Some methods have already been proposed to elaborate classification rules based on groups of variables (e.g. group lasso for logistic regression). However, to our knowledge, no tree-based approach has been proposed to tackle this issue. Here, we propose the Tree Penalized Linear Discriminant Analysis algorithm (TPLDA), a new-tree based approach which constructs a classification rule based on groups of variables. It consists in splitting a node by repeatedly selecting a group and then applying a regularized linear discriminant analysis based on this group. This process is repeated until some stopping criterion is satisfied. A pruning strategy is proposed to select an optimal tree. Compared to the existing multivariate classification tree methods, the proposed method is computationally less demanding and the resulting trees are more easily interpretable. Furthermore, TPLDA automatically provides a measure of importance for each group of variables. This score allows to rank groups of variables with respect to their ability to predict the response and can also be used to perform group variable selection. The good performances of the proposed algorithm and its interest in terms of prediction accuracy, interpretation and group variable selection are loud and compared to alternative reference methods through simulations and applications on real datasets.












Similar content being viewed by others
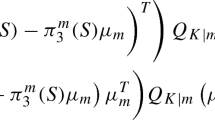
Notes
The number of groups included in the classification rule built by using TPLDA is lower than or equal to the number of splits in the final TPLDA tree. Note that it equals the number of splits in the final TPLDA tree when each selected group is used only once.
References
Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ (1999) Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci 96(12):6745–6750
Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT et al (2000) Gene ontology: tool for the unification of biology. Nat Genet 25(1):25
Bouveyron C, Girard S, Schmid C (2007) High-dimensional discriminant analysis. Commun Stat Theory Methods 36(14):2607–2623
Breiman L, Friedman J, Stone CJ, Olshen RA (1984) Classification and regression trees. CRC Press, Boca Raton
Brodley CE, Utgoff PE (1995) Multivariate decision trees. Mach Learn 19(1):45–77
Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP (2002) Smote: synthetic minority over-sampling technique. J Artif Intell Res 16:321–357
Dudoit S, Fridlyand J, Speed TP (2002) Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc 97(457):77–87
Engreitz JM, Daigle BJ Jr, Marshall JJ, Altman RB (2010) Independent component analysis: mining microarray data for fundamental human gene expression modules. J Biomed Inform 43(6):932–944
Friedman J, Hastie T, Tibshirani R (2001) The elements of statistical learning. Springer series in statistics, vol 1. Springer, New York
Friedman JH (1989) Regularized discriminant analysis. J Am Stat Assoc 84(405):165–175
Genuer R, Poggi JM (2017) Arbres CART et Forêts aléatoires,Importance et sélection de variables, preprint
Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA et al (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286(5439):531–537
Gregorutti B, Michel B, Saint-Pierre P (2015) Grouped variable importance with random forests and application to multiple functional data analysis. Comput Stat Data Anal 90:15–35
Grimonprez Q, Blanck S, Celisse A, Marot G (2018) MLGL: an R package implementing correlated variable selection by hierarchical clustering and group-lasso, preprint
Guo Y, Hastie T, Tibshirani R (2006) Regularized linear discriminant analysis and its application in microarrays. Biostatistics 8(1):86–100
Huang D, Quan Y, He M, Zhou B (2009) Comparison of linear discriminant analysis methods for the classification of cancer based on gene expression data. J. Exp. Clin. Cancer Res. 28(1):149
Huang J, Breheny P, Ma S (2012) A selective review of group selection in high-dimensional models. Stat Sci Rev J Inst Math Stat 27(4):481–499
Jacob L, Obozinski G, Vert JP (2009) Group lasso with overlap and graph lasso. In: Proceedings of the 26th annual international conference on machine learning, ACM, pp 433–440
Kaminski N, Friedman N (2002) Practical approaches to analyzing results of microarray experiments. Am J Respir Cell Mol Biol 27(2):125–132
Kanehisa M, Goto S (2000) KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res 28(1):27–30
Lange K, Hunter DR, Yang I (2000) Optimization transfer using surrogate objective functions. J Comput Graph Stat 9(1):1–20
Lee SI, Batzoglou S (2003) Application of independent component analysis to microarrays. Genome Biol 4(11):R76
Li XB, Sweigart JR, Teng JT, Donohue JM, Thombs LA, Wang SM (2003) Multivariate decision trees using linear discriminants and tabu search. IEEE Trans Syst Man Cybern Part A Syst Hum 33(2):194–205
Lim TS, Loh WY, Shih YS (2000) A comparison of prediction accuracy, complexity, and training time of thirty-three old and new classification algorithms. Mach Learn 40(3):203–228
Loh W (2014) Fifty years of classification and regression trees. Int Stat Rev 82(3):329–348
Loh WY, Shih YS (1997) Split selection methods for classification trees. Stat Sinica 7(4):815–840
Meier L, Geer SVD, Bühlmann P (2008) The group lasso for logistic regression. J R Stat Soc Ser B (Stat Methodol) 70(1):53–71
Mola F, Siciliano R (2002) Discriminant analysis and factorial multiple splits in recursive partitioning for data mining. In: International workshop on multiple classifier systems. Springer, Berlin, Heidelberg, pp 118–126
Murthy SK, Kasif S, Salzberg S, Beigel R (1993) OC1: a randomized algorithm for building oblique decision trees. In: Proceedings of AAAI, vol 93, pp 322–327
Picheny V, Servien R, Villa-Vialaneix N (2016) Interpretable sparse sir for functional data, preprint
Quinlan JR (1986) Induction of decision trees. Mach Learn 1(1):81–106
Quinlan JR (1993) C4.5: programs for machine learning. Morgan Kaufmann Publishers Inc, Burlington
Sewak MS, Reddy NP, Duan ZH (2009) Gene expression based leukemia sub-classification using committee neural networks. Bioinform Biol Insights 3:89
Shao J, Wang Y, Deng X, Wang S et al (2011) Sparse linear discriminant analysis by thresholding for high dimensional data. Ann Stat 39(2):1241–1265
Shipp MA, Ross KN, Tamayo P, Weng AP, Kutok JL, Aguiar RC, Gaasenbeek M, Angelo M, Reich M, Pinkus GS et al (2002) Diffuse large b-cell lymphoma outcome prediction by gene-expression profiling and supervised machine learning. Nat Med 8(1):68
Strobl C, Boulesteix AL, Zeileis A, Hothorn T (2007) Bias in random forest variable importance measures: illustrations, sources and a solution. BMC Bioinform 8(1):25
Tai F, Pan W (2007) Incorporating prior knowledge of gene functional groups into regularized discriminant analysis of microarray data. Bioinformatics 23(23):3170–3177
Tamayo P, Scanfeld D, Ebert BL, Gillette MA, Roberts CW, Mesirov JP (2007) Metagene projection for cross-platform, cross-species characterization of global transcriptional states. Proc Natl Acad Sci 104(14):5959–5964
Wei-Yin Loh NV (1988) Tree-structured classification via generalized discriminant analysis. J Am Stat Assoc 83(403):715–725
Wickramarachchi D, Robertson B, Reale M, Price C, Brown J (2016) HHCART: an oblique decision tree. Comput Stat Data Anal 96:12–23
Witten DM, Tibshirani R (2011) Penalized classification using Fisher’s linear discriminant. J R Stat Soc Ser B (Stat Methodol) 73(5):753–772
Xu P, Brock GN, Parrish RS (2009) Modified linear discriminant analysis approaches for classification of high-dimensional microarray data. Comput Stat Data Anal 53(5):1674–1687
Yin L, Huang CH, Ni J (2006) Clustering of gene expression data: performance and similarity analysis. BMC Bioinform 7(4):19–30
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Time complexity of TPLDA
In the following section, the maximal time complexity at a node t of the TPLDA method is detailed. We assume that there are:
-
\(n_{t}\) observations in the node t,
-
J groups of variables denoted \(X^j\), for \(j=1,\ldots ,J\) and
-
the group \({\mathbf {X}}^j\), with \(j=1,\ldots ,J\), includes \(d_j\) variables such as \({\mathbf {X}}^j = (X_{j_1},X_{j_2},\ldots ,X_{j_{d_j}})\).
To split a node t including \(n_{t}\) observations, TPLDA uses the following two steps:
-
Step 1: within group PLDA.
For any group \({\mathbf {X}}^j\) of variables, with \(j=1,\ldots ,J\), a PLDA is applied on the node t and the shrinkage parameter \(\lambda _j\) is selected by cross-validation.
-
Step 2: choosing the splitting group.
For any group \({\mathbf {X}}^j\) of variables, with \(j=1,\ldots ,J\), TPLDA computes the penalized decrease in node impurity resulting from splitting on group j and selects the group that maximizes it.
The time complexity of these steps are detailed below. Consider the group j, with \(j=1,\ldots ,J\).
\(\textit{Complexity when performing PLDA on group}\, j\):
PLDA computation steps are described in the original paper (Witten and Tibshirani 2011). We detailed here its maximal time complexity:
-
Complexity for constructing the estimated between covariance matrix \(\widehat{B}^j_{t}\) is \(\mathcal {O}\left( n_{t}d_j^2\right) \).
-
Complexity for constructing the diagonal positive estimate of the within covariance matrix \({\widehat{\Sigma }}^j_{t}\) is \(\mathcal {O}\left( n_{t}d_j\right) \).
-
Complexity of the eigen analysis of \(({\widehat{\Sigma }}^j_{t})^{-1}\widehat{B}^j_{t}\) is \(\mathcal {O}\left( d_j^2\right) \).
-
Complexity of the eigen analysis of \((\widehat{B}^j_{t})^{-1}\widehat{B}^j_{t}\) and the research for the dominant eigenvector is \(\mathcal {O}\left( d_j^2\right) \).
-
Complexity for estimating the penalized discriminant vector \({\hat{\beta }}^j\) by performing M iterations of the minimization-maximization algorithm (Lange et al. 2000) is \(\mathcal {O}\left( Md_j^2\right) \).
\(\Rightarrow \) So the maximal time complexity of performing PLDA on the group j in the node t is \(\mathcal {O}\left( n_{t}d_j^2\right) + \mathcal {O}\left( n_{t}d_j\right) + \mathcal {O}\left( d_j^2\right) + \mathcal {O}\left( Md_j^2\right) = \mathcal {O}\left( n_{t}d_j^2\right) \) by supposing that \(M< n_{t}\).
\(\textit{Complexity when selecting of the shrinkage parameter}\, \lambda _j\):
The value of shrinkage parameter \(\lambda _j\) is determined by using a K-fold cross-validation and a grid \(\lbrace v_1,\ldots ,v_L \rbrace \) containing L values for \(\lambda _j\). The maximal time complexity of this step is detailed below:
-
Complexity for dividing the \(n_{t}\) observations in the node t into K disjoint samples \(\lbrace S_1,\ldots ,S_K\rbrace \) is \(\mathcal {O}\left( n_{t}\right) \).
-
For each fold k, \(k=1,\ldots ,K\) and each value \(v_{\ell }\), \(\ell =1,\ldots ,L\):
-
Complexity for performing a PLDA on \(t\setminus S_k\) (i.e. all the disjoint sets \(\lbrace S_1,\ldots ,S_K\rbrace \) excepted \(S_k\)) with \(\lambda _j=v_{\ell }\) is \(\mathcal {O}\left( \frac{K-1}{K}n_{t}d_j^2\right) \).
-
Complexity for predicting the class of each observation in \(S_k\) using the resulted PLDA model computed on \(t\setminus S_k\) is \(\mathcal {O}\left( \frac{n_{t}}{K}d_j\right) \).
-
Complexity for computing the penalized decrease \(\Delta _j(t, v_{\ell })\) in node impurity is \(\mathcal {O}\left( n_{t}\right) \).
-
-
Complexity for choosing the value in the grid \(\lbrace v_1,\ldots ,v_L \rbrace \) which maximizes the penalized decrease in node impurity is \(\mathcal {O}\left( 1\right) \).
\(\Rightarrow \) So the complexity for selecting the value of \(\lambda _j\) is \( \mathcal {O}\left( n_{t}\right) + \mathcal {O}\left( L(K-1)n_{t}d_j^2\right) + \mathcal {O}\left( Ln_{t}d_j\right) + \mathcal {O}\left( Ln_{t}\right) + \mathcal {O}\left( 1\right) = \mathcal {O}\left( L(K-1)n_{t}d_j^2\right) \).
Complexity when choosing the splitting group
TPLDA selects among the J estimated splits the one which maximizes the impurity decrease. The complexity of this step is \(\mathcal {O}\left( 1\right) \).
Consequently, the maximal time complexity of TPLDA at a node t is in the worst case \(\mathcal {O}\left( Jn_{t}d_{\max }^2\right) + \mathcal {O}\left( JL(K-1)n_{t}d_{\max }^2\right) + \mathcal {O}\left( 1\right) = \mathcal {O}\left( JLKn_{t}d_{\max }^2\right) \) with \(d_{\max }= \max _j(d_j)\).
Additional figures about the illustration of the TPLDA method on a simple example
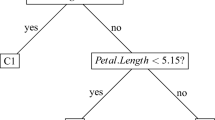
Figure 13 displays the two trees built by CART and TPLDA in the simple example used to illustrate TPLDA in Sect. 2.4. As mentioned previously, in this example, the TPLDA tree is much easier than the CART tree. Moreover, the simple TPLDA tree is as accurate as the complex CART tree (TPLDA AUC \(=\) 0.90, CART AUC \(=\) 0.89).
The two trees associated to the TPLDA and CART partitions displayed in Fig. 2. Circles define the nodes and the figure in each node indicates the node label. The splitting rule is denoted below each node
Additional information about the numerical experiments
This section provides additional results and figures about the simulation studies.
1.1 Justification for using PLDA instead of FDA in the splitting process
First of all, here we discuss the choice of using PLDA instead of FDA in the splitting process. In TPLDA, PLDA is replaced by FDA. This modified TPLDA is named TLDA and is applied on each sample of the first three experiments.
Table 9 displays the simulation results for TLDA in comparison with TPLDA. First, when data are not grouped, TPLDA and TLDA give almost the same results and can be then used interchangeably. Indeed, when the group size equals 1 and if the regularized parameter in the PLDA problem (3) is set to zero, the FDA problem and the PLDA problem are identical.
In the second and the third experiment, TLDA underperforms TPLDA. This can be explained by the fact that FDA performs badly in small nodes i.e. in the nodes where the number of observations is small relative to the size of some groups of variables (Shao et al. 2011; Friedman 1989; Xu et al. 2009; Bouveyron et al. 2007). Yet, tree elaboration is based on a recursive splitting procedure which creates nodes that becomes smaller and smaller whereas the sizes of input groups remain unchanged. Then FDA may not be appropriate for estimating recursively the hyperplane splits. This is well illustrated by the performances of TLDA in the third experiment where the groups of input variables are large compared to the number of observations in the training sample. Indeed, in the first split, the FDA used to split the entire data space overfits the training set. This can be seen in Fig. 14: the training misclassification error decreases much faster for TLDA and becomes smaller than the Bayes error from the first split while the test misclassification error for TLDA remains stable. Consequently, after applying the pruning procedure which removes the less informative nodes, the final TLDA tree is trivial in at least 25 % of the simulations (Table 9). Conversely, TPLDA does not seem to be affected by the high-dimension. Then, PLDA overcomes the weakness of FDA in high-dimensional situations.
1.2 Sensitivity to the pruning strategy for CART
Here, the performances of CART when using the cost-complexity pruning strategy are compared to those obtained by using the proposed pruning strategy based on the tree depth, in the first three experiments. The approach using the proposed pruning strategy is named CARTD (while the approach using the cost-complexity pruning is named CART). The results are given in Table 10. Figure 15 displays the group selection frequencies of CART and CARTD. Overall, the two pruning methods lead to similar CART trees and so similar classification rules. Indeed, the predictive performances and the tree depth are very close. CARTD trees may be slightly smaller. Moreover, the group selection frequencies do not really differ: they are lightly higher when using the proposed pruning strategy based on the depth. Thus, CART performances do not seem to be sensitive to the choice of one of the two pruning methods.
1.3 Additional results
Table 11 displays the simulation results for TPLDA, TLDA, CART and GL for the fourth and fifth scenarios. As previously, TLDA underperforms TPLDA. GL and CART overperform slightly TPLDA when no penalty function is used.
1.4 Additional figures
Additional figures about the simulation studies are displayed in this subsection. Figure 16 displays the predictive performances of TPLDA, CART and GL in the first three experiments. Figure 17 shows the distribution of the importance score for each group in the first three experiments.
Additional information about the application to gene expression data
Following Lee and Batzoglou (2003), we assume that each independent component refers to a putative biological process and that a group of genes is then created for each independent component. For a given independent component, the most important genes are the genes with the largest loads in absolute terms. Then, the group of genes associated to the given independent component includes the \(C\%\) of genes with the largest loads in absolute terms. The number of groups J (or equivalently the number of independent components) and the threshold parameter C are tuning parameters.
For each dataset, several values for the clustering parameters (J,C) are chosen in order to assess the sensitivity of the predictive performances of the methods TPLDA, CART, GL and SCRDA to the values of these parameters. For each dataset we show the results for two couples (J,C) (Table 12). In each dataset, genes are clustered into 15 or 50 non-mutually exclusive groups (Tables 7 and 13). Table 14 shows the results when genes are clustered into 50 groups of equal size. These results are not significantly different from those obtained when using 15 groups (Table 8).
Rights and permissions
About this article
Cite this article
Poterie, A., Dupuy, JF., Monbet, V. et al. Classification tree algorithm for grouped variables. Comput Stat 34, 1613–1648 (2019). https://doi.org/10.1007/s00180-019-00894-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-019-00894-y