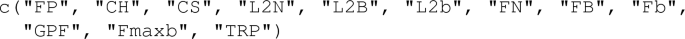fdANOVA: an R software package for analysis of variance for univariate and multivariate functional data

Abstract

Functional data, i.e., observations represented by curves or functions, frequently arise in various fields. The theory and practice of statistical methods for such data is referred to as functional data analysis (FDA) which is one of major research fields in statistics. The practical use of FDA methods is made possible thanks to availability of specialized and usually free software. In particular, a number of R packages is devoted to these methods. In the paper, we introduce a new R package fdANOVA which provides an access to a broad range of global analysis of variance methods for univariate and multivariate functional data. The implemented testing procedures mainly for homoscedastic case are briefly overviewed and illustrated by examples on a well known functional data set. To reduce the computation time, parallel implementation is developed and its efficiency is empirically evaluated. Since some of the implemented tests have not been compared in terms of size control and power yet, appropriate simulations are also conducted. Their results can help in choosing proper testing procedures in practice.

1 Introduction

In recent years considerable attention has been devoted to analysis of so called functional data. The functional data are represented by functions or curves which are observations of a random variable (or random variables) taken over a continuous interval or in large discretization of it. Sets of functional observations are peculiar examples of the high-dimensional data where the number of variables significantly exceeds the number of observations. Such data are often gathered automatically due to advances in modern technology, including computing environments. The functional data are naturally collected in agricultural sciences, behavioral sciences, chemometrics, economics, medicine, meteorology, spectroscopy, and many others. The main purpose of functional data analysis (FDA) is to provide tools for statistically describing and modelling sets of functions or curves. The monographs by Ramsay and Silverman (2005), Ferraty and Vieu (2006), Horváth and Kokoszka (2012) and Zhang (2013) present a broad perspective of the FDA solutions. The following problems for functional data are commonly studied (see also the review papers of Cuevas 2014 and Wang et al. 2016): analysis of variance (see Sect. 2), canonical correlation analysis, classification, cluster analysis, outlier detection, principal component analysis, regression analysis, repeated measures analysis, simultaneous confidence bands.

Many methods for functional data analysis have been already implemented in the R software (R Core Team 2017). The packages fda (Ramsay et al. 2017) and fda.usc (Febrero-Bande and Oviedo de la Fuente 2012) are the biggest and probably the most commonly used ones. The first package includes the techniques for functional data in the Hilbert space $L_2(I)$ of square integrable functions over an interval $I=[a,b]$. On the other hand, in the second one, many of the methods implemented do not need such assumption and use only the values of functions evaluated on a grid of discretization points (also non-equally spaced). There is also a broad range of R packages containing solutions for more particular functional data problems. The review of these packages is presented in the Supplementary Materials to save space.

Despite so many R packages for functional data analysis, a broad range of test for a widely applicable analysis of variance problem for functional data was implemented very recently in the package fdANOVA. Earlier, only the testing procedures of Cuevas et al. (2004) and Cuesta-Albertos and Febrero-Bande (2010) were available in the package fda.usc. The package fdANOVA is available from the Comprehensive R Archive Network at http://CRAN.R-project.org/package=fdANOVA. It is the aim of this package to provide a few functions implementing most of known analysis of variance tests for univariate and multivariate functional data, mainly for homoscedastic case. Most of them are based on bootstrap, permutations or projections, which may be time-consuming. For this reason, the package also contains parallel implementations which enable to reduce the computation time significantly, which is shown in empirical evaluation. Additionally, in this paper, some tests or their new versions are compared in terms of size control and power by simulation studies. Those comparisons were not presented anywhere else.

The rest of the paper is organized in the following manner. In Sect. 2, the problems of the analysis of variance for univariate and multivariate functional data are introduced. A review of most of the known solutions of these problems is also presented there. Some of the testing procedures are slightly generalized. Since it was not easy task to implement many different tests in a few functions, their usage may also be not easy at first. Thus, Sect. 3 contains a detailed description of (eventual) preparation of data and package functionality as well as a package demonstration on commonly used real data set. A series of experiments evaluating efficiency of parallel implementation is presented in Sect. 4. Simulation studies comparing some of the implemented tests in terms of size control and power are depicted in Sect. 5. Finally, Sect. 6 concludes the paper and notes on future extensions of the fdANOVA package. Supplementary Materials are described in Sect. 7.

2 Analysis of variance for functional data

In this section, we briefly describe most of the known testing procedures for the analysis of variance problem for functional data in the univariate and multivariate cases. All of them are implemented in the package fdANOVA.

2.1 Univariate case

We consider the l groups of independent random functions $X_{ij}(t)$, $i=1,\dots ,l,$$j=1,\dots ,n_i$ defined over a closed and bounded interval $I=[a,b]$. Let $n=n_1+\dots +n_l$. These groups may differ in mean functions, i.e., we assume that $X_{ij}(t)$, $j=1,\dots ,n_i$ are stochastic processes with mean function $\mu _i(t)$, $t\in I$ and covariance function $\gamma (s, t)$, $s,t\in I$, for $i=1,\dots ,l$. We also assume that $X_{ij}\in L_2(I)$, $i=1,\dots ,l,j=1,\dots ,n_i$, where $L_2(I)$ is a Hilbert space consisting of square integrable functions on I, equipped with the inner product of the form $\langle f,g\rangle =\int _{I}f(t)g(t)dt$. This is a common technical assumption. Of interest is to test the following null hypothesis

$$\begin{aligned} H_0:\mu _1(t)=\dots =\mu _l(t),\ t\in I. \end{aligned}$$

(1)

The alternative is the negation of the null hypothesis. The problem of testing this hypothesis is known as the one-way analysis of variance problem for functional data (FANOVA).

Many of the tests for (1) are based on the pointwise F test statistic (Ramsay and Silverman 2005) given by the formula

$$\begin{aligned} F_n(t)=\frac{\mathrm {SSR}_n(t)/(l-1)}{\mathrm {SSE}_n(t)/(n-l)}, \end{aligned}$$

where

$$\begin{aligned} \mathrm {SSR}_n(t)=\sum _{i=1}^l n_i(\bar{X}_i(t)-\bar{X}(t))^{2},\quad \mathrm {SSE}_n(t)=\sum _{i=1}^l\sum _{j=1}^{n_i}(X_{ij}(t)-\bar{X}_i(t))^{2} \end{aligned}$$

are the pointwise between-subject and within-subject variations respectively, and $\bar{X}(t)=(1/n)\sum _{i=1}^l\sum _{j=1}^{n_i}X_{ij}(t)$ and $\bar{X}_i(t)=(1/n_i)\sum _{j=1}^{n_i}X_{ij}(t),$$i=1,\dots ,l$, are respectively the sample grand mean function and the sample group mean functions.

Faraway (1997) and Zhang and Chen (2007) proposed to use only the pointwise between-subject variation and considered the test statistic $\int _I\mathrm {SSR}_n(t)dt$. Tests based on it are called the $L^2$-norm-based tests. Under Gaussian samples or large number of observations, the distribution of this test statistic can be approximated by that of $\beta \chi _{(l-1)\kappa }^2$, where $\beta =\mathrm {tr}(\gamma ^{\otimes 2})/\mathrm {tr}(\gamma )$ and $\kappa =\mathrm {tr}^{2}(\gamma )/\mathrm {tr}(\gamma ^{\otimes 2})$ ($\mathrm {tr}(\gamma )=\int _I\gamma (t,t)dt$, $\gamma ^{\otimes 2}(s,t)=\int _I\gamma (s,u)\gamma (u,t)du$) are obtained by comparing the first two moments of these random variables (see, Smaga 2017, for recent application of this method). The p-value is of the form $P(\chi _{(l-1)\kappa }^2\ge \int _I\mathrm {SSR}_n(t)dt/\beta )$. The parameters $\beta$ and $\kappa$ were estimated by the naive and biased-reduced methods (see, for instance, Zhang 2013, for more detail). Thus we have the $L^2$-norm-based tests with the naive and biased-reduced methods of estimation of these parameters (the $\mathrm {L}^{2}$N and $\mathrm {L}^{2}$B tests for short). In case of non-Gaussian samples or small sample sizes, the bootstrap $L^2$-norm-based test is also considered (the $\mathrm {L}^{2}$b tests for short).

A bit different $L^2$-norm-based test was proposed by Cuevas et al. (2004). Namely, they considered $\sum _{1\le i<j\le l}n_i\int _I(\bar{X}_i(t)-\bar{X}_j(t))^{2}dt$ as a test statistic and approximated its null distribution by a parametric bootstrap method via re-sampling the Gaussian processes involved in the limit random expression of their test statistic under $H_0$, i.e., $\sum _{1\le i<j\le l}\int _I(G_i(t)-\sqrt{p_i/p_j}G_j(t))^2dt,$ where $G_i(t)$, $i=1,\dots ,l$ are independent Gaussian processes with mean zero and covariance function $\gamma (s,t)$, and $n_i/n\rightarrow p_i>0$ as $n\rightarrow \infty$. Cuevas et al. (2004) investigated two testing procedures (the CH and CS tests for short) under homoscedastic and heteroscedastic cases. In heteroscedastic case, the processes $X_{ij}(t)$ and $G_i(t)$, $j=1,\dots ,n_i$ have covariance functions $\gamma _i(s,t)$, $s,t\in I$, which are not necessarily equal, $i=1,\dots ,l$. In homoscedastic (resp. heteroscedastic) case, the common covariance function $\gamma (s,t)$ (resp. the covariance function $\gamma _i(s,t)$ in the ith sample) is estimated based on observations from all groups (resp. the ith group).

Following test, which uses both the pointwise between-subject and within-subject variations, is known as the F-type test. More precisely, the test statistic is of the form

$$\begin{aligned} \frac{\int _I\mathrm {SSR}_n(t)dt/(l-1)}{\int _I\mathrm {SSE}_n(t)dt/(n-l)}. \end{aligned}$$

(2)

Tests of this type were considered by Shen and Faraway (2004) and Zhang (2011). Under Gaussian samples, the null distribution of the above test statistic is approximated by $F_{(l-1)\kappa ,(n-l)\kappa }$-distribution, where $\kappa$ is the same as for the $L^2$-norm-based test. The p-value is given by $P(F_{(l-1)\kappa ,(n-l)\kappa }>F_n)$, where $F_n$ denotes the test statistic (2). Depending on the method of estimation of parameter $\kappa$, the F-type tests based on naive and biased-reduced methods of estimation are considered (the FN and FB tests for short). For the same reasons as for $L^2$-norm-based test, the Fb test is also investigated, i.e., the bootstrap F-type test.

The next test, which also uses the test statistic (2), is the slightly modified procedure based on basis function representation of Górecki and Smaga (2015). We represent the functional observations by a finite number of basis functions $\varphi _m\in L_2(I),m=1,\dots$, i.e.,

$$\begin{aligned} X_{ij}(t)\approx \sum _{m=1}^{K}c_{ijm}\varphi _m(t),\quad t\in I, \end{aligned}$$

(3)

where $c_{ijm}$, $m=1,\dots ,K$, are random variables, $\mathrm {Var}(c_{ijm})<\infty$ and K is sufficiently large. By Górecki et al. (2015), the commonly used least squares method seems to be one of the best for estimation of $c_{ijm}$, so we use only that method for this purpose. The value of K can be selected for each $X_{ij}(t)$ using an information criterion, e.g., BIC, eBIC, AIC or AICc. From the values of K corresponding to all observations a modal, minimum, maximum or mean value is selected as the common value for all $X_{ij}(t)$. By using (3) and easy modifications of the results of Górecki and Smaga (2015), we proved that (2) is approximately equal to

$$\begin{aligned} \frac{(a-b)/(l-1)}{(c-a)/(n-l)}, \end{aligned}$$

(4)

where

$$\begin{aligned} a=\sum _{i=1}^l\frac{1}{n_i}\mathbf {1}_{n_{i}}^{\top }\mathbf {C}_{i}^{\top }\mathbf {J}_{{\varvec{\varphi }}}\mathbf {C}_{i}\mathbf {1}_{n_{i}},\ b=\frac{1}{n}\sum _{i=1}^l\sum _{j=1}^l\mathbf {1}_{n_{i}}^{\top }\mathbf {C}_{i}^{\top }\mathbf {J}_{{\varvec{\varphi }}}\mathbf {C}_{j}\mathbf {1}_{n_{j}},\ c=\sum _{i=1}^l\mathrm {trace}(\mathbf {C}_i^{\top }\mathbf {J}_{{\varvec{\varphi }}}\mathbf {C}_i), \end{aligned}$$

$\mathbf {1}_a$ is the $a\times 1$ vector of ones, $\mathbf {C}_i=(c_{ijm})_{j=1,\dots ,n_i;m=1,\dots ,K}$, $i=1,\dots ,l$, and $\mathbf {J}_{{\varvec{\varphi }}}:=\int _I{\varvec{\varphi }}(t){\varvec{\varphi }}^{\top }(t)dt$ is the $K\times K$ cross product matrix corresponding to ${\varvec{\varphi }}(t)=(\varphi _1(t),\dots ,\varphi _K(t))^{\top }$. The statistic (2) can be calculated based only on the coefficients $c_{ijm}$ and the matrix $\mathbf {J}_{{\varvec{\varphi }}}$, which can be approximated by using the function inprod() from the R package fda (For orthonormal basis, $\mathbf {J}_{{\varvec{\varphi }}}$ is the identity matrix.). Moreover, any permutation of the observations leaves b and c unchanged. For this reason, we considered the permutation test based on (4), and refer to it as the FP test. This test seems to have better finite sample properties than the F-type and $L^2$-norm-based tests. Moreover, for short functional data (i.e., observed on a short grid of design time points) it may also be better than the GPF test described in the following paragraph.

In the above test statistics, $\mathrm {SSR}_n(t)$ and $\mathrm {SSE}_n(t)$ were integrated separately. However, by the simulation results of Górecki and Smaga (2015), it follows that for example integrating the whole quotient $\mathrm {SSR}_n(t)/\mathrm {SSE}_n(t)$ is more powerful in many situations. Such test statistic of the form $\int _I F_n(t)dt$ was considered by Zhang and Liang (2014). They proposed the globalizing pointwise F test (the GPF test) based on this test statistic. Under Gaussianity assumptions or large sample sizes, the null distribution of test statistic can be approximated by that of $\beta \chi _d^2$ similarly as for the $L^2$-norm-based test, where

$$\begin{aligned} \beta =\frac{(n-l-2)\mathrm {tr}\left( \gamma _*^{\otimes 2}\right) }{(l-1)(n-l)(b-a)},\ d=\frac{(l-1)(n-l)^2(b-a)^2}{(n-l-2)^2\mathrm {tr}\left( \gamma _*^{\otimes 2}\right) } \end{aligned}$$

and $\gamma _*(s,t)=\gamma (s,t)/\sqrt{\gamma (s,s)\gamma (t,t)}$. Although integration seems to be a natural operation on $F_n(t)$ or its part, in some situations other using of $F_n(t)$ may be better in the sense of power, as was shown by Zhang et al. (2018). Instead of integral of $F_n(t)$, they used simply $\sup _{t\in I}F_n(t)$ as a test statistic and simulated the critical value of the resulting Fmaxb test via bootstrapping. By intensive simulation studies, Zhang et al. (2018) found that the Fmaxb (resp. GPF) test generally has higher power than the GPF (resp. Fmaxb) test when the functional data are moderately or highly (resp. less) correlated.

A different approach to test (1) was proposed by Cuesta-Albertos and Febrero-Bande (2010). Their tests are based on the analysis of randomly chosen projections. Suppose that $\mu _i\in L_2(I)$, $i=1,\dots ,l$, and $\xi$ is a Gaussian distribution on $L_2(I)$ and each of its one-dimensional projections is nondegenerate. Let h be a vector chosen randomly from $L_2(I)$ using the distribution $\xi$. When $H_0$ holds, then for every $h\in L_2(I)$, the following null hypothesis

$$\begin{aligned} H_0^h:\langle \mu _1,h\rangle =\dots =\langle \mu _l,h\rangle \end{aligned}$$

(5)

also holds. Moreover, Cuesta-Albertos and Febrero-Bande (2010) showed that for $\xi$-almost every h, $H_0^h$ fails, in case of failing of $H_0$. Thus, a test for $H_0^h$ can be used to test $H_0$. Cuesta-Albertos and Febrero-Bande (2010) propose the following testing procedure, in which k random projections are used:

• 1. Choose, with Gaussian distribution, functions $h_r\in L_2(I)$, $r=1,\dots ,k$.

• 2. Compute the projections $P_{ij}^r=\int _I X_{ij}(t)h_r(t)dt/\left( \int _I h_r^2(t)dt\right) ^{1/2}$ for $i=1,\dots ,l$, $j=1,\dots ,n_{i}$, $r=1,\dots ,k$.

• 3. For each $r\in \{1,\dots ,k\}$, apply the appropriate ANOVA test for $P_{ij}^r$, $i=1,\dots ,l$, $j=1,\dots ,n_i$. Let $p_1,\dots ,p_k$ denote the resulting p-values.

• 4. Compute the final p-value for $H_0$ by the formula $\inf \{kp_{(r)}/r,r=1,\dots ,k\}$, where $p_{(1)}\le \dots \le p_{(k)}$ are the ordered p-values obtained in step 3.

The tests based on the above procedure are referred to as the test based on random projections. Cuesta-Albertos and Febrero-Bande (2010) suggested to use k near 30, which was confirmed by the results of Górecki and Smaga (2017a). However, in the case of unconvincing results of the test, we should use a higher number of projections. We also have to choose a Gaussian distribution and ANOVA test appearing in steps 1 and 3 of the above procedure, respectively. We can do this in many ways and some of them are implemented in the package fdANOVA (see Sect. 3). In step 4, we can also use other final p-values instead of Benjamini and Hochberg procedure, as for example Bonferroni correction. However, according to our experience, the test with corrected p-value given in step 4 behaves best under finite samples, so we use only it. The procedure by Cuesta-Albertos and Febrero-Bande (2010) can also handle the heteroskedastic case. It only depends that such procedure exists for the projected data.

Most of the above testing procedures were compared via simulations in the papers of Górecki and Smaga (2015) and Zhang et al. (2018). As mentioned above, the GPF and Fmaxb tests seem to perform best among the tests considered in these articles. However, they were not compared with the testing procedure of Cuesta-Albertos and Febrero-Bande (2010). Such comparison of the finite sample behavior of these tests is given in Sect. 5. Different variants of the projection method proposed by Cuesta-Albertos and Febrero-Bande (2010) are also investigated there. As we will see the performance of this method usually depends on the choice of Gaussian distribution $\xi$ and on the choice of ANOVA test.

2.2 Multivariate case

Now, we study the multivariate version of the ANOVA problem for functional data as well as extensions of certain methods presented in the last section to this problem. The results of this section were mainly obtained by Górecki and Smaga (2017a).

Instead of single functions, we consider independent vectors of random functions $\mathbf {X}_{ij}(t)=(X_{ij1}(t),\dots ,X_{ijp}(t))^{\top }\in SP_p({\varvec{\mu }}_i,{\varvec{\Gamma }})$, $i=1,\dots ,l,$$j=1,\dots ,n_{i}$ defined over the interval I, where $SP_{p}({\varvec{\mu }},{\varvec{\Gamma }})$ is a set of p-dimensional stochastic processes with mean vector ${\varvec{\mu }}(t)$, $t\in I$ and covariance function ${\varvec{\Gamma }}(s, t)$, $s,t\in I$. We also assume that $\mathbf {X}_{ij}$ belong to $L_{2}^{p}(I)$ – a Hilbert space of p-dimensional vectors of square integrable functions on the interval I, equipped with the inner product: $\langle \mathbf {x},\mathbf {y}\rangle =\int _I\mathbf {x}^{\top }(t)\mathbf {y}(t)dt$. In the multivariate analysis of variance problem for functional data (FMANOVA), we have to test the null hypothesis as follows:

$$\begin{aligned} H_0:{\varvec{\mu }}_1(t)=\dots ={\varvec{\mu }}_l(t),\ t\in I. \end{aligned}$$

(6)

The first tests are based on a basis function representation of the components of the vectors $\mathbf {X}_{ij}(t)$, $i=1,\dots ,l$, $j=1,\dots ,n_i$, similarly as in the FP test. We represent the components of $\mathbf {X}_{ij}(t)$ in a similar way as in (3), i.e.,

$$\begin{aligned} \mathbf {X}_{ij}(t)\approx \left( \mathbf {c}_{ij1}^{\top },\dots ,\mathbf {c}_{ijp}^{\top }\right) ^{\top }{\varvec{\varphi }}(t)=\mathbf {c}_{ij}{\varvec{\varphi }}(t), \end{aligned}$$

(7)

where $\mathbf {c}_{ijm}=(c_{ijm1},\dots ,c_{ijmK_{m}},0,\dots ,0)\in R^{KM}$, ${\varvec{\varphi }}(t)=(\varphi _1(t),\dots ,\varphi _{KM}(t))^{\top },$$t\in I$ and $i=1,\dots ,l$, $j=1,\dots ,n_{i}$, $m=1,\dots ,p$, $KM=\max \{K_{1},\dots ,K_{p}\}$. The coefficients in $\mathbf {c}_{ij}$ and values of $K_m$ are estimated separately for each feature by methods described in Sect. 2.1. Similarly to MANOVA (Anderson 2003), the following matrices were used in constructing test statistics for (6):

$$\begin{aligned} \mathbf {E}&=\sum _{i=1}^l\sum _{j=1}^{n_{i}}\int _I \left( \mathbf {X}_{ij}(t)-\bar{\mathbf {X}}_{i}(t)\right) \left( \mathbf {X}_{ij}(t)-\bar{\mathbf {X}}_{i}(t)\right) ^{\top } dt,\\ \mathbf {H}&=\sum _{i=1}^l n_{i}\int _I \left( \bar{\mathbf {X}}_{i}(t)-\bar{\mathbf {X}}(t)\right) \left( \bar{\mathbf {X}}_{i}(t)-\bar{\mathbf {X}}(t)\right) ^{\top } dt, \end{aligned}$$

where $\bar{\mathbf {X}}_i(t)=(1/n_i)\sum _{j=1}^{n_i}\mathbf {X}_{ij}(t),$$i=1,\dots ,l$ and $\bar{\mathbf {X}}(t)=(1/n)\sum _{i=1}^l\sum _{j=1}^{n_i}\mathbf {X}_{ij}(t)$, $t\in I$. Modifying the results of Górecki and Smaga (2017a), we showed that these matrices can be designated only by the coefficient matrices $\mathbf {c}_{ij}$ and appropriate cross product matrix, i.e., $\mathbf {E}\approx \mathbf {A}-\mathbf {B}$ and $\mathbf {H}\approx \mathbf {B}-\mathbf {C}$, where

$$\begin{aligned} \mathbf {A}=\sum _{i=1}^l\sum _{j=1}^{n_{i}}\mathbf {c}_{ij}\mathbf {J}_{{\varvec{\varphi }}}\mathbf {c}_{ij}^{\top },\ \mathbf {B}=\sum _{i=1}^l\frac{1}{n_{i}}\sum _{j=1}^{n_{i}}\sum _{m=1}^{n_{i}}\mathbf {c}_{ij}\mathbf {J}_{{\varvec{\varphi }}}\mathbf {c}_{im}^{\top },\ \mathbf {C}=\frac{1}{n}\sum _{i=1}^l\sum _{j=1}^{n_{i}}\sum _{t=1}^l\sum _{u=1}^{n_{t}}\mathbf {c}_{ij}\mathbf {J}_{{\varvec{\varphi }}}\mathbf {c}_{tu}^{\top }, \end{aligned}$$

and $\mathbf {J}_{{\varvec{\varphi }}}$ is the $KM\times KM$ cross product matrix corresponding to ${\varvec{\varphi }}$. The following test statistics for (6) are constructed based on those appearing in MANOVA: the Wilk’s lambda $\mathrm {W}=\det (\mathbf {E})/\det (\mathbf {E}+\mathbf {H})$, the Lawley-Hotelling trace $\mathrm {LH}=\mathrm {trace}(\mathbf {H}\mathbf {E}^{-1})$, the Pillai trace $\mathrm {P}=\mathrm {trace}(\mathbf {H}(\mathbf {H}+\mathbf {E})^{-1})$, the Roy’s maximum root $\mathrm {R}=\lambda _{\max }(\mathbf {H}\mathbf {E}^{-1})$, where $\lambda _{\max }(\mathbf {M})$ is the maximum eigenvalue of a matrix $\mathbf {M}$. We consider the permutation tests based on these statistics and refer to them as the W, LH, P and R tests, respectively. Generally, we refer to them as the permutation tests based on a basis function representation. A quite fast implementation of these tests was obtained by observing that $\mathbf {A}$ and $\mathbf {C}$ are not changed by any permutation of the data.

The second group of tests for (6) is based on random projections similarly as in the FANOVA test based on random projections. Let a distribution $\xi$ be defined as in Sect. 2.1. Assume that $\mu _{ij}\in L_2(I)$, where $\mu _{ij}$ are the components of ${\varvec{\mu }}_i$, $i=1,\dots ,l$, $j=1,\dots ,p$. When (6) holds, then for every $\mathbf {H}=(h_1,\dots ,h_p)^{\top }\in L_2^p(I)$,

$$\begin{aligned} H_0^{\mathbf {H}}: (\langle \mu _{11},h_1\rangle ,\dots ,\langle \mu _{1p},h_p\rangle )^{\top }=\dots = (\langle \mu _{l1},h_1\rangle ,\dots , \langle \mu _{lp},h_p\rangle )^{\top } \end{aligned}$$

(8)

also holds, while if $H_0$ fails, for $(\xi \times \dots \times \xi )$-almost every $\mathbf {H}\in L_2^p(I)$, $H_0^{\mathbf {H}}$ also fails. Thus, a test for the MANOVA problem can be used to test the FMANOVA one by using it to test (8). For this reason, Górecki and Smaga (2017a) investigated the similar procedure based on k random projection as described in Sect. 2.1, which the first three steps are now as follows:

• 1. Choose, with Gaussian distribution, functions $h_{mr}\in L_2(I)$, $m=1,\dots ,p$, $r=1,\dots ,k$.

• 2. Compute the projections $P_{ijm}^r=\int _I X_{ijm}(t)h_{mr}(t)dt/\left( \int _I h_{mr}^2(t)dt\right) ^{1/2}$ for $i=1,\dots ,l$, $j=1,\dots ,n_{i}$, $m=1,\dots ,p$, $r=1,\dots ,k$.

• 3. For each $r\in \{1,\dots ,k\}$, apply the appropriate MANOVA test for $\mathbf {P}_{ij}^r=(P_{ij1}^r,\dots ,P_{ijp}^r)^{\top }$, $i=1,\dots ,l$, $j=1,\dots ,n_i$. Let $p_1,\dots ,p_k$ denote the resulting p-values.

In step 3 of this procedure, the well-known MANOVA tests were applied, namely Wilk’s lambda test (Wp test), the Lawley-Hotelling trace test (LHp test), the Pillai trace test (Pp test) and Roy’s maximum root test (Rp test). Their permutation versions are also investigated.

Remark 1

In multivariate analysis, the invariance of a procedure under linear transformations of the marginal distributions is usually important, since it is common, for instance, to standardize the data. For functional data, this issue is also considered. For example, Huang et al. (2008) investigated the functional principal components analysis invariant under scale transformation of functional data. So, it is worth to mention that the testing procedures under consideration for the FMANOVA problem are also invariant under such transformation. More precisely, conditioned on the basis representation and random permutations (resp. random projections and random permutations, if they are used) chosen and independent from the data, the permutation tests based on a basis function representation (resp. tests based on random projections) are invariant under scale transformation $X_{ijm}(t)\rightarrow c_mX_{ijm}(t)$, $t\in I$ for any $c_m\ne 0$, $i=1,\dots ,l$, $j=1,\dots ,n_i$, $m=1,\dots ,p$. This property indicates that the tests can also be applied, when the components of the functional data are measured in different units.

By the extensive Monte Carlo simulation studies of Górecki and Smaga (2017a), the performance of the tests considered except the Rp test is very satisfactory under finite samples. Unfortunately, the Rp test does not control the nominal type-I error level, and hence it can not be recommended. The other tests do not perform equally well, and there is no single method performing best. As a supplement to those simulation studies, the finite sample behavior of new variant of the tests based on random projections implemented in the package fdANOVA (i.e., different Gaussian distribution $\xi$ than the Brownian motion considered in Górecki and Smaga 2017a) is investigated in simulations of Sect. 5.

3 R implementation

In this section, we present the R package fdANOVA and illustrate the usage of it step by step using certain real data set. First, however, we mention about the eventual preparation of the functional data in the R program to use the functions of our package properly.

3.1 Preparation of the data

In practice, functional samples are not continuously observed, i.e., each function is usually observed on a grid of design time points. In our implementations of FANOVA and FMANOVA tests in the R programming language, all functions are observed on a common grid of design time points equally spaced in the interval $I=[a,b]$. We notice that not all tests need to be applied to functional data observed on design time points equally spaced in I. Nevertheless, since we assume that the considered functional data are dense, we can require that the design time points are equally spaced in I, which helps us in unifying the implementation of the tests.

In the case where the design time points are different for different individual functions or not equally spaced in I, we follow the methodology proposed by Zhang (2013). First, we have to reconstruct the functional samples from the observed discrete functional samples using smoothing technique such as regression splines, smoothing splines, P-splines or local polynomial smoothing (see Zhang 2013, Chapters 2–3). For this purpose, in R we can use the function smooth.spline() from the stats package (R Core Team 2017) or functions given in the packages splines (R Core Team 2017), bigsplines (Helwig 2016), pspline (S original by Jim Ramsey R port by Brian Ripley 2015) and locpol (Ojeda Cabrera 2012). After that we discretize each individual function of the reconstructed functional samples on a common grid of $\mathcal {T}$ time points equally spaced in I, and then the implementations of the tests can be applied to discretized samples. Such reconstruction largely removes the measurement errors from functional data, and hence may improve the finite sample performance of the tests, as it was noted, for example, in Zhang (2013) and Zhang and Liang (2014).

3.2 Package functionality

Now, we describe the implementation of the tests for analysis of variance problem for univariate and multivariate functional data in the R package fdANOVA. As we will see many of the implemented tests may be performed with different values of parameters. However, by simulation and real data examples presented in the present and previous papers (see Sects. 2 and 5), satisfactory results are usually obtained by using the default values of these parameters. Nevertheless, when the results are unconvincing (e.g., the p-values are close to the significance level), we have the opportunity to use other options provided by the functions of the package.

All tests for FANOVA problem presented in Sect. 2.1 are implemented in the function fanova.tests(), which is controlled by the following parameters:

• x = NULL – a $\mathcal {T}\times n$ matrix of data, whose each column is a discretized version of a function and rows correspond to design time points. Its default values is NULL, since if the FP test is only used, we can give a basis representation of the data instead of raw observations (see the list paramFP below). For any of the other testing procedures, the raw data are needed.

• group.label – a vector containing group labels.

• test = "ALL" – a kind of indicator which establishes a choice of FANOVA tests to be performed. Its default value means that all testing procedures of Sect. 2.1 will be used. When we want to use only some tests, the parameter test is an appropriate subvector of the following vector of tests’ labels (see Sect. 2.1):

  

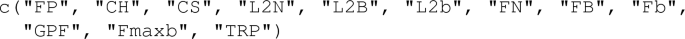
• params = NULL – a list of additional parameters for the FP, CH, CS, L$^2$b, Fb, Fmaxb tests and the test based on random projections. Its possible elements and their default values are described below. The default value of this parameter means that these tests are performed with their default values.

• parallel = FALSE – a logical indicating whether to use parallelization.

• nslaves = NULL – if parallel = TRUE, a number of slaves. Its default value means that it will be equal to a number of logical processes of a computer used.

The list params can contain all or a part of the elements paramFP, paramCH, paramCS, paramL2b, paramFb, paramFmaxb and paramTRP for passing the parameters for the FP, CH, CS, L$^2$b, Fb, Fmaxb tests and the test based on random projections, respectively, to the function fanova.tests(). They are described as follows. The list paramFP contains the following parameters of the FP test and their default values:

• int – a vector of two elements representing the interval $I=[a,b]$. When it is not specified, it is determined by a number of design time points.

• B.FP = 1000 – a number of permutation replicates.

• basis = c("Fourier", "b-spline", "own") – a choice of basis of functions used in the basis function representation of the data.

• own.basis – if basis = "own", a $K\times n$ matrix with columns containing the coefficients of the basis function representation of the observations.

• own.cross.prod.mat – if basis = "own", a $K\times K$ cross product matrix corresponding to a basis used to obtain the matrix own.basis.

• criterion = c("BIC", "eBIC", "AIC", "AICc", "NO") – a choice of information criterion for selecting the optimum value of K. criterion = "NO" means that K is equal to the parameter maxK defined below.

• commonK = c("mode", "min", "max", "mean") – a choice of method for selecting the common value for all observations from the values of K corresponding to all processes.

• minK = NULL (resp. maxK = NULL) – a minimum (resp. maximum) value of K.

• norder = 4 – if basis = "b-spline", an integer specifying the order of b-splines.

• gamma.eBIC = 0.5 – a $\gamma \in [0,1]$ parameter in the eBIC.

It should be noted that the AICc may choose the final model with a number K of coefficients close to a number of observations n, when a maximum K considered is greater than n. Such selection usually differs from choices suggested by other criterion, but it seems that this does not have much impact on the results of testing.

For the CH and CS (resp. L$^2$b, Fb and Fmaxb) tests, the parameters paramCH and paramCS (resp. paramL2b, paramFb and paramFmaxb) denote the numbers of discretized artificial trajectories for certain Gaussian processes (resp. bootstrap samples) used to approximate the null distributions of their test statistics. The default value of each of these parameters is 10,000. The parameters of the test based on random projections and their default values are contained in a list paramTRP with elements:

• k = 30 – a vector of numbers of projections.

• projection = c("GAUSS", "BM") – a method of generating Gaussian processes in step 1 of the testing procedure based on random projections presented in Sect. 2. If projection = "GAUSS", the Gaussian white noise is generated as in the function anova.RPm() from the R package fda.usc (Febrero-Bande and Oviedo de la Fuente 2012). In the second case, the Brownian motion is generated.

• permutation = FALSE – a logical indicating whether to compute p-values by permutation method.

• B.TRP = 10000 – a number of permutation replicates.

• independent.projection.tests = TRUE – a logical indicating whether to generate the random projections independently or dependently for different elements of vector k. In the first case, the random projections for each element of vector k are generated separately, while in the second one, they are generated as chained subsets, e.g., for k = c(5, 10), the first 5 projections are a subset of the last 10. The second way of generating random projections is faster than the first one.

A Brownian process in [a, b] has small variances near a and higher variances close to b. This means that the tests based on random projections and the Brownian motion may be more able to detect differences among mean groups, when those differences are much closer to b than to a.

To perform step 3 of the procedure based on random projections given in Sect. 2.1, in the package, we use five testing procedures: the standard (paramTRP$permutation = FALSE) and permutation (paramTRP$permutation = TRUE) tests based on ANOVA F test statistic and ANOVA-type statistic (ATS) proposed by Brunner et al. (1997), as well as the testing procedure based on Wald-type permutation statistic (WTPS) of Pauly et al. (2015).

The function fanova.tests() returns a list of the class fanovatests. This list contains the values of the test statistics, the p-values and the parameters used. The results for a given test are given in a list (being an element of output list) named the same as the indicator of a test in the vector test. Additional outputs as the chosen optimal length of basis expansion (the FP test), the values of estimators used in approximations of null distributions of test statistics (the L$^2$N, L$^2$B, FN, FB, GPF tests) and projections of the data (the test based on random projections) are contained in appropriate lists. If independent.projection.tests = TRUE, the projections of the data are contained in a list of the length equal to length of vector k, whose i-th element is an $n\times {\texttt {k[i]}}$ matrix with columns being projections of the data. When independent.projection.tests = FALSE, the projections of the data are contained in an $n\times \max ({\texttt {k}})$ matrix with columns being projections of the data.

The permutation tests based on a basis function representation for the FMANOVA problem, i.e., the W, LH, P and R tests are implemented in the function fmanova.ptbfr() with parameters x, group.label, int, B, parallel, nslaves, basis, own.basis, own.cross.prod.mat, criterion, commonK, minK, maxK, norder and gamma.eBIC. These parameters, which have a different meaning than in the function fanova.tests() (B corresponds to B.FP), are described as follows:

• x = NULL – a list of $\mathcal {T}\times n$ matrices of data, whose each column is a discretized version of a function and rows correspond to design time points. The mth element of this list contains the data of mth feature, $m=1,\dots ,p$. Its default values is NULL, because a basis representation of the data can be given instead of raw observations (see the parameter own.basis below).

• own.basis – if basis = "own", a list of length p, whose elements are $K_m\times n$ matrices ($m=1,\dots ,p$) with columns containing the coefficients of the basis function representation of the observations.

• own.cross.prod.mat – if basis = "own", a $KM\times KM$ cross product matrix corresponding to a basis used to obtain the list own.basis.

• criterion = c("BIC", "eBIC", "AIC", "AICc", "NO") – a choice of information criterion for selecting the optimum value of $K_m$, $m=1,\dots ,p$. criterion = "NO" means that $K_m$ are equal to the parameter maxK defined below.

• commonK = c("mode", "min", "max", "mean") – a choice of method for selecting the common value for all observations from the values of $K_m$ corresponding to all processes.

• minK = NULL (resp. maxK = NULL) – a minimum (resp. maximum) value of $K_m$.

The function fmanova.ptbfr() returns a list of the class fmanovaptbfr containing the values of the test statistics (W, LH, P, R), the p-values (pvalueW, pvalueLH, pvalueP, pvalueR), chosen optimal values of $K_m$ and the parameters used.

The function fmanova.trp() performs the testing procedures based on random projections for FMANOVA problem (the Wp, LHp, Pp and Rp tests). Its parameters are x, group.label, k, projection, permutation, B, independent.projection.tests, parallel and nslaves. The first two parameters of this function as well as the arguments parallel, nslaves are the same as in the function fmanova.ptbfr(). The other ones have the same meaning as in the parameter list paramTRP of the function fanova.tests() (B corresponds to B.TRP). The function fmanova.trp() returns a list of class fmanovatrp containing the parameters and the following elements ($|{\texttt {k}}|$ denotes the length of vector k): pvalues – a $4\times |{\texttt {k}}|$ matrix of p-values of the tests; data.projections – if independent.projection.tests = TRUE, a list of length $|{\texttt {k}}|$, whose elements are lists of $n\times p$ matrices of projections of the observations, while when independent.projection.tests = FALSE, a list of length $\max ({\texttt {k}})$, whose elements are $n\times p$ matrices of projections of the observations.

The executions of selecting the optimum length of basis expansion by some information criterion, the bootstrap, permutation and projection loops are the most time-consuming steps of the testing procedures under consideration. To reduce the computational cost of the procedures, they are parallelized, when the parameter parallel is set to TRUE. The parallel execution is handled by doParallel package (Revolution Analytics and Weston 2015). Some details of the parallel implementation and its efficiency are discussed in Sect. 4.

In the package, the number of auxiliary functions are also contained. The p-values of the tests based on random projections for FANOVA problem against the number of projections are visualized by the function plot.fanovatests() using the package ggplot2 (Wickham 2009), which is controlled by the following parameters: x – an fanovatests object, more precisely, a result of the function fanova.tests() for the standard tests based on random projections; y – an fanovatests object, more precisely, a result of the function fanova.tests() for the permutation tests based on random projections. Similarly, the p-values of the Wp, LHp, Pp and Rp tests are plotted by the function plot.fmanovatrp(). The arguments of this function are as follows: x – an fmanovatrp object, more precisely, a result of the function fmanova.trp() for the standard tests; y – an fmanovatrp object, more precisely, a result of the function fmanova.trp() for the permutation tests; withoutRoy – a logical indicating whether to plot the p-values of the Rp test. We can use only one of the arguments x and y, or both simultaneously.

Using the package ggplot2 (Wickham 2009), the function plotFANOVA() produces a plot showing univariate functional observations with or without indication of groups as well as mean functions of samples. The following parameters control this function:

• x – a $\mathcal {T}\times n$ matrix of data, whose each column is a discretized version of a function and rows correspond to design time points.

• group.label = NULL – a character vector containing group labels. Its default value means that all functional observations are drawn without division into groups.

• int = NULL – this parameter is the same as in the function fanova.tests().

• separately = FALSE – a logical indicating how groups are drawn. When separately = FALSE, groups are drawn on one plot by different colors. If separately = TRUE, they are depicted in different panels.

• means = FALSE – a logical indicating whether to plot only group mean functions.

• smooth = FALSE – a logical indicating whether to plot reconstructed data via smoothing splines instead of raw data.

The p-values and values of the test statistics for the implemented tests are printed by the functions print.fanovatests(), print.fmanovaptbfr() and print.fmanovatrp(). Additionally, summary.fanovatests(), summary.fmanovaptbfr() and summary.fmanovatrp() are functions for printing out information about the data and parameters of the methods.

When calling the functions of the fdANOVA package, the software will check for presence of the doBy, doParallel, ggplot2, fda, foreach, magic, MASS and parallel packages if necessary (Hojsgaard and Halekoh 2016; Revolution Analytics and Weston 2015; Wickham 2009; Ramsay et al. 2017; Hankin 2005; Venables and Ripley 2002). If the required packages are not installed, an error message will be displayed.

3.3 Package demonstration on real data example

In this section, we provide examples that illustrate how the functions of the R package fdANOVA can be used to analyze real data. For this purpose, we use the popular gait data set available in the fda package. This data set consists of the angles formed by the hip and knee of each of 39 children over each child’s gait cycle. The simultaneous variations of the hip and knee angles for children are observed at 20 equally spaced time points in [0.025, 0.975]. So, in this data set, we have two functional features, which we put in the list x.gait of length two, as presented below.

Similarly to Górecki and Smaga (2017a), for illustrative purposes, the functional observations are divided into three samples. Namely, the first sample consists of the functions for the first 13 children, the second sample of the functions for the next 13 children, and the third sample of the functions for the remaining children. The sample labels are contained in the vector group.label.gait:

We can plot the functional data by using the function plotFANOVA(). For example, we plot the observations for the first functional feature without (Fig. 1a) and with indication of the samples (Fig. 1b, c) as well as the group mean functions (Fig. 1d).

Fig. 1

The first functional feature of the gait data without (Panel a) and with indication of the samples (Panels b and c). Panel d depicts the group mean functions

From Fig. 1, it seems that the mean functions of the three samples do not differ significantly. To confirm this statistically, we use the FANOVA tests implemented in the fanova.tests() function. First, we use default values of the parameters of this function:

Besides of the p-values displayed above, the list of matrices of projections of the data may be of practical interest for the test based on random projections users. The reason for this is that we can check the assumptions of the tests used in step 3 of the procedure based on random projections (see Sect. 2.1), e.g., the normality assumptions of ANOVA F test. Such inspection may result in choosing the appropriate test used in this step. This is especially important when the tests based on random projections differ in their decisions.

As expected, neither FANOVA test rejects the null hypothesis. Now, we show how particular tests can be chosen and how the parameters of these tests can be changed. For the FP test, we use the predefined basis function representation of the data. For this purpose, we expand the data in the b-spline basis by using the functions from the fda package. They return the coefficients of expansion as well as the cross product matrix corresponding to the basis functions. For control, we choose the GPF test, which does not need any additional parameters. The Fmaxb test is performed by 1000 bootstrap samples. For the tests based on random projections, 10 and 15 projections are generated by using the Brownian motion, and p-values are computed by the permutation method.

The above examples concern only the first functional feature of the gait data set. Similar analysis can be performed for the second one. However, both features can be simultaneously investigated by using the FMANOVA tests described in Sect. 2.2. First, we consider the permutation tests based on a basis function representation implemented in the function fmanova.ptbfr(). We apply this function to the whole data set specifying non-default values of most of parameters. Here, we also show how use the function summary.fmanovaptbfr() to additionally obtain a summary of the data and test parameters. Observe that the results are consistent with these obtained by FANOVA tests.

Finally, we apply the tests based on random projections for the FMANOVA problem in the gait data set. In the following, these tests are performed with $k=1,5,10,15,20$ projections, standard and permutation methods as well as the random projections generated in independent and dependent ways. The resulting p-values are visualized by the plot.fmanovatrp() function:

Fig. 2

P-values of the tests based on random projections for the FMANOVA problem in the gait data set. The Wpp, LHpp, Ppp and Rpp tests are the permutation versions of the Wp, LHp, Pp and Rp tests. In the first (resp. second) row, the random projections were generated in independent (resp. dependent) way

The obtained plots are shown in Figure 2. As we can observe, except the standard Rp test, all testing procedures behave similarly and do not reject the null hypothesis. The standard Rp test does not keep the pre-assigned type-I error rate as Górecki and Smaga (2017a) shown in simulations. More precisely, this test is usually too liberal, which explains that its p-values are much smaller than these of the other testing procedures. That is why the function has option not to plot the p-values of this test.

4 Efficiency of the parallel implementation

As we mentioned in Sect. 3.2, the functions of the fdANOVA package provide the option of parallelization of the execution of the most time-consuming steps of performing the testing procedures, i.e., selection of optimal K in basis representation (3) by information criterion, permutation, bootstrap and projection methods. By default the parameter parallel is set to FALSE, which corresponds to sequential version. This option should be used when the data set is not too large or we have a single processor machine with one core, since the parallelization is very inefficient in such cases. When it is possible or needed, we specify parallel = TRUE to perform parallel computations using process forking based on the commonly used doParallel package (Revolution Analytics and Weston 2015). This parallel method can be performed on a single logical machine only.

The doParallel package uses the built-in parallel package (R Core Team 2017) and is supported on both Linux and Windows in contrast to other packages for parallelization, e.g., doMC for Linux and MAC OS (Revolution Analytics 2013) and doSNOW for Windows (Microsoft Corporation and Weston 2017). The doParallel package is essentially a merger of these two packages, and automatically uses the appropriate tool for system. The applied method of parallelization works by starting a specified number of regular R processes run on the available cores. The original R process controls the launch and stop of the those processes and the assignment of parallel tasks. The assignment of those processes to the cores is controlled by the OS.

In the fdANOVA package, we have possibility of controlling a number of parallel tasks by setting the parameter nslaves. This parameter is set to a number of logical processes of used computer by default, which is an optimal choice. Further information about parallel computing in R and its usage can be found for example in Schmidberger et al. (2009) and Teisseyre et al. (2016).

In the remainder of this section, we discuss the results of experiments evaluating efficiency of parallel implementation in the fdANOVA package. They were performed for one physical computer with 14 cores (processor Intel(R) Xeon(R) E5-2690 v4 @ 2.6 GHz, 3.5 GHz all-core turbo), 64 GB RAM, Windows 7 64-bit, R 3.3.3. We compared the execution time and speedup of the sequential and parallel versions. The number of slaves was set to 2, 4, 8 and 14. The experiments were performed by using the Graz and uWaveGestureLibrary data sets available in the mfds package (Górecki and Smaga 2017b). We present and discuss the results of the experiments based on these data sets and the FANOVA tests implemented via parallel method in the function fanova.tests(), i.e., the FP, CH, CS, L$^2$b, Fb, Fmaxb tests and the permutation test based on random projections. These tests were applied to the first features of these data sets by using default values of parameters, i.e., 1000, 10, 000 permutation replicates for the FP test and the tests based on random projections, respectively, 10,000 bootstrap samples and 30 projections. In the other settings, similar results have been obtained, and therefore, they are omitted for space saving.

Fig. 3

Execution time and speedup versus the number of slaves and the number of design time points $\mathcal {T}$ obtained for the Graz data set (one slave refers to the sequential version)

In the first experiment, the first feature of the Graz data set was considered. This data set contains $n=140$ three-dimensional functional observations, which were measured in $\mathcal {T}=1152$ design time points and divided into two groups each of 70 observations. In this experiment, we studied how the computational time and speedup depend on the number of design time points, i.e., we applied the tests to the truncated Graz data sets with $\mathcal {T}=100,400,800,1152$ design time points. The second experiment is based on the first feature of the uWaveGestureLibrary data set, which contains $n=4478$ three-dimensional functional observations measured in $\mathcal {T}=315$ design time points and divided into eight samples of 559 or 560 observations. In this case, we investigated how the computational time and speedup depend on the number of observations. For this purpose, we considered the subsets of the uWaveGestureLibrary data set consisting of $n=100,400,700,1000$ observations. Figures 3 and 4 depict the results of both experiments.

Observe that the parallel implementation results in satisfactory shortening the computational time. The usage of two slaves has already made calculations much faster. The execution time strictly decreases with increase of the number of slaves. The behavior of speedup also seems to be satisfactory, although it is not linear as there are other sequentially executed tasks in the functions. Nevertheless, for two and four slaves, the speedup is almost linear in both experiments, i.e., it is close to the numbers of parallel tasks. From the first experiment, however, it follows that the speedup for greater number of slaves may decrease with increase of the number of design time points (Fig. 3). Fortunately, the opposite usually holds when the number of observations increases as in the second experiment (Fig. 4). This can perhaps be explained by that the parallel tasks are more concerned in functional observations than their values in particular design time points. The implementation of the permutation tests based on random projections seems to be the most time-consuming. When one wants to perform this tests, it is recommended to use the parallel method even for not very large data sets. However, when we only choose other testing procedures for analysis, the parallelization should be used for larger data sets. Otherwise it may not make sense. Summarizing, the parallel implementation enables to reduce the computation time significantly, when it is used appropriately.

Fig. 4

Execution time and speedup versus the number of slaves and the number of observations n obtained for the uWaveGestureLibrary data set (one slave refers to the sequential version)

5 Simulation study

In this section, we consider simulation studies to compare the GPF, Fmaxb tests and the tests based on random projections. For the last one, two methods of generating Gaussian processes implemented in the fdANOVA package are considered. As a result, simulations indicate the recommended tests for different scenarios.

The simulations scenarios were inspired by a Monte Carlo study in Zhang and Liang (2014) and Zhang et al. (2018).

5.1 Simulation for FMANOVA tests

To compare the FMANOVA tests based on random projections with different methods of generating Gaussian processes, we consider three groups of two-dimensional functional data and two vectors $\mathbf {n}=(n_1,n_2,n_3)$ of sample sizes $\mathbf {n}_1=(10,10,10)$ and $\mathbf {n}_2=(10,20,15)$. Discrete functional samples are generated by using the model $x_{prs}(t)=\eta _{pr}(t)+v_{prs}(t)$, $t\in [0,1]$, $p=1,2,r=1,2,3$, $s=1,\dots ,n_r$. The functions $x_{prs}(t)$ are assumed to be observed at $\mathcal {T}=50$ design time points q / 51, $q=1,\dots ,50$.

The mean group functions are as follows: $\eta _{1r}(t)=\mathbf {c}_1^{\top }(1,t,t^2,t^3)^{\top }$ for $r=1,2$, $\eta _{13}(t)=(\mathbf {c}_1+2\delta \mathbf {u})^{\top }(1,t,t^2,t^3)^{\top }$ and $\eta _{2r}(t)=\mathbf {c}_2^{\top }(1,t,t^2,t^3)^{\top }$ for $r=1,2,3$, where $\mathbf {c}_1=(1, 2.3, 3.4, 1.5)^{\top }$, $\mathbf {c}_2=(2.2, 1.6, 1, 2.9)^{\top }$. Thus, the differences between appropriate group mean functions is controlled by $\delta$, whose values are contained in the tables of simulation results. Moreover, the direction of these differences is specified by $\mathbf {u}=(1,2,3,4)^{\top }/\sqrt{30}$.

For i.i.d. $v_{prs}(t)\sim SP(0,\gamma )$, we take $v_{prs}(t)=\mathbf {b}_{prs}^{\top }{\varvec{\varPsi }}(t)$, $\mathbf {b}_{prs}=(b_{prs,1},\dots ,b_{prs,11})^{\top }$, $b_{prs,w}{\mathop {=}\limits ^{d}}\sqrt{\lambda _w}y_{prs,w},w=1,\dots ,11$, where ${\varvec{\varPsi }}(t)=(\psi _1(t),\dots ,\psi _{11}(t))^{\top }$ is the orthonormal basis vector such that $\psi _1(t)=1$, $\psi _{2\omega }(t)=\sqrt{2}\sin (2\pi \omega t)$ and $\psi _{2\omega +1}(t)=\sqrt{2}\cos (2\pi \omega t)$, $\omega =1,\dots ,5$, $\lambda _w=1.5\rho ^w$, $\rho =0.1,0.3,0.5,0.7,0.9$, and $y_{prs,w}$ are independent random variables, $\mathrm {E}(y_{prs,w})=0$, $\mathrm {Var}(y_{prs,w})=1$. The Gaussian (resp. non-Gaussian) functional observations are obtained by considering $y_{prs,w}\sim N(0,1)$ (resp. $y_{prs,w}\sim t_4/\sqrt{2}$). Notice that $\gamma (s,t)$ is of the form ${\varvec{\varPsi }}(s)^{\top }\text {diag}(\lambda _1,\dots ,\lambda _{11}){\varvec{\varPsi }}(t)$ and the correlation increases with decreasing $\rho$.

For $\delta =0$ (resp. $\delta \ne 0$), the null hypothesis is true (resp. false) and we investigate the size control (resp. power) of the tests. This model will be referred to as FMANOVA model, and the simulation results obtained under it are depicted in Table 1 under Gaussian distribution and balanced design, while in Tables 1 and 2 in the Supplementary Materials, all results are presented.

All testing procedures based on random projections for FMANOVA except the Rp test control the nominal type-I error rate. They show a tendency of conservativity in most scenarios, but this is natural for tests based on random projection as indicated by Cuesta-Albertos and Febrero-Bande (2010) and Górecki and Smaga (2017a). The Pp (resp. LHp) test has the most conservative (resp. liberal) character. The standard version of the Rp test tends to be highly liberal for both methods of generating Gaussian processes. So, it is not comparable with the other tests. The permutation versions of all tests seem to behave better than the standard ones when the null hypothesis holds true, especially in the case of t-distribution.

Since the standard Rp tests do not maintain the pre-assigned type-I error rate, we do not compare their empirical powers with those of the other testing procedures. For completeness, however, they are presented in tables containing the simulation results. With increasing sample sizes, the empirical powers of the tests generally increase. Usually the LHp tests are more powerful than the Wp tests, which outperform the Pp ones. The permutation version of the LHp (resp. Wp or Pp) test has generally slightly smaller (resp. greater) empirical powers than the standard one. In terms of power, the permutation Rp testing procedure behaves similarly to the permutation Wp and LHp tests.

We also observe that the tests based on random projections using Brownian motion have higher (resp. lower) empirical powers than those using Gaussian white noise when the functional data are less (resp. highly) correlated, i.e., $\rho =0.7,0.9$ (resp. $\rho =0.1,0.3$). For moderately correlated functional data ($\rho =0.5$), both methods of generating Gaussian processes behave very similarly.

Table 1 Empirical sizes ($\delta =0$) and powers ($\delta \ne 0$), as percentages, of the tests based on $k=30$ random projections obtained under FMANOVA model and Gaussian distribution versus different methods of generating Gaussian processes (GAUSS and BM)

5.2 Simulation for FANOVA tests

The comparison of the GPF, Fmaxb tests and the tests based on random projections with two methods of generating Gaussian processes is made by generating three discrete functional samples by using the model $x_{rs}(t)=\eta _r(t)+v_{rs}(t)$, $t\in [0,1]$, $r=1,2,3$, $s=1,\dots ,n_r$, where the sample sizes are as in FMANOVA model and subject-effect functions $v_{rs}(t)$ are defined in the analogous way as in that model. We consider $\eta _r(t)=\mathbf {c}_1^{\top }(1,t,t^2,t^3)^{\top }$ for $r=1,2$ and $\eta _3(t)=(\mathbf {c}_1+2\delta \mathbf {u})^{\top }(1,t,t^2,t^3)^{\top }$, where $\mathbf {c}_1$, $\delta$ and $\mathbf {u}$ are as in FMANOVA model. This model will be referred to as FANOVA model. The simulation results are given in Table 2 under Gaussian distribution and balanced design, while in Table 3 in the Supplementary Materials, all results are depicted.

The GPF and Fmaxb tests keep the pre-assigned type-I error rate quite well, but the first one may be slightly liberal. The empirical sizes of the tests based on random projections are generally much lower than the nominal significance level. The tests based on ANOVA F test statistic are usually more conservative than the other testing procedures based on random projections. Observe also that the tests based on random projections and using ATS and WTPS and Gaussian white noise may be slightly liberal for less correlated functional data.

Table 2 Empirical sizes ($\delta =0$) and powers ($\delta \ne 0$), as percentages, of the GPF and Fmaxb tests and the tests based on $k=30$ random projections with two methods of generating Gaussian processes (GAUSS and BM) obtained under FANOVA model and Gaussian distribution

The conclusions about the empirical power of the tests based on random projections under two different methods of generating Gaussian processes are the same as in the multivariate case (see the last paragraph of Sect. 5.1). For very highly correlated functional data ($\rho =0.1$), the tests based on random projections using Gaussian white noise are the most powerful. When the functional data are a little less highly or moderately correlated ($\rho =0.3,0.5$), in terms of power, the best testing procedure is the Fmaxb method. Finally, for less correlated functional data ($\rho =0.7,0.9$), the GPF test and the tests based on random projections using Brownian motion outperform the remaining ones. Thus, there is not one method, which performs best, and the performance of the tests depends on the amount of correlation in functional data.

The tests based on random projections using different ANOVA methods do not perform equally well. It turns out that the tests based on random projections using ANOVA F test statistic and ATS have the highest power for normally distributed data, performing slightly better than those based on WTPS. The reason for this is that these testing procedures are constructed under normality assumption, while the WTPS one is not. The situation changes in case of t-distribution. There the tests based on random projections using WTPS are usually the best ones.

6 Conclusions and future work

Functional data analysis offers tools for solving statistical problems for high-dimensional data considered as curves or functions. An R package fdANOVA implements a broad range of the analysis of variance testing procedures for univariate and multivariate functional data. The implemented tests are usually very different solutions to the FANOVA and FMANOVA problems. Since their performance may depend on specifics of the functional observations, the package gives the opportunity to choose the most appropriate test for specific real data. The article presents the empirical evaluation of size control and power of some tests that were not compared elsewhere, which, together with previous simulation results (see, for example, Górecki and Smaga 2015, 2017a), may help in choosing appropriate procedures in practice. All the time-consuming parts of the package are parallelized, which makes it relatively fast, given that most of the testing procedures are based on permutation, projection and resampling methods.

When the testing procedures implemented in the fdANOVA package reject the null hypothesis about equality of group mean functions, it would be of interest to check which mean functions are significantly different and which are not. So, further developments of the package will include the implementation of post hoc and constrast analysis for functional data. Such testing procedures are considered, for instance, by Zhang (2013), who proposed the $L^2$-norm-based and F-type tests.