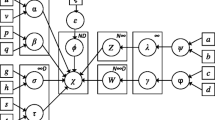
Appendix
Chinese Restaurant Process
In this section we recall the derivation of a Chinese Restaurant Process. Such a process will be used as the prior over cluster assignments in the model. This prior will then be updated through the likelihoods of the observations through the different views.
Imagine that every user u belongs to one of K clusters. \(z_u\) is the cluster of user u and \({\mathbf {z}}\) is a vector that indicates the cluster of every user. Let us assume that \(z_u\) is a random variable drawn from a multimomial distribution with probabilities \(\varvec{\pi }= (\pi _1,\ldots ,\pi _K)\). Let us also assume that the vector \(\varvec{\pi }\) is a random variable drawn from a Dirichlet distribution with a symmetric concentration parameter \(\varvec{\alpha } = (\alpha /K,\ldots ,\alpha /K)\). We have:
$$\begin{aligned} z_u | \varvec{\pi }&\sim \text {Multinomial}(\varvec{\pi })\nonumber \\ \varvec{\pi }&\sim \text {Dirichlet}(\varvec{\alpha }) \end{aligned}$$
The marginal probability of the set of cluster assignments \({\mathbf {z}}\) is:
$$\begin{aligned} p({\mathbf {z}}) =&\int \prod _{u=1}^U p(z_u | \varvec{\pi })p(\varvec{\pi } | \varvec{\alpha }) \text {d}\varvec{\pi }\\ =&\int \prod _{i=1}^K \pi _i^{n_i} \frac{1}{B(\varvec{\alpha })} \prod _{j=1}^K \pi _j^{\alpha /K-1} \text {d}\varvec{\pi }\\ =&\frac{1}{B(\varvec{\alpha })} \int \prod _{i=1}^K \pi _i^{\alpha /K + n_i - 1} \text {d}\varvec{\pi } \end{aligned}$$
where \(n_i\) is the number of users in cluster i and B denotes the Beta function. Noticing that the integrated factor is a Dirichlet distribution with concentration parameter \(\varvec{\alpha } + {\mathbf {n}}\) but without its normalizing factor:
$$\begin{aligned} p({\mathbf {z}})&= \frac{ B(\varvec{\alpha } + {\mathbf {n}}) }{B(\varvec{\alpha }) } \int \frac{1}{ B(\varvec{\alpha + {\mathbf {n}}}) } \prod _{i=1}^K \pi _i^{\alpha /K + n_i - 1} \text {d}\varvec{\pi }\\&= \frac{ B(\varvec{\alpha } + {\mathbf {n}}) }{ B(\varvec{\alpha }) } \end{aligned}$$
which expanding the definition of the Beta function becomes:
$$\begin{aligned} p({\mathbf {z}})= \frac{ \prod _{i=1}^K {\varGamma }(\alpha /K + n_i) }{{\varGamma } \left( \sum _{i=1}^K \alpha /K + n_i \right) } \frac{ {\varGamma } \left( \sum _{i=1}^K \alpha /K \right) }{ \prod _{i=1}^K {\varGamma }(\alpha /K) } = \frac{ \prod _{i=1}^K {\varGamma }(\alpha /K + n_i) }{{\varGamma } \left( \alpha + U \right) } \frac{ {\varGamma } \left( \alpha \right) }{ \prod _{i=1}^K {\varGamma }(\alpha /K) } \end{aligned}$$
(35)
where \(U=\sum _{i=1}^{K}n_i\). Note that marginalizing out \(\varvec{\pi }\) we introduce dependencies between the individual clusters assignments under the form of the counts \(n_i\). The conditional distribution of an individual assignment given the others is:
$$\begin{aligned} p(z_u = j| \mathbf {z_{-u}}) = \frac{p({\mathbf {z}})}{p({\mathbf {z}}_{-u})} \end{aligned}$$
(36)
To compute the denominator we assume cluster assignments are exchangeable, that is, the joint distribution \(p({\mathbf {z}})\) is the same regardless the order in which clusters are assigned. This allows us to assume that \(z_u\) is the last assignment, therefore obtaining \(p(\mathbf {z_{-u}})\) by considering how Eq. 35 before \(z_u\) was assigned to cluster j.
$$\begin{aligned} p({\mathbf {z}}_{-u}) =&\, \frac{ {\varGamma }(\alpha /K + n_j-1) \prod _{i\ne j} {\varGamma }(\alpha /K + n_i) }{{\varGamma } \left( \alpha + U -1 \right) } \frac{ {\varGamma } \left( \alpha \right) }{ \prod _{i=1} {\varGamma }(\alpha /K) } \end{aligned}$$
(37)
And finally plugging Eqs. 37 and 35 into Eq. 36, and cancelling out the factors that do not depend on the cluster assignment \(z_u\), and finally using the identity \(a {\varGamma }(a) = {\varGamma }(a+1)\) we get:
$$\begin{aligned} p(z_u = j| {\mathbf {z}}_{-u})&= \frac{\alpha /K + n_j-1}{\alpha + U -1} = \frac{\alpha /K + n_{-j}}{\alpha + U -1} \end{aligned}$$
where \(n_{-j}\) is the number of users in cluster j before the assignment of \(z_u\).
The Chinese Restaurant Process is the consequence of considering \(K \rightarrow \infty \). For clusters where \(n_{-j}>0\), we have:
$$\begin{aligned} p(z_u = j \text { s.t } n_{-j}>0 | {\mathbf {z}}_{-u})&= \frac{n_{-j}}{\alpha + U -1} \end{aligned}$$
and the probability of assigning \(z_u\) to any of the (infinite) empty clusters is:
$$\begin{aligned} p(z_u = j \text { s.t } n_{-j}=0 | \mathbf {z_{-u}}) =\;&\lim _{K\rightarrow \infty } (K - p)\frac{\alpha /K}{\alpha + U -1} = \frac{\alpha }{\alpha + U -1} \end{aligned}$$
where p is the number of non-empty components. It can be shown that the generative process composed of a Chinese Restaurant Process were every component j is associated to a probability distribution with parameters \(\varvec{\theta }_j\) is equivalent to a Dirichlet Process.
Conditionals for the feature view
In this appendix we provide the conditional distributions for the feature view to be plugged into the Gibbs sampler. Note that, except for \(\beta _{0}^\text {(a)}\), conjugacy can be exploited in every case and therefore their derivations are straightforward and well known. The derivation for \(\beta _{0}^\text {(a)}\) is left for another section:
1.1 Component parameters
1.1.1 Components means \(p(\varvec{\mu }_{k}^\text {(a)}| \cdot )\):
$$\begin{aligned} p(\varvec{\mu }_{k}^\text {(a)}| \cdot )&\propto p\left( \varvec{\mu }_{k}^\text {(a)}| \varvec{\mu }_{0}^\text {(a)}, \left( {\mathbf {R}}_{0}^\text {(a)}\right) ^{-1}\right) \prod _{u \in k} p\left( {\mathbf {a}}_u | \varvec{\mu }_{k}^\text {(a)}, {\mathbf {S}}_{k}^\text {(a)}, {\mathbf {z}}\right) \\&\propto {\mathcal {N}}\left( \varvec{\mu }_{k}^\text {(a)}| \varvec{\mu }_{0}^\text {(a)}, \left( {\mathbf {R}}_{0}^\text {(a)}\right) ^{-1}\right) \prod _{u \in k} {\mathcal {N}}\left( {\mathbf {a}}_u | \varvec{\mu }_{k}^\text {(a)}, {\mathbf {S}}_{k}^\text {(a)}\right) \\&= {\mathcal {N}}(\varvec{\mu ', {\varLambda }'}) \end{aligned}$$
where:
$$\begin{aligned} \varvec{{\varLambda }'}&= {\mathbf {R}}_{0}^\text {(a)}+ n_k {\mathbf {S}}_{k}^\text {(a)}\\ \varvec{\mu '}&= \varvec{{\varLambda }'^{-1}} \left( {\mathbf {R}}_{0}^\text {(a)}\varvec{\mu }_{0}^\text {(a)}+ {\mathbf {S}}_{k}^\text {(a)}\sum _{u\in k} {\mathbf {a}}_u\right) \end{aligned}$$
1.1.2 Components precisions \(p({\mathbf {S}}_{k}^\text {(a)}| \cdot )\):
$$\begin{aligned} p({\mathbf {S}}_{k}^\text {(a)}| \cdot ) \propto \;&p\left( {\mathbf {S}}_{k}^\text {(a)}|\beta _{0}^\text {(a)}, {\mathbf {W}}_{0}^\text {(a)}\right) \prod _{u \in k} p\left( {\mathbf {a}}_u | \varvec{\mu }_{k}^\text {(a)}, {\mathbf {S}}_{k}^\text {(a)}, {\mathbf {z}}\right) \\ \propto \;&{\mathcal {W}}\left( {\mathbf {S}}_{k}^\text {(a)}|\beta _{0}^\text {(a)}, (\beta _{0}^\text {(a)}{\mathbf {W}}_{0}^\text {(a)})^{-1}\right) \prod _{u \in k} {\mathcal {N}}\left( {\mathbf {a}}_u | \varvec{\mu }_{k}^\text {(a)}, {\mathbf {S}}_{k}^\text {(a)}\right) \\ =\;&{\mathcal {W}}(\beta ', {\mathbf {W}}') \end{aligned}$$
where:
$$\begin{aligned} \beta '&= \beta _{0}^\text {(a)}+ n_k\\ {\mathbf {W}}'&= \left[ \beta _{0}^\text {(a)}{\mathbf {W}}_{0}^\text {(a)}+ \sum _{u \in k} ({\mathbf {a}}_u - \varvec{\mu }_{k}^\text {(a)})({\mathbf {a}}_u- \varvec{\mu }_{k}^\text {(a)})^T \right] ^{-1} \end{aligned}$$
1.2 Shared hyper-parameters
1.2.1 Shared base means \(p(\varvec{\mu }_{0}^\text {(a)}| \cdot )\):
$$\begin{aligned} p(\varvec{\mu }_{0}^\text {(a)}| \cdot )&\propto p\left( \varvec{\mu }_{0}^\text {(a)}| \varvec{\mu _a}, \varvec{{\varSigma }_a}\right) \prod _{k = 1}^K p\left( \varvec{\mu }_{k}^\text {(a)}| \varvec{\mu }_{0}^\text {(a)}, {\mathbf {R}}_{0}^\text {(a)}\right) \\&\propto {\mathcal {N}}\left( \varvec{\mu }_{0}^\text {(a)}| \varvec{\mu _a, {\varSigma }_a}\right) \prod _{k = 1}^K{\mathcal {N}}\left( \varvec{\mu }_{k}^\text {(a)}| \varvec{\mu }_{0}^\text {(a)}, \left( {\mathbf {R}}_{0}^\text {(a)}\right) ^{-1}\right) \\&={\mathcal {N}}\left( \varvec{\mu '}, \varvec{{\varLambda }'}^{-1}\right) \end{aligned}$$
where:
$$\begin{aligned} \varvec{{\varLambda }'}&= \varvec{{\varLambda }_{a}} + K {\mathbf {R}}_{0}^\text {(a)}\\ \varvec{\mu '}&= \varvec{{\varLambda }'}^{-1} \left( \varvec{{\varLambda }_{a}} \varvec{\mu _{a}} + K {\mathbf {R}}_{0}^\text {(a)}{\overline{\varvec{\mu }_{k}^\text {(a)}}}\right) \end{aligned}$$
1.2.2 Shared base precisions \(p({\mathbf {R}}_{0}^\text {(a)}| \cdot )\):
$$\begin{aligned} p({\mathbf {R}}_{0}^\text {(a)}| \cdot ) \propto \;&p\left( {\mathbf {R}}_{0}^\text {(a)}| D, \varvec{{\varSigma }_a^{-1}}\right) \prod _{k = 1}^K p\left( \varvec{\mu }_{k}^\text {(a)}| \varvec{\mu }_{0}^\text {(a)}, {\mathbf {R}}_{0}^\text {(a)}\right) \\ \propto \;&{\mathcal {W}}\left( {\mathbf {R}}_{0}^\text {(a)}| D, (D\varvec{{\varSigma }_a})^{-1}\right) \prod _{k = 1}^K {\mathcal {N}}\left( \varvec{\mu }_{k}^\text {(a)}| \varvec{\mu }_{0}^\text {(a)}, \left( {\mathbf {R}}_{0}^\text {(a)}\right) ^{-1}\right) \\ =\;&{\mathcal {W}}(\upsilon ', \varvec{{\varPsi }}') \end{aligned}$$
where:
$$\begin{aligned} \upsilon '&= D+K\\ \varvec{{\varPsi }'}&= \left[ D\varvec{{\varSigma }_a} + \sum _k \left( \varvec{\mu }_{k}^\text {(a)}- \varvec{\mu }_{0}^\text {(a)}\right) \left( \varvec{\mu }_{k}^\text {(a)}- \varvec{\mu }_{0}^\text {(a)}\right) ^T \right] ^{-1} \end{aligned}$$
1.2.3 Shared base covariances \(p({\mathbf {W}}_{0}^\text {(a)}| \cdot )\):
$$\begin{aligned} p({\mathbf {W}}_{0}^\text {(a)}| \cdot ) \propto \;&p\left( {\mathbf {W}}_{0}^\text {(a)}| D, \frac{1}{D} \varvec{{\varSigma }_a}\right) \prod _{k=1}^K p\left( {\mathbf {S}}_{k}^\text {(a)}| \beta _{0}^\text {(a)}, \left( {\mathbf {W}}_{0}^{\text {(a)}}\right) ^{-1}\right) \\ \propto \;&{\mathcal {W}}\left( {\mathbf {W}}_{0}^\text {(a)}| D, \frac{1}{D} \varvec{{\varSigma }_a}\right) \prod _{k=1}^K {\mathcal {W}}\left( {\mathbf {S}}_{k}^\text {(a)}| \beta _{0}^\text {(a)}, \left( \beta _{0}^\text {(a)}{\mathbf {W}}_{0}^\text {(a)}\right) ^{-1}\right) \\ =\;&{\mathcal {W}}(\upsilon ', \varvec{{\varPsi }}') \end{aligned}$$
where:
$$\begin{aligned} \upsilon '&=D + K\beta _{0}^\text {(a)}\\ \varvec{{\varPsi }}'&= \left[ D\varvec{{\varSigma }_a}^{-1} + \beta _{0}^\text {(a)}\sum _{k=1}^K{\mathbf {S}}_{k}^\text {(a)}\right] ^{-1} \end{aligned}$$
1.2.4 Shared base degrees of freedom \(p(\beta _{0}^\text {(a)}| \cdot )\):
$$\begin{aligned} p\left( \beta _{0}^\text {(a)}| \cdot \right)&\propto p\left( \beta _{0}^\text {(a)}\right) \prod _{k=1}^K p\left( {\mathbf {S}}_{k}^\text {(a)}| {\mathbf {W}}_{0}^\text {(a)}, \beta _{0}^\text {(a)}\right) \\&=p\left( \beta _{0}^\text {(a)}| 1, \frac{1}{D}\right) \prod _{k=1}^K {\mathcal {W}} \left( {\mathbf {S}}_{k}^\text {(a)}| {\mathbf {W}}_{0}^\text {(a)}, \beta _{0}^\text {(a)}\right) \end{aligned}$$
where there is no conjugacy we can exploit. We may sample from this distribution with Adaptive Rejection Sampling.
Conditionals for the behavior view
In this appendix we provide the conditional distributions for the behavior view to be plugged into the Gibbs sampler. Except for \(\beta _{b_0}\), conjugacy can be exploited in every case and therefore their derivations straightforward and well known. The derivation for \(\beta _{b_0}\) is left for another section:
1.1 Users parameters
1.1.1 Users latent coefficient \(p(b_u | \cdot )\):
Let \({\mathbf {Z}}\) be a \(K\times U\) a binary matrix where \({\mathbf {Z}}_{k,u}=1\) denotes whether user u is assigned to cluster k. Let \(\mathbf {I_{[T]}}\) and \(\mathbf {I_{[U]}}\) identity matrices of sizes T and U, respectively. Let \(\varvec{\mu }^\text {(f)} = (\mu _1^{\text {(f)}},\ldots ,\mu _K^{\text {(f)}})\) and \({\mathbf {s}}^\text {(f)} = (s_1^{\text {(f)}},\ldots ,s_K^{\text {(f)}})\) Then:
$$\begin{aligned} p\left( {\mathbf {b}} | \cdot \right) \propto&\; p\left( {\mathbf {b}} | \varvec{\mu }^\text {(f)}, {\mathbf {s}}^\text {(f)}, {\mathbf {Z}}\right) p\left( {\mathbf {y}} | \mathbf {P, b}\right) \\ \propto&\; {\mathcal {N}}\left( {\mathbf {b}} | {\mathbf {Z}}^T\varvec{\mu }^\text {(f)}, {\mathbf {Z}}^T {\mathbf {s}}^\text {(f)} \mathbf {I_{[U]}}\right) {\mathcal {N}}\left( {\mathbf {y}}|{\mathbf {P}}^T \mathbf {b, \sigma _y I_{[T]}}\right) \\ =&\; {\mathcal {N}}\left( \mathbf {\varvec{\mu '}, \varvec{{\varLambda }'}^{-1}}\right) \end{aligned}$$
where:
$$\begin{aligned} \mathbf {{\Lambda }'}&= {\mathbf {Z}}^T {\mathbf {s}}^\text {(f)} \mathbf {I_{[U]}} + {\mathbf {P}}\sigma _\mathbf{y }^{-2} {\mathbf {I}}_{[T]} {\mathbf {P}}^T \\ \varvec{\mu '}&= \mathbf {{\varLambda }'}^{-1}\left( {\mathbf {Z}}^T {\mathbf {s}}^\text {(f)} {\mathbf {Z}}^T\varvec{\mu }^\text {(f)}+ {\mathbf {P}} \sigma _\text {y}^{-2} \mathbf {I_{[T]} y}\right) \end{aligned}$$
1.2 Component parameters
1.2.1 Components means \(p(\mu _{k}^\text {(f)}| \cdot )\):
$$\begin{aligned} p\left( \mu _{k}^\text {(f)}| \cdot \right)&\propto p\left( \mu _{k}^\text {(f)}| \mu _{0}^\text {(f)}, \left( r_{0}^\text {(f)}\right) ^{-1}\right) \prod _{u \in k} p\left( b_u | \mu _{k}^\text {(f)}, s_{k}^\text {(f)}, {\mathbf {z}}\right) \\&\propto {\mathcal {N}}\left( \mu _{k}^\text {(f)}| \mu _{0}^\text {(f)}, \left( r_{0}^\text {(f)}\right) ^{-1}\right) \prod _{u \in k} {\mathcal {N}}\left( b_u | \mu _{k}^\text {(f)}, s_{k}^\text {(f)}\right) \\&={\mathcal {N}}\left( \varvec{\mu '}, \varvec{{\varLambda }'}^{-1}\right) \end{aligned}$$
where:
$$\begin{aligned} \varvec{{\varLambda }'}&= r_{0}^\text {(f)}+ n_k s_{k}^\text {(f)}\\ \varvec{\mu '}&= \varvec{{\varLambda }'^{-1}} \left( r_{0}^\text {(f)}\mu _{0}^\text {(f)}+ s_{k}^\text {(f)}\sum _{u\in k} b_u\right) \end{aligned}$$
1.2.2 Components precisions \(p(s_{k}^\text {(f)}| \cdot )\):
$$\begin{aligned} p\left( s_{k}^\text {(f)}| \cdot \right)&\propto p\left( s_{k}^\text {(f)}|\beta _{0}^\text {(f)}, w_{0}^\text {(f)}\right) \prod _{u \in k} p\left( b_u | \mu _{k}^\text {(f)}, s_{k}^\text {(f)}, {\mathbf {z}}\right) \\&\propto {\mathcal {G}}\left( s_{k}^\text {(f)}|\beta _{0}^\text {(f)}, \left( \beta _{0}^\text {(f)}w_{0}^\text {(f)}\right) ^{-1}\right) \prod _{u \in k} {\mathcal {N}}\left( b_u | \mu _{k}^\text {(f)}, s_{k}^\text {(f)}\right) \\&= {\mathcal {G}}\left( \upsilon ', \psi '\right) \end{aligned}$$
where:
$$\begin{aligned} \upsilon '&= \beta _{0}^\text {(f)}+ n_k\\ \psi '&= \left[ \beta _{0}^\text {(f)}w_{0}^\text {(f)}+ \sum _{u \in k} \left( b_u - \mu _{k}^\text {(f)}\right) ^2 \right] ^{-1} \end{aligned}$$
1.3 Shared hyper-parameters
1.3.1 Shared base mean \(p(\mu _{0}^\text {(f)}| \cdot )\):
$$\begin{aligned} p\left( \mu _{0}^\text {(f)}| \cdot \right)&\propto p\left( \mu _{0}^\text {(f)}| \mu _{{\hat{b}}}, \sigma _{{\hat{b}}}\right) \prod _{k = 1}^K p\left( \mu _{k}^\text {(f)}| \mu _{0}^\text {(f)}, r_{0}^\text {(f)}\right) \\&\propto {\mathcal {N}}\left( \mu _{0}^\text {(f)}| \mu _{{\hat{b}}}, \sigma _{{\hat{b}}}\right) \prod _{k = 1}^K{\mathcal {N}}\left( \mu _{k}^\text {(f)}| \mu _{0}^\text {(f)}, \left( r_{0}^\text {(f)}\right) ^{-1}\right) \\&= {\mathcal {N}}\left( \mu ', \sigma '^{-2}\right) \end{aligned}$$
where:
$$\begin{aligned} \sigma '^{-2}&= \sigma _{{\hat{b}}}^{-2} + K r_{0}^\text {(f)}\\ \mu '&= \sigma _{{\hat{b}}}^{2'} \left( \sigma _{{\hat{b}}}^{-2} \mu _{{\hat{b}}} + K r_{0}^\text {(f)}{\overline{\mu _{k}^\text {(f)}}}\right) \end{aligned}$$
1.3.2 Shared base precision \(p(r_{0}^\text {(f)}| \cdot )\)
$$\begin{aligned} p\left( r_{0}^\text {(f)}| \cdot \right)&\propto p\left( r_{0}^\text {(f)}| 1, \sigma _{{\hat{b}}}^{-2}\right) \prod _{k = 1}^K p\left( \mu _{k}^\text {(f)}| \mu _{0}^\text {(f)}, r_{0}^\text {(f)}\right) \\&\propto {\mathcal {G}}\left( r_{0}^\text {(f)}| 1, \sigma _{{\hat{b}}}^{-2}\right) \prod _{k = 1}^K {\mathcal {N}}\left( \mu _{k}^\text {(f)}| \mu _{0}^\text {(f)}, \left( r_{0}^\text {(f)}\right) ^{-1}\right) \\&= {\mathcal {G}}\left( \upsilon ', \psi '\right) \end{aligned}$$
where:
$$\begin{aligned} \upsilon ' =&1+K\\ \psi ' =&\left[ \sigma _{{\hat{b}}}^{-2} + \sum _{k=1}^K \left( \mu _{k}^\text {(f)}- \mu _{0}^\text {(f)}\right) ^2\right] ^{-1} \end{aligned}$$
1.3.3 Shared base variance \(p(w_{0}^\text {(f)}| \cdot )\):
$$\begin{aligned} p(w_{0}^\text {(f)}| \cdot )&\propto p(w_{0}^\text {(f)}| 1, \sigma _{{\hat{b}}}) \prod _{r=1}^K p\left( s_{k}^\text {(f)}| \beta _{0}^\text {(f)}, w_{0}^\text {(f)}\right) \\&\propto {\mathcal {G}}(w_{0}^\text {(f)}| 1, \sigma _{{\hat{b}}}) \prod _{k=1}^K {\mathcal {G}}\left( s_{k}^\text {(f)}| \beta _{0}^\text {(f)}, \left( \beta w_{0}^\text {(f)}\right) ^{-1}\right) \\&= {\mathcal {G}}(\upsilon ', \psi ')\\ \upsilon '&= 1 + K\beta _{0}^\text {(f)}\\ \psi '&= \left[ \sigma _{{\hat{b}}}^{-2} + \beta _{0}^\text {(f)}\sum _{k=1}^K s_{k}^\text {(f)}\right] ^{-1} \end{aligned}$$
1.3.4 Shared base degrees of freedom \(p(\beta _{0}^\text {(f)}| \cdot )\):
$$\begin{aligned} p\left( \beta _{0}^\text {(f)}| \cdot \right)&\propto p\left( \beta _{0}^\text {(f)}\right) \prod _{r=1}^K p\left( s_{k}^\text {(f)}| w_{0}^\text {(f)}, \beta _{0}^\text {(f)}\right) \\&=p\left( \beta _{0}^\text {(f)}| 1, 1\right) \prod _{r=1}^K {\mathcal {G}} \left( s_{k}^\text {(f)}|\beta _{0}^\text {(f)}, \left( \beta _{0}^\text {(f)}w_{0}^\text {(f)}\right) ^{-1}\right) \end{aligned}$$
where there is no conjugacy we can exploit. We will sample from this distribution with Adaptive Rejection Sampling.
1.4 Regression noise
Let the precision \(s_{\text {y}}\) be the inverse of the variance \(\sigma _{\text {y}}^{2}\). Then:
$$\begin{aligned} p\left( s_{\text {y}} | \cdot \right)&\propto p\left( s_{\text {y}} | 1,\sigma _{0}^{-2}\right) \prod _{t=1}^T p\left( y_t | \mathbf {p^T b}, s_{\text {y}}\right) \\&\propto {\mathcal {G}}\left( s_{\text {y}} | 1,\sigma _{\text {0}}^{-2}\right) \prod _{t=1}^T {\mathcal {N}}\left( y_t | \mathbf {p^T b}, s_{\text {y}}\right) \\&= {\mathcal {G}}\left( \upsilon ', \psi '\right) \\ \upsilon '&= 1+T\\ \psi '&= \left[ \sigma _{\text {0}}^{2} + \sum _{t=1}^{T}\left( y_t-\mathbf {p^Tb}\right) ^2\right] ^{-1} \end{aligned}$$
Sampling \(\beta _{0}^\text {(a)}\)
For the feature view, if:
$$\begin{aligned} \frac{1}{\beta - D + 1} \sim {\mathcal {G}}\left( 1, \frac{1}{D}\right) \end{aligned}$$
we can get the prior distribution of \(\beta \) by variable transformation:
$$\begin{aligned} p(\beta ) =\;&{\mathcal {G}}\left( \frac{1}{\beta -D+1}\right) \left| \frac{\partial }{\partial \beta }\frac{1}{\beta -D+1}\right| \\&\propto \left( \frac{1}{\beta -D+1}\right) ^{-1/2} \exp \left( -\frac{D}{2(\beta -D+1)}\right) \frac{1}{(\beta -D+1)^2}\\&\propto \left( \frac{1}{\beta -D+1}\right) ^{3/2} \exp \left( -\frac{D}{2(\beta -D+1)}\right) \end{aligned}$$
Then:
$$\begin{aligned} p(\beta )&\propto (\beta - D + 1)^{-3/2} \exp \left( -\frac{D}{2(\beta - D +1)}\right) \end{aligned}$$
The Wishart likelihood is:
$$\begin{aligned} {\mathcal {W}}\left( {\mathbf {S}}_k | \beta , \left( \beta {\mathbf {W}}\right) ^{-1}\right)= & {} \frac{\left( |{\mathbf {W}}| \left( \beta /2\right) ^D\right) ^{\beta /2}}{{\varGamma }_D\left( \beta /2\right) } |{\mathbf {S}}_k|^{\left( \beta -D-1\right) /2} \exp \left( - \frac{\beta }{2}\text {Tr}\left( {\mathbf {S}}_k{\mathbf {W}}\right) \right) \\= & {} \frac{\left( |{\mathbf {W}}| \left( \beta /2\right) ^D\right) ^{\beta /2}}{\prod _{d=1}^{D} {\varGamma }\left( \frac{\beta +d-D}{2}\right) } |{\mathbf {S}}_k|^{\left( \beta -D-1\right) /2} \exp \left( - \frac{\beta }{2}\text {Tr}\left( {\mathbf {S}}_k{\mathbf {W}}\right) \right) \end{aligned}$$
We multiply both equations, the Wishart likelihood (its K factors) and the prior, to get the posterior:
$$\begin{aligned} p\left( \beta | \cdot \right)&= \left( \prod _{d=0}^D {\varGamma } \left( \frac{\beta }{2} + \frac{d-D}{2}\right) \right) ^{-K} \exp \left( -\frac{D}{2\left( \beta -D+1\right) } \right) \left( \beta -D+1\right) ^{-3/2} \\&\quad \,\times \left( \frac{\beta }{2}\right) ^{\frac{KD\beta }{2}} \prod _{k=1}^K \left( |{\mathbf {S}}_k||{\mathbf {W}}|\right) ^{\beta /2} \exp \left( -\frac{\beta }{2} \text {Tr}\left( {\mathbf {S}}_k{\mathbf {W}}\right) \right) \end{aligned}$$
Then if \(y = \ln \beta \):
$$\begin{aligned} p\left( y | \cdot \right)&= e^y \left( \prod _{d=0}^D {\varGamma } \left( \frac{e^y}{2} + \frac{d-D}{2}\right) \right) ^{-K} \exp \left( -\frac{D}{2\left( e^y-D+1\right) } \right) \left( e^y-D+1\right) ^{-3/2} \\&\quad \,\times \left( \frac{e^y}{2}\right) ^{\frac{KDe^y}{2}} \prod _{k=1}^K \left( |{\mathbf {S}}_k||{\mathbf {W}}|\right) ^{e^y/2} \exp \left( -\frac{e^y}{2} \text {Tr}\left( {\mathbf {S}}_k{\mathbf {W}}\right) \right) \end{aligned}$$
and its logarithm is:
$$\begin{aligned} \ln p\left( y | \cdot \right)&= y -K \sum _{d=0}^D \ln {\varGamma } \left( \frac{e^y}{2} + \frac{d-D}{2}\right) -\frac{D}{2\left( e^y-D+1\right) } -\frac{3}{2}\ln \left( e^y-D+1\right) \\&\quad +\frac{KDe^y}{2}\left( y - \ln 2\right) +\frac{e^y}{2} \sum _{k=1}^K \left( \ln \left( |{\mathbf {S}}_k||{\mathbf {W}}|\right) - \text {Tr}\left( {\mathbf {S}}_k{\mathbf {W}}\right) \right) \end{aligned}$$
which is a concave function and therefore we can use Adaptive Rejection Sampling (ARS). ARS sampling works with the derivative of the log function:
$$\begin{aligned} \frac{\partial }{\partial y} \ln p\left( y | \cdot \right)&= 1-K \frac{e^y}{2} \sum _{d=1}^D {\varPsi } \left( \frac{e^y}{2} + \frac{d-D}{2}\right) +\frac{De^y}{2\left( e^y-D+1\right) ^2} -\frac{3}{2}\frac{e^y}{e^y-D+1} \\&\quad \, +\frac{KDe^y}{2}\left( y - \ln 2\right) + \frac{KDe^y}{2} +\frac{e^y}{2} \sum _{k=1}^K \left( \ln \left( |{\mathbf {S}}_k||{\mathbf {W}}|\right) - \text {Tr}\left( {\mathbf {S}}_k{\mathbf {W}}\right) \right) \end{aligned}$$
where \({\varPsi }(x)\) is the digamma function.
Sampling \(\beta _{0}^\text {(f)}\)
For the behavior view, if
$$\begin{aligned} \frac{1}{\beta } \sim {\mathcal {G}}(1,1) \end{aligned}$$
the posterior of \(\beta \) is:
$$\begin{aligned} p(\beta | \cdot ) =&\, {\varGamma }\left( \frac{\beta }{2}\right) ^{-K}\exp \left( \frac{-1}{2\beta }\right) \left( \frac{\beta }{2}\right) ^{\left( K \beta -3\right) /2} \prod _{k=1}^{K} \left( s_k w\right) ^{\beta /2} \exp \left( -\frac{\beta s_k w}{2}\right) \end{aligned}$$
Then if \(y=\ln \beta \):
$$\begin{aligned} p\left( y | \cdot \right) =&\, e^y {\varGamma }\left( \frac{e^y}{2}\right) ^{-K}\exp \left( \frac{-1}{2e^y}\right) \left( \frac{e^y}{2}\right) ^{\left( K e^y -3\right) /2} \prod _{k=1}^{K} \left( s_k w\right) ^{e^y/2} \exp \left( -\frac{e^y s_k w}{2}\right) \end{aligned}$$
and its logarithm:
$$\begin{aligned} \ln p\left( y | \cdot \right) =&\, y -K\ln {\varGamma } \left( \frac{e^y}{2}\right) + \left( \frac{-1}{2e^y}\right) +\frac{Ke^y-3}{2}\left( y - \ln 2\right) \\&+ \frac{e^y}{2}\sum _{k=1}^{K} \left( \ln \left( s_k w\right) - s_k w \right) \end{aligned}$$
which is a concave function and therefore we can use Adaptive Rejection Sampling. The derivative is:
$$\begin{aligned} \frac{\partial }{\partial y} \ln p\left( y | \cdot \right) =&1 -K {\varPsi } \left( \frac{e^y}{2}\right) \frac{e^y}{2} + \left( \frac{1}{2e^y}\right) +\frac{Ke^y}{2} \left( y - \ln 2\right) + \frac{Ke^y-3}{2} \\&+ \frac{e^y}{2}\sum _{k=1}^{K}\left( \ln \left( s_k w\right) - s_k w\right) \end{aligned}$$
where \({\varPsi }(x)\) is the digamma function.
Sampling \(\alpha \)
Since the inverse of the concentration parameter \(\alpha \) is given a Gamma prior
$$\begin{aligned} \frac{1}{\alpha } \sim {\mathcal {G}}(1,1) \end{aligned}$$
we can get the prior over \(\alpha \) by variable transformation:
$$\begin{aligned} p(\alpha ) \propto ~&\alpha ^{-3/2} \exp \left( -1/(2\alpha )\right) \end{aligned}$$
Multiplying the prior of \(\alpha \) by its likelihood we get the posterior:
$$\begin{aligned} p(\alpha | \cdot ) \propto ~&\alpha ^{-3/2} \exp \left( -1/(2\alpha )\right) \times \frac{{\varGamma }(\alpha )}{{\varGamma }(\alpha +U)} \prod _{j=1}^{K} \frac{{\varGamma }(n_j + \alpha /K)}{\alpha /K}\\ \propto ~&\alpha ^{-3/2} \exp \left( -1/(2\alpha )\right) \frac{{\varGamma }(\alpha )}{{\varGamma }(\alpha +U)}\alpha ^K \\ \propto ~&\alpha ^{K-3/2} \exp \left( -1/(2\alpha )\right) \frac{{\varGamma }(\alpha )}{{\varGamma }(\alpha +U)} \end{aligned}$$
Then if \(y=\ln \alpha \):
$$\begin{aligned} p(y | \cdot ) = e^{y(K-3/2)} \exp (-1/(2e^y)) \frac{{\varGamma }(e^y)}{{\varGamma }(e^y +U)} \end{aligned}$$
and its logarithm is:
$$\begin{aligned} \ln p(y | \cdot ) = y(K-3/2) -1/(2e^y)+ \ln {\varGamma }(e^y) - \ln {\varGamma }(e^y+U) \end{aligned}$$
which is a concave function and therefore we can use Adaptive Rejection Sampling. The derivative is:
$$\begin{aligned} \frac{\partial }{\partial y} \ln p(y | \cdot ) = (K-3/2) +1/(2e^y)+ e^y{\varPsi }(e^y) - e^y{\varPsi }(e^y+U) \end{aligned}$$