An interactive graphical method for community detection in network data

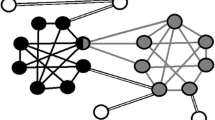
Abstract

The detection of community structures within network data is a type of graph analysis with increasing interest across a broad range of disciplines. In a network, communities represent clusters of nodes that exhibit strong intra-connections or relationships among nodes in the cluster. Current methodology for community detection often involves an algorithmic approach, and commonly partitions a graph into node clusters in an iterative manner before some stopping criterion is met. Other statistical approaches for community detection often require model choices and prior selection in Bayesian analyses, which are difficult without some amount of data inspection and pre-processing. Because communities are often fuzzily-defined human concepts, an alternative approach is to leverage human vision to identify communities. The work presents a tool for community detection in form of a web application, called gravicom, which facilitates the detection of community structures through visualization and direct user interaction. In the process of detecting communities, the gravicom application can serve as a standalone tool or as a step to potentially initialize (and/or post-process) another community detection algorithm. In this paper we discuss the design of gravicom and demonstrate its use for community detection with several network data sets. An “Appendix” describes details in the technical formulation of this web application built on the R package Shiny and the JavaScript library D3.

Technical appendix

gravicom utilizes three main pieces of software to establish interactive user control of a random graph as sketched out in Fig. 15, which are Shiny, D3, and igraph. These are used, respectively, for server/client interaction management, user interface and graph layout, and data formatting, respectively. In the following subsections, we describe the purposes of these three components in more detail.

Fig. 15

Relationship between client and server, specifically focusing on how data travels between the two

There are very minimal software requirements for a user of gravicom. The client simply needs to have a JavaScript enabled internet browser with HTML5 compatibility, something which almost any modern browser fulfills (an exception is IE8 and below).

The server side requirements are more extensive, but this does not affect the user of gravicom, only those wanting to host their own instance of the application. To host gravicom, a Linux server is required, with the following installed:

• Node.js (0.8.16 or later)

• R (2.15 or later)

• Shiny R package, installed into the machine-wide site library.

• Shiny Server

1.1 Shiny

Shiny RStudio Inc (2013) is an R package created by RStudio that enables R users to create an interactive web application that utilizes R as the background engine. Through default methods to build user interface elements in HTML and a handle to the server side code, Shiny is a simple way to turn R code into a website.

gravicom uses the Shiny functionality to create user controls, pass correctly formatted data to the client, and as a means to display summary information regarding the user’s interactions with a graph at any point in time. In this context, Shiny serves as the translator between the formatted data and what the user sees and interacts with on his screen.

1.2 D3

D3 Bostock et al. (2011) stands for “Data Driven Documents” and is a JavaScript library developed and maintained by Mike Bostock with the purpose of visualizing and interacting with data in a web-based interface. It is freely available from http://www.d3js.org. The library facilitates manipulation of HTML elements, SVG (scalable vector graphics), and CSS (cascading style sheets) with the end goal of rendering animations and providing user interactions that are tied to the underlying data. The key idea behind the library is that Document Object Model elements are completely determined by the data. The Document Object Model (DOM) is a convention for representing and interacting with objects in HTML, XHTML and XML. So, rather than adding elements to a web page to be viewed by users, D3 allows users to see and interact with graphical representations of their data in a web framework.

Fig. 16

Page lifecycle beginning from on load. User actions are highlighted in red, server actions in green, and actions completed on the client side are highlighted in blue (color figure online)

gravicom uses D3 to handle all graphical displays and user interactions with the graph. The data is passed to the client and able to be used through Shiny’s input bindings. It is crucial that the data has been formatted correctly at this point for the JavaScript to properly function. For this reason, we limit the file types being passed into the tool to a robust graph-specific type.

At this point in the page lifecycle, the graph nodes are tied to circles and the edges are tied to paths on the page. User manipulations such as selecting, dragging, and grouping are handled by D3 and data is passed back to the server via Shiny’s output bindings to allow for communication between user and the R engine underneath. This is illustrated in Fig. 16. What this means is that all visualization and user interaction with the graph are accomplished using JavaScript, more specifically the library D3. Shiny and R serve as the framework on which the data sits, but when the user touches the data they are doing so through the JavaScript elements.

1.3 igraph

igraph Csardi and Nepusz (2006) is a software package used for creating and manipulating undirected and directed graphs. It is a cross-language package available for C, R, python, and Ruby. igraph also supports multiple graph file formats and visualization of graph structures.

gravicom utilizes two parts of igraph, first is the conversion from a gml file to an XML file. The gml file format, short for Graph Modelling Language, is a hierarchical ASCII-based file format for describing graphs. Below is an example gml file of an undirected graph consisting of two nodes linked by a single edge. The important points to note are that node identifiers (id) have to be numeric. An edge consists only of source and target ids of the nodes it connects, while nodes can have other attributes, e.g. value in the example. For a directed graph, the parameter directed has to be set to 1, which will result in the edge information on target and source being evaluated accordingly.

For the conversion from an XML file to a JSON file we make user of the R package rjson Couture-Beil (2013). JSON is the native data format used in D3, which makes working with data in the D3 library incredibly straightforward. Here is our example in the finalized JSON format:

Our example data will yield the graph in Fig. 17.

Fig. 17

Graph created from sample gml file

The second use of igraph within gravicom is to compute initial x and y coordinates for the nodes of the graph using a force-driven layout. This provides the initialization for the force-layout algorithm in D3. This reduces the computational load on the clients’ side and helps minimize unnecessary movement by the nodes. This is critical as the extra movement at the loading of the pages creates an unnecessarily chaotic start to the user’s experience.