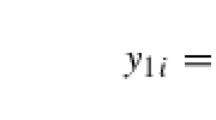Testing the hypothesis of absence of unobserved confounding in semiparametric bivariate probit models

Abstract

Lagrange multiplier and Wald tests for the hypothesis of absence of unobserved confounding are extended to the context of semiparametric recursive and sample selection bivariate probit models. The finite sample size properties of the tests are examined through a Monte Carlo study using several scenarios: correct model specification, distributional and functional misspecification, with and without an exclusion restriction. The simulation results provide some guidelines which may be important for empirical analysis. The tests are illustrated using two datasets in which the issue of unobserved confounding arises.

1 Introduction

We are concerned with testing the hypothesis of absence of unobserved confounding in the recursive and sample selection bivariate probit models (Heckman 1978, 1979; Maddala 1983; de Ven and Praag 1981; Greene 2012). Recursive bivariate probit models deal with a problem which arises in observational studies when confounders (i.e., variables that are associated with treatment and response) are unobserved; this issue is known in the econometric literature as endogeneity. These models control for unobserved confounders by using a two-equation structural latent variable framework, where one equation models a binary response as a function of a binary treatment and some covariates whereas the other determines whether the treatment is received based on some regressors. Recent economic and biostatistical applications of such models include the study of the effect of private health insurance on medical care utilization (Buchmueller et al. 2005), impact of diabetes on employment (Latif 2009), effect of physical activity on obesity (Kawatkar and Nichol 2009), and impact of insurance on mortality among HIV-infected individuals (Goldman et al. 2001).

Sample selection models address an issue which arises when observations are not from a random sample of the population. Instead, individuals may have selected themselves (or have been selected by others) into (or out of) the sample based on a combination of observed and unobserved characteristics. If the sample of selected individuals differs in important observed characteristics from the sample of unselected individuals, then selection bias can be avoided by controlling for these features. However, if the two samples differ in important unobserved characteristics then non-random sample selection arises. Sample selection bivariate probit models control for unobserved confounders by simultaneously estimating two regressions: a selection equation and a response equation. The former determines whether an individual is selected into the sample whereas the latter is used to examine the substantive question of interest. Applications of these models include the study of prevention program for high school dropouts (Montmarquette et al. 2001), quantification of the effect of family-related factors on foster approval (Cuddeback et al. 2004), estimation of HIV prevalence (Bärnighausen et al. 2011) and reject-inference to predict credit quality (Banasik and Crook 2007).

The classic recursive and sample selection bivariate probit models used for the applications mentioned above do not allow for flexible functional dependence of the responses on continuous covariates. To this end, Marra and Radice (2011, 2013a) introduced a penalized likelihood estimation framework to estimate simultaneously the parameters of a system of two binary equations that include smooth functions of continuous covariates. Alternative (Bayesian) approaches are available in the literature (e.g., Chib and Greenberg 2007; Chib et al. 2009). However the lack of user-friendly software makes them unfeasible for practitioners. The need for methods flexibly modeling covariate effects arises from the observation that all parameter estimates are inconsistent when the relationship between observed confounders and outcome is mismodeled (Marra and Radice 2011; Chib et al. 2009).

An important aspect of these binary bivariate models is that if the hypothesis of absence of unobserved confounding (i.e., exogeneity and random selection) can not be rejected then joint estimation of the model equations can be avoided. This is appealing because inference in simultaneous models with smooth components may become computationally demanding as the sample size and number of smooth terms increase. Therefore, before employing a complex simultaneous estimation approach, testing the hypothesis of absence of unobserved confounding is an important step that should be undertaken at the beginning of the empirical analysis. To this end, we extend Lagrange multiplier ($LM$) and, for comparison, Wald ($\mathcal {W}$) tests to the context of semiparametric bivariate probit models. $LM$ is particularly attractive as it is based on estimating the model equations separately. The finite sample size performance of the tests is investigated through a Monte Carlo simulation study that considers the scenarios of correct model specification, distributional and functional misspecification, with and without an exclusion restriction (ER). The simulation results allow us to infer some guidelines which may be crucial for applications. For instance, the good performance of $LM$ should be particularly attractive to practitioners wishing to test the null hypothesis of absence of unobserved confounding while avoiding simultaneous estimation. The tests are implemented in the R package SemiParBIVProbit (Marra and Radice 2013b).

The article is organized as follows. Section 2 provides a brief overview of the models of interest and their estimation; this is useful to define the notation and make some remarks that are relevant to the implementation of the tests. Section 3 discusses the construction of the $LM$ and $\mathcal {W}$ type tests in the context of semiparametric models, whereas Sect. 4 assesses their finite sample size performance through a Monte Carlo simulation study. Section 5 illustrates the tests using two datasets, and Sect. 6 provides a discussion. “Appendix 1” shows that, under the null hypothesis, the expected information matrix for the recursive bivariate probit model case is block diagonal, whereas “Appendix B” reports further simulation results.

2 Preliminaries

2.1 The models

The semiparametric recursive and sample selection bivariate probit models introduced by Marra and Radice (2011, 2013a) are a generalization of the parametric model versions introduced by Heckman (1978, 1979) in that continuous covariate effects are modeled flexibly.

The model structure consists of two equations. The first can be written as

$$\begin{aligned} y^*_{1i}=\mathbf m ^\mathsf{T}_{1i}\varvec{\theta }_{1} + \sum _{k_1=1}^{K_1} f_{1k_1}(z_{1k_1i}) + \varepsilon _{1i}, \quad i=1,\ldots n, \end{aligned}$$

(1)

where $n$ is the sample size, $y^*_{1i}$ is a latent continuous variable and $y_{1i}$ is determined via the rule $1(y^*_{1i}>0)$. The second can be defined as

$$\begin{aligned} y^*_{2i}=\vartheta y_{1i}+ \mathbf m ^\mathsf{T}_{2i}\varvec{\theta }_{2} + \sum _{k_2=1}^{K_2} f_{2k_2}(z_{2k_2i})+\varepsilon _{2i}, \end{aligned}$$

(2)

where, in the non-random sample selection case, $\vartheta$ is set to zero and $y_{2i}$ is determined as

$$ \begin{aligned} y_{2i}=\left\{ \begin{array}{l@{\quad }ll} 1 &{} \text {if} &{} \left( y^*_{2i}>0 \, \& \, y_{1i}=1\right) \\ 0 &{} \text {if} &{} \left( y^*_{2i}<0 \, \& \, y_{1i}=1\right) \\ - &{} \text {if} &{} y_{1i}=0 \\ \end{array} \right. , \end{aligned}$$

whereas, in the endogeneity case, $\vartheta$ is allowed to be different from zero and $y_{2i}$ is determined via the rule $1(y^*_{2i}>0)$. Vector $\mathbf m _{1i}$ contains $P_1$ parametric model components (such as the intercept, dummy and categorical variables), with corresponding parameter vector $\varvec{\theta }_1$, and the $f_{1k_1}$ are unknown smooth functions of the $K_1$ continuous covariates $z_{1k_1i}$. Each smooth term may also be multiplied by some predictor(s) (Hastie and Tibshirani 1993). Furthermore, smooth functions of two covariates such as $f_{11,12}(z_{11i},z_{12i})$ can be considered (e.g., Wood 2006). Similarly, $\mathbf m _{2i}$ is a vector containing $P_2$ parametric components, with coefficient vector $\varvec{\theta }_{2}$, and the other terms have the obvious definitions. Smooth functions are subject to constraints, i.e. $\sum _i f_{vk_v}(z_{vk_vi})=0, v=1,2$, for all smooth components in the model. The error terms are assumed to follow the distribution $\mathcal {N} ([0,0],[1,\rho ,\rho ,1])$, where $\rho$ is the correlation coefficient and the error variances are normalized to unity (e.g., Greene 2012, p. 686). To identify the parameters of Eq. (2) it is typically assumed that the ER on the exogenous variables holds. That is, the covariates in the first equation should contain at least one or more regressors (typically referred to as instruments) not included in the second equation. These regressors have to induce variation in $y_{1i}$, not to directly affect $y_{2i}$, and be independent of $(\varepsilon _{1i},\varepsilon _{2i})$ given covariates. However, under correct model specification, this restriction may not be necessary in estimation (Marra and Radice 2011; Wilde 2000).

The smooth functions are represented using regression splines (e.g., Eilers and Marx 1996). The basic idea is to approximate a generic function $f_k(z_{ki})$ by a linear combination of known spline basis functions, $b_{kj}(z_{ki})$, and regression parameters, $\beta _{kj}$, i.e. $\sum _{j=1}^{J_k} \beta _{kj} b_{kj}(z_{ki})= \mathbf B _{k}(z_{ki})^\mathsf{T}\varvec{\beta }_{k}$, where $J_k$ is the number of spline bases, $\mathbf B _{k}(z_{ki})=\left\{ b_{k1}(z_{ki}),\ldots ,b_{kJ_k}(z_{ki})\right\} ^\mathsf{T}$ is a vector of the basis functions evaluated at $z_{ki}$ and $\varvec{\beta }_{k}$ is the corresponding parameter vector. Note that subscript $v$ has been suppressed to avoid clutter. Basis functions have to be chosen to have convenient mathematical and numerical properties. Possible choices include B-splines, cubic regression and thin plate regression splines (see, e.g., Marra and Radice (2010) for an overview). Based on the result above, Eqs. (1) and (2) can be written as $y^*_{1i}=\mathbf m ^\mathsf{T}_{1i}\varvec{\theta }_{1} + \mathbf B _{1i}^\mathsf{T}\varvec{\beta }_{1} + \varepsilon _{1i}=\eta _{1i}+\varepsilon _{1i},$ and $y^*_{2i}=\vartheta y_{1i}+\mathbf m ^\mathsf{T}_{2i}\varvec{\theta }_{2} + \mathbf B _{2i}^\mathsf{T}\varvec{\beta }_{2} + \varepsilon _{2i}=\eta _{2i}+\varepsilon _{2i},$ where $\mathbf B _{vi}^\mathsf{T}=\left\{ \mathbf B _{v1}(z_{v1i})^\mathsf{T},\ldots ,\mathbf B _{vK_v}(z_{vK_vi})^\mathsf{T}\right\} , \varvec{\beta }_{v}^\mathsf{T}=(\varvec{\beta }_{v1}^\mathsf{T},\ldots ,\varvec{\beta }_{vK_v}^\mathsf{T})$ and $\eta _{1i}$ and $\eta _{2i}$ have the obvious definition.

2.2 Estimation

In the sample selection model the data identify only the three possible events $(y_{1i}=1,y_{2i}=1), (y_{1i}=1,y_{2i}=0)$ and $(y_{1i}=0)$ with probabilities $p_{11i}=\Phi _2(\eta _{1i},\eta _{2i};\rho ), p_{10i}=\Phi (\eta _{1i})-p_{11i}$ and $p_{0i} =\Phi (-\eta _{1i})$, where $\Phi$ and $\Phi _2$ are the distribution functions of a standardized univariate normal and a standardized bivariate normal with correlation $\rho$, respectively. Therefore, the log-likelihood function is

$$\begin{aligned} \ell (\varvec{\delta })=\sum _{i=1}^n\left\{ y_{1i}y_{2i}\log (p_{11i})+y_{1i}(1-y_{2i})\log (p_{10i})+(1-y_{1i})\log (p_{0i})\right\} ,\qquad \end{aligned}$$

(3)

where $\varvec{\delta }^\mathsf{T}=(\varvec{\delta }_1^\mathsf{T}, \varvec{\delta }_2^\mathsf{T}, \rho )$ and $\varvec{\delta }_{v}^\mathsf{T}=(\varvec{\theta }_{v}^\mathsf{T}, \varvec{\beta }_{v}^\mathsf{T})$, for $v=1,2$. In the recursive model $(y_{1i}=0)$ is replaced by $(y_{1i}=0,y_{2i}=1)$ and $(y_{1i}=0,y_{2i}=0)$ which have probabilities $p_{01i}=\Phi (\eta _{2i})-p_{11i}$ and $p_{00i}= 1 - p_{11i} - p_{10i} - p_{01i}$. Hence, in (3), $(1-y_{1i})\log (p_{0i})$ is replaced by $(1-y_{1i})y_{2i}\log (p_{01i}) + (1-y_{1i})(1-y_{2i})\log (p_{00i})$. To avoid overfitting, the model parameters are estimated by maximization of

$$\begin{aligned} \ell _p(\varvec{\delta })= \ell (\varvec{\delta }) -\frac{1}{2} \varvec{\beta }^\mathsf{T} \mathbf S _{\varvec{\lambda }} \varvec{\beta }, \end{aligned}$$

(4)

where $\varvec{\beta }^\mathsf{T}=(\varvec{\beta }_1^\mathsf{T},\varvec{\beta }_2^\mathsf{T}), \mathbf S _{\varvec{\lambda }}=\sum _{v=1}^{2} \sum _{k_v=1}^{K_v} \lambda _{vk_v} \mathbf S _{vk_v}$ and the $\mathbf S _{vk_v}$ are positive semi-definite known square matrices measuring the (second-order, typically) roughness of the smooth terms in the model, i.e. $\varvec{\beta }^\mathsf{T}\left( \sum _{v=1}^{2} \sum _{k_v=1}^{K_v} \lambda _{vk_v} \mathbf S _{vk_v}\right) \varvec{\beta }=\sum _{v=1}^{2} \sum _{k_v=1}^{K_v} \lambda _{vk_v} \int f_{vk_v}''(z_{vk_v})^2 d z_{vk_v}$. The $\lambda _{vk_v}$ are smoothing parameters controlling the trade-off between fit and smoothness. Because $\rho$ is bounded in $[-1, 1], \rho ^*=\tanh ^{-1}(\rho ) = (1/2) \log \left\{ \left( 1+\rho \right) \!/\!\left( 1-\rho \right) \right\}$ is used in optimization.

Estimation of $\varvec{\delta }$ and $\varvec{\lambda }=(\lambda _{1k_1},\ldots ,\lambda _{1K_1},\lambda _{2k_2},\ldots ,\lambda _{2K_2})$ is carried out in two steps. In particular, given a parameter vector value for $\varvec{\lambda }$, (4) is maximized using a trust region algorithm (Nocedal and Wright 2006) which is based on

$$\begin{aligned} \varvec{\delta }^{[a+1]}=\varvec{\delta }^{[a]}+ (\varvec{\mathcal {I}}^{[a]}+\tilde{\mathbf{S }}_{\varvec{\lambda }})^{-1} (\mathbf g ^{[a]}-\tilde{\mathbf{S }}_{\varvec{\lambda }}\varvec{\delta }^{[a]}), \end{aligned}$$

(5)

where $a$ is the iteration index and $\tilde{\mathbf{S }}_{\varvec{\lambda }}$ is defined as $\tilde{\mathbf{S }}_{\varvec{\lambda }}=\mathop {\mathrm {diag}}(0_{11},\ldots ,0_{1P_1},\lambda _{1k_1} \mathbf S _{1k_1}, \ldots ,\lambda _{1K_1} \mathbf S _{1K_1},0_{21},\ldots ,0_{2P_2},\lambda _{2k_2} \mathbf S _{2k_2},\ldots ,\lambda _{2K_2} \mathbf S _{2K_2},0)$. The gradient vector $\mathbf g$ is given by $\mathbf g _1=\partial \ell (\varvec{\delta })/\partial \varvec{\delta }_1, \mathbf g _2=\partial \ell (\varvec{\delta }) /\partial \varvec{\delta }_2$ and $g_3^*=\partial \ell (\varvec{\delta }) /\partial \rho ^*$, while the expected information matrix has a $3 \times 3$ matrix block structure with $(r,h)$th element $\varvec{\mathcal {I}}_{r,h}=-\mathbb {E}\left[ \partial ^2 \ell (\varvec{\delta })/\partial \varvec{\delta }_r \partial \varvec{\delta }_h^\mathsf{T}\right] , \ r,h=1,\ldots ,3,$ where $\varvec{\delta }_3=\rho ^*$. Given an estimate for $\varvec{\delta }$, multiple smoothing parameter estimation for (5) is then achieved by minimization of

$$\begin{aligned} \mathcal {V}_u^w(\varvec{\lambda })=\frac{1}{n_*}\Vert {\sqrt{ \mathbf{W}} } (\mathbf {z}-\mathbf{X}\varvec{\delta })\Vert ^2-1+\frac{2}{n_*}\text {tr}(\mathbf A _{\varvec{\lambda }}) \quad \text {w.r.t.} \quad \varvec{\lambda }, \end{aligned}$$

(6)

where $\mathbf z _i=\mathbf X _i \varvec{\delta }+\mathbf W _i^{-1}\mathbf d _i, \mathbf X _i=\text {diag}\left\{ \mathbf m ^\mathsf{T}_{1i},\mathbf B _{1i}^\mathsf{T},\mathbf m ^\mathsf{T}_{2i},\mathbf B _{2i}^\mathsf{T},1\right\} , \mathbf d _i=\left\{ \partial \ell (\varvec{\delta })_i/ \partial \eta _{1i},\right. \left. \partial \ell (\varvec{\delta })_i/ \partial \eta _{2i},\partial \ell (\varvec{\delta })_i/ \partial \eta _{3i}\right\} ^\mathsf{T}, \eta _{3i}=\rho ^*, \mathbf W _i$ is the $3 \times 3$ matrix with $(r,h)$th element

$$\begin{aligned} \left( \mathbf W _i\right) _{rh}=-\mathbb {E}\left[ \frac{\partial ^2 \ell (\varvec{\delta })_i}{\partial \eta _{ri}\partial \eta _{hi}}\right] , \ r,h=1,\ldots ,3, \end{aligned}$$

(7)

$n_*=3n, \mathbf A _{\varvec{\lambda }}=\mathbf{X}(\mathbf{X}^\mathsf{T}\mathbf{W}\mathbf{X}+\mathbf S ^*_{\varvec{\lambda }})^{-1}\mathbf{X}^\mathsf{T}\mathbf{W}$, and $\text {tr}(\mathbf A _{\varvec{\lambda }})$ represents the estimated degrees of freedom (edf) of the penalized model. The square root and inverse of W are obtained via eigen-decomposition. (To avoid clutter the superscript $[a]$ has been suppressed from the quantities above.) The two steps, one for $\varvec{\delta }$ and the other for $\varvec{\lambda }$, are iterated until convergence. Full details can be found in Marra and Radice (2011, 2013a).

For semiparametric bivariate probit models, the expected information matrix is the only option because the $\mathbf W _i$, as defined in (7), are positive-definite over a larger region of the parameter space as compared to those obtained without taking expectations. This is crucial given that $\sqrt{ \mathbf{W}}$ and $\mathbf W ^{-1}$ (via $\mathbf {z}$) are needed in (6).

3 Testing the hypothesis of absence of unobserved confounding

The hypothesis of absence of unobserved confounding can be stated in terms of $\rho$, which can be interpreted as the correlation between the unobserved variables in the two equations. If $\rho =0$ then $\varepsilon _{1i}$ and $\varepsilon _{2i}$ are uncorrelated and hence there is not a problem of unobserved confounding. On the contrary, $\rho \ne 0$ implies that there is a problem of unobserved confounding. This leads us to the definition of the following hypothesis

$$\begin{aligned} \left\{ \begin{array}{l} H_0:\rho =0 \\ H_1:\rho \ne 0 \end{array} \right. . \end{aligned}$$

Under $H_0$ function (4) becomes the sum of the penalized log-likelihood functions of two semiparametric univariate probit models. This implies that $\hat{\varvec{\delta }}_{H_0}^\mathsf{T} = \left( \hat{\varvec{\delta }_1}^\mathsf{T}, \hat{\varvec{\delta }_2}^\mathsf{T}, 0\right)$, where $\hat{\varvec{\delta }_1}$ and $\hat{\varvec{\delta }_2}$ are obtained by estimating the model equations separately. Therefore, consistent estimates for $\varvec{\delta }_2$ can be obtained by fitting Eq. (2) alone. Under $H_1$ simultaneous estimation is required to obtain consistent parameter estimates.

3.1 $LM$ type tests

In the context of the models described in this article, $LM$ (also known as score test) is an appropriate and computationally convenient tool for testing $H_0$. Its main advantage is that it does not require parameter estimates under $H_1$. This is appealing because the test is based on estimating the two model equations separately, hence obviating the need to fit the more computationally demanding semiparametric bivariate model. This implies that simultaneous estimation will be employed only if there is a problem of unobserved confounding.

The $LM$ statistic for the semiparametric bivariate models is

$$\begin{aligned} LM=\left\{ \mathbf g _{\hat{\varvec{\delta }}_{H_0}}-\tilde{\mathbf{S }}_{\varvec{\lambda }_{H_0}}\hat{\varvec{\delta }}_{H_0}\right\} ^\mathsf{T}\mathbf I ^{-1} \left\{ \mathbf g _{\hat{\varvec{\delta }}_{H_0}}-\tilde{\mathbf{S }}_{\varvec{\lambda }_{H_0}}\hat{\varvec{\delta }}_{H_0}\right\} \xrightarrow [H_0]{d} \chi ^2_1, \end{aligned}$$

(8)

where $\mathbf g _{\hat{\varvec{\delta }}_{H_0}}$ is the score vector evaluated at $\hat{\varvec{\delta }}_{H_0}, \tilde{\mathbf{S }}_{\varvec{\lambda }_{H_0}}$ is defined in Sect. 2.2 but with smoothing parameter estimates obtained by estimating the two univariate probit equations separately, and $\mathbf I ^{-1}$ is the inverse of the information matrix. Studying the limiting behavior of test statistics that involve penalty terms is not an easy task (e.g., Wood 2006, Sect. 4.8). However, because $\rho$ is not penalized, it is still possible to use the classic result that $LM$ has a $\chi ^2_1$ limiting distribution (Monfardini and Radice 2008). This can be seen by observing that $\big \{\mathbf{g }_{\hat{\varvec{\delta }}_{H_0}}-\tilde{\mathbf{S }}_{\varvec{\lambda }_{H_0}}\hat{\varvec{\delta }}_{H_0}\big \}^\mathsf{T}=\big \{\mathbf{0 },\mathbf{0 },\partial \ell (\hat{\varvec{\delta }}_{H_0})/\partial \rho \big \}$ which results from evaluating the penalized score in $\hat{\varvec{\delta }}_{H_0}$.

Different estimation methods for $\mathbf I$ may lead to different finite sample size performances. In this paper, we consider:

• The observed information matrix $-\varvec{\mathcal {H}}_{\hat{\varvec{\delta }}_{H_0}}+\tilde{\mathbf{S }}_{\varvec{\lambda }_{H_0}}$ (this expression derives from the penalized score in (8)). The test obtained using this matrix will be referred to as $LM_{\varvec{\mathcal {H}}}$ for notational convenience.

• The expected information matrix $\varvec{\mathcal {I}}_{\hat{\varvec{\delta }}_{H_0}}+\tilde{\mathbf{S }}_{\varvec{\lambda }_{H_0}}$. This test will be referred to as $LM_{\varvec{\mathcal {I}}}$.

The analytical expressions of $\mathbf g , \varvec{\mathcal {I}}$ and $-\varvec{\mathcal {H}}$ for the recursive and sample selection bivariate probit models are not reported here to save space and are implemented in function LM.bpm() of the R package SemiParBIVProbit (Marra and Radice 2013b).

For the recursive model, the expected information matrix becomes block diagonal under $H_0$ (see “Appendix 1”). Hence, $LM_{\varvec{\mathcal {I}}}$ can be simplified to

$$\begin{aligned} LM_{\varvec{\mathcal {I}}}= -\left\{ \frac{\partial \ell (\hat{\varvec{\delta }}_{H_0})}{\partial \rho }\right\} ^2\mathbb {E}\left[ \frac{\partial ^2 \ell (\hat{\varvec{\delta }}_{H_0})}{\partial \rho \partial \rho }\right] ^{-1}, \end{aligned}$$

(9)

which is computationally convenient since it does not require the inversion of the information matrix. This result does not hold for the non-random sample selection case given the different structure of the information matrix.

Note that, to implement the $LM$ type tests discussed above, we evaluate the score vector and information matrices at $\hat{\varvec{\delta }}_{H_0}$ (obtained from the univariate fits). Therefore, the arc-tangent transform for $\rho$ (used in the context of simultaneous equation estimation) is not required.

3.2 $\mathcal {W}$ test

The Wald test requires fitting the semiparametric bivariate model, hence it is not as advantageous as the $LM$ test. However, such a test is widely used in the applied literature and therefore we consider it for comparison.

$\mathcal {W}$ is based on estimating $\rho$ and is given by

$$\begin{aligned} {\mathcal {W}}=\frac{{\hat{\rho }}^2}{\mathrm{Var}\left( {\hat{\rho }}\right) } \xrightarrow [H_0]{d}\chi ^2_1. \end{aligned}$$

(10)

$\mathrm{Var}\left( {\hat{\rho }}\right)$ is estimated using the diagonal element of the inverse of $\varvec{\mathcal {I}}_{\hat{\varvec{\delta }}}+\tilde{\mathbf{S }}_{\varvec{\lambda }}$ corresponding to $\hat{\rho }$. This test will be referred to as $\mathcal {W}_{\varvec{\mathcal {I}}}$. In a semiparametric context this is the only option available. This is because model fitting can only be based on the expected information matrix, as explained in the final paragraph of Sect. 2.2. For the recursive model, $\mathrm{Var}\left( \hat{\rho }\right)$ can be estimated using the simplification described in the previous section, i.e. $\mathrm{Var}\left( \hat{\rho }\right) =-1/\mathbb {E}[\partial ^2 \ell (\hat{\varvec{\delta }})/\partial \rho \partial \rho ]$. Once again, this result does not hold for the non-random sample selection case. Because, in estimation, we make use of $\rho ^*$ rather than $\rho$ (see Sect. 2.2), using the delta method $\mathrm{Var}\left( \hat{\rho }\right) =4\mathrm{Var}\left( \hat{\rho }^*\right) \exp (2\hat{\rho }^*)/(\exp \left\{ 2\hat{\rho }^*\right\} +1)^2$.

The expected information matrix employed for computing $\mathrm{Var}\left( \hat{\rho }\right)$ corresponds to the Bayesian covariance matrix typically used for constructing ‘confidence’ intervals for the terms of a penalized regression spline model (e.g., Wood 2006). Such intervals have good frequentist coverage probabilities. This is because they include both a bias and variance component, a feature which is not shared by their frequentist counterpart; see Marra and Wood (2012) for full details. It may be argued that since $\rho$ is not penalized the frequentist covariance matrix, given by $\mathbf I ^{-1}(\mathbf I -\tilde{\mathbf{S }}_{\varvec{\lambda }})\mathbf I ^{-1}$, is also a sensible choice. Preliminary simulation evidence confirmed that $\mathrm{Var}\left( \hat{\rho }\right)$ is estimated well by both covariance matrices. However, the Bayesian version is computationally convenient since it can be obtained as a byproduct of the estimation procedure described in Sect. 2.2.

Another commonly used test which requires fitting the bivariate model is the likelihood ratio ($LR$) test. Here, the statistic is given by twice the difference of the model log-likelihoods under $H_1$ and $H_0$, and has a $\chi ^2_1$ limiting distribution for parametric models (Monfardini and Radice 2008). In the current context, we are however faced with a difficulty which inhibits the use of this approach for testing $H_0$. Specifically, in the semiparametric case the number of degrees of freedom for $LR$ is not guaranteed to be equal to 1, and can in fact be a positive or negative real value. For instance, if simultaneous estimation of the two equations leads to a model with edf (defined in Sect. 2.2) equal to 18.37 and estimating the equations separately yields a model with edf equal to 20.23 then the number of degrees of freedom for $LR$ is $-$1.86; the amount of smoothness required for the smooth functions of a model fitted via simultaneous estimation is likely to be different from that required when the equations are estimated separately. The same issue has been found when comparing generalized additive models (e.g., (Wood 2006, Sect. 4.10). It is not clear whether $LR$ can be rigorously extended to this context and further research is required.

4 Simulations

To compare the finite sample size properties of the $LM$ and $\mathcal {W}$ tests discussed in the previous section, we conducted simulation studies under correct and incorrect specification of both semiparametric bivariate probit models, with and without ER. The size and power of each test were calculated as the proportions of rejections based on simulation replications. All computations were performed in the R environment (R Development Core Team 2013) using the package SemiParBIVProbit (Marra and Radice 2013b).

The next sections provide details on the simulation and model fitting settings. The most salient features of the simulation results are then discussed. We present the endogeneity and non-random sample selection cases separately, starting with the former. Note that the study design detailed in Sects. 4.1.1 and 4.2.1 extends the simulation study of Monfardini and Radice (2008) to recognize the specific challenges that arise when there are nonlinear response-covariate relationships.

4.1 Endogeneity

4.1.1 Design of the experiments

Our experiments were based on two different data generating processes (DGPs): DGP1 and DGP2. In DGP1, the specification of the semiparametric recursive bivariate probit model contained main effects only, whereas in DGP2 an interaction term between the endogenous binary variable and a continuous regressor was also considered. That is,

$$\begin{aligned} \begin{array}{l} y^*_{1i}=\theta _{10} + \theta _{11}m_{1i}+ f_1(z_{1i}) + f_3(z_{2i}) +\varepsilon _{1i} \\ y^*_{2i}=\theta _{20} + \vartheta y_{1i} + \theta _{21}m_{1i} + f_2(z_{1i}) +\varepsilon _{2i} \end{array}, \end{aligned}$$

(11)

and

$$\begin{aligned} \begin{array}{l} y^*_{1i}=\theta _{10} + \theta _{11}m_{1i}+ f_1(z_{1i}) + f_3(z_{2i}) +\varepsilon _{1i} \\ y^*_{2i}=\theta _{20} + \theta _{21}m_{1i} + (1-y_{1i})f_2(z_{1i}) + y_{1i}f_4(z_{1i})+\varepsilon _{2i} \end{array}, \end{aligned}$$

(12)

where the binary outcomes $y_{1i}$ and $y_{2i}$ were determined according to the rules described in Sect. 2.1. The smooth functions were $f_1(z_{1i})=\gamma _1[z_{1i}^{2.5}+\exp \{\gamma _2(z_{1i}-\gamma _3)^ {2}\}], f_2(z_{1i})= \gamma _4 \{ \gamma _5 \exp (z_{1i})-z_{1i}^{3}\}, f_3(z_{2i})= \gamma _6 z_{2i}$ and $f_4(z_{1i})=\gamma _{7}\sin (\pi z_{1i})$. For both DGPs, we used three different parameter vector settings (see Table 1). These values were obtained randomly from a standardized normal distribution.

Table 1 Parameter value sets for the DGPs in the endogeneity and non-random sample selection cases

We also considered a variant of DGP2, for the three settings, useful to test what happens in the situation of distributional misspecification. Specifically, we generated data assuming uncorrelated gamma errors with shape and scale parameters equal to 2. This was achieved using rgamma(). The sample sizes considered were 1,000 and 4,000. Each design was replicated 1,000 times.

4.1.2 Fitting details

Let the two model equations be equal to

for DGP1 and

for DGP2. s() indicates that a smooth component is being used, and the by option is to allow the smooth to interact with a parametric term. Variables y1, y2, m1, z1 and z2 refer to $y_{1i},y_{2i}, m_{1i}, z_{1i}$ and $z_{2i}$. Using rmvnorm() in the package mvtnorm, regressors $m_{1i}, z_{1i}$ and $z_{2i}$ were obtained from a matrix of dimensions $n \times 3$ whose columns, called say reg1, reg2 and reg3, were generated from a multivariate normal distribution with zero means and covariance matrix characterized by correlations equal to 0.5 and variances equal to 1. reg1 and reg2 were then transformed using round() and pnorm(), respectively, to generate binary and uniform covariates. Note that the specifications for eq1 and eq2 are consistent with Eqs. (11) and (12).

$p$ values for $LM_{\varvec{\mathcal {H}}}$ and $LM_{\varvec{\mathcal {I}}}$ were calculated using LM.bpm() from SemiPar BIVProbit. That is,

corresponding to $LM_{\varvec{\mathcal {H}}}$ and $LM_{\varvec{\mathcal {I}}}$, respectively. data is a data frame containing the variables in the two equations generated according to the DGPs described in the previous section. $p$ values for $\mathcal {W}_{\varvec{\mathcal {I}}}$ were calculated using $\hat{\rho }$ and $\mathrm{Var}\left( \hat{\rho }\right)$ obtained from the output produced by SemiParBIVProbit(). That is,

The smooth components of the semiparametric models were represented using penalized thin plate regression splines with basis dimensions equal to 10 and penalties based on second-order derivatives (Wood 2006, pp. 154–160).

Regarding model misspecification, for DGP2, we generated data using gamma errors and employed the same tests. We also considered a scenario with functional form misspecification where the model equation for $y_2$ did not include the interaction term.

4.1.3 Monte Carlo results

Empirical size Table 2 provides rejection frequencies produced under $H_0:\rho =0$ and correct model specification using the three test statistics considered in this paper. Results are reported for the three typical critical values. The findings for the two DGPs share some important features, for the three settings. $LM_{\varvec{\mathcal {H}}}$ exhibits empirical sizes that are overall close to the nominal values. $LM_{\varvec{\mathcal {I}}}$ and $\mathcal {W}_{\varvec{\mathcal {I}}}$ yield unsatisfactory size results; the former under-rejects whereas the latter over-rejects. The good performance of $LM_{\varvec{\mathcal {H}}}$ is important for practitioners wishing to test the hypothesis of absence of unobserved confounding without coping with simultaneous estimation. In the current context, $-\varvec{\mathcal {H}}$ is a more adequate measure than $\varvec{\mathcal {I}}$ for estimating the information matrix. Monfardini and Radice (2008) found the same for parametric recursive bivariate probit models. This has also been confirmed in other contexts by Maldonado and Greenland (1994) and Louis (1982). In a notable article, Efron and Hinkley (1978) argued that the observed information should be used in preference to the expected information on the grounds that the former is ‘closer to the data’ whereas the latter is an a priori expectation. They showed this by using an appropriate ancillary statistic. The main practical limitation of their theoretical argument is the reliance on an ancillary statistic, which is often hard to specify in complex models such as the ones considered in this article. However, there are other examples (see Cavanaugh and Shumway (1996), Cao and Spall (2009) and references therein) where the expected information may more accurately estimate the true information. It emerges from the literature that there is not clear theoretical evidence about the superiority of $-\varvec{\mathcal {H}}$ on $\varvec{\mathcal {I}}$ (or vice versa) and that further research is needed towards this direction.

Table 2 Size results (in %) for the endogeneity case

The performance of $LM_{\varvec{\mathcal {I}}}$ and $\mathcal {W}_{\varvec{\mathcal {I}}}$ suggests that using $\varvec{\mathcal {I}}$ underestimates the variability of $\hat{\rho }$, hence causing them to produce zero and very high rejection frequencies, respectively. Note that the opposite rejection frequencies of the two tests is attributed to the way $-\mathbb {E}\left[ \frac{\partial ^2 \ell }{\partial \rho \partial \rho }\right]$ enters the statistics, which can be easily verified by looking at (9) and (10).

Empirical power For DGP1 and DGP2 we evaluated the empirical power of $LM_{\varvec{\mathcal {H}}}$ for $\rho =\left\{ 0.1,0,2,0.3,0.4,0.5,0.6,0.7,0.8,0.9\right\}$. Power curves are presented in Figs. 1 and 2. $LM_{\varvec{\mathcal {H}}}$ gives overall satisfactory results for all settings. Obviously the power improves as both $n$ and $\rho$ increase.

Fig. 1

Power curves for $LM_{\varvec{\mathcal {H}}}$ obtained under DGP1 and the three settings described in Sect. 4.1.1. The solid, dashed and dotted lines represent curves at the 10, 5 and 1 % significance levels, respectively

Fig. 2

Power curves for $LM_{\varvec{\mathcal {H}}}$ obtained under DGP2 and the three settings described in Sect. 4.1.1. The solid, dashed and dotted lines represent curves at the 10, 5 and 1 % significance levels, respectively

Empirical size under misspecification We applied $LM_{\varvec{\mathcal {H}}}$ to data generated according to model (12) with gamma errors. We also considered the situation of data generated according to model (12) with normal errors but using the test based on a misspecified functional form (i.e., the interaction term was omitted from the model). Size results are reported in Table 3 (see ER case). The results for setting 1 are not as good as those obtained under no misspecification but still reasonable. However, under settings 2 and 3 the sizes are overestimated. To gain more evidence, we considered other parameter sets; the results lead to similar conclusions (see “Appendix 2”, Table 7). Overall, this suggests that under misspecification the performance of $LM_{\varvec{\mathcal {H}}}$ worsens and the good results produced for setting 1 are due to sampling variability rather than to the robustness of the test.

Table 3 Size results (in %) for $LM_{\varvec{\mathcal {H}}}$ in the endogeneity case under the scenarios of no misspecification and misspecified error distribution and functional form

We also assessed the effectiveness of $LM_{\varvec{\mathcal {H}}}$ when the ER does not hold. Results are reported in Table 3 (see non-ER case). Overall, the test performs poorly. Comparing the ER and non-ER results, under misspecification, $LM_{\varvec{\mathcal {H}}}$ performs better when the ER holds, although it still has high rejection frequencies.

4.2 Non-random sample selection

4.2.1 Design of the experiments

Similarly to the endogeneity case, the sampling experiments were based on the two different DGPs: DGP3 and DGP4. In DGP3 the specification of the semiparametric sample selection bivariate probit model contained main effects only, whereas DGP4 also contained an interaction term between two regressors. That is,

$$\begin{aligned} \begin{array}{l} y^*_{1i}=\theta _{10} + \theta _{11}m_{1i}+ f_1(z_{1i}) + f_3(z_{2i}) +\varepsilon _{1i} \\ y^*_{2i}=\theta _{20} + \theta _{21}m_{1i} + f_2(z_{1i}) +\varepsilon _{2i} \end{array}, \end{aligned}$$

(13)

and

$$\begin{aligned} \begin{array}{l} y^*_{1i}=\theta _{10} + \theta _{11}m_{1i}+ f_1(z_{1i}) + f_3(z_{2i}) +\varepsilon _{1i} \\ y^*_{2i}=\theta _{20} + (1-m_{1i})f_2(z_{1i}) + m_{1i}f_4(z_{1i})+\varepsilon _{2i} \end{array}, \end{aligned}$$

(14)

where the binary outcomes $y_{1i}$ and $y_{2i}$ were determined according to the rules described in Sect. 2.1. For both DGPs, we considered the three different parameter settings reported in Table 1. We also considered a variant of DGP4, useful to test what happens in the situation of distributional misspecification. As before, we generated data assuming uncorrelated gamma errors with shape and scale parameters equal to 2. The sample sizes considered were 1,000 and 4,000. Each design was replicated 1,000 times.

4.2.2 Fitting details

We specified the two model equations

for DGP3 and

for DGP4. $p$ values for $LM_{\varvec{\mathcal {H}}}$ and $LM_{\varvec{\mathcal {I}}}$ were calculated using

where selection was set to TRUE to use the tests for the sample selection model case. $p$ values for $\mathcal {W}_{\varvec{\mathcal {I}}}$ were calculated using the quantities $\hat{\rho }$ and $\mathrm{Var}\left( \hat{\rho }\right)$ obtained from the output produced by SemiParBIVProbit(eq3, eq4, data, selection = TRUE).

In line with the endogeneity case, for DGP4, we generated data using gamma errors and employed the same tests. We also considered a scenario with functional form misspecification where the model equation for $y_2$ did not include the interaction term.

4.2.3 Monte Carlo results

Because the conclusions in this section are similar to those obtained in Sect. 4.1.3, we only report some of the results; “Appendix 2” contains the full set of results.

Regarding the empirical sizes, $LM_{\varvec{\mathcal {H}}}$ performs well, whereas the tests based on $\varvec{\mathcal {I}}$ perform poorly (see Table 4). The good performance of $LM_{\varvec{\mathcal {H}}}$ is also confirmed by the power results reported in Figs. 3 and 4 in “Appendix B”.

Fig. 3

Power curves for $LM_{\varvec{\mathcal {H}}}$ obtained under DGP3 and the three settings described in Sect. 4.2.1. The solid, dashed and dotted lines represent curves at the 10, 5 and 1 % significance levels, respectively

Fig. 4

Power curves for $LM_{\varvec{\mathcal {H}}}$ obtained under DGP4 and the three settings described in Sect. 4.2.1. The solid, dashed and dotted lines represent curves at the 10, 5 and 1 % significance levels, respectively

Table 4 Size results (in %) for the non-random sample selection case

As for model misspecification, the same conclusions as those for the endogeneity case are reached here; under functional and distributional misspecification the performance of $LM_{\varvec{\mathcal {H}}}$ worsens (see Table 8, ER case, “Appendix 2”). Also, the test’s performance is poor in the absence of ER and is slightly better in the presence of ER.

The main findings of our simulation study can be summarized as follows. 1) $LM_{\varvec{\mathcal {H}}}$ yields close to nominal empirical sizes and strongly outperforms the tests based on the expected information. $LM_{\varvec{\mathcal {I}}}$ and $W_{\varvec{\mathcal {I}}}$ are characterized by zero and very high rejection frequencies, respectively. 2) $LM_{\varvec{\mathcal {H}}}$ produces satisfactory power results which improve as $n$ and $\rho$ increase. 3) Under misspecification, the performance of $LM_{\varvec{\mathcal {H}}}$ worsens. 4) When the ER does not hold, the test is not reliable. 5) The good performance of $LM_{\varvec{\mathcal {H}}}$ is important for practitioners wishing to test the hypothesis of absence of unobserved confounding without coping with simultaneous estimation.

5 Real data illustrations

We illustrate the tests using two case studies in which the issues of endogeneity and non-random sample selection arise. The first concerns a study, conducted in Botswana, on the impact of education on women’s fertility (www.measuredhs.com) and contains around 4,300 observations. Education is equal to 1 if the woman had at least 8 years of education and 0 otherwise, and fertility is equal to 1 if the woman had at least one child. The proportion of 1’s for the two variables is 28.9 and 74 %, respectively. As suggested by many scholars, estimation of such an effect can be biased by the possible endogeneity arising because unobserved confounders (e.g., ability and motivation) are associated with both fertility and education; full details can be found in Marra and Radice (2011) and references therein. The second dataset considers an American survey of public opinion polls on school integration (www.electionstudies.org) where about 700 individuals were first asked if they had an opinion on the integration question (0 = no, 1 = yes) and then what that opinion was (0 = no integration, 1 = yes integration). This gave respondents an opportunity to opt out of the question answering process at an earlier stage. 64.57 % of the individuals chose to answer the integration question. Among these, the proportion of yes answers was 46.43 %. Because it is reasonable to assume that the decision to answer was not random, sample selection bias can occur when estimating the model parameters; full details can be found in Marra and Radice (2013a) and references therein.

In the fertility study, the direction of the bias due to unobserved confounding can not be determined a priori. The reason for this ambiguity is because of different substitution and income effects (Cygan-Rehm and Maeder 2012). As for the school integration study, the bias is expected to be negative because some individuals choose not to answer the integration question as they feel that their opinion may be perceived as socially unacceptable (Berinsky 1999).

5.1 Fertility dataset

Following previous work on the subject (Wooldridge 2010; Marra and Radice 2011; Sobotka et al. 2013), we specified a semiparametric recursive bivariate probit model with main terms only. The description of the variables used in the model are reported in Table 5. Specifically, the linear predictors of the treatment (ed) and outcome (child) equations included urb, em and el, whereas fhalf and ed entered the former and latter predictors, respectively. These variables entered the model as parametric components. Thin plate regression splines of age, with the same settings as those employed for the simulation study, were employed. The two equations are

$$\begin{aligned} \mathtt{ed }^*_i&= \theta _{10} + \theta _{11}\mathtt{el }_i + \theta _{12}\mathtt{urb }_i + \theta _{13}\mathtt{em }_i + \theta _{14}\mathtt{fhalf }_i + f_{1\mathtt{age }}(\mathtt{age }_i)+\varepsilon _{1i}, \\ \mathtt{child }^{*}_i&= \theta _{20} + \vartheta \mathtt{ed }_i + \theta _{21}\mathtt{el }_{i} + \theta _{22}\mathtt{urb }_{i} + \theta _{23}\mathtt{em }_{i} + f_{2\mathtt{age }}(\mathtt{age }_i)+\varepsilon _{2i}. \end{aligned}$$

As in Wooldridge (2010), the binary variable ‘born during the first 6  months of the year’ (fhalf) was used as an instrument on the grounds that it does not have a direct effect on fertility given covariates, influences education, and is unlikely to be associated with unobservable confounders such as ability and motivation. The nonparametric specification for age arises from the fact that this covariate embodies productivity and life-cycle effects that are likely to affect child non-linearly. Wooldridge (2010) considered a model for fertility that contains linear and quadratic terms in age, whereas Marra and Radice (2011) and Sobotka et al. (2013) specified a model containing a smooth function of age. Here, we found non-linear effects of age that are almost identical to those reported in Marra and Radice (2011); results are available upon request. The quantity of interest is the average treatment effect (ATE) of ed on child, which measures the effect of ed on the probability of having at least one child, i.e. $\mathbb {P} (\mathtt child =1)$.

Table 5 Variables in the education-fertility data set

Because the effect of education on fertility may be biased by the possible presence of endogeneity, as a first step of the analysis we tested the null hypothesis of absence of unobserved confounding. Specifically, we employed $LM_{\varvec{\mathcal {H}}}$ as, in simulation, it was shown to have good size and power properties. The $p$ value obtained using $LM_{\varvec{\mathcal {H}}}$ was 0.00, suggesting that there is an issue of endogeneity. For completeness, we also report the results of the tests based on the expected information; the $p$ values obtained using $LM_{\varvec{\mathcal {I}}}$ and $\mathcal {W}_{\varvec{\mathcal {I}}}$ were 0.94 and 0.00, respectively. The $p$ value of $\mathcal {W}_{\varvec{\mathcal {I}}}$ suggests that there is an issue of endogeneity, whereas that of $LM_{\varvec{\mathcal {I}}}$ suggests that endogeneity is not present. The conflicting conclusions can be attributed to the fact that, as shown in our simulations, $LM_{\varvec{\mathcal {I}}}$ and $\mathcal {W}_{\varvec{\mathcal {I}}}$ are not reliable as under the null they yield zero and high rejection frequencies, respectively. Based on the result produced by $LM_{\varvec{\mathcal {H}}}$, we estimated a recursive bivariate probit model and then calculated the ATE. The estimate in $\%$ (with 95 % confidence interval) was $-3.01 \ (-5.90,-0.08)$. This is statistically different from zero and suggests that having at least 8 years of schooling decreases the probability of having at least one child by 3 %.

5.2 School integration dataset

For the school integration dataset, using the variables in Table 6 and in line with the works by Berinsky (1999) and Marra and Radice (2013a), we specified a semiparametric sample selection probit model based on the two equations

$$\begin{aligned} \mathtt{opinion }^*_i&= \theta _{11} + \theta _{12}\mathtt{sex }_i + \theta _{13}\mathtt{race }_i + \theta _{14}\mathtt{reg.northeast }_i \\&+\, \theta _{15}\mathtt{reg.south }_i + \theta _{16}\mathtt{reg.west }_i + \theta _{17}\mathtt{chil } \\&+\, \theta _{18}\mathtt{discpol } + \theta _{19}\mathtt{moralcons } + \theta _{110}\mathtt{perslett } \\&+\, f_{1\mathtt{age }}(\mathtt{age }_i)+ f_{1\mathtt{educ }}(\mathtt{educ }_i) + \varepsilon _{1i}, \\ \mathtt{integration }^*_i&= \theta _{21} + \theta _{22}\mathtt{sex }_i + \theta _{23}\mathtt{race }_i + \theta _{24}\mathtt{reg.northeast }_i \\&+\, \theta _{25}\mathtt{reg.south }_i \!+\! \theta _{26}\mathtt{reg.west }_i \!+\! \theta _{27}\mathtt{chil }\!+\! \theta _{28}\mathtt{discpol } \\&+\, \theta _{29}\mathtt{moralcons } + f_{2\mathtt{age }}(\mathtt{age }_i)+f_{2\mathtt{educ }} (\mathtt{educ }_i)+\varepsilon _{2i}, \end{aligned}$$

where, the equations included sex, race, reg.northeast, reg.south, reg.west, discpol, moralcons and chil as parametric components, and smooth functions of age and educ. These two continuous covariates are expected to have non-linear impacts on integration as well as opinion. chil was included as a parametric component because it did not have enough unique covariate values to justify the use of a smooth function. The selection equation (opinion) also included perslett. This was because, according to Berinsky (1999), those individuals who are difficult to reach are also reluctant to answer specific survey questions. The inclusion of this variable in the selection equation served as ER. As in the fertility study, we found estimated linear and non-linear effects of the continuous variables that are almost identical to those reported in Marra and Radice (2013a).

Table 6 Variables in the school integration dataset

Table 7 Further size results (in %) for $LM_{\varvec{\mathcal {H}}}$ in the endogeneity case under the scenarios of misspecified error distribution and functional form

Table 8 Size results (in %) for $LM_{\varvec{\mathcal {H}}}$ in the non-random sample selection case under the scenarios of no misspecification and misspecified error distribution and functional form

The $p$ value obtained using $LM_{\varvec{\mathcal {H}}}$ was 0.00, whereas those obtained using $LM_{\varvec{\mathcal {I}}}$ and $\mathcal {W}_{\varvec{\mathcal {I}}}$ were 0.76 and 0.00. These lead to the same conclusions reached for the fertility study. In summary, $LM_{\varvec{\mathcal {H}}}$, which is the most reliable test, supports the presence of non-random sample selection. Therefore, we estimated the model parameters using the sample selection bivariate probit model and calculated the mean predicted probability (and associated confidence interval) of giving a supportive response. This was $0.34 \ (0.22, 0.45)$.

In both examples (fertility and school integration) $LM_{\varvec{\mathcal {H}}}$ suggests rejecting the null hypothesis of absence of unobserved confounding. In such cases, estimates of the parameters of interest (ATE and mean predicted probability) are obtained by using bivariate probit models. If we were not to reject the null hypothesis then we would estimate the quantities of interest by using univariate models, hence avoiding the use of a simultaneous estimation approach.

Following a reviewer’s suggestion, for both case studies, we obtained $p$ values using $LM_{\varvec{\mathcal {H}}}$ based on a parametric specification of the model equations (i.e., the continuous covariates were assumed to have a linear impact). The values were 0.12 and 0.03 for the fertility and school integration studies, respectively. In the first case, the conclusion would be that there is not an issue of endogeneity, which is not consistent with the results reported in this section as well as in the literature on this topic. In the second case, conclusions would not be altered. In general, we recommend using a model specification that reduces the risk of functional form misspecification which may have a detrimental impact on the reliability of the test.

6 Discussion

We extended $LM$ and $\mathcal {W}$ type tests for the hypothesis of absence of unobserved confounding to the context of semiparametric recursive and sample selection bivariate probit models. The finite sample size performance of the tests was examined via a Monte Carlo study under several scenarios: correct model specification, distributional and functional misspecification, with and without an ER. The results allowed us to derive some guidelines which may be important for empirical applications. First, under correct model specification, $LM$ based on $-\varvec{\mathcal {H}}$ (the observed information) performs well, whereas the statistics based on $\varvec{\mathcal {I}}$ (the expected information) are characterized by zero and very high rejection frequencies, suggesting these tests should not to be used for empirical analysis. Second, $LM$ performs satisfactorily only when the ER holds. Third, the availability of a valid instrument can alleviate but not eliminate the detrimental effect that model misspecification has on the empirical performance of the test.

The good performance of $LM_{\varvec{\mathcal {H}}}$ should be particularly attractive to practitioners wishing to test the null hypothesis of absence of unobserved confounding while avoiding simultaneous estimation. This implies that simultaneous estimation will be employed only if unobserved confounding is detected.

The $LM$ statistic presented here can in principle be generalized to any other model which controls for endogeneity or non-random sample selection. Examples are copula or count data endogenous and non-random sample selection models (Bratti and Miranda 2011; Winkelmann 2011; Zimmer and Trivedi 2006; Smith 2003). More generally, this test could be extended to any other context where there is a system of equations and testing their independence is important (Kiefer 1982; Yee and Wild 1996).

Appendix

1.1 Appendix A

For the recursive bivariate probit model case, matrix $\varvec{\mathcal {I}}$ becomes block diagonal under $H_0:\rho =0$. This is because $\varvec{\mathcal {I}}_{12},\varvec{\mathcal {I}}_{13}$ and $\varvec{\mathcal {I}}_{23}$, reported in Marra and Radice (2011), are equal to $\mathbf 0$ under the null. In what follows, we ignore the role of the penalty because it is block diagonal and hence does not affect the aforementioned quantities. Consider, for instance, $\varvec{\mathcal {I}}_{13}$. Under the null

$$\begin{aligned} \varvec{\mathcal {I}}_{13}&= \sum _{i=1}^{N}\phi ^2_{1i}\phi _{2i}\left[ \Phi _{2i}\left\{ \frac{1}{\Phi _{1i} \Phi _{2i}}+\frac{1}{(1-\Phi _{1i}) \Phi _{2i}}\right\} \right. \\&\left. -\,(1-\Phi _{2i})\left\{ \frac{1}{\Phi _{1i} (1-\Phi _{2i})}+\frac{1}{(1-\Phi _{1i}) (1-\Phi _{2i})}\right\} \right] \mathbf X _{1i} \\&= \sum _{i=1}^{N}\phi ^2_{1i}\phi _{2i} \left[ \frac{1}{\Phi _{1i}}+\frac{1}{1-\Phi _{1i}}- \frac{1}{\Phi _{1i}}-\frac{1}{1-\Phi _{1i}}\right] \mathbf X _{1i} =\mathbf 0 , \end{aligned}$$

where, using a shorthand notation, $\Phi _{1i}\Phi _{2i}, \Phi _{1i}(1-\Phi _{2i}), (1-\Phi _{1i})\Phi _{2i}$ and $(1-\Phi _{1i}) (1-\Phi _{2i})$ are the quantities for $p_{11i}, p_{10i}, p_{01i}$ and $p_{00i}$ obtained under $H_0$, and $\Phi _{1i}, \Phi _{2i}, \phi _{1i}$ and $\phi _{2i}$ denote the probability and density functions of a standardized normal evaluated at their corresponding linear predictors $\eta _{1i}$ and $\eta _{2i}$.

1.2 Appendix B