1 Introduction

The advent of advanced technologies, such as additive manufacturing (AM), has pushed designers and manufacturers to develop increasingly efficient and lightweight structures. The ability to manufacture free-shape components permits the exploration of complex features and tailored structures with enhanced mechanical properties, including energy absorption (EA) characteristics. In this regard, the capabilities of AM processes and the introduction of mathematical and bio-inspired geometries have accelerated the development of more efficient impact absorber devices. Considerable attention has been growing toward the design of head protection equipment applications, specifically helmets [1,2,3,4,5,6]. As an example, Khosroshahi et al. [3] showed that a hierarchical lattice liner structure manufactured in nylon via AM material extrusion (MEX) can decrease the peak linear acceleration (PLA) of a helmeted head to 60% compared with a conventional liner made of EPS (Expanded Polystyrene) foam. Similar studies have investigated the EA capabilities of additively manufactured components tested under multi-hit impacts [5, 6]. It was found that elastomeric lattice structures manufactured via AM technologies can guarantee lower PLA at multiple impacts compared to conventional polyurethane foams, which are the standard for sports applications [7].

Ideally, during the impact, an absorber should keep the instant peak force below a prescribed threshold with almost constant stress for a long deformation strictly proportional to the energy impact [8]. Consequently, several polymeric materials for AM have been investigated [9,10,11,12,13,14,15,16,17], looking for a balance between stiffness and elongation. In detail, polyamide and thermoplastic polyurethane (TPU) materials represent perfect candidates for absorber device production. These two materials show highly different strength and stiffness compared to each other. Additionally, AM offers the possibility of freely tailoring the geometry of the structure to obtain a substantial modification of the structure mechanical properties with respect to the corresponding bulk material.

An example of this design opportunity is cellular structure geometries characterised by a stochastic, periodic, or recursive repetition in the space of a single cell [18]. Among them, fractal geometry represents one of the natural cellular and mathematical objects that have barely been investigated in the structural engineering field. To date, their development has been limited due to the irregular, intricate, and self-similar 3D properties that make the production difficult. Although this problem can be overcome by AM technologies, studies on the feasibility and the characterisation of 3D fractal geometry are still limited. The works in Ref. [19,20,21] investigated the strength and deformation mechanisms under the quasi-static compression load of fractal-like nanolattice structures for nanotechnology applications. However, to the authors’ knowledge, only one study exists on the macroscale structural application of 3D fractal structures [22]. The study focused on characterising a single 3D Greek cross-fractal structure made in polyamide under quasi-static strain rate compression. The study shows the structure as promising for energy absorption applications. However, the response of the structure under higher strain-rate loads was not investigated.

In light of the results reported in Ref. [22], the 3D cross-based fractal structure (3D-CFS) is here investigated under both quasi-static and high-speed compression loads. An experimental study is carried out to evaluate the effects of the volume fraction variation on the manufacturing feasibility and mechanical responses. To further extend the characterisation of structure energy absorption performance, the structure is produced by polyamide and TPU. For comparison purposes, the Ideality efficiency index is employed to describe the EA performance of the tested samples with the literature data.

2 Materials and methods

2.1 Cross-based fractal design

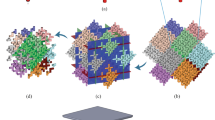
The 3D-CFS [22] is generated from the subsequent transformation of a 3D Greek cross initiator, i.e. a linear struts cross extruded along the three axes of a cartesian tern (Fig. 1a). The geometry of the structure is characterised by the diameter D and the length L of the beam of the initiator (Fig. 1a). These two geometrical factors will influence the volume fraction (VF) computed as the ratio between the actual volume of the reticular structure and the cubic envelope (Fig. 1b).

Fig. 1
figure 1

a 3D-CFS iterations: in red, the first step; in blue and green, the added branches of the second and third step, respectively. b Cubic compression sample. (adapted from Ref. [22])

Full size image

To analyse the effect of the structure design on the feasibility and the mechanical response of the structure, D and L were varied in a large range according to the following considerations.

As far as the diameter of the strut is concerned, D was selected to be higher than 1.5 mm. This constraint follows the findings reported in Ref. [22], in which various configurations of 3D-CFS were manufactured in PA12 using a Formiga P110Velocis and standard process parameters and tested under quasi-static compression. In that case, with the selected processing conditions, strut diameters lower than 1.5 mm showed an extremely low stiffness and higher amount of internal (porosity) and external defects, jeopardising the structure integrity and quasi-static performance. The same result was obtained when testing lattice structures under tensile load [23]. Since, as detailed in the next section, this study considers the same manufacturing system and process setting reported in Ref. [22], diameters lower than 1.5 mm were considered inappropriate for high-speed (HS) compression loads test.

L represents the length at the first iteration of the fractal design, that is, the actual height of the resultant structure constrained by the two base plates of the cubic sample (Fig. 1b). To ensure better fit with helmet liner applications and similar personal protective equipment (PPE), the upper limit of L was set equal to 40 mm.

A complete factorial plan was designed considering L and D at six different levels. In detail, the strut length varied from 20 to 40 mm, whereas the strut diameter from 1.6 to 2.6 mm. The designed plan consisted of 36 combinations of 3D-CFS structures with a volume fraction variation from 6.1 to 39%, as listed in Table 1. The VF value increases with the decrease of the length and decreases with the reduction of the strut diameter, as illustrated graphically in Fig. 2. Each design is named using a combination of L and D variables followed by identifying the set level. As an example, L20_D1.6 indicates a structure designed with a height equal to 20 mm and a diameter equal to 1.6 mm.

Table 1 Full factorial design plan for the manufacturing feasibility study with two factors, strut length (L) and strut diameter (D), whose combination generates different values of volume fraction (VF)
Full size table
Fig. 2
figure 2

Graphical illustration of the full factorial design plan reported in Table 1

Full size image

The best designs in terms of manufacturability were then selected and analysed to evaluate their mechanical properties at different compression strain-rates and with different materials. The main criterion for defining the degree of manufacturability is that the voids of the structure are free of powder. Selected designs were then grouped according to the parameters L, D, and volume fraction to evaluate the effect of the geometrical parameters on the mechanical response of the structure. The structures with stacked powder in the voids were excluded by the analysis because the powder may hinder the deformation mechanisms of the structure.

2.2 Production and testing

As mentioned above, the structure was analysed using two feedstock materials, PA12 and TPU, as powder. The PA12 material was supplied by the company EOS GmbH with the tradename PA2200 [24]. For TPU, the ESTANE® 3D TPU M95A-545 [25] was selected and supplied by Lubrizol. Table 2 summarises the mechanical properties of the material provided in the technical datasheet by the supplier.

Table 2 Primary material and mechanical properties of the PA2200 (PA12) [24] and ESTANE® 3D TPU M95A-545 powders (TPU) [25] as reported in the technical datasheet provided by the supplier
Full size table

To emulate an industrial production, both powders were a mix of virgin and recycled with a proportion according to the disposal of the supplier. PA12 was mixed with 50% virgin and 50% recycled powder, while ESTANE® 3D TPU M95A-545, shortly TPU, was mixed with 80% recycled and 20% virgin powder.

PA12 samples were manufactured via a Powder Bed Fusion-Laser (PBF-L/P) system of the EOS company, i.e. the Formiga P110 Velocis, which implements a CO2 laser for the powder sintering. The process parameters adopted were the standard parameters suggested by the machine supplier for the PA12. The laser power and speed were set equal to 21W and 2500 mm/s, respectively, while the hatch distance was fixed at 0.25 mm [22]. The temperature of the chamber was set equal to 172 °C [22].

TPU was processed by a Powder Bed Fusion-Infrared Light system (PBF-IrL/P) system of the Hewlett-Packard (HP®) company, JetFusion 4200 MultiJetFusion, which uses a combination of a fusing chemical agent and infrared light to solidify the powder. The fusing chemical agent is deposited in the section to be exposed and accelerates the agglomeration of the particles after the exposure. In addition, a so-called detailed agent is deposited at the contour of the section to be exposed and inhibits the dispersion of the heat from the exposed section to the surrounding powder [26]. The JetFusion 4200 MultiJetFusion is a closed system in which only the packing density and the lamp irradiance are disclosed and set equal to 2.2% and − 2%, respectively, as suggested by HP for TPU.

The layer thickness was set to 100 µm for both PBF systems.

Each sample was oriented into the build volume with the two base plates perpendicular to the build direction Z, as reported in Fig. 3.

Fig. 3
figure 3

PA12 and TPU printed samples with multiple configurations extracted by the full factorial design plan

Full size image

For each configuration, three replicas were produced and tested with quasi-static (QS) and high-speed (HS) compression loads.

After the production, the samples were naturally cooled, and the excess powder was removed with a sandblasting machine by the mechanical action of the same manufacturing powder mixed with glass microspheres. Figure 3 shows examples of the printed geometries.

The QS compression tests were performed on a universal testing machine, 3MZ Tensile (Easydur Srl, Italy), equipped with a 5-tonne load cell. The strain rate of the compression test was set to 2 × 10−3 s−1, corresponding to 5 mm/min, with a sampling rate of data recording equal to 100 Hz.

An in-house drop tower machine developed at the University of Aveiro was used to test the 3D-CFS specimens at HS impact. Force and displacement data were acquired using a 20-kN load cell and a position encoder. Data was synchronised and treated using Scilab software and a Savitzky-Golay type data filter [27].

A preliminary test was performed on a low VF structure (L40_D2.0) with an initial kinetic energy of 50 J to calibrate the impact energy for obtaining a reasonable compression response of the structure. After this preliminary test, the energy level was decreased to 25 J to adequately meet the structure strength response to the high-impact energy. The new energy level was maintained for the entire testing procedure on the samples of the selected configurations. The 25 J impact tests were subjected to a strain rate at an impact of 12.4 s−1.

The mechanical performances under compression and impact tests were calculated by extracting from the test machines the values of response force acquired by the load cell and the displacement of the impactor up to the complete densification of the sample. The uniaxial stress (σ) and strain (ε) were obtained from the acquired force and displacement by considering the height and minimum cross-section area of the sample.

2.3 Energy absorption descriptors

To evaluate the mechanical energy absorption performance of the tested structures, the energy per unit volume (W) was initially computed as reported in Eq. 1, i.e. the area under the stress vs. strain curve until the strain point from which starts the densification phase (εd).

$$W={\int }_{0}^{{\varepsilon }_{d}}\sigma \left(\varepsilon \right)d\varepsilon$$
(1)

To make the performance of different materials comparable, the specific energy absorption (SEA), defined as the ratio between the energy per unit volume W of the tested sample and the material density ρ (Eq. 2), was used.

$$SEA=\frac{W}{\rho }$$
(2)

To evaluate the efficiency of the absorber structure in absorbing energy by comparing its cushioning properties to an ideal absorber, the total Ideality index (It) was considered in this work. The It parameter is commonly used to evaluate the EA properties of a structure by considering its capability to be compressed with a low, almost constant stress level up to the starting point of the densification, as reported in Eq. 3.

$${I}_{t}=\frac{{\int }_{0}^{{\varepsilon }_{i}}\sigma \left(\varepsilon \right)d\varepsilon }{\underset{0\le \varepsilon \le {\varepsilon }_{i}}{{\text{max}}}\sigma \bullet {\varepsilon }_{i}}$$
(3)

A more detailed analysis of the EA indices meaning is reported in Appendix.

A further index of the capability to absorb energy considers the actual force recorded during the impact. Thus, the acceleration was calculated by deriving the values of the force vector. The acceleration values were expressed as multiples of the gravitational acceleration constant, or gravitational force, namely, g. When the acceleration is plotted against the time, it is common to consider the maximum value of the curve, i.e. the peak linear acceleration (PLA), as an indicator of the damage quantity the protected object can tolerate. Specific PPE applications typically require this value below a certain threshold [28].

3 Results and discussion

3.1 Manufacture feasibility

For this analysis, a total of 108 samples were produced. Owing to its reticular arrangement, the structure presents square porosities whose dimensions vary with the volume fraction. As evident from Fig. 4, the smaller porosities are concentrated at the centre of the fractal. The dimension of the minimum internal porosity gap is reported in Table 3.

Fig. 4
figure 4

Comparison between two 3D-CFS configurations (top, L40_D2.6; bottom, L20_D2.0) of the nominal minimum gap between central struts

Full size image
Table 3 Resume of the nominal minimum gap between the struts of the analysed configurations reported in Table 1
Full size table

Since the PBF for polymers is a hot process characterised by a pre-heating phase before the selective fusion of each layer, the heated powder combined with the fusion source increases undesired thermal effects on the area that should not be subjected to solidification. The smaller this area is and bordered by wider fused sections, the stronger the sintered is, and the more the powder remains entrapped. Therefore, the actual production via PBF can lead to the generation of trapped semi-sintered powder, which results impossible to remove from an intricate structure such as the 3D-CFS. Unremoved powder increases the structure geometry density and decreases the internal struts bending mechanisms when subjected to external loads.

To evaluate the feasibility of manufacturing, the percentage of powder removal was evaluated during the cleaning phase of the samples via the sandblasting machine. Figure 5 reports all the manufactured and cleaned samples highlighted by colours from red to green that qualitatively represent the number of pores free from powder.

Fig. 5
figure 5

Map of the powder-free percentage evaluated for the set of 36 3D-CFS configurations manufactured via PBF-L/P in PA12 material. Coloured areas represent the percentage of powder-free: red (< 70%), orange (70 ÷ 80%), yellow (81 ÷ 90%), light blue (91 ÷ 97%), green (> 97%). Dotted lines with different patterns enclose the configurations selected for the analysis of mini set, respectively, Set L, Set D, Set L × D

Full size image

The obtained results reveal that configurations with the higher capability of being fully powder-free are characterised by values of the nominal minimum gap of internal pores higher than around 1.40 mm, which corresponds to 3D-CFS with VF higher than 15%.

According to these results, the mechanical characterisation was restricted to three different sets of 3D-CFS structures extracted from the one characterised by a higher percentage of powder-free. The first set of configurations was analysed to investigate the effects of the strut length variation (Set L) by keeping the diameter constant at 1.6 mm. Conversely, the second set evaluates the variation of the strut diameter (Set D) by maintaining the length constant at 36 mm. Lastly, the third set studies the volume fraction variation by grouping the configurations in a matrix of three levels for two variables (Set L × D). Table 4 resumes the configurations of the three sets designed for mechanical characterisation.

Table 4 Resume of the IDs present in the three sets extracted from the manufacture feasibility study
Full size table

3.2 Compression test PA12

For the compression test, a total of 39 samples were produced. Figure 6 reports the results of the mechanical behaviour of 3D-CFS samples produced in PA12 material and tested in low strain rate (2 × 10−3 s−1) compression load. The decrease in the length of the fractal structure with constant strut diameter, corresponding to the increase of the VF, increases the sample strength with a progressive reduction of the plateau region. The densification point, detected in the point where the structure gives the maximum value of Ideality I, has a mean value of 30% for Set L (Fig. 6a). The stress after the first peak force is affected by fluctuated values for those structures characterised by low VF; however, these structures present low deviation from the mean plateau stress.

Fig. 6
figure 6

Stress vs strain curves of the compression test in quasi-static strain rate performed on PA12 samples with configurations belonging to a Set L, b Set D, and c Set L × D. d Resume table of volume fraction values of the tested structures

Full size image

In contrast, the increase of the VF (Fig. 6b), corresponding to the increase of the diameter with strut length constant (Set D), leads to a sharp decrease of the stress after the first peak force. These findings can be explained by considering the slenderness ratio of the struts: owing to the increase of D but with constant L, the strut slenderness decreases. This finding means stiffer behaviour of the structures that raises the stress thanks to the thicker struts parallel to the load direction. Nevertheless, when the bending behaviour of the structure occurs, i.e. after the elastic region, the thicker strut combined with the brittleness of the PA12 processed via PBF causes premature fractures corresponding to the stress collapse, as observed in Ref. [29].

Overall, the VF variation of the 3D-CFS geometry corresponds to a quasi-linear variation of the structure strength and onset of the densification point. Different deformation mechanisms among the struts can explain some deviations in the compressive curve trend, which can be affected by process-induced defects. Moreover, it is possible to note that 3D-CFS configurations with different combinations of L and D but similar VF report the same mechanical characteristics, as depicted in Fig. 6c. There is a relevant overlapping between the stress–strain curves of IDs L36_D1.8 and L32_D1.6 and IDs L36_D2.0, L32_D1.8, and L28_D1.6.

The results of the EA performance of the three 3D-CFS sets are illustrated on the bar plots reported in Fig. 7. The graphs indicate the specific energy absorption (SEA) value of each configuration and the related efficiency parameter It. All results are provided in ascending order of VF. The amount of absorbed energy increases with the VF, with some deviation from the trend among configurations with almost the same VF (see Fig. 7c). Therefore, despite higher VF samples reporting lower εd, the higher strength generates a higher level of absorbed energy. However, as Fig. 7 highlights, the efficiency in absorbing a significant quantity of energy decreases due to excessive stress recorded at the first part of the compression curve. Consequently, two opposite trends are observed between the SEA and the It with the increase of the VF. Overall, the investigated configurations report values of SEA and It between 6.5 ÷ 12.1 kJ/kg and 76 ÷ 84%, respectively.

Fig. 7
figure 7

Specific energy absorption (SEA) and total Ideality (It) bar plots of a Set L, b Set D, and c Set L × D. The graphs report the mean value and standard deviation evaluated among the three replicas of each tested configuration

Full size image

3.3 Impact test

For the impact test, a total of 36 samples were produced with both analysed polymeric materials. As mentioned above, the calibration test of the initial kinetic energy to set in the drop tower machine was performed at 50 J on L40_D2.0 (VF = 9.1%). The corresponding strain rate of the impactor is equal to 8.8 s−1. Both PA12 and TPU L40_D2.0 samples were tested. Figure 8 illustrates the results of the preliminary impact test of calibration.

Fig. 8
figure 8

Stress–strain curves of samples with configurations L40_D2.0 produced in PA12 and TPU materials and tested under high strain rate compression load equivalent to 50-J impact energy

Full size image

The exponential increase of the stress up to values close to 200 MPa indicates that the reticular structure collapses instantly at the impact. This finding can be explained by the brittle behaviour of the PA12, for which response is null due to the sudden and multiple internal fractures. Instead, the TPU sample immediately achieved densification due to the low stiffness of the material. Therefore, the reached high-stress value is associated with the force response at the impact between the mass impactor and the steel base plate on which the sample was placed. Considering all these evaluations, the energy level of the impact test was reduced to 25 J. At the same time, the selection of the 3D-CFSs was limited to five configurations reporting higher VF (Table 5).

Table 5 Configurations of the samples tested at high strain rate compression load and the related volume fraction (VF)
Full size table

For this second set of tests at high strain, the results for PA12 are reported in Fig. 9, in comparison with low strain (QS). The tests at high strain rate impact (12.4 s−1) loads on PA12 samples showed a significant discrepancy in terms of deformation mechanisms of the structure compared to the same configurations tested in quasi-static (QS) compression load (strain rate of 0.002 s−1). The high-speed movement of the impactor mass reduces the capability to compress and close the internal porosities of the struts with the axis parallel to the load direction exhibited in the low deformation regime, in agreement with the results reported in Ref. [22]. Therefore, the compression strength of the structure is reduced in the first part of the curve, which corresponds to a decrease in Young’s modulus compared to the QS samples. Moreover, except for the L36_D2.4 configuration, the plateau region shows an ascending behaviour that can be caused by a reduction of bending deformation among the struts combined with more rapid internal structure collapse.

Fig. 9
figure 9

Stress–strain curves of five PA12 3D-CFS configurations tested under low (0.002 s−1) and high (12.4 s−1) strain rate compression loads

Full size image

Despite the long strain reached before the densification stage, the SEA of some configurations tested in HS is slightly lower than the QS counterparts. In contrast to the QS samples (Fig. 10a), there is no correlation between the VF and SEA values for the HS samples. Also, there are appreciable deviations from the mean evaluated among the tested replicas. The presence of internal and external defects generated by the PBF process and the amount of impact load may lead to the rise of multiple fractures in stressed points. However, these fractures’ locations and propagation order may vary among the tested samples. This behaviour led to different energy absorption response levels. Moreover, as reported in the bar plot of Fig. 10b, the efficiency of the structure subject to HS impact is drastically affected by the energy loss generated by the lower Young modulus in the first part of the curve and by the not constant stress in the plateau region.

Fig. 10
figure 10

a Specific energy absorption (SEA) and (b) total Ideality (It) bar plots of PA12 3D-CFS configurations tested with quasi-static and high-speed compression loads. The graphs report the mean value and standard deviation evaluated among the three replicas of each tested configuration

Full size image

The comparison between 3D-CFS configurations in PA12 and TPU tested under the same load conditions of high strain rate impact is reported in Fig. 11. The substantial difference in stiffness and strength of the two investigated materials is evident. PA12 samples reached stress values almost double those of the TPU counterparts. However, the TPU structures showed a moderate elastic recovery with almost no fractures around the struts nodes compared to the PA12 counterparts. The low stiffness of the TPU material guaranteed that the structure accommodated the bending behaviour of vertical and horizontal struts more easily, as observed at low strain rate compression for PA12 [22]. These findings are confirmed by the constant stress value on the plateau region reported in most tested samples. In addition, thanks to the more controlled deformation mechanisms, the TPU samples show similar curves along the impact test with an identification of the densification point grouped in a limited range between 40 ÷ 60% of strain, in contrast to the PA12 counterparts (30 ÷ 70% of strain), as shown in the total Ideality graph of Fig. 11c and d.

Fig. 11
figure 11

Stress vs strain graph of high strain rate compression load tests of (a) PA12 and (b) TPU samples. Total Ideality (It) vs strain (ε) graph of (c) PA12 and (d) TPU samples

Full size image

The differences in strength between the two materials are emphasised by evaluating the SEA parameter (Fig. 12a). As mentioned before, the more controlled deformation mechanisms of TPU structures lead to low discrepancies in SEA values among the different configurations.

Fig. 12
figure 12

a Specific energy absorption (SEA) and (b) total Ideality (It) bar plots of PA12 and TPU 3D-CFS configurations tested with high-speed compression loads. The graphs report the mean value and standard deviation evaluated among the three replicas of each tested configuration

Full size image

Even if accentuated flatted stress–strain curves characterise the TPU samples, the lower stiffness generates lower EA efficiency than the PA12 (see Fig. 12b). As a visual example, the animation file provided as supplementary material compares the impact responses related to the L28_D2.0 structure manufactured in PA12 and TPU.

The acceleration vs. time graph is reported in Fig. 13. In general, PA12 samples absorb more energy with lower peak of acceleration (PA) values than the TPU samples. PA12 configurations are characterised by a decrease of the PA with the VF decrease. In contrast, the TPU counterparts depend on the PA with the diameter of the struts. As shown in Fig. 13b, the curves of the couples L24_D1.6/L28_D1.8 and L28_D2.0/L32_D2.0 overlap.

Fig. 13
figure 13

Acceleration vs. time graph of the 3D-CFS samples manufactured in (a) PA12 and (b) TPU materials. Each curve is centred around the main peak of acceleration

Full size image

Optimal PA values are achieved for both materials with the configuration L36_D2.4. This trend is also confirmed by the total Ideality index (Fig. 12b). The thicker diameter explains this superior performance of the L36_D2.4 over the other investigated configurations. These findings agree with the observation reported in Ref [22], for which the mechanical performances of artefacts produced via the PBF process are affected by the presence of internal pores that increase their damage effect with the decrease of the wall-thickness or diameter in the case of struts.

The detailed data of the energy performance parameters of the 3D-CFS configurations manufactured in PA12 and TPU materials and tested under high strain rate impact load are reported in Table 6.

Table 6 Energy absorption parameters mean values with the related standard deviation of the samples subjected to impact tests
Full size table

For comparison purposes, the EA performances of the 3D-CFS were compared with literature studies regarding cellular structures tested under HS, made PA12 or TPU, and manufactured via polymer-based AM technologies. The analysis is summarised in Table 7. For the sake of completeness, the value of EA performances of an EPS-60 [30] typically used in the head protection industry is also reported.

Table 7 Summary of energy absorption properties of AM polymeric cellular structures from the literature compared to a typical EPS foam of 60 kg/m3 used for impact applications
Full size table

Most structures reported in the literature are ordered and have multiple replications in the 3D space of a single-unit cell. As can be observed in Table 7, when axially compressed, the resulting structures can collapse slowly, reaching a high strain percentage with a low force response. Nevertheless, this behaviour represents a negligible quantity of absorbed energy per unit of volume. Therefore, despite a decent efficiency value, the low absorbed energy induces a high peak force generated from a dynamic impact load. Therefore, typically, the efficiency of such structures is much lower compared to EPS-60 [30]. In terms of SEA values, 3D-CFS TPU range between 2.5 and 3.5 kJ/kg, which is comparable to EPS-60 (2.76 kJ/kg), while PA12 3D-CFS performs considerably better (SEA between 7.5 and 17.4 kJ/kg), with a SEA value 170% higher than EPS-60, which is a reference for a typical material employed for head PPE.

4 Conclusion

The present research characterised the energy absorption capabilities of a 3D cross-based fractal structure (3D-CFS) manufactured via an advanced manufacturing technology: additive manufacturing. The fractal structure was designed and manufactured via the powder bed fusion (PBF) process with two different polymers, polyamide 12 (PA12) and thermoplastic polyurethane (TPU). The feasibility of the structure was investigated by varying the main geometrical parameters of the structure, the length (L), and the diameter (D) of the strut, which in turn generated 3D-CFS structures with different volume fractions. These experiments have determined a design window in which the structure was powder-free and corresponded to a volume fraction lower than 17% with a strut length higher than 20 mm. These structures were then tested under quasi-static compression loads to evaluate the energy absorption response. The results revealed that the increase of the VF implies an increase in specific energy absorption (SEA) but a decrease in the total Ideality parameter due to the high-stress response. Even if these findings have suggested that low VF 3D-CFS represent the optimal energy absorber under a low strain rate compression load, the impact tests (at high strain rate) revealed that these structures perform better with an average value of VF. Indeed, the brittle behaviour of the PA12 and the low stiffness of TPU affected the strength of the structure, which collapsed prematurely. Despite the permanent plastic deformation, PA12 3D-CFS guarantee superior EA performances with lower peak acceleration than the TPU counterparts. Compared to the literature data, PA12 3D-CFS is better, with a SEA value up to 170% higher than that of a typical material employed for head PPE. In contrast, TPU 3D-CFS looks more promising in the case of multiple impact conditions.

The limitation of this work can be found in the level of tested energy impact resistance, which should be, according to the standard for head PPE, at least equal to 50 J. However, it should be considered that the work investigated the properties of the single unit with limited dimension, while further experimental investigations are needed to evaluate the EA capabilities of the 3D-CFS inserted in a multiple-cell configuration. This configuration is expected to broadly enhance the dissipation of the impact energy while maintaining a high energy absorption [35]. The multiple-cell configuration may also consist of different 3D-CFS cells with tailored EA properties according to the helmet zone. In addition, the opposite behaviour of the two investigated materials suggests that their symbiosis could generate composite 3D-CFS structures with enhanced EA properties to address specific impact energy levels.