1 Introduction

Additive manufacturing (AM) is one of the pillars of the upcoming industry 4.0 revolution (4IR). This is a disruptive technology because of the reduction in waste and prototyping time, together with an increase in the digitalization of the manufacturing activity. Within AM framework material extrusion (MEX) plays an important role; it has become one of the most promising approaches to manufacture pneumatic actuators [1], microfluidic devices [2, 3], silicone implants [4], and composite structures [5,6,7].

The most widespread MEX process is fused filament fabrication (FFF). It consists in gradually melting a thermoplastic filament being conveyed in a heated cartridge by a pair of pushing gears; then, molten material is pushed through an extrusion nozzle and deposited on a built plate layer-by-layer, until the final part is built.

Nevertheless Pricci et al. [8] highlighted that FFF suffers of several limitations: the most critical for 4IR are the filament cost, limited range of printable materials, high environmental impact, and low productivity. In addition, the last step of product life cycle, which is the waste disposal, can be challenging.

More recently, pellet additive manufacturing (PAM) emerged as a promising MEX process: it consists in employing a screw-barrel system to convey, melt and pump pelletized thermoplastic material.

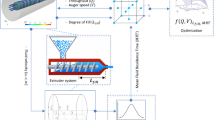
When dealing with large-screw extruders PAM has been also referred to as large-format additive manufacturing (LFAM). In the following, the general operations for a metering-type LFAM screw-barrel system are briefly recalled (Fig. 1).

Fig. 1
figure 1

Internal structure of a metering-type LFAM screw

Full size image

First, the pelletized feedstock is conveyed by gravity in a hopper. Then, it is compressed in the top vanes (solid-conveying zone) of a single-screw extruder (SSE). Next, pellet melts because of the heat supplied by a series of resistors placed on the external barrel (compression zone); according to Tadmor’s theory [9], the melting process takes place first near the external barrel wall. Subsequently, the rotational motion of the screw induces drag, which in turn moves the molten layer towards the screw flights, producing a lateral melt pool. Afterwards, molten material is conveyed (metering zone) towards the extruding nozzle. Finally, material is selectively deposited layer-by-layer to produce the final part.

Post et al. [10] highlighted the potential of LFAM for naval field; they illustrate the possibility to realize a boat hull mold by LFAM, without the need for expensive coating and steel substructures. Among the huge number of fields of applications, wind power is paramount; molds for a horizontal axis wind turbine were manufactured by means of one of the largest LFAM systems [11]. Next, blades were manufactured without any kind of wear on the original molds.

Cost saving is not the only relapse of LFAM with respect to 4IR paradigm. A comparison with respect to large-scale FFF has been performed in Table 1.

Table 1 Benefits and challenges of MEX processes in fulfilling 4IR’s requirements; \(\phi\) nozzle diameter
Full size table

It follows that LFAM is very promising in fulfilling several 4IR key requirements in the manufacturing field.

However, Post et al. [12] demonstrate that some disadvantages are related to difficult multi-material deposition and layer adhesion on large contact surfaces, poor part accuracy, and surface finish, which demands higher post-processing.

An accurate modeling of the thermophysical processes taking place in screw-barrel system is the basis for addressing the abovementioned challenges.

In 4IR, a second key pillar is the need for process simulations. To date, a complete and fast digital twin of the PAM process is still lacking. To achieve this goal, it is essential to elaborate reliable models for the screw-barrel system. This has been done both analytically and numerically [23,24,25,26,27]. Analytical tools are based on equations describing the process under a broad range of assumptions, which allow for a closed form solution. Numerical ones generally use commercial or home-made software to solve the original problem on a computational mesh. Solution accuracy is higher, but computing times are much longer.

On the other hand, semi-analytical methods are very promising since they allow solving more complex problems with reduced computational resources and times.

In screw-extrusion modeling, two commonly used assumptions are to (i) neglect channel curvature and (ii) assign the motion to the surrounding barrel instead of the screw. While the former results in a helical screw channel unwound into a rectangular one (parallel plate model, PPM) the latter consists in employing inverse kinematic conditions (IKC) [27].

Analytical solutions of the governing equations for the IKC-PPM model are possible for the one-dimensional and two-dimensional isothermal flow of Newtonian fluids [28].

Booy [29] has relaxed the PPM assumption for Newtonian fluids, taking in account the channel curvature. Rauwendaal et al. [30] studied the possibility to implement IKC in traditional PPM models, finding that the flow field does not depend on the exact kinematic conditions. Afterwards, Potente et al. [31] came to the same findings by means of finite element simulations. Habla et al. [32] showed that the abovementioned conclusion holds for the melt temperature rise.

However, the materials commonly employed in screw-extrusion processes usually show a shear-thinning behavior [33]. For that reason, the original Newtonian pumping model needs to be modified to account for non-Newtonian effects.

A very common non-Newtonian model used in literature is the power-law. Wilczyński et al. [34] studied the effect of the power-law and consistency indexes on the operating curves of screw-extruders, showing that they are highly non-linear especially at low power-law index values. Similar trends were found in [35] where a one-dimensional isothermal model for SSE was developed and compared with previously published experimental data, finding a very good agreement of pressure profiles and mass flow rates.

The governing equations are intrinsically non-linear and a general closed form analytical solution is not feasible. For that reason, semi-analytical IKC-PPM models are usually employed. Steller [23] studied the fluid flow of power-law fluids in high aspect ratio (AR) rectangular channels under isothermal flow conditions. Their theory has been extended in [36] to model the screw-barrel dynamics in injection moulding.

Das et al. [37] analyzed the conjugate heat transfer and fluid flow of power-law fluids in SSE via the finite volume method (FVM). Results match the experiments, confirming the FVM as a viable solution when simulating SSE.

The model proposed in [23] has been applied in PAM extrusion and the throughput limiting effect exerted by layer deposition has been accounted for in [33].

Recently, heuristic methods aiming at modeling the complex relation between process parameters, polymer rheology, and screw geometry have been formulated.

Roland et al. [38] addressed the effect of channel curvature for power-law fluids under IKC assumption; the error coming from neglecting curvature exceeds 10% when the barrel diameter to channel height ratio is lower than 10, which occurs in deep channel screw geometries. Then, Roland et al. [39] modeled the dimensionless throughput-pressure relationship by means of regression models.

However, thermoplastics usually show Newtonian and power-law behaviors at low and high shear rates, respectively. Rheological models as the Cross-WLF and Carreau-Yasuda are among the most representative of the viscous flow behavior in polymer processing. Unfortunately, the abovementioned models are highly non-linear and to date they have been studied only by means of computational fluid dynamics (CFD) simulations; in fact, the laminar flow along the streamwise and crosswise directions in screw vanes is governed by strongly coupled partial derivative equations.

Kadyirov et al. [25] investigated numerically the influence of screw geometry on the flow of a Cross fluid, finding a velocity profile along screw channel height flatter than for pure water, because of non-Newtonian flow characteristics. Compared to previous work, Vachagina et al. [26] considered also viscoelastic effects. However, a common problem in CFD is that it usually requires longer times to achieve a solution, if compared to analytical and semi-analytical methods.

In the present study, a semi-analytical IKC-PPM aiming at solving the isothermal flow of molten thermoplastics in the metering section of a metering-type industrial-scale SSE is presented.

The novelty is the applicability of the proposed approach to all generalized Newtonian fluid (GNF) models: the formulation is no longer restricted to the simple Newtonian and power-law rheologies.

The application is to the large metering-type screws typically employed in injection moulding, single-screw extrusion and LFAM.

The research paper is organized as follows: in Sect. 2.1, the properties of the material used in numerical validation have been stated. The mathematical model for the extrusion of power-law fluids is briefly recalled in Sect. 2.2. Next, the theory has been extended to GNF in Sect. 2.3. A design of experiment (DOE) has been introduced in Sect. 3.1 after finding the minimum set of dimensionless parameters. A comparison between CFD and both traditional (power-law) and proposed (GNF) methods has been performed in Sect. 3.2. Experimental validation with respect to available literature data has been done in Sect. 3.3. Finally, conclusions and further works have been outlined in Sect. 4.

2 Materials and methods

First, the material properties used in numerical validation of the proposed model have been declared. Then, the theory presented in literature for power-law fluids in the metering zone has been briefly recalled. Finally, the proposed GNF method is described.

All variables are listed in nomenclature.

2.1 Material properties

A particular grade of polylactic acid (PLA) manufactured by NatureWorks (NatureWorks Ingeo 3251D) was chosen for CFD validation against both traditional (power-law) and proposed (GNF) methods. The Moldflow software (Moldflow Plastics Labs. Ithaca, NY 14850, USA) was used to collect the material properties needed for CFD simulations.

The dynamic viscosity \(\eta \left(T; \dot{\gamma }\right)\) follows the Cross-WLF model:

$$\eta =\frac{{\eta }_{0}}{1{+\left(\frac{{\eta }_{0}\dot{\gamma }}{{\tau }^{*}}\right)}^{1-n}}$$
(1)

Here \({\eta }_{0}\) is the zero-shear viscosity:

$${\eta }_{0} ={D}_{1}{e}^{- \frac{A1\left(T-{T}_{g}\right)}{A2+T-{T}_{g}}}$$
(2)

Former parameters are detailed in Table 2.

Table 2 Rheological parameters for Ingeo 3251D
Full size table

2.2 A brief recall of the power-law model for SSE

The extrusion of power-law melts in SSE vanes (Fig. 2) has been modeled under the following assumptions:

  • Steady state extrusion process.

  • Incompressible flow.

  • Fully developed flow.

  • Isothermal flow.

  • Purely viscous flow: viscoelastic effects have been disregarded.

  • Gravity and inertia effects are negligible.

  • Constant channel geometry.

  • No vertical flow motion in the screw channel.

  • Unwound screw: the channel curvature is neglected (Fig. 2b).

  • Inverse kinematic conditions.

Fig. 2
figure 2

a Geometry of a single screw turn of the metering zone and b IKC-PPM geometry and operations, commonly used in theoretical models; W: channel width perpendicular to flight; S: screw lead; e: flight width; L: length of axial step; \(\varphi\): helix angle; Q: volumetric flow rate; N: screw speed; \({V}_{b}\): barrel velocity (IKC); \({V}_{bx}\): x-component of \({V}_{b}\); \({V}_{bz}\): z-component of \({V}_{b}\)

Full size image

Former assumptions have been recalled because they are the basis for formulating the GNF model (Sect. 2.3).

Steller showed that the flow problem in metering zone can be described by the following system of equations [23]:

$${\int }_{0}^{H}\frac{\partial {u}_{x}}{\partial y}dy={V}_{bx}$$
(3)
$${\int }_{0}^{H}\frac{\partial {u}_{z}}{\partial y}dy={V}_{bz}$$
(4)
$${\int }_{0}^{H}y\frac{\partial {u}_{x}}{\partial y}dy={V}_{bx}H$$
(5)
$$W{F}_{p}{\int }_{0}^{H}y\frac{\partial {u}_{z}}{\partial y}dy=Q-WH{V}_{bz}{F}_{d}$$
(6)

Former equations describe the one-directional (z-wise) flow of a molten thermoplastics. To account for the effect of the walls at low AR values, the correction factors for pressure (\({F}_{p}\)) and drag (\({F}_{d}\)) flows have been introduced [36].

The first equation is the integral form of the boundary condition for the velocity component along the \(x\) direction (\({u}_{x}={V}_{bx}\) and \({u}_{x}=0\) on barrel and screw surfaces, respectively); the second is the analogue for \({u}_{z}\) (\({u}_{z}={V}_{bz}\) and \({u}_{z}=0\) on barrel and screw surfaces, respectively); last two equations are the mass flow rate conservation principles along \(x\) and \(z\) directions, respectively.

Former system is valid no matter of the specific flow rheology. Therefore, it is the basis for the formulation of the GNF model in the next section.

The space derivatives in (3)–(6) have been specified for a power-law fluid [23]:

$$\frac{\partial {u}_{x}}{\partial y}={m}_{0}^{-\frac{1}{n}}\frac{\partial P}{\partial x}\left(y-{y}_{x}\right){\left[{\left(\frac{\partial P}{\partial x}\right)}^{2}{\left(y-{y}_{x}\right)}^{2}+{\left(\frac{\partial P}{\partial z}\right)}^{2}{\left(y-{y}_{z}\right)}^{2}\right]}^{\frac{1-n}{2n}}$$
(7)
$$\frac{\partial {u}_{z}}{\partial y}={m}_{0}^{-\frac{1}{n}}\frac{\partial P}{\partial z}\left(y-{y}_{z}\right){\left[{\left(\frac{\partial P}{\partial x}\right)}^{2}{\left(y-{y}_{x}\right)}^{2}+{\left(\frac{\partial P}{\partial z}\right)}^{2}{\left(y-{y}_{z}\right)}^{2}\right]}^{\frac{1-n}{2n}}$$
(8)

Here, \({m}_{0}\) is the consistency index, \({\text{n}}\) the power-law index, \(\partial P/\partial x\) the pressure gradient along \(x\) direction, \(\partial P/\partial z\) the one along \(z\), \({y}_{x}\), and \({y}_{z}\) both integration constants.

The system of Eqs. (3)–(6) consists of the following four unknowns:

$$\left\{\frac{\partial P}{\partial x}; \frac{\partial P}{\partial z};{y}_{x};{y}_{z}\right\}$$
(9)

It can be quickly solved by providing the Newtonian solution (\(n=1\)) as an initial trial.

The velocity components along the channel height \({u}_{x}(y)\) and \({u}_{z}(y)\) can be calculated based on previous trial solution.

2.3 Proposed approach: semi-analytical GNF model in SSE

Molten polymer flows typically exhibit complex rheological behavior, making it challenging to obtain an analytical solution (Fig. 3).

Fig. 3
figure 3

Transition from Newtonian to power-law behavior in Cross-WLF rheology (Material: Ingeo 3251D; temperature: \({T}_{b}\)=483.15 K); \(\eta\): dynamic viscosity; \({\Pi }_{d}\): shear rate

Full size image

At low shear rates, the fluid behaves as Newtonian (Newtonian regime), while at higher values it follows a power-law pattern (power-law regime). At intermediate shear rates, the material exhibits intermediate properties (transition regime).

An iterative method to deal with every GNF rheological model has been developed, and it follows some fundamental steps (Fig. 4):

  1. 1.

    Divide the channel height in \(k\) steps: the generic \(i\)-th position and spacing interval are therefore \({y}_{i}\) and \(\Delta {y}_{i}\), respectively.

  2. 2.

    Solve the system (3)–(6) assuming that the fluid behaves as a power-law fluid at barrel temperature \({T}_{b}\).

  3. 3.

    Evaluate local velocity derivatives (\({\left.{\dot{\gamma }}_{xy}\right|}_{{y}_{i}}\) and \({\left.{\dot{\gamma }}_{zy}\right|}_{{y}_{i}}\)) according to (7) –(8).

  4. 4.

    Calculate the shear rate at each location \({y}_{i}\):

    $${\left.{\Pi }_{d}\right|}_{{y}_{i}}=\sqrt{{{\left.{\dot{\gamma }}_{xy}\right|}_{{y}_{i}}}^{2}+{{\left.{\dot{\gamma }}_{zy}\right|}_{{y}_{i}}}^{2}}$$
    (10)
  5. 5.

    Get into the double logarithmic rheological chart of the molten polymer with the shear rates \({\left.{\Pi }_{d}\right|}_{{y}_{i}}\).

  6. 6.

    Find the tangent line at each \({\left.{\Pi }_{d}\right|}_{{y}_{i}}\) and calculate local values of consistency index (\({\left.{m}_{0}\right|}_{{y}_{i}}\)) and power-law index (\({\left.n\right|}_{{y}_{i}}\)).

  7. 7.

    Evaluate the solution to the modified system:

    $${\left.\frac{\partial {u}_{x}}{\partial y}\right|}_{{y}_{1}}\Delta {y}_{1}+\dots +{\left.\frac{\partial {u}_{x}}{\partial y}\right|}_{{y}_{n}}\Delta {y}_{n}={V}_{bx}$$
    (11)
    $${\left.\frac{\partial {u}_{z}}{\partial y}\right|}_{{y}_{1}}\Delta {y}_{1}+\dots +{\left.\frac{\partial {u}_{z}}{\partial y}\right|}_{{y}_{n}}\Delta {y}_{n}={V}_{bz}$$
    (12)
    $${\left.\left(y\frac{\partial {u}_{x}}{\partial y}\right)\right|}_{{y}_{1}}\Delta {y}_{1}+\dots +{\left.\left(y\frac{\partial {u}_{x}}{\partial y}\right)\right|}_{{y}_{n}}\Delta {y}_{n}={V}_{bx}H$$
    (13)
    $${F}_{p}\left[W{\left.\left(y\frac{\partial {u}_{z}}{\partial y}\right)\right|}_{{y}_{1}}\Delta {y}_{1}+\dots +{\left.W\left(y\frac{\partial {u}_{z}}{\partial y}\right)\right|}_{{y}_{n}}\Delta {y}_{n}\right]=Q-WH{V}_{bz}{F}_{d}$$
    (14)
Fig. 4
figure 4

Iterative method for the calculation of GNF fluid flow in screw channel

Full size image

Here each space derivative still follows Eqs. (7) –(8), but local consistency and power-law indexes are employed. Integrals are discretized as summations using the Gauss-Legendre quadrature. This discretization is particularly efficient, because it places more nodes near the channel boundaries, where boundary layer develops.

  1. 8.

    Iterate points 3 to 7 until the maximum deviation on consistency and power-law indexes between successive iterations goes below a threshold, set to 0.01% in all calculations; preliminary studies showed that a lower threshold value results in longer computational times and practically no significant enhancement in solution accuracy.

MATLAB R2021b was chosen to implement the calculation routine for both power-law and GNF methods.

The software used in CFD computations is Ansys Fluent v.19.2. The purpose is to describe numerically the flow field in the rectangular screw channel under the IKC-PPM assumptions. Details of the CFD model have been reported in section SI.1 (Supplementary Information), together with the indispensable mesh-independence study.

3 Results and discussion

In this section, the power-law and GNF methods were evaluated across a comprehensive range of operating conditions, encompassing the minimum set of dimensionless process parameters. It was found by applying Buckingham π theorem; then, two to three levels have been set for each parameter, and a full factorial plane was chosen. The theory has been compared with CFD results, for a particular material suitable for PAM applications (see Table 2). Lastly, the traditional (power-law) and proposed (GNF) methods have been applied to real screw extruders.

3.1 Buckingham analysis and design of experiment

The analysis of Eqs. (3)-(8) provides an indication of the fundamental operating parameters which affect the extrusion outcomes:

$$\left\{W;H;{D}_{b};{T}_{b};{T}_{g};u; N\right\}$$
(15)

By applying Buckingham analysis, it is possible to find the minimum number of dimensionless parameters.

First, it is worth noting that the abovementioned quantities are characterized by only three physical fundamental dimensions (denoted with square brackets, in the following): length \(\left[{\text{L}}\right]\), temperature \(\left[T\right]\) and time \(\left[S\right]\). Then, the full vector of operating parameters (15) is made dimensionless. To do this, some of the former parameters (base vector, in the following) are used to make dimensionless the remaining ones.

The base vector is made up of as many parameters as the physical dimensions. Here, three parameters must be chosen. Let’s call them generically \(({V}_{1};{V}_{2};{V}_{3})\).

Two conditions must be fulfilled by the chosen vector basis:

  • The parameters \(({V}_{1};{V}_{2};{V}_{3})\) shall include all fundamental physical dimensions (here \(\left[L\right]\), \(\left[T\right]\), and \(\left[S\right]\))

  • The product of the fundamental dimensions of \(({V}_{1};{V}_{2};{V}_{3})\) must give null vector, namely:

    $$\left[{V}_{1}\right]\left[{V}_{2}\right]\left[{V}_{3}\right]={\left[L\right]}^{0}{\left[T\right]}^{0}{\left[S\right]}^{0}$$
    (16)

A suitable base vector in (15) is:

$$\left\{{D}_{b};{T}_{g};N\right\}$$
(17)

As a result, the final set of dimensionless parameters is:

$$\left\{\frac{W}{{D}_{b}};\frac{{D}_{b}}{H};\frac{{T}_{b}}{{T}_{g}};\frac{u}{ND}\right\}$$
(18)

It is worth mentioning that last parameter is equivalent to the dimensionless flow rate (\({\Pi }_{{\text{V}}}\)) analyzed in [38] apart from a multiplicative constant:

$${\Pi }_{V}=\frac{2Q}{WH{V}_{bx}}$$
(19)

The final set of dimensionless parameters has been reported in Table 3.

Table 3 Minimum set of operating parameters
Full size table

Two values (low and high) were assigned to W*, H* and T* while three levels (low, intermediate and high) were set for \({\Pi }_{{\text{V}}}\), based on practical LFAM extrusion conditions. In Table 4, the full DOE has been outlined and both dimensional and dimensionless parameters have been shown; the dimensional ones have been reported to provide a quick insight in the order of magnitude of the different process parameters. In addition, the AR in each simulation has been reported, and the suitability of the GNF model for low AR has been verified numerically.

Table 4 Design of experiments
Full size table

The effect of curvature on screw pumping characteristics is significant if \({H}^{*}<10\), when dealing with shear-thinning fluid flowing in metering zone [38]. For that reason, it has always been set \({H}^{*}\ge 10\), which is typical of injection moulding and LFAM screws.

Lowest barrel temperature (\({T}_{b}=\) 433.15 K) was chosen according to the minimum processing temperature for INGEO 3251D suggested in the material technical data sheet. The highest value (\({T}_{b}=\) 483.15 K) was chosen based on the suggested printing temperature interval for this material (473 K to 493 K).

Moreover, most mass flow rate (\(G\)) values are typical of a 50 mm screw LFAM extruders. Duty et al. [13] show that larger screw-barrel systems employed in LFAM arrive up to 50 kg/h. Because of the continuous improvement in LFAM, even higher throughputs are investigated (see Table 4).

3.2 Result comparison

The methods introduced in Sects. 2.2 and 2.3 were compared first with numerical methods, based on the CFD model described in Supplementary Information.

The investigation was done with respect to former DOE (Table 4), and the flow field along \(x\) and \(z\) directions was found by applying:

  • Power-law, and

  • GNF methods

Results for the lower dimensionless temperature (\({T}^{*}\)=1.16) are reported in Fig. 5.

Fig. 5
figure 5

Analysis of \({u}_{x}\) and \({u}_{z}\) velocity components along channel height (\(y\)) at different values of dimensionless parameters (\({T}_{b}\)=433 K); square markers: power-law model; circular markers: GNF semi-analytical method; solid line: CFD results

Full size image

Each chart represents a DOE test point; both velocity components are represented as functions of the channel vertical coordinate (\(y\), in Fig. 4).

When considering the lowest value of the dimensionless flow parameter \({\Pi }_{V}\) both power-law and GNF methods agree well with CFD results.

It should be noted a marked deviation between the two semi-analytical models when higher values of \({\Pi }_{v}\) are set. This is especially true for the z-wise (\({u}_{z}\)) velocity component, which is although the only responsible for the mass flow rate conveying.

The GNF method agrees well with numerical results at all processing conditions, showing the limit of the traditional power-law model especially near the channel height centerline. The highest deviations of the traditional approach from CFD occur when considering low values of channel width and height, as shown in Fig. 6.

Fig. 6
figure 6

Analysis of \({u}_{x}\) and \({u}_{z}\) velocity components along channel height (\(y\)) in the most critical case (Index 3 in Table 4); square markers: power-law model; circular markers: GNF semi-analytical method; solid line: CFD results

Full size image

Maximum deviations reached 45.86% (at y = 1.5 mm) and 6.12% (at y = 2.5 mm) on \({u}_{x}\) and \({u}_{z}\) velocity components, respectively.

The discrepancy between CFD and power-law results is motivated as follows: near channel height centerline, velocity profile is flatter and local shear rate goes to approximately zero. At low shear rates, the material behaves as a Newtonian fluid (Fig. 3), and classical power-law model is not well suited because it predicts higher viscosity values. It brings to overall lower velocity values.

Similar conclusions can be drawn at higher \({{\text{T}}}^{*}\) (Fig. 7).

Fig. 7
figure 7

Analysis of \({u}_{x}\) and \({u}_{z}\) velocity components along channel height (\(y\)) at different values of dimensionless parameters (\({T}_{b}\)=483 K); square markers: power-law model; circular markers: GNF semi-analytical method; solid line: CFD results

Full size image

As highlighted in Table 5, the mean absolute deviation in overall flow speed \(\left(\sqrt{{u}_{x}^{2}+{u}_{z}^{2}}\right)\) when applying the GNF method and CFD \(\left({\left.\overline{{\varepsilon }_{{\text{rel}}} }\right|}_{{\text{GNF}}}\right)\) is very small, if compared to traditional power-law and CFD \(\left({\left.\overline{{\varepsilon }_{{\text{rel}}} }\right|}_{{\text{PL}}}\right)\), thus justifying the application of the proposed (GNF) approach:

Table 5 Mean relative error of the proposed (\({\left.\overline{{\varepsilon }_{rel} }\right|}_{GNF}\)) and traditional (\({\left.\overline{{\varepsilon }_{rel} }\right|}_{PL}\)) methods on total flow velocity with respect to CFD simulations
Full size table

Differences between traditional (power-law) method and CFD become significant when dealing with higher flow rates (up to 12.91%). On the other hand, the match between the proposed (GNF) method and CFD holds.

A significant improvement in computational time has been achieved; while CFD simulations performed on an Intel Core i5-6200U CPU with 2 physical cores took over two hours to get complete, the full DOE was solved in 3:57 min (time reduction 96.70%) and 2.30 min (time reduction 97.91%) with the proposed (GNF) and traditional (power-law) iterative methods, respectively. This comes mainly from the reduced-order nature of the iterative models, if compared to three-dimensional CFD simulations.

In addition, a maximum of 12 iterations were needed on the same hardware, with 30 Gauss–Legendre nodes placed along the channel height and a 0.01% threshold in each simulation, showing the fast-converging nature of the proposed method.

A comprehensive comparison among the three proposed methods has been shown in Table 6.

Table 6 Overview of the main features of the proposed (GNF) and traditional (power-law) methods compared to CFD solutions
Full size table

3.3 Experimental validation

The CFD validation provided important insights regarding the flow field in the screw vanes. Next, power-law and GNF methods were applied to predict the pressure drop in the last turns of industrial-scale metering-type screws.

The accuracy of the traditional power-law method was tested by means of the relative error with respect to the pressure drop data declared in literature:

$${\varepsilon }_{\%, PL}=100 \frac{\Delta {p}_{exp}-\Delta {p}_{PL}}{\Delta {p}_{exp}}$$
(20)

Here, \(\Delta {p}_{exp}\) is the experimental value of pressure drop, while \(\Delta {p}_{PL}\) is the one calculated by applying power-law rheology.

A similar formulation has been chosen to test out the proposed GNF method (pressure drop \(\Delta {p}_{{\text{GNF}}}\)):

$${\varepsilon }_{\%, GNF}=100 \frac{\Delta {p}_{exp}-\Delta {p}_{GNF}}{\Delta {p}_{exp}}$$
(21)

Han et al. [40] studied the fluid flow of power-law fluids in the metering zone; the authors propose an analytical method, comparing the pressure distribution along the screw with experiments for both a Davis-standard metering-type and a barrier type SSE. The focus of the present research is on former screw model.

Since molten thermoplastics (polystyrene and polycarbonate) follow the power-law model, the results of the power-law and GNF models are expected to be the same.

A direct comparison with experimental pressure drop has been provided in Table 7.

Table 7 Comparison between pressure drops declared in [40] (screw turns from number 17.91 to 23.73) and both power-law (PL) and present semi-analytical (GNF) methods; all pressure drops in MPa
Full size table

Power-law and GNF methods matched experiments in all conditions. The novelty lies in the better agreement of experimental pressure drop in the last screw vanes of a metering-type screw, if compared to Han’s analytical model (\({\varepsilon }_{\mathrm{\%},\mathrm{ Han}}\) in Table 7). Deviations are still present and are rooted in the non-isothermal nature of the flow field which develops also in the last screw turns.

A second validation was done with respect to the pressure profile declared in [24], where a low-density polyethylene resin was extruded with a metering-type screw at varying screw speeds.

The material behaves as a Cross-WLF fluid. Therefore, deviations from power-law model results are expected (Table 8).

Table 8 Comparison between pressure drops declared in [24] (axial screw positions from 750 to 1200 mm) and both power-law (PL) and present semi-analytical (GNF) methods; all pressure drops in MPa
Full size table

The experimentally measured mass flow rates were used as inlet boundary conditions for the power-law and GNF models. High discrepancies are found when applying former method to describe the fluid flow of a molten polymer which exhibit both Newtonian and non-Newtonian features (up to 62%). The error can be considerably reduced by using the GNF model. As in previous experimentation, the non-isothermal effects potentially can affect the pressure behavior along the screw extruder and are responsible for the modest difference with experimental data.

4 Conclusions

A fast and accurate method aiming at describing the fluid flow of molten thermoplastics in the last turns of SSE suited for LFAM applications has been presented. First, the minimal set of dimensionless parameters found via Buckingham analysis has been investigated. The goal was to evaluate how the proposed method deviates from both CFD and classical power-law theory. For that reason, a DOE (full factorial) was implemented based on the fundamental dimensionless parameters.

A modest deviation of the proposed GNF method from the classical power-law one was observed at low values of dimensionless flow parameter \({\Pi }_{v}\), when considering lower \({T}^{*}\). Discrepancies increase when dealing with higher flow rates, because the velocity profile near the channel height centerline becomes flatter; in this flow region a very low shear rate develops and fluid follows a Newtonian-like flow behavior. The power-law model overestimates the local dynamic viscosity, leading to overall lower velocities. This is even more true at higher \({T}^{*}\), which is more representative of real PAM temperature settings.

The mean error on overall flow speed reduces from 12.91% (traditional power-law method) to 1.04% (proposed GNF method), when high flow rates are considered.

In addition, a remarkable reduction in computational time with respect to CFD was observed (96.70 and 97.91% for GNF and power-law methods, respectively). The higher accuracy of the proposed GNF formulation with respect to traditional models justifies its application in real extrusion scenarios.

Then, experimentally measured pressure drops developing in industrial-scale SSE were compared with both power-law and GNF methods: when fluid flow exhibits both Newtonian and power-law characteristics, a significant discrepancy with real pressure drops is found, when adopting classical power-law theory (error ranging between 34.33 and 62%). The GNF method lowers this gap (error ranging between 5.34 and 10.97%).

The higher accuracy of the proposed GNF method with respect to traditional ones and its fast convergence paves the way for its application to enhance LFAM systems’ design.

To date, the proposed method does not account for non-isothermal and viscoelastic effects, which are very important to further reduce the abovementioned gaps. Further research will be dedicated to address the effect of elasticity and temperature gradients on the flow field in screw metering zones.