Modelling and simulation of heat flow in indexable insert drilling

Abstract

In machining, the heat generated during the process deforms the components and the final shape might not meet specified tolerances. There is therefore a need for a compensation strategy which requires knowledge of the workpiece temperature field and the associated thermal distortions. In this work, a methodology is presented for the determination of the heat load for indexable insert drilling of AISI 4140. Compared to previous research, this work has introduced a varying heat load. The heat load is extracted from thermo-mechanical finite element simulations for different nominal chip thicknesses and cutting speeds using the coupled Eulerian-Lagrangian formulation of an orthogonal turning process. The heat load is then transferred to a simplified 2D axisymmetric heat transfer model where the in-process temperature field in the workpiece is predicted. To verify the methodology, the predicted temperatures are compared to the experimentally measured temperatures for various feed rates. It is found that the model is capable of predicting the workpiece temperatures reasonably well. However, the methodology needs to be further explored to validate its applicability.

1 Introduction

The heat produced during machining processes is often a major concern in the manufacturing industry as the thermo-mechanical deformations can compromise the dimensional tolerances. In e.g. [3], the influence of heat load on the final shape is clearly demonstrated for several machining processes. The challenge this poses becomes even greater with the ongoing trend, driven by increasing environmental and cost requirements, to reduce the use of cutting fluids by using minimum quantity lubrication (MQL) or even better dry cutting. However, this leads to further increases in heat load on the workpiece and thus also the thermal distortions of the workpiece. In [9], the authors show that cutting fluids improve hole quality in drilling in both aluminium alloys and grey cast iron. The main explanation was the cooling effect of the cutting fluids. If the heat load is significant, residual stresses can also lead to final form errors. Depending on the shape of the component, residual stresses can be more or less of a concern where e.g. thin-walled components are usually more sensitive than stiffer solid geometries. This is illustrated e.g. in [8] where a compensation strategy is developed by a numerical study of both the residual stresses and the thermal stresses during face milling of steel plates.

To meet the dimensional tolerances in the presence of substantial heat loads, the thermal deformations needs to be accurately predicted and compensated for. Depending on the cutting parameters, material properties and the geometry of workpiece and cutting tool, the heat entering the workpiece and the resulting distortions are different. Extraction of this data through physical trials are costly and time-consuming, and it is therefore highly desirable to enable the use of modelling and simulation, e.g. the finite element (FE) analysis. FE modelling of cutting processes is however in general computationally demanding. As discussed in [12], where the authors provide a relatively recent overview of current status and challenges in FE modelling of machining processes, there are major challenges in modelling the extremely nonlinear processes at the cutting zone such as large plastic deformations, multiple contact surfaces and possibly crack propagations. To predict shape deviations driven by thermal deformations, however, the local processes near the cutting zone are often of secondary importance and instead a global idealized model can be used that only simulates the influence of the thermal load, and sometimes also the forces, acting on the workpiece. Such an approach is used in e.g. [6] where an axisymmetric FE model is developed to predict thermal distortions in drilling. The thermal load, represented as an analytically calculated surface heat flux, is subjected along the cutting edge where the imaginary tool is located and elements are continuously removed as the imaginary tool passes by. In this work, this modelling approach is referred to as the reduced heat transfer (RHT) methodology.

The thermal load on the workpiece and the resulting temperature field should be accurately computed for various cutting data. Several methods have been presented in the literature, and the most frequently used is the inverse heat transfer method where the heat load is determined by fitting the simulated temperatures to the experimentally measured counterparts (see e.g. [22]). In [19], the authors performed experiments and FE simulations of turning of aluminium. They calculate the heat flux from experiments for successive use in 2D axisymmetric FE simulations of a turning process. The final diameter deviation of the workpiece, due to thermal expansions and deflections of both the workpiece and the system tool-tool holder, was successfully predicted. Simulation-based approaches have also been presented in e.g. [16] for determination of the heat partition, i.e. the proportion of the total heat generated during cutting that flows to the workpiece, the chip and the tool, respectively. In [15], the authors studied longitudinal turning. They computed the heat flux from a transient 3D thermo-mechanical coupled Eulerian-Lagrangian method for subsequent use in a 2D implicit axisymmetric thermo-mechanical analysis that determined workpiece deformations with promising results. In [17], the authors predicted in-process temperatures during milling of S235 steel. The heat flux obtained from 2D simulations were used in a 3D transient heat transfer model of a more complex process for prediction of both the workpiece and tool temperatures. In the RHT methodology, the heat load can be applied in various ways depending on the purpose of the analysis. In [7], thermal deformations were analyzed during milling of a thin-walled component. The heat load was applied as a transient temperature field, and the model was able to predict the dimensional errors. In [5], different levels of abstraction were studied. The heat flux was not explicitly applied, but instead, a prescribed temperature was on the nodes near the cutting region. Three different approaches were adopted where the level of abstraction was refined between each analysis by prescribing the temperature in different sections and, in the next step, removing the material that has been “machined” in the previous step. They concluded that the results show great influence on the local temperature distribution which was important since they studied phase transformation near the cutting zone. However, refined models are computationally more expensive, and globally, the temperature field is not deviating considerably between the different types of analyses. Since it also is of interest to reduce computational times, the effect of model reductions was presented in [11]. In simulation of milling, they changed the width of the heat source and also the material removal width to analyze the influence of the temperature distribution. By comparing with experiments, it is found that the model was able to predict the temperature distribution and at the same time save 98$\%$ of the computation time.

In drilling, both the feed rate and the cutting speed strongly influence the workpiece temperature. Deep-hole drilling of an aluminium cast alloy with a twist drill was performed in [4] where also the effect of MQL was studied. They found that the feed rate is the determining factor for both the mechanical and thermal load on the workpiece, and the results indicate that the lower the feed rate, the higher the workpiece temperature. A similar study is presented in [20]. In this study, the aim is to predict the workpiece temperature during indexable insert drilling of AISI 4140. Indexable drilling has gained increased interest and offers a strong alternative to drill short holes at a low cost, but the number of studies of this process is limited. Especially, temperature predictions which are a prerequisite for dealing with thermal deformations have not yet been presented.

In this study, the RHT methodology is adopted to predict workpiece temperatures during an indexable drilling process. The method presented in [16] is used to compute the heat load where a FE model of orthogonal cutting using the CEL formulation is employed. A corresponding surface heat flux is subsequently determined and transferred to the RHT model for the prediction of the workpiece temperature. To verify the model, the temperatures from simulations are compared with experimental counterparts measured in indexable drilling tests for different feed rates. This work is an extension of the work by [14] by introducing a varying heat load since the indexable drill has a linear cutting speed in the radial direction of the tool.

Fig. 1

Schematic view of the RHT methodology used for indexable drilling

The paper is organized as follows: first, the RHT methodology is briefly described. Then, the method for extracting the heat is described. Then, the orthogonal experiments and simulations are explained where the extraction of the heat load is performed. After that, a section where the experimental set-up of the indexable drilling is described follows a description of the modelling approach used in this framework. Finally, the numerical and experimental results are presented. The paper ends with some conclusions and discussed along with suggestions for further work.

2 Methodology

In the RHT methodology, the cutting forces are of interest because they have a large impact on the heat contribution. Since the heat is controlling the in-process temperature of the workpiece and consequently the thermal expansion, this affects the distortion of the workpiece. Note that the deformation due to the forces themselves is not included in this approach. However, depending on the application, these forces might be of importance.

The RHT methodology is not restricted to indexable drilling. However, this process has a relatively long zone where the nominal chip thickness does not change that much along the cutting edge. This makes it suitable for the RHT methodology.

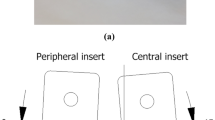
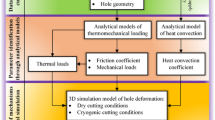
The methodology for indexable drilling is shown in Fig. 1. The indexable drill consists of two inserts placed in a tool holder. The inserts rotate around the central axis meaning that the cutting edge can potentially be cut with different cutting speeds and feed rates depending on the arrangement of the inserts. With a constant rotational speed, the cutting speed is linear in the radial direction from the axis. It is well known that the heat produced in a cutting operation is dependent on the above-mentioned parameters. In this work, a major assumption is that the cutting edge can be divided into small regions and that each region generates heat that only depends on the local cutting speed, $v_c$ and chip thickness, $h_a$ at this region. This is illustrated in Fig. 1 (top middle) where the heat load $\dot{Q}(h_a,v_c)$ at a specific region is the heat that enters the workpiece during a specific time.

In the RHT methodology used in this work, the cutting edge is divided into arbitrary small regions (or zones). Each region has the same cutting geometry except for at the corners of the insert as illustrated in Fig. 1. It is further assumed that the cutting process in each region occurs independently from the adjacent ones. This resembles an orthogonal cutting operation, and $\dot{Q}(h_a,v_c)$ is set individually for every region. To determine $\dot{Q}(h_a,v_c)$, several 3D orthogonal cutting simulations are performed using a 3D CEL transient thermo-mechanical FE analysis. These are performed with different cutting speeds and nominal chip thicknesses. The simulations are compared to orthogonal turning experiments to validate that the parameters are reasonable. Here, only the cutting force $F(h_a,v_c)$ is validated. With the heat load established, it is transferred to the RHT model which is a 2D axisymmetric transient heat transfer model of indexable drilling experiments of cylindrical test specimens. The heat load is given as a heat flux $\dot{q}(h_a,v_c)$ as this is needed in the FE simulation. Finally, temperatures at specific points are measured in experiments using thermocouples, and these are compared with simulations.

3 Method for extracting the heat load

The method to extract the heat is based on the work presented in [16] where a 3D CEL model is used to calculate the rate of internal heat of a moving control volume in the workpiece. The heat is emanating primarily from the plastic deformation in the primary zone but also from friction in the secondary shear zone and the flank face. This heat is transferred to different regions (see Fig. 2).

Fig. 2

Moving control volume for heat flux determination

In [16], the heat rate per unit width of the workpiece is shown to be given by

$$\begin{aligned} \dot{Q}_w = \frac{v_c}{l_w\, w_w} \int _V c_w \,\rho _w \, (T-T_0) \, \textrm{d}V \end{aligned}$$

(1)

where $v_c$ is the cutting speed, $l_w$ is the distance moved by the control volume, $w_w$ is the width of the control volume, $c_w$ is the specific heat capacity, $\rho _w$ is the density and $T-T_0$ is the temperature difference between the times $t-t_0$. In the actual simulations, it is sufficient to take the difference between the heat entering region 3 and region 1 since the moved control volumes share region 2. In steady state, the heat in region 1 is constant for all simulations meaning that it can be determined analytically. The simulation gives the temperatures in region 3 and consequently the increase of heat energy in the control volume.

The outcome of the CEL simulations is the rate of heat flow, $\dot{Q}_w$ entering the workpiece. By running the simulation with different nominal chip thicknesses, $h_a$ and cutting speeds, $v_c$, $\dot{Q}_w$ at steady state for all the combinations are determined. Then, it is transferred to the RHT models for which the details are given in a later section. No temperatures are measured, but instead, it is verified that the cutting forces are in line with experimentally obtained ones. Since this is the case, the model is judged suitable for obtaining the heat load.

4 Orthogonal turning experiments and simulations

4.1 Orthogonal turning experiments

Ribbed solid bars are prepared by producing 2-mm thick flanges through multiple external slots using a grooving tool with a width of 3 mm. For each specimen, there are in total six flanges (see Fig. 3).

All the orthogonal experiments are performed in a SOMAB 500 CNC lathe under dry conditions. In order to perform the orthogonal test, a tool bar is designed and manufactured. It is designed to adapt to inserts and the tool holder that is used with a Kistler force transducer model 9121 for the measurement of the cutting and the feed forces. The holder is also manufactured to fit the inserts to obtain a rake angle of $0^{\circ }$ and a clearance angle of $8^{\circ }$ as is used in the indexable drilling experiments. The insert is manufactured by KOMET and is designated SOEX 07T308-1. The force transducer is connected to a multichannel charge amplifier, and Matlab data acquisition toolbox is used for collecting the data.

Fig. 3

Experimental set-up for orthogonal turning

Four experiments for the feed rates 0.13, 0.16, 0.18 and 0.22 mm/rev are conducted resulting in 16 tests in total. These are the same feed rates as used in the indexable drilling experiments. The insert is rotated $90^{\circ }$ after each test, and after four experiments, the insert is replaced, i.e. a new cutting edge is used for each experiment. The cutting speed is 3 m/s for all the orthogonal experiments and is chosen based on the maximum cutting speed obtained from the indexable drilling experiments.

4.2 3D CEL model of orthogonal turning

Abaqus/Explicit CAE ver. 2017 is used for all the FE-models in this paper. Figure 4 shows the 3D CEL model. The model accounts for both thermal- and mechanical stresses, and therefore, a fully coupled 3D thermal-stress analysis is conducted. The large chip width/ thickness ratio and the fact that the problem is orthogonal suggest that a 2D plane strain model would suffice to represent the cutting process. However, since only 3D Eulerian elements are allowed in Abaqus/Explicit 2017, the assumed plane strain conditions are mimicked by letting one element model the width and suppressing the out-of-plane displacements. A 3D scanning of the insert used in the experiments is performed, and the model is transformed into a 3D CAD model. This model is sliced to obtain the 2D geometry used to model the insert. The light grey domain indicates the Euler space, and the embedded dark region of height 1.4 mm is initially filled with workpiece material.

Fig. 4

CEL orthogonal turning model. Dashed lines indicate surfaces with a prescribed velocity

The boundary conditions are imposed on the dashed-lined boundaries. The horizontal velocity of the workpiece, $v_x$, is varied and is set to 0.5, 1.0, 2.0 and 3.0 m/s. The cutting speed is set to 3 m/s, i.e. the same as in the indexable drilling experiments. In addition, the vertical velocity is $v_y=0$ for all analyses. The rigid tool is kept fixed in space and is oriented with a $0^{\circ }$ rake angle (excluding the chip breaker) and a $8^{\circ }$ clearance angle. For simplicity, all free surfaces of the Eulerian space are modelled as adiabatically insulated.

The flow stress for AISI 4140 is described by the commonly used Johnson-Cook (JC) model given by

$$\begin{aligned} \bar{\sigma } \!=\! \left[ A \!+\! B\left( \bar{\varepsilon }^p \right) ^n \right] \left[ 1\!+\!C\, \textrm{ln} \left( \frac{\dot{\bar{\varepsilon }}^{p}}{\dot{\varepsilon _0}} \right) \right] \left[ 1- \left( \frac{T-T_0}{T_m-T_0} \right) ^{m} \right] \end{aligned}$$

(2)

where A, B, C and m are constants; n is the strain hardening exponent; $\dot{\bar{\varepsilon }}^p$/${\dot{\varepsilon _0}}$ is the normalized equivalent plastic strain rate; T, $T_{m}$, $T_{0}$, $\bar{\varepsilon }^p$ and $\dot{\bar{\varepsilon }}^p$ represent the temperature, melting temperature, room temperature, equivalent plastic strain and equivalent plastic strain rate, respectively.

In [21], the same indexable drilling process is studied using the same tool and workpiece material. Therefore, the same material and contact parameters are used in this work, but they are for clarity also presented in this section. The JC parameters are taken from the literature [13] and are presented in Table 1. The thermo-mechanical parameters are also taken from literature [1] and are presented in Table 2. Damage initiation and evolution are not employed in the current model indicating that plasticity controls the behaviour of the material.

Table 1 Johnson-Cook constants for AISI 4140 [13]

Table 2 Thermo-mechanical parameters for the insert and the workpiece material [1]

The frictional shear stress is given by

$$\begin{aligned} \tau _f = \text {min} \left( \mu p,\tau _p\right) \end{aligned}$$

(3)

where $\mu$ is the friction coefficient, p is the contact pressure and $\tau _p$ is the maximum frictional shear stress. The sliding friction is modelled with Coulomb friction with $\mu = 0.4$, and the limit for the shear stress is $\tau _p = A/\sqrt{3}\approx 343$ MPa.

The heat conductance between the tool and the workpiece is assumed to be pressure-dependent. The heat conduction coefficient is taken from [18], is given in Table 3 and has been used in e.g. [23] and [2]. All the heat that are produced in the contact zone are transferred to the tool and the workpiece. The heat convection is assumed negligible and is set to zero.

Table 3 Pressure-dependent heat conduction coefficient

Fig. 5

a Tool holder with inserts. b Bottom view of tool with the two inserts. c Example of drilled test specimen

A mesh convergence study is also undertaken, and the initial mesh of the workpiece consists of roughly 35,000 EC3D8RT elements. The region containing the cutting zone is meshed with an element length and height of 25 $\upmu$m and 10 $\upmu$m, respectively. About 2200 thermally coupled 8-noded brick elements with an element edge length near the cutting edge of about 8.5 $\upmu$m are used to model the insert. The element size for the workpiece is then reduced in steps from the initial 25 $\upmu$m x 10 $\upmu$m to 22 $\upmu$m x 7 $\upmu$m and finally 20 $\upmu$m x 5 $\upmu$m.

5 Indexable drilling experiments and simulations

5.1 Indexable drilling experiments

The indexable drilling experiments are performed in a GROB G300 4-axis machining center under dry conditions. The tool holder and the inserts are shown in Fig. 5a and b. The holder provides a rake angle of $0^{\circ }$ if the chip breaker on the inserts is ignored. Moreover, the central and peripheral inserts are inclined approximately $3^{\circ }$ and $5^{\circ }$ from the rotational axis giving a point angle of $172^{\circ }$. The outer diameter of the holder is 22.7 mm, and with inserts placed in the holder, the outer diameter of the drill is 23.7 mm.

Fig. 6

Positions of thermocouples for variant A (left) and variant B (right)

Fig. 7

Test specimens with glued thermocouples. a Variant A. b Variant B

In this work, the primary objective is to study the influence of the feed rate on the heat load. Therefore, the same rotational speed of $\omega =2400$ rev/min is employed for all experiments, and it is selected to establish a cutting speed of 3 m/s at the peripheral corner edge of the insert. This speed is chosen to be the same as the maximum speed of the orthogonal experiments.

The experimental workpieces are delivered as long solid bars, and they are first cut in a sawing machine an then placed in a lathe to obtain the final dimensions of the test specimens with a diameter and length of 32 mm and 25 mm, respectively. A workpiece after a completed experiment is shown in Fig. 5c.

In the experiments, the temperatures are measured using four thermocouples (type K). Two types of experiments are conducted in this work, variant A and variant B, and the difference between these is the location of the thermocouples (see Figs. 6 and 7). Variant A has four thermocouples labelled 1–4 positioned in the mid plane of the workpiece with a $90^{\circ }$ angle between each one (see Fig. 6). Four holes are drilled with 3.0 mm in diameter and with depths of approximately 1.0, 1.7, 2.4 and 3.2 mm. The thermocouples are placed in the holes and glued using a heat-conductive adhesive with 0.87 W/mK. Variant B has four thermocouples positioned along the workpiece at 3.5, 9.5, 15.5 and 21.5 mm from the top surface of the workpiece as depicted in Fig. 7. For this variant, all holes are drilled with a depth of 3.15 mm meaning that the thermocouples are located 1 mm from the machined surface.

The set-up for the indexable drilling experiments is shown in Fig. 8. As shown, the specimen is clamped between two steel plates using four bolts that provide enough friction to support the torque in the drilling operation. The diameter of the hole in the upper plate is 27 mm, and the drill is 23.7 mm which means that the drill can move freely in the feed direction. The lower plate is connected to a HBM MCS10 multicomponent force-and-torque transducer. An additional thicker steel plate is mounted to the MSC transducer, and it is held in position using a vise that is connected to the machining table. The MSC transducer is measuring the forces and the torque produced by the drilling operation.

The feed rates are 0.13, 0.16 and 0.18 mm/rev, and three repeated tests are conducted for each feed rate. All specimens are drilled to a depth of roughly 15.9 mm so that around 9 mm thick bottom of the workpiece remains after drilling.

Fig. 8

Experimental set-up for indexable drilling

5.2 RHT models

In this section, the RTH methodology is used to create the 2D axisymmetric transient heat transfer models for the extraction of the in-process workpiece temperatures in indexable drilling. To develop these models, the cutting process for each insert is studied. Therefore, the uncut chip areas for each insert are schematically illustrated in Fig. 9.

Fig. 9

Uncut chip area for the a central insert and the a peripheral insert

It is observed that $h_a$ is essentially constant along the cutting edges and the same for both inserts except for at the overlapping region where $h_a$, as shown in Fig. 10, is varying in a rather complicated manner. However, as earlier mentioned, the influence of $h_a$ on $\dot{Q}_w$ is weak, and it is therefore assumed that the variation of $h_a$ along the cutting edges and its effect on $\dot{Q}_w$ can be neglected. This assumption implies that $\dot{Q}_w$ is only dependent on $v_c$. In addition, the overlapping region is passed twice each revolution, and $\dot{Q}_w$ should therefore be doubled. However, for simplicity, and the fact that the overlapping region is located some distance from the surface of the drilled hole, the influence of the overlapping region is also neglected in the calculation of the surface heat flux.

Fig. 10

Variation of uncut chip thickness along the cutting edges

To proceed further, it is assumed that the process is rapid enough so that $\dot{Q}_w$ can be averaged out on the complete cutting surface. Therefore, an axisymmetric transient heat transfer model of the process is assumed adequate. This is in line with the work in [5].

The load is applied as a surface heat flux, $\dot{q}_w$, and it is calculated as follows. From Fig. 21, the linear relationship between $\dot{Q}_w$ and $v_c$ is established, i.e. for each specific $h_a$

$$\begin{aligned} \dot{Q}_w = k \,v_c = k \, \omega \, r \end{aligned}$$

(4)

where k is a constant for the specific $h_a$, $\omega$ is the rotational speed and r is the radial coordinate from the hole axis. Furthermore, consider a small circular segment at radius r of the top surface with area $A_s = 2 \, \pi \,r \, w_s$ where $w_s$ is the width of the circular segment on which $\dot{Q}_w$ is acting. The heat flux applied in Abaqus finally becomes

$$\begin{aligned} \dot{q}_w = \frac{\dot{Q}_w \, w_s}{A_s} = \frac{k \, \omega }{2 \, \pi } \end{aligned}$$

(5)

That is, a constant independent of r and the same $\dot{q}_w$ is applied on the complete cutting surface as shown in Fig. 11.

Since k is different for each $h_a$, the heat flux $\dot{q}_w$ is calculated separately by means of Eq. 5 and k is determined by means of Fig. 21. The k-values are first generated for $h_a=0.10$ and $h_a=0.18$ mm from CEL simulations with these feed rates. The k-values for $h_a = 0.13$ and $h_a = 0.16$ mm are then obtained by linear interpolation. With a rotational speed of $\omega =2400$ rad/s, Eq. 5 gives the final values of $\dot{q}_w$ according to Table 4.

Fig. 11

RHT model 1

Two RHT models are created. Model 1 is shown in Fig. 11 where the geometry of the workpiece and the plates is taken from the experimental set-up. In this model, the upper plate is included but not the lower one because the heat is expected to reach this plate in a later stage in the process. In model 1, some heat can conduct through the plate, and therefore, a second model (model 2) is created to study this effect by preventing the heat from transferring through the interface between the test specimen and the upper plate. This is obtained by removing the upper plate. In the models, the diameter of the workpiece is 32 mm, and the height is 25 mm. The diameter of the hole of the upper plate for model 1 is 27 mm, the total length is 140 mm and the thickness is 12 mm. The workpiece consists of 11,120 elements (for the model with $f=0.18$ mm/rev) and the plate of 881 elements where type DCAX4 is used for both parts.

Table 4 Surface heat fluxes given in Abaqus

At the start, the heat flux $\dot{q}_w$ is initially applied on the top surface. All the free surfaces are assumed insulated, i.e. convection is omitted. The initial temperature is set to 25 $^{\circ }$C and is close to the one measured in the experiments. Perfect contact conditions are assumed to exist between the workpiece and the upper plate meaning that they are considered one part.

The central part of the workpiece is divided into thin rectangular sections as shown in Fig. 11. The height of each section is equal to the feed rate being modelled, and one element models the height of the section. As the simulation progresses, the elements that were subjected to the heat load in the previous step are deactivated, and the heat load is moved downwards and is applied to the new top surface as illustrated in Fig. 12.

Fig. 12

a Zoomed-in view of the RTH model (model 1) with the surface heat load after 35 revolutions. b Complete model after 35 revolutions

In addition, some heat also flows in the radial direction at the corner radius, R, of the insert. The deformation process in this region is more complex and consequently also the heat generated in this region [16]. In this study, the heat coming from the corner radius is divided into two parts as illustrated in Fig. 13.

Fig. 13

Chip thickness variation along the peripheral corner radius and illustration of applied surface heat fluxes

Fig. 14

Heat load for three element meshes

Fig. 15

Heat load vs. time

The first part is applied on the lower horizontal surface with an area of about $\pi DR$. This is set to have the same heat flux $\dot{q}_w$ as the surface cut by the main cutting edge, i.e. the surface from the hole axis to the start of the corner radius. The second part of the heat flux $\dot{q}_E$ is applied over a height $h_E$. In this work, $h_E$ is set to three times the feed per revolution, i.e. it is applied to three elements (except for the first three steps of the simulation). By requiring that the heat flow that enters the green dashed line is equal to the heat out, $\dot{q}_E$ is approximated as follows:

$$\begin{aligned} \dot{q}_w\, \pi ^2 \, D \, R /2 = \dot{q}_w\, \pi D \, R + \dot{q}_E\, \pi \, D \, h_E \end{aligned}$$

(6)

Note that the arc where $\dot{q}_w$ acts is approximated to $\pi R /2$ although this is actually somewhat larger. This gives

$$\begin{aligned} \dot{q}_E = 0.57 \,\dot{q}_w\, \frac{R}{h_E} \end{aligned}$$

(7)

Thus, $\dot{q}_E$ is set individually for each analysis. The temperature field from the previous step is transferred as the initial state in the following step and the simulation continues until the experimental drilling depth is reached.

Fig. 16

Cutting and radial forces from a experiment and b simulation with $h_a=0.18$ mm and $v_c=3.0$ m/s

Fig. 17

a Cutting forces from experiments and simulations. b Radial forces from experiments and simulations. Error bars are indicated

6 Results

6.1 Evaluation of the 3D CEL orthogonal model

6.1.1 Mesh convergence of heat load

It is observed that the forces converge fast, but $\dot{Q}_w$ needs smaller elements to converge to an acceptable level (see Fig. 14).

It is also noted in Fig. 15 that $\dot{Q}_w$ converges for the specific simulation. This is also verified for all simulations. From Fig. 15, it is observed that it takes time for the heat to reach the control volume before it starts to increase. However, after some time, it reaches a steady state. It should also be emphasized that most of the heat is transferred through the chip. This is the difference between the mechanical power and the sum of the other two curves in Fig. 15.

6.1.2 Cutting forces

In Fig. 16a, the cutting force and the radial force from a turning experiment with $h_a=0.18$ mm are shown. Note that $h_a=0.22$ mm is excluded since it is not used in the indexable drilling experiments. The forces reach a steady state in approximately 0.4 s. These curves appear quite smooth and steady, but some experiments exhibit a more oscillating behaviour. Figure 16b shows the simulation results. The cutting force is somewhat smaller compared to the experiments, but the deviation is considered acceptable. In contrast to the cutting force, the radial force is significantly smaller than the experimental counterpart.

In Fig. 17, a compilation of the mean values of the experimental and simulated steady-state cutting and radial forces is shown. The maximum deviation is 5% for the mean cutting force and is obtained for $h_a=0.13$ mm. For both the experiments and the simulation, a linear relation can be assumed to exist between the cutting force and $h_a$. However, the radial force is virtually unaffected by $h_a$, and the agreement between simulated and measured force is poor. It has been demonstrated by numerous authors e.g. [10] that the feed force is difficult to represent properly. Despite this deviation, it is assumed that the FE model is appropriate for extracting $\dot{Q}_w$ since the cutting force governs the mechanical power.

6.1.3 Temperatures and heat loads

The simulated temperature fields for $v_c$ = 3 m/s and $h_a$ = 0.05, 0.1, 0.18 mm are shown in Figs. 18, 19 and 20. The maximum temperature reaches almost 1000 $^{\circ }$C in all simulations. It is also observed that the temperature behind the tool edge is slightly higher for larger $h_a$. This also means that the $\dot{Q}_w$ is somewhat larger for larger $h_a$. This is visualized in Fig. 21 although the effect is not that apparent for the lowest $v_c$ used in this work.

Fig. 18

Steady-state temperature field for $h_a=0.05$ mm and $v_c=3.0$ m/s

Fig. 19

Steady-state temperature field for $h_a=0.10$ mm and $v_c=3.0$ m/s

Fig. 20

Steady-state temperature field for $h_a=0.18$ mm and $v_c=3.0$ m/s

In addition, from the results shown in Fig. 21, it is demonstrated that for a fixed $h_a$, almost a linear $\dot{Q}_w$-$v_c$ relation is obtained. It is also noticed that $\dot{Q}_w$ is nearly doubled when the cutting speed is doubled and that $h_a$, in principle, has a negligible effect on $\dot{Q}_w$.

Fig. 21

Heat load from orthogonal turning simulations

6.2 Evaluation of the RHT models

6.2.1 Predicted heat flow and temperature distribution using model 1

Simulation results for model 1 at two different time steps are shown in Fig. 22 for the case of $f=0.13$ mm/rev. The temperature fields and the heat fluxes are displayed at a drilling depth of 2.5 mm (Fig. 22a) and 15.5 mm (Fig. 22b). At a drilling depth of 2.5 mm, it is observed that the heat flow is largest near the peripheral corner edge, and it is directed slightly more in the axial direction than in the radial direction. This is due to the change of the temperature gradient. Although the top surface is connected to the upper plate, the area of connection is relatively small in comparison to the volume of the lower part of the workpiece which acts as a heat sink. At a drilling depth of 15.5 mm, there is no obvious change in direction for the flow. It is clear that the heat is flowing slightly more upwards because of the lower temperature in the top region. It should be emphasized that the FE model assumes perfect contact conditions between the workpiece and the upper plate, and therefore, the amount of heat that flows across the contact surface is overestimated.

Fig. 22

Temperature fields and heat fluxes from simulations with $f=0.13$ mm/rev a at depth 2.5 mm and b at depth 15.5 mm

It can also be noticed that the heat flow, at the larger part of the cut surface, is directed almost vertically and that most of the heat is removed as the top elements are deleted. However, the heat flows slightly faster than the feed rate, and as a consequence, the heated zone extends in the vertical direction.

Fig. 23

Temperature from simulations with the RHT model 1 (solid) and RHT model 2 (+- symbols) for feed rates 0.13 and 0.18 mm/rev. Curves for T1–T4 are presented from left to right, and they are offsetted 2 s in time for easier illustration

The lower plate is not modelled, and this also affects the results. By studying when the temperature rises at the bottom of the workpiece, the elapsed time can be calculated and consequently also the corresponding position of the tool. For $f=0.13$ mm/rev, the tool has reached a drilling depth of 11.7 mm when the temperature at the bottom surface starts to increase. When the tool reaches the final stage of 15.7 mm, the temperature at the bottom is between 29.2 $^{\circ }$C at the center and 27.1 $^{\circ }$C at the outer surface of the specimen. Since the bottom surface of the workpiece is assumed insulated, the heat instead flows in the radial direction. For $f=0.16$ and $f=0.18$ mm/rev, the corresponding drilling depths are 12.2 mm and 13.1 mm. When the tool reaches the final stage, the corresponding temperatures at the bottom are 26.7 $^{\circ }$C and 25.7 $^{\circ }$C at the center and 25.8 $^{\circ }$C and 25.3 $^{\circ }$C at the outer surface.

Table 5 RHT model 1 and variant A

Table 6 RHT model 1 and variant B

Fig. 24

Temperature from two experiments (solid lines) and simulations (model 1, dashed; model 2, +- symbols) for variant B and $f=0.18$ mm/rev

6.2.2 Comparison of the RHT models

In Fig. 23, predicted temperature-time curves from model 1 and model 2 are shown.

Nodal temperatures at the positions of the thermocouples in variant A and variant B are shown for feed rates $f=$ 0.13 and $f=$ 0.18. The curves for T1 to T4 are shown from left to right, and they are offsetted 2 s for easier illustration. It can be observed that the predictions from these two models are essentially identical until the maximum temperature is reached. That is, the upper plate in model 1 influences the temperature at these locations only after the maximum temperature has been recorded. The only exceptions, i.e. where the models predict slightly different maximum temperatures, are T1 and T2 of variant A, i.e. at the locations with the largest radial distance from the drilled hole. However, these deviations are relatively small. Post peak temperatures, the major difference between the models is that model 2 reaches a homogeneous temperature much faster and that the homogenized temperature is substantially higher due to its smaller volume.

6.2.3 Predicted vs. measured peak temperatures

Since the temperatures predicted by model 1 and model 2 only differ post peak temperature, the comparison of measured and predicted peak temperatures is only made between the experiment and model 1. In Tables 5 and 6, the predicted peak temperature and the mean values of the measured peak temperatures are compiled for variant A and variant B, respectively. The tables also indicate the prediction error calculated as $\varepsilon = (T_{p,sim}-\bar{T}_{p,exp})/\bar{T}_{p,exp}$.

For variant A, the overall trend in peak temperatures from experiment and simulation agrees well for all feed rates and thermocouples. It is expected that the peak temperature is higher the closer the thermocouple is to the surface of the drilled hole, i.e. that T4 gives a higher temperature than T3 and so on. All the simulations confirm this and, in general, so do the experiments, although there are a few exceptions. Furthermore, it is expected that the maximum temperature has an inverse relationship with the feed rate because the total engagement time becomes longer and a smaller proportion of the heat energy is removed in the cutting process. All the simulations confirm this behaviour and generally also the experiments. However, there are also a few exceptions that do not exhibit this behaviour. The largest peak temperature is approximately 64 $^{\circ }$C for the simulation and 61 $^{\circ }$C for the experiment, and these temperatures are obtained for T4 and $f=0.13$ mm/rev, i.e. at the thermocouple closest to the cut surface and for the lowest feed rate. Moreover, the lowest peak temperature is recorded at T1 for f = 0.18 where the predicted temperature of $45.6^{\circ }$C agrees well to the average measured temperature of 45.3 $^{\circ }$C. As shown, the maximum prediction error is about 10% for this variant.

For variant B, the feed rate has the inverse relation to the measured peak temperature for thermocouple T1–T3. However, at T4, this relationship does not hold, and the measured temperatures show no clear logic. The largest peak temperature is approximately 63 $^{\circ }$C for the simulations and is obtained for T3 and $f=0.13$. For the experiments, the highest temperature of about 62 $^{\circ }$C is obtained for T2 for $f=0.13$. Again, the peak temperatures from experiment and simulation agree fairly well for most feed rates and thermocouples. As shown in Table 6, the maximum error is relatively large, around 16 %, but in most cases, the prediction error is more acceptable. It should be noted that for $f=0.18$, the test failed because the insert was fractured during the test.

By taking the absolute value of each error in Tables 5 and 6, the mean value for each variant is calculated. As a general observation, the prediction errors are generally smaller for variant A compared to variant B. The average error for all thermocouples and feed rates for variant A is about 4%, and for variant B, it is about 7%.

6.2.4 Predicted vs. measured temperature histories

In Fig. 24, the predicted and simulated temperature vs. time curves for variant B and $f=0.18$ mm/rev are shown. Comparisons between simulations and experiments for other feed rates and for both variants show similar overall behaviours. That is, the peak temperatures are predicted fairly good, but the simulations show distinct temperature peaks while the experimental curves show wider peaks with a subsequent temperature decrease that is slower than in the simulations. The reason for this discrepancy is not determined, but it can possibly be explained by a poor connection of the thermocouples in the drilled holes and, although the adhesive is thermally conductive, the adhesive has a substantially lower conductivity compared to the steel material. Moreover, it is troublesome to ensure that all thermocouples are successfully mounted at the specified depth.

7 Conclusion and discussion

In this work, a methodology for the prediction of temperatures for indexable drilling has been developed. The basic idea is to calculate the heat from orthogonal thermo-mechanical CEL simulations for different feed rates and cutting speeds. This heat is then employed in RHT models where the temperature field can be calculated and compared to experiments. Two different types of experiments have been conducted, and they have also been compared to simulations for verification.

The main conclusions of the work are as follows:

• From the analysis of the heat flux from the CEL simulations, it is observed that the forces converge much faster than the heat flux.

• For the RHT models, the peak temperatures in both variants are predicted with an average error of less than 7%.

• For variant A, the predicted error is less than 10% for all thermocouples. For variant B, it is less than 16%.

In the modelling of the nose radius, the heat flux is also provided from orthogonal turning simulations. However, the deformation process is more complex in this region. This suggests that the heat flux could be provided from longitudinal turning simulations where the nose radius is modelled in detail [14, 17]. In addition, the heat flux in the model is acting on three elements in the axial direction to model the heat from the nose radius. This choice clearly affects the heat input to the workpiece. It would also be of interest to perform experiments with pre-drilled axial holes with different diameters to study the effect of the peripheral insert itself. For example, with this strategy, the influence of the corner radius can be studied independently since the cutting process is localized to the region of interest. The lower plate should also be included in the simulations to study its influence.

The difference in the width of the temperature peaks needs further investigation. The experiments show wide peaks, but the simulations show high and narrow peaks. The cause of this discrepancy is not determined, but as mentioned, it can be explained by a poor connection of the thermocouples in the drilled holes, and although the adhesive is thermally conductive, the adhesive has a significantly lower conductivity compared to the steel material.

It should also be emphasized that the results are dependent on an accurate CEL model. For example, this means that convergence in forces does not imply the same for the heat flux. With the adopted method used in this work, it is computationally demanding to obtain convergence of the heat flux. However, it is crucial to obtain reliable results.

Despite all the simplifications made, the developed RHT models can provide valuable results in terms of temperatures as indicated in Tables 5 and 6. However, the RHT methodology needs to be further explored to validate its applicability, and this is planned to be conducted in the near future.