1 Introduction

Tolerance allocation is the assignment of suitable values to the tolerances involved in a functional requirement. In general, a functional requirement is a geometric characteristic (most often a dimension) defined at assembly level, i.e. between features of different parts. A requirement has a nominal value and an allowed variation (the limits on its deviations), which are set as design specifications. At manufacturing stage, the variation of the requirement cannot be controlled directly, but is determined by the stackup of tolerances on features of some parts of the assembly. For example, the axial clearance of a transmission is a functional requirement involving a chain of dimensions on some connected parts (shaft, bearings, housing, covers, etc.). The tolerance limits on these dimensions must be chosen so that the clearance is neither too small, making assembly operations difficult, nor too large, causing malfunctioning and loss of quality (e.g. vibration, noise, wear).

In design practice, tolerances are often allocated with simple criteria. Each tolerance is given an initial value based on experience (e.g. depending on feature size and expected precision of manufacturing processes). The resulting variation on the requirement is calculated and compared to the specified variation; tolerances are then scaled either proportionally or depending of their contribution. Although acceptable in most situations, similar procedures do not take cost into account: an especially tight tolerance can require an excessive cost for the machining operations that will create the corresponding part feature. For this reason, many research studies treat tolerance allocation as an optimization problem: in the most common formulation, an optimal set of tolerances minimizes the total cost while satisfying the specified variation for the requirement [1,2,3].

The variation on the functional requirement must be specified as input to any tolerance allocation method. It is expressed as an assembly-level tolerance, and is equivalent to a variation budget that will have to be allocated among the part features involved in the requirement. Although it is generally set without further explanation in most cases presented in literature, it may deserve some more attention. Specifying too large a variation could cause defects in an unacceptable fraction of the assemblies produced, but this occurrence is not easy to predict without extensive prototype testing. On the other hand, too tight a variation would have an impact on cost, probably greater than that of a suboptimal allocation of tolerances.

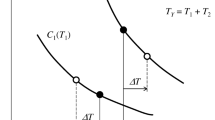
When confronted to the above task, designers may want to start with a tight variation to be on the safe side, and possibly accept some compromise on it to avoid excessive costs. Such decision would be easier if they knew the relationship between the cost of a functional requirement and its specified variation. This would be similar to the cost-tolerance functions defined for individual part features and used in tolerance allocation. The cost of the requirement is the sum of the costs of the involved tolerances when these have optimal values. This creates a difficulty in its estimation, which would require solving the allocation problem.

This paper proposes a method to estimate the cost-tolerance function of a functional requirement. The method avoids the prior optimization of the tolerances and allows an explicit evaluation of the contributions of the influencing factors related to the properties of the dimension chain. These include the materials of the parts and some attributes of part features such as shape, area and nominal dimension. The cost estimation procedure is based on some previous results, such as the extended reciprocal-power function and the optimal scaling method for tolerance allocation [4]. The paper also shows that the function can help solve allocation problems with a hierarchical approach: this consists of jointly optimizing part tolerances and variations of functional requirements, and using the latter as inputs for lower-level allocations.

Previous studies on the topic are recalled in Section 2. The proposed method is described in Section 3 along with its intended applications, and is demonstrated on examples in Section 4. The discussion in Section 5 highlights the advantages and limitations of the method. Section 6 summarizes the contribution of the work.

2 Background

The problem of tolerance allocation has been widely studied in literature. Traditionally, designers have set values of part tolerances using simple rules for typical dimension chains, e.g. [5]. Many research studies over four decades have proposed formal definitions and calculation procedures suitable for a wide variety of situations; these have helped improve the allocation, finding the right compromise between assembly quality and part manufacturing costs. Detailed discussions of the available methods can be found in the main reviews on the subject. The earlier ones [6, 7] define the general approaches (worst case, statistical) and the simplest methods, applying them to classic cases of 1D and 2D dimension chains. At a more mature stage of research, [1, 2] describe various formulations of the optimization problem with graphical, analytical, numerical, and simulation methods. More recently, [3] provides an extensive classification of basic assumptions, objective functions, constraints, and many special cases related to the properties of assemblies and mechanisms.

Among the available formulations, this work adopts the most common one for problems with a single dimension chain, i.e. minimization of cost subject to a constraint on the variation of the functional requirement to be controlled. The method of Lagrange multipliers [8, 9] is widely used because it allows to find analytical solutions under restrictive assumptions on cost functions and statistical distributions of part dimensions. Numerical solutions can be calculated with deterministic methods such as nonlinear programming [10, 11] and gradient search [12], or with stochastic methods such as simulated annealing [13, 14], genetic algorithms [15, 16] and particle swarm optimization [17]. Alternative formulations use cost as a constraint in minimizing quality-related functions such as expected quality loss [18, 19] and nonconforming rate [20,21,22,23]; in those cases, the solution methods are mostly based on either design-of-experiments (DOE) techniques [24,25,26] or numerical optimization [27,28,29].

For the optimization of tolerances, most studies use a mathematical function that expresses the relationship between cost and tolerance for each dimension involved in a functional requirement. Available cost-tolerance functions are discussed in some reviews [6, 30, 31] and comparative studies [14, 32,33,34,35]. In increasing order of complexity, they include the linear [36], reciprocal [10], reciprocal squared [8] and reciprocal-power [37] functions, as well as the Michael-Siddall function [38] and some combined and polynomial functions [39]. Simpler functions allow the analytical resolution of the allocation problem using Lagrange multipliers. Besides, they have fewer parameters, which can be evaluated without the need for large amounts of cost data. On the other hand, more complex functions are potentially more accurate.

Choosing the parameters of cost-tolerance functions is a non-trivial task, as discussed in a recent review [40]. The parameters are generally chosen without explicit reasons, and their values are often inconsistent among different sources. This is partially explained considering that different tolerances may require different machining processes, and the most cited datasets [41] provide relative cost data for individual processes. To allow a comparison between data relating to different processes, some sources provide cost-tolerance curves for combined processes, which approximate the envelope of curves relating to increasingly more precise processes as the tolerance decreases [7, 31, 39, 42, 43]. The parameters of the cost-tolerance functions are estimated from available cost data by linear regression, both for single processes [39, 44,45,46] and for combined processes [4, 47]. Alternative methods include neural networks [48, 49], fuzzy methods [50], and choice among process-constrained alternatives [51]. Other procedures use parametric data for elementary operations [52], codes for accessing company-specific databases [53], activity-based costing [54, 55], and qualitative assessment by company experts [26]. By regression of machining cost estimates, [4] extends the reciprocal-power function into a more complex expression that takes into account the specifications of a feature (material, area, type, nominal dimension). In principle, the use of such function can make the parameters consistent for all the features of a dimension chain, and for dimension chains related to different requirements of the same assembly. For this reason, it will be used to build the cost function for a functional requirement, which will turn out to have a similar expression.

Functional requirements (or assembly key characteristics) have been studied from various angles in the tolerancing literature. They are the assembly-level geometric conditions whose variation must be controlled within given limits; to do this, tolerances are specified on the parts to limit manufacturing errors on them. The design process that translates requirements into tolerances has also been called functional tolerancing [56, 57] or flowdown [58, 59].

An assembly generally has many functional requirements; some may have been predefined as product specifications, while others are implicit in the relational structure of the assembly and must be identified prior to any decision on part tolerances [60]. This requires a classification of the requirements, which has been done differently in relation to available tolerancing standards. In traditional practice based on dimensional tolerances, the requirement is essentially a “sum dimension” calculated as an algebraic function of a set of part dimensions (dimension chain); various types of sum dimensions have been described and compared in [42]. The progressive acceptance of geometric tolerancing has led to the requirement being defined as an assembly-level geometric control (e.g. orientation, position, runout), indicated on the assembly drawing with a special feature control frame [61]. High-level functional requirements have been classified in relation to technical functions such as clearance fit, sliding, sealing, etc. [62, 63]. Some classifications include rules for mapping requirements to appropriate types of part tolerances [64].

With the aim of allowing the identification and automatic flowdown of requirements, some studies have proposed models for their representation in computer-based procedures. They include virtual boundary requirements [65, 66], the structural–functional decomposition [67, 68], and a multi-level model based on hypergraphs [69]. Consistently with the correspondence between requirements and tolerances, a widely used model for tolerance representation (technologically and topologically related surfaces, TTRS [64]) has been extended to represent requirements (pseudo-TTRS, [70]) and used for translating high-level requirements into explicit geometric conditions [71]. In a similar extension, [72, 73] represent the requirements with a small displacement torsor model, so as to translate them into functional equations on geometric errors. In [74], requirements are defined as assembly-level extensions of orientation and position tolerances, allowing an effective graphical representation to support tolerancing decisions. In [75], the representation of tolerances and requirements in the same relational structure allows a consistency check on geometric tolerances specified by the designer.

The automatic identification of requirements uses input data about the assembly, usually structured in a graph of relations between part features. Most of the proposed methods consider 1D chains of dimensional tolerances, and are based on the search for loops in the relation graph [76,77,78]. Other approaches to the same problem include data extraction from CAD models [79] and a technique deriving from value analysis [80, 81]. Functional equations, which express the relationship between a requirement and the involved dimensions, are automatically generated in [82,83,84,85] with different methods for dimension chains of various complexity and dimensionality. In [86], some design rules are proposed to reduce the number of requirements of an assembly. The identification of requirements by loop detection has also been done for geometric tolerances, with the further complexity that the relations must be classified according to the associated direction [87]. In [88], the designer adds the requirements to a relation graph including a preliminary specification of the types of geometric tolerances on mating features; if this creates multiple loops, the designer is advised to eliminate the redundant ones to avoid overconstraints.

In the context of geometric tolerances, allocation is preceded by another task called tolerance specification [60], which generates the datum systems and the tolerance types on part features. Some proposed methods, such as recent ones based on axiomatic design [89,90,91] and machine learning [92,93,94], do not explicitly consider functional requirements. Others include procedures for the automatic flowdown of requirements. In [95, 96], the relational structure of the part features is completed with the requirements and iteratively simplified by recognizing some typical patterns of relations, until generating a hierarchy of toleranced features on each part. In [97], priority scores are calculated for part features involved in requirements to select datums, and rules are used to choose tolerance types. In [98], the same task is performed with a procedure structured in five phases, each including a set of detailed rules; these cover an especially wide diversity of cases and can be applied directly to the geometric models of the parts, without the need for further input data (e.g. the sequence of assembly operations). In [99], the specification procedure is based on a theory for jointly modeling product function (associated with requirements) and structure (associated with tolerances). With a different strategy, the method proposed in [100] carries out the allocation before specification, calculating bounds on linear and angular errors corresponding to the degrees of freedom constrained by the assembly relations.

The present study aims to combine the above mentioned concepts (cost-tolerance function, functional requirement) into a new concept that can help solving the tolerance allocation problem. This consists of a cost-tolerance function for the functional requirement. In allocation, the cost of a requirement is expressed simply as the sum of cost-tolerance functions for the dimensions of the associated chain. In some cases the expression of the sum includes a model of tolerance propagation, such as the small displacement torsor in [34]. However the variables of the cost function are invariably part tolerances, which are not known until the allocation problem is solved. The goal here is to obtain a cost function in only one variable, the allowable variation on the requirement (i.e. the assembly tolerance), which is an input data for the allocation. The proposed function will therefore be useful to support the choice of the variation of the requirement, a preliminary task to the allocation that does not seem to have been treated previously in literature.

3 Methods

The functional requirement is a geometric entity Y defined at assembly level, i.e. a linear or angular distance between features of different parts. It has nominal value Y0, and must be controlled within a variation ± TY to ensure either the correct joining of the parts or the function of the assembly. It is assumed that the requirement is related by a linear (or linearized) relationship to a set of n dimensions Xi of individual parts:

$$Y = \sum\limits_{i = 1}^{n} {S_{i} X_{i} }$$
(1)

where Si is the sensitivity of Y to dimension Xi, known from the analysis of the dimension chain.

Each dimension has a nominal value X0i and a tolerance ± Ti. It is assumed that the Xi are statistically independent and normally distributed with means X0i and standard deviations equal to Ti / 3 (or, more generally, to the same fraction of their tolerance). Consequently, the variation of the requirement is related to the tolerances by the root sum square (RSS) equation:

$$T_{Y} = \sqrt {\sum\limits_{i = 1}^{n} {S_{i}^{2} T_{i}^{2} } }$$
(2)

In a tolerance allocation problem, TY is given and the unknown tolerances minimize the total cost while satisfying the variation specified for the requirement:

$$\begin{gathered} \min C = \sum\limits_{i = 1}^{n} {C_{i} \left( {T_{i} } \right)} \hfill \\ {\mathrm{s}}{\mathrm{.t}}{. }T_{Y}^{2} = \sum\limits_{i = 1}^{n} {S_{i}^{2} T_{i}^{2} } \hfill \\ \end{gathered}$$
(3)

where Ci(Ti) is the cost-tolerance function for Xi, defined as the tolerance-dependent portion of the cost of machining the corresponding part feature. The goal discussed below is to directly estimate the cost C of the functional requirement as a function of TY without the need to explicitly solve the optimization problem (3).

3.1 Prior work

The expression of Ci(Ti) is based on the reciprocal-power cost-tolerance function [37], here limited to its variable part (the only one with an effect on optimal allocation):

$$C_{i} = \frac{{b_{i} }}{{T_{i}^{k} }}$$
(4)

An evaluation of the parameters in (4) has been provided in [4] by comparison with a feature-based method for the estimation of machining cost. According to those results, the exponent is set to k = 0.55, while the multiplicative factor is estimated as a function of nominal dimension Xi:

$$b_{i} = \beta \cdot f_{Mi} \cdot f_{Fi} \cdot f_{Ai} \cdot X_{i}^{{{k \mathord{\left/ {\vphantom {k 3}} \right. \kern-0pt} 3}}}$$
(5)

where:

  • β = 0.4 ⋅ 10–3;

  • fMi and fFi are coefficients depending respectively on the material and on the type of feature, with values listed in Table 1;

    Table 1 Coefficients related to material and feature type in the extended reciprocal-power cost-tolerance function
    Full size table

  • fAi is the area of the feature in cm2.

Equations (4) and (5) define an extended reciprocal-power function, which includes several cost-influencing factors beside tolerance. The same expression can then be used for all the features of a dimension chain by evaluating their coefficients separately. The function is expressed in machining minutes on computer numerically controlled (CNC) machine tools; in the following, the machining time will be converted into currency units CU (e.g. EUR or USD) assuming a suitable shop rate (60 CU/h).

Much like (4), the extended reciprocal-power function can be used for the analytical solution of the optimization problem (3) with the method of Lagrange multipliers. As shown in [4], the optimal tolerances turn out to be proportional to a factor depending on the coefficients of the cost-tolerance function and on the sensitivities of the requirement:

$$T_{i} \propto F_{i} = \left( {b_{i} S_{i}^{ - 2} } \right)^{{\frac{1}{k + 2}}}$$
(6)

where bi is calculated from (5). Such property suggests an “optimal scaling” procedure for tolerance allocation. The tolerances are set to initial values equal to Fi, and then scaled to the specified value of TY:

$$T_{i} = T_{Y} \cdot \frac{{F_{i} }}{{F_{Y} }}$$
(7)

where

$$F_{Y} = \sqrt {\sum\limits_{i = 1}^{n} {F_{i}^{2} } }$$
(8)

Equations (7) and (8) add nothing to the known analytical solution of (3), but express it in a convenient form that can be readily implemented in a spreadsheet. Compared to the common proportional scaling procedure, they guarantee that the initial values Fi set for the tolerances are optimal before being scaled to meet the stackup constraint (TY). Another advantage of optimal scaling is that factors Fi are in an explicit relationship, given by Eq. (5), with the nominal dimensions and with other properties of the parts (material, area and type of the toleranced features, nominal dimensions). Therefore, the designer can easily evaluate the sensitivity of the optimal allocation to the design variables. The procedure relies on the assumptions mentioned at the beginning of Section 3, which avoid the need for a numerical resolution of problem (3); this would not raise computational difficulties but would make it harder to evauate the influence of part properties on the allocated tolerances.

3.2 Cost of a functional requirement

The proposed method uses the extended reciprocal-power function and the optimal scaling method to find an estimate of the cost CY of a functional requirement Y. By definition, CY is the optimal value of C in the allocation problem (3) when the specified variation of the requirement is TY. While C is a function of the decision variables Ti (part tolerances), CY is a function of the parameter TY (assembly-level tolerance). As TY decreases, CY increases because the solution to (3) is a set of tighter optimal tolerances Ti and results in a higher value of the objective function C. The cost function CY(TY) is subject to the assumptions described in Eqs. (1–8).

In most design situations, the requirement does not fit into a typical pattern and includes every time a particular number of features, each different in type and geometric configuration. In these cases, what is needed is a function CY(TY) with one or more numerical coefficients. The shape of such a function can be easily identified: from (1), the cost of each feature is inversely proportional to the k-th power of its tolerance; besides, (7) shows that the tolerances are all directly proportional to TY. Consequently the cost function is simply

$$C_Y=\frac B{T_Y^k},\;B=F_Y^k\sum_{i=1}^n\frac{b_i}{F_i^k}$$
(9)

where bi, Fi and FY are calculated from (5), (6), and (8), respectively.

For some requirements common to a wide class of tolerance allocation problems, the above calculations may lead to a more detailed expression of CY as a function of TY and additional design parameters:

$$C_{Y} = C_{Y} \left( {T_{Y} ,p_{1} , \ldots ,p_{m} } \right)$$
(10)

where the parameters pj (j = 1, …, m) are appropriately chosen according to the type of requirement.

An example of requirement that occurs frequently in mechanical assemblies is the clearance fit between a pin and a hole (Fig. 1). Let D and H be the nominal diameter and depth of the hole, assumed to be approximately equal to the corresponding dimensions of the pin. The materials of the two parts are given, e.g. medium carbon steel for the pin and cast iron for the hole. The functional requirement is the clearance Y = X1 − X2, where X1 and X2 denote the actual diameters of the hole and of the pin, respectively.

Fig. 1
figure 1

Pin-hole clearance fit

Full size image

The cost of the requirement is

$$C_{Y} = \frac{{b_{1} }}{{T_{1}^{0.55} }} + \frac{{b_{2} }}{{T_{2}^{0.55} }}$$
(11)

The factors b1 and b2 of the cost-tolerance functions are calculated from (5). In Table 1 it is easy to recognize that fM1 = fM2 = 1.3, fF1 = 1.25 and fF2 = 1, fA1 = fA2 = πDH/100. Hence

$$b_1=1.25\cdot1.6\cdot10^{-5}H\cdot D^{1.18},\;b_2=1.6\cdot10^{-5}H\cdot D^{1.18}$$
(12)

The proportionality factors F1 and F2 for tolerance allocation are calculated from (6), considering that |S1| =|S2|= 1, and dropping the common elements:

$$F_1=1.25^{0.39}=1.09,\;F_2=1$$
(13)

From (8) it is

$$F_{Y} = \sqrt {1.09^{2} + {1}} = 1.48$$
(14)

The tolerances are then calculated from (7):

$$T_1=0.74\cdot T_Y,\;T_2=0.68\cdot T_Y$$
(15)

and Eq. (11) gives

$$C_{Y} = 4.4 \cdot 10^{ - 5} \frac{{H \cdot D^{1.18} }}{{T_{Y}^{0.55} }}$$
(16)

with H, D and TY in mm. The expression can be rewritten as

$$C_{Y} = 0.05\frac{H}{D}\left( \frac{D}{25} \right)^{2.18} \frac{1}{{T_{Y}^{0.55} }}$$
(17)

highlighting the steep increase of CY as a function of diameter D for a given aspect ratio H/D. The optimal allocation (15) and the cost function (17) can be calculated in a similar way for different materials of the two parts. For example, if the hole is machined in a rotational part made of a copper alloy (e.g. a bronze bushing), the corresponding results are

$$T_1=0.60\cdot T_Y,\;T_2=0.80\cdot T_Y$$
(18)

and

$$C_{Y} = 0.03\frac{H}{D}\left( \frac{D}{25} \right)^{2.18} \frac{1}{{T_{Y}^{0.55} }}$$
(19)

The previous expressions are also valid when geometric tolerances are specified on the two features. In those cases T1 and T2 must be replaced with equivalent tolerances, each calculated as half the difference between the diameters of the outer and inner boundaries of the feature. If TS is the size tolerance and TG is the geometric tolerance, it is easily found that the equivalent tolerance equals (TS + TG) if TG is specified regardless of feature size (RFS), and (3TS + TG) if TG is specified at maximum material condition (MMC). Since both TS and TG are specified on the same machined feature, their contributions to the cost cannot be separated. Therefore, the equivalent tolerance is optimized and then apportioned between TS and TG based on experience.

3.3 Use of the cost function

As shown before, the cost of a requirement can be estimated as a function of the variation allowed on it. This is equivalent to a generalization of the cost-tolerance function defined for single part features. The assembly-level cost function can support two main tasks:

  • choosing the variation on the requirement, as input data to a tolerance allocation problem;

  • solving a complex allocation problem with a hierarchical approach.

As a demonstration of the first task, the function in (17) can help specify the allowed variation on pin-hole clearances. To this end, Fig. 2 shows the graph of CY versus TY for D = 40 mm and H/D = 1. As a reference, the points corresponding to some IT tolerance grades on the two features are indicated. As the variation decreases, the cost of the requirement appears to increase more than linearly with respect to the variation. Absolute and relative values of cost are useful in evaluating the economic impact of the specification, with possible trade-offs with other performance-related considerations. For example, a variation of ± 0.14 mm (IT10) is relatively narrow and may even not require finish machining at all. Compared to that, a choice of ± 0.03 mm (IT7) would cost about twice as much, with a difference of 400 CU per 1000 units produced. Reducing variation to as little as ± 0.02 (IT6), the cost ratio and difference would increase to about 3 × and 800 CU per thousand units, respectively.

Fig. 2
figure 2

Cost of pin-hole clearance

Full size image

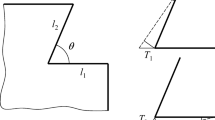
The second task is motivated by the fact that some functional requirements may depend on many part features. In such cases, identifying the dimension chain requires special attention to avoid errors in the tolerance propagation model. This occurs especially in assemblies with clearance fits between cylindrical or prismatic features of size.

For example, Fig. 3a shows the schematic layout of a slider-crank mechanism where the requirement to be controlled is the position Y of the slider relative to the center of the crankpin when the mechanism is at its top dead center. The assembly includes some cylindrical fits, whose clearances affect the variation of Y. Therefore the diameters of the pins and holes should appear explicitly in the dimension chain, and their sensitivities should be evaluated considering the misalignments between the centers of the mating features. By doing that, the actual contacts between the features would result in a chain of 10 dimensions.

Fig. 3
figure 3

Complex dimension chain: a with mating features; b with clearances

Full size image

The problem can be simplified by removing the diameters from the dimension chain, and replacing them with the clearances of the respective pin-hole fits. As shown in Fig. 3b, this reduces the chain to only 7 dimensions. Some of these (X2, X5, X7) are defined on individual parts, and therefore will be associated to cost-tolerance functions defined as in (4) and (5). Others (X1, X3, X4, X6) involve features of different parts, and can be associated with cost functions for clearance requirements as in (17). In other words, dimensions and requirements can be treated similarly in a tolerance allocation problem. The solution to the problem provides both the optimal tolerances on the dimensions and the optimal amounts of variation to be specified for the clearances. The latter can then be used as inputs to optimize the tolerances on the diameters of the mating features, thus completing the allocation with a hierarchical procedure. The same approach may be used when the assembly includes subassemblies, whose dimensions can be grouped into a single requirement and then optimized separately.

4 Results

The procedure for estimating the cost of a functional requirement is demonstrated below on two simple examples. The first concerns the choice of the variation on requirements defined by geometric characteristics. The second is a case of hierarchical tolerance allocation including pin-hole clearances.

4.1 Specification of requirement variation

Figure 4a shows a two-axis positioning mechanism including a table, a longitudinal slide, and a cross slide, all made of medium carbon steel. The two slides have translational motions allowed by a dovetail guide and a T-guide. The functional requirements Y1 and Y2 are the profile errors of two surfaces of the cross slide with respect to reference surfaces on the table, when the parts are in the positions shown. The part drawings in Fig. 4b specify both size and geometric tolerances, which are unknown and will have to be optimized by solving two tolerance allocation problems. Before doing this, the allowable variation on each of the requirements must be specified taking into account its impact on cost.

Fig. 4
figure 4

Positioner: a assembly with functional requirements; b parts with tolerances

Full size image

The first step consists in calculating the sensitivities of the two requirements to the involved part features. To do this, a dimension chain is identified for each requirement. For Y1 it is assumed that, due to possible vertical loads, the parts are always in actual contact on their horizontal mating planes. Furthermore, if form errors are neglected, the same surfaces are horizontal in the worst cases allowed by their tolerances. Consequently, the profile tolerance TY1 is equivalent to a dimensional tolerance on height h, which is the sum of the dimensions h1, h2 and h3 on the three parts (Fig. 5). Table 2 provides the tolerances on all dimensions, calculated based on the meaning of the geometric tolerances on the related features. The sum of the tolerances gives the following linear functional equation:

$$T_{Y1} = T_{{{\mathrm{P}}1}} + T_{{{\mathrm{P}}5}} + T_{{{\mathrm{P}}9}}$$
(20)
Fig. 5
figure 5

Dimension chain for Y1 on the positioner

Full size image
Table 2 Tolerance stackup for Y1 on the positioner
Full size table

Equation (20) is the worst-case relationship between the part tolerances and the variation on the requirement. To account for the compensation of errors on random parts, it will have to be replaced by the corresponding RSS stackup equation. However, it provides the values of the sensitivities to be used in subsequent calculations.

The next step is the resolution of the tolerance allocation problem using TY1 as a parameter, in order to estimate the corresponding cost function. Table 3 shows the results of the calculation of the cost factors bi from (5), evaluating the coefficients fMi, fFi and fAi from Table 1. The factors Fi for the optimal scaling are calculated from (6) considering the sensitivities in (20). The ratios between the individual tolerances Ti and the variation TY are calculated from (7) and (8) with FY = 0.756.

Table 3 Cost-tolerance factor and optimal scaling for Y1 on the positioner
Full size table

Expressing all tolerances in proportion to TY and adding their costs calculated from (4), the resulting equation for the cost of Y1 is

$$C_{Y1} = \frac{0.49}{{T_{Y1}^{0.55} }}$$
(21)

Figure 6 shows the graph of the cost function (21). Although the choice of TY1 is likely to be mainly driven by the desired positioning accuracy, it is apparent that the specification can be set without a significant impact on cost up to about 0.1 mm, which keeps the cost within about 2000 CU per thousand units or about two times that corresponding to a much wider variation (0.5 mm). The cost would double by reducing the variation to 0.02 mm, and it would triple at 0.01 mm. For high production volumes, these figures should be carefully considered in comparison with other cost items.

Fig. 6
figure 6

Cost of Y1 on the positioner

Full size image

The profile tolerance TY2 corresponds to an angular error θ over a horizontal dimension of 32 mm. This angle is the sum of 5 angles θ23, θ34, θ46, θ67 and θ78 (Fig. 7). Table 4 shows the tolerances on all the angular dimensions in radians. In their expressions, the denominator is the length over which the relative rotation between the features occurs, which allows the angle of rotation in radians (approximately equal to its tangent) to be calculated from a linear deviation. The numerator is either a geometric tolerance specified at RFS (θ78), or the maximum value of a geometric tolerance specified at MMC (θ23, θ46), or the sum of equivalent tolerances for the mating features of a prismatic fit (θ34, θ67), calculated as explained in subSection 3.2 for a cylindrical fit.

Fig. 7
figure 7

Dimension chain for Y2 on the positioner

Full size image
Table 4 Tolerance stackup for Y2 on the positioner
Full size table

The sum of the tolerances gives

$$T_{Y2} = 0.96 \cdot T_{3} + 0.64 \cdot T_{4} + 1.28 \cdot T_{6} + 0.64 \cdot T_{7} + 0.64 \cdot T_{8}$$
(22)

where T3, T4, T6, T7 and T8 have the expressions shown in Table 5. Each feature is therefore associated with a single tolerance, which will be optimized by solving the allocation problem. Its value will be apportioned freely between the size and geometric tolerances specified on the same feature, since their separate contribution to the cost is not known. Table 5 also shows the calculation of the factors bi from the related coefficients, and the sensitivities Si from (22). The factors Fi are scaled on their RSS FY = 1.201.

Table 5 Cost-tolerance factor and optimal scaling for Y2 on the positioner
Full size table

Finally, the cost function for Y2 is

$$C_{Y} = \frac{1.18}{{T_{Y2}^{0.55} }}$$
(23)

The graph in Fig. 8 shows that the cost estimates are higher than for Y1, due to the greater number of tolerances involved. The maximum variation of about 0.5 mm corresponds approximately to an angular error of ± 1°, and has a baseline cost of approximately 2,000 CU per thousand units. The cost would increase by 2 or 3 times if the variation were reduced to 0.1 mm (± 0.2°) or 0.05 mm (± 0.1°), but would probably be too high with even tighter specifications.

Fig. 8
figure 8

Cost of Y2 on the positioner

Full size image

4.2 Hierarchical tolerance allocation

Figure 9 shows a shaft carrying a gear wheel and fitted to two bearing bushes mounted in a housing. The shaft and the gear wheel are made of medium carbon steel, while the bushings are made of bronze and are sourced as custom parts (or available in a wide range of tolerance grades). The parts are in contact at cylindrical features, which are designed with size tolerances and position tolerances; the latter are assumed as RFS for the sake of simplicity (the case with MMC modifiers could be treated as described in subSection 4.1). The bushings are fitted to the housing bores without clearance and with negligible geometric errors.

Fig. 9
figure 9

Gear assembly

Full size image

The functional requirement to be controlled is the eccentricity Y of the outer surface of the gear wheel with respect to the common axis of the two bores in the housing. The variation TY on the requirement is assumed to be given, and the goal is to optimize the part tolerances that are related to it. It can be noted that Y is a dimension involving the axis of a generic cylindrical surface, and does not depend on specific properties of the gearing. A requirement established on the pitch cylinder of the gear wheel would be treated similarly but with more complex calculations.

The problem could be solved by expressing TY as a function of the 10 tolerances TS1, TP1, TS2, TS3, TP3, TS4, TS5, TP5, TS6, TP7, and evaluating the cost-tolerance functions for the related features. Alternatively, it can be considered that some tolerances are involved in pin-hole clearance fits, and the method described in subSection 3.2 allows to associate clearances with cost functions. The problem can therefore be tackled with a hierarchical approach, expressing Y as a function of both clearance variations and part tolerances. The dimension chain turns out to be simpler, and can be set up without analyzing the role of each single mating feature. A first tolerance allocation allows to optimize the clearances. Once the variation on each clearance is set, lower-level allocations are carried out to optimize the related part tolerances, again with very simple dimension chains.

The worst-case equation of the dimension chain is

$$T_{Y} = \frac{b}{{2\left( {a + b} \right)}} \cdot \left( {T_{{{\mathrm{P}}1}} + T_{12} } \right) + \frac{a}{{2\left( {a + b} \right)}} \cdot \left( {T_{{{\mathrm{P}}3}} + T_{34} } \right) + \frac{1}{2} \cdot \left( {T_{{{\mathrm{P}}5}} + T_{56} + T_{{{\mathrm{P}}7}} } \right)$$
(24)

where a = 100 mm and b = 150 mm are the distances between the midsections of the gear wheel and the two bushings. In addition to the part tolerances TP1, TP3, TP5 and TP7 defined in Fig. 8, Eq. (24) includes the variations on the three clearance requirements between the shaft and either the left-side bushing (T12), the right-side bushing (T34), and the gear wheel (T56).

The cost functions are evaluated as shown in Table 6. For each part tolerance, the factor bi of the cost-tolerance function (4) is calculated from (5) from appropriate coefficients and nominal dimensions. For each clearance requirement, the cost factor B in (9) is calculated from the diameter and the aspect ratio of the fit: considering part materials, Eq. (19) is used for T12 and T34, while Eq. (17) is used for T56.

Table 6 Cost-tolerance factor and optimal scaling for Y on the gear assembly
Full size table

The result of the allocation is also shown in Table 6. The sensitivities of Y to all part tolerances and clearance variations are taken from (24). The factors Fi for the optimal scaling are calculated from (6) for the part tolerances, and from the corresponding expression

$$F_{i} = \left( {B_{i} S_{i}^{ - 2} } \right)^{{\frac{1}{k + 2}}}$$
(25)

for the clearance variations. The Fi are scaled using Eqs. (7) and (8) with FY = 1.710. This gives the optimal values of the first-level specifications in proportion to TY.

Table 7 shows the second-level allocations: the variation of each clearance is optimally distributed to the related features. This is done using the expressions found in subSection 3.2 for pin-hole clearances: considering again the materials of the parts, (18) is used for T12 and T34, and (15) for T56. All tolerances are now set in proportion to TY; the assembly specification could have been known from the beginning as input data, or chosen after estimating the cost function of Y at the first allocation level as in the example in subSection 4.1.

Table 7 Tolerance allocation for the pin-hole features on the gear assembly
Full size table

5 Discussion

The above examples suggest some considerations about the two main applications intended for the cost function of a requirement.

The case in subsection 4.1 demonstrates how the choice of the variation TY allowed for a requirement can be helped with an estimation of its cost CY. In practice, a precision specification is unlikely to be driven by cost constraints alone; it is equally unlikely, however, that it is completely determined by technical constraints. Two typical situations can be mentioned in this regard:

  • If the requirement is related to ease of assembly, the condition to be satisfied usually involves only one of the two variation limits. For the axial clearance of a shaft, the lower limit must be greater than zero, but the upper limit can be chosen freely as long as no functional problems arise.

  • If the requirement influences essential aspects of the operation of a mechanism (precise positioning, backlash, sealing, etc.), the choice is mainly technical but usually with no known rules to help setting the variation. Even after preliminary calculations or experimental tests, a designer would tend to overspecify for safety if this did not lead to excessive cost penalties.

In both situations, using cost estimation as a further support for design decisions seems useful. In the proposed approach, the cost of the requirement is expressed in machining minutes, which are readily translated into currency units according to an appropriate shop rate. This makes it possible to evaluate the impact of tolerancing decisions on both productivity and cost.

It may be difficult to find the right trade-off between variation and cost for a requirement. From this point of view, a linear graph of the cost function seems effective enough because it clearly shows the progressive steepness of the curve. When possible, as in the case of a chain of two dimensions such as the gap of a cylindrical fit, the visualization can be further improved by adding notable points such as those corresponding to IT tolerance grades.

The case in subsection 4.2 demonstrates a hierarchical approach that can be applied in principle to any tolerance allocation method. It consists in solving the problem by mixing part-related variables (tolerances) with assembly-related variables (variations of requirements); the latter then become the data for further allocations at a lower level. The most apparent effect is that a lower number of dimensions is involved at each level. The benefit is of limited importance using optimal scaling, but other optimization methods (possibly needed under less restrictive assumptions) might reach convergence more quickly with fewer variables. Other potential advantages of hierarchical allocation include:

  • an easier inspection of the dimension chain, which helps to avoid errors in the functional equation;

  • a logical aggregation of features that have a combined effect, as in the case of cylindrical fits;

  • a consistency with the well-known charting methods for tolerance analysis, e.g. [101], which introduce the misalignment between mating features (assembly shift) in the dimension chain to avoid explicitly considering the involved dimensions (e.g. diameters of shafts and holes).

Beyond the two applications described, the proposed method might provide design support in a broader sense. The cost function can help estimate the relative effects of different design variables on the cost of a generic functional requirement. For example, let Y be the sum of n dimensions associated to features with equal types and sizes on parts made of the same material. The cost of the requirement is

$$C_{Y} = n\frac{b}{{T^{0.55} }}$$
(26)

where the tolerance for all dimensions is

$$T = \frac{{T_{Y} }}{\sqrt n }$$
(27)

and the common cost factor is

$$b = \beta \cdot f_{M} \cdot f_{F} \cdot f_{A} \cdot X^{0.18}$$
(28)

where the coefficients fM, fF and fA as well as the nominal value X are the same for all dimensions. Substituting (27) and (28) into (26), it results that

$$C_{Y} = \frac{{\beta \cdot n^{0.83} \cdot f_{M} \cdot f_{F} \cdot f_{A} \cdot X^{0.18} }}{{T_{Y}^{0.55} }}$$
(29)

The above expression shows how the tolerance-dependent cost depends on the design variables associated with the requirement. Doubling the number n of features, the cost is multiplied by 20.83 = 1.77. Doubling the nominal dimension X, the cost is multiplied by 20.18 = 1.13. Changing materials and feature geometries so as to double fM, fF, or fA doubles the cost.

Similar what-if analyses can lead to cost reduction criteria. For example, it is interesting to have a feel of how the total cost would change if the features involved in a requirement had very different properties (material, type and size). For this purpose, let Y be the sum of two dimensions whose cost factors bi are in the ratio b1/b2 = q > 1. For consistency with the previous case, it is also b1 + b2 = 2b. Therefore

$$b_1=\frac q{q+1}\cdot2b,\;b_2=\frac1{q+1}\cdot2b$$
(30)

With unit sensitivities and dropping the common factors, Eq. (6) gives

$$F_1=\left(\frac q{q+1}\right)^{0.39},\;F_2=\left(\frac1{q+1}\right)^{0.39}$$
(31)

It is easily found from (7) and (8) that the optimal tolerances are

$$T_1=\frac{q^{0.39}}{\sqrt{1+q^{0.78}}}T_Y,\;T_2=\frac1{\sqrt{1+q^{0.78}}}T_Y$$
(32)

Substituting (30) and (32) in (4) and adding the costs of the two features, it results that

$$C_Y=\frac{\left(1+q^{0.78}\right)^{0.73}}{1+q}C_0,\;C_0=\frac{2b}{T_Y^{0.55}}$$
(33)

Figure 10 shows that, for a given TY, CY decreases considerably as the ratio q between the cost factors increases. It can be generally said that, if some features have optimal tolerances that are very different from one another, the cost decreases due to the wider tolerances more than it increases due to the tighter tolerances.

Fig. 10
figure 10

Cost of a requirement involving two features with b1/b2 = q

Full size image

It would also be interesting to use the cost of a requirement to compare alternative designs of an assembly. Such chance, however, is limited by the fact that the proposed method estimates only the fraction of the cost that depends on the tolerances, corresponding to the time taken by the finish machining operations. If the two compared designs have very different geometries and require different amounts of rough machining or raw material, the cost differences resulting from those factors should be estimated separately.

For all the applications described, the proposed cost function seems to provide an acceptable trade-off between convenience and accuracy. The first takes advantage of the explicit mathematical expression, calculated directly without the need for optimization procedures. The second relies on the extended reciprocal power function, which accounts for multiple design variables and was validated in [4] using a proven method for machining cost estimation. It cannot be denied, however, that the estimation uncertainty of the requirement cost is affected by the simplicity of the underlying assumptions; the potentially most critical one is the use of general cost data that do not consider the actual equipment available in specific manufacturing settings. From this point of view, better results have recently been obtained with a new approach to tolerance allocation, which constrains the optimization to the use of given resources. In [102], these are modeled through exponential cost-tolerance functions with different parameters for alternative machine tools. In [103, 104], the cost model is more complex and takes into account further activities influenced by tolerances, such as inspection of parts and assemblies. In both methods, the resources chosen for each part dimension are additional optimization variables, and the conformity ratio on the assembly is estimated along with cost for the optimal solution. The process-based approach is suitable for complex assumptions and is likely to be more accurate as a company can use first-hand, easy to update cost data. Furthermore, as shown in [103], it can highlight further limits on the allowable variation for a requirement: with given resources, an especially tight variation can cause excessive nonconformities, while an especially wider one gives no marginal cost reduction. On the other hand, it requires a numerical solution of the optimization problem, which can make it more difficult to integrate in the design workflow.

6 Conclusions

The paper has described a procedure for estimating the cost of a functional requirement as a function of the allowed variation. In a tolerance allocation problem, the variation of a requirement is a given specification and is generally treated as a constraint in the minimization of cost. The proposed cost function allows to predict how the minimum cost will be influenced by the specification without the need to solve the optimization problem. This is made possible by the use of two previously developed concepts: the extended reciprocal-power cost-tolerance function and the optimal scaling method. The first expresses the cost of tolerances homogeneously for different types of part features, making explicit the influence of some design variables (part material, feature shape and size). The second solves the allocation problem by scaling initial tolerance values in optimal proportions. The examples have shown that the procedure is suitable for parts designed with either dimensional tolerances or geometric tolerances with possible modifiers.

The cost of a functional requirement has a particularly simple expression and has three main applications:

  • supports the choice of the variation of the requirement, which is usually specified without in-depth discussion but can have a relevant impact on the manufacturing cost;

  • allows a hierarchical approach to tolerance allocation, which simplifies the dimension chain by using requirements as optimization variables;

  • suggests design criteria for the reduction of the cost associated with tolerances, showing the effect of some choices such as the number of involved features and their design attributes.

Like its parent method (the optimal scaling for tolerance allocation), the estimation of requirement cost is suitable for manual calculations as it does not require numerical optimization procedures that can possibly be an obstacle to practical use in mechanical design. However, it could easily be implemented in a spreadsheet template for generic dimension chains. This would allow the designer to quickly evaluate the economic impact of alternative specifications on the requirement. At a more sophisticated level, the proposed method could be integrated into existing CAD-based applications for the automatic recognition of functional requirements and dimension chains.

In principle, the proposed method might be used to define an assembly-level allocation problem. This would consist of optimizing all requirements identified for an assembly before solving the respective allocation problems. The problem could be solved with a different formulation than the classical allocation of part tolerances, e.g. minimizing a quality-based objective function (fraction of rejects, risk of functional defects, quality loss on the requirement, etc.) within a given cost budget. The feasibility of such an approach will be investigated in upcoming studies.