1 Introduction 

The current industry is highlighting the growing need for green, renewable, and ecological materials, particularly biocomposites, as part of the drive for sustainable solutions. In response to these demands, current research is focused on exploring various biocomposites for additive manufacturing (AM), with a specific emphasis on fused deposition modelling (FDM), a widely adopted AM technology [1,2,3].

Polylactic acid (PLA) has been a prominent choice for FDM due to its affordability, favorable thermal properties, and biodegradability. However, the practical application of FDM-manufactured PLA parts as fully functional engineered components is limited by their lack of strength. The addition of organic fillers of various kinds to virgin PLA has the potential to both improve the mechanical properties of virgin PLA, increase the cost-effectiveness, and preserve the biodegradability of the material [4,5,6].

Various organic additives, such as hemp and wood fibers, wood flour, coconut, and lignocellulose particles, have been successfully applied into virgin PLA. Despite their potential benefits, certain technical challenges have been reported during the printing process. Uneven distribution and significant hydrophilicity of the organic additives in PLA filaments have been identified as factors that may adversely affect processability [7, 8].

It is noteworthy to address the potential risks associated with technical issues in FDM of PLA biocomposites, which may lead to significant defects in manufactured components. To minimize such defects, it is of crucial importance to recognize the presence of additives during the decision-making process for selecting FDM process parameters. Previous research has indicated that the introduction of organic additives to PLA complicates the process-structure–property relationship within FDM manufacturing. Despite extensive research efforts exploring the effects of various parameters, such as raster angle, additive volume, and layer height, on the mechanical properties and geometric precision of PLA/biocomposite components, a comprehensive understanding of the threshold relationship remains elusive [9, 10].

To address this knowledge gap, several numerical models have been proposed to predict the dimensions and mechanical properties of FDM-manufactured specimens. Yang et al. [11] proposed a numerical model calculating the different temperature fields in honeycomb structures manufactured by FDM. Scapin et al. [12] developed a tool for designers to predict the real mechanical properties of printed components based on finite element analysis. Similarly, Comminal et al. [13] proposed a numerical model to simulate the strand extrusion of partially molten material on a moving substrate, based on CFD paradigm. However, contemporary numerical models mainly focus on virgin materials, neglecting the specific nature of PLA/biocomposites with organic additives. Consequently, the current numerical models may not accurately predict the potential peculiarities and specific defect formation associated with the addition of organic particles to virgin filaments. Therefore, there is a continuous need for the numerical models explicitly designed to handle the unique structure of biocomposites reinforced with natural fillers.

As a response to current lack of numerical models simulating the FDM process of biocomposites reinforced with natural fillers, the current study proposes a novel FEM numerical model based on thermo-mechanical coupling able to predict the distortions and surface defects in blocks produced by FDM from biocomposites. The numerical model considers the composite-like nature and heterogeneity of the PLA-based biocomposite filaments. The introduced numerical model was validated by the comparison of simulated dimensional deviations and surface defects of 9 FDM-manufactured cubes from PLA/wood biocomposite with the ones of experimental cubes manufactured with same process parameters.

2 Materials and methods

2.1 Sample preparation

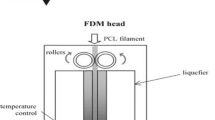
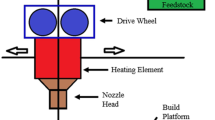
Nine cubical specimens with dimensions of 20 × 20 × 20 mm were manufactured via FDM using RepRam manufacturing system, as it is schematically demonstrated in Fig. 1. Wood-reinforced PLA filaments (Sunlu, China) were applied in fabrication of the cubes. The filaments were composed by a 20% of recycled wood and 80% of polylactic acid (PLA), and they had the diameter of 1.75 mm, with a dimensional accuracy of ± 0.03 mm.

Fig. 1
figure 1

Schematic representation of the manufacturing process 

Full size image

The selected process parameter included variable layer height (LH) and nozzle temperature (NT), while the adopted experimental methodology abided the principles of design of experiment (DOE). Adopted full factorial design has resulted in 9 experimental units (Table 1).

Table 1 FDM process parameters 
Full size table

All specimens were manufactured with same printing speed (PS) and same building strategy. The applied building strategy consisted of parallelly standing stripes with full infill pattern, diagonally scanning the square-like areas of each of building layer. The building path rotates of 90° between each successive layer, as shown in Fig. 2.

Fig. 2
figure 2

Diagonal building strategy

Full size image

The present study conducted dimension analysis of cubes in their as-built state by examining their x-, y-, and z-dimensions. The examined dimensions were determined as the mean of the distances between parallel planes assessed at five measuring points distributed across all faces of the cubes. The distribution of measuring points was symmetrical, with one point placed in the middle of the face and the remaining four at edges, as demonstrated in Fig. 3.

Fig. 3
figure 3

Symmetric distribution of measuring points

Full size image

Furthermore, the deviations from each assessed dimension (Dx, Dy, Dz) were assessed as the difference between the measured or simulated dimension with the nominal dimension designed in CAD file (20 mm). The relative error between experimental and simulated dimension deviations was determined.

Within the study, the surface defect evaluation relied on a rigorous qualitative analysis through meticulous observations. Comprehensive scrutiny and analysis were conducted on each specimen, entailing the meticulous documentation and description of any defects or deviations. This facilitated a rigorous comparison between the simulated and experimental results.

The present study examines the temperature distribution of manufactured specimens at 3.5 s after the termination of the building process, while the cubes were in a partially cooled state. Moreover, the research analyzes the complete temperature history of a single measuring point, positioned at the upper front left edge of the first layer, during both the processing and cooling phases. The measuring point is visually demonstrated in Fig. 4.

Fig. 4
figure 4

Location of measuring point for which temperature history is determined

Full size image

2.2 Numerical model

In the present numerical model, the material deposition was simplified into deposition of full layers all-at-once. Such simplification has resulted in significant decrease of computational time. The deposition of new layers was represented through birth-and-death technique.

The time between deposition of two successive layers is equal to deposition time of a layer applying the real deposition strategy (1):

$${t}_{deposition}=\frac{{s}_{deposition}}{{v}_{deposition}}$$
(1)

where \({s}_{deposition}\) denotes the real deposition path of 1 layer and \({v}_{deposition}\) is a deposition speed.

The PLA/wood material was described as composite including PLA matrix and filler in form of wooden particles. Similarly, as in material used in experimental part of the work, the filler and matrix ratio were 20:80. The filler was represented by spherical particles with diameter of 0.15 mm to realistically capture the medium characteristics of the wooden powder according to Das et al. [14]. Unlike in experimental build, the wooden particles were evenly distributed across deposited layers, as it is demonstrated in Fig. 5. In order to simplify the model, the friction between the filler and the matrix was neglected. The perfect bonding between wooden particles and matrix was considered and the interface between the two materials was identified as “identity pairs” [15].

Fig. 5
figure 5

Schematic representation of composite nature of wood-filled PLA

Full size image

The PLA, as a matrix was characterized by Three Network Model, capturing the viscoplastic nature of polymer, as it is represented in Fig. 6 [16, 17].

Fig. 6
figure 6

Rheological representation of thermoplastic nature of PLA

Full size image

A, B, and C elements are parallelly interconnected. First two frames within the scheme, the Maxwell elements represent the damping of the system, absorbing the applied deformation. On the other hand, the third element, C, defines the elastic behavior of the system under loading. The plastic behavior is represented by element B, which is evolving with plastic strain.

Given the connections between A, B, and C elements, the total Cauchy stress equal to Cauchy stresses in all elements, therefore (2,3,4,5):

$$\sigma ={\sigma }_{A}+{\sigma }_{B}+{\sigma }_{c}$$
(2)
$${\sigma }_{A}=\frac{{\mu }_{A}}{{J}_{A}^{e}\overline{{\lambda }_{A}^{e*}}}\frac{{L}^{-1}(\frac{\overline{{\lambda }_{A}^{e*}}}{{\uplambda }_{L}})}{{L}^{-1}(\frac{1}{{\uplambda }_{L}})}dev\left[{{\varvec{b}}}_{A}^{e*}\right]+k\left({J}_{A}^{e}-1\right){\varvec{I}}$$
(3)
$${\sigma }_{B}=\frac{{\mu }_{B}}{{J}_{B}^{e}\overline{{\lambda }_{B}^{e*}}}\frac{{L}^{-1}(\frac{\overline{{\lambda }_{B}^{e*}}}{{\uplambda }_{L}})}{{L}^{-1}(\frac{1}{{\uplambda }_{L}})}dev\left[{{\varvec{b}}}_{B}^{e*}\right]+k\left({J}_{B}^{e}-1\right){\varvec{I}}$$
(4)
$${\sigma }_{C}=\frac{{\mu }_{C}}{J\overline{{\lambda }^{*}}}\frac{{L}^{-1}\left(\frac{\overline{{\lambda }^{*}}}{{\uplambda }_{L}}\right)}{{L}^{-1}\left(\frac{1}{{\uplambda }_{L}}\right)}dev\left[{{\varvec{b}}}^{*}\right]+k\left({J}_{A}^{e}-1\right){\varvec{I}}$$
(5)

where \({\sigma }_{A}\), \({\sigma }_{B}\), \({\sigma }_{c}\) denote the Cauchy stresses in elements A, B, and C. \({\mu }_{A}\) and \({\mu }_{C}\) stand for constant shear moduli in elements A and C, respectively, while \({\mu }_{B}\) stand for current shear modulus in element B. \({J}_{A}^{e}\), \({J}_{B}^{e}\), and J are the Jacobian terms for respective parts of the system, which can be expressed as the determinant of the force in the respective part of the mechanical system. \({\lambda }_{A}^{e*}, {\lambda }_{B}^{e*}\), and \(\overline{{\lambda }^{*}}\) describe the effective distortional chain stretches in respective parts of the mechanical system, inherently described by trace of Cauchy-Green deformation tensor b. \({\uplambda }_{L}\) denotes the chain locking stretch and \(k\) denotes the bulk modulus.

The temperature-dependent viscoplasticity of the examined material is described by temperature-dependent values of shear and bulk moduli, as it is depicted in Fig. 7 [18, 19].

Fig. 7
figure 7

Temperature-dependent shear and bulk moduli of PLA matrix

Full size image

The plastic behavior of system, represented in element B, was described by evolution rate of shear modulus (6).

$$\dot{{\mu }_{B}}=-\beta ({\mu }_{B}^{i}-{\mu }_{B}^{f})\dot{{\gamma }_{A}}$$
(6)

where \(\beta\) is the evolution rate of \({\mu }_{B}\), \({\mu }_{B}^{f}\) is the total shear modulus in element B, and \(\dot{{\gamma }_{A}}\) is the deviatoric flow rate.

Consequently, the deviatoric flow rate can be described as follows (7).

$$\dot{{\gamma }_{A}}=\dot{{\gamma }_{0}}(\frac{{\tau }_{A}}{\widehat{{\tau }_{A}}+{a}_{v}R({p}_{A})}{)}^{{m}_{A}}$$
(7)

where \(\widehat{{\tau }_{A}}\) represents the flow resistance of network A, \({a}_{v}\) describes the pressure dependence of the flow, \({m}_{A}\) is the stress exponent of network A, \({p}_{A}\) is the hydrostatic pressure, and \(R\) is the ramp function.

Some of the PLA material parameters applied in numerical model are demonstrated in Table 2 [17].

Table 2 Selected PLA material parameters used in numerical model
Full size table

Considering the significantly higher plasticity of PLA than the one of the wood, the wood was considered purely elastic in the present model. Its material properties are demonstrated in Table 3 [20, 21].

Table 3 Mechanical properties of wood
Full size table

Von Mises yield function was applied for both filler and matrix included in the model (8,9).

$$F={\sigma }_{Mises}-{\sigma }_{ys}$$
(8)
$$F=Q$$
(9)

Finally, the mass conservation equation valid throughout the model can be expressed as (10):

$$\rho \frac{{\partial }^{2}{\varvec{u}}}{\partial {t}^{2}}=\nabla .s+{{\varvec{F}}}_{v}$$
(10)

where \(\rho\) is the density of referential volume, \({\varvec{u}}\) is the displacement field, \(s\) is the stress tensor, \({{\varvec{F}}}_{v}\) is the body force. Within the presented model, the body force includes also gravity fields.

Thermal expansion represents the coupling feature between thermal and mechanical analysis within both designed materials (11,12, 13).

$${\epsilon }_{th}=\alpha (T)(T-{T}_{ref})$$
(11)
$$Q={Q}_{d}$$
(12)
$${Q}_{d}=-T\frac{\partial (s:\alpha )}{\partial t}$$
(13)

\({\epsilon }_{th}\) denotes the thermal strain, \(\alpha\) is the coefficient of thermal expansion, \({T}_{ref}\) is the reference temperature, \({Q}_{d}\) represents the thermoelastic damping of the system, and \(s\) relates the elastic strain.

Newly deposited layers were given the nozzle temperature at the moment of deposition, but they started to immediately cool down, with both convective heat flux and heat radiation to outer environment (14,15, 16).

$${q}_{0}=h({T}_{amb}-T)$$
(14)
$$-{\varvec{n}}.{\varvec{q}}=\varepsilon \sigma ({T}_{amb}^{4}-{T}^{4})$$
(15)
$$-n.q={q}_{0}$$
(16)

where \(h\) is heat transfer coefficient, \({T}_{amb}\) is the ambient temperature, \({\varvec{q}}\boldsymbol{ }\mathrm{is the heat flux vector},\) \(\varepsilon\) denotes the surface emissivity, and σ is the Stefan-Boltzmann constant.

The numerical model abides the governing partial heat balance equation and Fourier law of heat conduction (17, 18):

$$\rho {C}_{p}\frac{\partial T}{\partial t}+\rho {C}_{p}{\varvec{u}}.\nabla T+\nabla .{\varvec{q}}=Q$$
(17)
$${\varvec{q}}=-k\nabla T$$
(18)

where \({C}_{p}\) is the heat capacity, \({\varvec{u}}\) is the velocity field, \(Q\) denotes the heat source, and \(k\) represents the thermal conductivity. Table 4 compares the thermal characteristics of both PLA matrix and wooden filler [22,23,24,25].

Table 4 Thermal properties of PLA matrix and wooden filler
Full size table

The building platform and biocomposite layers were discretized into tetrahedral meshing elements using a physics-driven approach for this study. Specifically, the PLA/wood layers were simulated with a minimum element size of 0.0525 mm, resulting in a notably finer mesh compared to that employed for the building platform. We tailored the mesh size for each layer to match its respective thickness, ensuring that thinner layers were discretized into finer elements. Conversely, the mesh for the building platform was deliberately coarser, as our investigation did not encompass an analysis of temperature distribution or platform distortion. A representation of the mesh for both the building platform and PLA/wood biocomposite layers with a thickness of 0.25 mm is depicted in Fig. 8.

Fig. 8
figure 8

Specimen and building platform discretized into meshing elements

Full size image

3 Results and discussion

3.1 Dimension accuracy

Table 5 represents a comparison between the dimensions of PLA specimens manufactured under varying process parameters through experimentation and simulation. The results reveal that all specimens exhibit dimensions larger than their intended values, a phenomenon that may be attributed to the thermal expansion of the building material [3, 25]. Moreover, the specimens’ dimensions in the x- and y-axes exceed those in the z-axis, implying the influence of gravity and body mass forces on the material's flow, resulting in viscous flow in the XY plane.

Table 5 Comparison of experimental and simulated dimensions of PLA cubes manufactured with variable process parameters
Full size table

Table 6 demonstrates the calculated relative errors between simulated and experimentally assessed deviations from designed dimensions in x-, y-, and z-direction of FDM-manufactured cubes. Positive values of relative error indicate that simulated value of dimension deviation exceed the experimentally assessed dimension deviation, and conversely, negative values of relative error represent that simulated dimension deviation is lower than the experimental one.

Table 6 Calculated relative errors (%) between simulated and experimentally assessed deviations from designed dimensions in x-, y-, and z-direction in function of layer thickness (LT) and nozzle temperature (NT)
Full size table

The obtained results indicate a promising level of concurrence between the simulated and experimental data, with a low relative error of dimension deviation calculated. The calculated higher relative errors correlate with the very low dimension deviation and coarser mesh applied in simulation that did not provide the sufficient sensitivity to determine the dimension deviation more precisely. Based on the results obtained in this study, it is evident that the numerical model demonstrates significant promise as a robust and dependable tool for accurately predicting distortion phenomena in cubes produced through the FDM technology.

Similar trend of distribution of displacement fields was observed in all specimens, regardless of the applied process parameters. Figure 9 displays a comparison of distribution of displacements in cubes manufactured with LH of 0.15 and 0.25 mm 3 s after finishing their building process. Significant gradation of distortions in the direction of the z-axis was observed in both cubes. Lower distortions were observed in the lower part of the cubes, which can be attributed to the strong adhesion of the lower layers to the building platform [26]. This phenomenon is frequently observed in PLA specimens due to PLA’s inherent resistance to warping. Nevertheless, the uppermost layers of the cube, fabricated with a layer height (LH) of 0.15 mm, did not substantially contribute to the progressive distortion observed in the specimen. In fact, their distortion levels were approximately one-third lower than those observed in the preceding layers. This behavior can be explained by incomplete cooling of the specimen. Several irregularities located in central areas of the fabricated faces were observed, suggesting the formation of defects. Additionally, in cube manufactured with layer thickness of 0.25 mm, higher displacements were located also around the edges of manufactured specimens.

Fig. 9
figure 9

Distribution of displacement fields in PLA cubes manufactured with layer height of 0.15 mm and 0.25 mm

Full size image

Figure 10 confirms the simulated results of difference in distortion distribution in case higher layer height is applied to build the specimen. The distortions located around the edges are easily observable in cube manufactured with LH of 0.25 mm but seem undetected in cube manufactured with LH of 0.15 mm. The defects and their possible causes are further discussed in the subsequent part of the paper.

Fig. 10
figure 10

The distortions I experimental specimens built with LH of 0.15 and 0.25 mm

Full size image

3.2 Defects and distortions

Several defects and distortions were observed in manufactured cubes. The size and range of these defects were found to be highly dependent on the applied layer thickness and nozzle temperature, as illustrated in Fig. 11, where the contours circle up the sets of process parameters within which the respective defects were observed. It can be thus interpreted that the process parameters outside the contours tend to create the cubes without the respective defects. It is noteworthy that the defects identified through experimental qualitative analysis were found to be consistent with the simulated defects.

Fig. 11
figure 11

Distribution of defects in FDM specimens manufactured with variable layer thickness and nozzle temperature

Full size image

The results indicate that cubes produced with a layer thickness of 0.15 mm exhibit relatively low levels of defects, which are of smaller range. On the contrary, augmenting the layer thickness has yielded a notable upsurge in the occurrence of defects, encompassing a broader spectrum of types and magnitudes. More precisely, cubes characterized by a layer thickness of 0.15 mm predominantly exhibit undulating surfaces and minute voids. These observations hold true across simulated and empirical samples, as illustrated in Fig. 12. While the wavy edges represent relatively common defect in PLA specimens manufactured by FDM [27], the additive of wooden particles might possibly contribute to range of such effects especially in more moist environments, where the wooden particles start to bud and increase their volume [28]. The effect of wooden particles would be especially observable in case of uneven distribution of filler, where the wooden particles are clustering to larger aggregates [29].

Fig. 12
figure 12

Wavy faces of simulated and experimental cubes

Full size image

Increasing the layer height to 0.20 mm has led to a higher variety and range of defects in manufactured cubes. The identified defects included wavy sides, larger-scale holes, and defects caused by splattering of molten material. The latter defect was observed only in specimens manufactured at a high nozzle temperature (220 °C), likely due to the higher flowability of the molten material [30]. These findings are supported by the observed distribution of defects, which demonstrated that splattering only occurred in specimens manufactured at this temperature. Figure 13 provides a comparison of both the simulated and experimental defects caused by splattering of molten material.

Fig. 13
figure 13

Simulated and experimental defects caused by splattering of molten material

Full size image

The effect of increasing layer height from 0.20 to 0.25 mm consisted of a greater variety and larger scale of observed defects, including those previously identified in specimens manufactured with layer heights of 0.15 and 0.20 mm. Notably, holes observed in specimens manufactured with a layer height of 0.25 mm exhibited considerably larger diameters than those observed in the cubes manufactured with lower layer heights, with protrusions of material penetrating to the outer space (Fig. 15a). The inclusion of wooden additives could potentially facilitate the development of these defects. Differing densities between the matrix and filler materials may lead to the formation of distinct sublayers within the deposited structure. Specifically, gravitational forces may result in the creation of a denser PLA sublayer positioned in the lower portion of the deposited layer, while a less dense wooden sublayer forms in the upper region of the deposited layer [31]. The uneven material distribution correlates with the different flowability inside the layers, which can lead to holes and material protrusions. The reduced incidence of defects of this particular nature, as evidenced in cubes produced with thinner layers, can be likely attributed to the closer alignment between smaller layer thickness and the dimensions of the wooden particles. This assumption was later confirmed by numerical model. As it is observable in Fig. 14, demonstrating the volume of fillers in solidified layer with the height of 0.25 mm, the higher volume of wooden particles is located in the top parts of deposited layers.

Fig. 14
figure 14

Solidified layer with height of 0.25 mm

Full size image

Furthermore, largely distorted edges and adjacent areas in cubes manufactured with large layer thickness were observed. The edges exhibited a striking resemblance to inwardly oriented, subtly irregular seams, whereas the regions adjacent to these edges exhibited an inward orientation, giving rise to shallow sinkholes, as illustrated in Fig. 15b.

Fig. 15
figure 15

Defects in cubes manufactured with layer height of 0.25 mm

Full size image

Additionally, in specimen manufactured with layer thickness of 0.25 mm and nozzle temperature of 220 °C, the failure of the lower edge was identified (Fig. 15c). This failure can be attributed to the high flowability of the molten material, which is exacerbated by the temperature-induced softening of slowly cooling material, as well as the higher body mass forces of the thicker layers [29]. Both different thermal behavior and different flowability between PLA and wooden particles have potential to significantly contribute to observed edge failure [27]. These findings suggest that careful consideration of material properties and printing parameters is necessary to prevent failure in additive manufacturing processes.

3.3 Residual stresses

Residual stresses in PLA/wooden cubes cooled for 3.5 s after completion of the FDM manufacturing process were found to be significantly influenced by the employed process parameters. The present study revealed that the residual stresses were lowest in cubes fabricated with the lowest layer thickness and the lowest nozzle temperature. The application of higher nozzle temperature and thicker layer thickness resulted in an increase in residual stresses. However, the impact of layer thickness on residual stresses was found to be substantially greater than that of nozzle temperature, as evident from the results presented in Fig. 16.

Fig. 16
figure 16

Residual stresses in FDM cubes manufactured with different process parameters

Full size image

The results of numerical simulation showed that the residual stresses were similarly distributed in all specimens, with the highest stresses observed around the edges in the lower half of the specimens. A gradual decrease of residual stresses in the direction of the z-axis was also observed. The accumulation of high residual stresses in the lower part of the specimens was found to be correlated with the adherence of the bottom layers to the building platform [26]. In contrast, the upper parts of the fabricated specimens were less constrained, allowing for more freedom in temperature-induced material expansion and shrinkage, resulting in higher distortions but lower residual stresses in this area [32].

The values of residual stresses observed in the manufactured specimens exhibited a clear dependence on the adopted layer thickness. Specifically, the lowest residual stresses were observed in specimens fabricated using a layer thickness of 0.15 mm, with a maximal value of 27.7 MPa. An increase of layer thickness to 0.20 mm resulted in a corresponding increase of the maximum residual stress to 42 MPa. Further increase of the layer thickness led to even higher residual stress values, with a maximum of 48 MPa observed. The identified residual stresses are in good agreement with the results in literature. In contrast, differences in residual stress values among specimens fabricated with the same layer thickness but varying nozzle temperatures were found to be much less significant [33]. More significant effect of nozzle temperature was however observed in cubes manufactured with layer thickness of 0.25 mm. This can be explained by the fact that such high layers undergo less heating cycles, which would normally work as in situ thermal treatment, eventually minimizing the residual stresses of the specimens. The missing in situ thermal treatment in higher layers might thus emphasize the effect of nozzle temperature on thermal gradients in the faster-cooling corners of the building cubes. The different thermal gradients therefore lead to different residual stresses in corners of the cubes manufactured with layer thickness of 0.25 mm and different nozzle temperature. This behavior was later confirmed by the temperature analysis, where only one heating cycles were observed in layers with the thickness of 0.25 mm.

3.4 Temperature

The temperature distribution in a partially cooled (for 3.5 s after finishing the manufacturing process) cube fabricated using FDM is presented in Fig. 17. It is noteworthy that the temperature distribution is consistent across all fabricated cubes, regardless of the applied process parameters. Differences in thermal behavior of PLA matrix and wooden fillers seemingly did not influence the global thermal behavior of the manufactured cubes.

Fig. 17
figure 17

Temperature distribution in FDM specimen after 3.5 s of cooling

Full size image

The lowermost layers maintained continuous contact with the preheated platform, thus preserving their initial preheated state. A progressive elevation in temperature was discernible, extending from the lower to the upper parts of the specimen, due to the incomplete cooling of recently deposited layers. Notably, the cooling rates differed substantially between the peripheral and central regions, primarily attributable to the enhanced exposure of the periphery to the ambiental lower temperature. This temperature gradient holds potential ramifications for both the mechanical attributes and dimensional precision of objects produced through FDM [34].

The temperature data presented in Fig. 18 demonstrates the comparison of the temperature history curves, taken in pre-defined measuring point in the first deposited layer in specimens manufactured with same layer thickness of 0.15 mm, but varying nozzle temperature (220, 210, and 200 °C). The results showed that there were only minor differences in the temperature history. This finding was consistent across all examined layer thicknesses.

Fig. 18
figure 18

Comparison of temperature history in cubes manufactured with same layer thickness and variable nozzle temperature

Full size image

The results show that rapid cooling occurs immediately after layer deposition in all examined specimens. At the end of the first cooling phase, the temperature of the examined point approached the preheating temperature of the building platform. Upon deposition of the second layer, the material in the examined point underwent another rapid heating, but the maximal temperature did not reach the nozzle temperature and remained at approximately 370 K. Subsequently, a few cycles of rapid cooling and heating with decreasing temperature amplitude were observed until the temperature stabilized at the value of 320 K, which corresponds to the temperature of the heated building platform. These findings correspond with the literature [35, 36].

The number of observable cycles of rapid heating and cooling depended on the thickness of the deposited layers. Thinner layers resulted in a higher number of thermal cycles. The material underneath the deposited layers reacts thermally to subsequent layers, resulting in a more complex thermal history of the deposited layers [36]. Figure 19 illustrates the relationship between layer thickness and the number of observable thermal cycles.

Fig. 19
figure 19

Thermal history curves of specimens manufactured with same nozzle temperature and varying layer thickness

Full size image

4 Conclusions

In this present study, we introduced a comprehensive coupled thermomechanical 3D numerical model aimed at simulating distortions, defect formations, residual stresses, and temperature variations in cubes fabricated using the fused deposition modeling (FDM) technique. To ensure the accuracy and reliability of our numerical model, rigorous validation was conducted through a meticulous comparison of the simulated dimensions of fabricated components with experimental measurements, revealing a high level of concordance between the two sets of data. As a result of our investigation, several pertinent conclusions have been deduced and are elucidated below. Displacement fields of fabricated specimens showed increasing tendency in the direction of z-axis, attributed to the strong adhesion of the lower layers to the building platform. Furthermore, in specimens manufactured with higher thickness, high displacement fields were located around the edges.

  • The FDM building process might create several types of defects and distortions in manufactured components. The size and range of these defects highly depend on the applied process parameters.

  • The presence of wooden additives might contribute to defect formation due to higher flowability of PLA matrix, increase of the volume of wooden filler in moist environment, clustering of the wooden particles and the difference in thermal properties between matrix and filler material.

  • The proposed numerical model was able to sufficiently capture the defect formation in FDM manufactured cubes as the simulated defects corresponded well to the defects identified within qualitative analysis of experimental specimen.

  • The numerical stresses were influenced mainly by the applied layer thickness. Specifically, specimens fabricated using a layer thickness of 0.15 mm exhibited the lowest residual stresses, with a maximal value of 27.7 MPa. An increase of layer thickness to 0.20 mm resulted in a significant increase of the maximum residual stress to 42 MPa. Further increase of the layer thickness led to yet another increase of residual stresses up to 48 MPa.

  • The thermal curves showed considerable impact of layer thickness on thermal history of the deposited layers. Thinner layers undergo more cycles of rapid heating and cooling what might further influence the mechanical properties and overall quality of fabricated parts.