1 Introduction

In high-performance geared transmissions, accurate static and dynamic models are fundamental for obtaining a realistic characterization of the system’s behavior by which the transmission’s performances can be improved. Static models study the transmission at low angular speeds (typically a few hundred revolutions per minute), neglecting the influence of any gear-induced vibration on the meshing conditions. On the contrary, dynamic models include several high-frequency vibrating motions superimposed on the nominal gear constant angular speed, which may be different depending on the working regime considered. Moreover, as the working regimes are often characterized by intersections with the system’s resonance frequencies (amplifying gear-induced vibrations), it is necessary to consider either the static or dynamic behavior of the transmission.

Öezgüven and Houser [1] and Wang et al. [2] reviewed the mathematical models used to model gear transmissions up to the 1990s and indicated the parameters of paramount importance when analyzing the system dynamics. Of all these parameters, profile modifications are essential for any geared transmission system. Profile modifications are defined as the amount of material removed in the direction normal to the nominal profile of the tooth, in general a circular involute, to obtain the desired tooth profile. The profile modifications can be uniform along the gear width (i.e., tip relief), a local modification of the tooth’s external edges (i.e., tip crowning), or a combination of the two. A suitable profile modification, usually optimized for specific working regimes with static analyses, prevents collisions when a new teeth pair engages, increases the overall efficiency of the transmission, reduces noise and vibrations, and so on.

Kahraman studied the effect of the involute contact ratio on the torsional dynamics of spur gears using gears with the same geometry but different outer diameters [3]. Other researchers studied standard profile modifications (i.e., linear or parabolic tip relief) [4, 5] and analyzed their influence on the dynamic tooth root strain. Eritenel and Parker [6] derived an analytical solution for the nonlinear vibrations of spur gears with tooth profile modifications and analyzed their influence on total and partial contact loss. Moreover, tooth surface microscopic features can influence the meshing stiffness and the overall efficiency of the transmission [7, 8]. Narrow-faced spur and helical gears [9], multimesh gear vibration with profile modifications [10], and gear manufacturing errors [11] have also been studied.

In this context, several studies demonstrated that the profile modifications play a fundamental role both in the static and dynamic behavior of geared transmission systems [12,13,14]. The profile modifications influence meshing stiffness, load distribution, contact ratio, corner contacts, and transmission error. Consequently, optimizing the shape and entity of the profile modification can improve the behavior of the transmission. Several authors have studied methods to optimize the gear profile and the static performance of gear trains [15,16,17,18,19,20]. Sankar et al. [21, 22] optimized the gear tooth profile design using finite element models to increase the overall tooth strength. Other studies [23,24,25,26,27] have explored the optimal profile modification to minimize the maximum contact pressure. Genetic algorithms have been successfully employed to optimize the macro and micro-geometry of spur gears [28, 29]. The main limitation of these studies is that, with some exceptions [25, 30], only the static behavior of the transmission is considered.

From a manufacturing point of view, introducing a profile modification increases the complexity of the production process, the overall cost, the production time, and the material waste. The commonly adopted profile modification is usually linear or parabolic, starts from the pitch point, and is defined by the maximum entity of the modification at the tooth tip. This produces a significant quantity of removed material, especially for high-profile modifications, and determines contact conditions that involve the nominal involute profile only up to the pitch point, with an increase in the maximum contact pressures. The design for manufacturing of the profile modification can reduce the volumes of removed material and manufacturing time compared with the commonly adopted profile modifications, and also improve both the static and dynamic meshing conditions.

To respond to the critical issues described so far, the present work proposes a method to improve spur gear profiles based on the transmission error. The transmission error is the most used index to represent the non-ideal behavior of the meshing gears due to the gear compliance and tooth profile modifications (compared to the ideally rigid nominal involute profile). Modifying the transmission error in static conditions through a profile modification can reduce the meshing stiffness fluctuations in the working regimes of interest, thereby achieving better dynamic performances. Following this logic, the static transmission error function was calculated for the nominal involute profile. After selecting the nominal torque of the transmission, two profile modification functions with improved dynamic performances were obtained using an iterative algorithm. The proposed profile modifications were compared in terms of peak-to-peak static transmission error and maximum contact pressure in static conditions. A lumped parameter model was introduced to compare the dynamic performances of the modified profiles in terms of dynamic overload factor and dynamic transmission error. The grinding wheel profiles used to machine the proposed profile modifications were defined. Lastly, the volume of material removed was evaluated for several profile modifications.

2 Profile modification definition

As the main purpose is to reduce the vibrations induced by a non-constant meshing stiffness, the definition of the improved profile modification is based on the minimization of the peak-to-peak static transmission error \(q_\textrm{PTP}\), which is the difference between the maximum and the minimum static transmission error in a single meshing cycle (Fig. 1). Ideally, if the peak-to-peak static transmission error was identically zero in a complete meshing cycle at a given constant torque, the meshing stiffness would be constant, and the self-induced vibrations would be absent. As a consequence, minimizing the peak-to-peak static transmission error is expected to improve the static and dynamic behavior of the transmission. In the proposed method, the static transmission error is evaluated and assigned to the tooth profile as a material subtraction until a minimum peak-to-peak transmission error is reached, allowing to uniquely determine the tooth profile points to be modified and to intervene on any gear geometry without losing generality.

For a gear pair, the first step to define the improved profile modification is the calculation of the static transmission error curve. The nominal torque \(M_\textrm{N}\) is chosen based on the actual working regimes of the transmission. A static finite element model [31] is used to calculate the static transmission error \(q_0\) under a static torque \(M_\textrm{T}\) equal to the nominal one \(M_\textrm{T}=M_\textrm{N}\), thus obtaining the starting point of the iterative algorithm. In the present work, the gear parameters (reported in Table 1) are taken from [32], and the static transmission error obtained for \(M_\textrm{T}=M_\textrm{N}=200\) Nm as a function of the normalized roll angle \(\psi \) (the ratio between the roll angle \(\phi \) and the gear angular step \(\phi _0\)) is shown in Fig. 1.

Table 1 Parameters of the transmission
Full size table
Fig. 1
figure 1

Static transmission error curve at \(M_\textrm{T}=M_\textrm{N}=200\) Nm

Full size image

The gears feature a contact ratio equal to 1.37, meaning that the meshing teeth pairs vary between 1, in the Single Teeth Contact (STC) zone, and 2, in the Double Teeth Contact (DTC) zone. As can be observed in Fig. 1, the transition from the STC to the DTC zone is gradual and the peak-to-peak static transmission error of the nominal involute profile is equal to 3.72 \(\mu \)m.

Considering the nominal involute profile, the variation of the static transmission error is generated by the compliance of the spur gears, which cannot be eliminated or significantly modified. Consequently, the peak-to-peak static transmission error can be reduced only through a profile modification, which increases the static transmission error in the DTC zone due to a rigid motion of the gears. Moreover, the peak-to-peak static transmission error cannot be reduced identically to zero, as a lower limit is given by the tooth compliance in the STC zone (Fig. 1). For this purpose, the next step of the algorithm consists in identifying the value of the static transmission error to which all points along the meshing arc must tend, which is given by the minimum value of the static transmission error when only two teeth are in contact \(q_\textrm{min}\) (Fig. 2). The intersection of the horizontal line passing through \(q_\textrm{min}\) and the static transmission error curve defines the starting point of the profile modification \(\phi _\textrm{in}\). The ending point of the profile modification is at the tooth tip. The difference between \(q_\textrm{min}\) and the static transmission error defines the total profile modification assigned at each meshing point in the direction normal to the nominal involute profile \(h(\phi )\), as shown in Fig. 2 and Eq. (1).

$$\begin{aligned} h(\phi )= {\left\{ \begin{array}{ll} q_\textrm{min}-q_0(\phi ) \hspace{0.125cm} \textrm{if} \hspace{0.125cm} q_\textrm{min}-q_0(\phi )\ge 0\\ 0 \hspace{2.15cm} \textrm{else} \end{array}\right. } \end{aligned}$$
(1)
Fig. 2
figure 2

Definition of the profile modification

Full size image

The static transmission for \(M_\textrm{T}=M_\textrm{N}\) is calculated with the updated geometry (Fig. 3) and used as the new profile to be modified. The profile modification increases the static transmission error in the transition region between the STC and the DTC zone (tooth tip modification), causing an increase in the lower limit of the peak-to-peak transmission error and the need to avoid excessive profile modifications. Consequently, the procedure is applied iteratively until the difference between \(q_\textrm{PTP}\) and its lower limit (Fig. 1) is lower than 10%. The proposed algorithm (reported in Fig. 4) can be applied to improve the material removal of any tooth profile, regardless of whether it is the nominal involute profile or an existing profile modification. There are infinite solutions with equal peak-to-peak transmission error, allowing the application of other constraints or starting points to satisfy different requirements (for example, static or endurance requirements).

Fig. 3
figure 3

Updated gear tooth profile

Full size image
Fig. 4
figure 4

Optimization algorithm

Full size image

It is worth noting that the algorithm can be applied to any gear type. However, most advantages are obtained for spur gears, which feature higher contact irregularity, lower contact ratio, and a higher margin of improvement for the transmission’s dynamics. For example, the intrinsic meshing regularity of hypoid or helical gears makes profile modifications less relevant to reduce vibrations, thus the profile modifications are mainly employed to avoid edge contact or modify the meshing contact pattern for those gears.

Fig. 5
figure 5

Type 1 profile modification as a function of \(\psi \)

Full size image

In the present work, the method was applied to obtain two different profile modifications calculated for the gears from [32]:

  • The first profile modification is obtained by applying the iterative algorithm to the nominal involute profile without any constraint on the modification shape (hereafter defined as “Type 1”). The maximum profile modification at the tooth tip is limited by strength requirements (not exceeding the scuffing limit) and is oriented to improve the dynamic behavior of the transmission.

  • The second profile modification is obtained by applying the iterative algorithm to a profile calculated in static conditions to reduce the maximum contact pressures in one meshing cycle and derived from [24] (hereafter defined as “Type 2”). The starting modification shape is a parabolic and linear spline, which produces an initial static transmission error different from the nominal involute profile. In this case, the purpose of the algorithm is to modify the material removal at each point, improving the dynamic performances of the starting tooth profile while maintaining the same static performances. As in the previous case, the maximum profile modification at the tooth tip is limited by strength requirements.

The spur gears from [32] were previously characterized using a dynamic model based on a novel meshing stiffness definition, featuring high precision and the capability to replicate the experimental behavior of the transmission [31]. As the model can simulate any profile modification while maintaining the same accuracy, the theoretical results presented in the following may be considered accurately representative of the actual dynamic behavior of the transmission.

2.1 Type 1

The type 1 profile modification was obtained by applying the iterative algorithm starting from the nominal involute profile. In Fig. 5, the profile modification h is represented as a function of the normalized roll angle \(\psi \). It can be noticed that convergence needs only a few steps, and a profile modification different from commonly used shapes is obtained. The differences between the curves at each iteration are the starting point of the profile modification and the maximum profile modification at the tooth tip \(h_{\max }\), which is adjusted to avoid corner contacts (i.e., based on the maximum contact pressure).

Fig. 6
figure 6

Static transmission error at \(M_\textrm{T}=M_\textrm{N}=200\) Nm with the type 1 profile modification

Full size image

The static transmission error at \(M_\textrm{T}=M_\textrm{N}=200\) Nm for the type 1 profile modification is represented in Fig. 6 for all the iterations required to reach convergence. All the static transmission error curves show the same trend in the STC zone, which is unaltered by the profile modification. The minimum value of the static transmission error in the DTC zone reaches the value of \(q_\textrm{min}\) for all the iterations considered. The static transmission error of the modified profiles in the transition from the STC to the DTC zone is slightly increased due to the presence of a profile modification, causing an increase of \(q_\textrm{PTP}\) and a negligible angular extension of the STC zone. At convergence, \(q_\textrm{PTP}\) is reduced from 3.72 to 0.70 \(\mu \)m, thus obtaining an 81% reduction compared to the unmodified profile.

The obtained profile modification was included in a static finite element model to calculate the response surface of the modified gear pair. The results obtained for any loading regime and angular configuration are reported in Fig. 7, in which \(q_0\) is represented as a function of \(\psi \) for several torque regimes. The variability of the gear pair compliance with the contact position along the tooth flank, the number of teeth in contact, and the transmitted torque can be observed. The STC zone, the DTC zone, and the static transmission error at zero load \(q_\textrm{u}\) are highlighted. Compared to the nominal involute profile, the static transmission error at zero load is non-null and constitutes the main component of the static transmission error at low nominal torques (idle regimes). Moreover, the static transmission error at zero load is uniform in the DTC zone.

Fig. 7
figure 7

Response surface of the gear pair with the type 1 profile modification

Full size image
Fig. 8
figure 8

Type 2 profile modification as a function of \(\phi \)

Full size image

2.2 Type 2

The type 2 profile modification was obtained by applying the iterative algorithm to a profile modified using a spline, which is made of a parabolic and a linear function of \(\phi \) [24].

The tip relief h is represented as a function of the roll angle \(\phi \) in Fig. 8. Three steps are needed to reach convergence, obtaining the improved spline. Compared to the initial curve, the entity of the tip relief at each value of \(\phi \) is increased. The position of the spline node moves towards the starting point of the profile modification, extending the linear part of the spline. The maximum profile modification is unaffected by the iterative algorithm.

The static transmission error at \(M_\textrm{T}=M_\textrm{N}=200\) Nm for the type 2 profile modification is represented in Fig. 9 for all the iterations considered. The final curve shows the same features of the type 1 profile modification, with a slight difference in the static transmission error trend in the DTC zone. At the final step, \(q_\textrm{PTP}\) is reduced from 3.72 to 0.62 \(\mu \)m, obtaining an 83% reduction.

Fig. 9
figure 9

Static transmission error at \(M_\textrm{T}=M_\textrm{N}=200\) Nm with the type 2 modification

Full size image
Fig. 10
figure 10

Response surface of the gear pair with the type 2 profile modification

Full size image

The type 2 profile modification was included in a static finite element model to obtain the related response surface (Fig. 10). Compared to the type 1 profile modification, the response surface obtained presents the same features, but the maximum unloaded transmission error is not uniform and shows a peak at the center of the DTC zone.

3 Static behavior

The profile modifications obtained were compared considering the maximum contact pressure in a meshing cycle and peak-to-peak transmission error as a function of the applied torque.

The maximum contact pressure \(p_{\max }\) is represented as a function of \(\psi \) in Fig. 11. As expected, \(p_\mathrm {\max }\) is uniform along the STC zone. The maximum value of \(p_\mathrm {\max }\) is experienced in the transition from the STC to the DTC zone and is higher for the type 1 profile modification, reaching a maximum value of 1630 MPa. Considering a maximum contact pressure of 2 GPa to avoid scuffing failure (typical of case-hardened steel gears), the safety factors obtained for the type 1 and 2 profile modifications are equal to 1.25 and 1.74, respectively. The relative difference between the two profile modifications in the transition zone is about 40%.

Fig. 11
figure 11

Maximum contact pressure \(p_{\max }\) for the two profile modification as a function of \(\psi \) for \(M_\textrm{T}=M_{\textrm{N}}=200\) Nm

Full size image
Fig. 12
figure 12

Peak-to-peak static transmission error represented as a function of \(M_{\textrm{T}}\)

Full size image

The peak-to-peak static transmission error \(q_{\textrm{PTP}}\) is represented as a function of \(M_{\textrm{T}}\) in Fig. 12. For the unmodified profile, \(q_\textrm{PTP}\) monotonically increases with \(M_\textrm{T}\). For the modified gears, the peak-to-peak static transmission error shows a minimum for the nominal torque and then increases as the static torque is either increased or decreased, depending on which component prevails in the determination of the total relative mesh displacement (i.e., the static transmission error at zero load at lower static torques and the compliance of the gear elements at the highest static torques). Regardless of the adopted profile modification, the minimum value of \(q_\textrm{PTP}\) is obtained at the nominal torque \(M_\textrm{T}=M_\textrm{N}=200\) Nm. For \(M_\textrm{T}>M_\textrm{N}\), the peak-to-peak static transmission error of the modified profiles increases with \(M_\textrm{T}\) and is always lower than the value obtained for the nominal involute profile. For \(M_\textrm{T}\le M_\textrm{N}\), the peak-to-peak static transmission error of the modified profiles increases as the nominal torque is reduced and becomes higher than the value obtained for the nominal involute profile when \(M_\textrm{T}<90\) Nm.

The static results show that the two profile modifications are equivalent from the point of view of peak-to-peak static transmission error. However, the type 2 profile modification features a more regular profile (produced by the initial constraints), leading to lower maximum pressures experienced in a single meshing cycle during the transition from the STC to the DTC zone.

4 Dynamic behavior

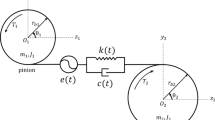
The dynamic behavior of the geared transmission system was studied using a lumped parameter model [31]. In particular, a meshing frequency \(f_\textrm{m}\) up to 5 kHz was considered, allowing the investigation of the resonance peaks in the dynamic response of the system in this range. Three static torques \(M_\textrm{T}=[100,200,400]\) Nm were considered to investigate the usefulness of the proposed profile modification outside the working regime at the nominal torque. At each static torque, the dynamic response was simulated by increasing (Ramp-Up or RU) and decreasing (Ramp-Down or RD) the meshing frequency to highlight the effect of any bifurcation phenomena, which may lead to a different dynamic response depending on the sign of the gear’s angular acceleration [31]. In all the simulations, a reasonable damping value was estimated using the results of previous studies [33]. At each static torque and meshing frequency, the dynamic overload \(K_\textrm{v}\) (defined as the ratio between the maximum instantaneously transmitted torque and the static one) and the root mean square of the total relative displacement \(q_\textrm{rms}\) were used to compare the unmodified gears against the two proposed profile modifications.

4.1 Nominal torque

The comparison between the dynamic overload at \(M_\textrm{T}=M_\textrm{N}=200\) Nm for the unmodified gears and the proposed profile modifications is represented in Fig. 13.

Fig. 13
figure 13

Dynamic overload for the unmodified gears and the proposed profile modifications at \(M_\textrm{T}=M_\textrm{N}=200\) Nm

Full size image

At least three resonance peaks, attributed to the main harmonic of the meshing frequency and its super-harmonics, can be identified (points 1, 2, and 3 in Fig. 13). A bifurcation in the dynamic response of the system is experienced during the Ramp-Down simulation at all the resonance peaks of the system when no profile modifications are present. Moreover, the maximum \(K_\textrm{v}\) is about 4.25 and is experienced during the Ramp-Down phase at 4.5 kHz (point 3). The implementation of the type 1 profile modification produces a significant improvement in the dynamic response. Outside any near-resonant condition \(K_\textrm{v}=1\), meaning that no dynamic overload is experienced by the transmission system. In resonant conditions, the bifurcation phenomena are reduced (points 2 and 3) or eliminated (point 1). Any resonance peak of the system is narrower and less intense. The maximum \(K_\textrm{v}\) is still experienced during the Ramp-Down phase at 4.5 kHz (point 3) but is equal to 2.75. A 35% reduction compared to the gears without profile modifications was consequently expected. The dynamic response of the type 2 profile modification shows the same features as the type 1 profile modification, but the improvement is limited: the resonance peaks are wider and more intense (points 2 and 3). Overall, the maximum \(K_\textrm{v}\) is still experienced at 4.5 kHz (point 3) and is equal to 3, with a 30% reduction compared to the gears without profile modifications.

Fig. 14
figure 14

Root mean square of the total relative mesh displacement for the gears without profile modifications and for the proposed profile modifications at \(M_\textrm{T}=M_\textrm{N}=200\) Nm

Full size image

The same improvements in the dynamic response at \(M_\textrm{T}=M_\textrm{N}=200\) Nm can be observed considering \(q_\textrm{rms}\) (Fig. 14). For the modified gears, \(q_\textrm{rms}\) is null outside any resonant condition, thus indicating no dynamic amplification of the nominal load (as observed in Fig. 13). All the resonance peaks of the system of the modified gears are narrower and less intense, denoting a significant reduction in the transmission’s noise. For the gears without profile modifications, the maximum value of \(q_\textrm{rms}\) is about 22.5 \(\mu \)m and is experienced during the Ramp-Down phase at 4.5 kHz (point 3). Compared to the unmodified gears, the maximum value of \(q_\textrm{rms}\) for the type 1 profile modification is obtained at the same frequency, but it is 44.5 % lower. The maximum \(q_\textrm{rms}\) for the type 2 profile modification is obtained during the Ramp-Down phase at 2.25 kHz (point 2), obtaining a 33.3 % reduction compared to the gears without profile modification.

4.2 Half the nominal torque

The comparison between the dynamic overload at \(M_\textrm{T}=100\) Nm for the gears without profile modifications and the proposed profile modifications is represented in Fig. 15.

Fig. 15
figure 15

Dynamic overload for the gears without profile modifications and for the proposed profile modifications at \(M_\textrm{T}=100\) Nm

Full size image

Compared to the nominal torque, the three main resonance peaks of the system are shifted at lower frequencies due to the lower instantaneous meshing stiffness (points 1, 2, and 3). The unmodified gears show a bifurcation in the dynamic response at each resonance peak. The maximum \(K_\textrm{v}\) is experienced at 4.25 kHz (point 3) and is equal to 4.5. Even outside the nominal torque regime, the proposed modifications improve the dynamic behavior of the system. \(K_\textrm{v}\) is reduced by at least 25\(\%\) outside resonant conditions for both the proposed profile modifications. The type 1 profile modification shows bifurcation phenomena at each resonance peak. The maximum \(K_\textrm{v}\) is experienced at 2 kHz and is 28\(\%\) lower than the unmodified gears. At 4.25 kHz (point 3), the type 1 modification achieves a 53\(\%\) reduction of \(K_\textrm{v}\). The type 2 tip relief eliminates some of the bifurcation phenomena present (points 1 and 3). The maximum \(K_\textrm{v}\) is experienced at 2 kHz and is 34\(\%\) lower than the unmodified gears. At 4.25 kHz (point 3), the type 2 modification achieves a 60\(\%\) reduction of the dynamic overload.

The same considerations about the dynamic response of the system can be made considering \(q_\textrm{rms}\) (Fig. 16). The proposed modifications produce a significant reduction of \(q_\textrm{rms}\) outside the resonant conditions. For the unmodified gears, the maximum value of \(q_\textrm{rms}\) is experienced at 1 kHz (point 1) and is equal to 13.5 \(\mu \)m. At 1 kHz (point 1), the reduction of \(q_\textrm{rms}\) obtained with the proposed modifications is about 60\(\%\). For the modified gears, the maximum \(q_\textrm{rms}\) is experienced at 2 kHz and is 22 \(\%\) (type 1) and 33 \(\%\) (type 2) lower than the unmodified gears.

Fig. 16
figure 16

Root mean square of the total relative mesh displacement for the gears without profile modifications and for the proposed profile modifications at \(M_\textrm{T}=100\) Nm

Full size image
Fig. 17
figure 17

Dynamic overload for the gears without profile modifications and for the proposed profile modifications at \(M_\textrm{T}=400\) Nm

Full size image

4.3 Double the nominal torque

The comparison between the dynamic overload at \(M_\textrm{T}=400\) Nm for the gears without profile modifications and the proposed profile modifications is represented in Fig. 17.

Compared to the nominal torque, the three main resonance peaks of the system are shifted at higher frequencies due to the higher instantaneous meshing stiffness (points 1, 2, and 3). The unmodified gears show a bifurcation in the dynamic response only at 1.2 kHz and 4.5 kHz (points 1 and 3). The maximum \(K_\textrm{v}\) is experienced at 4 kHz (point 3) and is equal to 3.5. Moreover, the resonance peak at 4.5 kHz shows a sudden change in shape compared to the lower torques. The proposed modifications produce an improvement in the dynamic response of the system outside the resonant conditions. The \(K_\textrm{v}\) values obtained with the type 1 profile modification are lower or at most equal to the values obtained with the unmodified gears, so the usage of such a modification can still improve the dynamic behavior of the transmission. The \(K_\textrm{v}\) values obtained with the type 2 profile modification are higher than the ones obtained for the unmodified gears at 1.2 kHz and 2.4 kHz (points 1 and 2), so the use of such a modification at the considered torque regime becomes questionable.

Fig. 18
figure 18

Root mean square of the total relative mesh displacement for the gears without profile modifications and for the proposed profile modifications at \(M_\textrm{T}=400\) Nm

Full size image

Despite the results obtained for \(K_\textrm{v}\), the proposed profile modifications reduce \(q_\textrm{rms}\) at all the working regimes even at \(M_\textrm{T}=400\) Nm (Fig. 18). In particular, a 50 \(\%\) reduction of \(q_\textrm{rms}\) is achieved outside the resonant conditions. For the unmodified gears, the maximum value of \(q_\textrm{rms}\) is experienced at 2 kHz (point 2) and is equal to 32.5 \(\mu \)m, for which a 14\(\%\) reduction is obtained with the proposed profile modifications.

The modified gears significantly improve the dynamic behavior of the transmission. Bifurcation phenomena are reduced or eliminated, the maximum overload is reduced by at least 25%, and the gearbox is less noisy at all the working regimes considered.

The type 1 profile modification, obtained without any initial constraint on the profile shape, produces better dynamic results. As the two profile modifications feature the same peak-to-peak static transmission error, the different dynamic behavior can be attributed to the static transmission error trend in a single meshing cycle. The type 1 profile modification shows a constant static transmission error in the DTC zone (Fig. 6), producing constant meshing stiffness and lower self-induced dynamic overloads. On the contrary, the static transmission error in the DTC zone obtained with the type 2 profile modification features the superimposition of a higher frequency wave (Fig. 9), producing higher fluctuations of the meshing stiffness and slightly worse dynamic behavior.

5 Design for manufacturing

For the sake of simplicity, the manufacturing was characterized by considering the mass production of spur gears designed to operate with the same nominal torque.

As is typical in high-performance applications with high production volumes, it was assumed that the initial roughing phase is performed via gear hobbing, which is a process with a higher production rate than other gear generation processes. The gear hob shapes the nominal involute profile starting from the raw disk combining a cutting motion of the tool with a relative piece-tool movement that simulates the gear meshing. The typical output obtained at the end of the hobbing phase is a nominal involute profile characterized by a roughness average in the range of [1.6 \(\div \) 3.2] \(\mu \)m. Hobbing is followed by a finishing process that produces the profile modifications and the required tooth surface tolerances by removing the machining allowance. Considering that high-performance spur gears are often characterized by heat treatments which increase hardness and make the finishing process difficult to be performed with standard tools, it was assumed that the finishing is performed with a properly shaped grinding wheel, whose active surface replicates the final shape of the tooth flank. As schematically shown in Fig. 19, the grinding wheel is first brought into position outside the gear at a radial position equal to the total cutting depth. The feeding motion is parallel to the gear rotational axis, and the opposite tooth flanks of each tooth vane are machined simultaneously, achieving the required surface finish and final tooth shape. After machining each tooth vane, the gear rotates by an angular step around its axis, preparing the next tooth vane.

Fig. 19
figure 19

Tooth vane and profile modification finishing

Full size image
Table 2 Grinding wheel active surface profiles
Full size table
Fig. 20
figure 20

Grinding wheel active surface obtained for the type 1 and the type 2 profile modifications. The interpolation of the profile is represented using a dashed line

Full size image

Table 2 shows the characteristic points of the grinding wheel surface, measured in a reference system having its origin at the intersection between a plane perpendicular to the grinding wheel axis and its external diameter (Fig. 19). All the points were calculated considering a high-precision execution of the grinding wheel profile (resolution lower than 1 \(\mu \)m). Neglecting the tooth root profile, typically obtained through other machining processes, the grinding wheel profiles can be approximated by a single-node spline, which is made of the nominal involute circle and a second-order polynomial function (Fig. 20). The two profiles share the initial curve, a perfect involute circle, and diverge from the modification starting point, which is moved forward for the type 2 profile modification. Macroscopically, the tooth profiles appear to be identical. The difference between the calculated profiles and their quadratic interpolation is lower than a micron (Fig. 21). The profile modifications proposed, despite their apparent complex shape, are obtainable through low-degree polynomials, justifying their ease of execution in industrial practice.

Fig. 21
figure 21

Vertical difference between the calculated grinding wheel profiles and their quadratic interpolation

Full size image
Fig. 22
figure 22

Normalized volume of material removed for the tip relief functions considered

Full size image

The manufacturing of the proposed profile modifications was also compared in terms of productivity with two standard profile modifications for industrial applications: the linear and the parabolic tip reliefs applied starting from the pitch point. The initial manufacturing process used to obtain the nominal involute profile was assumed to be the same for all the modifications considered, as it depends only on the gear macro-geometry. The comparison was thus made considering only the finishing phase, which can be obtained using differently shaped grinding wheels depending on the tooth profile to be obtained. The profile modifications were compared under the same maximum profile modification at the tooth tip (6 \(\mu \)m) using the total volume of removed material per gear during the finishing phase normalized with respect to the type 2 profile modification \(V_\textrm{n}\), which is directly related to the productivity of the manufacturing process.

Compared to the nominal involute profile (Fig. 22), the total volume of removed material for each gear (Table 1) is about 5 mm\(^3\) for either of the proposed profile modifications, with a negligible difference between type 1 and type 2 profiles. \(V_\textrm{n}\) is higher for the standard profile modifications, with a \(150\%\) and a \(73\%\) increase for the linear and the parabolic tip relief modifications, respectively. Our profile modifications can thus be obtained faster and with less material waste than standard profile modifications obtained using the same manufacturing process. Furthermore, the lower volume of material removed reduces the grinding wheel wear experienced during the finishing phase, increasing process productivity and reducing production downtime, especially in the mass production of spur gears.

6 Conclusions

An iterative algorithm based on the static transmission error was used to define a profile modification capable of improving the dynamic behavior of spur gears. The proposed approach was applied to a nominal involute profile (type 1) and to a profile calculated to reduce the maximum contact pressure in one meshing cycle (type 2). In both cases, the calculation was based on the minimization of the peak-to-peak static transmission error, and only three steps were needed to reach convergence.

The static results show that the proposed modifications radically modify the peak-to-peak static transmission error curves, which present a minimum for the nominal torque considered. In addition, the maximum contact pressure experienced during a single meshing cycle was reduced with the proposed type 2 profile modification.

The proposed modifications can be adopted to reduce the dynamic overload and the transmission noise, even outside the nominal torque regime. The dynamic overload obtained with the modified gear profiles was significantly reduced outside any resonant condition and all the resonance peaks were narrower and less intense compared to the unmodified gears. In addition, some of the bifurcation phenomena experienced by the unmodified gears during the Ramp-Down were eliminated. The type 1 profile modification showed a very different shape from any industrial standard but obtained a significant reduction in the dynamic overload and the transmission noise at any static torque considered, outperforming the typical profile modifications.

The proposed profile modifications can be manufactured through a gear hobbing process followed by a finishing phase with a suitably shaped grinding wheel. The grinding wheel profiles were calculated using a CAD model and interpolated using third-degree polynomial functions, demonstrating the feasibility of the profile modifications manufacturing. The total volume of material removed during the gear tooth finishing was calculated. The results obtained considering the same maximum amount of profile modification show that the proposed profiles are characterized by a lower volume of removed material, meaning they can be obtained faster and with less material waste than standard industrial profiles. In summary, the proposed modifications are feasible, less impacting, and produce a significant improvement in the static and dynamic performances of the whole transmission system.

Our iterative approach could be applied to define several profile modifications for different industrial applications. In particular, the constraints and requirements could be changed, thus obtaining a tooth profile that could improve several aspects of gear meshing and manufacturing.