1 Introduction

Friction stir welding is a joining procedure developed for the welding of parts difficult to join with conventional processes [1]. Aluminum triggered the development of the process, which was published in 1991 by the British Welding Institute [1]. As expected, aluminum has been thoroughly studied ever since in various grades and forms [2,3,4,5,6,7,8,9], such as AA6061 [10,11,12,13,14,15] and AA5083 [16, 17]. All these works achieved high-weld qualities, employing tools such as the analysis of variances (ANOVA) modeling tool [14]. Due to its characteristics (non-consumable welding tool, energy-efficient, autogenous welding process, etc.), it rapidly gained popularity [2], in applications in the automotive, aerospace, shipbuilding, and household applications among others [18, 19]. Research indicated and reports that the processing factors, such as the travel speed of the tool, the rotational speed of the weld tool, and the geometry of the weld tool [20], highly affect the performance of the weld [21, 22].

Polymers are among the materials which are difficult to join, so, as expected, the FSW joining process was expanded in these materials as well [23,24,25] and their composites [26]. The feasibility of the process was the first challenge faced in the research [27]. Afterward, settings, such as the efficiency of the weld tool toward the improvement of the weld performance, were investigated [28, 29], on thermoplastics such as HDPE (high-density polyethylene) [30]. As expected, popular polymers such as ABS (acrylonitrile butadiene styrene) [31] and poly(methyl methacrylate) (PMMA) [32] have been investigated for their performance in the process. The effect of the welding condition on polymer composites has been reported [33, 34]. Similar and dissimilar polymers have been welded with the FSW process [35, 36] and hybrid polymer-metal joints have been achieved as well [37,38,39,40]. The process was also applied to 3D-printed thermoplastics, which have additional challenges, due to their 3D printing structure [41]. Among the polymers reported for their performance in the FSW process are ABS [42], polycarbonate (PC) [43], polylactic acid [44], poly(methyl methacrylate) (PMMA) [45, 46], and polyamide 6 [47]. Research focuses on the effects of the FSW variables on weld performance [48]. The performance of dissimilar joints has also been reported [46, 49], focusing again on the impact of the FSW settings on the process. Composites, such as high-density polyethylene/carbon black, have also been investigated, with research focusing on parameters such as the impact of the developed temperature on the response of the weld [50].

Polycarbonate (PC) is a transparent engineering thermoplastic featuring high impact and toughness properties. It is a versatile thermoplastic applied in various applications from the automotive sector to electronics [51]. In coatings, it has been applied in the automotive sector, in optical [52], electronics [53], and medical applications [54]. In composites form, it has been employed for biomedical [55], electronics, electrical, aircraft, automobiles, construction, and other types of applications [56]. In 3D printing, its performance has been investigated [57,58,59] in pure form and polymer/ceramic composites [60,61,62,63]. For the study and optimization of the experimental data, tools for statistical modeling are the common approach followed [64,65,66,67]. This is obligatory due to the usual complex relations of the experiment parameters, which make the estimation of their effect on the parts’ performance a difficult, not straightforward task [68, 69]. Therefore, a similar approach was used in the current research, although it was further developed and optimized to employ more suitable control parameter levels, as will be explained below.

In the FSW joining method, PC, as expected, has been extensively studied. Dissimilar joints have been achieved [70]. The effect of the developed loads and temperature on the weld morphology has been reported [43]. Modeling implements, such as finite element analysis, have been incorporated into the process [71]. The effect of lubrication has been reported [72], and also the quality of the joint [73]. Modeling tools investigated the material flow [74], and the effect of tilt angle has been reported [75], as well as the influence of the tool geometry on generated loads [76]. Sensors have been used to monitor the process [77]. It has been reported that the FSW parameters highly influence the mechanical response of the welds, by investigating the rotational and travel speed, and the tilt angle, on 10 mm thick PC sheets, using one welding tool (25 mm shoulder, 7 mm pin) [78]. The impact of the welding tool’s rotational speed on the mechanical performance of the weld has been studied [79]. Spot [80] and lap [81] joints have also been achieved.

The study herein for the first time investigates in depth the weld tool geometry, the rotational speed, and the travel for their effect on the mechanical response of 4 mm thick PC sheets incorporated into the FSW procedure. Regarding the tool geometry, the shoulder and the pin diameter were individually investigated for their effect on the performance of the welds, which were evaluated on both tensile and flexural tests. Research on the shoulder geometry for polymeric materials is still limited [82]. The shoulder-to-pin ratio is an important metric for the efficiency of the weld tool in the FSW process, as it has been reported in the literature, and investigated only for the joining of aluminum parts so far [83], to the authors’ best knowledge. The effect on the weld geometry and morphology, along with the developed temperatures during the process, was also investigated. Moreover, for the determination of the control parameter levels, a two-step screening process was applied for the first time. First, an L9 Taguchi array was formed, and the control parameter levels that produced acceptable results were then used to form a successive L9 Taguchi array to derive the optimum results for the response metrics, related to the performance of the produced welds. Through this analysis, the importance of the FSW factors on the joint’s behavior was highlighted. Additionally, valuable information regarding the control parameter values producing improved welds is provided for direct use, along with modeling equations with proven reliability for the estimation of the performance-related response measures studied.

2 Materials and methods

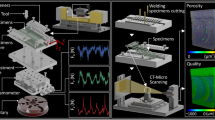
Figure 1 highlights the primary experimental and methodological procedures undertaken in the present study for the FSW course and the assessment of joint performance.

Fig. 1
figure 1

On the left side the algorithm followed in the study is presented. Point no 6 (decision making) highlights the feedback in the system regarding the efficiency of the control parameter levels during the selection of their values. On the right side, screenshots from the processes are presented (a) preparation of the sheets, (b) manufacturing of the welding tools, (c) FSW of the samples, (d) the completed weld sample, (e) quality control, (f) welded tensile test samples, (g) mechanical testing (three-point-bending), and (h) morphological analysis

Full size image

2.1 Materials and welding tool preparation

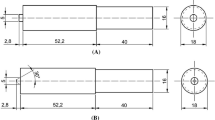
Four millimeter thick solid PC sheets were procured from Isik Plastic (Kocaeli, Turkey) [42, 44]. The tensile strength of the specific PC grade, according to the datasheet of the manufacturer, is >60 MPa (ISO 527), its density is 1.2 g/cm3 (ISO 1183), Vicat temperature (50 N, 50°C, ISO 306) of 148°C, nominal operating temperature 120°C, and class B1 fire resistance. Their thermal behavior was verified with thermogravimetric analysis (TGA) (Perkin Elmer Diamond, 30–550°C heating course with a 10°C/min step) and differential scanning calorimetry (from TA Instruments DSC 25 apparatus, 25-220–25°C heating cycle, 15°C/min step). This was necessary to verify that the material’s solid state remains during the FSW treatment, to be compatible with the process. Samples for the FSW processing were prepared in the Haas VF2 vertical machining center. The fixture used for the FSW process was designed, and manufactured by this research team and is analytically presented in previous works [42, 44]. Welding tools were produced using AISI304L stainless steel bars on a Haas SL20 CNC lathe. The welding tools were designed with different shoulder and pin diameters to assess their impact on the process.

2.2 FSW experiments and welding performance

In each FSW experimental course, two samples were welded on their long side, producing a linear seam. The welded part was then cut off (with a flat-end cutting milling tool of 2 mm diameter) in three (3) sets of four (4) samples, welded with different FSW conditions (twelve samples in total). The procedure is analytically presented in previous works of this research team [47]. The FSW process was carried out in a Haas VF2 vertical machining center. Throughout the joining FSW process in each set of samples, the developed temperature in the seam was monitored (Flir One Pro thermal imaging camera). This was necessary to guarantee the samples’ solid state during the process.

The weld performance was evaluated through two standard mechanical tests, i.e., tensile and three-point-bending flexural tests (52 mm span). For the tensile tests, the welded specimen was cut off into dumbbell shape specimens, while for the flexural tests, prismatic shape samples were cut off. All experiments were performed on an Imada MX2 material testing machine with the elongation speed set at 10 mm/min. Reference samples with identical dimensions to the welded ones were also prepared from the PC sheets and tested as control samples.

Apart from the mechanical response, the weld performance was also assessed through its morphological characteristics. A high-quality caliper was used to quantify the weld thickness, and optical microscopy (Kern OKO 1) and stereoscopy (KERN OZR5) were used to analyze the weld region (NZ, TMZ, and HAZ). Images were captured with a 5-MP KERN ODC 832 digital camera. SEM was also employed to evaluate the morphological characteristics of the welds, on a field emission SEM, model JSM-IT700HR by Jeol. Samples were gold-sputtered to avoid charging since a 20-kV accelerating voltage was set for the SEM observations.

2.3 Two-step screening and optimization design of experimental process

As mentioned above the FSW parameters, and more specifically, the travel speed, the rotational speed, and the weld tool geometry highly affect the performance of the produced weld [78]. Therefore, they were selected in the current study as the control parameters. The weld tool geometry was evaluated with two control parameters, i.e., the shoulder (SD) and the pin diameter (PD). As mentioned above, these parameters were evaluated and it was found that the shoulder-to-pin ratio achieves the best results regarding the performance of the weld, justifying also for the polymeric materials the importance of this metric in the efficiency of the weld. Since there are no similar research studies on 4 mm thick PC sheets, the specific grade, and the exact control factors, as well as their levels could not be accurately estimated. An L9 Taguchi array was initially formed with the four control settings, each having three levels. The values were estimated by the literature and are presented in Table 1. By analyzing the conducted experiments, the spectrum of the control parameter values that produced acceptable outcomes (seams without visual defects, etc.) was used to form a second L9 Taguchi array, with the same control parameters, which is shown in Table 2. With this approach, the range of the control parameter values was initially optimized. Based on this second L9 array, a second round of experiments was conducted for the analysis of the impact of each control parameter in the response metrics and the optimization of the process. Eight different response metrics were evaluated and optimized, i.e., the welding temperature, the thickness of the weld zone (compared to the nominal specimen’s dimensions), the tensile and flexural strength, toughness, and modulus of elasticity (energy absorbed by the specimen during the mechanical test, derived by the integration of the produced stress vs strain as shown in the plot of the experimental data). Following, an analysis of variance (ANOVA) was employed and equations for the eight (8) response measures were created, as a function of the control variables. Their expected accuracy was calculated, and their reliability was evaluated with confirmation runs.

Table 1 Taguchi L9 design: control factors and levels for screening
Full size table
Table 2 Taguchi L9 design: control factors and levels
Full size table

3 Results

3.1 Screening process results

The screening process experimental results are depicted in Fig. 2 for various runs carried out. The different issues that occurred are evident in the images in specific runs, due to the control parameter values, with the produced seams having discontinuities and cavities. In specific runs, such as run 6, a pseudo tool was formed, as shown in Fig. 2d. Such formation has been reported in the literature and negatively affects the weld tool wear [84] and as a result the produced seam. The morphological characteristics of the produced welds during the screening process were also examined with stereoscopic microscopy, to observe the topography of the welds on a micro-scale (Fig. 3). In specific runs, the produced runs faced defects, such as cracks in the HAZ and welding debris (Fig. 3a), micro-inclusions at the HAZ and cavitations at the TMZ (Fig. 3b), material pile up around the weld zone and surface downside (Fig. 3c), and cavitations at the sample’s base (Fig. 3d). Such issues in the specific runs showed the importance of the control parameter values on the weld result and that in the specific runs the control parameter levels were not appropriate for the process, so these values should be excluded. By examining the produced seams and evaluating the results, the control parameter values for the second step of the process, as explained above, were formed.

Fig. 2
figure 2

Screening process results demonstrating the issues occurred (a) run 3 (seam quality issues), (b) run 4 (discontinuities in the seam), (c) run 7 (discontinuities in the seam), (d) run 6 (pseudo tool), (e) run 6 welding process

Full size image
Fig. 3
figure 3

SEM and microscopic morphological analysis of the samples of run 8 during the screening process (a) SEM image depicting cracks and welding debris formation in the HAZ, (b) stereoscopic image from the side of the sample showing the welding zone; the surface downside and the material pile up at the limits of the welding zone are visible (c) stereoscopic image from the size focused on the limits between the TMZ and the HAZ, depicting micro inclusions at HAZ and cavitations at the TMZ, respectively, (d) stereoscopic image from the size showing the welding zone, in which cavitations at the base of the sample are visible

Full size image

3.2 Experimental results by optimized control parameters (second experimental round)

Figure 4 presents the FSW process for runs 1, 5, and 9, of the second stage of the experimental procedure, in which the control parameter values were the optimized ones, as they were determined by the screening process. These three runs are selected to be presented, as they have low (run 1), medium (run 5), and high (run 9) control parameter values. The highest developed temperature in each run is depicted in the photos (Fig. 4a, d, and g) along with the temperature distribution in the region in a color scale. As shown, the increase in the travel speed increases the developed temperatures, with their values, still below the temperature at which the material begins to melt. The maximum recorded temperature as shown in Fig. 4g was 114.3°C, 31.2°C higher than the maximum temperature of run 1 (83.1°C). In aluminum welds produced with the FSW process, an increase in the traverse speed leads to a reduction in the heat input while an increase in the rotational speed leads to an increase in the heat input. This is not the case here, attributed to the different tribological responses of the polymeric materials, compared to the aluminum ones. The current findings are in agreement with the corresponding literature on the FSW of polymeric materials [42, 44,45,46,47].

Fig. 4
figure 4

Maximum developed temperature during the FSW process for run 1 (a), along with the completed seam (b) and the tensile specimens produced, along with the sample cross-section and the tool used (c). (d), (e), and (f) present the corresponding results for run 5, while (g), (h), and (i) for run 9

Full size image

The resulting seam in the three runs is depicted in Fig. 4b, e, and h correspondingly. As shown, at least visually, a defect-free continuous seam is produced. This was examined and verified afterward by microscopic observations. Figure 4c, f, and i show the welded dumbbell shape sample, with the weld tool of the run. The inset images show the weld region. The transparency of the material facilitates the visual qualitative evaluation of the welded joint.

Figure 5a shows a randomly selected produced seam weld of each one of the nine runs implemented according to the L9 array, along with a photo of the corresponding weld tool. Figure 5b shows the tensile stress vs strain graph of a randomly selected sample from each one of the nine runs, comparatively to the control sample’s graph (not welded sample). As shown, run 8 (TS 6 mm/min, RS 800 rpm, SD 8 mm, and PD 4 mm, SD/PD 2) is the least efficient weld, while run 6 (TS 4 mm/min, RS 1000 rpm, SD 8 mm, and PD 3 mm, SD/PD 2.66) is the most efficient one. All graphs illustrate the welding efficiency of 100%, which represents the ratio of the strength of the welded sample to the strength of the unwelded sample on a percentage scale. A welding effectiveness of 60% has been reported for the ABS polymer [85]. For polymeric materials (polypropylene), efficiency up to 89% has been reported with preheating of the materials [86]. Herein, without preheating or any other processing, welding efficiency up to almost 90% was achieved, as presented in Fig. 5b for run 6. Figure 5c shows the corresponding results for the flexural tests. In this case, experiments were terminated at 5% strain, to be consistent with the ASTM D690 standard. Again, run 8 showed an inferior mechanical response in the test, while the differences between the responses of the remaining runs were not that high. Run 9 had the highest flexural strength among the runs, the same as the tensile tests. In this test, welding efficiency of up to almost 73% was achieved, which is a well-acceptable result. As expected, samples failed in the weld region, which is the downside of the cross-section in this area, due to the weld, contributing further to this outcome. The variations between the performance of the specimens in the various runs justify the need for further analysis and optimization of the control parameter levels, to achieve the best possible mechanical performance in the samples.

Fig. 5
figure 5

a Seam weld and tool for the nine runs of the optimized step, (b) tensile stress vs strain curves from a random sample of each one of the nine runs, and (c) the corresponding flexural stress vs strain curves

Full size image

Figure 6 presents top-view stereoscopic pictures from the fracture area of a randomly chosen sample from each one of the nine runs. The fracture mechanism of parts welded with the FSW process has been investigated and reported in the literature [87,88,89]. As shown, the fracture mode differs between the runs, with samples having failed with a clear brittle failure (no visual deformation, for example, run 9, Fig. 6i), while in other cases a more ductile fracture occurred (for example, run 1, Fig. 6a). Figure 7 shows the corresponding stereoscopic images of the fracture. Such fracture morphology and mechanism have been reported before in the literature for polymeric materials joined with the FSW process [42, 44,45,46,47].

Fig. 6
figure 6

Stereoscopic images of the fractured area (top view) after the tensile test of a random specimen from each one of the nine optimization runs (a)–(i) (magnification 2.5×)

Full size image
Fig. 7
figure 7

Stereoscopic images of the fractured area after the tensile experiment of a random specimen from each one of the nine optimization runs (a)–(i) (magnification 5.0×)

Full size image

The observations from the top verified in these images what was estimated from the top-view images. Run 9 showed a brittle failure, along with runs 2, 4, 5, and 6. The remaining runs show some limited deformation but again the failure can be characterized as brittle. Run 8, which had the lower mechanical performance, shows slightly higher deformation in the fractured surface. Overall, the brittleness of the failure does not seem to be somehow connected to the performance of the samples, as both runs 8 and 9 showed a brittle failure, with run 8 showing the lowest mechanical performance and run 9 the highest. Still, in run 9, the deformation on the fractured surface was slightly higher as mentioned above. Figure 8 shows top-view images of the fractured areas captured with SEM, at 25× magnifications, and the fractured areas at two different magnifications, i.e., 22× and 300×. Again, one randomly selected sample from each run is depicted. In the top-view images, the boundaries of the weld region along with the circular pattern formed in the region due to the FSW process are visible. In the cross-section, SEM micrographs, the fracture mechanism observed in the stereoscopic images was again evident. In run 1 (Fig. 8b), part of the cross-section has developed sufficient deformation before failure. This phenomenon is decreased in run 5 (Fig. 8e), while the run 9 sample (Fig. 8h) has failed with a clear brittle failure.

Fig. 8
figure 8

25× SEM image from the top of the run 1 sample (a), along with 22× SEM image (b) and 300× SEM image from its fractured surface (c). (d), (e), and (f) show the related micrographs from a run 5 sample, and (g), (h), and (i) from a run 9 sample

Full size image

Figure 9a presents the DSC curve produced for the PC polymer. The solid-state of the polymer is preserved up to 260°C. Overall, most of the developed temperatures during the FSW of the various cases studied are below the glass transition point of the PC polymer. Still, in some cases, they are around or marginally higher than the glass transition point. As shown below, the run with such developed temperatures (run 8) showed inferior mechanical performance than the runs with lower temperatures, which obviously can be attributed also to the phase change of the PC polymer during the FSW process. Because of the rapid strain rate experienced by the polymers while being stirred and subsequently cooled, voids resulting from shrinkage are generated [90]. This is more evident in the microscope images of the fractured surface of run 8. With an increase in heat input, there is a corresponding rise in peak temperature, which in turn impacts the crystallinity and molecular weight of the polymer being processed [27]. As a result, there is a proportional growth in shrinkage, leading to the creation of larger pores within the stirred zone [26]. This formation of shrinkage voids contributes to a reduction in the mechanical strength of the welded polymer [90].

Fig. 9
figure 9

a Recording of the highest temperature values throughout the FSW procedure, correlated with the corresponding DSC graph, and (b) the TGA graph

Full size image

Figure 9b shows the corresponding TGA graph for the PC polymer, which shows that the PC thermoplastic starts to degrade at 470°C. The temperature was recorded throughout the FSW process, as explained above and the maximum recorded temperatures are correlated with the DSC curve (Fig. 9a). It was verified that the PC polymer’s solid state was retained throughout the process. Additionally, no thermal degradation of the PC polymer occurred throughout the FSW processing. As shown, the maximum developed temperature during the FSW process was marginally higher than 150°C.

3.3 L9 experimental process results

Table 3 presents the mean values and the calculated deviation for the thickness (surface downside) of the samples in each run. The second column shows the % percentage from the nominal sample dimension. As shown, in run 8, the sample downside is impressively more intense than the remaining runs, justifying the inferior mechanical performance of the samples of the specific run. The third column shows the maximum developed temperature and its deviation for each run. Table 4 presents the corresponding results for the tensile strength, toughness, and modulus of elasticity. The second column depicts welding efficiency. Table 5 depicts the corresponding results for the flexural tests. The analytic experimental results for each sample in each run are exhibited in the supplementary file of the study.

Table 3 Mean values and standard deviations of calculated responses for residual thickness, residual thickness to nominal, and maximum welding temperature
Full size table
Table 4 Mean values and standard deviations of calculated responses for tensile strength, tensile welding efficiency, tensile modulus of elasticity, and tensile toughness
Full size table
Table 5 Mean average values and standard deviations of calculated responses for flexural strength, flexural welding efficiency, flexural modulus of elasticity, and flexural toughness
Full size table

Figure 10 displays the main effect plots (MEP) for the control factors studied vs two response metrics, i.e., the welding temperature and the residual thickness. The welding temperature needs to satisfy the smaller-the-better criterion, while the residual thickness needs to satisfy the higher-the-better criterion. The TS is the dominant parameter for the welding temperature (rank 1), while the SD is the least important parameter for the welding temperature (rank 4). The increase of TS increases the welding temperature by almost 30°C. The increase in the welding tool pin diameter also increases the welding temperature. The residual thickness is significantly decreased at the highest TS tested (6 mm/min). TS is rated as the no 1 control factor for the metric. The median RS (800 rpm) decreases the residual thickness, while the lowest and highest RS values maintain high residual thickness values. The increase in SD increases the residual thickness, while the increase in PD has the opposite effect.

Fig. 10
figure 10

Main influence plots for (a) WT and (b) residual thickness

Full size image

Figure 11 exhibits the MEP for the tensile test metrics (tensile strength, modulus of elasticity, and toughness). The higher-the-better criterion needs to be satisfied for these metrics. The RS control parameter is rated as the no 1 control factor for all three metrics. The SD control parameter is the no 4 ranked control parameter for the tensile strength and the tensile toughness, while TS is rated as the no 4 control factor for the tensile modulus of elasticity. Median TS and PD values and high RS and SD values optimize all three metrics. Figure 12 exhibits the associated MEP for the flexural test metrics. SD was the no 1 ranked control parameter for flexural strength and flexural toughness, while TS was the no 1 ranked control parameter for flexural modulus of elasticity, while it was rated as the no 4 control factor for the other two metrics, showing the complication of the relations of the control settings with the response metrics. Median TS, SD, and PD values increase flexural strength, while the highest RS value increases the metric. High flexural modulus of elasticity is achieved with high TS and PD values, median RS values, and low SD values. TS has a mild effect on flexural toughness. High flexural toughness values are achieved with high RS and SD values and median PD values.

Fig. 11
figure 11

Main effect plots for (a) tensile strength, (b) tensile modulus of elasticity, and (c) tensile toughness

Full size image
Fig. 12
figure 12

Main effect plots for (a) flexural strength, (b) flexural modulus of elasticity, and (c) flexural toughness

Full size image

From the MEP graphs, the complex relations involving the control factors are evident (antagonistic and synergistic relations), but MEP diagrams provide no such information. To derive such information, interaction plots were formed for each response metric. For the welding temperature (Fig. 13a), only the TS and PD relation is synergistic and the remaining relations between the control parameters are antagonistic. For the residual thickness, all the control parameters show antagonistic relations (Fig. 13b). The same is observed for the tensile strength (Fig. 14a) and the tensile modulus of elasticity (Fig. 14b). For the flexural strength (Fig. 14c), the SD and PD, and the SD and RS show synergistic relations; the remaining control parameter relations are antagonistic. For the flexural modulus of elasticity (Fig. 14d), the TS and PD relation is synergistic, and the remaining control parameter relations are antagonistic. The interaction plots supported the complexity of the interactions among the three control variables and the investigated response factors. Traditional mathematical models lack the capability to adequately describe these relationships or accurately forecast their impact on the response settings.

Fig. 13
figure 13

Interaction plot charts (a) welding temperature and (b) residual thickness

Full size image
Fig. 14
figure 14

Interaction plot charts (a) tensile strength, (b) tensile modulus of elasticity, (c) flexural strength, and (d) flexural modulus of elasticity.

Full size image

3.4 ANOVA analysis and modeling

The reduced quadratic regression model (RQRM) for each performance is computed:

$${Y}_k={a}_k+\sum_{i=1}^n{b}_{i,k}{x}_i+\sum_{i=1}^n{c}_{i,k}{x}_i^2+{e}_k$$
(1)

where k stands for the quality result (e.g., temperature, thickness, tensile strength, tensile toughness, tensile modulus of elasticity, flexural strength, flexural toughness, flexural modulus of elasticity), a is the steady value, b is the coefficients of the linear stipulations, c is the coefficients of the quadratic stipulations, e is the error and xi the six (n = 4) control factors, i.e., the welding tool shoulder diameter and pin diameter, the welding travel, and rotation speed.

In the supplementary file of the study, the ANOVA tables for each performance are presented. In all response metrics, the R values are very high, higher, or almost 90% in most cases, while only in flexural toughness, and R value was calculated to be 76.47%. These results of the calculated models are sufficient for the prediction of the response metrics studied. Based on the ANOVA tables, corresponding modeling equations were formed for the expectation of each response metric, as a function of the control settings investigated [91]. The compiled equations for each response metric are presented in the following equations (2)–(9):

$$Tensile\ Strength=-313.9+14.16\bullet TS-0.3939\bullet RS+81.8\bullet SD+61.68\bullet PD-1.960\bullet T{S}^2+2.67\bullet {10}^{-4}\bullet R{S}^2-4.25\bullet S{D}^2-11.07\bullet P{D}^2$$
(2)
$$Tensile\ Mod. of\ Elasticity=-3142+96.2\bullet TS-5.409\bullet RS+1013\bullet SD+517.9\bullet PD-13.94\bullet T{S}^2+3.461\bullet {10}^{-3}\bullet R{S}^2-52.7\bullet S{D}^2-91.0\bullet P{D}^2$$
(3)
$$Tensile\ Toughness=10.8+2.202\bullet TS-2.794\bullet {10}^{-2}\bullet RS-2.23\bullet SD+3.704\bullet PD-0.2654\bullet T{S}^2+2.0\bullet {10}^{-5}\bullet R{S}^2+0.153\bullet S{D}^2-0.720\bullet P{D}^2$$
(4)
$$Flexural\ Strength=-1118+20.04\bullet TS-0.4417\bullet RS+264.0\bullet SD+78.66\bullet PD-2.662\bullet T{S}^2+2.97\bullet {10}^{-4}\bullet R{S}^2-14.13\bullet S{D}^2-13.83\bullet P{D}^2$$
(5)
$$Flexural\ Mod. of\ Elasticity=-2384-195.0\bullet TS+9.92\bullet RS+642\bullet SD-827\bullet PD+39.72\bullet T{S}^2-6.288\bullet {10}^{-3}\bullet R{S}^2-45.9\bullet S{D}^2+160.5\bullet P{D}^2$$
(6)
$$Flexural\ Toughness=-36.90+0.322\bullet TS-5.81\bullet {10}^{-3}\bullet RS+7.48\bullet SD+3.530\bullet PD-3.83\bullet {10}^{-2}\bullet T{S}^2+5\bullet {10}^{-6}\bullet R{S}^2-0.3928\bullet S{D}^2-0.6079\bullet P{D}^2$$
(7)
$$Welding\ Temperature=444.7+4.53\bullet TS+0.2985\bullet RS-84.4\bullet SD-55.89\bullet PD+0.327\bullet T{S}^2-2.01\bullet {10}^{-4}\bullet R{S}^2+4.349\bullet S{D}^2+10.427\bullet P{D}^2$$
(8)
$$Thickness=-11.92+0.3652\bullet TS-1.5907\bullet {10}^{-2}\bullet RS+4.316\bullet SD+0.8958\bullet PD-6.142\bullet {10}^{-2}\bullet T{S}^2+1.0\bullet {10}^{-5}\bullet R{S}^2-0.2292\bullet S{D}^2-0.1842\bullet P{D}^2$$
(9)

To depict the statistically influential control factors for each response measure, Pareto charts were formed and are depicted in the supplementary material of the work. Along with the Pareto charts, actual vs predicted graphs are formed, indicating how the actual values converge with the predicted ones. In this direction, two metrics are calculated, i.e., average absolute proportion error (MAPE) [92] and Durbin Watson (indicating positive, <2, neutral, between 2 and 3, or negative >3 autocorrelation of the results) [93]. For all response metrics, the reliability of the prediction models was verified since the indicators were more than acceptable. Figure 15 presents in a three-dimensional surface graph the relationship between the response metrics and the two highest-ranked control parameters for each metric.

Fig. 15
figure 15

Surface charts of the tensile strength (a), (b), the tensile modulus of elasticity (c), flexural strength (d), (e), flexural modulus of elasticity (f), residual thickness (g), (h), and WT (i)

Full size image

3.5 Confirmation experiments

Two additional runs, i.e., runs 10 and 11, were carried out, to estimate the accuracy of the prediction models. The control parameter values for the two confirmation runs are depicted in Table 6. Tables 7, 8, and 9 show the response metrics’ average values and deviations for each run. The convergence with the nominal values is also depicted. The analytic experimental results for each sample in each run are depicted in the supplementary file of the study. In Table 10, the real (experimental) and the anticipated values for the response metrics are shown, alongside their deviation in percentage scale. As shown, the absolute error is as low as 3.95%, while the highest deviation found was 13.21% in the tensile strength of run 10, which is still a very accurate calculation, confirming the reliability of the prediction models presented herein. Such high accuracy can be credited to the screening procedure followed initially for the selection of the control parameters levels. Still, it is expected that the precision of the prediction models will decrease when control parameter values are selected outside the range of the values used in the study.

Table 6 Control parameters and levels for the confirmation runs
Full size table
Table 7 Mean values and standard deviations of calculated responses for residual thickness, residual thickness to nominal one, and maximum welding temperature for the verification runs
Full size table
Table 8 Mean average values and standard deviations of measured responses for tensile strength, tensile welding efficiency, tensile modulus of elasticity, and tensile toughness for the verification runs
Full size table
Table 9 Mean average values and standard deviations of calculated responses for flexural strength, flexural welding efficiency, flexural modulus of elasticity, and flexural toughness for the verification runs
Full size table
Table 10 Validation table
Full size table

4 Discussion

The initial screening process conducted established the value of the control parameters levels on the quality of the weld. Specific runs produced seams with obvious defects when inspected visually. On the other hand, the levels selected, following the outcome of the screening process, produced good-quality seams. Still, as expected, differences were evident in the mechanical performance of the welded samples and the morphological characteristics of the produced seams, justifying the need for the modeling process followed. The accuracy and reliability of the developed prediction models were high, which can also be attributed to the selection of proper control parameter levels by considering the screening process outcome.

The RS was the most significant parameter regarding the tensile properties of the welded samples, where the median value produced low tensile properties and the highest value was achieved with the high RS value. The differences between the highest and the lowest tensile strength only by changing the RS value reached 40%. The SD was the dominant factor for the flexural strength with the difference between the highest and the lowest flexural strength reaching 30% only by changing the SD. Such differences in the mechanical performance of the produced welds show the importance of the FSW parameter values in the process. The complex interactions between the control factors also justify the need for modeling and consideration of the experimental outcomes.

Additionally, for the first time, a thorough investigation of the weld tool geometry was conducted, by evaluating the effect of the SD and the PD in the weld performance individually. By this investigation, the SD/PD ratio, studied in metal parts only so far, as mentioned above, was assessed herein. The SD/PD ratio was between two and four, with the weld tool dimensions studied. It was found that the best mechanical performance occurred when the SD/PD ratio was between 2.5 and 3. Lower and higher SD/PD ratio values produced inferior results in the mechanical response of the welded parts. Overall, the welding effectiveness accomplished reached 90%, which is higher than the welding efficiency usually reported for polymeric materials, as mentioned above. This can be also attributed to the control parameter values derived from the screening process.

As mentioned, PC sheets have been investigated before in FSW for the performance of the welds, among other parameters. Still, no research has investigated 4 mm thick PC sheets in the FSW parameter value range studied herein and the weld tool geometry. Therefore, the outcomes reported cannot be directly associated with the literature. By comparing the tensile properties from the conducted experiments herein with works in the literature on the FSW of PC sheets, the results are very similar [73, 79]. Still, in these works, significantly higher TS were investigated, RS was rather similar, and the welding tool was different, with works not studying the weld tool geometry. The outcomes reported herein are in good agreement also with a study on spot welds [80]. Another study on lap joints conducted both tensile and flexural experiments, the same as the current work, and the presented outcomes are also in good accordance with the findings provided herein [81]. These comparisons verify the reliability of the research conducted herein and highlight its novelty, which is toward different directions, i.e., the screening process followed, the specific grade and thickness PC sheets, the modeling approach implemented, the study on the weld tool geometry, and finally the range of the FSW parameters’ values.

5 Conclusions

In this study, the mechanical performance of welds produced with the FSW process on 4 mm thick PC sheets is presented. A two-step L9 Taguchi design of experiments was implemented, to analyze and optimize the effect of optimum control parameter levels on metrics related to the geometrical characteristics of the produced weld and the mechanical properties of the welded samples. Regarding the weld tool geometry, SD/PD ratio was evaluated for the first time in polymeric materials in the FSW process. The solid-state of the PC sheets throughout the FSW process was confirmed with temperature measurements. The TS was the most important parameter regarding the developed temperature and the geometry of the weld, while the RS affected more the tensile strength and the SD the flexural strength. The samples welded with TS 4.0 mm/min, RS 1000 rpm, SD 8 mm, and PD 3 mm (2.66 SD/PD ratio) showed the greatest mechanical behavior in both the tensile and the flexural tests. On the other hand, the specimens welded with TS 6 mm/min, RS 800 rpm, SD 8 mm, and PD 4 mm (2 SD/PD ratio) showed the lowest mechanical performance in both the tensile and the flexural tests. The produced ANOVA prediction models proved their reliability in the confirmation runs carried out, providing valuable calculation tools. Such tools can be directly employed in the industry for the prediction of the mechanical performance of PC sheets welded with the FSW process. The outcome can be used as a roadmap on the control parameter levels, providing instructions for the selection of the appropriate value range that will produce better performance and quality seams. In future work, the range of the control factor levels can be extended, and supplementary control factors can be assessed for a more complete assessment of the behavior of 4 mm thick PC sheets when joined with the FSW process.