Skip to main content
SpringerLink
Log in

Machining vibration suppression of cantilever parts of aerospace structure using robot-assisted clamping system

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

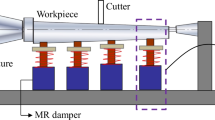
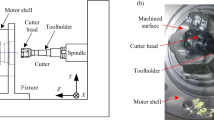
Cantilever parts are extensively used in aerospace applications. However, machining vibrations readily arise under the action of cutting forces due to the poor fixed stiffness of cantilever parts mounted on large structures, compromising working accuracy and efficiency. To address the shortcomings of traditional special vibration suppression fixtures including lengthy development cycles, high costs and limited universality, a mobile robot-assisted clamping system was proposed to fulfill the vibration suppression requirements of diverse cantilever parts on large structures. Furthermore, to analyze the vibration responses under different clamping states, a workpiece-fixture dynamics model incorporating the mobile robot-assisted clamping system is established using the transfer matrix method for multibody systems (MSTMM). Then, the effects of different clamping states on cantilevered part vibration are explored using acceleration responses as the metric. Finally, the effectiveness of the vibration suppression method and the accuracy of the dynamics model are validated through experiment and simulation. This work provides a solution for vibration suppression and optimal clamping states selection of different cantilever parts.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Data availability

Not applicable.

Code availability

Not applicable.

References

  1. Zhou X, Zhang DH, Luo M, Wu BH (2015) Chatter stability prediction in four-axis milling of aero-engine casings with bull-nose end mill. Chin J Aeronaut 28:1766–1773

    Article  Google Scholar 

  2. Yang Y, Zhang WH, Ma YC, Wan M (2016) Chatter prediction for the peripheral milling of thin-walled workpieces with curved surfaces. Int J Mach Tool Manuf 109:36–48

    Article  Google Scholar 

  3. Moradi H, Vossoughi G, Behzad M, Movahhedy MR (2015) Vibration absorber design to suppress regenerative chatter in nonlinear milling process: application for machining of cantilever plates. Appl Math Model 39:600–620

    Article  MATH  Google Scholar 

  4. Li B, Cui GY, Tian W, Liao WH (2022) Vibration suppression of an industrial robot with AGV in drilling applications by configuration optimization. Appl Math Model 112:614–631

    Article  MathSciNet  Google Scholar 

  5. Shamoto E, Mori T, Nishimura K, Hiramatsu T, Kurata Y (2010) Suppression of regenerative chatter vibration in simultaneous double-sided milling of flexible plates by speed difference. CIRP Ann-Manuf Technol 59:387–390

    Article  Google Scholar 

  6. Khorshidi K, Rezaei E, Ghadimi AA, Pagoli M (2015) Active vibration control of circular plates coupled with piezoelectric layers excited by plane sound wave. Appl Math Model 39:1217–1228

    Article  MathSciNet  MATH  Google Scholar 

  7. Fei JX, Lin B, Xiao JL, Ding M, Yan S, Zhang XF, Zhang J (2018) Investigation of moving fixture on deformation suppression during milling process of thin-walled structures. J Manuf Process 32:403–411

    Article  Google Scholar 

  8. Yuan H, Wan M, Yang Y (2019) Design of a tunable mass damper for mitigating vibrations in milling of cylindrical parts. Chin J Aeronaut 32:748–758

    Article  Google Scholar 

  9. Kono I, Miyamoto T, Utsumi K, Nishikawa K, Onozuka H, Hirai J, Sugita N (2017) Study on machining vibration suppression with multiple tuned mass dampers: vibration control for long fin machining. Int J Auto Tech-Jpn 11:206–214

    Article  Google Scholar 

  10. Qin P, Liu YA, Wang M, Zhang YL (2021) Milling vibration control of semiconical shell workpiece with multiple distribution tuned mass dampers. Int J Adv Manuf Technol 115:2175–2190

    Article  Google Scholar 

  11. Kolluru K, Axinte D, Becker A (2013) A solution for minimising vibrations in milling of thin walled casings by applying dampers to workpiece surface. CIRP Ann-Manuf Technol 62:415–418

    Article  Google Scholar 

  12. Christian M, Hans CS, Philip K, Christian B, Simon-Markus K, Jörg W, Wolfgang H (2017) Machining of large scaled CFRP-Parts with mobile CNC-based robotic system in aerospace industry. Procedia Manuf 14:17–29

    Article  Google Scholar 

  13. Smith S, Wilhelm R, Dutterer B, Cherukuri H, Goel G (2012) Sacrificial structure preforms for thin part machining. CIRP Ann-Manuf Technol 61:379–382

    Article  Google Scholar 

  14. Slamani M, Gauthier S, Chatelain J-F (2015) A study of the combined effects of machining parameters on cutting force components during high speed robotic trimming of CFRPs. Measurement 59:268–283

    Article  Google Scholar 

  15. Kaliński Krzysztof J, Mazur Michał R, Galewski Marek A (2013) The optimal spindle speed map for reduction of chatter vibration during milling of bow thruster blade. Solid State Commun 198:686–691

    Google Scholar 

  16. Zhang XM, Ding H (2013) Note on a novel method for machining parameters optimization in a chatter-free milling process. Int J Mach Tool Manuf 72:11–15

    Article  Google Scholar 

  17. Wang H, Zhang KY, Wu DB, Yu T, Yu J, Liao YP (2021) Analysis and optimization of the machining fixture system stiffness for near-net-shaped aero-engine blade. Int J Adv Manuf Technol 113:3509–3523

    Article  Google Scholar 

  18. Luo M, Zhang XF, Zhang DH, Wu BH (2015) On-line compressor blade stiffness enhancement in multi-axis machining process. IFAC-PapersOnline 48:664–667

    Article  Google Scholar 

  19. Atsushi M, Hiroaki N, Nils K, Daisuke K (2018) Influence of contact condition between flexible plate and passive pivot support on machining vibration. Procedia CIRP 77:557–560

    Article  Google Scholar 

  20. Zeng SS, Wan XJ, Li WL, Yin ZP, Xiong YL (2012) A novel approach to fixture design on suppressing machining vibration of flexible workpiece. Int J Mach Tool Manuf 58:29–43

    Article  Google Scholar 

  21. Raghu A, Melkote SN (2004) Analysis of the effects of fixture clamping sequence on part location errors. Int J Mach Tool Manuf 44:373–382

    Article  Google Scholar 

  22. Wan X, Zhang Y, Huang X (2013) Investigation of influence of fixture layout on dynamic response of thin-wall multi-framed work-piece in machining. Int J Mach Tool Manuf 75:87–99

    Article  Google Scholar 

  23. Wang SY, Song QH, Liu ZQ (2019) Vibration suppression of thin-walled workpiece milling using a time-space varying PD control method via piezoelectric actuator. Int J Adv Manuf Technol 105:2843–2856

    Article  Google Scholar 

  24. Nagamatsu S, Shiraishi T (2021) Semi-active vibration suppression of a structure by a shear-type damper using magnetorheological grease. In: Oberst S, Halkon B, Ji J, Brown T (eds) Vibr Eng Sustain Future. Springer, Cham, pp 241–247

    Chapter  Google Scholar 

  25. Ma JJ, Zhang DH, Wu BH, Luo M, Chen B (2016) Vibration suppression of thin-walled workpiece machining considering external damping properties based on magnetorheological fluids flexible fixture. Chin J Aeronaut 29:1074–1083

    Article  Google Scholar 

  26. Sallese L, Grossi N, Tsahalis J, Scippa A, Campatelli G (2016) Intelligent fixtures for active chatter control in milling. Procedia CIRP 55:176–181

    Article  Google Scholar 

  27. Li YG, Liu CQ, Hao XZ, Gao JX, Maropoulos PG (2015) Responsive fixture design using dynamic product inspection and monitoring technologies for the precision machining of large-scale aerospace parts. CIRP Ann-Manuf Technol 64:173–176

    Article  Google Scholar 

  28. Li B, Tian W, Zhang CF, Hua FF, Cui GY, Li YF (2022) Positioning error compensation of an industrial robot using neural networks and experimental study. Chin J Aeronaut 35:346–360

    Article  Google Scholar 

  29. Cui GY, Li B, Tian W, Liao WH, Zhao W (2022) Dynamic modeling and vibration prediction of an industrial robot in manufacturing. Appl Math Model 105:114–136

    Article  MathSciNet  MATH  Google Scholar 

  30. Rui XT, Wang XP, Zhou QB, Zhang JS (2019) Transfer matrix method for multibody systems (Rui method) and its applications. Sci China Technol Sci 62:712–720

    Article  Google Scholar 

  31. Rui XT, Zhang JS, Wang X, Rong B, He B, Jin Z (2022) Multibody system transfer matrix method: the past, the present, and the future. Int J Mech Syst Dyn 2:3–26

    Article  Google Scholar 

Download references

Funding

This work was co-supported by the National Natural Science Foundation of China (Nos. 52005254, 52075256 and U22A20204), and the Fundamental Research Funds for the Central Universities (No. NT2022016).

Author information

Authors and Affiliations

  1. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Pinzhang Wang, Wei Tian & Bo Li

  2. Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Bo Li

Authors
  1. Pinzhang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wei Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bo Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Pinzhang Wang: experiments design, dynamics modeling, data analysis, writing—original draft. Wei Tian: experiments design, data analysis, writing—reviewing and editing. Bo Li: investigation, supervision, reviewing and editing.

Corresponding authors

Correspondence to Wei Tian or Bo Li.

Ethics declarations

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

We confirm that this work is original and has not been published elsewhere, nor is it currently under consideration for publication elsewhere. All the authors listed have agreed to publish the manuscript that is enclosed.

Competing interests

The authors declare no competing interests.

Additional information

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1

The transfer equation of the state vector \({\boldsymbol{\rm Z}}_{r,O}\) with respect to \({{\varvec{Z}}}_{r,I}\) is defined as

$${{\varvec{Z}}}_{r,O}={{\varvec{U}}}_{r}{{\varvec{Z}}}_{r,I}(r=\mathrm{2,5},\mathrm{8,11,15,17,19,21,23,25,27,29})$$
(12)

where \({{\varvec{U}}}_{r}\) is the transfer matrices of the rigid body, it is expressed as

$${{\varvec{U}}}_{r}=\left[\begin{array}{cccc}{{\varvec{I}}}_{3}& -{\widetilde{{\varvec{l}}}}_{IO}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ m{\omega }^{2}{\widetilde{{\varvec{l}}}}_{CO}& -{\omega }^{2}\left(m{\widetilde{{\varvec{l}}}}_{IO}{\widetilde{{\varvec{l}}}}_{IC}+{{\varvec{J}}}_{I}\right)& {{\varvec{I}}}_{3}& {\widetilde{{\varvec{l}}}}_{IO}\\ m{\omega }^{2}{{\varvec{I}}}_{3}& -m{\omega }^{2}{\widetilde{{\varvec{l}}}}_{IC}& {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}\end{array}\right]$$
(13)

where

$${\widetilde{{\varvec{l}}}}_{IO}=\left[\begin{array}{ccc}0& -{z}_{O}& {y}_{O}\\ {z}_{O}& 0& -{x}_{O}\\ -{y}_{O}& {x}_{O}& 0\end{array}\right],{\widetilde{{\varvec{l}}}}_{IC}=\left[\begin{array}{ccc}0& -{z}_{C}& {y}_{C}\\ {z}_{C}& 0& -{x}_{C}\\ -{y}_{C}& {x}_{C}& 0\end{array}\right],{{\varvec{J}}}_{I}=\left[\begin{array}{ccc}{J}_{x}& -{J}_{xy}& -{J}_{xz}\\ -{J}_{xy}& {J}_{y}& -{J}_{yz}\\ -{J}_{xz}& -{J}_{yz}& {J}_{z}\end{array}\right]$$

where \({\widetilde{{\varvec{l}}}}_{CO}={\widetilde{{\varvec{l}}}}_{IO}-{\widetilde{{\varvec{l}}}}_{IC}\), I and O are the input and output end respectively, C is the center of mass, and \({\widetilde{{\varvec{l}}}}_{PQ}\) is the coordinate matrices of point Q relative to P. \({{\varvec{J}}}_{I}\) is the moment of inertia with respect to I, m is the mass of the body, \(\omega\) is the system natural frequency.

The transfer equation and the geometric relationship between multiple input ends are

$$\left\{\begin{array}{c}{{\varvec{Z}}}_{13,O}=\sum_{m=1}^{4}{{\varvec{U}}}_{13,m}{{\varvec{Z}}}_{13,m}\\ {{\varvec{H}}}_{13,n}{{\varvec{Z}}}_{13,n}={{\varvec{H}}}_{13,1}{{\varvec{Z}}}_{13,1}\end{array}\right.\left(n=2,3,4\right)$$
(14)

where the transfer matrix \({{\varvec{U}}}_{\mathrm{13,1}}\) is consistent with the form of \({{\varvec{U}}}_{r}\) in Eq. (13), the transfer matrices of the output end with respect to input ends n (\(n=\mathrm{2,3},4\)) are represented as

$${{\varvec{U}}}_{13,n}=\left[\begin{array}{cccc}{{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}& {\widetilde{{\varvec{l}}}}_{{I}_{r}O}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}\end{array}\right]$$
(15)

The geometrical relationship of the first end with respect to itself is

$${{\varvec{H}}}_{13,1}=\left[\begin{array}{cccc}{{\varvec{I}}}_{3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\end{array}\right]$$
(16)

The additional geometrical equations describing geometrical relationships between the first and nth \(\left(n=2,3,4\right)\) input ends can be expressed as

$${{\varvec{H}}}_{13,n}=\left[\begin{array}{cccc}{{\varvec{I}}}_{3}& {\widetilde{{\varvec{l}}}}_{{I}_{1}{I}_{n}}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\end{array}\right]$$
(17)

The transfer matrix of workpiece 31 can be obtained according to the above method.

The transfer matrix of spatial elastic hinge is

$${{\varvec{U}}}_{v}=\left[\begin{array}{cccc}{{\varvec{I}}}_{3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{K}}}_{v}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}& {{\varvec{K}}}_{v}{\prime}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}\end{array}\right]$$
(18)

where v = 1, 3, 4, 6, 7, 9, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, and

$${{\varvec{K}}}_{v}=\left[\begin{array}{ccc}-1/{K}_{v,x}& 0& 0\\ 0& -1/{K}_{v,y}& 0\\ 0& 0& -1/{K}_{v,z}\end{array}\right],{{\varvec{K}}}_{v}{\prime}=\left[\begin{array}{ccc}1/{K}_{v, x}{\prime}& 0& 0\\ 0& 1/{K}_{v, y}{\prime}& 0\\ 0& 0& 1/{K}_{v, z}{\prime}\end{array}\right]$$

in which \({K}_{v,x},{K}_{v,y}\), and \({K}_{v,z}\) donate the stiffnesses of springs in the \(x,y\), and \(z\) directions, respectively. Moreover, \({K}_{v,x}{\prime},{K}_{v,y}{\prime}\), and \({K}_{v,z}{\prime}\) are the torsional stiffnesses of rotary springs about the \(x,y\), and \(z\) directions, respectively.

According to the automatic deduction, the main transfer equation is established as follows

$${{\varvec{T}}}_{31-32}{{\varvec{Z}}}_{\mathrm{32,0}}+{{\varvec{T}}}_{31-1}{{\varvec{Z}}}_{\mathrm{1,0}}+{{\varvec{T}}}_{31-4}{{\varvec{Z}}}_{\mathrm{4,0}}+{{\varvec{T}}}_{31-7}{{\varvec{Z}}}_{\mathrm{7,0}}+{{\varvec{T}}}_{31-10}{{\varvec{Z}}}_{\mathrm{10,0}}={{\varvec{Z}}}_{\mathrm{31,0}}$$
(19)

where \({{\varvec{Z}}}_{k,0}\) reprintings the state vector of the output end of element k, and

$$\begin{array}{c}{{\varvec{T}}}_{31-32}={{\varvec{U}}}_{31,32}{{\varvec{U}}}_{32}\\ {{\varvec{T}}}_{31-1}={{\varvec{U}}}_{31,30}{{\varvec{U}}}_{30}{{\varvec{U}}}_{29}{{\varvec{U}}}_{28}{{\varvec{U}}}_{27}{{\varvec{H}}}_{X}\left({\theta }_{6}\right){{\varvec{U}}}_{26}{{\varvec{U}}}_{25}{{\varvec{H}}}_{Y}\left({\theta }_{5}\right){{\varvec{U}}}_{24}{{\varvec{U}}}_{23}{{\varvec{H}}}_{X}\left({\theta }_{4}\right){{\varvec{U}}}_{22}{{\varvec{U}}}_{21}{{\varvec{H}}}_{Y}\left({\theta }_{3}\right)\\ {{\varvec{U}}}_{20}{{\varvec{U}}}_{19}{{\varvec{H}}}_{Y}\left({\theta }_{2}\right){{\varvec{U}}}_{18}{{\varvec{U}}}_{17}{{\varvec{H}}}_{Z}\left({\theta }_{1}\right){{\varvec{U}}}_{16}{{\varvec{U}}}_{15}{{\varvec{U}}}_{14}{{\varvec{U}}}_{13,3}{{\varvec{U}}}_{3}{{\varvec{U}}}_{2}{{\varvec{U}}}_{1}\\ {{\varvec{T}}}_{31-4}={{\varvec{U}}}_{31,30}{{\varvec{U}}}_{30}{{\varvec{U}}}_{29}{{\varvec{U}}}_{28}{{\varvec{U}}}_{27}{{\varvec{H}}}_{X}\left({\theta }_{6}\right){{\varvec{U}}}_{26}{{\varvec{U}}}_{25}{{\varvec{H}}}_{Y}\left({\theta }_{5}\right){{\varvec{U}}}_{24}{{\varvec{U}}}_{23}{{\varvec{H}}}_{X}\left({\theta }_{4}\right){{\varvec{U}}}_{22}{{\varvec{U}}}_{21}{{\varvec{H}}}_{Y}\left({\theta }_{3}\right)\\ {{\varvec{U}}}_{20}{{\varvec{U}}}_{19}{{\varvec{H}}}_{Y}\left({\theta }_{2}\right){{\varvec{U}}}_{18}{{\varvec{U}}}_{17}{{\varvec{H}}}_{Z}\left({\theta }_{1}\right){{\varvec{U}}}_{16}{{\varvec{U}}}_{15}{{\varvec{U}}}_{14}{{\varvec{U}}}_{\mathrm{13,6}}{{\varvec{U}}}_{6}{{\varvec{U}}}_{5}{{\varvec{U}}}_{4}\\ {{\varvec{T}}}_{31-7}={{\varvec{U}}}_{31,30}{{\varvec{U}}}_{30}{{\varvec{U}}}_{29}{{\varvec{U}}}_{28}{{\varvec{U}}}_{27}{{\varvec{H}}}_{X}\left({\theta }_{6}\right){{\varvec{U}}}_{26}{{\varvec{U}}}_{25}{{\varvec{H}}}_{Y}\left({\theta }_{5}\right){{\varvec{U}}}_{24}{{\varvec{U}}}_{23}{{\varvec{H}}}_{X}\left({\theta }_{4}\right){{\varvec{U}}}_{22}{{\varvec{U}}}_{21}{{\varvec{H}}}_{Y}\left({\theta }_{3}\right)\\ {{\varvec{U}}}_{20}{{\varvec{U}}}_{19}{{\varvec{H}}}_{Y}\left({\theta }_{2}\right){{\varvec{U}}}_{18}{{\varvec{U}}}_{17}{{\varvec{H}}}_{Z}\left({\theta }_{1}\right){{\varvec{U}}}_{16}{{\varvec{U}}}_{15}{{\varvec{U}}}_{14}{{\varvec{U}}}_{\mathrm{13,9}}{{\varvec{U}}}_{9}{{\varvec{U}}}_{8}{{\varvec{U}}}_{7}\\ {{\varvec{T}}}_{31-10}={{\varvec{U}}}_{31,30}{{\varvec{U}}}_{30}{{\varvec{U}}}_{29}{{\varvec{U}}}_{28}{{\varvec{U}}}_{27}{{\varvec{H}}}_{X}\left({\theta }_{6}\right){{\varvec{U}}}_{26}{{\varvec{U}}}_{25}{{\varvec{H}}}_{Y}\left({\theta }_{5}\right){{\varvec{U}}}_{24}{{\varvec{U}}}_{23}{{\varvec{H}}}_{X}\left({\theta }_{4}\right){{\varvec{U}}}_{22}{{\varvec{U}}}_{21}{{\varvec{H}}}_{Y}\left({\theta }_{3}\right)\\ {{\varvec{U}}}_{20}{{\varvec{U}}}_{19}{{\varvec{H}}}_{Y}\left({\theta }_{2}\right){{\varvec{U}}}_{18}{{\varvec{U}}}_{17}{{\varvec{H}}}_{Z}\left({\theta }_{1}\right){{\varvec{U}}}_{16}{{\varvec{U}}}_{15}{{\varvec{U}}}_{14}{{\varvec{U}}}_{\mathrm{13,12}}{{\varvec{U}}}_{12}{{\varvec{U}}}_{11}{{\varvec{U}}}_{10}\end{array}$$
(20)

where \({{\varvec{U}}}_{i}\) is the transfer matrix corresponding to the element i, \({{\varvec{U}}}_{31,30}\) and \({{\varvec{U}}}_{31,32}\) are the transfer matrices of workpiece 31 with respect to input ends 30 and 32, \({{\varvec{U}}}_{13,3}\),\({{\varvec{U}}}_{13,6}\),\({{\varvec{U}}}_{13,9}\) and \({{\varvec{U}}}_{13,12}\) are the transfer matrices of AGV 13 with respect to input ends 3, 6, 9, and 12.

Furthermore, the coordinate transformation matrices are

$${{\varvec{H}}}_{X}\left({\theta }_{k}\right)=\left[\begin{array}{cccc}{{\varvec{h}}}_{X}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{X}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{X}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{X}\left({\theta }_{k}\right)\end{array}\right],k=1,2,{3,4},\mathrm{5,6}$$
(21)
$${{\varvec{H}}}_{Y}\left({\theta }_{k}\right)=\left[\begin{array}{cccc}{{\varvec{h}}}_{Y}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{Y}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{Y}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{Y}\left({\theta }_{k}\right)\end{array}\right], k=1,2,\mathrm{3,4},\mathrm{5,6}$$
(22)
$${{\varvec{H}}}_{Z}\left({\theta }_{k}\right)=\left[\begin{array}{cccc}{{\varvec{h}}}_{Z}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{Z}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{Z}\left({\theta }_{k}\right)& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{h}}}_{Z}\left({\theta }_{k}\right)\end{array}\right],k=1,2,\mathrm{3,4},\mathrm{5,6}$$
(23)

where \({\theta }_{k}\) is the angle of the joint k, and

$${{\varvec{h}}}_{X}(\theta )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{cos}\theta & \mathrm{sin}\theta \\ 0& -\mathrm{sin}\theta & \mathrm{cos}\theta \end{array}\right],{{\varvec{h}}}_{Y}(\theta )=\left[\begin{array}{ccc}\mathrm{cos}\theta & 0& -\mathrm{sin}\theta \\ 0& 1& 0\\ \mathrm{sin}\theta & 0& \mathrm{cos}\theta \end{array}\right],{{\varvec{h}}}_{Z}(\theta )=\left[\begin{array}{ccc}\mathrm{cos}\theta & \mathrm{sin}\theta & 0\\ -\mathrm{sin}\theta & \mathrm{cos}\theta & 0\\ 0& 0& 1\end{array}\right]$$
(24)

The elements with multiple input ends in the ARGW system include workpiece 31 and vehicle body 13, so system geometric equations can be found as

$$\begin{array}{c}{{\varvec{G}}}_{31-32}{{\varvec{Z}}}_{\mathrm{32,0}}+{{\varvec{G}}}_{31-1}{{\varvec{Z}}}_{\mathrm{1,0}}+{{\varvec{G}}}_{31-4}{{\varvec{Z}}}_{\mathrm{4,0}}+{{\varvec{G}}}_{31-7}{{\varvec{Z}}}_{\mathrm{7,0}}+{{\varvec{G}}}_{31-10}{{\varvec{Z}}}_{\mathrm{10,0}}={{\varvec{O}}}_{6\times 1}\\ {{\varvec{G}}}_{13-1}{{\varvec{Z}}}_{\mathrm{1,0}}+{{\varvec{G}}}_{13-4}{{\varvec{Z}}}_{\mathrm{4,0}}={0}_{6\times 1}\\ {{\varvec{G}}}_{13-1}{{\varvec{Z}}}_{\mathrm{1,0}}+{{\varvec{G}}}_{13-7}{{\varvec{Z}}}_{\mathrm{7,0}}={0}_{6\times 1}\\ {{\varvec{G}}}_{13-1}{{\varvec{Z}}}_{\mathrm{1,0}}+{{\varvec{G}}}_{13-10}{{\varvec{Z}}}_{\mathrm{10,0}}={0}_{6\times 1}\end{array}$$
(25)

where \({{\varvec{O}}}_{6\times 1}\) denotes a 6 × 1 zero column matrix, and the parameters in Eq. (25) can be expressed as.

$$\begin{array}{c}{{\varvec{G}}}_{13-1}=-{{\varvec{H}}}_{13,3}{{\varvec{U}}}_{3}{{\varvec{U}}}_{2}{{\varvec{U}}}_{1}\\ {{\varvec{G}}}_{13-4}={{\varvec{H}}}_{13,6}{{\varvec{U}}}_{6}{{\varvec{U}}}_{5}{{\varvec{U}}}_{4}\\ {{\varvec{G}}}_{13-7}={{\varvec{H}}}_{13,9}{{\varvec{U}}}_{9}{{\varvec{U}}}_{8}{{\varvec{U}}}_{7}\\ {{\varvec{G}}}_{13-10}={{\varvec{H}}}_{13,12}{{\varvec{U}}}_{12}{{\varvec{U}}}_{11}{{\varvec{U}}}_{10}\\ {{\varvec{G}}}_{31-1}={{\varvec{H}}}_{31,30}{{\varvec{U}}}_{31,30}^{-1}{{\varvec{T}}}_{31-1}\\ {{\varvec{G}}}_{31-4}={{\varvec{H}}}_{31,30}{{\varvec{U}}}_{31,30}^{-1}{{\varvec{T}}}_{31-4}\\ {{\varvec{G}}}_{31-7}={{\varvec{H}}}_{31,30}{{\varvec{U}}}_{31,30}^{-1}{{\varvec{T}}}_{31-7}\\ {{\varvec{G}}}_{31-10}={{\varvec{H}}}_{31,30}{{\varvec{U}}}_{31,30}^{-1}{{\varvec{T}}}_{31-10}\\ {G}_{31-32}=-{{\varvec{H}}}_{31,32}{{\varvec{U}}}_{32}\end{array}$$
(26)

where

$${{\varvec{H}}}_{i,o}=\left[\begin{array}{cccc}{{\varvec{I}}}_{3}& {\widetilde{{\varvec{l}}}}_{io}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\\ {{\varvec{O}}}_{3\times 3}& {{\varvec{I}}}_{3}& {{\varvec{O}}}_{3\times 3}& {{\varvec{O}}}_{3\times 3}\end{array}\right]$$
(27)

where \({l}_{io}\) represents the displacement matrix of the input point end o relative to first input end i, \({\widetilde{{\varvec{l}}}}_{io}\) refers to the skew-symmetric matrix of \({{\varvec{l}}}_{io}\). In this paper, i includes 13, and 31, o is the corresponding 3, 6, 9, 12, and 30, 32.

Combing the system main transfer equation Eq. (18) and the system geometric equations Eq. (25), the system overall transfer equation can be obtained as

$$\left[\begin{array}{cccccc}-{{\varvec{I}}}_{12}& {{\varvec{T}}}_{31-32}& {{\varvec{T}}}_{31-1}& {{\varvec{T}}}_{31-4}& {{\varvec{T}}}_{31-7}& {{\varvec{T}}}_{31-10}\\ {{\varvec{O}}}_{6\times 12}& {{\varvec{G}}}_{31-32}& {{\varvec{G}}}_{31-1}& {{\varvec{G}}}_{31-4}& {{\varvec{G}}}_{31-7}& {{\varvec{G}}}_{31-10}\\ {{\varvec{O}}}_{6\times 12}& {{\varvec{O}}}_{6\times 12}& {{\varvec{G}}}_{13-1}& {{\varvec{G}}}_{13-4}& {{\varvec{O}}}_{6\times 12}& {{\varvec{O}}}_{6\times 12}\\ {{\varvec{O}}}_{6\times 12}& {{\varvec{O}}}_{6\times 12}& {{\varvec{G}}}_{13-1}& {{\varvec{O}}}_{6\times 12}& {{\varvec{G}}}_{13-7}& {{\varvec{O}}}_{6\times 12}\\ {{\varvec{O}}}_{6\times 12}& {{\varvec{O}}}_{6\times 12}& {{\varvec{G}}}_{13-1}& {{\varvec{O}}}_{6\times 12}& {{\varvec{O}}}_{6\times 12}& {{\varvec{G}}}_{13-10}\end{array}\right]\left[\begin{array}{c}{{\varvec{Z}}}_{\mathrm{31,0}}\\ {{\varvec{Z}}}_{\mathrm{32,0}}\\ {{\varvec{Z}}}_{\mathrm{1,0}}\\ {{\varvec{Z}}}_{\mathrm{4,0}}\\ \begin{array}{c}{{\varvec{Z}}}_{\mathrm{7,0}}\\ {{\varvec{Z}}}_{\mathrm{10,0}}\end{array}\end{array}\right]=0$$
(28)

Furthermore

$${{\varvec{U}}}_{\text{all}}{{\varvec{Z}}}_{\text{all}}={{\varvec{O}}}_{72\times 1}$$
(29)

Appendix 2. Calculation of the dynamic equation

The form of the coefficients in the overall dynamic equations are

$$\begin{array}{c}M={\text{d}}{\text{i}}{\text{a}}{\text{g}}\left({{\varvec{M}}}_{2},{{\varvec{M}}}_{5},\cdots ,{{\varvec{M}}}_{31}\right)\\ K={\text{d}}{\text{i}}{\text{a}}{\text{g}}\left({{\varvec{K}}}_{2},{{\varvec{K}}}_{5},\cdots ,{{\varvec{K}}}_{31}\right)\\ v={\left[{{\varvec{v}}}_{2}^{\text{T}},{{\varvec{v}}}_{5}^{\text{T}},\cdots ,{{\varvec{v}}}_{31}^{\text{T}}\right]}^{\text{T}}\\ f={\left[{{\varvec{f}}}_{2}^{\text{T}},{{\varvec{f}}}_{5}^{\text{T}},\cdots ,{{\varvec{f}}}_{31}^{\text{T}}\right]}^{\text{T}}\end{array}$$
(30)

And the augmented eigenvector of the kth model is defined as

$$\left\{\begin{array}{c}{{\varvec{V}}}_{i}^{k}={{\varvec{H}}{\varvec{Z}}}_{i}^{k}, \, \, i=\mathrm{2,5},\cdots 30,H={\left[{{\varvec{I}}}_{6*1 }, {{\varvec{O}}}_{6*1 }\right]}^{\mathrm{T}}\\ {{\varvec{V}}}^{k}={\left[{\left({{\varvec{V}}}_{2}^{k}\right)}^{\text{T}},{\left({{\varvec{V}}}_{5}^{k}\right)}^{\text{T}},\cdots ,{\left({{\varvec{V}}}_{30}^{k}\right)}^{\text{T}}\right]}^{\text{T}}\end{array}\right.$$
(31)

The damping \({\varvec{C}}=2\zeta \omega {\varvec{M}}\), where \(\zeta\) is the modal damping ratio. According to the orthogonality of the augmented eigenvectors, the relation between M, K, and the augmented eigenvector \({{\varvec{V}}}^{j}\) is satisfied

$$\begin{array}{c}\langle {{\varvec{M}}{\varvec{V}}}^{k},{{\varvec{V}}}^{j}\rangle ={\delta }_{k,j}{M}^{j}A\\ \langle {{\varvec{K}}{\varvec{V}}}^{k},{{\varvec{V}}}^{j}\rangle ={\delta }_{k,j}{({\omega }^{j})}^{2}{M}^{j}\end{array}$$
(32)

where \({M}^{j}\) and \({K}^{j}={({\omega }^{j})}^{2}{M}^{j}\) are the jth-order modal mass and stiffness, respectively. Only when k = j, \({\delta }_{k,j}=1\), in other situations, \({\delta }_{k,j}=0\).

Appendix 3. Parameters in the simulation

Tables 8 and 9

Table 8 The physical parameters
Full size table
Table 9 The physical parameters
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, P., Tian, W. & Li, B. Machining vibration suppression of cantilever parts of aerospace structure using robot-assisted clamping system. Int J Adv Manuf Technol 128, 4103–4121 (2023). https://doi.org/10.1007/s00170-023-12090-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-023-12090-w

Keywords

Search

Navigation