1 Introduction

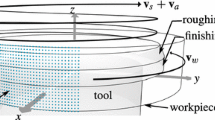
In tool grinding, the workpiece quality as well as the economic efficiency is highly affected by process planning. In this context, the use of cooling lubricants has a significant influence in order to manufacture workpieces in accordance to the quality requirements. Typical challenges in grinding of cemented carbide are given in the context of cooling lubrication. Process planning of flute, peripheral, and tool tip grinding influences the surface quality, shape deviation, surface layer properties, and cutting performance of the tool. The fluid dynamic processes of cooling lubricants and their effects on the thermal workpiece load are largely unknown and not considered in process planning. Furthermore, the grinding wheel topography is not considered but has a significant influence on the surface quality, thermal effects, and residual stresses. Additionally, bond layer modeling received little attention in previous studies, which would allow fluid dynamic simulation of cooling lubrication in the contact zone. Previous studies show methods for modeling the wetting behavior of microstructured silicon surfaces. The wetting angle with distilled water was analyzed for regular and irregularly structured surfaces. A correlation between the surface structure and the droplet spreading could be established. The contact angle and drop shape vary as a function of the structuring direction and shape [1]. However, the findings of these investigations cannot be applied directly to the grinding wheel bond layer, since the surface of the grinding wheel is also porous. Differences between distilled water and cooling lubricants are also of great importance. The topography and the supply with cooling lubricant determine the occurrence of boundary zone defects. The main function of the cooling lubricant is to cool the grinding wheel and the workpiece. It also reduces friction, removes chips, and cleans the grinding wheel [2, 3]. Figure 1 shows the different influences in process planning of helical flute grinding and shows in this context also the cooling lubrication.

Fig. 1
figure 1

Influences helical flute grinding [4]

Full size image

Current investigations on cooling lubricant supply address the flow field measurement. For this purpose, optical measurement methods such as the measurement of coolant flow fields by means of particle image velocimetry (PIV) and the tracing of patterns in shadowgraphs were used [5]. Investigations were carried out with rotating grinding slides without workpiece machining. The results show that the reduction in cooling efficiency from a grinding wheel to fluid velocity ratio of 0.8 [6] correlates with increased bouncing of the coolant jet when it hits the grinding wheel. Computational fluid dynamic (CFD) simulations are dedicated to the fluid mechanics of the coolant in the grinding zone [7]. As a result, it was found that the most efficient emulsion feed is given at an angle of inclination of the feed nozzle of 30°. With regard to mathematical modeling, the boundary conditions between cooling lubricant, grinding wheel, and workpiece are important. Recent investigations on the fluid behavior between free fluids and porous media (similar to grinding wheel topography) indicate a complex behavior depending on the geometry and the flow parameters at the boundary layer [8, 9]. Tencio et al. also describe the influence of topography on the wetting angle and surface free energy of a material [10]. For thermal modeling, it is important to understand the heat transfers between cooling lubricant, grinding wheel, and workpiece [11, 12].

The boundary conditions within the wetting of grinding wheels with coolant are complex and currently unknown due to the porous surface. In this context, modeling approaches are required to perform fluid simulations. The 2D radially symmetric thin film equation is used to identify the slip parameters, whereas the same would be prohibitively expensive to realize in a 3D Navier-Stokes framework.

In this work, we investigate the wetting behavior of different grinding wheels via droplet experiments and use the droplet dynamic to identify slip parameters in the thin-film equation which is used to simulate these experiments. Similar droplet experiments were conducted and analyzed in [13] and [1], where the wetting of porous surfaces and microstructured surfaces was investigated. This research is an intermediate step in getting to a better understanding of the interactions between cooling lubricant and grinding wheels during tool grinding. In particular, we aim to identify the important characteristics informing the wetting behavior of the cooling lubricant/grinding wheel system. More concretely, the identified slip parameters for different grinding wheel specifications appear in the interface conditions between grinding wheel and lubricant in the form of the Beavers-Joseph law [14]. This allows a transfer to 3D Navier-Stokes simulations to describe the fluid dynamics of an overall grinding process.

2 Modeling approach

We describe the time evolution of a single droplet on both dry and pre-wetted grinding wheel topographies within the framework of the thin-film equation. A two-dimensional approximation to the Navier-Stokes system where the free fluid-air interface is characterized by the droplet film height h = h(t, x). It is based on the Navier-Stokes system describing the fluid dynamic of the cooling lubricant and its interaction with both the grinding wheel and the surrounding air. For general details regarding the thin film equation, we refer to [13, 15,16,17].

For our specific scenario, we work with the thin-film equation with slip and refer to [17, 18] for details and its derivation. Let T > 0 be the time horizon of interest and Ω the surface of the grinding wheel where the drop is observed. The time evolution of this film height can then be described via a balance equation in the form of

$${\partial}_th=-\mathit{\operatorname{div}}\ {q}_h+f\kern1em \textrm{in}\ \left(0,T\right)\times \varOmega$$
(1)

where qh denotes the fluid flux density and f a possible volume source density. With this approach, mass conservation is satisfied when f = 0. In the unwetted scenario, the source term can therefore be used to model the extraction of fluid into the porous surface structure of the grinding wheel. The flux takes the general form

$${q}_h=Q(h)\left(\nabla \varDelta h\right)$$
(2)

for a mobility function Q(h) leading to a non-linear fourth-order parabolic PDE. The exact form of the mobility function depends on the specific situation considered in the Navier-Stokes system (e.g., boundary conditions, wetted or dry condition). As we are interested in characterizing the slip via the rough, porous substrate of the grinding wheel under dry and pre-wetted conditions, we consider the Navier-slip mobility function given by

$$Q(h)=\frac{1}{3\mu}\left({h}^3+\beta {h}^2\right).$$
(3)

Here, μ denotes the dynamic viscosity of the fluid and iβ the slip parameter. Generally speaking, a higher parameter β corresponds to faster wetting behavior.

In all experiments, complete wetting was observed; i.e., there are no stationary contact angles. To avoid the free-boundary part of the problem that comes with explicitly modeling the contact angle evolution, we additionally assume the existence of a small background fluid film 0 < hbg ≪ 1.

As we are considering a fourth-order parabolic PDE, two sets of boundary conditions are needed in addition to the initial condition for the film height to arrive at a well-posed problem. In our study, we assume both homogeneous Neumann (no in-/outflow)

$$-\nabla h\cdot n=0\kern1.25em \textrm{on}\ \left(0,T\right)\times \partial \varOmega$$
(4)

and Dirichlet condition (fixed background film height at the boundary)

$$h={h}_{\textrm{bg}}\kern1em \textrm{on}\ \left(0,T\right)\times \partial \varOmega .$$
(5)

While most parameters in this model are given as part of the setup, the goal is to use the free parameter β to characterize the wetting properties of the different grinding wheels, specifically with regard to the grain size, bonding system, and dry or pre-wetted state. Due to the high complexity of the composition of the porous medium and the cooling lubricant, the surface energy of the materials could not be determined directly. Consequently, experiments investigating these properties are needed, to describe these effects empirically. With the thin-film equation, droplet experiments are usually a good starting point as they are easily comparable to the simulation and clearly interpretable.

3 Experimental investigation

The focus of this research study is the experimental investigation of the wetting behavior in order to compare the simulation. In the first step, the wetting behavior is investigated under stationary conditions. For this purpose, grinding wheels are wetted with cooling lubricant and the wetting is recorded. In further investigations, the influence of the grinding wheel surface temperature is planned.

3.1 Experimental setup

To investigate the wetting behavior of different grinding wheel specifications with the used grinding oil (SintoGrind MP 830), different wetting tests were carried out with an electronic pipette (Sartorius Picus). Figure 2 shows the experimental setup. The wetting speed of the grinding wheel topography was determined by varying the grain size, grain concentration, angle of attack, droplet volume, and wetting condition. The wetting process was recorded with the aid of a high-speed camera Photron FastCam SA5 model 775K-M1 and evaluated by means of developed scripts for image processing. For the experiments, a frame rate of 2000 fps and an area of 1024 × 1024 pixels were chosen to capture the entire width of each droplet. Using such a camera system enables a highly accurate analysis of the droplet behavior over a defined period of time. In the experimental study, droplet development from the side view was investigated. For this purpose, an extended selection of grinding wheels with suitable hybrid bonds for flute grinding from Saint-Gobain (D33, D54) and Dr. Müller (D15, D39, D46, D91) was examined (Table 1). The porous grinding wheel surfaces consist of a polyamide resin bond with bronze as a sintered metal additive. Deviations are possible depending on the manufacturer. A detailed analysis of the individual ingredients was not carried out due to the large number of grinding wheel types examined. In total, 36 video recordings were evaluated regarding the drop height and width at five times. All experimental settings were carried out three times at different positions on the grinding wheel both with a dry surface and with a pre-wetted surface (8 μl).

Fig. 2
figure 2

Experimental setup

Full size image
Table 1 Parameters of the wetting experiments
Full size table

3.2 Evaluation and experimental results

The recorded videos of the wetting experiments were evaluated by using the software Matlab and its image processing toolbox (Fig. 3). Using a customized script, the video recordings can be evaluated automatically. First, the user defines the frame in which the droplet is located on the grinding wheel in its initial state. Then, five frame intervals from 0 to 1.5 s are automatically evaluated. For this purpose, the binary image is generated by the script, in which the width and height of the drop are analyzed at each of the time intervals. Taking measurement uncertainties and interference into account, the results show the following tendencies (Fig. 4). It can be seen that the droplet height of the pre-wetted surface is smaller than for the dry surface for most of the grain sizes. A correlation of the droplet height after 1.5 s with the grain size is clearly shown regarding the dry state. This correlation is less present for the pre-wetted state.

Fig. 3
figure 3

Experimental evaluation

Full size image
Fig. 4
figure 4

Droplet height after 1.5 s

Full size image

Considering the drop height of the initial state (Fig. 5), a significantly lower dependency on grain size can be seen. These results led to the assumption that the observation of the development of drop height and drop width over time is significant for the wetting simulations.

Fig. 5
figure 5

Droplet height at the initial state

Full size image

4 Wetting simulation

The aim of the simulations is to identify the optimal slip parameter for different grinding wheels that best explains the observed wetting behavior. For the corresponding numerical simulations, we implemented a finite element approach for a radially symmetric 2D situation. This is justified by the experimental setup (no lateral movement of the wheels, no wind, and no inclination) and the videos of the actual experiments where symmetry was closely observed.

The simulations, shown in Fig. 6, were done in Matlab (R2018b) based on a framework proposed in [19]. The corresponding FEM implementation for a 1D scenario was extended for the 2D radially symmetric situation in a way to also be compatible with a background film, the mobility function given by Eq. (3) and our boundary conditions (Eqs. (4) and (5)).

Fig. 6
figure 6

Optimal slip parameter

Full size image

At the beginning, for both pre-wetted and dry grinding wheel experiments, the initial height functions were extracted from the high-speed videos via a polynomial fit using edge detection (cf. binary image in Fig. 3). From there, for each set of experimental values, a naive optimization search in the parameter space β > 0 was conducted to find the value that best explains the observations by punishing deviations from the measured height and width values over time.

With the dry simulations an additional uncertainty is the amount of cooling lubricant flowing into the porous layer of the grinding wheel. This second parameter was identified by observing the droplet volume lost over the time interval before, again, conducting a parameter search for the slip parameter. The results can be found in Fig. 6; it shows a more volatile situation, where, due to the dry wheel, the surface structure is more pronounced. It should be noted that the parameters in the wetted and dry situation are not directly comparable due to the additional fluid flow inside the porous layer in the dry case.

5 Discussion

The grinding wheel specification (grain size, grain concentration, and bonding) influences the wetting behavior with the cooling lubricant. As shown in Fig. 6, there is a small but clear correlation between grain size and wetting behavior in the pre-wetted case, where grinding wheels with larger grains tend to exhibit stronger slip properties. Even more important seem to be the specific bonding structure and therefore the topography of the porous layer of the grinding wheels. Although both manufacturers (Saint-Gobain and Dr. Müller) use the same type of hybrid bonding (resin and metal), we found clear differences in the wetting behavior (Fig. 6). This should not be interpreted as a statement of quality, but only as an observation of difference. In summary, the wetting of the grinding wheel and the resulting cooling effectiveness are influenced by the individual grinding wheel characteristics including the specific bonding structure used by the manufacturer.

In the dry case, however, the differences with respect to grain size and bonding structure are far less pronounced. In addition, the variation of the wetting behavior in the experiments for the individual wheels is larger. This is most likely a consequence of the local variation in the surface and structure of the porous layer (the wheels were rotated between the three droplet experiments). In the wetted case, these local differences were at least partially smoothed out by the existing fluid film.

The general combined and normalized mean-squared errors (MSE) between the experimental data and simulated results with optimized slip parameters (considering both height and width at the measured time steps) for the 36 experiments were found to be in the range of 0.00008 and 0.005 showing overall good agreement. Figure 7 shows the comparison between experiments and simulations results for the droplet heights specifically after 1.5 s for the dry and the pre-wetted topography. In both cases, the overall trend for droplet height after 1.5 s is captured with observed deviations in the range of 2–10% (with the D91 grinding wheel simulations in the pre-wetted experiments having the highest disagreement). These deviations are partially a consequence of potential inaccuracies in the measurements (e.g., due to the rough surface structure of the wheel or the unclear transition from droplet to wheel surface especially in the flat end-states) as well as, at least in the dry case, local differences in the surface structure. Even more importantly, it must be pointed out as well that the parameter was not optimized to best describe the height at 1.5 s but rather to achieve good agreement with the time evolution of the droplets measured via height and width over several time steps, as measured via the MSE mentioned above.

Fig. 7
figure 7

Comparison of experimental results and simulation with fitted slip parameters for the droplet height after 1.5 s

Full size image

6 Conclusion

In tool grinding process steps like helical flute grinding, the cooling lubrication plays an important role for the properties of the boundary zone, e.g., residual stresses. For an adequate thermo-fluid-dynamical modeling and simulation of local cooling, an identification and parametrization of the relevant interface conditions between grinding wheel and lubricant are necessary. Based on the temporal wetting behavior from grinding oil droplet experiments, slip parameters could be successfully identified. It was established that the grain size negatively correlates with the slip properties and that the bonding structure of the grinding wheel is particularly important.

The results of our investigations (namely, the identified slip parameters) are necessary for 3D Navier-Stokes simulations of the overall grinding situation. More specifically, the connection between grain size and slip parameter will be used in the Navier-slip condition (Beavers-Joseph) on the interface between the and grinding wheel. Additional validation experiments are planned, in which, e.g., droplet dynamics on inclined grinding wheels are investigated. Further experiments are planned to investigate the influence of surface temperature and energy.