1 Introduction

Nowadays, non-rigid parts, meaning parts that endure deformation during assembly such as injection moulded plastic and thin sheet-metal components, are more and more common in industrial products. Due to the manufacturing process, some parts can show large deformation, i.e., exceeding functional limits, that in some instances can be significantly reduced during the assembly process, obtaining a functional part. Therefore, the functional geometrical specifications (i.e., ISO GPS), relevant to the assembly, cannot be directly transferred to the single sub-assembly parts, whose manufacturing geometrical specifications should be based on a “free state condition” (see ISO 10579 [1]). A clarifying example can be found in appendix A.

In industry, the relations that arise among functional and manufacturing specifications are often not managed systematically, at least in many industrial cases encountered by the authors. The multi-pole structure created by the different documents (i.e., functional, manufacturing, and verification specifications) relies on hierarchical relations, consequently, a rigorous correlation is needed (see ISO/TS 21619/2018 [2]). When dealing with rigid parts and assemblies, tolerance stack-ups can be used to achieve this correlation; the tolerance transfer method [3] represents a valid option. On the other side, there is a lack of standardized procedures to correlate the functional specification (or “as assembled”) to the manufacturing specification (“free state”), of deformable (or compliant) assemblies.

When dealing with to non-rigid bodies, literature provides approaches based on Finite Element Method simulation (FEM). Many contributions focus on sheet metal parts and assemblies which are commonly used in the aerospace and automotive sector. A mechanical approach, using influence coefficient matrices aiming to compute tolerances in the case of welded, bolted, riveted, or glued sheet metal parts, is proposed by Sellem and Rivière [4]. A mono-dimensional strategy called “offset finite element model” is presented by Liu and Hu [5] to predict sheet metal assembly variability when the parts are spot welded. The differences between “series” and “parallel” assemblies are discussed by Liu, Hu, and Woo [6]: a smaller variability in the assembly is found for parallel assemblies when compared to the single part variability. The influence coefficient method [7] was then developed, a sensitivity matrix links the spring-back of the assembly to the free-state condition allowing to determine the “as assembled” configuration. Further developments to this method presented strategies to consider both shape defects and contact modelling [8, 9]. All these approaches are limited to thin walled parts; a summary of all these methodologies can be found in the literature [10].

An approach considering the elastic deformation in sheet metal parts for tolerance stack-ups is presented by Stockinger et al. [11]. Experimental results were used to validate the approach; it was also compared to different commercial solutions integrating 3DCS™ by Dimensional Control Systems® and CATIA V5™ workbench TAA™ (Tolerance Analysis of deformable Assemblies) by Dassault Systèmes® where FEM simulation is used to analyse the assembly process deviations.

A methodology to perform fixtureless inspections of freeform surfaces on non-rigid thin-walled parts, called Generalized Numerical Inspection Fixture (or, GNIF), is presented by Radvar-Esfahlan and Tahan [12]. The deformation of the part is considered to be isometric, meaning that the geodesic distance between any two internal points does not change during deformation. Using this assumption, correspondent points, between the CAD model and the free form acquired model, are defined. Further developments to this framework introduced improved boundary conditions [13] and automation [14]. To compensate the information lost in a fully clamped configuration, such as internal stresses and inherent tendency to deform after the clamps are released, Lindau et al. [15] proposed a method to perform the measure on a three point supporting set-up, simulating the clamped state with FEM simulation, and the method of influence coefficient. Worth noting the contribution by Morse and Grohol [16] who developed an efficient methodology to perform fixtureless inspection of non-rigid parts executing FEM simulation on the nominal geometry independently from actual data.

A methodology allowing to perform virtual measurement of thin-walled parts made of polymers in a constrained state was proposed by Raymauld et al. [17].

Recent trends driven by the digitizing of product systems and the implementation of the digital twin concept enabled to predict the geometrical quality of the product still in the early design phase as discussed by by Maropoulos and Ceglarek [18]. The Digital Twin concept was first developed at NASA and presented in 2010 [19] where it is defined as “an integrated multi-physics, multi-scale, probabilistic simulation of a vehicle or system that uses the best available physical models, sensor updates, fleet history, etc., to mirror the life of its flying twin.” As it concerns mechanical assemblies, the main purpose of a Digital Twin is the verification and validation of the product design and the definition of its characteristics [20] allowing a digital variation management [21, 22]. One of the main characteristics of a Digital Twin is the double way real time communication: physical-digital and digital-physical. Its implementation for geometrical assurance enables the selective assembly and real-time process adjustment [23-26]. The use of neural networks embedded in Digital Twin or as meta-models for predicting assembly variability [24, 27] and spring back during manufacturing [28] has also been tested.

Full model simulation might be suitable in early design phases for development and optimization purposes; simplified models are crucial for real time application during production [22]. However, the concurrent engineering paradigm implies that an early design phase alone can not be strictly defined and the product geometry itself is developed parallel to the production process [29]. Therefore, the needs for simplified meta-models or surrogate models extend also to the design phase.

In literature, sheet metal and/or parts with thin-walled geometry were mainly addressed, with no specific works on general non-rigid large parts. In the following, it is referred to “non-rigid large part” as a part where not all the geometry equally influenced by the assembly process, meaning that local stiffer portions are not deformed but only translated and/or rotated. It is also considered that the part, once assembled, reaches a stable configuration. Furthermore, the methodologies presented in the literature are optimized for inspection or tolerance stack-up applications. Since they represent a post-processing of the acquired data, if used for quality control, they need to be routined after each inspection cycle. The need for simplified generic models was also underlined by Kaufmann et al. in an in-depth analysis of the model presented by the literature [30].

In a recent work by the authors [31], a procedure for the correlation of the functional geometrical specification to the manufacturing specification applied to large injection moulded parts has been presented. This methodology suggests a correlation procedure between the geometric specifications at “as produced” (i.e., free) state to the “as assembled” (functional) state to be performed at start-up of production in order to define free state tolerance limit for inspection during mass production. The procedure uses FEM simulation and it is based on a formal definition of datum systems and geometric tolerances as defined by the ISO GPS (Geometrical Product Specification) standards. However, the methodology relies on the non-realistic hypothesis that the assembly process can completely recover the initial deformation, at the assembly features, resulting in the best-case scenario where the maximum possible reduction is found.

Thus, in order to fill this gap, the authors aim to describe a methodological framework to correlate the manufacturing specification and the functional specification applied to large non-rigid parts taking into consideration the elastic spring-back of the assembly. The spring-back is evaluated using the influence coefficient method, which has been widely applied in sheet metal assemblies. This model is used to find the spring back of the assembly features. In particular, this contribution presents and discusses a methodology that allows to create a linearized model for simulating the constrained state using a “restricted skin model” approach.

2 Materials and methods

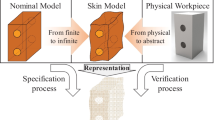
The overall proposed methodology can be seen in Fig. 1. In brief, parts at free state are inspected based on the manufacturing specification, the free state deviations are recorded and the free state restricted skin model is generated. The assembled state restricted skin model is simulated starting from the free state restricted skin model through a linearized model, and it is virtually inspected based on the functional specification. The assembled state deviation are recorded and correlated to the free-state ones.

Fig. 1
figure 1

General workflow to correlate functional (design) and manufacturing specifications

Full size image

The core concepts described in this article comprehend the definition of the restricted skin model and the linearized model discussion.

The methodology is presented through the evaluation of the assembly between two large non-rigid parts. If more than two parts need to be assembled, the result of the first assembly operation can be considered a new single part that receives a third part, etc. For both parts, a coherent functional specification is considered available. For both parts, two classes of geometrical features can be labelled: the mutual assembly features (i.e., the features that are put in contact when the two parts are assembled) and other functional features. Among these, the functional datum system for both parts should be found if a correct geometrical specification is given.

The assembly process is considered to be composed of four general steps: locating and placement in the fixture, clamping, joining, and releasing [32, 33]. No deformation caused by the joining process is considered, even though its contribution might be easily added as presented in [9].

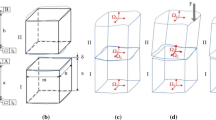
Considering the first part, n degrees of freedom are assigned to the assembly features and a total of m degrees of freedom are assigned to the other functional features. The degrees of freedom could be a rigid geometrical deviation (i.e., rigid translation or rotation), a set of point deviations of a given feature (e.g., a point sampling on a flat surface to consider form deformations) or a derived geometry (i.e., axis or mid-plane) deviation. An example of each kind of input-output degrees of freedom, and its geometrical interpretation can be seen in Fig. 2. The use of a set of points for tolerance analysis, still not considering deformability, is also postulated in [34]. The same concept is also proposed for multi-stage manufacturing process simulation [35, 36].

Fig. 2
figure 2

Types of possible input-output degrees of freedom, a integral "rigid" feature, b point sampling over an integral feature, c derived feature

Full size image

2.1 Matrix computation

Throughout a simulation, a sensitivity matrix [A1] (m× n) linking the m outputs degrees of freedom to the n input degrees of freedom is evaluated. At the same time, a reduced stiffness matrix [K1] (n× n) linking the n input degrees of freedom to the n constrain forces is also computed. To obtain these reduced matrices, n FEM simulation shall be carried out by applying a unit deviation in one input degree of freedom at the time and a null deviation to all the others. It is noteworthy to highlight that being the FEM simulations an input to the model, its reliability will impact considerably to the accuracy of the proposed methodology. Case by case, the simulation parameters (mesh, boundary conditions, contact modelling, etc) need to be carefully evaluated.

The same matrices are evaluated also for the second component: [A2] (p× n) and [K2] (n× n). It must be noted that the degrees of freedom applied to the assembly features of the second component must be mapped from the first one, Fig. 3.

Fig. 3
figure 3

The input degrees of freedom are mapped on the second part mating feature creating an assembly link per each of them

Full size image

The assembly needs to be evaluated since it becomes stiffer compared to both single parts. Considering only the input degree of freedom a reduced stiffness matrix can be evaluated for the assembly [Kasm] (n× n) linking the assembly deviation to the constraining forces.

2.2 Assembly feature deviation

Once the matrices are evaluated, the first step is the evaluation of the deviation of the assembly features by applying the influence coefficient method [7], equation (1). The derivation of the formula is omitted for the sake of brevity.

$$\left\{{\updelta}_{\mathrm{n}}\right\}={\left[{\mathrm{K}}_{\mathrm{asm}}\right]}^{-1}\left[{\mathrm{K}}_1\right]\left\{{\updelta}_1\right\}+{\left[{\mathrm{K}}_{\mathrm{asm}}\right]}^{-1}\left[{\mathrm{K}}_2\right]\left\{{\updelta}_2\right\},$$
(1)

where

{δn} is the deviation associated with the n input degrees of freedom after the assembly;

{δ1} is the free state deviation associated with the n input degrees of freedom for the first part;

{δ2} is the free state deviation associated with the n input degrees of freedom for the second part.

2.3 Deviation of other functional elements

The overall methodology is based on the assumptions of linear constitutive relations and small deviations from nominal. Consequently, the superposition principle is used to determine the deviation from the nominal of an actual geometry, when constrained, summing the different contributions.

Three contributions are considered: the free state deviation, the deviation due to the fixturing and the elastic spring back, obtaining the final formula.

$${\left\{{\updelta}_{\mathrm{m}}\right\}}_{\mathrm{TOT}}={\left\{{\updelta}_{\mathrm{m}}\right\}}_{\mathrm{FREE}}-\left[{\mathrm{A}}_1\right]\left\{{\updelta}_1\right\}+\left[{\mathrm{A}}_1\right]\left\{{\updelta}_{\mathrm{n}}\right\},$$
(2)

The formula is written for the first part of the assembly, where

{δm}TOT is the deviation associated with the m output degrees of freedom after the assembly;

{δm}FREE is the free state deviation associated with the m output degrees of freedom for the first part and should be evaluated by means of inspection of the part in free state condition;

− [A1] {δ1} are the deviations associated with the m output degrees of freedom for the first part if the n input degrees of freedom, of the non-ideal actual part, are forced to their nominal position (i.e., fixturing);

[A1] {δn} are the deviations associated with the m output degrees of freedom for the first part due to the elastic spring back.

Equation (2) can also be rewritten in a more structured way as follows:

$${\left\{{\updelta}_{\mathrm{m}}\right\}}_{\mathrm{TOT}}={\left\{{\updelta}_{\mathrm{m}}\right\}}_{\mathrm{FREE}}+\left\{-\left[{\mathrm{A}}_1\right]+\left[{\mathrm{A}}_1\right]{\left[{\mathrm{K}}_{\mathrm{asm}}\right]}^{-1}\left[{\mathrm{K}}_1\right]\right\}\left\{{\updelta}_1\right\}+\left\{\left[{\mathrm{A}}_1\right]{\left[{\mathrm{K}}_{\mathrm{asm}}\right]}^{-1}\left[{\mathrm{K}}_2\right]\right\}\left\{{\updelta}_2\right\},$$
(3)

If considering the second part, the equation becomes:

$${\left\{{\updelta}_{\mathrm{p}}\right\}}_{\mathrm{TOT}}={\left\{{\updelta}_{\mathrm{p}}\right\}}_{\mathrm{FREE}}+\left\{\left[{\mathrm{A}}_2\right]{\left[{\mathrm{K}}_{\mathrm{asm}}\right]}^{-1}\left[{\mathrm{K}}_1\right]\right\}\left\{{\updelta}_1\right\}+\left\{-\left[{\mathrm{A}}_2\right]+\left[{\mathrm{A}}_2\right]{\left[{\mathrm{K}}_{\mathrm{asm}}\right]}^{-1}\left[{\mathrm{K}}_2\right]\right\}\left\{{\updelta}_2\right\},$$
(4)

Besides the two sensitivity matrices, [A1] and [A2], already defined, four more sensitivity matrices can be defined:

  • [A11] = − [A1] + [A1] [Kasm]-1 [K1] assembled state sensitivity matrix for the first part relative to the first part deviations;

  • [A12] = [A1] [Kasm]-1 [K2] assembled state sensitivity matrix for the first part relative to the second part deviations;

  • [A22] = − [A2] + [A2] [Kasm]-1 [K2] assembled state sensitivity matrix for the second part relative to the second part deviations;

  • [A21] = [A2] [Kasm]-1 [K1] assembled state sensitivity matrix for the second part relative to the first part deviations.

Both Equations (3) and (4) can then be written compactly.

$${\left\{{\updelta}_{\mathrm{m}}\right\}}_{\mathrm{TOT}}={\left\{{\updelta}_{\mathrm{m}}\right\}}_{\mathrm{FREE}}+\left[{\mathrm{A}}_{11}\right]\left\{{\updelta}_1\right\}+\left[{\mathrm{A}}_{12}\right]\left\{{\updelta}_2\right\},$$
(5)
$${\left\{{\updelta}_{\mathrm{p}}\right\}}_{\mathrm{TOT}}={\left\{{\updelta}_{\mathrm{p}}\right\}}_{\mathrm{FREE}}+\left[{\mathrm{A}}_{21}\right]\left\{{\updelta}_1\right\}+\left[{\mathrm{A}}_{22}\right]\left\{{\updelta}_2\right\},$$
(6)

These two equations, plus Equation (1), can be used to evaluate the constrained state. These three equations are the core of the proposed linearized model.

It is noteworthy that these three equations may also be used to propagate the uncertainty associated with the input quantities such as the free-state measurement uncertainty.

A summary of the procedure to create the proposed linearized model can be seen in Fig. 4.

Fig. 4
figure 4

The general workflow to generate the proposed linearized model. DoF stands for degree of freedom

Full size image

2.4 Specification correlation

Using the abovementioned workflow, for both free state and simulated constrained state, grants the geometrical deviations of the functional features to be known. These deviations could be in the form of rigid feature translation and/or rotation or as a set of point deviations allowing to take into account the form error. Therefore, the result can be considered a “restricted skin model” representation compared to the “full” skin model that considers all the topological boundaries of the part as including form deviations [37].

Digital inspection can be performed according to ISO GPS standard, for the free state part using the manufacturing specification and for the constrained state part using the functional specification, thus obtaining the geometrical deviations according to ISO 17450-1:2011 and ISO 1101:2017 [38, 39] for both states.

Consequently, it is possible to create a statistical correlation model between the free state deviation and the simulated constrained state, testing all possible combinations of assembly among the available parts. This correlation model can be used to define the free state (manufacturing) limits that, statistically, guarantee the pre-defined functional limit.

2.5 The case study

The proposed methodological framework has been tested in order to verify and validate its assumptions. Testing was performed for different case studies designed to test and stress different steps of the procedure.

In particular, a simplified mono-dimensional case for which it was possible to find an analytical definition for all the sensitivity matrices previously described was tested. Therefore, no FEM simulation was needed, allowing to highlight the methodological flaws independently from FEM model inaccuracies.

Secondly, a case study designed to prove the effectiveness of the sensitivity matrix to simulate the output degrees of freedom based on FEM simulation is presented. This case study was used to prove that the reduced model can obtain the same result as a full FEM simulation.

Thirdly, a case study looking exclusively at the elastic spring back at the assembly features is proposed.

Lastly, based on the third case study, two samples were produced and the result was compared to actual measurements.

2.5.1 Case study 1

The monodimensional test case setup can be seen in Fig. 5. It consists of two idealized components and each of them has one input and one output. Each elastic element, nominally, is 100 mm long.

Fig. 5
figure 5

The monodimensional case study

Full size image

In Table 1, all the configurations tested can be seen. Different combinations of stiffness and free state deviation are tested to check the framework results.

Table 1 Configurations tested to verify the framework
Full size table

Each of the combinations has been chosen in order to stress the model and obtain particular cases in which the final output could have been deduced. The list of expected outcomes can be seen in Table 2.

Table 2 Expected simulation results
Full size table

2.5.2 Case study 2

The case study set up to prove the effectiveness of the sensitivity matrix as proposed in the framework can be seen in Fig. 6. Assuming that the elastic spring back is correctly estimated by the model (MIC), the results obtained through the reduced model are compared to the result obtained with full FEM simulation to prove that the proposed sensitivity matrix can correctly estimate the output degrees of freedom deviations.

Fig. 6
figure 6

The case study used to prove the sensitivity matrix’s effectiveness, a CAD model, b FEM model

Full size image

The assembly feature is defined as a deformable planar surface and is described with 12 degrees of freedom. The output degrees of freedom are considered the translation and rotation of the upper cylinder, see Fig. 6a.

To perform FEM simulations, the software Patran/NASTRAN was used. The geometry is discretized with bidimensional FEM elements (CQUAD4). To record the deviation of the output degrees of freedom, two service nodes are placed in the nominal position at the extreme points of the cylinder axes, and connected to one node of the cylinder in the corresponding extreme section with a rigid link (RBE2), see Fig. 6b. To check the assumption that the cylinder behaves as a rigid element, the same service node is connected with the relevant FEM node in the corresponding section with spring elements (CELAS1). If the cylinder behaves as a rigid element, no stress should be recorded within the spring elements.

Five different free-state deviations for the assembly feature were tested and can be seen in Table 3. The deviation values were randomly generated based on a truncated Fourier series.

Table 3 Configuration tested for case study 2
Full size table

2.5.3 Case study 3

Case study 3 is designed to test the elastic spring back at the assembly features. The setup can be seen in Fig. 7: two simple parts (base, Fig. 7b and Fig. 7e and top, Fig. 7a and Fig. 7d) are considered and the assembly is performed by glueing together the two parts using a fixture.

Fig. 7
figure 7

The case study used to test the elastic spring back, a top CAD model, b base CAD model, c assembly CAD model, d top FEM model, e base FEM model, f assembly FEM model

Full size image

Both assembly features are described with 12 degrees of freedom, see Fig. 7a and Fig. 7b. The simulations are performed using Patran/NASTRAN; the geometry is discretized with bidimensional FEM elements (CQUAD4), see Fig. 7d, e, f.

Since the FEM simulation gives a polynomial approximation of the result, it is unavoidable to have numerical errors in the stiffness matrix. Theoretically, the sum of any raw of the stiffness matrix should be equal to one; actually, a residual error is always present. The effect of this error gives a resultant fixturing force even for rigid translation of the assembly features, which is not real. Even if this residual force is small (compared to the forces due to the actual assembly feature deformation) when it passes through the inverse of the assembly stiffens matrix it estimates a rigid spring back translation which has no actual physical meaning. For this reason, the input deviations need to be filtered by their mean value which describes a rigid translation. By doing so, this numerical error is avoided.

One of the reasons for the residual errors lies in the fact that only a certain amount of significant digits are computed by the FEM solver. In some cases, the residual error is high enough to make the solution unstable: the elastic spring back is larger than the input deviations, or even on the opposite side. This effect was studied on a simplified geometry, see Fig. 8. In this case, two identical parts are joined together and deformations on only one part are considered.

Fig. 8
figure 8

The geometry used to test the instability of the problem, a part FEM model, b assembly FEM model

Full size image

The full model, in this case, shows a physically sound behaviour, but if the stiffness matrices are truncated, the less significant digits are used the more the spring back diverges on the opposite side compared to the input deviations, Fig. 9.

Fig. 9
figure 9

Effect of the truncation of the stiffness matrices on the elastic spring back simulation

Full size image

To avoid this numerical effect, only the diagonal component of the stiffness matrices are retrieved: the fixturing forces (−[K] · {δ1}) do not have actual values, but since the same transformation is done for both component and assembly stiffness matrices, the resultant assembly forces are correctly converted into spring back deviations, see Fig. 9. It can be seen as the diagonal model is more stable than the full model: even with only two significant digits in the stiffnesses matrices, the spring back is comparable to the one obtained with the full model. Therefore, to avoid numerical instability, only the diagonal element of the stiffness matrixes are used in the model for case study 3.

The different configurations tested for case study 3 can be seen in Table 4.

Table 4 Configuration tested for case study 3
Full size table

Test case 3.1 is proposed to check whether the model can correctly handle rigid translations; the expected result is a null spring back since no deformation at the assembly feature is applied during the joining operation. Test case 3.2 checks whether the simulated spring back is physically sound; part 1 is considered nominal and part 2 has a simulated deviation with a zero average value. It is expected that the spring back will be in the same direction as the free state deviation of part 2 with a lower value. Test case 3.3 proposes mirrored free-state deviations between the two parts. Since part 1 (base) is stiffer than part 2 (top) is expected to have a small spring back towards the free state deviation of part 1. Finally, test case 3.4 presents some random free state deviation; therefore, it is not straightforward to expect any particular spring back result.

2.5.4 Case study 4

Case study 4 is designed to check the model against actual data. The same geometry presented for case study 3 was additively manufactured using a formlabs® Form 3™ apparatus and the formlabs® Tough 1500 resin, see Fig. 10a, b, c, d. The geometry was manually distorted to obtain high deviations from the nominal. The base and top parts were 3D scanned using a 3D-structured light scanner (Aurum3D) and the data were elaborated in GOM Inspect to extract the twelve free state deviations at the assembly features. The two parts were glued together using epossidic glue. During the glueing process, the two parts were kept flat using a custom gig. The assembly, Fig. 10e, f, was measured with the same procedure used for the single free-state parts.

Fig. 10
figure 10

Actual geometries used for case study 4, a first actual base part, b first actual top part, c second actual base part, d second actual top part, e first actual assembly, f second actual assembly

Full size image

The Free state deviations were used as input for the model as explained in case study 3 and the results were compared with the actual values measured in the assembly.

3 Results

3.1 Result case study 1

3.1.1 Matrices computation

For the presented case study, the matrices collapse into numbers. The analytical formulation, for each of them, is described below.

$$\left[{A}_1\right]=\frac{k_{21}}{k_{11}+{k}_{21}},$$
(7)
$$\left[{K}_1\right]=\frac{k_{11}\cdot {k}_{21}}{k_{11}+{k}_{21}},$$
(8)
$$\left[{A}_2\right]=\frac{k_{12}}{k_{12}+{k}_{22}},$$
(9)
$$\left[{K}_2\right]=\frac{k_{12}\cdot {k}_{22}}{k_{12}+{k}_{22}},$$
(10)
$$\left[{K}_{asm}\right]=\frac{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}\cdot {k}_{22}\right)+\left({k}_{12}+{k}_{22}\right)\left({k}_{11}\cdot {k}_{21}\right)}{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}+{k}_{22}\right)},$$
(11)

In a non-simplified case, these matrices should be found using FEM simulation. Therefore, no analytical solution for any further sensitivity matrix needs to be studied.

3.1.2 Assembly feature deviation

In this simple case, all the sensitivity matrices can be analytically defined. Equation (1) can then be written as follows.

$$\begin{aligned} \left\{{\updelta}_n\right\}=\frac{\left({k}_{11}\cdot {k}_{21}\right)\left({k}_{12}+{k}_{22}\right)}{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}\cdot {k}_{21}\right)+\left({k}_{12}+{k}_{22}\right)\left({k}_{11}\cdot {k}_{21}\right)}\left\{{\updelta}_1\right\}+\\\kern2em+\frac{\left({k}_{12}\cdot {k}_{22}\right)\left({k}_{11}+{k}_{21}\right)}{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}\cdot {k}_{21}\right)+\left({k}_{12}+{k}_{22}\right)\left({k}_{11}\cdot {k}_{21}\right)}\left\{{\updelta}_2\right\},\end{aligned}$$
(12)

3.1.3 Deviation of other functional elements

The compact equation derived to directly evaluate the deviation of the other functional elements, Equations (5)–(6), can be expressed as follows.

$$\begin{aligned} {\left\{{\updelta}_m\right\}}_{TOT}={\left\{{\updelta}_m\right\}}_{\mathrm{FREE}}+\\ +\frac{k_{21}}{\left({k}_{11}+{k}_{21}\right)}\left[\frac{\left({k}_{11}\cdot {k}_{21}\right)\left({k}_{12}+{k}_{22}\right)}{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}\cdot {k}_{21}\right)+\left({k}_{12}+{k}_{22}\right)\left({k}_{11}\cdot {k}_{21}\right)}-1\right]\left\{{\updelta}_1\right\}+\\ +\left[\frac{\left({k}_{21}\cdot {k}_{12}\cdot {k}_{22}\right)}{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}\cdot {k}_{21}\right)+\left({k}_{12}+{k}_{22}\right)\left({k}_{11}\cdot {k}_{21}\right)}\right]\left\{{\updelta}_2\right\},\end{aligned}$$
(13)
$$\begin{aligned} {\left\{{\updelta}_p\right\}}_{TOT}={\left\{{\updelta}_p\right\}}_{\mathrm{FREE}}+\\ +\left[\frac{\left({k}_{11}\cdot {k}_{21}\cdot {k}_{12}\right)}{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}\cdot {k}_{21}\right)+\left({k}_{12}+{k}_{22}\right)\left({k}_{11}\cdot {k}_{21}\right)}\right]\left\{{\updelta}_1\right\}+\\ +\frac{k_{12}}{\left({k}_{12}+{k}_{22}\right)}\left[\frac{\left({k}_{12}\cdot {k}_{22}\right)\left({k}_{11}+{k}_{21}\right)}{\left({k}_{11}+{k}_{21}\right)\left({k}_{12}\cdot {k}_{21}\right)+\left({k}_{12}+{k}_{22}\right)\left({k}_{11}\cdot {k}_{21}\right)}-1\right]\cdot\\\cdot\left\{{\updelta}_2\right\}, \end{aligned}$$
(14)

3.1.4 Test case results

The result obtained using the described methodology for the test cases described in Table 1 can be seen in Table 5.

Table 5 Simulation results
Full size table

The results obtained from the first six tests (Table 5) are in line with the expected results (as presented in Table 2) except for the spring-back of test 1.5 and the deviation of the second component of test 1.6. These two discrepancies are legitimate because it is not possible to impose a stiffness value of zero and, therefore, the result diverges.

The results for test case 1.7 are summarized in Fig. 11. It can be highlighted that the spring-back due to the deviation of part one decreases linearly with the influence that the very same part has on the assembly stiffness.

Fig. 11
figure 11

Result for test case 7

Full size image

3.2 Results case study 2

The assumption of rigid behaviour for the output feature is verified: stresses in all spring elements is 0.0 N.

The comparison between the reduced model (sensitivity matrix) and the full FEM model can be seen in Table 6 for all configurations of test case 2.

Table 6 Case study 2, reduced model results compared to full FEM model results
Full size table

3.3 Results case study 3

The result of the three test cases relevant to case study 3 can be seen in Fig. 12. At first glance, it is possible to see that the expected result summarized in subsection 2.5.3 are met although, especially for test case 3.3 it is difficult to see the elastic spring back. In Table 7 the numerical values for the spring back can be seen.

Fig. 12
figure 12

Result for case study 3

Full size image
Table 7 Configuration tested for case study 3
Full size table

3.4 Results case study 4

The results of the comparison between the proposed framework and the actual value measured in the two samples are summarized in Fig. 13. It can be noted that in both cases the differences are in the range ±0.2 mm even if the scale of the deviations is different.

Fig. 13
figure 13

Comparison between the result obtained with the proposed framework and the actual values measure in the assembly, a first assembly results, b second assembly results

Full size image

4 Discussion

The proposed procedure aims to create a linearized model able to simulate the assembled state of non-rigid parts that can be used for correlating the free-state manufacturing deviations to the constrained state.

4.1 Limits of application

The test cases from 1.1 to 1.6 were used to check if the proposed model can react accordingly to what is physically sound.

Test case 1.1 considers that the second element had the nominal geometry while being infinitely rigid; the only deviation was on the assembly feature of the first component. Unfortunately, since an infinite rigidity cannot be imposed, a value of 109 N/mm (i.e., 108 times the first component rigidity) was used instead. Even with this approximation, the result is compliant with the theoretical result: there is no spring-back at the assembly feature, the second component is undeformed, and the first component output degree deviation is opposite to the free state deviation of the assembly feature, coherently with the assembly procedure.

Test case 1.2 introduced a finite rigidity to the second component; therefore, a spring-back, in agreement with the free state deviation of the assembly feature of the first component, was expected and seen through simulation. The deviation of the first part output decreases when compared to the previous case where, starting from the nominal position, its deviation was due to the fixturing only; due to the spring-back, it now leans back to its nominal position. This time also the second component output shows a deviation in the same direction as the spring-back.

Test case 1.3, starting from the previous one, introduces a deviation in the assembly feature (i.e., input) of the second component in the same direction as the deviation on the first component. In this configuration, both parts contribute to the spring-back; therefore, they can be considered two distinct contributions. Each contribution points in the same direction as the free state deviation. Therefore, compared to the previous case, a greater spring-back value is expected. The model provides a result that is in line with the theoretical assumption. In this case, the deviation of the output degrees of freedom is disregarded.

Test case 1.4 assumes an opposite deviation to the second part assembly feature. This time the spring-back should be lower than test case 2 since the deviations of the two parts compensate for each other. The output degree of freedom on the first part should be greater compared to the second test case in absolute value. Both results given by the model are coherent.

Test case 1.5 introduces a deviation on all functional features and a null rigidity on the stiffnesses k21 and k12 which are the elements that link the assembly features to the output degrees of freedom. Therefore, during assembly no force is needed, consequently, no further deviation should be seen in output degrees of freedom and no spring-back should happen. In this case, the model results are in line with the theoretical assumption for the output degree of freedom but a non-null spring-back is predicted. Nevertheless, this incongruence can be explained. The model does not allow to use a stiffness equal to zero, for this reason, the used value was 10-9 N/mm. Even though this value is very small, the assembly force is different from zero. At the same time, the assembly stiffness has the same order of magnitude as the, near-zero, imposed stiffness. Therefore, even a small assembly force results in a non-null spring-back.

Test case 1.6 used a null stiffness on the second part. Therefore, the second part should not exchange forces with the first one resulting in a complete spring-back: deviation on part one and the deviation of the output degree of freedom of part two should not change. The model correctly simulates the deviation in part one but the deviation due to the spring-back in the second part is not null. The discrepancy can be explained by the same effect seen in the previous case: the impossibility to set null stiffnesses makes the result diverge.

Besides the monodimensional case study, the model was tested with FEM simulation, case study 3. The expected results for the proposed case are met showing no unexpected behaviours. The case study was designed to be far away from the problematic cases shown in the monodimensional case study.

Considering all the evidences, it can be stated that the proposed model is generally able to correctly interpret the theoretical behaviour. The cases in which it fails are due to the impossibility of correctly setting the required stiffness for the specific case. Nevertheless, a null stiffness is not realistic in an actual application. However, the model definition requires particular care in all of those cases in which the stiffness ratio between the two parts is high.

4.2 Assembly with more than two parts

The result of test case 1.7 shows a linear correlation between the spring-back due to the deviation of the first component with the part influence on the assembly stiffness. In other words, the stiffer the component the greater the spring-back. In the example, a two components assembly was considered; applying the superimposition of the effects for an assembly with more than two parts, the overall spring-back will be the sum of every single contribution. The higher the number of parts that create the assembly the lesser each of them will contribute to the assembly stiffness. This means that the overall spring-back will be the sum of different terms that will be significantly lower with respect to the free state deformation. Each contribution of the spring-back is likely to be randomly directed in the space, therefore, compensating for each other. Hence, for an assembly where the mean free state deviations of the mating features are randomly distributed a small spring-back, compared to the free state deviation, is expected.

4.3 The advantages of a hybrid approach

This methodology can be considered a hybrid approach, hereinafter referred to as restricted skin model. Some features are discretized as skin models, therefore considering their form deviations, others as rigid features considering just its derived element and/or the associated degrees of freedom. The result is a lighter model (i.e., a low number of degrees of freedom) compared to traditional skin model approaches in which the number of degrees of freedom is higher. If a “full” skin model approach is used, the creation of a linearized model linking all the possible sources of variation results may not be practically feasible. In industrial applications, where form error is not functionally relevant, the proposed method allows to neglect it from the linearized model. At the same time, the model can be much more accurate than non-skin model approaches where it is not possible to use any form of contact model.

The use of a linearized model requires performing FEM simulations at the beginning, needed for its creation (i.e., 3n simulations), and then all the combinations can be simulated in real-time solving the three equations (equations (1)-(5)-(6)). The simulation process (FEM) may also be optimized using the super-element method [40]. The model is completely independent from the actual mean deviations; therefore, it also allows quick reuse of the model during production to adjust the manufacturing specification limits in case of process deviations. It can also be used to set dedicated limits for different production lines or different production plants with almost no further effort.

Case study 2 was designed to check whether the sensitivity matrix applied to the restricted skin model can correctly estimate the deviations of the output degrees of freedom when compared to the full FEM simulation. From the result presented in Table 6, it can be seen the difference between the reduced model and the full FEM model is negligible. For this reason, it can be concluded that the proposed hybrid approach can effectively estimate the result of a full model with reduced computational effort.

4.4 Experimental validation

Case study 4 enables to experimentally validate the proposed model. Two assemblies were considered and deterministically evaluated. In the first assembly, the deviations of the two mating surfaces were almost opposite in direction resulting in a mitigation of the effects. As expected, the simulated spring-back is small when compared with the simulated spring-back of the second assembly where the free state deviations were almost concordant: in this second case, there is no mitigation. The reduced spring-back, compared to the free state deviations, is due to the assembly stiffness that increases super-linearly while the spring-back force is given by a linear sum of the fixturing forces.

The difference between the simulated spring-back and the actual values is in the range ±0.2 mm even if the spring-back of the first assembly is much smaller that the one of the second assembly. The result is that for the second assembly, there is a better fit between the simulated and actual values due to the scale. Since the error is similar in both cases it might be interpreted as an effect of the glue layer thickness that appears to be non-uniform adding a level of uncertainty. Considering the uncertainty given by the glue layer and the measuring process, the methodology is considered experimentally validated.

5 Conclusions

The aim of this paper is to present and discuss a linearized model for simulating the constrained state using a restricted skin model approach.

The inspiration for this work comes from the experience gained by the authors working with Electrolux on the geometric specification development for a washing machine tub; in this case, the tub is composed of two polymer flanges that are deformed and friction welded together; at the same time, the bearing seats and shoulders are not deformed. This case falls within the scope of the paper.

The proposed framework using a linearized model is conceived for allowing correlation of the “as assembled state” to the “as produced state” and finding proper free state tolerances limits that fulfil functional (as assembled) tolerances. It is particularly suited for large non-rigid parts where considering the full body as skin model may be non-convenient. Moreover, it allows a possible real-time application during production.

The model was tested on a simplified mono-dimensional assembly and resulted in having appropriate and coherent outcomes when compared to the theoretical assumption. Discrepancies were found when using null stiffnesses; however, the application of the model is not limited since this condition does not occur in actual industrial cases. The use of the sensitivity matrix applied to the proposed reduced skin model approach was tested with FEM simulation to test whether the results of the proposed reduced model are congruent to the full FEM simulation. Differences were found to be negligible; the maximum difference was 2.1 · 10−7 mm for traslations and 6.0 · 10−3 deg for rotations. The framework was also tested to check the spring-back simulation at the assembly features; the results were in line with the expected theoretical deviations and were experimentally validated finding errors in the range ±0.2 mm for two actual assemblies.

Further developments will require deepening the knowledge about FEM simulations specificities (i.e., boundary conditions, contact modelling) and closing the loop creating the statistical correlation model. In this instance, it will be also important to check whether the stresses induced by the fixturing are compatible with the material strength.