Abstract
Laser welding of copper hairpins is required to produce a conductive connection in electric stators. Past manufacturing processes introduce misalignments that lead to poor weld connections with increased electrical resistance. In this work, we discuss correlations between the electrical resistance of the weld connection and possible misalignment types. Misalignments lead to a deformed surface topography of the weld. We correlate inline measurements of the weld topography by optical coherence tomography (OCT) with misalignment types and hence erroneous weld connections. We identify a connection between surface topographical weld features with the electrical resistance of the weld. As a result, a quantified separation of process results is possible with a surface topographical feature of the hairpins that allows for concluding the electrical resistance of the pin-pair connection. Correlation coefficient is identified as the most relevant feature indicating a linear trend in the height profile. Reference measurements with a symmetrical weld pearl show a correlation coefficient of around 0, whereas misalignments with a skewed surface topography show increased absolute correlation coefficient values up to 0.75. The identified correlation between the electrical resistance and different misalignment types can be depicted with the correlation coefficient for the given boundary conditions. Defective weld results with electrical resistances above 6 µΩ can be identified with feature values above 0.5, whereas reference welds with an electrical resistance below 5 µΩ can be identified with an absolute correlation coefficient below 0.2.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hairpin technology is used for reliable and automated production of stator windings for electric motors. The manufacture of stators follows several process steps: First, copper pins are cut to size and stripped of paint. Second, the hairpins are shaped and assembled in the stack of lamination. Finally, the pins are bent into pin-pairs (twisting) and then contacted with each other by laser welding to form a closed winding [1]. A current limitation of this process is that after twisting, the hairpins might be misaligned. The application of laser welding to misaligned hairpins can lead to poor electrical contact resulting in an increase in electrical resistance possibly resulting in a defective stator. Monitoring technology is essential for quality control of serial production to identify an increase in electrical resistance and ultimately defective stators.
Inline cameras can give feedback on two-dimensional misalignments and can be used for the identification of spatter [2]. However, this approach is not able to detect axial height offsets between the pin-pairs. One potential inline monitoring technology that overcomes this limitation is optical coherence tomography (OCT). OCT is an interferometric measurement technology that enables the assessment of the welding bead by non-destructive distance measurement [3,4,5,6,7]. OCT can be applied to identify misalignments in pre-process monitoring, the weld depth in in-process monitoring, and the shape of the resulting weld in the post-process monitoring stage [8, 9]. Baader et al. [8] analyzed the potential of OCT for process monitoring of laser welding hairpin windings. The authors identified the potential for post-process characterization of welded hairpins, where a misalignment results in deformed surface topography of the weld shape.
Deformed welding shape can be used as an indicator for a reduced connection area of the joint partners and an increase in electrical resistance. Data processing is required to make use of the surface topographical information from the welding bead, and for this, machine learning approaches and artificial intelligence can be used. This allows extraction of relevant features from OCT data for the identification of quality-relevant characteristics [4, 7]. One potential method for feature extraction is feature extraction based on scalable hypothesis tests (FRESH) [10, 11]. FRESH applies various time-series characterization methods and predicts statistically significant features of targets being investigated.
In this work, we apply the FRESH algorithm to identify a quality-relevant feature for the classification of hairpin weld results based on different misalignments from surface topographical OCT data for the prediction of electrical resistance. We first discuss different misalignment types and their impact on the weld result. Second, we identify a feature to correlate inline measurements of the weld topography by OCT with misalignment types and erroneous weld connections. Finally, we demonstrate the correlation between the identified surface topographical weld feature with the electrical resistance of the hairpins.
2 Experimental methods
2.1 Experimental setup
Hairpin welding is conducted with a programmable scanning optic with cross-jet, processing laser with fiber, OCT, and inline camera (see Fig. 1a). Laser welding is performed using a continuous wave disk laser (Trumpf TruDisk 8001) at a wavelength of 1030 nm (maximum average power of 8 KW). Laser light is coupled into programmable focusing optics (Trumpf PFO 33–2) that allow for scanning in an elliptical field of 240 × 140 mm2 with galvanometer scanners. Focusing optics with an F-theta lens have a focal length of 345 mm resulting in a laser spot diameter of 228 µm.
Experimental setup consisting of process monitoring technologies like inline camera and OCT as well as processing laser equipment (laser fiber, programmable focusing optic, and cross-jet) (a). b shows the welding process strategy in two phases on the hairpins. c shows the measurement positions with the OCT measurement line on the hairpins
The OCT for inline process observation is attached to the programmable focusing optics and enables a coaxial positioning of the measurement beam for post-process welding bead analysis (Lessmüller OCT). The OCT is an SD-OCT with a superluminescent diode in a wavelength range from 820 up to 860 nm with an axial resolution of 11 µm, while the lateral resolution is 24 µm. The measurement beam is detected on a 2048-pixel line sensor with a maximum measurement frequency of 70 kHz. The inline camera for inline process observation is a monochromatic camera that enables coaxial measurement of the joint partners and is used for a qualitative observation of the weld (inline camera Trumpf VisionLine camera).
2.2 Experimental procedure and evaluation
Laser welding experiments are performed in a clamping device with pure copper hairpins (Cu-ETP) in the size of 140 × 4.5 × 3.2 mm3. Two I-pins are welded within a weld area of 6.3 × 4.5 mm2 in the focus position. The weld geometry is constant with movements around the I-pins and follows two phases (see Fig. 1b). Phase 1 aims for a uniform preheating of the workpiece and the transition of the joint partners to the fluid phase. Here, the processing laser performs circular movements with welding speeds of 12 m/min and 18 m/min at an average laser power of 6.0 kW. Phase 2 aims for an increase in weld depth and sufficient wetting of the contact area. Here, a welding speed of 48 m/min is used in a rectangular weld geometry at an average power of 3.7 kW.
Processing parameters are adjusted according to misalignment type (see Table 1). Misalignment types can occur in three dimensions: axial misalignment with a height difference in processing laser direction (z-direction), lateral misalignment with a relative misalignment between pins lateral to processing laser direction (x-direction), and radial misalignment with a gap between the pin-pair (y-direction) (illustrated in Fig. 2). Misalignments are introduced with increments of 0.2 mm for lateral and radial misalignment and with increments of 0.4 mm for axial misalignment. The upper limit for axial misalignment is set to 4.0 mm due to a lack of practical relevance. The upper limits for lateral and radial misalignment are chosen as 1.6 mm and 1.0 mm, respectively, as a further increase in offset would lead to no weld contact. Additionally, reference measurements are performed with no offset to quantify the impact of each misalignment type. Each set of parameters is repeated five times. Reference measurements are repeated 20 times.
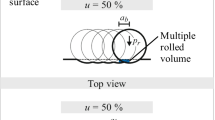
Each figure section shows a misalignment type (top) with a corresponding OCT measurement after the welding process (bottom). OCT images for a reference measurement, b axial misalignment with an offset of 3.6 mm; c radial misalignment with an offset of 0.8 mm, and d lateral misalignment with an offset of 1.6 mm
After laser welding, three OCT measurement lines are applied for post-process observation of the weld topography (see Fig. 1c). Each measurement line has a length of 10 mm with 1000 measurement points. The measurement line x0 is positioned central and is used for a qualitative analysis of the welding bead (see also Fig. 2). The measurement lines x1 and x2 are at a distance of 1.1 mm above/below the central measurement line x0. This distance is chosen to enable a balanced sensitivity towards most possible misalignment parameters.
The resulting height profiles from each measurement line (x0, x1, and x2) can be considered as time-series and are individually used for feature extraction with the FRESH algorithm [10, 11]. FRESH identifies meaningful features based on scalable hypothesis tests and applies three functionalities: feature extraction, ranking of features by relevance based on hypothesis tests, and multiple testing.
The data is labeled for the FRESH algorithm in four categories according to the misalignment type with reference, axial misalignment, lateral misalignment, and radial misalignment.
The feature extraction combines 63 time-series characterization methods that calculate 794 time-series features with feature mappings (e.g., skewness and kurtosis). Afterward, the significance of each feature is tested with a hypothesis test. Each feature is evaluated concerning its significance for predicting the target (e.g., lateral misalignment). A p-value is calculated for each feature to quantify the probability of a feature’s relevance for the target prediction. At last, multiple testing is applied for the identification of relevant features. Hypothesis tests like the Kolmogorov–Smirnov test are configured based on the target being binary. Finally, the Benjamini–Yekutieli procedure controls the FDR and identifies which hypotheses need to be rejected [11].
Even though a first reduction of the feature set is performed based on the p-value (< 0.05), further reduction of the feature set is necessary. For this reason, the coefficient of determination R2 is calculated for each feature with a linear model. This should allow for a linear correlation of the identified feature with the different misalignment types. As a result, the feature with the highest cumulated R2 and second lowest cumulated p-value (1.37 × 10−4) is chosen for the classification with the measurement line x1 (“agg_linear_trend__attr_rvalue__ chunk_len_50__ f_agg_min” [12]).
The feature can be explained as follows (see Fig. 3): For the calculation of the aggregated linear trend (agg_linear_trend), each height profile is divided into 50 segments (= chunks) (chunk_len = 50). The data of each segment is aggregated over the minimum in a single data point per chunk (f_agg = min). This reduces the number of measurement points to the number of segments. A linear least-squares regression line is calculated for the remaining data points, described by attributes like the Pearson correlation coefficient r (attr = rvalue). Here, the feature is named correlation coefficient r. The correlation coefficient r is dimensionless and describes a linear relationship between two variables:
Schematic representation of the feature calculation (aggregated linear trend) in the example of a height profile. Division of the height profile into N segments (segmentation). The minimum of each segment b (e.g., for segment a) is determined via an aggregation function and condensed here (aggregation). The summarized data can then be described using a specific attribute of the linear least-squares regression line c (correlation coefficient)
In this case, it is the linear trend of the height information z along the height profile position y. The correlation coefficient r can take values between negative 1 and positive 1. The absolute value 1 means a full linear relationship of the variables, whereas the value 0 signifies no linear relationship between the variables.
This feature should allow for the identification of misalignment types and electrical resistance based on surface topographical information.
Further measurements are necessary for an assessment of the offset categories and electrical resistance of the hairpin connection. Computer tomography (CT) measurements (General Electric Type Phoenix 180 kV) with a resolution of 12 µm enable insights into two areas: First, the analysis of the welding bead as a cut-section in 2D as well as in a whole in 3D. Second, the assessment of pores in the weld which may influence the resulting electrical resistance. The electrical resistance R can be calculated from the electrical resistivity of the material ρ, the length l, and the cross-sectional area of the conductor A:
The electrical resistance of the hairpin connection is determined over the ratio of the voltage U and the electrical current I with a micro-ohmmeter (T&R DMO 200) at a constant 200 A. Resistance measurements are repeated three times for each sample, have a resolution of 0.1 µΩ, and show a small variance coefficient of 4.3% over 20 measurements.
3 Results and discussion
In this section, we present results demonstrating the prediction of electrical resistance in hairpin connections based on surface topographical information. First, we discuss the influence of each misalignment type on the electrical resistance qualitative with X-ray measurements and quantitative with electrical resistance measurements. Second, we discuss the applicability of the identified feature for the classification of misalignment types. Third, we discuss the ability of the identified feature for the determination of the electrical resistance.
3.1 Influence of the misalignment on the electrical resistance
Weld results for each misalignment type as well as a reference weld can be seen in Fig. 4. Pores are detected for all misalignment types and did not result in an impact on the electrical resistance.
Qualitative analysis of the weld topography by misalignment types with X-ray measurements indicating the size of pores in false colors and inline camera images showing the top view of the weld result. a shows a reference weld, b shows the axial misalignment type, c shows the radial misalignment type, and d shows the lateral misalignment type
A reference measurement for a good hairpin weld can be seen in Fig. 4a. The welding bead is formed as a symmetrical pearl (the standard for a good weld [8]). Figure 4b shows the weld result for an axial misalignment of 3.6 mm between both joint partners. The resulting welding bead is skewed towards the lower joint partner both being molten and connected. It can be assumed that most of the molten material on the lower joint partner may originate from melt flow from the upper joint partner likely due to the position of the upper joint partner in the focus position. The lower joint partner has a lower energy input by the processing laser and is unlikely to contribute. Figure 4d shows a weld with a lateral misalignment of 1.6 mm giving a relatively flat welding bead. Only pin A is fully molten, whereas pin B is partially molten. This is because pin B is not within the laser weld contour. The molten material from pin A flows in the laser weld direction into the gap between pin A and pin B and solidifies. An example for radial misalignment with a gap of 0.8 mm is shown in Fig. 4c, resembling the welding bead is like the welding bead of the lateral misalignment: relatively flat and left-skewed. The surface topography shows a small bulge between the two pins as molten material can flow into the gap. This is possible as the processing laser remains in a constant welding path. The constant processing laser path results in fully molten material of pin A in comparison to pin B as only pin B was moved to introduce the misalignment. This meant pin B remained intact at its outer contour.
Figure 5 shows the electrical resistance for each misalignment type. The reference weld with no misalignment shows the lowest electrical resistance values with a mean of 3.1 µΩ. Increasing axial misalignment up to 4 mm shows only a slight trend towards increasing electrical resistance. The mean electrical resistance of 3.3 µΩ remains in the order of the reference measurements. A full connection with the wetting of both joint partners is possible for axial misalignments. Due to this, the length and the cross-sectional area of the conductor remain unchanged for axial misalignments up to 4 mm showing a relatively constant electrical resistance. Lateral and radial misalignments show a stronger impact on electrical resistance. Radial misalignments exhibit a strong linear correlation between the misalignment and the electrical resistance. The resistance is at an increased level for offsets between 0.2 and 1 mm. Latter offset is reduced to two analyzed samples due to poor contacting and consequently shows the highest electrical resistance above 8 µΩ. The increase in electrical resistance for radial misalignments can be explained by the increasing air gap between both pins which works as an insulator. At last, lateral misalignment also exhibits an increase in electrical resistance for increasing offset. However, misalignments between 0.4 and 1.2 mm result in similar values in electrical resistance like the reference. A strong increase in electrical resistance only can be found for an offset of 1.6 mm. Large lateral offsets lead to reductions in the cross-sectional area of the conductor, increasing electrical resistance.
To conclude, the electrical resistance of reference welds is shown to be lowest when compared to misaligned welds. Lateral and radial misalignments show a trend towards increasing electrical resistance for increasing misalignment and therefore defective welds. Axial misalignments did not exhibit a relevant increase in electrical resistance for the given data. A further increase in electrical resistance can be expected for axial misalignments in the case of no wetting of both joint partners.
Each misalignment type shows specific surface topographies in comparison to reference welds. Welds with high electrical resistance tend to show a flat surface, whereas axial misalignment and reference welds with lower electrical resistance exhibit strongly skewed or round surface topographies (compare Fig. 4). In the following, it is necessary to derive a surface topographical feature that allows for identifying defective welding results based on the surface topographical information.
3.2 Correlation between the misalignment and the identified surface topographical feature
The correlation coefficient r is used for the description of the topographical information based on the evaluation by the FRESH algorithm. Figure 6 shows the correlation coefficient r for reference welds, axial, radial, and lateral misalignment.
The correlation coefficient r for the reference weld ranges from − 0.17 to 0.09, with a mean value of 0.0. A correlation coefficient of 0.0 is expected due to the symmetrical round shape of the weld surface. The correlation coefficient r increases or decreases towards a value of + 1 or − 1 for a linear trend of the height profile. The value is positive or negative depending on whether the welding bead is skewed to the left or right, respectively. All misalignment types show a good linear correlation of the correlation coefficient for increasing offset and are in accordance with the identified deviations of surface topography from the reference weld. Small misalignments up to 0.8 mm for axial misalignments as well as offsets up to 0.4 mm for lateral and axial misalignments cannot be distinguished from a reference weld. Maxima of radial and lateral misalignments are in the order of an absolute value of 0.75, whereas the feature reaches a maximum value of 0.45 for axial misalignment. These maxima are reached at 1.6 mm for lateral misalignment, at 1.0 mm for radial misalignment, and 3.6 mm for axial misalignment. This shows a stronger influence of radial and lateral misalignment on the resulting surface topographical shape in comparison to axial misalignments. Radial and lateral misalignments also showed a stronger impact on the electrical resistance (compare Fig. 5). From these measurements, a correlation between electrical resistance and surface topographical feature should be possible. Deviations from the 0.0 value indicate a deviation from the symmetrical weld pearl and may indicate an increase in electrical resistance.
3.3 Correlation between electrical resistance and the identified surface topographical feature
For a prediction of the electrical resistance based on the surface topographical shape of the welding bead, a correlation between electrical resistance and the identified feature is necessary. For further analysis, only the absolute value of the correlation coefficient is considered, as the sign of the feature contains only the information whether pin A or pin B shows the relative offset. The absolute correlation coefficient depending on the electrical resistance can be seen for all misalignment types in Fig. 7.
Reference measurements with an ideal symmetrical weld pearl and correlation coefficient of 0.0 show electrical resistances in the range from 2 up to 4 µΩ. This range is the tolerance band for reference welds and is not expected to be differentiated by the correlation coefficient. The correlation coefficient for axial misalignments shows the smallest trend towards increasing electrical resistance in comparison to lateral and radial misalignment. This is in line with data presented in Fig. 5, where the axial misalignment shows the smallest influence towards increasing electrical resistance. Apart from one stray bullet, the electrical resistance remains below 6 µΩ for a correlation coefficient below 0.5 for axial misalignments. Same indication can be found for radial and lateral misalignments. Here, a correlation coefficient above 0.5 indicates an electrical resistance above 6 µΩ. The trend for axial misalignments gives rise for assuming a similar relationship between electrical resistance and correlation coefficient.
In consequence, the surface topographical feature shows good potential for identifying welds with high electrical resistance. A prediction of “bad” welds with high misalignment and electrical resistance above 6 µΩ is possible with an absolute feature value above 0.5. “Good” welds with 5 µΩ and below can be identified in the regime of reference welds with an absolute feature value below 0.2. We performed additional tests to approve this hypothesis. As misalignments do not occur isolated in practical application, we performed a proof-of-concept with three welds that exhibit a combination of all misalignment types (axial misalignment 0.8 mm, lateral misalignment 0.4 mm, radial misalignment 0.2 mm). This configuration resulted in feature values r between 0.05 and 0.18 with an electrical resistance R between 4 and 5 µΩ meaning the hypothesis holds true. Limitations of this hypothesis include indeterministic area for feature values between 0.2 and 0.5, dependence of the feature value on the boundary conditions of the experimental setup (e.g., pin size and number of measurement points), and insufficient number of experiments that exhibit a combination of all misalignment types. Further experiments are necessary to identify a cohesive hypothesis for the correlation between surface topography and electrical resistance requiring the consideration of different hairpin geometries, measurement strategies, and measurement resolution.
4 Conclusion
In this work, experimental work was performed to assess the influence of misalignments in copper pin-pairs on the electrical resistance. It was shown that radial and lateral misalignments have a bigger impact on the resulting electrical resistance than axial misalignments. This is due to the wetting of both joint partners for axial misalignments, whereas radial and lateral misalignments increase the electrical resistance due to an increase in electrical resistivity by an air gap and a reduction in the cross-section of the conductor.
Inline OCT measurements offer surface topographical information of the welding bead. The height profiles were analyzed with the FRESH algorithm for the identification of a significant feature. The most relevant feature is the correlation coefficient which indicates a linear trend in the height profile. Reference measurements with a symmetrical weld pearl show a correlation coefficient around 0, whereas misalignments with a skewed surface topography show increased absolute correlation coefficient values up to 0.75.
The identified correlation between the electrical resistance and different misalignment types can be depicted with the correlation coefficient. Defective weld results with electrical resistances above 6 µΩ can be identified with a correlation coefficient above 0.5, whereas reference welds with an electrical resistance below 5 µΩ can be identified with absolute values below 0.2.
Consequently, a quantified separation of process results is possible with the identified feature and enables the prediction of poor weld connections for the given experimental setup.
We expect these findings beneficial for the quality assessment in hairpin welding. Future work will focus on the identification of a universal feature to correlate the surface topography with the electrical resistance of the hairpins under arbitrary geometrical conditions. Further future work will consider the adaption of the methodology for alternative laser welding configurations and sensing technologies as well as the integration in an industrial context.
Data availability
The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Glaessel T, Seefried J, Masuch M, Franke J (2019) Process reliable laser welding of hairpin windings for automotive traction drives. In 2019 International Conference on Engineering, Science, and Industrial Applications (ICESI), IEEE, pp 1–6
Hartung J, Jahn A, Bocksrocker O, Heizmann M (2021) Camera-based in-process quality measurement of hairpin welding. Appl Sci 11(21):10375
Stadter C, Schmoeller M, Zeitler M, Tueretkan V, Munzert U, Zaeh MF (2019) Process control and quality assurance in remote laser beam welding by optical coherence tomography. J Laser Appl 31(2):022408
Stadter C, Schmoeller M, von Rhein L, Zaeh MF (2020) Real-time prediction of quality characteristics in laser beam welding using optical coherence tomography and machine learning. J Laser Appl 32(2):022046
Schmoeller M, Stadter C, Liebl S, Zaeh MF (2019) Inline weld depth measurement for high brilliance laser beam sources using optical coherence tomography. J Laser Appl 31(2):022409
Kogel-Hollacher M, André S, Beck T (2018) Low-coherence interferometry in laser processing: a new sensor approach heading for industrial applications. SPIE 10749, Interferometry XIX, vol. 10749. International Society for Optics and Photonics, p 1074912. https://doi.org/10.1117/12.2501295
Hartung J, Jahn A, Stambke M, Wehner O, Thieringer R, Heizmann M (2020) Camera-based spatter detection in laser welding with a deep learning approach. In Forum Bildverarbeitung 2020. KIT Scientific Publishing, p 317
Baader M, Mayr A, Raffin T, Selzam J, Kühl A, Franke J (2021) Potentials of optical coherence tomography for process monitoring in laser welding of hairpin windings,” in 2021 11th International Electric Drives Production Conference (EDPC), IEEE, p 1–10
Dupriez ND, Denkl A (2017) Advances of OCT technology for laser beam processing: precision and quality during laser welding. Laser Tech J 14(4):34–38
Christ M, Kempa-Liehr AW, Feindt M (2016) Distributed and parallel time series feature extraction for industrial big data applications. arXiv preprint arXiv:1610.07717
Christ M, Braun N, Neuffer J, Kempa-Liehr AW (2018) Time series feature extraction on basis of scalable hypothesis tests (tsfresh–a python package). Neurocomputing 307:72–77
Christ M, Braun, N, Neuffer J, Kempa-Liehr A. “tsfresh.feature_extraction package.” https://tsfresh.readthedocs.io/en/latest/api/tsfresh.feature_extraction.html. Accessed 15 Feb 2022
Funding
Open Access funding enabled and organized by Projekt DEAL. The authors gratefully acknowledge funding of the Erlangen Graduate School in Advanced Optical Technologies (SAOT) by the Bavarian State Ministry for Science and Art. The authors received research support from Vitesco Technologies Germany GmbH.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics approval
The authors respect the ethical guidelines of the journal.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Will, T., Müller, J., Müller, R. et al. Prediction of electrical resistance of laser-welded copper pin-pairs with surface topographical information from inline post-process observation by optical coherence tomography. Int J Adv Manuf Technol 125, 1955–1963 (2023). https://doi.org/10.1007/s00170-022-10796-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-022-10796-x