1 Introduction

Industrial articulated robots are one of the key enablers of modern manufacturing environments. They are characterised by flexibility and lower cost per unit of working space compared to other specialised machinery such as machining centres. These capabilities have allowed the integration of industrial robots across important industries in a variety of applications, and commodities such as consumer electronics, industrial machinery, or vehicles, since 1961 [1].

Some of the most significant disadvantages of articulated industrial manipulators in contact applications, such as robotic milling [2], are their comparably lower accuracy [3] and higher vibrations [4] in contrast to the benchmark machinery used for these applications. The improvement of positioning accuracy is the subject of the study of robot calibration [5]. Positioning accuracy is the distance between the commanded and the attained position of an articulated robot’s end effector (EE) [6]. As described by Mooring [7], robot calibration intends to improve the positioning accuracy by:

  1. 1.

    Modelling the kinematics (imperfect geometries and configurations [8] as well as gear backlash [9]) and non-kinematic parameters (joint and link compliance [10]) and thermo-elasticity errors [11]

  2. 2.

    Measuring the positioning accuracy of the actual robot [12]

  3. 3.

    Identifying its model parameters from the measurements [13]

  4. 4.

    Implementing the model parameters to optimise the accuracy of the manipulator [14].

Robot original equipment manufacturers (OEMs) offer working space calibration services to improve the mean and maximum positioning accuracy to typically less than 0.5 mm and 1.0 mm [12] for all the robot working space.

Contact applications [15] such as machining [16] and especially high material removal rate operations [17], require tight workpiece tolerances. They commonly demand an accuracy better than ± 0.25 mm on the location of features. This may require calibration for operating spaces rather than the OEM calibration for the working space [18]. This operating space calibration, done for a limited set of manipulator configurations in close vicinity, should yield a local optimum in positioning accuracy.

Garnier and Subrin [19] provided recently a summary of measurement instruments and procedures used for compliance calibration. All the described measurement procedures evaluate the industrial manipulator in static configurations and follow ISO 9283 [6] recommendations. These measurement procedures are less complex and minimise the uncertainty associated with the manipulator’s configuration. However, when the actual contact application is performed, geometric and non-geometric (motion dependent) errors contribute to the robot’s positioning accuracy [20]. Therefore, Theissen et al. [21] proposed a measurement scheme in which the industrial manipulator moved at velocities from 50 to 250 mm s− 1. In preceding research work, the authors reported an apparent difference between static and quasistatic (QS) deflections of industrial manipulators. To investigate this phenomenon further, this article analyses and quantifies the effect of Cartesian velocity on the measured deflections of industrial manipulators to evaluate the suitability of quasi-static stiffness measurements for robotic compliance calibration.

This paper is organised as follows: Section 2 discusses the concept and the rationale for measurements under motion. Section 3 summarises the experimental measurement procedures carried out to analyse and quantify the effect of velocity. Section 4 focuses on the measurement results as well as an analysis of the validity of the measurement results from a metrological point of view.

2 Quasi-static compliance

The mechanical stiffness of a system can be defined as its capacity to sustain loads, which results in a change in its geometry [22]. The magnitude of a structure’s mechanical stiffness depends on the frequency of the displacement, vibration, or excitation force. This magnitude is minimal, close to or at an eigenfrequency of the mechanical structure. The inverse of stiffness is named compliance.

This article differentiates between static and quasi-static deflections. The static deflections are measured at discretised static configurations along trajectories, while the quasi-static deflections are measured under motion along the same trajectories. Thus, in the static state, the wrenches and the deflections have a frequency component at 0 Hz. In the quasi-static state, the wrenches and the deflections have frequency components higher than 0 Hz and lower than approximately 10% of the first eigenfrequency of the industrial manipulator [23, 24]. In other words, this article uses the terminology quasi-static to indicate that the machine under investigation is moving. At the same time, the frequency components of the displacement and the excitation force are at least five to ten times smaller than the first eigenfrequency of the system. In this frequency range, it should be feasible to approximate the behaviour of the mechanical system accurately through static models instead of dynamic models. This approximation can be visualised in Fig. 1. The dynamic compliance of the industrial manipulator remains almost constant close to 0 Hz and up to 5 Hz, while it starts changing and then increases significantly close to the first eigenfrequency at approximately 14 Hz.

Fig. 1
figure 1

Dynamic compliance of an ABB IRB 6700 measured at [625 − 950 1300]mm in RBCS

Full size image

Other authors have used the term quasi-static to indicate that the robot [2] or machine tool [25] are moving during the measurement phase. In that sense, the term quasi-static compliance refers to the parameterisation of a compliant manipulator model by using a tuple, which consists of the configuration in terms of joint angles Θ, the quasi-static wrench WQS, and the deflection ΔXQS vector, as follows:

$$ \left\Vert K_{\theta}^{-1} J({\Theta})^{T} \cdot W_{QS} - J({\Theta}){\Delta}{X}_{QS} = 0 \right\Vert^{2} $$
(1)

Here K𝜃 denotes the diagonal joint stiffness matrix, and the term J(Θ) expresses the configuration of the articulated robot as a function of the joint angles. In short, the quasi-static compliance modelling phase may adopt any model, from the basic six degree of freedom (DOF) torsional spring [26] to the elaborate 258 DOF link and joint compliance model [10], but uses measurement data from a quasi-static measurement instead of a static one to identify the model parameters.

3 Methodology

3.1 Measurement procedure — description

The proposed measurement procedure quantified the QS deflections. Those are the EE deflections while moving along a trajectory. The trajectories under investigation were circular due to the design constraints of the utilised measurement instrument, the loaded double ball bar (LDBB) [27]. A more detailed description of the measurement procedure can be found in [21] and [28].

This work aimed at quantifying the influence of varying velocity of a QS measurement on a single industrial articulated robot (ABB IRB 6700). Furthermore, it applied the same QS measurement for a single Cartesian velocity on two more manipulators (KUKA KR 270 and a Stäubli TX 200) to evaluate the transferability of the findings.

The experiments comprised measurements with an ABB IRB 6700 at 0, 1, 5, 50, 150, and 500 mm s− 1. The label 0 mm s− 1 was meant to express a static measurement in accordance with the ISO standard. There were two additional sets of measurements performed on a KUKA KR 270 and a Stäubli TX 200 at 0 and 50 mm s− 1. The measurement of the deflections on the ABB IRB 6700 was recorded using both a laser tracker (LT) and the linear variable displacement transducer (LVDT) located inside the LDBB. The LT’s maximum sampling rate is 1000 Hz. Thus, the potential incorrect attribution of the movement as deflection may lead to significant errors at velocities from 150 onwards, e.g. close to 500 μm for LT measurements at the velocity of 500 mm s− 1. Therefore, no data is presented from the LT for the velocities of 150 and 500 mm s− 1.

In short, the measurement procedure provided data to identify the wrench WQS and the quasi-static deflections ΔXQS at a manipulator measurement configuration Θ. These data were synchronised to avoid a biased attribution of the former two to the latter. This is discussed in detail starting in the next Section 3.2.

The manipulator measurement configurations (MMC) were generated using offline programming. The circular trajectory for these experiments and the poses along the trajectory can be visualised through coordinate systems in Fig. 2. For the static measurement, these MMCs correspond to the discretised Cartesian poses along the circular trajectory. Configuration or target T01 and T37 were at the same position, meaning that the static circle path had the same start and end point.

Fig. 2
figure 2

The targets along the circle for the static (above) and QS measurement (below). The targets along the circle’s first quadrant are exemplified for the static measurement

Full size image

For the quasi-static measurement, there were only four nominal MMCs. These were the vertices on two arcs that described a circle using the circular movement functions, namely, ABB’s RAPID MoveC, KUKA’s KRL CIRC, and Stäubli’s VAL3 movec. The whole trajectory was created to obtain several MMC in between the vertices, which equaled the number of measurement points along the trajectory. First, the manipulator executed a trigger movement of 3 mm in the Z-axis direction at the start point of the circle. Then, the manipulator moved two times clock-wise (CW) about the same circular trajectory (see Fig. 3).

Fig. 3
figure 3

LDBB quasi-static manipulator measurement; CW signal was the sum of the measurement data and the angular overshoot (AOS) movement

Full size image

The quasi-static wrench exerted multiple force components simultaneously. The Z-axis component’s magnitude equalled approx. \(\frac {1}{3}\) of the total load, while the remaining \(\frac {2}{3}\) were split between the X- and Y -axis components. Their contribution depended on the position of the LDBB along the circular trajectory [28]. For the static measurement, once the manipulator reached a stable position, the static loads were induced at the tool centre point (TCP).

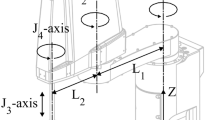
The measurement application point (MAP) for the LVDT is located at the TCP of the EE. The spherically mounted retroreflector (SMR), target for the MAP of the LT, is located close to the TCP. The MAPs for the LVDT and the LT can be visualised in Fig. 4. The experiments on the KUKA KR 270 and Stäubli TX 200 were measured using only the LVDT. Additional parameters such as the position of the centre of the circular trajectory in the robot base coordinate system (RBCS), AOS, and apparent load (AL) for each of the three industrial manipulators can be seen in Table 1. Each industrial manipulator has different boundary constraints in terms of time, operating space availability, and control system. This led to varying implementations of the measurement procedure on each manipulator. Each measurement was repeated five times.

Fig. 4
figure 4

Visualisations of the three industrial manipulators with their EEs and MAPs. Robot (a) has a dummy tool which has one MAP for the LT close to the TCP, and the MAP for the LVDT is in the TCP. Robots (b) and (c) are equipped with motor spindles for machining

Full size image
Table 1 Experimental conditions for the comparison of static and quasi-static deflections of three different industrial manipulators
Full size table

3.2 Measurement procedure — error separation analysis

This subsection evaluates all factors associated with the measurement procedure that could have introduced bias to the measurement data.

3.2.1 Transient measurement data

In the context of this work, transient measurement data can be defined as data that was acquired from the industrial manipulator during the change from equilibrium or steady state to a moving state. There were mainly two different kinds of transient phases in the measurement stages associated with loaded circular testing, which corresponded to acceleration and deceleration as well as trigger movements. For instance, for the measurement of quasi-static stiffness, the industrial manipulator is moving along a trajectory at a constant velocity [21]. At the beginning of the test, the manipulator had to accelerate until it reached constant velocity and, at its end, decelerate back to zero velocity. The measurement data captured during these stages contained contributions from the manipulator’s dynamics. This would have introduced bias in the identification of the static mechanical stiffness, as the model does not look to quantify the effect of the inertia and velocity terms. Hence, an overshoot travel, also known as AOS, is employed. The magnitude of the AOS selected was 180∘ as the transient behaviour was assumed to be contained within this domain.

Furthermore, the controller of the industrial manipulators under investigation and the measurement instrument did not communicate bilaterally. Even if they could communicate, there could have existed a significant delay [29]. Thus, trigger signals were employed to facilitate data synchronisation. Trigger signals are usually mechanical movements that involve the fast movement of the TCP by a significant distance compared to the measurand from the referenced starting position and orthogonal to the commanded trajectory. The trigger movement is usually employed at the measurement’s beginning and end to highlight the measurement data. Both the AOS and the trigger movement can be visualised in Fig. 3.

3.2.2 Mechanical base load reference

All measurements presented in this analysis featured a mechanical base load reference (MBLR). The deflections of the industrial manipulators were not derived as the difference between the unloaded and loaded configuration but as the difference of a loaded configuration with respect to another loaded configuration at the MBLR. This approach can also be considered as a pre-loading of the components in the force loop [25]. This procedure was meant to reduce errors in the measurement resulting from play or backlash (out of the scope of this work). Moreover, some industrial manipulators may exhibit hysteresis that could be reflected in the measurements if the comparison included both CW and counter clock-wise (CCW) trajectories. Therefore, this comparison was excluded from this investigation.

In general, the measurements were intended to capture the compliance of the industrial manipulator without contributions from other error sources. Thus, a suitable MBLR needed to be selected. By default, the MBLR in all tests equalled 125 N. The MBLR was adjusted depending on the payload and reach of the industrial manipulator if additional information was available. The wording AL is used to highlight the idea that a MBLR has been used. An AL of 250 N indicated that the system is loaded with 375 N, but the deflection was estimated with respect to the MBLR of 125 N. This is visualised in Fig. 5. The figure is a schematic reproduction of the measurement data, which means that the data is qualitatively accurately represented, but not quantitatively. The magnitudes were changed to highlight the observations. The figure shows the two reference trajectories at 50 and 500 mm s− 1 as well as the trajectories for the AL of 250 and 500 N. It can be assumed that at lower velocities, the kinematic errors predominantly affect the position of the reference trajectory. In comparison, dynamic and controller errors should be more dominant at higher velocities. The concept of the MBLR should ensure that these error sources do not bias the compliance evaluation, as one would expect the kinematic and control errors for the trajectory at AL of 125 and 50 mm s− 1 and AL of 250 and 50 mm s− 1 to have the same magnitude. Therefore, their difference can be considered as an accurate reflection of the compliance of the industrial manipulator. In addition, it could be seen in Fig. 5 that the reference trajectories were offset from one another based on their velocity. This shift of the reference trajectory did not introduce an error because the deflections of the industrial manipulators are calculated as the relative difference to each corresponding (velocity-wise) reference trajectory.

Fig. 5
figure 5

Schematic representation of the measurement data at a velocity of 50 and 500 mm s− 1 (solid and dashed line, respectively) and ALs of 250 and 500 N. The circle centers of the 50 and 500 mm s− 1 circular trajectories appear as offset due to the change in velocity (a phenomenon which was observed from the measurements)

Full size image

3.2.3 Measurement instruments

The measurement instruments require the ability to exert a controllable mechanical load while measuring the deflection in terms of distance and position. This subsection evaluates the influences of the measurement procedure on the deflection measurement and the mechanical load exertion.

This article presented measurement data, which were obtained from a LVDT as well as a LT. The measurements were performed using a Micro-Epsilon DTA-3G8-3-CA®; [30] LVDT for all velocities and with a Leica AT901®; [31] LT up to a velocity of 50 mm s− 1. The sampling rate of the measurement instruments was selected to ensure that at least one data point was measured at a nominal travel distance of 50 μm, i.e. at a Cartesian velocity of 50 mm s− 1 the sampling rate equals 1000 Hz. For both measurement instruments, there was no technical specification about their accuracy for dynamic measurements such as the QS measurements used in this work. The uncertainty associated with the position measurement of the LT and the distance measurement of the LVDT are stated in Table 2.

Table 2 Investigated type B uncertainty contributors associated with the proposed measurement procedure. It is assumed that these uncertainty contributors are normally distributed
Full size table

The LDBB induces load by controlling the pressure in the chamber using a proportional pressure control valve (PPCV) [32]. The PPCV and its measurement systems are not affected by this static load, as the load is not exerted on them. However, the load fluctuated for the quasi-static measurement at higher velocities. For a trajectory at 50 mm s− 1, there existed a steady-state control error but no fluctuations. The load fluctuated within approximately 2% at 500 mm s− 1. The force along the static and quasi-static trajectory was also measured on the side of the link (TL), by mounting the TL to a Kistler 9255C Dynamometer®; [33]. The test measured the loads on the TL for both the static and quasi-static measurements. The results differed by less than 1 N on average for all ALs. This experiment was repeated five times. The uncertainty associated with the control of the magnitude of the static force to push between the two objects is stated in Table 2.

4 Results and discussion

The effect of the velocity of the movement on the difference between static and QS compliance of industrial manipulators is shown in Figs. 6 and 7 and Table 3. The figures illustrate the average Cartesian deflections and uncertainty for the static and QS procedures for the ABB IRB 6700. Figure 7 shows that the static and QS deflections are significantly different in magnitude but similar in trend. The same phenomenon was observed in two other manipulators included in the study. Table 3 summarises the average deflections and their uncertainty for the static and the QS measurement data for the three industrial manipulators. The static measurement data were considered the reference, see the column Static 0 mm s− 1. It can be seen that for each QS measurement, the deflections are greater than for the static deflections. At 50 mm s− 1, the QS deflections are 8 to 17% bigger than the static deflections.

Fig. 6
figure 6

Comparison of the average static deflection and QS deflections measured at different speeds for the IRB 6700. The static measurement data were considered as the reference (100%)

Full size image
Fig. 7
figure 7

Mean Cartesian deflections of the ABB IRB 6700 and their uncertainty in the RBCS

Full size image
Table 3 Comparison of average static and QS deflections of three different industrial manipulators
Full size table

For the ABB IRB 6700, see Fig. 6, the results suggest that the Cartesian velocity has a proportional relationship to the measured deflections. The LVDT data imply that beyond a velocity of 50 mm s− 1, the higher the velocity, the higher the QS deflections. Additionally, both the LVDT and LT data suggest that for velocities between 1 and 50 mm s− 1, a constant change in magnitude can be expected.

Additionally, as shown in Fig. 5, the positions of the circular trajectory varied at different velocities. The smaller the levers created by the configuration, the higher the robot’s Cartesian stiffness [10]. Other authors have attributed the difference in the deflection of the robot to link weights and to the effect of the gravity compensator [34]. Therefore, a change is expected in the Cartesian stiffness and measured deflections as the manipulator is not always measured at the same position. The same notion of position shift also applies to the repetition of the circular trajectory at each velocity as defined by the path positioning repeatability of the industrial manipulator [6]. Under the assumption that it is only the change in configuration 𝜃 that influences the Cartesian stiffness KX, the change in Cartesian stiffness dependent on the change of the configuration can be quantified according to Eq. 1. For the investigation of the ABB IRB 6700, the change in configuration from the QS trajectories of 1 to 500 mm s− 1 equalled on average a positioning change of 1.5 mm. Equation 1 was used to simulate the effect of the change in position on the expected Cartesian deflection with the following set of parameters: normally distributed translational offsets with an average of ± 2 mm and normally distributed orientation offsets with an average of ± 20 m deg in the Cartesian components at 100 000 samples around the circular trajectory. According to the simulation results, this systematic change in the configuration should have contributed with less than 1% to the difference in deflection between the static and QS trajectories.

Theoretically, as the excitation frequencies in the QS wrench or the manipulator’s movement are well below the first eigenfrequency, one would expect no significant differences between static and QS deflections. The frequency components of the quasi-static measurements at the different velocities have been identified using a fast Fourier transform (FFT) of the LVDT and LT measurement data. The maxima of the spectral magnitude occur at frequencies less than 1 Hz. Nevertheless, the performed measurements have shown the opposite. Thus, it could be argued that the combined effect of manipulators mechanics in terms of the inertial forces, and backlash as well as the control in terms of the control loop gains, and the criterion of passage of the position control might explain the difference between the static and QS deflections. This difference can be perceived as a relative loss of stiffness between static and moving industrial articulated robots. An error separation analysis of these effects can support the understanding of the systematic difference between static and QS deflections. This work presented how the QS measurement procedure might have influenced the measurand, and it was not possible to find an associated systematic bias.

4.1 Uncertainty

The investigated type B uncertainty contributors, presented in Table 2, can be considered insignificant in comparison to the measurands. This is expressed through the combined expanded (k = 2) uncertainty presented in Table 2. The measurand is assumed to be normally distributed. This information has been used to create the visualisation of the error bars in Fig. 7 and to calculate the uncertainty presented in Table 2.

5 Conclusion

The work presented in this article quantifies the influence of Cartesian velocity on quasi-static deflections of industrial manipulators and analyses how the QS measurement procedure could have influenced the presented measurands. For all industrial articulated robots in this experimental investigation, the static and quasi-static deflections were significantly different in magnitude but similar in trend, being the quasi-static deflections larger. No systematic error in the measurement procedure could be found to explain this difference.

From the authors’ points of view, this implies that the manipulator’s calibrated compliant model obtained according to ISO 9283 may have systematic inaccuracies associated with the robot motion. Therefore, a calibrated compliant manipulator model derived from a QS measurement may yield more accurate estimates for trajectory optimisation compared with conventional static stiffness identification procedures. A successful implementation of quasi-static compliance calibration requires a measurement procedure that produces accurate results with fewer resource requirements. For this scheme to be economically viable, it is preferential to perform the calibration faster, i.e. reducing the required downtime of the industrial manipulator. In a quasi-static compliance calibration, the downtime consists of the setup and measurement time. The measurement time is proportional to the velocity of the motion. Therefore, the effect of the Cartesian velocity on the measured deflections was investigated. According to the results obtained, the magnitude of the quasi-static deflections had a proportional relationship to the Cartesian velocity above above 50 mm s1. Based on the observed influence of the velocity on the load-induced deflections, the suggestion is to perform a quasi-static compliance calibration that considers not only the combination of force and motion, but pays special attention to the Cartesian velocity of the trajectory for the intended application.