1 Introduction

Welding residual stress is a major issue in welded joints, as in service it may combine with the applied stress to cause unexpected failure or shorten the component lifetime. It is a fact that residual stress could be detrimental to the integrity of components and structure being responsible of brittle fracture, buckling deformation, reduced fatigue life, and stress-corrosion cracking; extensive reviews on the various aspects of the problems related to the onset of residual stresses in welding have been given by Masubuchi [1] and Radaj [2]. Hence, the presence of residual stresses is currently taken into account in the assessment of engineering components under working conditions [3]. However, the most common practices, such as overdesigning, give rise to weight and cost increases; therefore, residual stress prediction and control would be desirable in a context of stable service performance and economic efficiency. In this respect, many efforts have been devoted to optimize welding parameters in order to obtain effective welded joint with the required quality, minimizing residual stresses and distortion [4].

Residual stress in welding is mainly the result of a sequence of thermal contractions and expansions due to an uneven temperature distribution in the workpiece [5]. The portions of material inside the weld joint tend to expand when heated and shrink as they cool: as a result, residual stress develops because the nearby material pulls back to maintain a bond with the shrinking weld material. Since residual stress is not caused by external loads, the associated stress field on a macro-scale has necessary resultant force and moment equal to zero: in general, tensile stresses take place around the weld pool and are perfectly balanced by compressive stresses, lower and widely distributed over an area that extends farther from the weld line [6].

The welding residual stress distribution is rather complex, and its determination is an arduous task [7]. It cannot be measured directly, and as consequence, other methods have been considered, such as measurements of strains or strain increments by extensometric gauges [8] or by digital image correlation technique [9], deformations at the atomic level by X-ray [10] or neutronic diffraction [11], or indirect methods based on the detection of alternative physical quantities, such as magnetization [12], or propagation velocity of elastic waves [13].

As for designing of components and prediction of their lifetime in service, several studies have been aimed at predicting the residual stress state due to welding. Advances in computational simulation techniques make it possible to tackle the simulation of the complex thermo-mechanical phenomena associated with welding processes, at the same time modeling with great accuracy the geometry of welded joints, which significantly affects the residual stress distribution and magnitude [14]. Particularly, the use of the finite elements method (FEM), coupled with experimental verification, is the most widespread approach for welding deformation and residual stress assessment [15]. However, huge computation times are required for an accurate numerical analysis, since weld phenomena lead to transient problems with strong nonlinearity [16]. With regard to the considered configuration, a 2D FEM analysis can be performed under appropriate simplifying assumptions [17]. Therefore, in some case, 2D models have been utilized instead of more complex 3D simulations [18]. A further simplification can be achieved by carrying out an uncoupled thermo-mechanical FEM analysis [19]. Significant results in terms of shortening the calculation time can also be obtained by adopting models with high effective instantaneous heat sources coupled to coarser mesh density [20].

Despite the efforts made, some critical issues in numerical simulation of stress–strain cycles due to welding effects on joined materials still remain difficult to be overcame [21]. Particularly, transient thermal field, combined with mechanical constraints in joint geometry, and thermo-elastic–plastic response of materials, on which the evolution of thermo-mechanical strain depend as weld pool solidifies, remain too complex to be considered accurately.

In any case, a detailed analysis of the thermal field in the fused zone (FZ) and heat affected zone (HAZ) is needed to accurately set the preconditions for the development of the residual stress distribution, also taking into account the effect of the variation of the main thermo-physical properties with temperature. Recently, several studies have developed FEM simulations of the welding thermal field (for a review see the work by Marques et al. [22]). These numerical simulations require increasing computing capacity and time, according to the degree of accuracy of the mesh by which the joint is modeled [23], and need to be validated by experimental measurements that, by their nature, are specific of the considered welding conditions [24]. Furthermore, the direct estimation of thermal field needs considering both conduction and convection modes of heat transfer [25], and this further increases the complexity of the modeling, making the calculation more and more computationally intensive. This is the reason why conduction-based heat transfer models are widely used to predict the temperature field even in the most refined numerical simulations [21].

Concerning the specific case of laser welding, the approach based on the phenomenological laws of heat conduction, less complex from the point of view of the thermal field calculation, has also received substantial interest from the point of view of the development of analytical modeling [26]. According to this approach, also, the “keyhole” full penetration welding mode, characteristic of the high-power laser, can be simulated by means of mobile heat sources.

In the case of high-power laser beam welding, however, a model based only on heat conduction would not take into account the complex fluid dynamics phenomena inside the keyhole, which affect thermal distribution and are difficult to simulate analytically, even when trying to make the best use of alternative combinations of heat sources [27]. In order to compensate for the simplification inherent in the modeling carried out according to the laws of heat conduction, a parameterized multipoint-line system of thermal sources, fitted on the experimentally-detected weld bead profile, was introduced [28], and its potential in predicting final composition, solidification mode, and microstructure of weld, was proven [29].

The theoretical bases for the evaluation of welding-induced residual stress by analytical modeling of the thermal field have roots in the first studies on the subject [30,31,32], and have been further outlined in a more recent past [33, 34], but they have rarely been applied to the detailed calculation of the distribution of residual stresses [35].

The proposed work presents a novel simplified approach to the theoretical estimation of residual stresses distribution due to laser welding, which use the conduction-based analytical method fitted on the experimentally-detected weld bead profile, previously introduced in [28], to evaluate the thermal field. Reference is made to the case of CO2 laser beam single pass on two squared edged AISI 304L plates 10 mm thick, which were butt-positioned. The “keyhole” full penetration welding mode, characteristic of the high-power laser, was simulated by means of a mobile conductive heat sources system whose parameters were chosen in order to generate a fusion profile that fits on the one detected experimentally.

The solution of the thermal field allows the analytical calculation of the distribution of the longitudinal residual stresses in two ways: one that makes use of a simplified formulation of the distribution, well known in the literature [6]; a second modality that, by defining a procedure for residual stress generation, based on a combined processing of thermal profiles and heating–cooling cycles and its mathematical modeling, allows the distribution of the longitudinal residual tensile stresses to be constructed by points with greater accuracy.

The latter approach, based on the detailed analysis of the thermal field in the base metal, assumes a perfect elastic–plastic behavior of the material in the residual stress generation mechanism, according the Masubuchi’s model [1], and takes into account the main thermo-physical and mechanical properties variations vs. temperature, whose effects on welding simulation have been demonstrated cannot be overlooked [36].

The paper is structured as follows: Sect. 2 describes the process and materials used, introduces the thermal field modeling, and defines the basic residual stress generation model; in Sect. 3, a detailed application to the analyzed experimental case is developed according to two different approaches for calculating the residual stress distribution, and the main results are reported; Sect. 4 presents the validation of results; final remarks on the substantial differences between the two approaches and their field of application are collected in Sect. 5.

2 Materials and methods

2.1 Process and materials used

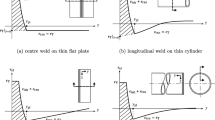
The welding of the plates, butt-positioned on a flat surface (Fig. 1a, b), was performed using a CO2 laser device and consumable inserts as filler material, according to a procedure that is easier to perform than using wire filler metal and also able to increase tolerance towards any geometric imperfections in the edge preparation or deviations of the beam alignment [37].

Fig. 1
figure 1

Sketch of the welded joint with mobile heat source and reference system positioning (a) and consumable inserts assembly (b)

Full size image

The process parameters are shown in Table 1. They correspond to an incident energy of the beam so high that the “keyhole” full penetration welding mode was obtained: the portion of irradiated material melts and vaporizes, forming a capillary cavity called “keyhole”, surrounded by molten metal.

Table 1 Welding process parameters
Full size table

The welding was carried out by means of a single pass on square plates with dimensions of 1000 × 1000 mm2, with a thickness of 10 mm. The base metal (BM) is AISI 304 L austenitic stainless steel, characterized by excellent weldability due to the low carbon content. The borders have been squared to allow the interposition of the filler material (FM) in the form of AWS 309 L consumable inserts (Fig. 1b). The compositions of the materials used are reported in Table 2.

Table 2 Compositions of base and filler metals (% weight)
Full size table

2.2 Thermal field modeling

The highly unstable processes that govern the “keyhole” phenomenon give it a dynamic behavior that involves considerable difficulties in modeling [38]. Thermal field models based on the laws of heat conduction neglect this aspect, and bring the advantage of using the analytic solutions developed starting from the well-known Rosenthal equations [39]. They describe the three-dimensional thermal field T(x, y, z) in a generic point of a solid, generated by mobile point sources, and the two-dimensional field T(x, y) generated by mobile sources distributed in line along the thickness of the medium (z axis), which in both cases move along the welding axis with constant speed v (m/s).

A modeling of this type, based on heat conduction, does not take into account the complex fluid dynamics phenomena that characterize the “keyhole” mechanism, and are very difficult to simulate analytically. To compensate for this basic simplification in the modeling, the simulation of the thermal field was obtained using a multipoint-line system of thermal sources previously proposed [28]. Using this approach, the actual heat input generated by the “keyhole” and its real effects on the melt pool and on the cross-sections of the joint are reproduced by fitting some parameters that define the layout and power distribution between the sources, on the profile of the fused zone, experimentally detected in a cross-section of the joint. The objective of the fitting is to calibrate the virtual system of the thermal sources in order to make the theoretical profile of the fused zone coincide as much as possible with the experimental one, in order to simulate as accurately as possible the effect of the real thermal source.

With this premises, the following formulation for the overall thermal field can be used, with reference to the mobile system xyz shown in Fig. 1a, integral with the point of incidence of the laser beam on the upper surface of the plates:

$$T\left( {x,y,z} \right) = T_{o} + \sum\nolimits_{i = 1}^{n} { \, \frac{{Q_{P \, i} }}{{c_{i} \pi \, k \, r_{P \, i} }}} \, e^{{ - \frac{v}{2\alpha }\left( {r_{P \, i} + x} \right)}} + \frac{{Q_{L} }}{2 \, \pi \, k} \, e^{{ - \frac{v}{2\alpha }x \, }} \, K_{o} \left( {\frac{{v \, r_{L} }}{2\alpha }} \right)$$
(1)

In Eq. (1), the first term To is the initial temperature of the system, which can be assumed equal to the room temperature or to a preheating temperature; the second term expresses the thermal field due to n point sources; the third term is due to the line source.

It also results that QPi (W) and QL (W/m) are respectively the power of the ith point source and the power per unit of length of the line source; v (m/s) is the welding speed; k is the thermal conductivity (W/mK); α is the thermal diffusivity (m2/s); Ko is the modified Bessel function of the second type of zero order; ci is a numerical coefficient equal to 2 or 4 for point sources placed respectively on the surface of the solid or inside the solid; rPi and rL (m) are respectively the radial distance from the ith point source, and from the line source, and are expressed as

$$r_{P \, i} = \sqrt {x^{2} + y^{2} + \left( {z - z_{P \, i} } \right)^{2} } \quad \quad r_{L} = \sqrt {x^{2} + y^{2} }$$
(2)

where zPi is the height of the ith mobile source with respect to the origin of the axes.

The fitting on the experimental profile of the fused zone allows to determine the values of the power coefficients γPi and γL, which distribute the overall power of the laser beam P between the point sources and the line source used, respectively, and the absorption coefficient η.

These parameters ultimately allow to calculate the powers QPi and QL delivered by each source, which appear in Eq. (1), by using the following expressions:

$$Q_{P \, i} = \gamma_{P \, i} \, \eta \, P \quad \quad Q_{L} = \gamma_{L} \, \eta \, P/z_{L}$$
(3)

where zL is the length of the line source.

The point solutions in the second term of Eq. (1) basically apply to infinite or semi-infinite workpieces. Their use can be extended to plates of finite thickness if the latter are thick enough, that is, for the effect on the temperature distribution of the lower boundary to be negligible. According to Dowden, this condition occurs if the thickness h of the plate is significantly greater than the factor 2α/v [40]. Otherwise, the use of corrective approaches in point sources modeling, such as the “method of images”, is necessary.

2.3 Residual stress generation

The material subject to fused welding undergoes localized heating; therefore, the resulting temperature distribution will not be uniform, because the weld metal and the heat-affected zone immediately close reach temperatures substantially higher than those of the thermally unaffected base metal.

Considering the case of butt-welding of two plates (Fig. 2a), during the heat source travel, ahead the melt pool (above section 1–1) material is not yet interested by heating, and thus, the internal stress is almost zero. Stress is zero also in the weld pool (between sections 1–1 and 2–2) because the liquid metal cannot support loads; but in the solidified zone, between sections 2–2 and 3–3, the material is compressed since its thermal expansion is constrained by the surrounding metal that is at lower temperature. In this zone, the temperature is so high that the material reaches the yield limit. Far from the melt pool, between sections 3–3 and 4–4, the material is cooled down: as it attempts to shrink, tensile stresses are induced due to the constrain exerted by the neighboring material, which is not subject to the thermal cycle.

Fig. 2
figure 2

Schematization of the thermal effects in butt-welding of two plates by the three-bar model (a) and stress-temperature diagram in the weld bead (b)

Full size image

Typically, the process that leads to the residual stress onset and distribution is well described by the three-bar model [6] (Fig. 2a, on the right): the weld bead and the adjacent zones subjected to high temperatures are schematized by the thin central bar, while the lateral wider bars represent the material that is not affected by high temperatures. This model reproduces a constraint condition that opposes any deformation of the central bar, giving rise first to macrostress of compression (during the heating stage), and then of traction (during the final cooling). Generally, the two lateral bars have considerably larger sections; thus, they are subjected to stresses of opposite sign that are much lower than those arising in the central bar.

Assuming an elastic behavior of material, followed by a perfectly plastic stage once the yield strength is reached, the mechanism that leads to the onset of the longitudinal residual stress σx in the central bar can be interpreted using the model introduced by Masubuchi [1], subsequently formalized by Murakawa [41], and represented by the qualitative stress-temperature diagram in Fig. 2b. It should be noted that the curves represented in this diagram must take into account the effect of the temperature variation on the thermo-physical properties of the material, particularly the reduction of the yield strength σo and the Young’s modulus E, and the increase in the coefficient of thermal expansion λ, as the temperature increases.

With these premises, the conditions that can occur are the following:

  • Heating up to TA: Due to the dilatation, the central bar in A is subjected to a compressive stress E(TA) λ(TA) [TA–To], being E(TA) and λ(TA) the values of Young modulus and thermal expansion at temperature TA, respectively, and TA–To the increment of temperature respect to the initial temperature To. A subsequent cooling to the temperature To, along AO, occurs in the elastic field, and therefore leaves the material free from stress.

  • Heating up to TB: In this case, the stress due to thermal expansion reaches the compression yield stress of the material at TB temperature σo″(TB), and the following condition occurs:

    $$\sigma_{o}\,^{\prime \prime} \left( {T_{B} } \right) = E\left( {T_{B} } \right) \, \lambda \left( {T_{B} } \right) \, \left[ {T_{B} - T_{o} } \right]$$
    (4)

    TB is the limit temperature up to which the material remains in the elastic field, and therefore free from internal stresses at the end of cooling along BO.

  • Heating up to TC: When the material is heated beyond the limit temperature TB, it yields and enters the plastic field, and the compressive stress state stabilizes on the yield limit σo″(T), varying with it as a function of the temperature along BC. When cooled along CE, first, the compressive state reduces up to vanishes, and then, a residual tensile state arises, due to the constraint conditions that prevent the shrinkage of the central bar. In this case, at To, a longitudinal residual stress is established. It is quantified by the stress value corresponding to point E, that is lower than the tensile yield strength σo′(To), and can be expressed by:

    $$\sigma_{x} \left( {T_{C} } \right) = E\left( {T_{C} } \right) \, \lambda \left( {T_{C} } \right) \, \left[ {T_{C} - T_{o} } \right] - \left| {\sigma_{o}\,^{\prime \prime } \left( {T_{C} } \right)} \right|$$
    (5)

  • Heating up to TD: The heating temperature is so high that during cooling from D, the tensile yield strength curve is intercepted in F. Therefore, the stress state as the cooling continues, varies along FG; consequently, the final residual tensile stress in G is equal to the value of the tensile yield strength at To temperature σo′(To).

It can be concluded that temperature TB, defined by the equilibrium condition (4), constitutes the limit within which the material remains in the elastic field, and at cooling returns to the initial zero stress state; therefore, it is also the limit beyond which residual tensile stresses arise, the maximum value of which does not exceed the tensile yield strength value of the material at temperature To.

Equations (4) and (5) refer to the condition in which the central bar is completely constrained by the two lateral ones, and so the mismatch between them, due to the shrinkage of the former, completely turns into stress. This condition clearly occurs in the specific case analyzed (butt-positioned 1000 × 1000 mm2 square plates), as the stiffnesses of the two lateral bars are much higher than the stiffness of the central bar, due to the great difference in the areas of the corresponding cross-sections: assuming that the central bar represents the weld bead and the adjacent zones subjected to high temperatures, the lateral bars represent the large portions of the plates that are not affected by significant thermal variations (starting from a distance of about 30 mm from the welding axis, the heating of the plates due to the passage of the heat source is negligible [28]).

In general terms, the fully constrained condition in the three-bar model may not occur. In this case, to take into account that a part of the mismatch turns into deformation, it is possible to introduce in Eqs. (4) and (5) a multiplicative parameter β ≤ 1 that expresses the degree of restraint from the two lateral bars on the central one, as a function of their stiffnesses [41].

2.4 Experimental measurements

For the experimental validation of theoretical results, the hole-drilling strain gage method was used to measure the surface residual stress. This technique allows to assess the residual stresses present in a workpiece before drilling by measuring the relaxation due to metal removal [42]. The test procedure described in Micro-Measurements Technical Note TN-503–6 [43], which extends the basic ASTM E837 standard [44] to applications at higher residual stress (up to 70% of the yield strength of the material), was followed. Both procedures assume that the residual stresses are essentially uniform with hole depth.

Three-element strain gauge rosettes of CEA-06-062UM-120 type were used, with narrow grids to permit their close grouping on one side of the hole, facilitate positioning, and allow measurement closer to welds and adjacent holes.

A carbide-tipped cutter was used to drill blind holes with diameter Do = 1.6 mm in the center of the strain gauge rosettes; in compliance to the technical note, the depth was set equal to 0.4D = 2.052 mm (being D = 5.16 mm the grid central circle diameter), so sufficiently small compared to the thickness of the plates (10 mm). Calibration coefficients a and b equal to 0.126 and 0.358, respectively, corresponding to Do/D = 0.31 blind hole, were used to calculate the stresses by the measured strains.

3 Application and results

3.1 Analysis of the thermal field

As anticipated in Sect. 2.2, the thermal field model expressed by Eq. (1) can be applied to plate of finite thickness if the latter is significantly greater than the factor 2α/v. In the present application, this condition can be considered verified, as the ratio between the plate thickness h and the factor 2α/v exceeds 18 (being h = 10 mm, α = 5.42 × 10−6 m2/s, v = 1.2 m/min).

The comparison between the profile of the fused zone calculated theoretically and that detected experimentally in a cross-sectional plane of the welded joint allows the fitting of the thermal field model (1). Figure 3a shows the macrography of a cross-section of the welded joint, with the boundary of the fused zone (FZ) marked in red.

Fig. 3
figure 3

Macrography of a cross-section of the joint with relief of the profile of the fused zone (a), 3D model of the melt pool and projection of the profile on the joint cross-section (b), comparison and fitting between theoretical profile and experimentally-detected profile (c)

Full size image

To simulate full penetration welding, best reproducing the experimental profile of the FZ, the thermal sources system was configured by: one point source on the upper surface (zP1 = 0 mm); a second point source inside the weld bead, at the focus of the laser beam (zP2 = 5.5 mm); the line source along the entire thickness of the joint (extension of the source zL = 10 mm).

This configuration of the thermal sources system, with the number of point sources n = 2, was set on the basis of the peculiarities of the profile of the welded section (Fig. 3a): the line source contributes to the formation of a regular fused zone along the entire thickness, while the two point sources give rise to the convexities that characterize the experimental profile, respectively, in the vicinity of the surface exposed to the laser beam, and of the focal point of the beam, inside the joint.

Figure 3b, c shows the 3D modeling of the melt pool generated by the set system of thermal sources, together with the comparison between the profile of the fused zone calculated theoretically, and that detected experimentally in the cross-sectional plane of the joint (from Fig. 3a). The construction of the surface of the melt pool is carried out by obtaining, by means of Eq. (1), the isothermal curves at the solidus temperature on horizontal planes as the depth z varies. By projecting the maximum amplitude contour of the weld pool on the yz plane, the theoretical profile of the fused zone on the cross-section of the welded joint is obtained (Fig. 3b).

For the thermo-physical properties of AISI 304 L steel, constant values were considered (corresponding to a temperature of 700 °C) [45]: density ρ = 7682 kg/m3, thermal conductivity k = 25 W/mK, diffusivity α = 5.42 × 10−6 m2/s. The solidus temperature was set equal to 1673 K.

The fitting of the model parameters to be calibrated γPi, γL, and η was obtained by minimizing the sum of the square distances along the y axis, between the theoretical profile and the experimental one, obtaining a solution that closely approximates the latter (Fig. 3c). A value of 0.51 was obtained for the absorption coefficient η. The thermal field model so defined has been validated previously by comparison with thermal profiles detected by direct experimental measures [28].

Once the analytical model has been calibrated, using Eq. (1), it is possible to simulate the thermal field in different forms. For the purposes of this work, the thermal profiles that develop during the single pass welding in fixed points inside the material, at different distances y from the welding line, will be analyzed.

3.2 Calculation of the residual stress distribution

The information on the thermal field can be processed to analytically evaluate the distribution of the longitudinal residual stresses σx according to two approaches.

  1. 1.

    By using the formula that Masubuchi et al. attribute to Uhlig [6], which describes this distribution as a symmetric function vs. the distance (y) from the welding axis

    $$\sigma_{x} \left( y \right) = \sigma_{m} \left[ {1 - \left( \frac{y}{b} \right)^{2} } \right] \, e^{{ - \frac{1}{2}\left( \frac{y}{b} \right)^{2} }}$$
    (6)

    where σm is the maximum tensile residual stress along the centerline of the weld, which is usually assumed as high as the yield strength σo at the initial temperature of the base metal [46]; b is the value of the distance from the welding axis (y) for which the residual longitudinal stress vanishes (σx = 0) and there is the inversion between tensile and compression stresses. In other words, b represents the half width of the longitudinal tensile residual stress distribution, measured at the intersection with the y axis.

  2. 2.

    By performing a thermal field analysis to obtain the thermal profiles for y < b, which combined with the stress-temperature diagram (qualitatively described in Fig. 2b), allows to construct point by point the tensile zone of the distribution of the longitudinal residual stresses (that is the part of the stress distribution of greatest interest); in this case, according to the residual stress generation process described in Sect. 2.3, the maximum tensile residual stress σm depends on the maximum peak of the thermal profiles, and at most, it can reach the tensile yield strength σo′ at the initial temperature of the base metal.

In both cases, it is first necessary to construct the stress-temperature diagram corresponding to the case analyzed (Fig. 4), and determine the point of intersection between the heating–cooling cycles and the curves that represent the trends of the tensile and compressive yield strength with the temperature, σo′(T) and σo″(T). Here, the same yield strength value of the base metal AISI 304 L at room temperature (250 MPa at To = 20 °C) and the same variation with the temperature were assumed for both tension and compression, i.e., σo′(T) = σo″(T) = σo(T). As stated above, the curves shown in the stress-temperature diagram, such as the one in Fig. 4, take into account not only the variation of the yield strength σo, but also the variations of the Young’s modulus E, and of the coefficient of thermal expansion λ with temperature. For the AISI 304 L, the reductions of the mechanical properties σo and E as functions of temperature were expressed by reduction coefficients [47], the increase in the thermo-physical property λ by means of an analytical formula as a function of temperature [45].

Fig. 4
figure 4

Condition of equality (4) represented in the stress-temperature diagram, and corresponding value of limit temperature TB (To = 20 °C)

Full size image

3.2.1 First approach: calculation using Uhlig’s formula

With regard to the first approach for the analytical calculation of the longitudinal residual stresses, the resolution of the thermal field allows to precisely define the value of the term b on which Eq. (6) depends. For this purpose, it is necessary to determine the value of the temperature TB (according to the nomenclature adopted in Fig. 2b) in correspondence with which the condition of equality (4) is verified; that is, the temperature corresponding to the condition in which the stress due to thermal expansion reaches the compressive yield limit of the material without exceeding it (zero internal stress). The condition of equality (4) is satisfied for TB = 84 °C (357 K), when the initial temperature is the room one (To = 20 °C); this condition is represented in the stress-temperature diagram of Fig. 4.

To determine the value of b to be used in Eq. (6), it is necessary to analyze the thermal profiles of the points on a line orthogonal to the welding axis, as their distance y from this axis varies, and determine the value of y that corresponds to a thermal profile whose maximum value is TB = 357 K. This value is determined by the analysis of the thermal profiles synthetized in Fig. 5.

Fig. 5
figure 5

Thermal profiles in points outside the fused zone and their analysis to determine the value of the parameter b in the residual stress distribution (z = 5 mm, v = 1.2 m/min, To = 20 °C)

Full size image

Assuming the initial temperature To equal to the room one (20 °C), these profiles have been calculated by means of the fitted thermal field model (1), for points positioned along the y direction, at the height z = 5 mm (i.e., at the center of the plate), and outside the fused zone (whose limit at z = 5 mm, for the fixed speed v = 1.2 m/min, is equal to 1.37 mm). The thermal profiles in these points are represented by temperature trends as a function of time, i.e., as the position of the heat source varies during the translation at the welding speed v.

In Fig. 5, in addition to the thermal profiles corresponding to the points in the range 2 ≤ y ≤ 15 mm, the curve that interpolates their maximum values (dashed red line) and the thermal profile for which the maximum value coincides with TB are shown. The latter profile has been calculated in a point located at a distance y = 21.3 mm from the welding axis; here, the maximum temperature TB is reached as the heat source has moved along the x axis for 38 s after passing the intersection with the y axis on which the point lies (according to the scheme in Fig. 5). As a result, b = 21.3 mm is the half width of the longitudinal residual stress distribution at the intersection with the y axis. With this value of b, and by imposing in Eq. (6) σm equal to the yield strength at room temperature (σo = 250 MPa), the distribution of the longitudinal residual stresses σx described in Fig. 6 by the continuous red line indicated with AC-U (analytical calculation using Uhlig’s formula) is obtained.

Fig. 6
figure 6

Distributions of the residual stresses obtained by the different approaches to calculation (v = 1.2 m/min, To = 20 °C): Uhlig’s formula (AC-U) and thermal field analysis (AC-TFA)

Full size image

3.2.2 Second approach: calculation by thermal field analysis

The second approach to the calculation of the residual stresses is based on the detailed analysis of the thermal field in the points on a line orthogonal to the welding axis, as their distance y from this axis varies within the limit of tensile residual stresses (y < b). Therefore, in this case, the analytical calculation of the longitudinal residual stresses focuses on the tensile part of the distribution.

As can be seen in Fig. 7, for points with y < 21.3 mm, the condition is created whereby in the heating phase of thermal cycle, the compression stress due to thermal expansion exceeds the yield strength of the material. In all these cases, therefore, knowing the maximum value of the temperature profile corresponding to the specific value of y (highlighted by the dashed line of the maximum values in Fig. 5), it is possible to determine the point on the compression yield strength curve σo″(T) in Fig. 7 from which cooling begins, and in turn the corresponding cooling path down to the initial temperature. The stress value corresponding to the end of the cooling path indicates the residual stress, for each value of y analyzed (e.g., for the point at y = 20 mm, the corresponding value of longitudinal residual stress is σx = 39.4 MPa).

Fig. 7
figure 7

Calculation of the residual stresses by thermal field analysis (v = 1.2 m/min, To = 20 °C): construction of the heating–cooling curves in the stress-temperature diagram

Full size image

In general terms, being y the distance of the generic point from the welding axis, with y < b, and Tm = Tm(y) the maximum value of the temperature profile at that point, the value of the corresponding longitudinal residual stress can be expressed by means of Eq. (5), which becomes:

$$\sigma_{x} \left( y \right) = E\left( {T_{m} } \right) \, \lambda \left( {T_{m} } \right) \, \left[ {T_{m} - T_{o} } \right] - \left| {\sigma_{o}\,^{\prime \prime } \left( {T_{m} } \right)} \right|$$
(7)

Performing the calculation of the residual stress σx(y) as y varies in the tensile region of longitudinal residual stresses (within the limit value b), two conditions can occur:

  1. 1.

    For no value of y, the longitudinal residual stress σx(y) reaches the tensile yield strength of the material at Tm temperature σo′(Tm). In this case, the maximum value of the distribution of residual tensile stresses σm will match the maximum value of σx(y) calculated by Eq. (7) for y < b, and will be lower than the yield strength of the material at the initial temperature σo′(To). This condition can be expressed as

    $$\sigma_{x} \left( y \right) < \sigma_{o}\, ^{\prime}\left( {T_{m} } \right) \, \quad\forall \, y < b \quad \Rightarrow \quad \sigma_{m} = \max \left[ {\sigma_{x} \left( y \right)} \right] < \sigma_{o}\, ^{\prime}\left( {T_{o} } \right)$$
    (8)
  2. 2.

    There exists a point at y = y* in which the thermal profile has a maximum value Tm* such that the longitudinal residual stress σx(y*) reaches the tensile yield strength of the material at the initial temperature σo′(To). In this case, for all values of y < y*, the longitudinal residual stress σx(y) reaches the tensile yield strength of the material at the corresponding Tm temperature σo′(Tm), and the last part of the cooling phase continues by stabilizing the internal stress up to the tensile yield strength at the initial temperature σo′(To). As a result, the maximum value of the distribution of residual tensile stresses σm stabilizes on σo′(To) for all the points corresponding to y ≤ y*. This condition can be expressed as

    $$\exists \, y^* \, : \, \sigma_{x} \left( {y^*} \right) = \sigma_{o}\, ^{\prime}\left( {T_{o} } \right) \quad \Rightarrow \quad \sigma_{x} \left( y \right) = \sigma_{o}\, ^{\prime}\left( {T_{o} } \right) \quad \forall \, y \le {y^*} \quad and \quad \sigma_{m} = \sigma_{o}\, ^{\prime}\left( {T_{o} } \right)$$
    (9)

  • Also considering the part of the residual stresses distribution curve on the negative side of the y axis, mirroring that considered up to now, σm is stabilized on σo′(To) for all points belonging to the interval [−y*, y*], and a central plateau with constant value at the top of the residual stress distribution is formed, straddling the welding axis x. To characterize this specific condition of maximum residual stress stabilization on the yield strength, the parameter bm = y* is defined, which expresses the half width of the plateau of the maximum residual stress.

As shown by the diagram in Fig. 7, by applying condition (9), it can be deduced that y* = 13 mm is the limit point for which the residual stress reaches the value of the tensile yield strength of the base metal at To temperature σo′(To) = 250 MPa. For all points such that y < 13 mm (e.g., y = 12 mm in Fig. 7), during the cooling phase, the corresponding value of the tensile yield strength σo′(Tm) is reached, and the cooling continues by stabilizing the internal stress up to the yield strength at the initial temperature σo′(To). Therefore, the maximum value of the longitudinal residual stresses σm stabilizes on σo’(To) for all points belonging to the interval [− y*, y*], forming the central plateau with constant value.

By means of this combined processing of thermal profiles and heating–cooling cycles in the stress-temperature diagram, it is possible to construct point by point (each one corresponding to a value of y < b) the distribution of the longitudinal residual tensile stresses, obtaining the curve in Fig. 6 indicated with AC-TFA (analytical calculation by thermal field analysis). As can be seen in the same figure, the distribution determined in this way is characterized by three main parameters:

  1. 1.

    b, the half width of the residual stress distribution for σx = 0, which corresponds to the value of the coordinate y of the point where the maximum temperature of the thermal profile is equal to TB (Figs. 5 and 7);

  2. 2.

    bm, the half width of the plateau of the maximum stress, i.e., the value of y corresponding to the limit point for which the tensile residual stress reaches the yield strength of the base material (Fig. 7); this parameter bm occurs only in cases, such as the one in question, in which the maximum tensile residual stress σm stabilizes on the yield strength at the initial temperature To, according to previously introduced condition (9): as a consequence, the distribution of the residual stresses is characterized by the central plateau with constant value, as shown in Fig. 6.

  3. 3.

    σm, the maximum tensile residual stress along the centerline of the weld, which in the present case results equal to the yield strength σo of the base metal at the initial temperature To (assumed equal to 20 °C in Fig. 7).

The AC-TFA distribution has in common with the AC-U one only the parameter b, and the maximum value of the residual stress σm. The trends of the two curves in Fig. 6 are instead substantially different, highlighting a clear underestimation of the residual stresses in the analytical calculation performed by Uhlig’s formula.

4 Validation of results

The construction by points, through the analysis of the thermal field, allows to obtain a more realistic distribution of longitudinal residual stresses, and in accordance with trends of longitudinal tensile residual stress available in the literature. In this regard, Fig. 8 shows a comparison between the AC-TFA distribution obtained on AISI 304 L through the proposed approach, and the distributions of the longitudinal residual tensile stresses in full penetration CO2 laser welded joints on affine materials (austenitic stainless steels of similar composition than the one used in the present investigation): FEA(304) and FEA(301L) distributions were assessed by finite element numerical simulations on AISI 304 [48] and 301L [49] steels, respectively; XRD(304) distribution was assessed by X-ray diffraction on ANSI 304 steel [50].

Fig. 8
figure 8

Calculation of the residual stresses by thermal field analysis: comparison with results from the literature obtained by numerical simulations and experimental detection

Full size image

To compare these cases, characterized by different process conditions (beam power, welding speed, plates thickness), the corresponding longitudinal residual stress distributions have been normalized according to two parameters: the maximum value of the residual stress σm, and the half width of the stress distribution b. Consequently, the distribution profiles have been represented and compared in a reference system with σx/σm and y/b in the axes.

The normalization adopted allows to compare the shape of the distributions. As it is possible to notice, the proposed calculation model defines a trend of the normalized distribution that is markedly similar to the results obtained by numerical simulations and experimental detection (if in the latter case the detection on the positive side of the y/b axis is taken into account). In all cases, the condition of maximum residual stress stabilization on the yield strength occurs, and the distribution is characterized by the central plateau with constant value. The affinity of the results can also be confirmed with regard to the half width of the plateau of the maximum stress, whose deviation in AC-TFA profile is maintained within − 10% compared to the results from the literature.

For a direct validation of the theoretical results obtained, some values of residual stresses have been experimentally detected by the hole-drilling strain gage method. The preliminary measures adopted in the application of the technique, in accordance with the Micro-Measurements technical note TN-503–6, are reported in Sect. 2.4.

It should be noted that this method allows to detect the relieved surface strains caused by the introduction of the hole, and then to calculate the near surface stresses present before removing the material by drilling. The stress distribution obtained by the proposed theoretical approach, which is reported in Fig. 6 and compared in Fig. 8 with the results from literature, refers instead to the central position along the thickness of the plates (z = 5 mm). To evaluate the sensitivity of the residual stresses calculation based on the analysis of the thermal field (AC-TFA curve in Fig. 6), with respect to the z axis, the distribution obtained point by point for z = 5 mm was compared in Fig. 9 with those obtained for z = 0 mm and z = 10 mm, i.e., at upper and lower surfaces of the plates, respectively. The comparison is represented in the graph of Fig. 9 (on the left side with respect to the symmetry axis of the theoretical distribution, which coincides with the welding line). As can be seen, the results are superimposable, from which it can be deduced that in the case under consideration, the calculation model provides a distribution of the residual stresses substantially invariant with respect to z. This finding outlines a condition of uniformity of the stresses with the depth, which moreover is one of the prerequisites for the stress field to be detected by the hole-drilling method, thus confirming the suitability of the experimental technique used.

Fig. 9
figure 9

Residual stresses calculation by thermal field analysis and experimental validation: residual stress distributions as the depth z varies along the thickness of the plates (left side of the graph), and comparison with experimentally-measured stresses for z = 0 mm (right side of the graph)

Full size image

The experimental measurements were obtained at four points, positioned according to the scheme shown in Fig. 9. The choice of positioning was guided by two needs:

  • carry out the measurements in order to verify the reliability of the theoretical stress distribution constructed by points, which on the upper surface (z = 0 mm) extends with respect to the y axis between the values 13 ÷ 21.1 mm;

  • respect a minimum distance between the holes of 5 to 6 times the diameter (8–10 mm), ensuring that the stress released in one point made negligible effects on the other ones [51].

To satisfy both of these needs, the detection points had to be positioned on different lines perpendicular to the welding axis x. In this way, actually, some points of the same theoretical distribution of longitudinal residual stresses corresponding to a cross-section of the welded joint are compared to experimental measurements carried out in correspondence with different sections of the welded joint. However, the comparison by points is consistent since, despite the experimentally measured stresses at the same distance from the welding axis may vary as x varies, the theoretical distribution of longitudinal residual stresses can be considered uniform along the welding axis. The latter condition occurs because the points of the theoretical distribution of the residual stresses have been derived from temperature cycles estimated by a thermal field model which was found to be robust (not affected by significant variations) with respect to the position of its origin on the welding axis [28]. Therefore, the measurements obtained were collected on the same graph in Fig. 9, and compared to the points of the theoretical stress distribution calculate for z = 0 mm (on the right side of the graph, with respect to the welding line).

The results of the experimental investigation show a good agreement with the theoretical construction of the distribution, with deviations in the values of the residual stresses within 7%, compared to the corresponding theoretical values. The experimental value detected at point P1 only is an exception. While in fact the points P2, P3, P4 (with distance from the welding line y = 16, 18, 21 mm, respectively) are subject to stress states that do not exceed the accuracy limit of the experimental technique (70% of the yield strength, i.e. 175 MPa) [43], the point P1 (y = 13 mm) is well beyond this limit. According the theoretical construction, the yield point is reached at P1, and therefore, the stress state strongly deviates from the linear-elastic behavior assumed as one of the basic conditions in the calculation of residual stresses using the hole-drilling method. This deviation leads to larger margins of error in the experimental measurement, which has been estimated as positive and in the range 10 ÷ 30% for thick sections where blind holes are used [52]. The deviation between experimental and theoretical data estimated for point P1, equal to 16.2%, falls within this range, confirming that the residual stress at y = 13 mm exceeds the proportional limit and enters the yield field, in agreement with the theoretical construction of the stress distribution.

As a final consideration on the validation of the theoretical results, it can be concluded that within the limit of tensile residual stresses b:

  • the results found in other comparable investigations reported in the literature fully confirm the trend in the distribution of residual stresses (Fig. 8);

  • the results obtained by direct experimental measurements substantially confirm the values of the stress distribution in the part constructed point by point (Fig. 9).

5 Final remarks

Although the first approach to the calculation of the distribution of the longitudinal residual stresses (Sect. 3.2.1), based on the Eq. (6), exploits the analysis of the thermal field to accurately calculate the parameter b, it provides an approximate evaluation. The aspect that makes the approach particularly limited in accuracy concerns the setting of σm, which cannot be estimated, and is usually equated to the yield strength of the material at the initial conditions σo. By doing so, in fact, it is imposed that the residual stress always reaches the yield point, but only on the welding line (y = 0) and in its close proximity (as shown by curve AC-U in Fig. 6). It follows that:

  • it is not possible to determine the cases in which the distribution of the longitudinal stresses remains below the yield strength of the material;

  • in the event that the residual stresses reach the yield point, it is not possible to determine the distance from the welding line at which this occurs (bm), and the consequent plateau σm = σo.

This latter condition, clearly detected and characterized in the presented case by means of the approach based on the analysis of the thermal field (Sect. 3.2.2), can be associated with the high heat input due to process settings (being P = 14 kW and v = 1.2 m/min from Table 1, and having determined an absorption coefficient by model fitting η = 0.51, the actual value of the heat input per unit length is ηP/v = 357 J/mm). This determines thermal profiles with high temperature peaks, and favors reaching the yield strength in the generation of the residual stresses, and the occurrence of the condition of maximum residual stress stabilization on the yield strength.

The same condition, however, also occurs in the similar cases presented in the literature and mentioned in the previous section (Fig. 8), even though they are obtained through lower heat inputs (48 ÷ 225 J/mm nominal values, which do not take into account the reduction due to the absorption coefficient). These evidences outline a common trend in the distribution of residual stresses due to laser welding of type 304 stainless steels or affine materials, even for low heat input values, in accordance with the results obtained here by the second approach, and therefore the need to use the latter to overcome the limitations inherent in the first approach.

In conclusion, the construction by points of the longitudinal residual stresses distribution, based on thermal field analysis, compared to the use of Uhlig’s formula (6), has substantial advantages:

  • it allows to outline the modality in which the maximum residual tensile stresses develop, by verifying the conditions (8) or (9), and to fully characterize the distribution, by defining in detail the parameters b, bm, and σm;

  • it provides a more accurate prediction of the distribution of longitudinal residual tensile stresses, consistent both with the results found in other comparable investigations reported in the literature and with those obtained by direct experimental validation.

This latter approach can be used in all cases in which the three-bar model is adequate to represent the real welding condition. The case in which the volume of material represented by the central bar is subject to significant variations in the cooling phase of the thermal cycles is an exception, as when the volumetric expansion due to the martensitic transformation occurs at high cooling rates [6]. This is because the construction by points, based on the three-bar model and the associated thermal cycles analysis, is intrinsically unsuitable to take into account the effect of thermal rates on the generation of residual stresses. In applications for which this aspect is significant, it would be necessary to use other approaches, such as experimental investigations, or multi-physics modeling and numerical simulation. In all other cases, where the materials are not affected by microstructural transformations with significant volume change, as for austenitic steels, or where the process parameters are such that they do not determine the conditions under which these transformations occur [53], the effect of cooling rate can be neglected and the proposed theoretical model can be considered effective for predicting residual stresses.

6 Conclusions

Two different modes have been defined to use the analysis of the thermal field due to laser beam welding for the theoretical calculation of the distribution of the longitudinal residual stresses. The first one makes use of a simplified formula well-known in the literature, which describes this distribution as a function of two fundamental parameters: the value of the distance b from the welding axis for which the residual longitudinal stresses reverse their sign (tension–compression), and the yield strength of the base metal at room temperature. In this case the simulation of the thermal field allows to calculate with precision the value of the parameter b, but the approach shows substantial limitations in the stress distribution modeling it provides. The second mode, which is based on a combined processing of thermal profiles and heating–cooling cycles, allows a full characterization of the longitudinal residual tensile stresses, obtaining results more detailed and compliant to the known distribution trends reported in the literature. A comparison of these results with the ones obtained by experimental measurements confirms the reliability and greater accuracy of the second approach to the theoretical calculation of residual stresses.