The relevance of wall roughness modeling for simulation of powder flows in laser metal deposition nozzles

Abstract

Point-particle large-eddy simulations and high-speed imaging are used to investigate effects of wall roughness and particle size on characteristics of a powder flow issuing from a vertical, round nozzle. Wall roughness effects on dynamics of particles can be characterized by the standard deviation of the roughness angle distribution $\Delta \gamma$, which is a hybrid roughness parameter that represents a combination of amplitude and spacing roughness parameters. We optically scan the inner nozzle surface to obtain the two-dimensional roughness profiles, using which $\Delta \gamma$ is estimated. We adopt a stochastic approach in the numerical simulations to model the wall roughness. We find that this modeling is essential to obtain a good agreement between simulation and experimental results. The wall roughness is found to enhance the transverse dispersion of particles and to eliminate the preferential accumulation of particles in the near-wall region, giving rise to reduction of the mean particle velocity within the nozzle and to clustering of the particles in the nozzle core. Results also reveal that an increase in the particle size (characterized by Stokes number) and in the wall roughness leads to a reduction of the particle velocity and to an enhancement of the particle-stream divergence throughout the jet region. However, a saturation behaviour is observed in the particle-stream divergence with the Stokes number. All this dependence is rationalized by the fact that the Stokes number characterizes the particle response to the gas flow and the wall roughness determines the inelastic particle-wall collision frequency.

1 Introduction

Powder-based laser metal deposition (LMD) is an additive manufacturing process, which progressively attracts more attention in the field of production technology owing to its broad application for coating, rapid prototyping, rapid manufacturing, and rapid tooling [1]. Despite several advantages of the LMD over traditional manufacturing methods, including high build rate, easy material change, and reduced material wastes [2], the LMD is still away from being a mainstream production technology [3]. Some of the relevant issues limiting its industrial application are the high cost of specialized powder flowstock and laser equipment and the low build resolution, such that a certain level of post-processing like mechanical machining, polishing, or blasting is often needed [4]. In addition, the deposited track geometry in the LMD and accordingly the quality of deposited components depends on a large number of process parameters [5], whose effects still need to be thoroughly understood. The main objective of this research is therefore to advance the current knowledge of fundamental aspects of powder flows in the LMD process since a comprehensive understanding of participating sub-systems in any technology is necessary to improve it.

The powder flow, which is one of the key elements among others such as laser power rate and laser spot size that determine the deposited track geometry in the LMD process [6], depends on several parameters including the gas and powder flow rates, the size distribution of powder, and the geometry of nozzles [7]. Effects of these parameters on powder flow characteristics have been studied by means of laboratory experiments [5] and numerical simulations [8]. Balu et al. [6] conducted a parametric study on a coaxial multi-material powder flow by means of a high-speed CCD camera and numerical simulations, showing that an increase in the gas flow rate leads to the growth of the divergence angle of powder, which accordingly results in a larger powder focus diameter. In contrast, Jeromen et al. [9] reported insignificant influence of the gas flow rate on the powder focus diameter by experimentally investigating a discrete, axial nozzle. A powder flow issuing from a coaxial-type nozzle with two paths has been studied by Takemura et al. [10] using a high-speed camera and numerical simulations, where a high gas flow rate was found to result in an increased sputter generation during the deposition process. Smurov et al. [11] investigated effects of the particle size on the divergence angle of particles for annular gap nozzles using a CCD camera-based diagnostic tool and numerical simulations, and showed that the divergence of particle flow grows with the particle size. A single-jet lateral nozzle has been studied by Kebbel et al. [12] via digital holographic particle image velocimetry, illustrating a reduction of the particle velocity with increasing powder-feed rate. A Gaussian-like powder distribution has been documented in different configurations such as a single-jet lateral nozzle [12], a discrete coaxial nozzle with four jets [6], and nozzles with an annular gap [13]. Nonetheless, a comprehensive understanding of underlying mechanisms as well as a precise quantification of the observed dependence of powder flow on controlling parameters remains difficult. In this paper, we investigate a particle-laden jet issuing from a vertical, round nozzle to understand and quantify the dependence of powder flow properties on the wall roughness and the particle size.

We apply a high-speed imaging technique to perform an experimental analysis of the powder flow and employ an Eulerian-Lagrangian point-particle approach to numerically simulate the powder flow. Turbulence models along with discrete phase random walk and wall functions are usually applied for numerical simulations of the turbulent flow in previous literature of LMD process (see [14], and references therein). The most commonly used turbulence model is the standard $k-\varepsilon$, where k is the turbulent kinetic energy and $\varepsilon$ is the dissipation rate of the turbulent kinetic energy [6]. The turbulence modeling approach is in principle based on a strict assumption, that is the flow is fully turbulent. This assumption is, however, often violated in additive manufacturing applications because of the wide range of parameter space usually considered, covering from laminar to fully turbulent regimes. To overcome this limitation and also to increase fidelity of the solution, we employ wall-resolved large-eddy simulation (LES) with a reasonable computational cost. This approach resolves the large eddies, as they contain most of the turbulent kinetic energy, and model effects of the eddies smaller than the grid size, which are more isotropic and homogeneous. We also use dimensional analysis to formulate the problem in terms of non-dimensional parameters, allowing us to perform a systematic study and to generalize the acquired results. We note that any conclusion drawn for the studied values of non-dimensional parameters can be applied to all different combinations of control parameters that create those values of the non-dimensional parameters.

Wall roughness is well known to play a considerable role in the particle-wall collision process [15]. Indeed, the wall roughness substantially alters the rebound behaviour of particles, resulting, on one hand, in a pronounced enhancement of the transverse dispersion of the particles [16], and on the other hand, in a significant reduction of the mean axial velocity of the particles [17]. It is important to point out that collisions of irregularly shaped particles with a smooth/rough wall have similar effects [18]. Thoroughly investigating the particle-wall collision process in a particle-laden horizontal channel flow using particle tracking velocimetry, Sommerfeld and Huber [15] showed that the distribution of the wall roughness angle experienced by particles is well approximated by a normal distribution function, whose standard deviation is denoted as $\Delta \gamma$. This parameter, referred to as a hybrid parameter that combines both amplitude and spacing roughness parameters, depends not only on roughness structure but also on particle size. Novelletto Ricardo and Sommerfeld [19] have proposed a model to estimate $\Delta \gamma$ from the two-dimensional roughness profile of the inner nozzle surface using the mean arithmetic average height (i.e. an amplitude parameter) and the mean spacing at the mean line (i.e. a spacing parameter). We explain this method in detail in Sect. 2.

Novelletto Ricardo and Sommerfeld [19] have recently investigated the changes in surface roughness of the aluminium, copper, and brass wall samples exposed to quartz sand and spherical glass bead particles. An impingement jet facility has been used to obtain experimental data for erosion times of 2.5, 5 and 10 h and wall inclination angles of 10, 20, 30 and $40^\circ$. Although the arithmetic average height and the mean spacing roughness asperities were found to vary differently at various inclination angles, the standard deviation of the roughness angle distribution, $\Delta \gamma$, appeared to behave similarly for most of the cases. This parameter showed a sharp increase within the first 5–10 h of erosion, but its variation remained almost unchanged afterwards. For instance, a fresh aluminium wall sample with an initial value of $\Delta \gamma \simeq 3^\circ$ reached almost three times higher value, i.e. $\Delta \gamma \simeq 9^\circ$, after about 5 h of erosion but changed very slightly afterwards. This study suggests that the particle velocity and concentration distributions obtained for a worn nozzle are fairly robust as $\Delta \gamma$ remains almost unchanged with time.

Particle-wall and particle-particle collisions need to be appropriately modeled to obtain a reliable numerical simulation of confined particle-laden flows [15]. To model the particle-wall collisions in numerical simulations, we employ the soft-sphere collision model, in which the contact forces and torques are mathematically represented using springs, dash-pots, and sliders [20]. To model wall roughness effects on particle-wall collisions in numerical simulations, we adopt a stochastic approach in the soft-sphere collision model [21, 22]. This approach is established on the concept of virtual wall and assumes that the real impact angle of a particle comprises the trajectory angle with respect to the smooth pipe wall plus a stochastic contribution owing to the wall roughness. It follows that the local wall at every particle-wall collision is reoriented with a random angle, which is sampled using the normal distribution function with the standard deviation $\Delta \gamma$ [16]. Therefore, we need to specify $\Delta \gamma$ in each simulation as an additional constant parameter in the wall-particle collision model. Inter-particle collisions are usually neglected in previous work (see [23], and references therein). However, our preliminary analysis indicates that the bulk-mean particle volume fraction inside the nozzle for typical conditions in the LMD process appears to be of the order of $0.01\%$. Because recent work of confined particle-laden flows has shown that inter-particle collisions play a significant role in the dynamics of particle-laden confined flows even for such a low bulk-mean particle volume fraction [24, 25], we consider the inter-particle collisions in this work using the soft-sphere collision model.

One main aspect of the LMD process is a normally used short nozzle, which complicates showing a good agreement between results of experiments and numerical simulations. This lies in the fact that numerical simulation results of a short nozzle appear to depend on boundary conditions at the nozzle inlet. Kovalev et al. [26] have studied this dependence and showed that the inlet boundary conditions are not forgotten within a short nozzle, and therefore, the particle velocity at the inlet needs to be carefully adjusted in the numerical simulations to obtain an acceptable agreement between experimental and simulation results. This conclusion was consistent with results of Smurov et al. [11]. Such a conclusion devalues application of numerical simulations for the LMD process because the particle velocity at the nozzle inlet is a priori unknown property. This implies that reliable results can not be obtained from a numerical simulation for a new parameter space, for which no experimental data is available. In this work, we elaborate on this relevance and illustrate that considering wall roughness effects substantially reduces the entrance length that is the required nozzle length to forget the inlet boundary condition and to reach the fully developed particle-laden flow. We additionally show that our considered nozzle with the length of 100 mm is long enough to reach the fully developed particle-laden flow at the nozzle outlet.

The structure of the paper is as follows. In Sect. 2, we describe the material, the experimental setup, and the measurement techniques. In Sect. 3, we define the mathematical formulation, describe the simulation setup, and verify the point-particle LES code and the implemented stochastic wall roughness model using the available experimental results of Kussin and Sommerfeld [16] for a horizontal particle-laden channel flow. In Sect. 4, we first study effects of the wall roughness on the particle statistics using numerical simulation results, and then make a comparison between our simulation and experimental results. We then investigate dependence of the particle statistics at the nozzle outlet and inside the jet region on the particle size. We finally summarize the results and draw conclusions in Sect. 5.

2 Experimental investigation

2.1 Material

We use stainless steel $316\,\mathrm {L}$ powder with a size of $45 \ \mu\mathrm {m}$ to $106\ \mu\mathrm {m}$, a flow rate of $16.9~\mathrm {s}/50~\mathrm {g}$, and an apparent density of $4.03~\mathrm {g}\, \mathrm {cm}^{-3}$, according to the manufacturer, i.e. Deutsche Edelstahlwerke Specialty Steel GmbH & Co. KG. The powder is sieved before conducting the experiments using the following mesh sizes: 45, 53, 63, 71, 80, 90, 100, and $106\ \mu\mathrm {m}$, resulting in seven different size fractions. In the present work, however, we only use three size fractions, namely 45–53 ${\mu}\mathrm {m}$, 71–80 $\mu\mathrm {m}$, and 90–100 ${\mu}\mathrm {m}$. Morphology of these particle size fractions is assessed by SEM pictures, as shown in Fig. 1. This figure indicates that each experiment can be considered as a monodisperse case with fairly spherical particles. To characterize the powder flow in the LMD process, we use a configuration of reduced complexity, that is a powder jet issuing from a vertical, round nozzle. The sieved powder, whose feed rate is accurately controlled by the powder feeder TWIN-150 from Oerlikon Metco, is uniformly fed into a single vertically aligned nozzle using Argon as the carrier gas. The nozzle consists of a ceramic inner tube supplied by Buntenkötter Technische Keramik GmbH with a copper outer shielding and has an inner diameter of $D=1.7~\mathrm {mm}$ and a length of $L=100~\mathrm {mm}$, resulting in a pipe length-to-diameter ratio of $L/D \simeq 58.8$.

Fig. 1

SEM images of the sieved powder fractions used in this work

2.2 Roughness of inner nozzle surface

To determine the roughness properties of the inner nozzle surface, we cut the ceramic nozzle in half along its axis and optically scan its inner surface using a Keyence VK 9700 laser confocal microscope with a 50$\times$ lens with a numerical aperture of 0.55. Figure 2a shows the obtained three-dimensional morphology of the inner nozzle surface. Using the Keyence VK Analyzer, we additionally export two-dimensional roughness profiles over six parallel lines, which are equally distributed along the width of the sample (see Fig. 2b).

Fig. 2

a 3D morphology of the inner nozzle surface. (The sample is 3 mm long but the bottom image in panel (a) only shows $15\%$ of the sample for a better visualization.) b 2D roughness profiles over six parallel lines equally distributed along the sample width. The location of these lines is shown in the bottom image of panel (a) with dashed lines

Several parameters can be determined from the two-dimensional roughness profiles to describe the surface roughness. These parameters, according to their functionality, are classified into three groups, namely amplitude, spacing, and hybrid parameters [27]. The amplitude parameters like the arithmetic average height Ra indicate vertical characteristics of roughness, the spacing parameters like the mean spacing at the mean line $RS_m$ represent horizontal characteristics of roughness, and the hybrid parameters illustrate a combination of vertical and horizontal characteristics of roughness. Sommerfeld [28] has argued that wall roughness effects on particle-wall collisions can not be solely characterized by an amplitude parameter. Rather, a spacing parameter also needs to be taken into account. Following the same line of reasoning, Sommerfeld and Huber [15] showed that wall roughness effects on particle-wall collisions can be completely characterized by a hybrid parameter that is the standard deviation of the roughness angle distribution $\Delta \gamma$. This parameter depends on roughness structure and particle size. Two scenarios, as shown in Fig. 3, are considered to estimate $\Delta \gamma$ from the two-dimensional roughness profile [19, 28]. If particle size is larger than the mean spacing at the mean line, $\Delta \gamma$ is estimated as $tan^{-1}[ Ra/(2\,RS_m)]$, and if particle size is smaller than the mean spacing at the mean line, $\Delta \gamma$ is estimated as $tan^{-1}[ 2\,Ra/RS_m]$. We determine the values of Ra and $RS_m$ for each of the two-dimensional roughness profiles and calculate the corresponding mean values. This approach decreases the uncertainty in calculating the roughness parameters. We obtain the mean arithmetic average height $Ra \simeq 1.7\ \mu\mathrm {m}$ and the mean spacing at the mean line $RS_m \simeq 8.2\ \mu\mathrm {m}$. Since the particles considered in the present work are larger than the mean spacing at the mean line, the standard deviation of the roughness angle distribution is estimated as $\Delta \gamma = tan^{-1}[Ra/(2\,RS_m)] \simeq 5.9^\circ$. As explained in the introduction, the calculated $\Delta \gamma$ remains almost unvaried with time according to findings of Novelletto Ricardo and Sommerfeld [19], given that our nozzle can be considered as a relatively worn nozzle, which has been used for more than a few hours.

Fig. 3

Sketch of the model proposed by Novelletto Ricardo and Sommerfeld [19] to estimate $\Delta \gamma$ from 2D surface roughness profile for: a large particles and b small particles

2.3 Experimental setup

We employ a high-speed camera (Vision Phantom Research VEO410L) in combination with an illumination laser (CAVITAR CAVILUX HF) to observe the powder flow. The laser is directed at a white sheet of paper located behind the powder flow to achieve a high contrast between the powder particles and the background. The setup for the high-speed imaging experiments is depicted in Fig. 4a. All high-speed videos are recorded at $30~\mathrm {kHz}$ with an image size of $384~\mathrm {px} \times 376~\mathrm {px}$, where one pixel width is equivalent to $26.27\ \mu\mathrm {m}$. The evaluation window is then approximately $10~\mathrm {mm}$ in width and height. Each experiment is recorded in at least 13000 frames, which correspond to approximately $0.433~\mathrm {s}$. To analyse the obtained videos, we use a LabView based program, in which a background model is at first created by averaging 5000 frames from the video (see Fig. 4b). This step is repeated every 5000 frames to compensate for changing lighting conditions. The absolute difference between the input frame and background model is used to eliminate constant interference (e.g. spots on the camera) as well as the nozzle itself. The frame is then binarized and run through a particle detection. These steps are taken for each frame. Through the analysis of two consecutive frames, trace of particles can be detected. The particle velocity is then calculated by dividing the length of trace with the shutter time of the camera. In addition, we obtain powder concentration distribution by superposing all binarized individual images. Since we have placed the white sheet paper behind the powder flow, the acquired concentration distributions correspond to the whole ejected particles not to the symmetry axis of the nozzle. In this work, we carry out three experiments to study effects of the particle size on the powder flow characteristics. Effects of the wall roughness on particle properties is only studied using the numerical simulations. A detailed description of the considered parameter set is explained in Sect. 3.2.

Fig. 4

a Sketch of the experimental setup for high-speed imaging, b left to right: full frame from high-speed video, frame after binarization, particle detection within ROI

3 Numerical simulation

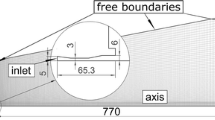
We consider a particle-laden turbulent jet issuing from a round nozzle (see Fig. 5a). For the gas phase, the inner nozzle surface is considered to be smooth. For the particle phase, the inner nozzle surface is considered to be smooth and rough. The nozzle is vertical and both phases flow in the same direction as the gravitational force. The computational domain is composed of a round pipe with the diameter of $D=1.7~\mathrm {mm}$, and the length of $L=100~\mathrm {mm}$ attached to a cylinder with the length of $20\,D$ and the diameter of $40\,D$.

Fig. 5

a Sketch of the computational domain and the cylindrical coordinate system. The mesh b at a horizontal cross section in the pipe nozzle and c at the vertical cross section on the centerline plane focusing on the jet exit region

The open-source software OpenFOAM is used to apply an Eulerian-Lagrangian point-particle approach, in which the carrier phase is described as a continuum and calculated by solving the incompressible Navier-Stokes equations, and the dispersed phase is treated as point particle and calculated by solving Lagrangian equations of motion for each particle. The coupling between two phases is ensured via the inter-phase momentum exchange. In addition, we take particle-particle interactions into account.

3.1 Governing equations

The governing equations for the gas phase are the incompressible Navier-Stokes equations, which in the framework of LES read

$$\begin{aligned} \begin{aligned} \varvec{\nabla } \varvec{\cdot } \varvec{\overline{u}_g}&= 0\;, \\ \frac{\partial \varvec{\overline{u}_g}}{\partial t}+\varvec{\overline{u}_g} \varvec{\cdot } \varvec{\nabla } \varvec{\overline{u}_g}&= -\varvec{\nabla } \overline{p} + \varvec{\nabla } \varvec{\cdot } \Big (\nu _g \varvec{\nabla } \varvec{\overline{u}_g} - \varvec{\tau } \Big ) + g\, \varvec{e}_z - \varvec{\overline{S}}_p. \end{aligned} \end{aligned}$$

(1)

The subscript g denotes the gas, the overbar indicates the LES filtering, $\varvec{\overline{u}_g}$ is the instantaneous filtered gas velocity vector, t the time, $\overline{p}$ the modified filtered pressure divided by the constant gas density, $\nu _g$ the gas kinematic viscosity, $g=9.81\,\mathrm {m}\, \mathrm {s}^{-2}$ the gravitational acceleration, and $\varvec{e}_z$ is the downward pointing vertical unit vector. The variable $\varvec{\tau }$ is the subgrid scale stress tensor, whose deviatoric part is modeled using the dynamic subgrid scale model based on the turbulent kinetic energy. Further details of this model can be found in Kim and Menon [29]. The last term describes the filtered gas-particle interaction force per unit mass of the gas and is expressed as

$$\begin{aligned} \overline{\varvec{{S}}}_p = \frac{1}{\rho _g\, (1-\Phi _v)\, V_\mathrm {cell}} \sum ^{N_p}_{p=1} \frac{V_p\, \beta }{\Phi _v} (\overline{\varvec{{u}}}_g - \varvec{u}_p)\;, \end{aligned}$$

(2)

where the subscript p denotes the particle, $\rho _g$ is the gas density, $\Phi _v$ the particle volume fraction, $V_p$ the particle volume, $V_\mathrm {cell}$ the volume of the computational cell, $N_p$ the number of particles in the corresponding cell, and $\varvec{u}_p$ the translational velocity of the particle. The inter-phase momentum exchange coefficient is defined by [30]

$$\begin{aligned} \beta = \frac{3}{4}\, C_D\, \frac{(1-\Phi _v)\, \Phi _v\, \rho _g\, \mid \overline{\varvec{{u}}}_g - \varvec{u}_p \mid }{d_p}\,(1-\Phi _v)^{-2.65}\;, \end{aligned}$$

(3)

and the coefficient of drag is given by [31]

$$\begin{aligned} C_D = {\left\{ \begin{array}{ll} \frac{24 }{Re_p} \big (1+0.15\, Re_p^{0.687} \big ) &{} \text {if } Re_p < 1000 \\ 0.44 &{} \text {if } Re_p \ge 1000 \;, \end{array}\right. } \end{aligned}$$

(4)

where $Re_p = \mid \overline{\varvec{{u}}}_g - \varvec{u}_p \mid \, d_p /\nu _g$ is the particle Reynolds number with $d_p$ the particle diameter.

The governing equations for the motion of an individual solid particle read:

$$\begin{aligned} \frac{\partial \varvec{x}_p }{\partial t} =&\, \varvec{u}_p, \end{aligned}$$

(5a)

$$\begin{aligned}m_p \frac{\partial \varvec{u}_p }{\partial t} =\, \frac{V_p\, \beta }{\Phi _v} (\overline{\varvec{{u}}}_g - \varvec{u}_p) + m_p\ g\, \varvec{e}_z + \varvec{F}_{c},\end{aligned}$$

(5b)

$$\begin{aligned}I_p \frac{\partial \varvec{\omega }{}_p }{\partial t} =&\, \varvec{T}_{c}, \end{aligned}$$

(5c)

where $\varvec{x}_p$ is the position of particle, $\varvec{\omega }_p$ the angular velocity of particle, $m_p$ the mass and $I_p$ the moment of inertia of particle. The variables $\varvec{F}_c$ and $\varvec{T}_c$ are the contact force and torque acting on a particle by its adjacent contact, which can be a particle or a wall. We employ the soft-sphere collision model, in which the inter-particle and wall-particle contact forces and torques are modeled using simple mechanical elements, such as springs, dash-pots, and sliders. A precise description of the collision model can be found in [22, 32]. We adopt a stochastic approach in the soft-sphere model to consider the pronounced effects of the wall roughness on particle-wall collisions. A thorough explanation of this approach can be found in [21, 22].

3.2 Description of simulations

Two sets of simulations, as shown in Table 1, are carried out to study effects of the wall roughness and the particle size. In each set, we only change one parameter. Particles are considered to be spherical and monodisperse, owing to the fairly narrow size distribution obtained from the sieve analysis (see Fig. 1). In the first set, we consider three standard deviations of the roughness angle distribution, namely $\Delta \gamma =0$, 3, and $6^\circ$ with $d_p=50\mu\mathrm {m}$, $\dot{m}_p=4~\mathrm {g~min^{-1}}$, and $\dot{v}_g = 5~\mathrm {L~min}^{-1}$. We refer to these cases as R0, R3, and R6, respectively. In the second set, we consider three classes of particles with different sizes, namely $d_p = 50$, 75, and $95\mu\mathrm {m}$, with $\Delta \gamma =6^\circ$, $\dot{m}_p=4~\mathrm {g~min^{-1}}$, and $\dot{v}_g = 5~\mathrm {L~min}^{-1}$. We refer to these cases as D50, D75, and D95, respectively. We note that the cases R6 and D50 are identical. The experiments are only conducted for the second set.

Table 1 Parameter space. The prefixes R and D indicate the roughness of wall and the diameter of particle, respectively. Here $\Delta \gamma$ is the standard deviation of the roughness angle distribution, $d_p$ the particle diameter, $\dot{m}_p$ the powder mass flow rate, and $\dot{v}_g$ the gas volumetric flow rate. The parameters Re, St, and $\Phi _m$ are the Reynolds number, the Stokes number, and the mass loading all defined by Eq. (6). $\overline{\Phi }_v$ is the bulk-mean particle volume fraction at the nozzle outlet defined by Eq. (8), $u_b$ the gas bulk velocity, and $N_p$ the number of particles in the whole system. The cases R6 and D50 are identical

Three relevant non-dimensional parameters that prove useful for the discussion of results in particle-laden flows are the Reynolds number, the Stokes number, and the mass loading, respectively defined as [22]

$$\begin{aligned} Re = \frac{\rho _g u_b D}{\mu _g}\;,~~ St = \frac{\rho _p d_p^2 u_b }{18\,\mu _g D}\;,~~ \mathrm {and} ~~ \Phi _m = \frac{\dot{m}_p}{\rho _g \dot{v}_g}\;. \end{aligned}$$

(6)

Here, $\rho _p$ is the particle density, $u_b$ the gas bulk velocity, and $\mu _g$ the gas dynamic viscosity. In this work, we fix the Reynolds number and the mass loading ($Re=5000$ and $\Phi _m=0.45$) and cover the Stokes number ranging from 1050 to 3790, given that the density of Argon is $\rho _g = 1.78~\mathrm {kg~m^{-3}}$, the dynamic viscosity of Argon is $\mu _g = 2.225 \times 10^{-5}~\mathrm {kg~m^{-1}~s^{-1}}$, and the density of stainless steel is $\rho _p=7780~\mathrm {kg~m^{-3}}$.

The required parameters for the inter-particle and particle-wall collisions in the soft-sphere model rely on the properties of the wall and particles [33], namely, on the friction coefficient, on the restitution coefficient, on the Young’s modulus, and on the Poisson ratio. For the stainless steel (particles) and ceramic (internal nozzle surface), we consider the Young’s modulus and the Poisson ratio to be 210 $\mathrm {G Pa}$ and 70 $\mathrm {G Pa}$ and 0.27 and 0.3, respectively. Although wall roughness influences friction coefficient, and restitution coefficient depends on impact velocity [34], it is a general practice in the literature to consider constant values for the friction and restitution coefficients independent of wall roughness properties and impact velocity, for simplicity [21, 35]. Hence, we consider in all simulated cases the friction and restitution coefficients for both stainless steel and ceramic to be 0.4 and 0.9, respectively. The latter value is obtained from Stevens and Hrenya [34], where the coefficient of restitution for the stainless steel has been experimentally shown to vary from $\simeq 0.93$ to $\simeq 0.85$ for the impact velocity changing from $\simeq 0.4$ to $\simeq 1.4$ m/s.

The commercial tool ANSYS ICEM CFD is used to generate a structured mesh with $\simeq 8 \times 10^5$ cells. As indicated in Fig. 5, we cluster the majority of cells in the near-wall region and the jet shear layer. We choose the grid spacing based on the resolution requirements for the wall-resolved LES of shear-driven flows [36]. In particular, we sufficiently resolve the viscous sublayer and the buffer layer inside the nozzle. As one limitation in the point-particle approach, the gird cells must be larger than the particle size [24, 37]. This limitation is satisfied in our generated mesh.

At the nozzle inlet, we use the TurbulentInlet boundary condition of OpenFOAM for the gas velocity, which imposes a fluctuating inlet condition by adding a random component to the bulk gas velocity, and the Neumann boundary condition for the pressure. At the nozzle wall, we apply the no-slip boundary condition for the gas velocity and the Neumann boundary condition for the pressure. On the jet exit boundary and on the open lateral boundaries, we use the Neumann boundary condition for the gas velocity and the constant total pressure. Particles are injected at the nozzle inlet with a random position and a random initial particle velocity according to $\varvec{u}_{p,\mathrm {inlet}} = a\, ( \varvec{e}_z + b\, \varvec{Y})$, where a and b are considered to be $20~\mathrm {m~s}^{-1}$ and 0.5 and $\varvec{Y}$ is a normally distributed random vector. Having performed a sensitivity analysis, we ascertained that the results at the nozzle exit as well as throughout the jet region are independent of the considered inlet boundary condition. This analysis is discussed in detail in Appendix, for completeness.

The unladen flow simulation is conducted until $t=0.01\,\mathrm {s}$ to reach the statistically steady state. Random injection of particles at the nozzle inlet begins at $t=0.01\,\mathrm {s}$ and the simulations run until $t=0.1\,\mathrm {s}$ to reach the statistically steady-state particle-laden flow. The statistical temporal averaging is then performed between $t=0.1\,\mathrm {s}$ and $t=1\,\mathrm {s}$. This time window is approximately two times larger than the one for the experiments. To improve the clarity of the results, we apply an averaging spatial filter with an interval of $\Delta r/D = 0.1$ for the radial distribution profiles of the particle properties, and an averaging spatial filter with an interval of $\Delta z/D = 0.5$ for the axial distribution profiles of the particle properties. Here r and z indicate radial and axial directions, respectively (see Fig. 5a).

3.3 Verification of the code

To examine the performance of our point-particle LES code and particularly to validate the implemented wall roughness model, we simulate a particle-laden flow in a horizontal channel and compare the obtained results with those of experimental work of Kussin and Sommerfeld [16]. The results of this previous work have been also used by Mallouppas and van Wachem [21] to verify their point-particle LES code. Our main reasons to choose this previous work as the verification case are their high Stokes number particles and their precisely measured standard deviation of the roughness angle distribution. Following Mallouppas and van Wachem [21], we consider a rectangular prism computational domain with the size of $L_x=0.175~\mathrm {m}$, $L_y=0.035~\mathrm {m}$, and $L_z= 0.035~\mathrm {m}$, where the subscripts x, y, and z indicate the streamwise, the wall-normal, and the spanwise directions, respectively. The domain is periodic in the x and z directions. Air and glass beads are considered as the carrier and the dispersed phases, respectively. We fix the bulk air velocity $u_{b,\mathrm {air}}=19.7~\mathrm {m~s^{-1}}$, which results in $Re=42585$ given that $\rho _\mathrm {air}=1.15~\mathrm {kg~m^{-3}}$ and $\mu _{air} = 1.862 \times 10^{-5}~\mathrm {kg~m^{-1}~s^{-1}}$. Monodisperse spherical particles are considered with an average diameter of $d_p=195\mu m$, the density of $\rho _\mathrm {glass} =2500~\mathrm {kg~m^{-3}}$, the coefficient of friction of 0.3, and the coefficient of restitution of 0.95, which are the same values as in [24]. We consider the mass loading $\Phi _m = 1$, which results in the number of particles to be $N_p \simeq 25000$. We take into account gas-particle and particle-particle interactions, and conduct one simulation with the smooth wall and one simulation with the rough wall, in which $\Delta \gamma$ is set to be $5^\circ$, according to Lain et al. [38].

Figure 6 compares the numerical simulation and experimental results for the mean velocities, the root-mean-square of velocities, and the particle distribution as a function of the normalized channel height. Angle brackets denote averaging over time, and $\overline{\Phi }_v$ is the bulk-mean particle volume fraction. It is immediately evident that the wall roughness plays an indispensable role in determining the dynamics of particles, leading to stronger transverse dispersion of the particles. This in turn results in a considerable reduction of the mean particle velocity and in the uniform distribution of the particles throughout the channel. The observed good agreement between the results of the experiment and the rough-wall simulation corroborates that our code is capable of producing trustworthy results.

Fig. 6

Comparison of the simulation and experimental results for the particle-laden flow in a horizontal channel. a The mean gas and particle streamwise velocity, b the fluctuation intensity of gas and particle streamwise velocity, and c the mean particle volume fraction normalized by the bulk-mean value in the particle-laden horizontal channel flow. Lines indicate the simulation results and symbols the experimental results of Kussin and Sommerfeld [16]

4 Results and discussion

In this section, we first investigate effects of the wall roughness on different particle properties using the numerical simulations and then compare the simulation and experimental results, illustrating that modeling of wall roughness is of essence to obtain a good agreement between them. Finally, we discuss and rationalize dependence of the particle properties on the particle size.

4.1 Effects of wall roughness

Figure 7 illustrates the instantaneous snapshots of the gas velocity on the vertical plane together with the position and the velocity of particles for cases R0, R3, and R6. Images only show a small part of the nozzle, and the particles are enlarged by a factor of ten for a better visualization. No discernible effects of particles on turbulent structures are observed, and the preserving core of length few nozzle diameters, through which a low rate of gas velocity decay occurs, is captured in all simulations. The most striking features are that with increasing $\Delta \gamma$, the divergence of the powder flow grows and the particle velocity reduces. This dependence is attributed to the higher frequency of the inelastic particle-wall collision in cases with higher $\Delta \gamma$, causing that the particles in these cases lose more kinetic energy within the nozzle and leave it with a larger angle with respect to the nozzle axis. We note that a smaller particle velocity results in a larger number of particles in the system, according to

$$\begin{aligned} \dot{m}_p =\frac{\pi D^2}{4} \rho _p\, \overline{\Phi }_v\, u_{p,b}\;, \end{aligned}$$

(7)

given that the particle mass flow rate is constant among the considered cases (cf. Table 1). Here $\overline{\Phi }_v$ is the bulk-mean particle volume fraction defined as

$$\begin{aligned} \overline{\Phi }_v = \frac{8}{D^2} \int _{0}^{D/2} \langle \Phi _v(r) \rangle _{z=0}\, r\, \mathrm {d}r\;, \end{aligned}$$

(8)

and $u_{p,\mathrm {bulk}}$ is the bulk-mean velocity of particles defined as

$$\begin{aligned} u_{p,\mathrm {bulk}} = \frac{8}{D^2} \int _{0}^{D/2} \langle u_p(r) \rangle _{z=0}\, r\, \mathrm {d}r\;, \end{aligned}$$

(9)

where $\langle \Phi _v \rangle _{z=0}$ and $\langle u_p \rangle _{z=0}$ are the mean particle volume fraction and the mean particle velocity at the nozzle exit [22]. Figure 7 also indicates that those particles that can reach the jet edge have smaller velocity. This is well explained by the fact that these high-inertia particles very likely had a collision with the nozzle wall in the proximity of the nozzle outlet, in the process of which a large amount of their momentum is lost. It is important to point out that considerably larger scattering rate of the particles and smaller particle velocity in case R6 compared to case R0 are partly a consequence of the larger bulk-mean particle volume fraction, $\overline{\Phi }_v$, as this non-dimensional parameter determines the frequency of inelastic inter-particle collisions.

Fig. 7

Dependence of the gas and particle statistics on the wall roughness. Instantaneous snapshots of the gas velocity, $\overline{u}_f$, on the vertical plane together with the particle position and the particle velocity, $u_p$, for a the unladen case, b R0, c R3, and d R6. (Images only show a small part of the nozzle, and the particles are enlarged by a factor of ten for a better visualization. Opacity mapping for the vertical plane is used to also show the particles behind the plane)

Figure 8 shows the axial distribution of the centerline normalized mean particle velocity, $\langle u_p \rangle _\mathrm {c}/u_b$, and the centerline mean particle volume fraction, $\langle \Phi _v \rangle _\mathrm {c}$. The subscript c denotes the centerline, and $z/D = -58.8$ and $z/D=0$ indicate the nozzle inlet and outlet, respectively. Consistent with visualizations in Fig. 7, we observe that with increasing the standard deviation of the roughness angle distribution, the mean particle velocity considerably decreases and thus the mean particle volume fraction substantially increases, according to Eq. (7). Figure 8 also indicates that considering the wall roughness considerably reduces the required nozzle length to reach the fully developed particle-laden flows. The entrance length for the case with the smooth wall is $\simeq 40\,D = 68~\mathrm {mm}$, while this length for the rough-wall case with $\Delta \gamma =6^\circ$ is $\simeq 18\,D = 30~\mathrm {mm}$. This finding is of particular relevance for the LMD applications, as nozzles used in these applications are usually short. We note that the entrance length depends on other parameters such as the Stokes number and the mass loading, as well.

Fig. 8

Dependence of the particle statistics on the wall roughness. The axial distribution of a the centerline mean particle velocity normalized by the gas bulk velocity and b the centerline mean particle volume fraction

Particles in reality are accelerated not only within the nozzle but also inside the powder-transport system [11]. Therefore, the entrance length in reality might be smaller than the ones obtained in our numerical simulations, in which the boundary conditions at the inlet have been intentionally chosen as the worst conditions to ascertain that our nozzle is sufficiently long for any cases occurring in reality to establish the fully developed flow at the nozzle outlet. Nonetheless, we stress that the main conclusion from Fig. 8 that considering the wall roughness considerably reduces the entrance length is independent of the evolution of particles throughout the powder-transport system. Owing to the common differences in the properties of the hoses and the nozzles as well as a possible bending along the hoses, the particle velocity and concentration distributions at the nozzle inlet are definitely different than the ones at the nozzle outlet, meaning that even in reality with a long hose, particle properties evolve inside the nozzle.

The particles appear to accelerate right after the nozzle exit (see Fig. 8a). The acceleration of particles mainly lies in the fact that the inelastic wall-particle collisions, which act as a braking mechanism inside the nozzle, suddenly disappear in the jet region. This feature has been also documented in previous work of powder flow simulations for the LMD process [11, 26]. The acceleration of particles in the near field of the jet is a relevant characteristic of the particles with very large Stokes number, as previous work of particle-laden jets has shown that particles with the Stokes number of the order of 10 retain their velocity within the preserving core but remarkably decelerate in the jet far field [22, 39, 40]. The acceleration of particles continues as long as the relative velocity between two phases is large enough (i.e. up to $z \simeq 5\,D$), and particles retain their inertia afterwards (see Fig. 8a). It is important to point out that sufficiently resolving the near-field of the jet is essential to precisely capture the acceleration behaviour. The acceleration rate of particles increases with the wall roughness. The reason is that the braking caused by the wall-particle interaction is stronger in cases with larger $\Delta \gamma$ due to the higher wall-particle collision frequency in these cases. It is worth mentioning that the evolution of the particle velocity within the jet region is important for the LMD process, as the magnitude of the particle velocity primarily determines the particle-laser interaction time [41].

Particles congest at early stage of the nozzle (i.e. at $z \simeq -55\,D$), which is accompanied by a strong reduction of the particle velocity in that region (see Fig. 8). This is because of the chosen boundary condition of particles at the nozzle inlet, which imposes an early collision of particles with the wall. Such a behaviour accounts for insensitivity of the results on initial and boundary conditions such that these conditions are rapidly forgotten inside the nozzle. Particles gradually accelerate after the early congestion due to the drag force exerting on them from the fluid flow, and accordingly, the centerline particle volume fraction declines for $z \gtrsim -55\,D$ (see Fig. 8b). The centerline particle concentration decays right after the nozzle exit, whose rate strongly increases with the wall roughness. This is inferred from the observation in Fig. 8b that, although $\langle \Phi _v \rangle _\mathrm {c}$ at the nozzle outlet for case R6 is approximately three times larger than the one for case R0, this quantity for case R6 drops below the one for case R0 for $z \gtrsim 5\,D$.

Figure 9 illustrates the radial distribution of the normalized mean particle velocity and the normalized mean particle volume fraction at different levels. These results correspond to the symmetry axis of the nozzle, and the top panel shows the results at the nozzle outlet and the bottom panel within the jet region at $z=5\,D = 8.5~\mathrm {mm}$. It is evident that a large number of particles accumulate in the near-wall region in the simulation with the smooth wall, causing that the particle velocity profile becomes convex. The observed preferential accumulation of particles occurs mainly because of the small value of the coefficient of restitution, which leads to the fact that the particles lose a large amount of their kinetic energy after a collision with wall such that they can not reach the nozzle core anymore.

Fig. 9

Dependence of the particle statistics on the wall roughness. The radial distribution of a, c the normalized mean particle velocity and b, d the normalized mean particle volume fraction at different levels. Panels (a, b) show the results at the nozzle outlet, $z=0$, and panels (c, d) inside the jet region at $z=5\,D$. $\mathrm {R0-COR0.99}$ corresponds to the extra simulation with the same parameter space as R0 but the coefficient of restitution of 0.99

The wall roughness enhances the transverse dispersion of particles by increasing the particle-wall collision frequency. It follows that with increasing $\Delta \gamma$, first, the preferential accumulation of particles in the near-wall region monotonically diminishes (see Fig. 9b), and second, the profile of the mean particle velocity flattens and its magnitude considerably reduces (see Fig. 9a). The former behaviour is attributed to the fact that those particles colliding with a rough wall in average tend to be suspended into the bulk of the flow instead of remaining near the wall. The latter behaviour is explained by the inelastic particle-wall collision process, through which the particle kinetic energy is lost. We note that the convex-shape profile for the particle concentration has been also reported in previous literature of particle-laden jets with two orders of magnitude smaller Stokes number but comparable bulk-mean particle volume fraction as in our simulations [42, 43].

The preferential accumulation of particles in the near-wall region, to the best of our knowledge, has not been reported in previous numerical simulations of powder flows for the LMD process. Our further analysis indicated that considering a nonphysically large value for the restitution of coefficient with smooth wall could eliminate the particle accumulation near wall. However, the mean velocity of particles appears to be much larger than in the rough-wall cases. To clarify this, we conduct an extra numerical simulation with the smooth wall and the coefficient of restitution of 0.99. We refer to this case as $\mathrm {R0-COR0.99}$, whose results are also incorporated in Fig. 9 by circle symbols. As shown, the particle accumulation in the near-wall region vanishes, but the centerline mean velocity of particles is by a factor of $\simeq 1.5$ larger than in the rough-wall case with $\Delta \gamma = 6^\circ$. As explained in the introduction, the nozzle considered in previous work was normally very short such that inlet boundary conditions were not sufficiently forgotten at the nozzle outlet. A good agreement was, hence, obtained between numerical simulation and experimental results by carefully adjusting the particle velocity at the nozzle inlet [11, 26]. We recall that our results within the jet region are independent of the chosen initial and boundary conditions.

Fig. 10

A method to determine the concentration distribution corresponding to all particles from the numerical simulations. In panel (g), $\widetilde{\Phi }_v$ is the integrated particle concentration over y direction and $\overline{\widetilde{\Phi }}_v$ is its corresponding bulk value at the nozzle exit

The radial profiles of the particle velocity inside the jet region, as shown in Fig. 9c, indicate that the deviation in the particle velocity among different cases at the nozzle outlet is retained in the core region of the jet. This means that the particle velocity in the jet region reduces with the wall roughness. The divergence of the powder flow appears to grow with $\Delta \gamma$, as the radial profiles of the normalized particle volume fraction at $z=5\,D$ monotonically widen (see Fig. 9d). Consistent with previous work [6, 13], we find these profiles to resemble the Gaussian profile.

Careful attention must be paid to compare simulation and experimental results in a consistent framework. To calculate the average particle velocity within the evaluation window in numerical simulations in a robust manner, we first take the integral of the mean particle velocity at different levels below the nozzle outlet with an interval of $1~\mathrm {mm}$ by taking into account the mean particle concentration as the weighting factor. We then calculate the mean value using the ones corresponding to all levels. We determine the powder concentration distribution from the experiments by normalizing the distribution of the number of detected particles obtained from the superposition of the binarized images by their corresponding bulk value at the nozzle exit. This distribution, as indicated in Sect. 2.3, correspond to the whole ejected particles not to the symmetry axis of the nozzle as the white sheet paper has been placed behind the powder flow. To obtain an equivalent particle concentration distribution corresponding to all particles from the simulations, we first calculate the mean particle volume fraction distribution at several vertical planes that are parallel to but uniformly deviated from the symmetry axis of the nozzle (see Fig. 10a). We then integrate the distributions by taking into account the interval of $0.25\,D$ and finally normalize the obtained distribution, i.e. $\widetilde{\Phi }$, by its corresponding bulk value at the nozzle exit, i.e. $\overline{\widetilde{\Phi }}$. This analysis is shown in Fig. 10 for case R6. Comparison of Fig. 10b and g illustrates that considering the whole ejected particles to determine the particle concentration distribution results in an up-scaled particle concentration at far away from the nozzle exit with respect to the symmetry axis of the nozzle. In the following, we show that this observation is analytically supported and we determine the scaling factor between the integrated particle concentration profile corresponding to all ejected particles and the particle concentration profile corresponding to the symmetry axis.

Fig. 11

The distribution of the mean particle volume fraction along x direction for case R6 at $z/D=4$ for the different vertical cross sections as well as the corresponding integrated and the modeled profiles

We approximate the mean particle concentration distribution at each height with the normal distribution function

$$\begin{aligned} \langle \Phi _v (r_*) \rangle &= \Phi _{v,\mathrm {max}}\, \mathrm {exp}\bigg [-\frac{r_*^2}{2\,\sigma ^2}\bigg ] \Rightarrow \\ \langle \Phi _v (x_*, y_*) \rangle &= \Phi _{v,\mathrm {max}}\, \mathrm {exp}\bigg [-\frac{x_*^2 + y_*^2 }{2\,\sigma ^2}\bigg ]\;, \end{aligned}$$

(10)

where the subscript $*$ indicates normalization with the pipe diameter, x and y are the Cartesian coordinate system with $r=\sqrt{x^2+y^2}$, $\Phi _{v,\mathrm {max}}$ is the mean particle volume fraction value at $x=0$, and $\sigma$ is the standard deviation of the normal distribution function. Integrating Eq. 10 in y direction also yields a normal distribution as

$$\begin{aligned} \begin{aligned} \widetilde{\Phi }_v (x_*) &= \int _{-\infty }^{\infty } \langle \Phi (x_*, y_*) \rangle dy_*\\&= \Phi _{v,\mathrm {max}}\, \mathrm {exp}\bigg [-\frac{x_*^2 }{2\,\sigma ^2}\bigg ] \times \int _{-\infty }^{\infty } \mathrm {exp}\bigg [-\frac{y_*^2 }{2\,\sigma ^2}\bigg ] dy_* \\&= \Phi _{v,\mathrm {max}}\, \mathrm {exp}\bigg [-\frac{x_*^2 }{2\,\sigma ^2}\bigg ]\, \times \sqrt{2\,\pi \,\sigma ^2} \;. \end{aligned} \end{aligned}$$

(11)

Comparison of Eqs. 10 and 11 leads us to propose a model for the integrated particle volume fraction as

$$\begin{aligned} \widetilde{\Phi }_v (x_*)= \sqrt{2\,\pi \,\sigma ^2} \times \langle \Phi _v(x_*) \rangle _{y=0}\;. \end{aligned}$$

(12)

This relationship supports the observation in Fig. 10 that considering the whole ejected particles to determine the particle concentration distribution leads to an up-scaled particle concentration with respect to the nozzle symmetry axis. The scaling factor $\sqrt{2\,\pi \,\sigma ^2}$ can be determined using the normal distribution approximation and the calculated standard deviation from the numerical simulation results. Figure 11 shows the radial distribution of the mean particle volume fraction for case R6 at $z/D=4$ for the different vertical cross sections as well as for the integrated profile. Approximating the concentration distribution profile corresponding to the symmetry axis, i.e. $y=0$, with the normal distribution, we obtain $\sigma ^2 \simeq 0.4$. The modeled concentration distribution profile according to Eq. (12) appears to fit very well with the calculated integrated profile, as shown in Fig. 11.

Fig. 12

Dependence of the particle statistics on the wall roughness. Comparison of simulation and experimental results of the average particle velocity and the integrated concentration distribution of all particles within the evaluation window

Figure 12 compares the experimental and numerical simulation results of the average particle velocity as well as the concentration distributions corresponding to all particles for the cases with $d_p = 50\mu\mathrm {m}$, $\dot{m}_p=4~\mathrm {g~min^{-1}}$, and $\dot{v}_g = 5~\mathrm {L~min}^{-1}$. Results clearly indicate that modeling of the wall roughness is essential to obtain a good agreement between the simulation and experimental results. In particular, Fig. 12b confirms that no particles in reality accumulate in the near-wall region, rather they preferably cluster within the nozzle core. The best agreement in terms of the average particle velocity and the particle concentration distribution between the experimental and simulation results is obtained for $\Delta \gamma \simeq 6^\circ$, which is consistent with the calculated value of $\Delta \gamma$ from the two-dimensional roughness profiles of the inner nozzle surface in Sect. 2.2.

4.2 Effects of particle size

In the following, we study effects of the particle size on particle statistics by considering three cases with $d_p=50$, 75, and 95 ${\mu}\mathrm {m}$. We note that a variation of the particle size with keeping other parameters constant modifies not only the Stokes number but also slightly the bulk-mean particle volume fraction according to Eq. (7), as the bulk particle velocity varies with the particle size. A good agreement between the numerical simulation and experimental results is observed in Fig. 13, confirming again that the employed point-particle LES with the implemented wall roughness model produce reliable results for a wide range of the parameter space occurring in the LMD processes. It is also evident in Fig. 13a that larger particles move slower. While the mean velocity of particles for the experiment case with $d_p=50\mu \mathrm {m}$ is $10.29~\mathrm {m~s}^{-1}$, this value is $9.14~\mathrm {m~s}^{-1}$ and $8.7~\mathrm {m~s}^{-1}$ for the experiment cases with $d_p=75$ and $95\mu \mathrm {m}$, respectively. The reason is that the Stokes number in case D50 is approximately two and four times smaller than the ones in cases D75 and D95, respectively (see Table 1). The bulk-mean particle volume fraction at the nozzle outlet increases with Stokes number, according to Eq. (7). We obtain $\overline{\Phi }_v \simeq 0.047\%$, $0.051\%$, and $0.059\%$ for cases D50, D75, and D95, respectively (see Table 1). The particle size appears to have negligible effect on the particle concentration distribution, which is attributable to the very large Stokes numbers considered in this work.

Fig. 13

Dependence of the particle statistics on the particle size. Comparison of simulation and experimental results of the average particle velocity and the integrated concentration distribution of all particles within the evaluation window

To provide more insight into the dependence of the particle properties on the particle size, we plot in Fig. 14 the radial profiles of the normalized mean particle velocity and the normalized particle concentration at different levels using the simulation results. These profiles, in contrast to the contours in Fig. 13, correspond to the symmetry axis of the nozzle. The dotted lines indicate the results at the nozzle outlet, the dashed lines at $z=2\,D = 3.4~\mathrm {mm}$, and the solid lines at $z=5\,D = 8.5~\mathrm {mm}$. The particle velocity profiles inside the nozzle are almost uniform independent of the Stokes number. We note that the reason is not only high particle mixing due to wall-particle and inter-particle collisions, but also the fact that high-inertia particles are efficient in transferring momentum from the nozzle centre towards the near-wall region. Consistent with Fig. 13a, we observe that the particle velocity decreases with the Stokes number inside the nozzle. This dependence remains unchanged throughout the jet region, even though particles accelerate in the near field of the jet independent of the considered Stokes numbers. Particles accumulate in the nozzle centre and disperse throughout the jet region. Owing to the very large Stokes numbers considered in this work, it is difficult to discern clear effects of the particle size on the concentration distributions. To shed more light on these effects, we extend the range of the considered parameter space for the Stokes number by conducting one extra numerical simulation with the same parameter space as in D50 but with smaller particle size, i.e. $d_p=25\ \mu\mathrm {m}$, which corresponds to $St=263$ according to Eq. (6). We refer to this case as D25, whose results are also incorporated in Fig. 14b. It is evident that in this case more particles cluster within the nozzle core and particles disperse less throughout the jet region. These results allow us to infer a saturation pattern in the variation of the particle scattering rate with the Stokes number such that the Stokes number effects on the particle dispersion behaviour is negligible for $St \ \gtrsim\ 1000$. We note that the same variation of the powder divergence with the particle size has been documented in Jeromen et al. [9]. In particular, they have observed that the powder-stream diameter at a workpiece-standoff distance of 8 mm grows by $\simeq 20\%$ with increasing the mean particle size from $22\ \mu\mathrm {m}$ to $82\ \mu\mathrm {m}$, while the powder-stream diameter remains almost unchanged with increasing the mean particle size from $82\ \mu\mathrm {m}$ to $132\ \mu\mathrm {m}$.

Fig. 14

Dependence of the particle statistics on the particle size. The radial distribution of a the normalized mean particle velocity and b the normalized mean particle volume fraction corresponding to the symmetry axis at different levels

5 Conclusion

An analysis of effects of wall roughness and particle size on characteristics of a powder flow issuing from a vertical, round nozzle has been performed by means of high-speed imaging and point-particle large-eddy simulations. The standard deviation of roughness angle distribution $\Delta \gamma$, which is a hybrid parameter that represents a combination of amplitude and spacing roughness parameters, can fully characterize wall roughness effects on particle-wall collisions. The inner nozzle surface has been optically scanned to obtain the 2D roughness profiles, using which $\Delta \gamma$ is estimated based on the model proposed by Novelletto Ricardo and Sommerfeld [19]. In the numerical simulations, the soft-sphere model has been used to consider both gas-particle and inter-particle interactions, and a stochastic approach has been taken to model the wall roughness. The employed code has been verified by simulating a particle-laden horizontal channel flow and comparing the obtained first- and second-order statistics with those of experimental work of Kussin and Sommerfeld [16]. Dimensional analysis enabled us to study effects of the aforementioned parameters in a systematic manner using a Stokes number, St, and the standard deviation of the roughness angle distribution, $\Delta \gamma$. We study effects of these parameters for the range $St \simeq 1050$–3790 and $\Delta \gamma = 0^\circ - 6^\circ$ for the fixed values of the Reynolds number $Re=5000$ and the mass loading $\Phi _m=0.45$. The considered parameter space corresponds to the typical conditions in the laser metal deposition processes.

We found that wall roughness needs to be appropriately modeled in numerical simulations to obtain an acceptable agreement between results of simulations and experiments. Our results additionally revealed the main characteristics of the powder flow in laser metal deposition process: (i) The particles cluster in the nozzle centre, forming a convex-shape particle distribution profile. This feature was attributed to interaction of particles with the rough wall. (ii) The particles spread right after the nozzle outlet. (iii) The particle velocity profiles inside the nozzle are almost uniform mainly owing to the high particle-wall collision frequency. (iv) Particles accelerate in the near field of the jet because inelastic wall-particle collisions, through which a large amount of particle momentum is lost, suddenly disappears in the jet region.

Results indicated that the Stokes number and the wall roughness have significant impacts on the particle velocity and concentration fields. The dependence of the aforementioned main characteristics of the powder flow on these non-dimensional parameters is as follows. (i) The degree of convexity in the particle concentration profile inside the nozzle considerably grows with increasing $\Delta \gamma$ but slightly reduces with an increase in St. (ii) The divergence of the powder flow grows with St and $\Delta \gamma$. However, a saturation pattern in the variation of the particle scattering rate with the Stokes number was observed such that the Stokes number effects on the particle dispersion behaviour was found to be negligible for $St \gtrsim 1000$. (iii) The mean particle velocity strongly reduces with St and $\Delta \gamma$. (iv) The acceleration rate of particles within the near field of the jet grows with St and $\Delta \gamma$. All this dependence is well explained by the fact that the wall roughness and the Stokes number characterize the inelastic particle-wall collision frequency and the particle response to the gas flow, respectively.

The main practical implications of this research for laser metal deposition process are as follows: Firstly, we conclude that a higher powder catchment efficiency, owing to a smaller powder diameter, can be achieved using a nozzle that has a smooth, wear-resistant inner surface. This conclusion is consistent with recent experimental results of Jeromen et al. [9], where smaller powder-stream diameter has been reported for smoother inner surface of nozzles. Secondly, we conclude that relevant effects of wall roughness on particle dynamics need to be considered to develop a precise numerical simulation of laser metal deposition. This numerical simulation, owing to providing fast solutions with much lower cost in comparison to expensive and technically difficult experiments, can be used to optimize parameter set in laser metal deposition.

Appendix

1.1 Sensitivity analysis of the inlet boundary condition for particles

Here we perform a sensitivity analysis to ascertain that our considered nozzle with the length of 100 mm is long enough to forget the inlet boundary conditions, and hence, the particle statistics of interest at the nozzle exit as well as throughout the jet region are independent of the chosen inlet boundary condition for particles. As explained in the main text, particles are injected at the nozzle inlet with a random position and a random initial particle velocity according to

$$\begin{aligned} \varvec{u}_{p,\mathrm {inlet}} = a\, ( \varvec{e}_z + b\, \varvec{Y})\;, \end{aligned}$$

(13)

where a and b are constant and $\varvec{Y}$ is a normally distributed random vector. To conduct the sensitivity analysis, we consider five cases with $d_p = 50\ \mu\mathrm {m}$, $\Delta \gamma =6^\circ$, $\dot{m}_p=4~\mathrm {g~min^{-1}}$, $\dot{v}_g = 5~\mathrm {L~min}^{-1}$ and different values of a and b (see Table 2). Figure 15 shows the axial evolution of the centerline mean particle velocity and the centerline mean particle volume fraction for these cases. It is immediately evident that the inlet boundary conditions are forgotten within the first $\simeq 40$ mm of the nozzle, as the particle statistics for all cases fall on top of each other at $z/D \simeq -45$ and remain unchanged afterwards. We recall that the required nozzle length to reach the fully developed particle-laden flows increases with decreasing $\Delta \gamma$ as discussed in the main text. The small value of b in Case IV accounts for the moderate, continuous reduction of the particle velocity within the first $\simeq 40$ mm of the nozzle, since the parameter space in the LMD process corresponds to the inertia- or collision-dominated regime [22] and considering a small value of b in Eq. (13) postpones first collisions of particles with the nozzle wall.

Table 2 Values of constants a and b in Eq. (13) for different cases. Case I corresponds to the case presented in the main text

Fig. 15

The axial distribution of a the centerline mean particle velocity normalized by the gas bulk velocity and b the centerline mean particle volume fraction