1 Introduction

Laser-based powder bed fusion of plastics (PBF-LB/P), which is also referred to as laser sintering, is an additive manufacturing (AM) process that enables the production of parts with a high level of geometric freedom. In addition to market-dominating polyamides (PA12, PA11, PA6), only a small number of polymers such as polyether ether ketones (PEEK), polypropylene (PP), and thermoplastic polyurethanes (TPU) are commercially available. To open further fields of application, the available range of materials needs to be expanded. Therefore, new types of plastic powders and filled systems are increasingly being investigated [1]. However, the qualification of new plastic powders is associated with an extensive design of experiments as illustrated by studies on PA12 [2], PEEK [3], PP [4], or polystyrene (PS) [5]. The predominant topic of these investigations is the influence of process parameters (e.g., laser power, scan speed, or process temperatures) on part properties such as mechanical properties, density, or porosity [1].

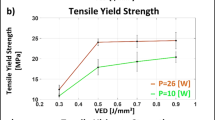
The tensile strength of thermoplastics primarily depends on the energy delivered by the laser beam to the polymer powder. For PA12, a plateau of mechanical properties is reached at volumetric energy density values between 0.25 and 0.4 J/mm3. However, the properties of PA12 parts exhibit comparatively low reproducibility, as illustrated in Fig. 1. Bourell et al. [6] further emphasize the low level of reproducibility based on 68,000 PA11 tensile test bars which were manufactured over 10 years. Therefore, it is still state-of-the-art to reevaluate the influence of all process parameters on the properties of the resulting parts each time a new feedstock material is qualified. To enhance the reproducibility of the part properties and to increase the range of available materials, efforts are being made to improve the understanding of the process based on process simulation and process visualization or, rather, monitoring. Consequently, process monitoring systems are increasingly used in research to analyze the interaction between input variables (e.g., process parameters, part geometry, or build job layout), intermediate process variables (e.g., melt and powder temperatures or condition of the build surface), and part properties.

Fig. 1
figure 1

Ultimate tensile strength of PBF-LB/P test samples made from PA12 as a function of volumetric energy density with a plateau region of the mechanical properties between 0.25 and 0.4 J/mm.3. Aggregation of data from the published literature [7,8,9,10,11,12]

Full size image

In situ monitoring systems normally rely either on geometrical or temperature data. Optical coherence tomography (OCT) and fringe projection are methods that utilize geometrical data to detect PBF-LB/P process defects. An OCT is an optical setup with an interferometer, whose beam can be coaligned with the CO2 laser beam, to gather information about surface texture and subsurface powder, which is not sufficiently melted [13]. Furthermore, OCT systems can detect process defects, such as curling, or part defects, such as pores and their position [14]. Possible applications are the verification of process stability or part integrity [15]. Since these methods only process localized geometrical data, they do not provide further structural information, such as the pore size distribution or the resulting part density. In situ monitoring systems based on fringe projection analyze the surface topography of the powder bed [16]. This method can detect the contours of exposed cross-sections [17] and identify various types of structural defects such as curling [18]. In addition to the identification of surface irregularities, fringe projection can also be applied to assess contour accuracy by reconstructing the 3D shape of the part layer by layer [19]. While geometric data enable layer-wise anomaly detection to avoid the failure of a build process, a derivation of correlations between process parameters and part properties is not possible.

In contrast, the implementation of infrared cameras allows the analysis of temperature profiles of the powder and the melt pool in time and space. Bourell et al. [20] used infrared thermography to identify a homogeneous temperature distribution on the powder surface as a prerequisite for improved reproducibility. In addition, Abdelrahman et al. [21] define peak temperature during exposure and the temperature before material coating as important intermediate process variables. Also, the varying return times of the laser beam, which are a function of the underlying part geometry, scan speed, and hatch distance, influence the resulting melt pool temperature [22, 23] as well as the mechanical properties [24]. Greiner et al. [25] correlate the influence of exposed cross-sectional area, scan, and laser parameters at constant energy density ED on melt pool temperatures with part density and morphology. Furthermore, the peak temperatures of the melt pool are correlated with the tensile strength and elongation at the break by Wroe et al. [26]. Phillips et al. [27] use this finding to design a feed-forward laser control that adjusts the laser power to achieve a uniform peak melt temperature and improve the reproducibility of the mechanical properties. Schlicht et al. [28] also illustrate that uniform geometry-invariant temperature fields are a decisive factor in PBF-LB/P processing by utilizing exposure patterns with a scale-invariant structure to process parts in non-isothermal conditions. However, the influence of the interactions between the underlying part geometry and the used exposure parameters on the melt pool properties have so far only been assessed qualitatively. Only mean and maximum temperatures during exposure, as well as a temperature at an arbitrary moment after exposure at which the melt has cooled down to process temperature, are analyzed in the literature. However, it is hypothesized that the cool down from peak temperature to process temperature must also be considered to derive correlations between exposure parameters, part geometry, and part properties. This assumption is supported by the findings of Chatham et al. [29], which relate the transition in the consolidation regime from viscous coalescence to bubble diffusion to the lower boundary of the plateau of the mechanical properties by evaluating the temperature of the melt as a discrete function of the time at which viscous flow can occur. Since absolute process temperatures serve as input variables and due to other simplifications in the analytical process model, unphysical solutions are calculated, e.g., for incompletely melted powders at low energy inputs. This is in part due to the temperature-dependent emissivity of plastic powders, which depends on the aggregate state [30]. Therefore, analytical process models are not suitable to evaluate the influence of the interaction of exposure parameters and component geometry on the resulting part properties. Melt pools generated with energy densities outside the plateau of mechanical properties need to be investigated further to still quantify these effects with thermal process data from in situ monitoring systems. Furthermore, representative thermal metrics that are based on relative instead of absolute melt pool temperatures need to be identified. However, there is currently no method available to quantitatively evaluate the cooling behavior in a reproducible way. Therefore, decay values, which can be used to characterize the cool down behavior of the melt and are derived from the cooling rate of the melt pool, as well as coefficients of functions, which fit transient temperature profiles, are evaluated for this purpose within the scope of this work.

2 Materials and methods

2.1 Material and powder characterization

A PA12 powder (PA2200, EOS GmbH) with the properties listed in Table 1 is used for the experiments. The powder is a 50:50 mixture of virgin and recycled powder, which corresponds to the industrial standard. The rheological properties are determined using a melt flow indexer (Mflow, Zwick Roell GmbH & Co.KG). The melt volume rate is measured according to DIN EN ISO 1133 at 230 °C under a load of 2.16 kg. The bulk density measurement is performed according to DIN EN ISO 60. The results show that no noticeable effects on the processability or infrared thermography are expected.

Table 1 Material properties of the polyamide 12 powder used
Full size table

2.2 Experimental setup

The experiments are performed on a Formiga P100 (EOS GmbH). A high-speed infrared camera is mounted at an angle of approx. 14° to the vertical axis (ImageR 8300, InfraTec GmbH: spectral range from 1.5 to 5.7 µm, detector format of 640 × 512 pixel, frequency of 200 Hz). A window made of sapphire glass protects the camera from reflected laser radiation. The resulting field of view (diameter of approx. 35 mm) is close to the center of the build surface (200 × 250 mm). The mounted macro-lens resolves the build surface with approx. 80 µm/px. This setup is used to monitor the exposure of single-layer specimens with a cross-section of 10 × 10 mm2. Thus, four single-layer specimens are placed in the field of view of the infrared camera in each layer. The combinations of parameters analyzed are divided into groups A and B, which are positioned in an alternating sequence along the z-axis. The order of exposure within a layer is from the lowest to the highest energy density. Twelve samples are manufactured for each of the 8 different parameter sets (96 samples in total). The exact arrangement and positioning of the single-layer specimens are visualized in Fig. 2.

Fig. 2
figure 2

(I) Schematic sketch of the experimental setup and the PBF-LB/P system used (II) with a visualization of the position and arrangement of the single-layer specimen on the build surface and (III) within the build volume, and (IV) of the assigned process parameters

Full size image

2.2.1 Processing parameters

The processing temperatures are set to 170 °C for the powder surface and 150 °C for the building chamber. Contour exposure is deliberately omitted to avoid edge effects, which are undesirable in the evaluation of the process-specific cooling behavior. The single-layer specimens are exposed with the parameters listed in Table 2. The layer height is 100 µm, and the layer time is constant for all specimens. The selection of process parameters is based on industrial standards and the findings of Wegner [8] who previously characterized PA2200 powder on an identical PBF-LB/P system. The process parameters cover a wide range of energy densities with varying scan parameters to enable the development of a robust and reproducible method to characterize melt pool temperatures during and after laser exposure. A full factorial design of experiments with an analysis of the corresponding properties of multilayer test specimens, such as density cubes of varying sizes or tensile tests, will be carried out at a later stage of this research.

Table 2 Exposure parameters for single-layer specimen
Full size table

2.2.2 Part characterization

The surface roughness is analyzed (VK-X1000, Keyence) to characterize the properties of the single-layer specimen. Following Heinl et al. [31], the focus variation technique is chosen to evaluate the area roughness of the up-skin surface of the additively manufactured parts. The mean arithmetic height Sa and the root mean square height Sq are determined according to DIN EN ISO 25,178–2 with suitable filter options based on DIN EN ISO 25,178–3. Thus, a square-shaped measuring area with an edge length of 5 mm is defined in the center of the samples (Fig. 3). The microscope is also used for visual examination since the entire surface of the single-layer specimens is imaged for the surface roughness measurement.

Fig. 3
figure 3

Visualization of the measuring area for the surface roughness measurement

Full size image

2.2.3 Data processing

Infrared thermography is used to monitor the mean temperature Tmean in the exposed cross-section of the single-layer specimens as visualized in Fig. 4. The temperature decay following the exposure T(t) is fitted to remove noise. Furthermore, this approach simplifies data storage since only the fit coefficients must be archived and the raw data can be discarded. Thus, the transient temperature profiles can be reconstructed for later evaluations. For reference, in this experiment, the size of time series files (Tmean) is approx. 1 MB/layer while the final matrix, which includes fit coefficients and decay values, is less than 4 KB/layer.

Fig. 4
figure 4

Visualization of the recording and processing of the mean temperatures of the exposed cross-section of the single-layer specimens with subsequent extraction of the decay time tdecay, the decay temperature Tdecay, the peak of the mean temperature Tpeak, and their temperature difference ΔT from a transient temperature profile at an arbitrary cooling rate i

Full size image

The surface temperature following laser exposure in a PBF process can be calculated from laser power P, scan speed v, hatch distance h, density ρ, thermal diffusivity α, specific heat capacity cp, absorption coefficient µa, and an empirically determined correction factor k (Eq. 1) [32]. This model includes simplifications such as a static heat source that releases energy into the volume in a flash. This is comparable to the present approach which evaluates Tmean in a measurement area that corresponds with the exposed cross section.

$$T\left(t\right)=\frac{k {\mu }_{a} P}{v h {c}_{p} \rho \sqrt{\pi \alpha }} \frac{1}{\sqrt{t}}+{T}_{0}$$
(1)

The temperature data, which is recorded with infrared cameras, does not correspond to the actual melt pool temperatures since the emissivity ε is temperature dependent and not constant during the phase transition from solid powder to liquid melt [33]. However, it is common practice to evaluate the cooling of objects with a constant ε by interpreting temperatures to a reference standard (e.g., in non-destructive testing using active thermography) [34]. Following this approach, the melt pool temperatures are analyzed for ε = 1 and the transient temperature profiles as well as the deduced decay values are compared relative to each other. Furthermore, Eq. 1 is simplified to account for effects, such as a changing emissivity, which are caused by the measurement technique. Therefore, the temperature data is fitted with four coefficients a, b, c, and d (Eq. 2). Alternative fit functions, the fit quality, and the interpretation of the fit coefficients, are further discussed in Sect. 3.1.

$$T\left(t\right)=a \frac{1}{{(t+b)}^{c}}+d$$
(2)

In the literature, a decay time tdecay is recently determined in addition to the maximum and mean temperatures during and at the end of the exposure. Greiner et al. [25] define tdecay as the duration required for Tmean to reach a state of equilibrium after the end of the exposure. Chatham [12] instead determines tdecay at the moment at which an exponential fit of the maximum temperature of the exposed cross-section Tmax comes within 0.2 K of a linear baseline-fit of the transient temperature profile. Since these two approaches only qualify the melt in the equilibrium state, the cooling behavior itself is not quantified. For this purpose, decay values are introduced in this work. By deriving the cooling rate dT/dt from the pre-processed transient temperature profile, tdecay can be further defined as the duration from the end of exposure to the point in time in which the transient temperature profile reaches a specific cooling rate. The decay values are illustrated for cooling rates from − 2 to − 0.25 K/s (Δ 0.25 K/s) to identify a suitable cooling rate that can be used to evaluate the cooling behavior of polymer melts in PBF-LB/P. This range was determined a posteriori to cover time frames in which the influence of the cooling rate, and the energy input on the decay values can be visualized. Therefore, the cooling rates result in decay times after which the melt pool temperature is considered to be in an equilibrium state (e.g., 2 s [12] or 10 s [8]).

The decay values are based on Tmean, since Tmax resembles the temperature of a random pixel with the highest temperature during cooling. In addition, the decay temperature Tdecay is recorded for each tdecay. The peak of the mean temperature Tpeak is also determined. Tpeak is extracted from the raw data to avoid data processing errors. Additionally, the difference ΔT between Tdecay and Tpeak is calculated to assess the temperature decay over the corresponding tdecay. These values serve as simplified metrics that represent transient temperature profiles.

An automated data stream is designed for quick and easy analysis of the thermal process data. The infrared camera software records the process temperatures for 30 s after the start of the exposure, as well as 0.5 s before exposure, using an internal buffer. The time series of Tmean of the exposed cross sections is exported to a script (Python 3.8). This tool computes the sequence of decay values at different cooling rates for each exposed cross-section. Additionally, the origin of the time series (t = 0 s) is automatically set at the end of the exposure. The cooling rate at an arbitrary point in time is calculated from the difference of the mean temperature between two discrete time steps i and i + 1 and the frequency of the thermal recording f (Eq. 3). All individual decay values, Tpeak and the fit coefficients, as well as the mean value and standard deviation of each underlying parameter set, are written to an export file for further evaluation.

$$\frac{dT}{dt }=\frac{{T}_{(i+1)}-{T}_{(i)}}{{t}_{(i+1)}-{t}_{(i)}}={(T}_{(i+1)}-{T}_{\left(i\right)}) f$$
(3)

3 Results and discussion

3.1 Influence of energy density on temperatures of the melt pool

Representative temperature–time curves are generated for each parameter set by averaging the coefficients of the individual fit functions of the transient temperature profile. The resulting mean values and standard deviations of the coefficients are listed in Table 3. Data before the end of exposure are supplemented as a temperature average of all corresponding transient temperature profiles at each discrete time step. Since Tpeak is extracted from the raw data and the decay values are extracted from pre-processed thermal data, these representative transient temperature profiles are for qualitative graphical evaluation only. However, the visualization of the transient temperature profiles in Fig. 5 indicates a significant difference in the cooling behavior. During the exposure of the single-layer specimen, Tmean continuously increases until it reaches its peak at the end of exposure for all parameter sets. Higher energy inputs result in increased Tpeak. Hereafter, the melt pool cools down to process temperature. The higher the energy input, the longer it takes for the melt to reach an equilibrium state.

Table 3 Mean of coefficients for the fit of the transient temperature profile for the individual parameter sets
Full size table
Fig. 5
figure 5

Representative transient temperature profiles of single-layer specimens manufactured with different energy densities

Full size image

Equation 2 shows a good balance between high fit quality (RMSE of approx. 0.1) and short processing times, which are necessary for in situ quality assurance. Coefficient d represents the baseline of the temperature decay which depends on the temperature control of the powder bed surface. Therefore, coefficient d is nearly constant for all parameter sets. In contrast, the coefficient a scales with energy input since it is a function of laser and scan parameters. Coefficients b and c are introduced to compensate for the fact that the cross-section of the components is scanned with a laser beam instead of releasing the energy into the volume at once, as assumed by Eq. 1. Compared to Eq. 1, the exponent c is not constant and increases with higher energy inputs while b is nearly constant for all parameter sets. However, c is close to 0.5 as predicted by the model of the surface temperature (Eq. 1). It can be assumed that the influence of a varying ε during phase transition and temperature cool down affects the raw thermal data. The fit function was found to be not robust with a constant c or without b. An alternative to Eq. 2 with a similar accuracy (RMSE of approx. 0.3) is a two-term exponential fit as used in the literature [12]. Further research is required to evaluate which fit function is better suited to evaluate and distinguish physical effects and distortions caused by the measurement technique. The influence of process parameters, part geometry, and material properties on the coefficients of these and other fit functions will be analyzed in subsequent studies. However, the decay values can already be interpreted independently of the used fit function.

3.2 Influence of energy density and cooling rates on decay values

Following the hypothesis that the cooling rate of the polymer melt influences the properties of PBF-LB/P parts, the transient temperature profile itself determines if a homogenous melt pool is formed. Therefore, tdecay and ΔT are determined at multiple cooling rates to characterize the cooling behavior. The resulting sequence of decay values at different cooling rates contains more information than a single snapshot of the temperature at an arbitrary point in time after the melt has decayed to process temperature. The decay values for an energy input of 0.031 J/mm2 are plotted with their corresponding temperature distributions of the exposed cross-sections in Fig. 6. A larger negative cooling rate increases tdecay and decreases Tdecay. Although Tdecay only changes slightly after a cooling rate of − 2 K/s is reached, tdecay is significantly affected by a change of the cooling rate, especially at small negative cooling rates.

Fig. 6
figure 6

Exemplary result for the decay values and their corresponding thermograms for single-layer specimen manufactured with ED = 0.031 J/mm.2

Full size image

Tpeak corresponds with the maximal cooling rate of a transient temperature profile. Both increase with higher energy inputs. Therefore, Tpeak is not detected accurately at the underlying frame rate at large energy inputs. Since this results in a lower reproducibility of Tpeak, the standard deviation of ΔT is also increased at high energy densities. Tpeak could be determined more precisely in the future by choosing a higher frame rate. However, Tdecay still exhibits a high reproducibility for all cooling rates. This behavior is visualized in Fig. 7 for Tdecay at a cooling rate of − 1 K/s.

Fig. 7
figure 7

Temperature difference between the decay temperature at a cooling rate of − 1 K/s and the peak of the mean temperature

Full size image

Note that Tpeak does not correspond to the actual maximal temperature in the laser spot during exposure. Thus, Tmax could be used to estimate if the melt pool temperature is above the melting temperature of the polymer in future studies. In turn, ΔT can alternatively be calculated as the difference between Tmax and Tdecay, which is still extracted from the time series of Tmean. However, Tmax can increase during exposure depending on the combination of exposure parameter and scan vector length and Tmax exhibits a high noise [23]. Therefore, more data needs to be generated to assess which approach is more suitable in the long run. Nevertheless, the choice of the upper reference value for ΔT does not influence the method of determining the decay values.

Although Tdecay also tends to decrease with larger negative cooling rates, the dominant influence on ΔT remains Tpeak (Fig. 8, right). Therefore, the variation in the cooling rates does not significantly affect ΔT and Tdecay at small negative cooling rates. However, the cooling rate is a determining factor for tdecay. Additionally, the standard deviation of tdecay increases the more time has elapsed since the exposure (Fig. 8, left). This is due to a low-frequency oscillation in the raw data of the transient temperature profiles. It is conceivable that this results from the control of infrared radiators. This phenomenon reduces fit quality and therefore the reproducibility of high tdecay, especially at smaller negative cooling rates.

Fig. 8
figure 8

Decay time (left) and temperature difference between the decay temperature and the peak of the mean temperature (right) at varying cooling rates as a function of surface energy density

Full size image

The combination of tdecay and ΔT can be treated as an indicator for the consolidation of particles since both values correlate with energy input. The overall trends in transient temperature profiles can be determined in a reproducible way before the temperature has decayed to an equilibrium state if cooling rates around − 1 K/s are chosen. The process parameters for PA12 result in part properties within the plateau region [8] if tdecay is between 3.7 and 4.3 s, while ΔT ranges from 32 to 47 K for cooling rates of − 1 K/s and emissivity of 1 (Fig. 8). Thus, suitable processing parameters can theoretically be identified through the representation of the decay values. However, the prerequisite for the quantification of interaction between process parameters, part geometry, and materials properties with decay values is an additional correlation to part properties which is discussed next.

3.3 Correlations between transient temperature profiles and part properties

Although surface roughness in the x–y plane is dominated by powder properties and the resulting bulk density [35], a plateau region forms for Sa and Sq of the manufactured single-layer specimens between energy inputs of 0.02–0.04 J/mm2 (Fig. 9, left). Similar results are reported by Czelusniak et al. [36] who analyzed the surface roughness of PA12 (PA2200) parts in a wider spectrum of energy densities. A significant increase in surface roughness is only detected at energy inputs below 0.013 J/mm2 due to insufficiently molten particles between hatch lines [36]. Since the porosity of PA12 (PA2200) parts increases at energy densities smaller than approx. 0.025 J/mm2 [11], the single-layer specimens manufactured in that processing range exhibit slightly increased standard deviations for Sa and Sq. This is also indicated by microscope images in Fig. 10. However, the influences of energy density, hatch distance, and scan speed on the surface roughness are partially opposite [37] and depend on the scan vector length [38]. This opposite behavior is also reported for the resulting melt pool temperatures [22, 25]. Therefore, it can be assumed that the interactions between processing parameters and the geometry of the exposed cross-section will affect the decay values. The analysis of the surface roughness as a function of tdecay in Fig. 9 (right) indicates that the plateau region exists for a defined range of tdecay. Further research on different sizes of multilayer parts manufactured with various parameter sets is required to analyze how and to what extent individual decay values affect the resulting part properties.

Fig. 9
figure 9

Surface roughness of the single-layer specimen as a function of energy density and decay time

Full size image
Fig. 10
figure 10

Exemplary microscopy images of the single-layer specimen surfaces with corresponding decay values for a cooling rate of − 1 K/s

Full size image

Nevertheless, already existing process knowledge can be used to identify correlations between specific sequences of decay values and the resulting part properties since ε is set to a constant value. The anisotropy of parts manufactured with energy densities close to the upper boundary of the plateau region (0.031 and 0.037 J/mm2) usually decreases due to improved mechanical properties in z-orientation [8]. Tdecay of melt pools processed in this range is initially above Tdecay of melt pools with energy inputs close to the lower boundary (0.022 and 0.026 J/mm2) and drops below them at smaller negative cooling rates while tdecay increases (Fig. 11). Consequently, this behavior should be an indication of homogeneous melting. Therefore, decay values can also be used to differentiate parameter sets which result in components with properties inside and close to the plateau region.

Fig. 11
figure 11

Transient temperature profiles of single-layer specimens manufactured with different energy densities and their corresponding decay values at different cooling rates with exemplary microscopy images of the surface

Full size image

In addition, decay values also enable a quantitative analysis of parameter sets outside the plateau region. At constant cooling rates, Tdecay decreases with increasing energy inputs at an overall low energy density level (0.016 and 0.018 J/mm2), while tdecay is almost identical. Therefore, the increased ΔT at an energy input of 0.018 J/mm2 likely indicates that there are higher proportions of unmolten particles (Fig. 11). However, further studies are required to validate these assumptions and to identify more patterns within the thermal process data.

The melt pools reported in the literature are in an equilibrium state within a range from 2 [12] to 10 s [8] after laser exposure. However, the cooling rates within this range span from − 4.7 K/s (0.050 J/mm2, 2 s) to − 0.16 K/s (0.016 J/mm2, 10 s) for the parameter sets used in this work. Furthermore, it is reported that the temperature of the first layers of multilayer components increases if a new layer of powder material is recoated before the melt pool has decayed to the process temperature [23]. In addition, various studies also suggested that consolidation continues after recoating if the underlying layers are reheated due to subsequent laser exposure [12, 39]. Therefore, the layer time and the duration from recoating to laser exposure (closed-time) as well as the time from laser exposure to recoating (open-time) are further relevant process variables. The effect of closed-time and open-time on mechanical properties has already been emphasized by Josupeit [40]. Thus, decay values can be used to systematically quantify those time scale effects in future studies. Consequently, the use of decay values can potentially enable new process strategies that decrease build time while maintaining part properties.

4 Conclusion and outlook

PBF-LB/P parts often exhibit a comparatively low reproducibility since plastic powders require precisely defined process parameters for robust processing. Recent progress in process monitoring of PBF-LB/P suggests that the melt pool temperatures during and after exposure correlate with part properties. Therefore, the low reproducibility can be attributed to interactions between exposure parameters and the geometry of the exposed cross section, which affect the resulting melt pool temperatures. So far, these findings could only be used qualitatively for the development of new processing strategies, which generate uniform temperature fields and thereby increase the reproducibility of part properties [27, 28]. A quantitative analysis of the resulting transient temperature profiles to qualify the extent of these effects is still pending, since transient temperature profiles of melt pools have been analyzed only in the peak, in an equilibrium state after cool down, or at an arbitrary point in the time in the literature. Following the hypothesis that the cooling behavior—or rather the cooling rate of the melt pool—is a determining factor for robust processing, a method that evaluates the melt pool temperatures at different cooling rates is introduced within the scope of this work. These decay values provide the necessary context to interpret thermal process data. By varying the energy density during the production of PA12 single-layer specimens, the following conclusions are derived:

  • Decay values (tdecay, Tdecay, and ΔT), which are a function of the cooling rate of the melt pool, correlate with energy input and can be used to quantify the cooling behavior in a systematic and reproducible way at a cooling rate of − 1 K/s.

  • tdecay is strongly affected by changes in the cooling rate and the energy density.

  • Negative cooling rates smaller than − 2 K/s and changes in energy input have a minimal effect on ΔT and Tdecay.

  • ΔT is heavily dependent on Tpeak, which increases with higher energy inputs.

  • The sequence of tdecay and the corresponding ΔT at different cooling rates can be combined with existing process knowledge to further differentiate process regimes, such as homogenous melting or the presence of incompletely molten particles. However, further studies are required to validate these assumptions.

Furthermore, potential improvements in the data processing such as the optimization of the fit function or the use of Tmax instead of Tpeak are identified. The next step of this research is the transfer of the results to other plastic materials. Therefore, the manufacturing of three-dimensional multilayer specimens will be monitored and analyzed. During this, the influence of parameters such as scan vector length, scan speed, laser power, hatch distance, process temperature, and layer time on the decay values can be evaluated with a statistical design of experiments. Correlations between decay values and part properties, such as tensile strength, elongation at break, or density, are especially of interest. A conceivable application of the process knowledge generated in this way is an in situ quality assurance with the design of a digital twin of the build job to make post-process material testing redundant.