1 Introduction

3D printing is a form of additive manufacturing that is revolutionising the manufacturing industry by providing an efficient method for producing complex, customised, and lightweight structures such as lattices [1, 2] which cannot be manufactured by common manufacturing methods. A lattice is a cellular structure which has been widely used in aerospace [3,4,5] and medical industries [6,7,8,9] with great properties, such as high specific stiffness and strength [3, 10, 11], heat insulation [12], and energy damping attenuation [13]. One of the most common filament arrangements in lattice structures is body-centred cube (BCC) which has been extensively used for energy absorption applications [14]. Moreover, open lattices has specific advantages compared to the conventional foam cores such as the capability of core ventilation that eliminates the property degradation caused by moisture absorption [15, 16]. Therefore, the BCC lattice structures bear excellent capabilities for structural design. The mechanical properties of BCC lattices are determined by the size of the unit cell and the arrangement and connectivity of the filaments [17,18,19]. Along with advances in additive manufacturing methods of BCC lattices and efficient design of these structures, efforts are underway to precisely determine the mechanical properties of BCC lattices. Maconachie et al. [18] fabricated AlSi10Mg BCC lattices and other topologies to evaluate static and dynamic performance. They performed micro-scale finite element modelling with beam elements to directly simulate geometric defects such as joint effects that result from 3D printing manufacturing methods. Also, they used an elastic/plastic material model with properties determined from tensile testing of a dog-bone sample. They found that the relative density of manufactured BCC lattices is higher than the expected predicted value from CAD design. This is due to the different manufacturing orientations of the constituent filaments. It impacts the arrangements of filaments within the lattices. Wang et al. [20] also investigated the mechanical properties of an optimised graded BCC lattices. They implemented a numerical simulation to capture stress distributions through a graded BCC lattice beam under compression loading. They found that an optimised fillet at filament joints can increase structural stiffness. Energy absorption of a micro BCC lattice cube manufacture by SLM was investigated at [21]. The authors studied the dynamic behaviour of micro-scale lattices through a combination of FE simulation and experiments. They found that the face-truss joints behave the locations of high stress concentration. Lee et al. [22] studied elastic modulus of stainless steel BCC lattices using an analytical model for a single unit cell without considering shear effects. They implemented a 2D FE simulation to validate analytical studies. They concluded that discrepancies between FE simulation and experimental results are caused by the inconsistent lattice filament diameter and the 2D simplification in the FE modelling. Lei et al. [23] fabricated AlSi10Mg BCC multilayer lattices using SLM to investigate the effect of geometrical imperfections on the compressive properties using FE simulation and experimental validation. They found that compressive modulus of lattices with finite dimensions reduced as the number of layers added.

They concluded that the traditional analytical formulation is not adequate to predict this behaviour. Yang et al. [24] proposed an analytical model based on propagation of a filament deformation pattern to predict mechanical properties of metallic sandwich BCC lattice structures and used a 2D FE model to validate their analytical approach. The authors found that boundaries and their connection to the lattice joints have a major impact on the mechanical properties of sandwich BCC lattices. Boniotti et al. [25] presented an experimental investigation of a BCC AlSi10Mg micro lattices using digital image correlation (DIC) technique to determine the localisation of deformation on the unit cell. They observed significant strain concentrations on the vertical filaments and joint areas. Also, an ideal CAD model without considering material overlapping effects and imperfections cannot accurately estimate the strength and does not accurately describe the real behaviour of the printed lattice structure. Quasi-static compressive behaviour of stainless steel micro BCC lattices with the effect of material overlapping was investigated in Gumruk and Mines [26]. They proposed an analytical approach for micro lattices and validated mechanical properties with a combination of 2D FE simulation and experimental tests. They found that 2D beam elements are not accurate for modelling of manufactured lattices including block nodes. Moreover, discrepancies between predictive FE simulation and experimental results after elastic section was observed which is due to the change in filament/filament thickness. Ptochos and Labeas [27] analytically calculated Young’s modulus and Poisson’s ratio of an irregular micro BCC lattice. Compressive properties of stainless steel micro lattices using Euler–Bernoulli assumption were defined by Ushijima et al. [28]. They found a great match between predicted theoretical formulation and experimental results for low filament aspect ratio (d/l < 0.1). However, these studies focused on metallic micro lattices without considering influence of filament joints and material overlapping effect. Moreover, to the best of our knowledge, material parameters of an individual 3D-printed polymeric microstructure have been rarely determined for analytical models and FE simulation of lattice structures. Though several analytical and FE simulation models have been proposed for micro lattices, one should note that the filament/filament joints at higher aspect ratio (d/l) [29] impact overall mechanical properties of a lattice cube. FE simulation of a large-scale lattice structures, containing material overlapping effect at joints, are computationally intensive. Therefore, further investigation on the geometries of 3D-printed filaments and connectivities should be carried out to accurately design the lattice structures. In this paper, we aim to develop a combination of an analytical formulation, FE simulation, and experimental tests to elucidate the impact of connectivity and material overlapping on static mechanical properties of a polymeric macro lattice structure.

A theoretical formulation utilising Timoshenko’s beam theory and the impact of material overlapping at nodes for a micro lattice structure is proposed. The propagation of filament-deformation patterns of a macro lattice constrained between two rigid platens is shown to represent the sections with different elastic constants. Based on FE simulation, 3D solid hexahedral elements are used to predict compressive behaviour of a macro lattice structure. The stress–strain curve and material properties of an individual 3D-printed single filament is determined using a custom-made experimental setup and inverse calibration approach. To verify the analytical model and FE simulation, the compressive experimental tests using digital image correlation technique are also carried out. Results are validated in terms of elastic stiffness, plastic collapse strength, and deformation for lattice cubes. These findings provide a combination of predictive analytical model, simulation, and experiments to investigate the effect of imperfections and material overlapping effect on static compressive behaviour and failure modes of 3D-printed macro lattice structures.

2 Analytical formulation of a macro-BCC lattice cube

The topology of a Body-Centre Cubic (BCC) unit cell and individual lattice filament is given in Fig. 1. The main assumption in this work is to consider the material overlapping at the filament/filament joint. Effective length leff is defined as a moment length which is less than length of filament as mentioned in Eq. (3). The geometrical parameters of the unit cell are defined as follows in Eqs. (1) to (4). In Fig. 1, manufacturing nodes connecting filaments to each other assumed the rigid parts to consider the node effect in lattice blocks and there is a little deformation and rotation exist in the nodes. These assumptions are aligned with the experimental results given in [26].

Fig. 1
figure 1

I 3D representation of BCC unit cell; II individual filament geometry with boundary conditions and simplifications. (X is local coordinate system in filament longitudinal axis)

Full size image

Due to imperfections of block nodes, a distance “x” that is about half of diameter is defined where both force and moment act [26].

$$\frac{L}{2}=\frac{\sqrt{{h}^{2}+{a}^{2}+{b}^{2}}}{2}$$
(1)
$$\theta ={\mathrm{tan}}^{-1}\frac{h}{\sqrt{{a}^{2}+{b}^{2}}}$$
(2)
$${l}_{eff}=\frac{L}{2}-2x=\frac{\sqrt{{h}^{2}+{a}^{2}+{b}^{2}}}{2}-d$$
(3)
$$c=\frac{d}{2}tan\theta$$
(4)

2.1 Relative density

The volume of the unit cell block is Vblock = abh. Since the BCC unit cell is made of eight filament (or filament) with length leff and one sphere with radius c, the relative density (R) is then given by Eq. (5) [26]:

$$\begin{aligned}R&=\frac{{V}_{unit\;cell}}{{V}_{unit\;cell\;block}}=\frac{\left(2\pi {d}^{2}{l}_{eff}+\frac{4}{3}\pi {c}^{3}\right)}{abh}\\&= \frac{\left(2\pi {d}^{2}\left(\frac{\sqrt{{h}^{2}+{a}^{2}+{b}^{2}}}{2}-d\right)+\frac{\pi {d}^{3}}{6}{tan}^{3}\theta \right)}{abh}\end{aligned}$$
(5)

For a regular lattice block (a = b = h = l) without considering material overlapping effect (and hence the absence of the second term), Eq. (5) is matched with Eq. (6) as defined in several other studies such as [28]:

$$R=\sqrt{3}\pi {\left(\frac{d}{l}\right)}^{2}$$
(6)

2.2 Compressive modulus of a micro lattice

An analytical formulation for predicting the initial linear compressive stiffness of an unconstrained BCC micro lattice is introduced. In Fig. 2, a schematic representation of the stress, which is defined as the ratio of filament forces divided by the area, in the y-directions of BCC unit cell is presented. As it can be revealed from Fig. 2, one end of the individual filament is fixed and the other one is free to translate. Considering the compression loading scenario, as shown in Fig. 2, the single filament is under compressive loading scenario such that a normal stress \({\sigma }_{y}\) is induced in the unit cell.

Fig. 2
figure 2

Filament loading condition for calculation of Young’s modulus in y-direction

Full size image

Strain \({\varepsilon }_{y}\) and the elasticity modulus in y-direction (\({E}_{y}\)) can be determined as follows:

$${E}_{y}=\frac{{\sigma }_{y}}{{\varepsilon }_{y}}$$
(7)
$${\varepsilon }_{y}=\frac{{\delta }_{y}}{h/2}$$
(8)

The engineering stress \({\sigma }_{y}\) is calculated as:

$${\sigma }_{y}=\frac{{4F}_{y}}{ab}$$
(9)

By substituting Eqs. (8) and (9) into Eq. (7), the elastic modulus is formulated as:

$${E}_{y}=\frac{{2F}_{y}h}{ab{\delta }_{y}}$$
(10)

The compressive load \({F}_{y}\) results in filament deflections \({\delta }_{x}\), \({\delta }_{y}\), and \({\delta }_{z}\). \({F}_{y}\) can be decomposed into two components \({F}_{{x}{{\prime}}}={F}_{y}sin\theta\) and \({F}_{{y}{{\prime}}}={F}_{y}cos\theta\) which result in the displacement \({\delta }_{{x}{{\prime}}}\) and \({\delta }_{{y}{{\prime}}}\) (as shown in Fig. 2). Using Timoshenko beam theory including considering the shear effect, the solution of \({\delta }_{{x}{{\prime}}}\) and \({\delta }_{{y}{{\prime}}}\) in the local coordinate system are as follows:

$${\delta }_{y\prime}=\frac{{F}_{y\prime}{{l}_{eff}}^{3}}{12E{I}_{y\prime}}+\frac{{F}_{y\prime}{l}_{eff}}{kAG}$$
(11)
$${\delta }_{x\prime}=\frac{{F}_{x\prime}{l}_{eff}}{AE}$$
(12)

where I, E, G, and A are second moment of area, stiffness of the individual filament, shear modulus, and cross-section area, respectively. The Timoshenko shear coefficient k for solid circular cross-section is as follows [30]:

$$k=\frac{6(1+\nu )}{7+6\nu }$$
(13)

where \(\nu\) is the Poisson’s ratio of the constitutive material.

The filament deformations in the global coordinate system (x, y, z) are calculated using transformation law:

$${\delta }_{x}=\left(-{\delta }_{x\prime}cos\theta +{\delta }_{y\prime}sin\theta \right)cos\beta$$
$${\delta }_{y}=\left({\delta }_{x\prime}sin\theta +{\delta }_{y\prime}cos\theta \right)$$
$${\delta }_{z}=\left(-{\delta }_{{x}{{\prime}}}cos\theta +{\delta }_{{y}{{\prime}}}sin\theta \right)sin\beta$$
(14)

where \(\beta\) is the angle between x- and z-direction in global coordinate system as follows:

$$cos\beta =\frac{a}{\sqrt{{a}^{2}+{b}^{2}}}$$
(15)

By combining Eqs. (11) and (12), the global filament deformation in y-direction \({\delta }_{y}\) is formulated as:

$${\delta }_{y}={F}_{y}\left(\frac{{l}_{eff}}{AE}{sin}^{2}\theta +\left(\frac{{{l}_{eff}}^{3}}{12E{I}_{{y}{{\prime}}}}+\frac{{l}_{eff}}{kAG}\right){cos}^{2}\theta \right)$$
(16)

By substituting Eq. (16) into Eq. (10), the elastic modulus is formulated as:

$${E}_{y}=\frac{2h}{ab\left(\frac{{l}_{eff}}{AE}{sin}^{2}\theta +\left(\frac{{{l}_{eff}}^{3}}{12E{I}_{{y}{{\prime}}}}+\frac{{l}_{eff}}{kAG}\right){cos}^{2}\theta \right)}$$
(17)

For a regular unit cell without considering the effect of filament joints, the derived formulation is consistent with literature and can be found as follows [24]:

$${E}_{y}=\frac{9\sqrt{3}\pi E}{\left(17+12\nu \right){\left(\frac{L}{d}\right)}^{2}+2{\left(\frac{L}{d}\right)}^{4}}$$
(18)

2.3 Plastic collapse strength

For modelling of the plastic collapse of a micro unit cell, it is assumed that a single circular filament can plastically collapse under the plastic bending moment. The plastic bending moment at a section is the first moment of normal stress on the cross-section about the centroid [31]. The bending moment is calculated by elastic and plastic bending moments and it is stated as [26]:

$$M=2{\sigma }_{0}\left\{0.0625{d}^{3}\left(1-\alpha \right)\left(0.33{A}^{2}+0.5\right)\sqrt{A}+0.0156B\frac{{d}^{4}}{c}\right\}$$
(19)

where A and B are constant parameters and can be determined from [26]:

$$c=\frac{{\sigma }_{0}d}{2E\varepsilon }$$
(20)

Also, \({\sigma }_{0}\) and \(\alpha\) denote yield stress for the material and the ratio of tangent modulus to elastic modulus, respectively. c is the distance from the neutral axis to the initially yielded filament and depends on the deformation of the filament in the cross-section [32]. Therefore, compression experiments of lattices will be utilised to define the strain value corresponding to plastic collapse strength (refer to the Sect. 4.2). After finding the collapse strain value from an experimental test, the plastic moment for elastic–plastic material can be obtained as follows:

$$M=\gamma {\sigma }_{0}{d}^{3}$$
(21)

where \({\sigma }_{0}\) and \(\gamma\) are yield stress and a coefficient that is determined using experimental tests of lattices. Mathematical formulation of plastic strength considers the uniform compression and bending deformation. So, the bending moment for a single filament is defined as:

$$M(x=0)=\frac{{F}_{y}{l}_{eff}}{8}cos\theta$$
(22)

where \({F}_{y}={\sigma }^{*}ab\). \({\sigma }^{*}\) is a plastic collapse. For a regular lattice structure (a = b = h = L), we have:

$$M(x=0)=\frac{{\sigma }^{*}{L}^{2}{l}_{eff}}{8}cos\theta$$
(23)

If the statement for M(x = 0) and bending plastic moment (M) are equal to each other, the plastic collapse stress is obtained as follows:

$${\sigma }^{*}=\frac{9.79\gamma {\sigma }_{0}}{0.86-\left(\frac{d}{L}\right)}{\left(\frac{d}{L}\right)}^{3}$$
(24)

2.4 Compressive stiffness of a micro lattice block constrained with two rigid platens

When a lattice cube is constrained within upper and lower rigid platens, it leads to variation of elastic properties such as compressive stiffness of the structure [24]. As is shown in Fig. 3, transverse displacement of an individual filament in x- and z-direction (compressive loading direction is in y-direction) are zero.

Fig. 3
figure 3

Propagation of filament-deformation patterns for a single unit cell under constrained boundary (CB) condition at the bottom

Full size image

The derived deformation formulation (Eq. (14)) in x- and z-directions are zero; \({\delta }_{x}=0, {\delta }_{z}=0\).

$${\delta }_{x}=\left(-{\delta }_{x\mathrm{^{\prime}}}cos\theta +{\delta }_{y\mathrm{^{\prime}}}sin\theta \right)cos\beta =0\to {\delta }_{{x}^{\mathrm{^{\prime}}}}cos\theta ={\delta }_{y\mathrm{^{\prime}}}sin\theta$$
(25)

By substituting Eq. (11) and (12) into Eq. (25), \({F}_{y\mathrm{^{\prime}}}\) is obtained as follows:

$$\left(\frac{{F}_{{x}^{\mathrm{^{\prime}}}}{l}_{eff}}{AE}\right)cos\theta =\left(\frac{{F}_{{y}^{\mathrm{^{\prime}}}}{{l}_{eff}}^{3}}{12E{I}_{{y}^{\mathrm{^{\prime}}}}}+\frac{{F}_{{y}^{\mathrm{^{\prime}}}}{l}_{eff}}{kAG}\right)sin\theta$$
$${F}_{y\mathrm{^{\prime}}}={F}_{{x}^{\mathrm{^{\prime}}}}\frac{\sqrt{{a}^{2}+{b}^{2}}}{h}\frac{{l}_{eff}}{AE}\frac{1}{\frac{{{l}_{eff}}^{3}}{12E{I}_{{y}^{\mathrm{^{\prime}}}}}+\frac{{l}_{eff}}{kAG}}$$
(26)

By substituting the statement for \({F}_{y\mathrm{^{\prime}}}\) into Eq. (10), the Young’s modulus of unit cell with the CB conditions is obtained as follows:

$${E}_{y}=\frac{4h\left(sin\theta +cos\theta \times \left(\frac{\sqrt{{a}^{2}+{b}^{2}}}{h}\frac{{l}_{eff}}{AE}\frac{1}{\frac{{{l}_{eff}}^{3}}{12E{I}_{{y}{{^{\prime}}}}}+\frac{{l}_{eff}}{kAG}}\right)\right)}{2ab\left(\frac{{l}_{eff}sin\theta }{AE}+cos\theta \times \left(\frac{\sqrt{{a}^{2}+{b}^{2}}}{h}\frac{{l}_{eff}}{AE}\frac{1}{\frac{{{l}_{eff}}^{3}}{12E{I}_{{y}^{{{\prime}}}}}+\frac{{l}_{eff}}{kAG}}\right)\times \left(\frac{{{l}_{eff}}^{3}}{12E{I}_{{y}^{{{\prime}}}}}+\frac{{l}_{eff}}{kAG}\right)\right)}$$
(27)

2.5 Compressive stiffness of a macro lattice block constrained with two rigid platens

Figure 4 shows the macro lattice block constrained with upper and lower rigid platens. As it can be seen, we have a distribution of elastic modulus within a structure [24].

Fig. 4
figure 4

I sketches of distributions of unit cells; II CAD model, 10 × 10 × 10 unit cells

Full size image

In Sect. 2.2 and 2.4, the compressive Young’s modulus for free and constrained boundary conditions for the single unit cell was defined, respectively (Eqs. (18) and (27)). The effective Young’s modulus of a regular macro lattice structure (Lx = Ly = Lz = L) should satisfy the below equation:

$${\delta }_{y}={\delta }_{y1}+{\delta }_{y2}={\varepsilon }_{y1}\times {c}_{1}+{\varepsilon }_{y2}\times {c}_{2}$$
(28)

where c1 and c2 are the distance from the top and bottom of the rigid platens to the centre of the lattice cube, respectively (for the regular cube c1 = c2 = L/2).

$${\delta }_{y1}={\varepsilon }_{y1}\times h=\frac{{\sigma }_{y}}{{E}_{eff}}\times h$$
(29)

The lattice is split in the top and the bottom sections. The Young’s modulus of the entire lattice (\({E}_{eff}\)) in the y-direction is as follows:

$$\frac{1}{{E}_{eff}}=\frac{{c}_{1}}{h}.\frac{1}{{E}_{1}}+\frac{{c}_{2}}{h}.\frac{1}{{E}_{2}}$$
(30)

where E1 and E2 are the Young’s modulus of the top and bottom sections in the y-direction, respectively.

Yang (2019) developed the effective Young’s modulus of a macro sandwich BCC lattice with different dimensions (regular and irregular lattices) [24]. It is noted that they did not consider the effect of imperfections such as material overlapping effect at the vicinity of the joints. It is also recommended to use the formulation when the number of unit cells along sides are larger than 5 [24]. They showed effective E for a cubic regular structure formulated as follows:

$${E}_{eff}=-\frac{2{E}_{CB}\left[1+\frac{ln\left(\frac{{E}_{CB}}{{E}_{FB}}\right)}{1-\frac{{E}_{CB}}{{E}_{FB}}}\right]}{1-\frac{{E}_{CB}}{{E}_{FB}}}$$
(31)

where ECB and EFB are elastic modulus of unit cell with the constrained and free boundary conditions, respectively. By substitution of Eqs. (17) and (27) into Eq. (31), the Young’s modulus of a regular macro-BCC lattice with considering the effect of material overlapping at joint is formulated as follows:

$${E}_{eff}=-\frac{1.333\left({a}^{2}EB+{l}_{eff}\right)}{\mathrm{B}{l}_{eff}}\left(\frac{\left[1+\frac{ln\left(\frac{0.667\left({a}^{2}EB+{l}_{eff}\right){l}_{eff}\left(1+2{a}^{2}EB\right)}{6\mathrm{aEB}{l}_{eff}}\right)}{1-\frac{0.667\left({a}^{2}EB+{l}_{eff}\right){l}_{eff}\left(1+2{a}^{2}EB\right)}{6\mathrm{aEB}{l}_{eff}}}\right]}{1-\frac{0.667\left({a}^{2}EB+{l}_{eff}\right){l}_{eff}\left(1+2{a}^{2}EB\right)}{6\mathrm{aEB}{l}_{eff}}}\right)$$
(32)

where B is defined as follows:

$$B=\frac{{{l}_{eff}}^{2}}{12E{I}_{{y}^{\mathrm{^{\prime}}}}}+\frac{1}{k{a}^{2}G}$$
(33)

3 Computational modelling of a 3D-printed BCC lattice

3.1 Characterisation of material parameters

Stress–strain distribution and deformation pattern will be obtained by finite element simulation [33]. Also, the failure modes can be predicted, which is important for biomedical implants [10]. FEM also enables large deformations, non-linear material properties, and dynamic effects to be included, if needed. The validity of FE model is highly dependent on the material properties. Therefore, material properties of 3D-printed filaments need to be characterised, since this information will affect the predicted deformation mode, initial compressive stiffness, and plastic collapse [34]. Nylon filaments with 2 mm diameter were fabricated using selective laser sintering (SLS) process. It is often the case with SLS that material properties exhibit a certain degree of anisotropy [35]. Yang et al. [36] studied that the 3D printing orientation of 45° could provide a reasonable estimation for Young’s modulus of 3D-printed materials. Therefore, all filaments were 3D-printed in the orientation of ± 45° with respect to the loading axis. After manufacturing, it was found that the cross-section of the filament is quite elliptical. The average diameter that runs through the shortest part and the longest part were 2.04 mm and 2.38 mm, respectively.

A single filament compaction experimental setup was developed at Centre for Advanced Composite Materials (CACM) [37]. The overall experimental setup is illustrated in Fig. 5.

Fig. 5
figure 5

Single filament compressive experimental setup

Full size image

Each filament was placed centrally on a transparent glass plate with 19 mm thickness and 100 mm diameter. In order to mitigate the effect of friction on the measured compression response of the filament, the metallic compaction and glass plates were finely polished. A high-resolution iDS UI-1490SE-M-GL camera was attached to the inner wall of this hollow structure. The detail of the compressive experimental setup can be found at [37]. The cameras captured the images of the bottom surfaces of the sample at a rate of 2 frames/s. An image processing and segmentation algorithm in MATLAB was used to determine sample width and the length at each frame. Figure 6 shows the example images at two different frames (first and final frame) to show visually the change in width and length of the filament.

Fig. 6
figure 6

Example images of the filament under compression at the first frame and the last frame

Full size image

An inverse calibration method using MCalibration software version 5.1.2 was used in combination with a FEA model of a single filament under compaction test [38]. The detail of an inverse calibration method can be found in authors’ works [38].

The inverse method was used to determine an appropriate material constitutive model and input parameters for the 3D-printed Nylon lattices which behaves permanent plasticity deformation under compression tests [38]. A FE simulation of the test using ABAQUS 2019 with an elasto-plastic isotropic hardening material model was compared to the experimental data to fully characterise the behaviour of the material. Figure 7 shows the experimental results for true stress and true strain and FE model of the filament under the compression test. By importing the experimental data and FE model of a single filament into the MCalibration software, material parameters for a fitness value (NMAD) of 0.38% were obtained by the inverse calibration technique. The obtained Young’s modulus was 152.3 MPa. Plastic material properties are listed in Table 1.

Fig. 7
figure 7

a Compression experimental data and true stress and true strain curve obtained from the MATLAB algorithm. b Total deformation in loading direction of 3D-printed Nylon filament under 25% of compressive strain

Full size image
Table 1 Material parameters of 3D-printed Nylon obtained by inverse calibration algorithm via MCalibration software-used for ABAQUS elastic–plastic isotropic hardening material model
Full size table

3.2 Finite element simulation

To predict the deformation pattern of the macro lattices, finite element simulation was performed using ABAQUS 2019. The regular BCC configuration has an isotropic material behaviour with three independent parameters including elastic modulus (Ex = Ey = Ez), Poisson’s ratio, and Shear modulus. The dimension of a single unit cell is 5 × 5 × 5 mm with filament diameter 1 mm and lattice structure is composed of 10 unit cells in directions x, y, and z. The BCC unit cell and lattice structures are designed and meshed using Micromechanics [39] as a plugin in ABAQUS (shown in Fig. 8). The main reason to use Micromechanics plugin for creating a geometry instead of conventional CAD software is because it has more flexibility in selecting element types and generating structured meshes. 3D solid elements of hexahedral type (C3D8R) were employed to mesh the lattice models. A convergence study with respect to the mesh size is first performed to ascertain the level of finite element refinement necessary to obtain accurate results. The total number of elements and nodes was 839,808 and 1,152,685, respectively. The model is given the input material properties which were obtained from inverse calibration algorithm of a compaction test of a single filament as shown in Table 1.

Fig. 8
figure 8

a BCC unit cell 5 × 5 × 5 mm. b Lattice cube

Full size image

Top and bottom rigid plates were modelled to represent boundary conditions applied in the experimental test in which the bottom plate was moved 12 mm compression displacement at a constant velocity and fixed in the other directions, whereas the top plate was fully constrained. Moreover, the type of contact between the connected filaments of the cells within lattice structure was defined as general contact with a friction coefficient of 0.25 as tangential behaviour and “hard” contact as normal behaviour. Moreover, all the top and bottom surfaces of lattice structure were connected as tie constrains with the rigid plates. The applied boundary condition and constraints are shown in Fig. 9.

Fig. 9
figure 9

a Applied boundary condition and constrains. b Hexahedral mesh

Full size image

4 Experimental methodology

4.1 Lattice manufacturing

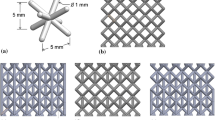
In order to design the lattices of dimensions 50 × 50 × 50 mm, PTC™ Creo Parametric 5.0.2.0 software was used. The cell filament diameter was selected as 1 mm for a relative density of 0.17. Figure 10a represents the computer-aided design (CAD) models of the lattice cube which was saved in.STL format. A selective laser sintering (SLS)-based 3D printer, EOS Formiga P110 Velocis at Creative Design and Additive Manufacturing Lab at University of Auckland, was used to print the samples using default settings including the chamber being heated to 150 °C and laser power of 40 W. The specimens were made of Polyamide 12 Nylon. Three samples of each filament diameter were fabricated and the unprocessed material was blown off after printing. The fabricated final samples for experiments are shown in Fig. 10b.

Fig. 10
figure 10

a Sample design in Creo Parametric. b Two samples with different filament diameters fabricated by SLS 3D printing

Full size image

4.2 Compression test

In order to determine strain and deformation response of the manufactured lattices, uniaxial compression experiments were performed using an Instron 1185 universal testing machine with 100kN load capacity. During the tests, the lattice structures were centrally located between two platens as shown in the experimental compression rig (Fig. 5). The top plate was fixed, and the bottom plate which is attached to the developed compaction rig (refer to Fig. 5) was moved upwards with a constant displacement rate of 0.5 mm/min. One face of the specimen was monitored using a pair of high-resolution digital cameras (iDS UI-2280SE-M-GL USB incorporating 5-megapixel Sony ICX655 monochrome sensors) to monitor two orthogonal specimen surfaces. Macroscopic engineering strains were calculated through digital image correlation (DIC) using an in-house developed system called MODEM (MATLAB Optical Displacement and Strain Measurement) [40]. A programme called “uEye Sequence Capture” has been developed to facilitate the capturing of images using the iDS uEye cameras for the purpose of DIC [40]. To gain the optimal accuracy for the strain measurement, a speckle pattern is applied. Figure 11 shows the experimental setup with the DIC system employed.

Fig. 11
figure 11

a DIC setup for compression test. b Lattice structure with speckle pattern

Full size image

A schematic of compressive stress–strain behaviour of a lattice is shown in Fig. 12 with having four regions including elastic loading, elastic–plastic collapse, plastic collapse, and densification. The slope of elastic region represents the initial compressive stiffness and plastic collapse stress is calculated from the intersection point of elastic–plastic collapse and plastic collapse regions.

Fig. 12
figure 12

Schematic representation for defining elastic and collapse strength and stiffness for manufactured polymeric BCC lattice cube

Full size image

5 Results

5.1 Analytical model validation

Figure 13 shows the variation of the relative density versus aspect ratio d/l for proposed analytical model, Ushijima approach [28], and CAD predictions. As can be seen, there is a significant difference between Ushijima model and CAD predictions as the aspect ratio becomes larger which, later explained, causes significant error for analytical formulation of Young’s modulus.

Fig. 13
figure 13

Comparison of the predictions for relative density from analytical formulation and CAD models

Full size image

The values of initial stiffness from theories and experiments performed by literature according to aspect ratio for stainless steel with modulus of elasticity 97 GPa are shown in Fig. 14. The proposed analytical model matches with experimental data form Gumruk and Mines [26] for all aspect ratio ranges. Ushijima considered only axial and bending effects showing an error of up to 42% with increase of aspect ratio [28]. In contrast, the Yang model considered shear effect that is important for higher aspect ratio (d/l > 0.1) [24].

Fig. 14
figure 14

Variation of compressive Young’s modulus versus aspect ratio

Full size image

Therefore, it has been found that the effect of material overlapping at joints and shear is much more important for large aspect ratios rather than small aspect ratios.

Figure 15 shows a comparison of Young’s modulus for free and constrained boundary BCC lattices with and without considering the material overlapping effect (MOE) at the nodes.

Fig. 15
figure 15

Variation of compressive Young’s modulus versus aspect ratio for free and constrained boundaries of micro lattices with considering the material overlapping effect (MOE)

Full size image

It can be seen that the material overlapping effect (MOE) must be taken into consideration for the modelling which is important for higher aspect ratio. For instance, when the length of an individual structure is five times bigger than its diameter, the difference of Young’s modulus is 24%. Moreover, as is expected, elastic modulus for constrained boundaries’ (CB) lattices are greater than free boundaries’ (FB) lattices as the unit cells of the CB have higher effective stiffness compared to the unit cells of the FB.

5.2 Initial stiffness and plastic collapse

In Fig. 16, a comparison of compressive force–displacement curve obtained from the FE simulation and experiments using DIC approach for 1 mm filament diameter and the dimension of unit cell 5 × 5 × 5 mm (relative density 17%) under 12 mm compression displacement is given. The FE model with solid elements predicts very similar initial stiffness as the experimental data although a lower elastic–plastic region. Possible reasons for this difference in behaviour (lower elastic–plastic region) include the variable filament diameter, unprocessed materials during 3D printing, and partially melted material on filament surfaces [29]. An FE model based on a perfect geometry of the lattice cube cannot consider the changing thickness and semi melted powders on filament surfaces. Figure 17 represents a microCT scan photo of deformed BCC lattice that shows some imperfections such as material overlapping at the vicinity of filament joints.

Fig. 16
figure 16

Comparisons of simulation and experimental compressive force–displacement curve

Full size image
Fig. 17
figure 17

MicroCT detailed photo of the deformed lattice [26]

Full size image

In Fig. 18, a comparison of initial Young’s modulus from analytical formulation, numerical simulation, and experimental data of lattice structure with relative density of 17% is given. It can be seen that analytical modelling overestimates the stiffness of the lattice structure by 6.2% as it is based on fully constrained boundaries at the top and the bottom of the lattice structure. Due to the undesired unprocessed materials during 3D printing and post-processing, the 3D-printed lattice cube shows higher stiffness than the FE simulation with a difference of less than 2%.

Fig. 18
figure 18

Comparison of initial elastic modulus from analytical, simulation, and experimental data

Full size image

For analytical calculation of plastic collapse, as it was mentioned earlier in Sect. 2.3 and Eq. (21), experimental results of lattice cubes will be used to determine the strain value corresponding to plastic collapse strength. Figure 19 shows the experimental data of the lattice compression curve under 60% strain. As seen from Fig. 19, the collapse strength value of the lattice block nearly corresponds to \(\varepsilon =0.16\) overall compressive strain. By substituting in Eq. (20), c is found, and therefore, the plastic moment (Eq. (19)) can be approximately obtained. Table 2 shows the values of plastic collapse for a range of strain values corresponding to plastic collapse. If the strain value corresponding to plastic collapse strength is chosen 0.18, the result only changes by 9%. Therefore, \(\varepsilon =0.16\) values are selected.

Fig. 19
figure 19

Experimental stress–strain curve of lattice structure with filament diameter 1 mm and lattice cell size 5 mm

Full size image
Table 2 Analytical values of plastic collapse with respect to different values of strain
Full size table

The values of initial plastic collapse from formulation, FE simulation, and experiments are shown in Fig. 20. The simulation result gives close prediction to experiments with an error less than 13%. The proposed analytical model shows a discrepancy from experiments of up to 22% although it reveals more precise responses to experimental data than Ushijima’s model [28] with 0.302 MPa without considering joint overlapping effect. Therefore, it can be concluded that the consideration of imperfections in analytical models becomes important in lattices with high aspect ratio (d/l > 0.1).

Fig. 20
figure 20

Comparison of plastic collapse strength from analytical, simulation, and experimental data

Full size image

5.3 Deformation of lattice structure

In this work, the actual deformation of the lattice structures can be directly obtained from the digital image correlation (DIC) data. In order to obtain a good calibration result, the chessboard calibration pattern should be viewed from a wide range of camera angles and positions that as a collection should cover as much of the field of view (of both cameras) as can be practically achieved. With a good variation in the position and orientation of the calibration pattern, the calibration error reached 0.903 pixels.

The photos in Fig. 21 show typical images at macroscopic deformation σelastic, σplastic collapse, and an image at the final frame (12 mm displacement) which are compared with the simulation results at the same time frame. The corresponding values are highlighted in Fig. 19 by circles. The final frame shows a barrel shape deformation for lattice block. Also, the middle horizontal row shows the highest distortion compared to the other rows. As mentioned earlier (refer to Fig. 4) when considering the top and the bottom surfaces as constrained boundaries, it influences both mechanical properties of outer and inner unit cells which leads to a nonuniform displacement pattern under compression loading scenario. The deformation patterns of outer filaments will be propagated to inner filaments, as represented in the FE simulation displacement plot which causes variations of mechanical properties such as stiffness. The quantitative results and strain maps of the lattice will be explained later.

Fig. 21
figure 21

Comparison of deformation between optical images at increasing compression steps, σelastic, σcollapse, and σfinal frame (circles in Fig. 19) and FE simulation

Full size image

The corresponding displacement and strain maps for stress values of σelastic/2, σelastic, σcollapse, and σfinal frame for the main diagonals are shown in Fig. 22. The selected main diagonal regions are shown in Fig. 23. The first reason for selecting a diagonal region was to investigate the symmetric and heterogeneity pattern of strain contour. Also, the filaments located in the main diagonal undergo larger deformation than other diagonals [26] and this diagonal row is responsible for the failure of the lattice. Due to the discontinuous nature of a lattice, it is also difficult to use DIC for full tracking of open cell structures. Nonuniform stress pattern is due to strain component parallel to the vertical loading direction εyy. As seen from the strain contour, localisation first happens at the intersections between the lattice and moving and fixed platens, while the other part of the lattice remains perfect up to σelastic/2. With increasing macroscopic stress level, the localisation is visible as early as the middle of the macroscopic elastic region σelastic.

Fig. 22
figure 22

Displacement and strain εyy counter at increasing macroscopic stress levels

Full size image
Fig. 23
figure 23

Tracked features for main diagonals of the lattice cube

Full size image

Figure 24 shows the strain profile along a vertical row at the centre line (x = 25 mm) at the final frame and compares with simulation results. The simulation results are in a close agreement with the DIC data with a discrepancy less than 5% in a mean strain value for the vertical row. The graph represents intermittent changes that correspond to the periodicity of filaments and joints and indicates that each inclined filament behaves differently. The inclined filaments clearly support the majority of the deformation of the lattice cube. The middle filaments in the deformed shaped (starting from y = 15 to y = 20 mm), for example, show a mean strain value approximately 0.005 which is 20% higher than a mean strain value for the whole vertical row within the deformed lattice cube (0.0042).

Fig. 24
figure 24

a Tracked features for the vertical row at the centre (x = 25 mm) and b profile plot on a red tracked vertical row at macroscopic strain 25% (final frame)

Full size image

6 Conclusions

Materials overlapping at the vicinity of the 3D-printed filament joints were considered as one of the 3D-printing manufacturing defects and imperfections. This paper presents the structural performance of an imperfect macro lattice cubes utilising a combination of analytical, numerical, and experimental analyses to precisely model the impact of material overlapping manufacturing defect. The impact of block nodes or material overlapping effect was taken into account in Young’s modulus and plastic collapse strength in theoretical formulation. Moreover, the shear effect was considered by using Timoshenko beam model in analytical formulation. The use of a custom-made compression rig and associated inverse calibration approach were utilised to fully determine material parameters for a 3D-printed micro filament. The obtained elastic–plastic material parameters were used in a commercial FEA package to simulate static compression of macro lattice cube. Finally, a series of macro lattice cubes were manufactured using SLS additive manufacturing process to conduct a macro-scale validation study. An in situ testing procedure using DIC method was implemented. The key findings of this work are:

  • The effect of shear and material overlapping effect become very important for large aspect ratios (d/l > 0.1) rather than small aspect ratios for a micro unit cell.

  • A series of simulations confirmed the capability of the parent material model obtained from a single filament compression and inverse calibration method in replicating the nonlinear response of real 3D-printed lattices.

  • The developed theoretical predictions for stiffness and collapse strength showed a very close agreement to the numerical and experimental results.

  • The determined localised displacement and failure modes from DIC method have been obtained as quite consistent with FE simulation.

To achieve even more accurate numerical predictions of static and dynamic mechanical properties of real 3D-printed lattice geometries, it would be necessary to include all imperfections and local variations in filament dimensions.