1 Introduction

Growing demands for high-strength and difficult-to-machine materials in conjunction with high manufacturing precision result in increased requirements on the design of the corresponding manufacturing processes. Electrochemical machining (ECM) and its variants, such as pulsed electrochemical machining (PECM), have great capability to meet the mentioned requirements [1,2,3,4,5]. By adapting the cathode geometry and pulse regime, and by selecting suitable electrolytes and flow conditions, the material removal rates , the precision and the surface roughness achieved can be specifically influenced [6, 7].

A literature review reveals that a superimposed magnetic field offers the potential to influence electrochemical processes [8,9,10,11] such as electrochemical metal deposition by increasing depletion rates [12,13,14] and to enhance the detachment of hydrogen bubbles from the electrodes, which results in more efficient machining [15,16,17]. However, the influence of the magnetic field on ECM cannot be derived from other electrochemical processes since current density values and flow velocities are comparatively large. Nevertheless, a few applications of magnetic field–assisted ECM are reported in the literature. Bradley and Samuel [18,19,20] investigated the influence of a static magnetic field on the flow of the electrolyte in the working gap and the influence on the machining results. As a result, Bradley and Samuel. showed that a superimposed magnetic field increases the material removal rate and decreases the surface roughness for the considered materials and experimental setup. Long et al. [21,22,23] showed that applying a magnetic field to the ECM of LY12 aluminium alloy, with increasing magnetic flux density, the surface roughness decreases for the magnetic field direction perpendicular to the flow direction of sodium nitrate electrolyte. Tang and Gan [24] showed that a magnetic field can improve the precision of machining complex cavities in S-03 stainless steel by reducing stray current. Enache and Opran [25] provide basic mathematical modelling of magnetic field–assisted ECM and showed theoretically that a magnetic field would influence the electrolyte flow as well as the electric field with specific orientation of the magnetic field. The literature review leads to the conclusion that a magnetic field can influence electrochemical processes on a macro- and microscale. A macroscale effect such as the Lorentz force changes the flow field between the electrodes and results in a stirring effect [11, 26, 27]. An example for a microscale effect are Lorentz force–induced convection cells around surface roughness peaks, which results in an increased limiting current [8].

Thus far, it has not been studied how the magnetic field’s influence on the ECM process varies over different length scales and in which scale it is most dominant. Furthermore, investigations to determine the interactions between process parameters for the electric, magnetic, and flow field are crucial to evaluate the limits of the influence of a magnetic field on ECM. Consequently, the influence of a superposed magnetic field on the electrochemical machining process has to be examined experimentally and its representation in suitable simulation models has to be analysed accordingly.

In this study, fundamental work is presented to clarify the following questions: “Can the influence of a magnetic field on ECM be measured by optical experimental methods, and which are the relevant measurement parameters?” and “Are the developed simulation approaches suitable to predict the flow field of magnetohydrodynamic flow of sodium nitrate electrolyte under ECM conditions?” The outcome of the present work (Fig. 1, Step 1) will be transferred to a mesoscale analysis cell (Fig. 1, Step 2), which represents an ECM setup, to analyse the influence of the magnetic field in a measurable scale. In a last step (Fig. 1, Step 3), the influence of the magnetic field on the ECM-process and machining results will be investigated in the actual ECM machining process.

Fig. 1
figure 1

General approach to analyse superposition of magnetic field and ECM by measurements and numeric simulation models. Step 1: Starting with a simplified measuring cell (present work). Step 2: Transfer to a mesoscale analysis cell, to analyse the influence of the magnetic field in a measurable scale. Step 3: Investigation within the actual ECM-process

Full size image
Fig. 2
figure 2

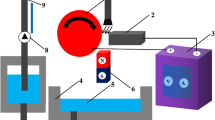
a Schematic illustration of the measuring cell. b Experimental setup and resulting Lorentz force ⊙, which is expected to be dominant close to the magnetic surface. c Plane for investigation with particle image velocimetry at 3 mm away from the reservoir wall. When comparing experiment and simulation, identical planes are considered

Full size image

Therefore, an experimental setup (Fig. 1, Step 1) was designed with the following requirements:

  • optically accessible flow field,

  • reproducible initial conditions,

  • easily represented by a simulation model.

By the construction of a reservoir with an octagonal base, the optical accessibility and the efficient realization for the experiment and the simulation are ensured. To account for the influence of the Lorentz force in the electrolyte, the magnetic and electric field lines must be aligned in a specific angle to each other. This simple setup is chosen for good comparability between the experiments, using particle image velocimetry, and the modelling, using magnetohydrodynamic (MHD) and multiphase (MP) simulations.

2 Methods

2.1 Experimental setup

A 3D model of the optical measuring cell is shown in Fig. 2a. To ensure optical accessibility, the reservoir is made of acrylic glass with a wall thickness of 2 mm and an octagonal base area with 20 mm side length. The electrodes are made of stainless-steel (type DIN EN 1.4301, AISI 316) with a thickness of 1 mm and a width of 20 mm; their minimum distance is 46.29 mm. Distance and material of the electrodes are chosen to minimize the influence of the electrochemical reaction. The choice of stainless steel for the electrodes is to avoid disturbances of the magnetic field due to its low magnetic permeability of approximately 1 H/m [28]. An aqueous solution with sodium nitrate (9.5% mass fraction, balance for mixing: LC 1200 S, Sartorius AG) is used as electrolyte. The permanent magnet is made of neodymium, iron, and boron (NdFeB N45) and has a dimension of 80 mm in length and 20 mm in width. During the experiment, the level of the electrolyte in the reservoir \({h}_{\mathrm{El}}\) is equal to the height of the magnet of 80 mm.

Due to the experimental arrangement, the Lorentz force is expected to be highest close to the surface of the magnet (Fig. 2b, c). Depending on the polarity of the two electrodes, the Lorentz force should result in an upward or downward electrolyte flow. For this reason, the examination area is located 3 mm away from the reservoir wall near the magnet.

To create different magnitudes of the Lorentz force, the electric current is varied by using a variable constant current power source (EA-PSI 5080–20 A, EA-Elektro-Automatik GmbH) and the magnetic field by using magnets with different magnetic flux densities (Table 1). Measurements of the magnetic flux were conducted through the wall next to the reservoir surface using a magnetic flux meter (PCE-MFM 3000-ICA, PCE Instruments™).

Table 1 Parameters of the measurement system
Full size table

Particle image velocimetry (PIV) is used to investigate the electrolyte flow in the examination area (Fig. 2). The PIV system consists of a CCD camera (TSI Powerview 4MP CCD Camera) and a 532-nm double-pulse laser (TSI, YAG200-15-LIT: Nd:YAG, max. power per pulse: 1200 mJ; repetition rate: 15 Hz; max. pulse duration 4 ns). All images are processed with the software Insight 4G™ (Version 10.1, TSI).

2.2 Dimensional analysis

In order to gain insight into the dynamics and general behaviour of the above-described physical system, a dimensional analysis is carried out. This will also help to reduce the experimental and numerical effort by revealing relations between different sets of parameters that should lead to a similar system behaviour.

The physical phenomena taken into account within the dimensional analysis are single-phase fluid dynamics and electromagnetism. Consequently, relevant physical parameters are the geometrical length scale \(L\), the average normal electric current density \(J\) on the electrode surfaces, the normal magnetic field \(B\) on the magnet side face of the reservoir, the fluid’s mass density \(\rho\), and its dynamic viscosity \(\eta\). Here, for the geometrical length scale \(L\), the distance of opposed side faces of the measuring cell as shown in Fig. 2 is used.

Please note that none of the above parameters relates to electrochemical gas production. Therefore, gas production will be neglected in our dimensional analysis. Table 2 represents the dimensional matrix according to the relevant physical parameters.

Table 2 Structure of the dimensional matrix regarding the characteristic length \({\varvec{L}}\) (here the distance between opposite sides of the measuring cell), the average normal electric current density on the electrode side faces \({\varvec{J}}\), the magnetic field \({\varvec{B}}\), the density of the fluid \({\varvec{\rho}}\), and the dynamic viscosity of the fluid \({\varvec{\eta}}\)
Full size table

The numbers in Table 2 correspond to the exponents of the dimensions mass, length, time, and electric current that the parameters’ units involve. This results in \(n=\) 5 input parameters and a dimensional matrix rank of \(r=\) 4. According to the Buckingham \(\pi\) theorem, there is only one dimensionless \(\pi\) group, as a result of \(n-r=\) 1 [29]:

$${\pi }_{1}=J B {L}^{3} \rho {\eta }^{-2}$$
(1)

This dimensionless group can be interpreted in different ways, e.g., as a ratio of Lorentz forces \({F}_{\mathrm{L}}=J B {L}^{3}\) and viscous forces \({F}_{\mathrm{visc}}={\eta }^{2} {\rho }^{-1}\) so that \({\pi }_{1}={F}_{\mathrm{L}}/{F}_{\mathrm{visc}}\). Alternatively, it can be understood as the product of a characteristic shear rate \({\dot{\gamma }}_{\mathrm{char}}=J B L {\eta }^{-1}\) of the Lorentz force induced flow and a measure of the system’s relaxation time \({t}_{\mathrm{relx}}={L}^{2} \rho {\eta }^{-1}\) so that \({\pi }_{1}={\dot{\gamma }}_{\mathrm{char}} {t}_{\mathrm{relx}}\).

If the above-described notion of the physical phenomena involved — which this analysis is based on — is accurate, then all parameter sets that yield the same value of \({\pi }_{1}\) will lead to a similar system behavior. This dimensional analysis can be used to scale the process parameters and the relationships between the physical phenomena to the mesoscale analysis cell (Fig. 1, Step 2), where forced convection and electrochemical reactions will be investigated additionally. It is one aim of this study to validate the demonstrated approach for dimensional analysis by experiments and simulations.

2.3 Simulation

Two simulation methods are combined to realistically represent the process. One is a magnetohydrodynamic simulation (MHD simulation) approach based on the commercial Finite-Volume-Element software StarCCM + provided by Siemens. The second method is a multiphase simulation (MP simulation) approach implemented in m-AIA, which is developed at the Institute of Aerodynamics at RWTH Aachen University.

The MHD simulation involves the assumption that there is no gas production, and in the present MP simulation, no Lorentz force can be calculated. By transferring the calculated Lorentz force values from the MHD simulation approach to the MP simulation approach, a more detailed simulation model of the magnetic field–assisted electrochemical process can be achieved.

Further assumptions for both simulation approaches are:

  • no Joule-heating of the electrolyte,

  • steady boundary conditions.

For the MHD simulation, the 3D-model geometry was derived from the experimental setup representing only the electrolyte domain, while the magnet and electrodes are modelled as boundary conditions, not physical continua, to reduce numerical effort. In Fig. 3, the simulation geometry and the numbering of the boundary conditions are shown. The definitions for each boundary depend on the simulation approach and are given in Table 3.

Fig. 3
figure 3

Simulation geometry and numbers of boundary conditions (Table 3). 1: cathode, 2: anode, 3: magnet, 4: wall, 5: free surface

Full size image
Table 3 Boundary conditions for the MHD and MP simulation model. The symbols describe \({\varvec{F}}\) Faraday constant, \({\varvec{J}}\) electric current density, \({\varvec{M}}\) molar mass, \(\dot{{\varvec{m}}}\) mass flow rate, \(\overrightarrow{{\varvec{n}}}\) normal vector, \({\varvec{p}}\) pressure, \(\overrightarrow{{\varvec{u}}}\) velocity vector, \({\varvec{z}}\) oxidation number, and \(\boldsymbol{\varphi }\) electric potential
Full size table

The modelled phenomena result from fluid-dynamics and electrodynamics including electric and magnetic field distributions. Field variables to be solved for are the velocity field, the electric potential field, and the magnetic vector potential field. The electromagnetism is described by Maxwell’s equations, and the electric field \(E\) is a result from the electric potential difference between the electrodes \(V\).

Based on the electric conductivity of the electrolyte and the electric field, the electric current distribution \(J\) is calculated. The Lorentz force \(F\) is defined as the cross product of the electric current density and the constant electric field. By adding the Lorentz force as external force to the Navier–Stokes equations, the impact on the electrolyte flow field can be described.

Table 3 lists the different boundary conditions for the MHD simulation. Boundary No. 1 represents the cathode with an electric current density towards the \(x\)-direction \({J}_{x}\). The anode (boundary no. 2) represents the ground with an electric potential of 0 V. Walls of the reservoir and magnet are electrically insulated, which means the electric current through the wall equals zero. The magnetic field strength is determined based on measurements directly on the reservoir surface with a magnetic flux meter. The magnet source is modelled as magnetic vector potential at the reservoir surface at boundary no 3. At the reservoir walls (nos. 1, 2, 3, 4), a no slip boundary condition is defined. Boundary condition no. 5 represents the top surface of the electrolyte and is defined with a slip condition.

The MP simulations are conducted to incorporate the influence of the gas generation on the electrolyte flow. Therefore, a Eulerian-Eulerian bubbly flow method was chosen. It employs two sets of conservation equations, each representing the mass and momentum balance of one phase, similar to Haji Mohammadi et al. [30].

The gas phase is modelled by a finite-volume method, while a lattice Boltzmann solver is used for the liquid phase. Both solvers operate on a shared uniform Cartesian grid that is also used to transfer interfacial momentum terms, leading to a two-way coupled system. Validation of the method has been done previously with experimental data of a bubble column [31].

Equivalent to the MHD simulations, only the electrolyte-filled domain of the experiment is considered for the MP simulations. The Cartesian simulation grid of the MP model contains 1,232,640 cells with a width of 0.503 mm.

As listed in Table 3, the liquid solver uses no-slip conditions at all boundaries. For the gas solver, no-slip boundary conditions are applied to all boundaries except for the top surface, where a pressure outflow condition is used instead to enable the gas to leave the domain.

The gas is injected into the domain through the boundary cells neighbouring the electrodes. For each experiment, the gas production rate \({\dot{m}}_{i}\) for hydrogen and oxygen generation is calculated by Faraday’s law, given by Eq. (2). Here, the parameter \({M}_{i}\) is the molar mass of the element of the injected gas, \({z}_{i}\) represents the valence, \(F\) is the Faraday constant, and \({J}_{n}\) is the normal current density at the surface.

$${\dot{m}}_{i}=\frac{{M}_{i}}{{z}_{i}\cdot F\cdot {J}_{n}}$$
(2)

Due to low current density values less than 1 A/cm2, a small amount of anodic material dissolution is expected during the considered process time leading to the assumption that 100% of the electric charge at the anode surface is used for gas production. Since the present model only supports a single gas, both the H2 and O2 gases are modelled as an equivalent volume of H2 gas. This simplification is justified by the fact that the difference in buoyancy of both gases in water is negligible (< 0.15%). As average diameter of the spherical gas bubbles that form at the surface of the electrodes, 0.35 mm are estimated based on the experiment. This value is considered constant for the simulation.

To incorporate the influence of the Lorentz force on the flow field, the stationary force field generated by the MHD simulations is used. The forces are evaluated at 21 X–Z planes in the MHD simulations that are distributed uniformly throughout the domain of the electrolyte. In between these planes, the values are linearly interpolated to achieve coupling of the force field in 3D.

3 Results

3.1 Parameter definition

For comparing the results of the experiment and the two sets of simulations, we defined five cases shown in Table 4. The case selection was done so as to ensure that the influences of low and high current density (\(J=\) 80 A/m2: case 1, case 2; \(J=\) 200 A/m2: case 4, case 5) as well as installed and removed magnet (\(B=\) 0 T: case 1, case 4; \(B=\) 0.239 T: case 2, case 5) are captured. In addition, we defined another case (3) with the same dimensionless number \({\pi }_{1}\) as in case 2. Here, case 3 is defined with a different electric current density and a different magnetic flux density (case 3: \(J=\) 125 A/m2; \(B=0.151\)). Due to the higher electric current density, case 3 is likely to have a higher gas production than case 1. This is, however, considered neither in the MHD model nor the dimensional analysis described above.

Table 4 Definition of the five test settings for comparison of the experiment, the MHD, and MP simulations
Full size table

3.2 Field distributions

The calculated electromagnetic field distributions and the resulting magnitude of the Lorentz force of the MHD-simulations exemplary for case 2 can be seen in Figs. 4, 5 and 6. The qualitative distributions of magnetic flux density, current density, and Lorentz force are similar across the different cases.

Figure 4 shows the magnitude of the magnetic flux density B for case 2. A non-uniform magnetic field is formed in front of the magnet-side. A high density of magnetic field lines leads to an increase of the magnetic flux density at the edges between boundary nos. 3 and 4 (see Fig. 3). Maximum values of approximately 0.8 T can be observed. Towards negative Z-direction, the magnetic flux density decreases reaching values of approximately 0.2 T in the plane of investigation (see Fig. 2) for case 2.

Fig. 4
figure 4

False colour rendering of the magnitude of the magnetic flux density B (T) for case 2 (I = 0.13 A; B = 0.239 T; π1 = 2.2 × 106) in Z-X plane (Y = 0.06 m); arrows (uniform length) indicate direction of magnetic field lines for case 2

Full size image

Figure 5 shows the magnitude of the electric current density J for case 2. A non-uniform distribution is formed between the cathode and the anode. At the anode surface, a constant value of approximately 80 A/m2 can be observed, which corresponds to the defined boundary condition (Table 3). At the anode surface, the calculated electric current density distribution reaches maximum values of approximately 150 A/m2 in the area of the sharp edges between the anode and the insulated walls of the reservoir due to a high density of electric field lines. At the examined area in front of the magnet surface, current density values of approximately 27 A/m2 can be observed.

Fig. 5
figure 5

False colour rendering of magnitude of the electric current density J (A/m2) for case 2 (I = 0.13 A; B = 0.239 T; π1 = 2.2 × 106) in Z-X plane (Y = 0.06 m); arrows (uniform length) indicate direction of electric field lines for case 2

Full size image

In Fig. 6, the result of the calculated magnitude of the Lorentz force can be seen. The false colour plot shows the magnitude in X–Y-, Z-X-, and Y–Z planes. A non-uniform distribution of the Lorentz force can be observed because of the present electromagnetic fields. Maximum values of about 10 N/m3 can be found next to the magnet surface. In the area of the PIV-measurements, the Lorentz force density reaches values of approximately 6 N/m3. Furthermore, the action of the Lorentz force within the afore-mentioned plane is in the positive direction of the Y-axis. As a result, an acceleration of the electrolyte in the same direction is to be expected.

Fig. 6
figure 6

False colour rendering of the magnitude of the Lorentz force FL (N/m3) for case 2 (I = 0.13 A; B = 0.239 T; π1 = 2.2 × 106) in X–Y plane (z = 0.0 m), Z-X plane (Y = 0.06 m), Y–Z plane (X = 0.0 m); arrows (uniform length) indicate direction of force for case 2

Full size image

In order to compare the results of the simulations and the experiment, the area parallel to the magnetic surface at a distance of 3 mm from the wall in the electrolyte is chosen. In this area, a nearly homogeneous Lorentz force can be assumed based on the simulated Lorentz force as illustrated in Fig. 6.

Figure 7 shows the maximum and mean velocity magnitudes in the examined area over 1 min, starting at 120 s of process time for all cases. In addition, Fig. 8 provides an impression of the flow conditions in the examination area after 150 s of process time. The results for each case are given in the columns and each investigation technique (experiment, MHD/MP simulation) in the rows.

Fig. 7
figure 7

Distribution of a the maximum and b the mean velocity magnitudes \({\varvec{v}}\) between 120 and 180 s of process time in the examination area measured with PIV, calculated from the MHD simulation, and calculated from the MP simulation. The upper limit of the bar shows the median, while the lower and upper limits of the error indicator mark the 25% and the 75% quantiles, the x marks the temporal maximum value, and the + marks the temporal minimum value

Full size image
Fig. 8
figure 8

Surface plots of the velocity magnitude \({\varvec{v}}\) (based only on the velocity vectors in X and Y directions) in the examination area for each case (columns 1–5) at a process time of 150 s, measured using PIV (row 1), calculated from the MHD simulation (row 2), and calculated from the MP simulation (row 3)

Full size image

3.3 Process without magnet

Before investigating the influence of the magnetic field on the electrolyte flow field, the electrolyte flow during electrolysis without magnet was measured and simulated (cases 1 and 4: 80 A/m2 and 200 A/m2). As shown in Fig. 8a, d, k, and n, the resulting flow fields are similar in both cases. Both the experiment and the MP simulations exhibit a main flow from the upper right corner (side of the cathode) spreading into the examination area. Another secondary flow from the upper left corner (side of the anode) appears at the beginning but is soon suppressed by the main flow. These characteristic flow patterns are a result of the electrochemical process characterized by hydrogen and oxygen production at the electrodes. Hence, the electrolyte is displaced and set into motion due to the buoyancy of the gases. As expected, because of the higher gas production rate, the velocities for case 4 are higher than in case 1, see Fig. 7.

For the MHD simulation, both the velocities over time (Fig. 7) and the snapshot after 150 s of process time (Fig. 8f, i) amount to zero. This deviation occurs due to the focus on the electromagnetic behaviour in the fluid domain, while ignoring the electrochemical gas production in the MHD simulations.

3.4 Process with magnet

In cases 2, 3, and 5, a superimposing magnetic field is added. This creates a Lorentz force as demonstrated in Fig. 6. From the direction of the electric current and the magnetic field results an upward-directed Lorentz force and, thus, an upward electrolyte flow near the magnet surface. This flow is experimentally verified and simulated with both the MHD and the MP simulation (Fig. 8).

Comparisons between cases 1 and 2 as well as cases 4 and 5 show that the resulting velocities are significantly larger than the velocities without magnet (Fig. 7). However, according to Sect. 2.2, this depends largely on the magnitude of the dimensionless number. For cases 2 and 3, the pairing of magnetic flux density and electric current density is chosen to result in the same dimensionless number. Comparing both cases, the resulting velocities are nearly identical. This similar flow field between the cases is confirmed by all three investigation methods.

Case 5 has considerably larger deviations, independent of the investigation method, compared to cases 2 and 3 (Fig. 7). While comparing different snapshots of case 5, it became clear that also the flow pattern changes over time. For cases 2 and 3, these changes do not appear or at least in the case of the experiment, the changes are significantly smaller and appear over larger time periods. This change from a quasi-static flow to a chaotic flow could be reproduced experimentally between \({\pi }_{1,\mathrm{low}}=\) 2.5 × 106 and \({\pi }_{1,\mathrm{up}}=\) 4 × 106. Therefore, in this case, a flow characterization based on \({\pi }_{1}\) is equivalent to a characterization of the flow conditions by a Reynolds number, which turns out to be a valid option.

3.5 Experiment and simulation

3.5.1 Experimental uncertainty

The uncertainty of the experimental velocity determination is estimated according to “GUM: Guide to the Expression of Uncertainty in Measurement” [32]. For calculating the expanded uncertainty \(U(v)\) (k = 2), Eq. (3) is used:

$${U(\nu )\left({\left[{\left(\frac{\partial v}{\partial s}\right)}_{\tau }\cdot U\left(\Delta x\right)\right]}^{2}+{\left[{\left(\frac{\partial v}{\partial \tau }\right)}_{s}\cdot U\left(\Delta \tau \right)\right]}^{2}{+\left[{\left(\frac{\partial v}{\partial {F}_{L}}\right)}_{q,L}\cdot U\left({F}_{L}\right)\right]}^{2}\right)}^{0.5}$$
(3)

The first two terms of Eq. (3) describe the influence of the PIV setup, i.e., optical setup and software settings, on the velocity \(v\). This is based on the relation between the calculated displacement \(\Delta s\) and the time difference \(\Delta \tau\), \(v=\Delta s/\Delta \tau\).

The time difference is equal to the laser pulse time difference. Laser pulses are software-controlled, and stability and precision were confirmed by measurements. Additional light sources, which influence the uncertainty of the time difference \(U(\Delta \tau )\), were carefully covered. Therefore, the influence of uncertainties in the time difference is considered negligible.

However, the influences on the calculated displacement are manifold. According to the available literature, e.g., see Sciacchitano and Wienecke [33] and Wienecke [34], the dominant element originates from the calibration. In this case, graph paper was used for the calibration. This resulted in an uncertainty of 1.67%. Seeding particles (hollow glass spheres, diameter 8–12 μm, particle density 1050–1150 g/cm3), seeding density, and software settings were all chosen to fit the manufacturer’s specifications for reliable results. Therefore, these influences are assumed to be negligible.

The third term in Eq. (3) is based on the reproducibility of the velocity field depending on the electric, chemical, and magnetic setup.

This can be described using the influence of the Lorentz force, see Eq. (1). Thereby, Eq. (3) is based on the relationship for the dimensionless number, while Eq. (4) describes the Lorentz force \({\overrightarrow{F}}_{\mathrm{L}}\) on moving charges \(q\).

$${\overrightarrow{F}}_{\mathrm{L}}=q\overrightarrow{v}\times \overrightarrow{B}$$
(4)

In the experimental setup, the electric current density \(J\) is set by the electric current \(I\) over the wetted electrode areas \(A\): \(J=I/A\).

The power source can be adjusted accurate to \(U\left(I\right)=\) 0.01 A and the reproducible electrolyte height of \(U\left(h\right)=\) 0.001 m and constant width; the uncertainty of the current density for different currents can be calculated.

To calculate the Lorentz force, the magnetic flux density is required. This varies for both magnets over the surface around an average of \({B}_{\mathrm{weak}}=\) 0.151 T for the weaker magnet and \({B}_{\mathrm{strong}}=\) 0.239 T for the stronger magnet with a standard deviation of \(U\left({B}_{\mathrm{weak}}\right)=\) 7.956 × 10–3 T and \(U\left({B}_{\mathrm{strong}}\right)=\) 10.871 × 10−3 T. The preparation of the electrolyte solution was carried out with an uncertainty of 0.005 g for 800 g of electrolyte, which results in an uncertainty of \(U\left(x\right)=\) 1.2569 × 10−5 in the mass fraction and is, therefore, considered negligible. All those influences result in a maximum combined expanded (\(k=\) 2) uncertainty of 0.0032 m/s at a maximum velocity in the field of 0.0209 m/s (which corresponds to a relative uncertainty of 18.2%) and case 5.

The same uncertainties must be considered for comparing the experimental results for equal dimensionless numbers \({\pi }_{1}\) Eq. 1). Using the same approach as for the velocity, this results in a maximum combined expanded (\(k=\) 2) uncertainty of 4.0 × 105 m/s (17.9%).

3.6 Experiment and MHD simulation

Cases 2, 3, and 5 are used to compare the MHD simulations with the experiments. According to Fig. 8 b/g, c/h, and e/j, both experiment and simulation show similar flow patterns. For those, the relative differences for the average maximum and mean velocity magnitudes over 60 s are the highest with 6.0% and 61% (Fig. 7). With respect to the experimental uncertainty, the MHD simulation reproduces the experimental result very well.

In the simulation, the flow in case 1 becomes completely stationary after an initial time. However, this is not the case in the experimental result. Also, after around 5 min, gas bubbles appear in the whole reservoir. This means that gas produced at the electrodes has mixed into the bulk electrolyte. In addition to these effects, the similarities in the results show that the Lorentz force is the dominant on the electrolyte flow in the chosen setup. Thus, the setup can be used for further investigations, e.g., with modified magnet arrangement. To transfer the results to investigation on the electrode surfaces with a superimposed magnetic field (mesoscale analysis cell, Fig. 1, Step 2), however, gas production rates must be taken into account.

3.7 Experiment and MP simulation

The comparison of the MP simulations with the experimental data for cases 1 and 4 shows good agreement. Although the simulation results exhibit slightly higher values for the velocity magnitude, the measured instantaneous velocity fields are reproduced very well (Fig. 8). These differences in the maximum velocities could be explained by the simplified modelling of the bubbles with an estimated and constant diameter since no precise measurements for the bubble size were available. The simulations of case 1 reach nearly a steady state within about 60 s from the start, with slight fluctuations remaining. This agrees well with the observations made in the experiment. In case 4, fluctuations in the velocity remain throughout the duration of the experiment and the simulation, resulting in a wider distribution of the statistics in Fig. 7.

Cases 2, 3, and 5 are also reproduced very well. The averaged maximum and mean values of the velocity and their fluctuations are slightly underestimated but match the experimental values even better than the MHD simulations (Fig. 7). The instantaneous velocity fields at a time of 150 s also agree well with the results of the other methods. Some deviations regarding the shape and the location of the regions of maximum velocity can be observed due to the unsteady behaviour of the flow, especially at higher electrical currents. It was also demonstrated that the relative influence of the gas bubbles on the flow in the measurement area is low, since the different gas production rates between cases 2 and 3 do not result in large differences in the flow fields.

Therefore, the MP approach is not strictly required for the present cases 2, 3, and 5, as can be seen by the excellent results of the MHD simulations. The MP modelling approach, however, is considered to have great potential for investigations on the electrode surfaces with a superimposed magnetic field (Fig. 1, Step 2), where the influence of the gas production is stronger.

4 Summary and conclusions

The aim of this work was to investigate the influence of the Lorentz force on an electrolyte flow without forced convection. Thus, the following questions were to be answered: “Can the influence of a magnetic field on ECM be measured by optical experimental methods, and what are the measurement parameters?” and “Are the available simulation models suitable to predict the flow field of magnetohydrodynamic flow of sodium nitrate electrolyte under ECM conditions?” Within the process described in Fig. 1, the focus of this paper is to test the existing experimental and simulation methods on a specific setup (Fig. 2).

We have shown that despite the wide distance between the electrodes, the gas production leads to a buoyancy flow in the fluid (Fig. 8a, d , cases 1 and 4). However, in cases with superimposed magnetic field (cases 2, 3, and 5), an upward flow dominates in the examination area. This experimental observation confirms the MHD simulation results regarding the prediction of the Lorentz force (Fig. 6). Although, the gas production is not considered, the MHD simulation results for cases with magnetic field agreed excellently with the experimental results (Figs. 7 and 8).

Application of the MP simulation enables the consideration of gas production at the electrodes. For the cases without superimposed magnetic field (cases 1 and 4), the flow pattern is similar to the experiment (Fig. 8 a/k and d/n). However, the velocity magnitude is significantly larger. This is probably due to the calculation based on a constant bubble size. To simulate the behaviour with a superimposed magnetic field by the MP simulation (cases 2, 3, and 5), the Lorentz force is set according to the results from the MHD simulation. This coupled simulation approach leads to accurate reproduction of the experimental flow velocities, similar to the results of the MHD simulations. Finally, the results for cases 2 and 3 are almost equally independent of the investigation method. Both cases have the same dimensionless number. Due to the same electrolyte flow in these two cases, the dimensionless number can justifiably be used to characterize the flow.

To answer the initial questions, the optical method (PIV) can be successfully used to investigate processes in ECM, and the presented simulation approaches can reproduce important phenomena, e.g., Lorentz force and the electrolyte flow. For the upcoming investigations of influence of the magnetic field in the electrode area (Fig. 1, Step 2), the described methods for experimental and simulation-based investigations will be further improved. This approach will close the gap between the machining conditions provided in this paper and real ECM conditions (Fig. 1, Step 3). Therefore, transferring the findings to the manufacturing scale will be the main objective of upcoming work. Experimental and simulation-based results will be compared with respect to process variables such as the electric current, produced process gas, and reaction products.

For a successful simulation of the processes in the area of the electrodes, the MHD and MP simulation approaches will be more closely linked to each other. This approach aims to improve future process simulations and thus shorten the process design of electrochemical machining with superimposed magnetic fields.