1 Introduction

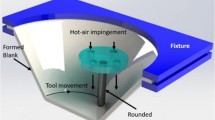
Thin-gauge pressure negative thermoforming is a process for the production of thin-walled thermoplastic parts like coffee cups or blisters. The manufacturing process begins with heating the thin-walled plastic raw material over its glass transition temperature, and then placing it on top of the mold. After closing the pressure box air-tight around the sheet, the deformation process as depicted in Fig. 1 starts.

Fig. 1
figure 1

Common thin-gauge thermoforming: a heated sheet of plastic is inflated into the mold by one-sided pressure application

Full size image

Pressurized forming air is led into the pressure box, so that the plastic sheet inflates into the mold, thereby taking its form. At mold contact, wall sticking can be assumed [8, 11, 15, 28], which implies uneven stretching and thinning of the raw material, with the end product’s thinnest point at the bottom radius for cup-like molds. Air trapped between sheet and mold escapes through venting bores, which in thin-gauge thermoforming applications are usually limited to fractions of a millimeter.

The wide range of applicability for packaging, especially for food products, makes thermoforming a widely used process in plastics processing. Due to this specific interest, a substantial amount of research targeted the analysis of the common process. While even analytical studies have been conducted [14], most of the research was using simulations [8, 15, 32], partially backed by experimental data [12]. Difficulties in understanding and simulating the process arise from the non-linearities in the contact boundary condition, the plastic material models and the large deformation [16, 28].

As thermoforming is a versatile technology with a broad range of applicability, thermoformed products account for a notable portion of plastic consumption and plastic waste. The amount of used raw material is usually determined by the thinnest wall part [25], so that a more uniform wall thickness distribution allows for a reduction in raw material thickness and hence provides economical as well as ecological advantages. The optimum is considered to be a completely uniform wall thickness for most applications [23, 25, 26].

With plug prestretching as shown in Fig. 2 and the application of a suitable temperature profile onto the sheet before inflation, two process enhancements for improving the wall thickness distribution are known.

Fig. 2
figure 2

Thermoforming process with plug-prestretching

Full size image

Within the past decades, both were subject to scientific investigation. Notable research work has been conducted focused on improving plug prestretched thermoforming using simulations and experiments. An early contribution by Koziey et al. already highlights the importance of sliding at plug contact [16]. Nam et al. focused on a method to compute the ideal plug geometry, but adopted the debatable assumption of perfect slip between plug and sheet [26]. Over several years, the research group around O’Connor, McCool, Martin et al. published notable findings of their systematic research on the influence of plug heat transfer, plug contact friction, plug speed, and further process parameters on the thermoforming process [22,23,24, 30]. In summary, the literature supports the conclusion that plug prestretching not only can lead to a significantly improved wall thickness distribution, but also unveils the intrinsic drawbacks arising from the temperature- and material-dependent behavior for modeling the process, especially at the contact between plug and sheet.

Pre-heating with a non-uniform temperature profile on the other hand requires a good understanding of the heating process, the peculiarities of which have been treated in a range of publications [10, 18, 19]. The effect of nonuniform heating has been partially treated as a side effect [5, 9, 27, 28], but there has also been published work on finding a suitable temperature distribution for a more even wall thickness distribution. In an early contribution, Wang et al. point out that already small changes in temperature may have a significant effect on the wall thickness distribution [38], implying that the temperature profile must be projected onto the sheet with a high accuracy. Bach et al. used ceramic heaters to apply a favorable temperature profile obtained using simulations of the thermoforming process, leading to an increase of the wall thickness minimum by more than \(100\%\), showcasing the potential of the approach [1]. More recently, Cha presented a simulation model which computed improvements of \(30\%\) in a type of vacuum forming process, although with notable deviations to experimental data, which underlines the challenging modeling of such a process [6]. Like thermoforming with plug prestretching, also the profiled pre-heating method comes with the drawback of increased machinery and maintenance cost and naturally relies on accurate modeling of the temperature-dependent stress-strain behavior of the material under consideration.

The forming air impact technology for thermoforming (FIT) comprises a novel approach with the potential to combine an improved wall thickness distribution with only little increase in thermoforming device complexity, maintenance effort, and running costs.

2 Forming air impact technology for thermoforming

The FIT process extends the common thermoforming process by utilizing the pressurized inflation air flow through the favorably arranged inlet nozzles for an improved deformation behavior.

Among the parameters which are deemed to be influential, there are process parameters like pressure increase over time, and heating temperature as well as geometry parameters like the nozzle size and standoff distance. Detailed knowledge of the parameters’ effect and mutual interaction is required in order to allow for reliable prediction and optimization of the resulting wall thickness distribution. Due to the large number of influential parameters, experimental exploration of the whole parameter space in order to gain insight into their mutual influence is very costly [23].

The interaction of the nozzle jet impinging onto the plastic sheet is twofold: by dynamic pressure increase and by local increase of heat transfer. Local pressure differences that can be achieved are small compared to the average forming pressures applied onto the sheet; therefore, the latter is assumed to be the more important effect. By exploitation of the temperature-dependent material behavior, it has been proven experimentally that the wall thickness distribution can be influenced favorably [37]. In conclusion, the idea behind this approach can be thought of a just-in-time application of pre-heating with an appropriate temperature profile, but without the need for an additional profile—pre-heating device to the thermoforming machine. Only exchangeable nozzle geometries, e.g., using nozzle plates, and an elaborate flow control for pressurized air are required. This implies the further advantage of making this approach suitable for retrofitting to existing thermoforming machines.

On the downside, the interaction between inflation air flow and the plastic sheet via heat transfer and dynamic pressure is of complex nature, making the FIT process harder to investigate by simulations and experiments.

For the complete interaction and the expected complex highly turbulent flow field in the pressure box to be captured, a thermally and dynamically coupled fluid-structure interaction (FSI) simulation would be mandatory, but the huge computational demand of FSI simulations would preclude the application of simulations for extensive parameter studies and iterative parameter optimization runs. Hence, the seemingly best possibility for simulating the process is to use a purely structural simulation, with modeled interaction between flow field and plastic sheet.

2.1 Aim and scope of this study

The goal of this study is to set up and validate a structural simulation model for the FIT process, which reproduces the final wall thickness distribution accurately enough for allowing parametric studies with qualitatively correct results. Possible delay of the deformation due to counter-pressure by the air trapped between sheet and mold receives special attention. An axis-symmetric mold geometry as depicted in Fig. 3 is used as a sample geometry.

Fig. 3
figure 3

Cross-sectional sketch of the axis-symmetric mold with venting bore at the bottom radius and dimensioning. Numbered measurement points of wall thickness are shown as white circles

Full size image

Two axis-symmetric nozzles are considered for inlet of pressurized inflation air: a round nozzle along the symmetry axis termed central nozzle with diameter \(D_{CN}\), and a concentric annular nozzle defined by its diameter \(D_{AN}\) and gap width \(g_{AN}\). Figure 4 shows a cross-sectional view of the nozzles and the expected flow paths of the jets emerging from the nozzles.

Fig. 4
figure 4

Sketch of nozzle arrangement and expected jet flow paths. Above the plastic sheet, there is the pressure box fluid domain, while between the sheet and the mold there is the mold fluid domain where counter-pressure may build up

Full size image

The reasoning behind the annular nozzle is to project a cooled ring-shaped area onto the plastic sheet, such that most stretching happens outside that ring of increased stiffness, at the to-be side walls of the mold, leading to a thicker bottom including the most critical part, the bottom radius.

2.2 The role of mold counter-pressure

Publications on simulations of common thermoforming so far consider only the pressure applied to the sheet upper side, while pressure build-up in the mold is neglected. As inertial effects are usually negligible in these cases, the omission of mold counter-pressure does not have a detrimental effect on simulation accuracy because the deformation for the hyperelastic material models often used is then only dependent on the effective pressure acting on the sheet, and not on time. On the contrary, correct time resolution of the deflection during inflation is crucial for thermoforming using the FIT process. This is due to the cooling potential of the nozzles in use that depends significantly on the jet path length, which is the distance between nozzle exit and impingement point at the sheet surface. Common approximative relations assume a decay of the heat transfer coefficient along the jet path length, usually according to a power function. Therefore, the decay is strongest for small jet path lengths, with the maximum at process start, so that correct modeling of the deflection from simulation start on is indispensable. Basic consideration of a common simplified thermoforming process for the mold shown in Fig. 3, assuming full deformation within 200 ms and 24 venting bores with a diameter of 0.25 mm each (total venting area is \(A_{Vent} = 1.18 \text { mm}^2\)), implies an average flow velocity of 156 \(\text {ms}^{-1}\). This in turn, neglecting flow contraction and assuming a pressure loss coefficient of 1, would already lead to a pressure difference over the venting nozzles of 0.14 bar, which is only one order of magnitude below the commonly applied forming pressures. Considering that deflection speed changes with time, mold counter-pressure may have an impact on the deformation process even for larger venting bore diameters that imply less counter-pressure. Apart from the given example, the effect arising from undersized venting geometries has been treated in the literature. Throne stresses the implications of too small venting holes, slowing down the escaping air flow, as well as of too large venting holes, possibly leading to unwanted visible nipples [35]. Due to the potential effect of counter-pressure on cycle time and therefore wall thickness distribution, a method to include the counter-pressure effect in the simulation in an implicit manner has been developed, and will be presented together with a description of the modeling of the pressure box fluid flow impact on the plastic sheet during deformation.

3 Experimental setup

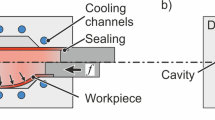
Data for validation of the simulation model has been obtained on a thermoforming test bench, a picture of which is given in Fig. 5.

Fig. 5
figure 5

Thermoforming test bench used for experimental data generation. A revolvable metal plate to which the sheets of raw material are clamped moves the sheets to the heating, and after that, forming station

Full size image

At its core, it consists of a circular metal plate which is revolvable around its central axis. Several tool stations for heating, forming, or additional other steps are placed along its circumference. For conduction of an experiment, a sheet of plastic is clamped onto the metal plate, and then by rotation of the latter moved to the tools’ stations by mechatronics control, allowing for high repeat accuracy. The figure explicitly shows the actual heater and thermoforming tool stations, used for the experiments in this study. Air-tightness during forming is achieved by moving the upper part of the thermoforming tool downwards and the mold from below upwards, clamping the sheet in between.

4 Simulation setup

Simulations were conducted using the ANSYS Mechanical finite element software in version 2020R1. The system of equations to be solved for nodal deflections \(\mathbf {u}\) is given as Eq. (1).

$$\begin{aligned} \mathcal {M} \; \ddot{\mathbf {u}}(t) + \mathcal {C} \; \dot{\mathbf {u}}(t) + \mathcal {K} \; \mathbf {u}(t) = \mathcal {F}^a(t) \end{aligned}$$
(1)

Due to axis-symmetry of the mold geometry, only a small azimuthal section of \(5^\circ\) of sheet and mold are modeled for the simulation, reducing the computational cost considerably. Nonetheless, a brick-like continuum finite element type featuring thermal-mechanical coupling, named SOLID226 in ANSYS terminology, was favored for the sheet instead of an axis-symmetric element type, in order to facilitate a future extension to configurations where the assumption of axis-symmetry no longer holds. The sheet mesh consists of three element layers, with overlaid contact elements on the sheet lower side, while the mold mesh consists of contact-target elements only with no extent in thickness direction. A picture of the mesh colored according to equivalent true plastic strain contours at the middle of the inflation process is given in Fig. 6. Blue coloring indicates low strain, while red coloring indicates large strain. The contact elements of the mold are shown in light gray. Furthermore, the figure illustrates the adaptive mesh sizing with refinement where high bending occurs, in order to accurately capture the radii while keeping the computational cost low. In an enhanced view, the three elements in thickness direction can be distinguished.

Fig. 6
figure 6

Solid mesh of \(5^\circ\) extent in azimuthal direction showing the sheet mesh colored by equivalent true plastic strain and the mold mesh in light gray. An enhanced view focuses on the upper bend radius

Full size image

In total the number of finite elements amounts to around 600, including contact elements. Mesh refinement studies with up to 2400 elements yielded a maximum difference of \(2\%\) in wall thickness averaged over the eight measurement points, depending on the test case. Since this is significantly lower than the deviations to the measurements presented in the results section, the mesh with 600 elements was considered fine enough for this study.

4.1 Simulation sequence

Fig. 7
figure 7

Flowchart of simulation steps

Full size image

The basic simulation process is depicted in Fig. 7. Starting with the first time step, the initial conditions are set up. Secondly, in a cooling step without mechanical load, sheet cooling during transport from heating to forming station is simulated. A constant heat transfer coefficient at upper and lower sides of the sheet and ambient reference temperature are applied. In the next step, gravitational acceleration is switched on, so that sagging of the sheet due to its own weight is considered, which has been shown to be able to have significant impact on the final wall thickness distribution [36].

Beginning with the fourth step, a venting phase is simulated, in which local cooling with the nozzles is possible while a venting valve of the pressure box remains opened, such that no pressure build-up and therefore cooling without inflation occurs. A fixed number of 20 time steps is used for simulating the venting process. For the scope of this study, this possibility has not been made use of. After venting, the actual thermoforming process with closed venting valve starts and runs until full deformation is reached.

4.2 Forming simulation

In the forming time steps, the deformation state of the sheet depends mainly on the effective pressure applied on the sheet, which is the difference between forming pressure in the pressure box \(p_{Box}\) and the counter-pressure from within the mold \(p_{Mold}\):

$$\begin{aligned} p_{Eff} = p_{Box} - p_{Mold} \end{aligned}$$
(2)

Mold pressure is due to the pressure loss at the venting bores, through which the air initially between mold and plastic sheet escapes, displaced and compressed by the deforming plastic sheet. Air compressibility must hence be taken into account, such that modeling of the thermodynamic behavior within the mold is mandatory. Forming pressure \(p_{Box}\) is known from measurements and prescribed as a function depending on time.

The dependence of mold pressure on total volumetric displacement of the plastic sheet, which in turn depends on the effective pressure and thus in turn on mold pressure, constitutes a circular dependency as depicted in Fig. 8.

Fig. 8
figure 8

Circular dependency between total displacement and mold pressure. Solid lines represent deterministic arithmetic relationships. In contrary, the dashed line connection is evaluated either via simulation or approximated by extrapolating from previous time steps

Full size image

In mathematical formulation, the circular dependency can be expressed as Eq. (3), or rewritten in fixed-point formulation for the total volumetric displacement TD, as Eq. (4).

$$\begin{aligned} TD(p_{Eff})&= TD(p_{Box} - p_{Mold}(TD)) \end{aligned}$$
(3)
$$\begin{aligned} TD^{k+1}&= TD(p_{Box} - p_{Mold}(TD^{k})) \end{aligned}$$
(4)

A compatible state with the circle’s variables must be found for each time step. While the solid connections in Fig. 8 from total displacement over the venting mass flow rate and counter-pressure to effective pressure can be calculated based on arithmetic modeling relations, the link between effective pressure and total displacement is more difficult to resolve. In order to find the final compatible solution, a costly call to the finite element solver is inevitable. However, for an estimate, an extrapolation of the dependency of total displacement on the effective pressure from the previous time steps can be used, which is exploited to find a reasonable guess in a compatibility loop, as explained below.

In order to be resolve the circular dependency in the simulation, an inner loop within each forming time step is run through, in which the model is solved for a combination of forming pressure and mold pressure, until the resulting displacement is compatible with the applied effective pressure. Figure 9 shows a flowchart of the time stepping procedure, including the time step inner loop.

Fig. 9
figure 9

Flowchart of time stepping loop, including inner loop and compatibility loop highlighted in light and dark gray

Full size image

Because of the strong dependence between mold pressure and sheet deflection, this approach converges slowly or even tends to diverge in case of a unreasonable initial guess for the total volumetric displacement. Furthermore, the evaluation of the total displacement requires a solution of the simulation model for the time step, increasing the necessary computational effort. Consequently, in order to improve convergence and execution speed, within the inner loop, a combination of deflection, pressure box pressure, and mold pressure is to be found, which is compatible with prior knowledge of deflection-pressure relationships from previous time steps. The search for a compatible combination is implemented in a nested loop, as discussed below. After a seemingly compatible and therefore promising combination is found, the boundary conditions are recomputed for the estimated displacement and pressures and the solver is called. Convergence of the inner loop is judged by the relative or absolute change of total volumetric displacement between succeeding inner iterations: the relative change is required to drop below \(1\%\) or the absolute change is required to drop below \(0.4\%\) of the targeted displacement for the time step.

Detection of process end

The end of the thermoforming simulation is deemed to be reached after the total volumetric sheet displacement exceeds a value close to the initial mold volume and no further notable deflection over a few time steps occurs. This approach using two criteria is necessary due to contact penetration and geometrical discretization errors, both of which may lead to slight differences between theoretically and practically achievable full deformation. In addition, upper limits for the number of time steps and the used wall-time ensure that simulations, which do not reach full deformation, are aborted.

Time step size

In the first forming steps, a very small time step size around \(\Delta t = 0.1\) ms is required for maintaining stability. As the simulation advances, the time step size may be increased. The target time step size is computed such that, based on linear extrapolation, a prescribed relative mold deflection happens in the next time step. A portion of \(1\%\) of the total volumetric displacement proved to be a good compromise between simulation execution speed and stability in preliminary test runs. Close to the end of the deformation, this target deflection must again be reduced in order to maintain stability of the simulation. Limiters ensure gradual increases between time steps.

4.3 Compatibility loop

At each time step inner loop, the solver enters a compatibility loop as included in Fig. 9, which iterates until a combination of total volumetric displacement TD and effective pressure \(p_{Eff}\) is found that matches with the expected sheet deflection.

Assuming a locally linear dependence of total displacement on effective pressure as expressed by Eq. (5), based on the two previously computed data points, a simple estimation for TD based on \(p_{Eff}\) can be constructed using linear extrapolation, as given in Eq. (6).

$$\begin{aligned} \frac{\partial TD}{\partial p_{Eff}} \approx \frac{\Delta TD}{\Delta p_{Eff}} = \frac{TD^n-TD^{n-1}}{p_{Eff}^n-p_{Eff}^{n-1}} = \left. \frac{\partial TD}{\partial p_{Eff}}\right| _{Est} \end{aligned}$$
(5)
$$\begin{aligned} TD_{Est} = TD^{n} + (\Delta p_{Eff}) \; \left. \frac{\partial TD}{\partial p_{Eff}}\right| _{Est} \end{aligned}$$
(6)

In other words, in order to check for presumable compatibility, the circular dependency visualized in Fig. 8 is closed by adopting an approximation instead of the costly simluation. When converged, the compatibility loop gives a reasonable estimates for \(p_{Mold}\) and TD, that then will be solved for within this inner loop iteration.

In order to counter divergence problems arising from overshoots in the prediction of \(TD_{Est}\), an incremental search algorithm is applied. It works similar to under-relaxation, but instead of reducing the estimated value \(TD_{Est}\) to a certain portion of the difference to the previous result, only a prescribed change \(\Delta TD_{max}\) is allowed as shown in Eq. (7) and reduced each time the search direction is reversed.

$$\begin{aligned} \begin{aligned} TD^{n+1} = \max (\min (TD_{Est},\;&TD^n+\Delta TD_{max}), \\&TD^n-\Delta TD_{max}) \end{aligned} \end{aligned}$$
(7)

It thus corresponds to limiting with an adaptively updated threshold. Convergence is achieved faster than with constant under-relaxation, due to strong required relaxation by the first iteration steps. Compatibility loop convergence is judged the absolute and relative changes of estimated displacement between two succeeding loop iterations, with the criteria of a fraction of 1e-11 times the mold volume and 5e-5, respectively. As a consequence, a minimum of two compatibility loops per time step is required for the convergence criterion to be computable.

4.4 Mold counter-pressure calculation

In order to correctly consider the effect of mold counter-pressure, an implicit computing approach had to be adopted. Especially at the beginning, very small time steps are required in order to incorporate mold counter-pressure explicitly without stability issues. This is due to a notable sheet deflection already for small initial pressure increments. As the simulations continues, due to increased material and geometrical stiffness, the deflection gradient with respect to pressure differences decreases considerably, alleviating this problem. Finally, close to deformation end, the relative error in the mold volume computation increases due to contact penetration, so that in turn the mold pressure accuracy drops. Therefore, for the last portion of the deformation, the mold counter-pressure is relaxed to 0.

The mass leaving the mold in a certain time step can be computed using two approaches given as Eqs. (8) and (9).

$$\begin{aligned} \Delta m_1= & {} V_{Begin} \; \rho _{Begin} - V_{End} \; \rho _{End} \end{aligned}$$
(8)
$$\begin{aligned} \Delta m_2= & {} \int _{t, \; Begin}^{t, \; End} \; c_{Vent}(t)\; A_{Vent} \; \rho _{Vent}(t) \, \mathrm {d}{t} \end{aligned}$$
(9)

Here, \(c_{Vent}\) is the flow velocity through the venting bores, which have a total cross-section area of \(A_{Vent}\), and \(\rho _{Vent}\) is the density of the escaping air. Both relations 8 and 9 must be satisfied, which in turn allows for a computation of the unknown quantities at the end of the time step. Values at time step begin are known as the values of the end of the previous time step. In order approximate the integral using known values, the relations (10) and (11) for venting flow velocity and density as well as the trapezoidal rule for integral approximation are used, which ultimately leads to Eq. (12).

$$\begin{aligned} c_{Vent}(t)= & {} \sqrt{\frac{2 \; p_{Mold}}{\xi \; \rho _{Vent}}} \end{aligned}$$
(10)
$$\begin{aligned} \rho _{Vent}= & {} \frac{1}{2} (\rho _{Mold}+\rho _{Ambient}) \end{aligned}$$
(11)
$$\begin{aligned} \begin{aligned} \ \quad \Delta m_2 \approx \frac{1}{2}\; \Delta t\; A_{Vent} (\,&c_{Vent, \; Begin}\;\rho _{Vent, \; Begin}&\\ + \,&c_{Vent,\; End}\;\rho _{Vent, \; End})&\end{aligned} \end{aligned}$$
(12)

The pressure loss coefficient \(\xi\) has been estimated to 3, due to the very small venting hole diameter and therefore comparatively large impact of surface irregularities, air compressibility, sharp edges at the venting nozzle inlet and flow contraction. Furthermore, the thermodynamic description of the compressed mold air with polytropic coefficient n and with \(p_{Mold}\) relative to ambient pressure \(p_{Amb}\) according to Eq. (13) is required in order to make the unknowns computable.

$$\begin{aligned} p_{Mold} = p_{Amb} \; \left( \left( \frac{\rho _{Mold}}{\rho _{Amb}} \right) ^n -1 \right) \end{aligned}$$
(13)

Now, three Eqs. (8, 12, and 13) are available for computing the unknown mold pressure at time step end \(p_{Mold,\; End}\), mold density at time step end \(\rho _{Mold, \; End}\), and venting velocity at time step end \(c_{Vent, \; End}\). A polytropic coefficient of \(n=1.4\) has been chosen, which corresponds to isentropic behavior of the trapped mold air. As an analytical solution for \(\Delta m\) given the equations above is not possible, several numerical approaches for the solution have been implemented, as discussed below.

Incremental search approach

From Eq. (8), by rearrangement an iterative procedure according to Eq. (14) can be derived, with \(\Delta m^{m}\) computed using the mass outflow Eq. (12) and the previous iteration’s value for \(\rho _{End}\).

$$\begin{aligned} \rho _{End}^{m+1} = \frac{\Delta m^{m} + V_{Begin} \; \rho _{Begin}}{V_{End}} \end{aligned}$$
(14)

For stability, strong under-relaxation or limiting after each iteration is mandatory. As the former would require under-relaxation factors close to 0 in order to prevent divergence at the beginning of the loop, convergence in this case is delayed significantly. Hence, this method is not suitable for practical application and an incremental search approach using limiting is adopted, analogously to the incremental search approach outlined for the computation of \(TD_{Est}\) in the compatibility loop. After each iteration, the new density \(\Delta \rho _{End}^{m+1}\), computed from the iterative formula, is clipped to the range \(\rho _{End}^{m} \pm \Delta \rho _{Max}\). The limiting value \(\Delta \rho _{Max}\) is computed basing on the density change of the previous time step. Each time the search direction changes, \(\Delta \rho _{Max}\) is reduced by a constant factor, so that the search range continues to narrow, until the difference between successive iterations \(\Delta \rho _{End}^{m+1} - \Delta \rho _{End}^{m}\) drops below a convergence threshold. The outlined iterative search technique provides results significantly faster than a simple under-relaxation approach, but in rare cases may suffer from resulting unphysical intermediate values for the mold pressure.

Grid-search approach

Another approach is to find the according mold pressure using a grid search, where a range of different pressures are tested for compatibility. For the correct pressure, the mass error computed as

$$\begin{aligned} m_{Err} = \Delta m_1 - \Delta m_2 \end{aligned}$$
(15)

is 0. With \(m_{err}\) computed for a range of guessed pressures \(p_{Mold}\), using interpolation a compatible pressure can be found for which the mass error approximately vanishes. In order for this approach to work reliably, a good estimate for the pressure range in which to search the compatible mold pressure is required, which can be derived from the changes within the previous time step and can be widened adaptively between iterations. By limiting the searched range of mold pressures to physically meaningful values, unphysical results are assuredly prevented.

4.5 Boundary and initial conditions

Initially, the sheet is at rest and plane. At its outer boundary nodes, for all directions, a zero deflection condition is prescribed, corresponding to fixed support. On the sheet boundaries in azimuthal direction, symmetry conditions are adopted. This implies that the deflection and temperature field do not vary along the circumference, and hence implements the assumption of axis-symmetry. Figure 10 illustrates the boundary conditions in a top-view sketch of the simulated section of the sheet

Fig. 10
figure 10

Illustration of boundary conditions in top view onto the simulated azimuthal section of the plastic sheet

Full size image

Movement of the sheet lower side is furthermore constrained by contact with the mold. Contact behavior is set to bonded in order to prohibit sliding of the sheet along the mold wall after the first contact, which is the behavior commonly observed and adopted for thermoforming simulations [8, 11, 15, 28]. Best convergence properties in the considered cases were achieved using the Augmented Lagrangian algorithm for finding contact equilibrium. Thermal conductance over the area in contact is activated to capture the rapid cooling at wall contact. Although contact heat transfer, in particular for soft materials of unknown surface roughness, is difficult to model properly [7], values for the thermal conductance coefficient in the range of 250 W \(K^{-1}m^{-2}\) and 400 W \(K^{-1}m^{-2}\) seem to be suitable [20, 23]. In this study, a value of 300 W \(K^{-1}m^{-2}\) was specified.

Boundary conditions for heat transfer coefficient at jet impingement spots and for dynamic pressure depend on the inlet nozzle’s velocity, which is computed from the time step’s mass inflow rate. Thermodynamic modeling within the pressure box is based on the ideal gas law and the assumption of isentropic behavior. With the volume and density at time step start and expected volume and density at time step end known, the mass entering the pressure box during the current time step is obtained. Using Eq. (16), the inflow velocity \(c_{inlet}\) is computed, from which then the heat transfer and dynamic pressure load boundary conditions are derived.

$$\begin{aligned} c_{inlet} = \frac{\Delta m}{\Delta t \; \rho _{inlet} \; A_{inlet}} \end{aligned}$$
(16)

With the values at time step end being estimates in the inner iteration loop, this constitutes an explicit contribution, which may lead to instabilities. As a countermeasure, smoothing over the last five time steps and limiting to a certain deviation from the previous time step’s value are applied to the computed inlet velocity.

At the sheet upper side, the effective pressure \(p_{Eff}\) according to Eq. (2) is acting on the sheet. In addition, dynamic pressure due to the jet impingement may be applied in an approximate fashion. This is done in such a way that the inlet jet dynamic pressure force, computed according to Eq. (17), is approximately conserved.

$$\begin{aligned} F_{p,dyn} = \frac{1}{2}\;\rho _{inlet} \; A_{inlet} \; c_{inlet}^2 \end{aligned}$$
(17)

Assuming a constant spreading angle of \(9^\circ\) for the jet flow, the approximate impingement area is obtained using nozzle size and current standoff distance. With the further assumption of a profile with trapezoidal cross section for the dynamic pressure distribution, as shown in Fig. 11, the local dynamic pressure at the mesh nodes is computed and applied as an additional pressure boundary condition to the effective pressure.

Fig. 11
figure 11

Assumed development of jet width and impingement wall pressure profile for a single nozzle

Full size image

In addition to using the smoothed and limited velocity values like for the heat transfer computation, for stability reasons, the dynamically computed jet force is also limited to only contribute a certain portion to the total force acting on the sheet. This in turn means that force conservation may be violated especially at simulation start, where the force from effective pressure may be comparatively small to the dynamic pressure. As the dynamic pressure influence is considered to be small, and a lot of modeling assumptions are introduced during the calculation, the expected error from this limiting was deemed to be negligible.

During forming steps, a thermal boundary condition is applied to the sheet upper side, while the lower side is considered isolated due to the convective transport being considered negligible when compared to the upper side forced convection. Upper side cooling is modeled using correlations for heat transfer from the literature. A comprehensive summary of the effects and characteristics of jet impingement heat transfer is given by Zuckerman [41]. Relations from literature imply a notable uncertainty, as they usually exhibit quite limited ranges of validity. In addition, the case at hand with convex impingement area and a moving, free-form impingement plane may lead to further deviations. Both for central and annular nozzles, the formulas from literature for the average Nusselt number up to a given distance from the nozzle impingement point, marked by an overbar, had to be transformed to formulas for the Nusselt number Nu at a certain distance from the impingement spot using the relations

$$\begin{aligned} Nu(r)= \frac{\mathrm {d}{(\overline{Nu}(r) \; r^2})}{\mathrm {d}{(r^2)}} \end{aligned}$$
(18)
$$\begin{aligned} Nu(x)= \frac{\mathrm {d}{(\overline{Nu}(x) \; x })}{\mathrm {d}{x}} \end{aligned}$$
(19)

for round nozzles and for slot nozzles, respectively.

The effect of curvature at the jet impingement spot and of inclined impingement as treated in literature [3, 13, 17, 40], is neglected at the current stage, as it contradicts the objective of model simplicity. For correct inclusion of this effect, not only the sheet curvature but also the jet path curvature would have to be taken into account, which is hardly feasible without empirical or experimental data providing this information. Furthermore, a shift of the heat transfer maximum from the impingement spot is hard to implement.

Central nozzle

The correlation of Wen and Jang [39], which hardly differs from the parametrization published by Tawfek [34], appears to be a suitable choice for the central nozzle heat transfer calculation, although it turned out that the range of validity does not completely cover the range of all simulations. The formulas for average and local heat transfer are given as Eqs. (20) and (21).

$$\begin{aligned} \overline{Nu}(r)= 0.442 \; Pr^{\frac{1}{3}}\; Re^{0.696} \; \left( \frac{H}{D}\right) ^{-0.2} \; \left( \frac{r}{D}\right) ^{-0.41} \end{aligned}$$
(20)
$$\begin{aligned} Nu(r)= \frac{2-0.41}{2} \; \overline{Nu}(r) \end{aligned}$$
(21)

In order to avoid unrealistically large values for the heat transfer coefficient at low distances to the impingement spot, clipping is introduced such that \(\frac{r}{D} \ge 0.5\).

Annular nozzle

For annular nozzles, no suitable heat transfer correlations exist in the literature. In the case at hand, with the gap width way smaller than the annulus diameter, a slot nozzle like characteristic can be expected. Hence, for the annular nozzle the slot nozzles heat transfer correlation from Schlünder et al. [21, 33], given in Eqs. (22) to (24), was adopted.

$$\begin{aligned} b_1(x)= \frac{x}{S} + \frac{H}{S} + 1.39 \end{aligned}$$
(22)
$$\begin{aligned} b_2(x) = 0.695 - \frac{1}{\frac{x}{S} + \left( \frac{H}{S}\right) ^{1.33} + 3.06} \end{aligned}$$
(23)
$$\begin{aligned} \overline{Nu}(x)= 1.53 \; Pr^{0.42} \; \frac{Re^{b_2(x)}}{b_1(x)} \end{aligned}$$
(24)

The final result for the local heat transfer coefficient is given as Eq. (25).

$$\begin{aligned} \begin{aligned} Nu(x) = &1.53\; Pr^{0.42} \; \frac{Re^{b_2(x)}}{b_1(x)} \; \biggl ( 1+ \biggr . \\&\left. \ln (Re)\;x\; \frac{(b_2(x)-0.695)^2}{S} - \frac{x}{b_1(x) \; S} \right) \end{aligned} \end{aligned}$$
(25)

Analogously to the central nozzle, \(\frac{r}{2B}\) is clipped to values greater than 0.5. For the annular nozzle air curtain, deflection must be considered. As static pressure rise will be equal for the whole pressure box, the annular nozzle jet is assumed to split at impingement according to the relative portion of the volume inside and outside the air jet curtain, which is a further assumption adopted for simplicity and lack of more detailed insight into this complex phenomenon. The jet deflection angle is limited from \(1^\circ\) to \(30^\circ\) which is deemed to be the realistic range. Alternatively, a specific deflection angle of the annular jet may be defined, but this possibility has not been made use of in this study.

4.6 Material modeling

In order to simulate the thermoforming process, the deformation behavior of the plastic sheet is reproduced in material models. They link the thermal conditions applied on the sheet by the forming air flow field to the mechanical behavior during inflation. Hence, obviously accurate modeling of the dependence on temperature is mandatory for reasonable wall thickness distribution results. To describe the mechanical behavior, the models are divided into elastic, for example Mooney-Rivlin or Odgen model, and plastic models like Johnson-Cook or Multilinear Isotropic Hardening (MISO) [2]. For thermoforming applications, in the thermoforming literature mostly hyperelastic [4, 5, 8, 11, 15, 16, 27, 31] and, in rather few cases, hypoelastic [4] material models are adopted. Occasionally, also viscoelastic effects are considered [6, 11, 14, 15, 29, 32].

The development of the material model and reproduction of the elastic and plastic forming behavior of polyvinyl chloride (PVC) were accomplished in reverse-engineering method. In the first step to determine the relevant temperature range, a differential scanning calorimetry (DSC) analysis of the material was done, with the result that the material begins to melt above a temperature of \(140\; {}^\circ \text {C}\). Based on this measurement result, \(23 \, {}^\circ \text {C}\) to \(140 \, {}^\circ \text {C}\) was selected as the relevant temperature range. The reverse-engineering method is characterized by the fact that a selected measuring method is reproduced in a numerical simulation model. Afterwards, the material model is fitted to the measured data. As a suitable measuring method, the uni-axial tensile test was selected. For the used molded part, the areal draw ratio is \(282\%\). Based on this pre-analysis, the parameters of the uniaxial tensile tests have been set to the temperature of \(23 \, {}^\circ \text {C}, \, 105\, {}^\circ \text {C}, \, 115\, {}^\circ \text {C}, \, 125\, {}^\circ \text {C}\) and the measurements were conducted until a stretching threshold was achieved or the sample ruptured. The uni-axial tensile tests were conducted on the testing device BZ2 as sketched in Fig. 12 in combination with a heating chamber from Zwick/Roell.

Fig. 12
figure 12

Sketch of the uni-axial tensile test

Full size image

The clamping length is 40 mm at a width of 15 mm and the speed of stretching is 40 mm \(\text {min}^{-1}\). Figure 13 shows the result of the experimental study for PVC. The curves show a typical behavior of an amorphous plastic material. These do not have significant yield strength and the stress increases continuously with increasing strain. In addition, the stress is lower at higher temperatures.

Fig. 13
figure 13

Forming behavior of PVC at different temperatures and the comparison with the material model

Full size image

For simulating the forming behavior of plastic materials, a range of different material models exists. Due to the changeable streaming during the thermoforming step, elastic models are not suitable. Furthermore, the approach was chosen for the material model to not consider the influence of strain rate and material direction. For these reasons, the multi-linear hardening model termed MISO is suitable to reproduce the forming behavior of PVC during the thermoforming with directed air flow. For the present study, this model type proved to provide advantages regarding stability when compared to other material model types. Essentially, MISO is defined as a data table containing data points for strains and the corresponding stresses at a range of temperatures. Elastic and plastic contributions are determined implicitly from the curve slope at the origin, which defines the elastic modulus. The data points for the chosen model were determined by fitting the behavior of the material model of the tensile test to the experimental data. For each measured temperature curve, around 100 data points are used to reproduce the measured behavior, leading to a virtually smooth model curve despite the piecewise definition. As shown in Fig. 13, the resulting material model describes the stress-strain behavior of the PVC material under consideration very well.

5 Simulation results

Cases with two different inlet nozzle types were studied, in both of which the raw material was a sheet of PVC with an initial thickness of \(520 \, \mu m\). In nozzle configuration 1, a central nozzle with a diameter of \(D_{CN}=5\) mm was used for pressurized air supply, while in nozzle configuration 2 it was an annular nozzle of dimensions \(D_{AN}=20\) mm and \(g_{AN}=1\) mm. The simulation models for both nozzles were run with different parameters for the venting calculations in order to quantify the effect of counter-pressure on the final wall thickness distribution and to compare the incremental search and grid search counter-pressure computation implementations. A summary of the studied simulation configurations is given in Table 1.

Table 1 Simulation test cases configuration
Full size table

The computing times on a desktop machine with three processors lay in the range of 0.5 to 1.5 h.

5.1 Wall thickness distribution

All wall thickness data presented is relative to the initial sheet thickness. Measurements from experiments were available for eight points along the wall side length as depicted in Fig. 3. The first measuring point lies at the outermost part of the upper mold radius. With the following three data points, the wall side thickness is captured. Points 5 to 8 represent the bottom wall thickness, from the bottom radius to the bottom center.

Figure 14 shows a comparison of the wall thickness distributions from experiments and simulations.

Fig. 14
figure 14

Wall thickness distributions of two simulation test cases compared to the experimental results, including estimated uncertainty

Full size image

All curves show qualitatively the same behavior: the initial thickness is nearly retained at the upper mold radius, then dropping along the mold side wall until the minimum is reached at the bottom radius. From bottom radius to bottom center, the wall thickness increases again. Notably, the maximum relative deviation in almost all cases occurs at the bottom corner radius, which also is the thinnest point as it is the last to get in contact with the mold and undergoes the largest stretching. While most of the data points lie within the estimated uncertainty range for the experimental data, it can clearly be observed that the simulations overestimate the wall thickness at the mold bottom and have a tendency to underestimate the side wall thickness.

Table 2 lists the deviations between simulations and experiments, quantified using the mean absolute error of the relative wall thickness distribution at the measurement point locations.

Table 2 Simulation test cases with resulting deviation from the measured wall thickness distribution
Full size table

According to the available data, hardly any difference between the results of different configurations of both test cases can be seen. However, both for central and annular nozzles, the most obvious difference occurs in the hypothetical test cases 1D/2D with reduced venting bore diameter and in turn the lowest deformation speed.

5.2 Inflation over time

Sheet deflection and thickness in cross-sectional view are depicted in Fig. 15 for different time steps of the simulation of test case 1A.

Fig. 15
figure 15

Deflection and thickness in cross-sectional view for different times in simulation of test case 1A. Thickness is enhanced by a factor of two for better visibility

Full size image

Initially there is a free inflation phase, where the sheet is only constrained by the mold contact at the upper bend radius and takes the shape of a spherical cap. Notably, the curvature of the upper radius is closely, but not exactly followed by the sheet at this stage. Thinning of the sheet happens quite homogeneously in the free inflation phase. As the process continues, the sheet comes in contact with the mold side wall and the deformation outline becomes more flattened towards the axis of symmetry at the center. Finally, bottom contact is reached at the center and the sheet inflation continues until it lastly covers the mold’s bottom corner radius. The thickness profiles indicate clearly that the inhomogeneities in the wall thickness distribution to a large extent stem from the final phase of the inflation process, after first contact at the bottom center has been reached.

5.3 Mold counter-pressure

In Fig. 16, the total relative volumetric mold displacement over time is compared for different simulations of the central nozzle case.

Fig. 16
figure 16

Relative total displacement over time for different counter-pressure configurations of case 1

Full size image

In all simulated cases, the last few percent of the deformation took long to complete, which is evident through the flattened curves close to \(100\%\) displacement, corresponding to full deformation. The time dependence of bulk of the deformation, however, strongly depends on the chosen configuration. Unsurprisingly, without counter-pressure considered, the deviation happens fastest. In case 1B, with counter-pressure considered and the actual venting nozzle hole diameter, the deflection was delayed by almost a factor of 2 and even more with smaller venting holes, as in case 1D. The same behavior could be observed analogously for the displacement over time curves of cases 2A–2D, which are not included here.

For the case 1A, the rise of forming pressure, mold counter-pressure, and effective pressure are shown together with the relative volumetric displacement over time in Fig. 17.

Fig. 17
figure 17

Forming pressure, mold counter-pressure, and the difference effective pressure (left vertical axis) and relative volumetric displacement over time (right vertical axis) for case 1A

Full size image

Virtually full displacement of more than \(99\%\) in this case was reached after 190 forming time steps. It can be seen that mold counter-pressure initially rises almost as fast as the forming pressure, then the increase slows down and after 75 ms begins to drop. The linear rise of forming pressure implies that the effective pressure acting on the inflating sheet, computed as the difference of forming to mold pressure, initially increases slowly, but starts to rise with a steeper slope from the time on that mold pressure starts to drop.

Figure 18 shows the number of inner loop iterations over the forming time steps.

Fig. 18
figure 18

Number of inner loop iterations over the time steps for case 1A

Full size image

Before forming, not shown in this graph, for cooling, sagging, and venting steps, one inner iteration suffices because mold venting is not yet considered. Directly after forming start, up to four inner iterations are required. In the further course of inflation, the number of inner iterations reaches values of up to 4, while in the majority of time steps convergence of the inner loop is reached after only two inner iterations.

5.4 Adaptive time stepping

Adaption of time step sizing works reliably as depicted in Fig. 19.

Fig. 19
figure 19

Time step size and relative volumetric displacement over the forming steps for case 1A

Full size image

At the very beginning of the inflation process, a small time step size is mandatory due to the strong inter-dependency of mold pressure, forming pressure, and sheet deformation. The small value then gradually increases as being adapted in order to obtain a prescribed volumetric displacement per time step. With ongoing deformation, the sheet stiffness changes, automatically leading to time step size adjustment. When the sheet is close to full deformation, for stability reasons the target deflection per time step is reduced, but due to increasing stiffness, time step size nonetheless rises.

6 Discussion

The observed qualitative wall thickness distribution is the commonly expected one for thermoforming of simple cups, like the one used in this contribution. Smoothness of the simulation result indicates that the known eight measured points are enough to adequately reflect the quantitative wall thickness distribution. The match between experimental and simulation results is satisfactory, yet the differences between the experimental wall thickness distributions are more pronounced than between the simulation results, suggesting that some influential effect is not reproduced in adequate magnitude by the simulation model. At the bottom, the occurring average error is larger than at the side wall. Furthermore, in almost all cases, the simulation overpredicts the bottom thickness, while the side wall thickness is partially underpredicted. This suggests that there is some systematic deviation between simulation and experiment. A possible cause is the material model, which is based on data for uni-axial stretching, while the real deformation at the bottom is way closer to bi-axial stretching, which may happen at a lower stiffness.

The inflation behavior of the sheet complies with the expectations, starting with a sphere-like initial deflection pattern. Apparently, while bending moments appear to be small, they are not negligible, as the mold upper bend radius is not exactly followed by the sheet for rather small deflections. Considering that wall-sticking was assumed for the simulations, the qualitative wall thickness distribution as presented above is a logical result of the time-dependent inflation progress. Against the background of the simulated wall thickness being too high at the bottom and too low at the side walls, one can deduce that the actual deformation profile would have been even more flattened to a more plug-like shape before bottom contact happens.

It could be shown that counter-pressure consideration notably effects the speed of inflation, in the chosen test configurations by roughly a factor of 2. Surprisingly, this difference is not reflected by the wall thickness distributions of the according configurations. For the test cases in this study, mold counter-pressure and its parametrization seem to have no relevant effect on the final wall thickness distribution. A cause of this may be that the nozzle influence is still underpredicted in all simulations. In light of the fact that the used correlations were obtained for idealized test cases instead of the thermoforming process with moving boundary, curvature, and a free-form surface, this appears to be quite plausible. Another possible explanation is that what matters for deformation is mostly the projected temperature profile of the sheet right at the beginning of the process, and not the minor changes that occur during the course of the deformation.

Two counter-pressure implementations, namely incremental search and grid search, have been compared, which run stable until the simulation finished. As expected, both implemented methods yield the same results. The incremental search procedure may suffer from unfavorable input data, which in turn may cause numerical errors like the square root of a negative number during velocity computation, if in an intermediate step the mold pressure is negative. Furthermore, convergence may be slow if no good first estimate is known, and the relaxation and limiting parameters must be chosen carefully so that stability is guaranteed with only minor detrimental impact on convergence speed. On the plus side, the incremental search approach allows for computation of the pressure with nearly arbitrary accuracy. In contrast, the number of operations for the grid-search approach remains constant if the number of tested pressures does not vary. As a certain test grid density is required for good accuracy, its computational cost is likely higher. Advantageously, for the grid search approach, with grid density, a lever for trade-off between accuracy and execution speed exists, such that this approach is to be considered nearly as versatile as the incremental search procedure. Between time steps, only relatively small changes in pressure will occur; therefore, it is easy to find reliable upper and lower bounds for reasonable mold pressures to be tested, making this approach both accurate and stable. In consideration of the fact that simulation time will be dominated by the actual finite element solution, the computational requirements of both approaches do not play a significant role, although they are called at the third level of nested loops. Arbitrary accuracy is not important due to uncertainties in other modeling aspects of the simulation, so the stability of the approaches becomes the decisive criterion. Although in the presented cases, the incremental search approach did not cause stability issues, the grid search approach is supposed to be more stable, and therefore is considered the better variant. Independent of the adopted calculation method, the modeling is based on a range of assumptions, which for confirmation and parametrization would require dedicated experimental data that is not available. Hence, it is not possible to definitely conclude if the computed counter-pressures are close to the real values, although the run of the curves appears to be plausible.

The inner loop, which includes the compatibility loop, has proven to work reliably. In most time steps, the minimum number of two iterations per time step suffices for convergence, highlighting the effectiveness of the implemented approach. Only when the prediction of the gradient of volumetric displacement by effective pressure is not very reliable, i.e., is subject to significant changes, more iterations are necessary. At simulation begin and around forming time step 100 when the sheet touches the mold bottom, this is the case for example.

Adaptive time stepping allows for fast execution of the simulation while maintaining stability. The chosen target value of \(1\%\) for the main part of inflation in combination with small time steps at the beginning and adaptive reduction close to full deformation yielded good results in all cases presented in this study.

7 Conclusions

A simulation model for forming air impact thermoforming has been presented. It includes via approximations the dynamic and thermal effect of the nozzle jets on the plastic sheet. In addition, delay of the deformation due to build-up of counter-pressure in the mold has been implemented using different methods.

While the model validation yielded satisfactory results, further improvements appear to be necessary in order to allow for quantitatively reliable simulation results. The assumed significant influence of counter-pressure could not be confirmed. Contrarily, results with simulations using this model show only little sensibility with regard to the counter-pressure parametrization, although the accuracy of the resulting curves cannot definitely be judged due to the number of assumptions involved in the computation. Both implemented counter-pressure computation methods have proven stable, but the grid search method is considered advantageous due to its presumed superior stability in other cases.

In summary, the main finding of this contribution was that it is possible to set up a stable simulation model of reduced complexity in order to simulate the FIT thermoforming process, so that qualitatively correct and quantitatively satisfactory results can be obtained. Numerous approximations and simplifications were imposed in order to include all effects deemed to be relevant and to make the numerical model computable on a desktop machine.

Ongoing research will attempt to further improve the simulation regarding agreement with experimental data. Further work towards the development of formulas suited for the heat transfer computation for the air-flow conditions found in thermoforming, with consideration of sheet deflection and curvature during inflation, appears to be reasonable. Especially the annular nozzle jet behavior should be investigated in more detail. The goal is to create a reliable tool for numerical investigations of the thermoforming process with directed air flow, which can then be used both for large-scale parameter studies as well as for black-box optimization of the wall thickness distribution.