A combined experimental and numerical approach that eliminates the non-uniqueness associated with the Johnson-Cook parameters obtained using inverse methods

Abstract

Johnson-Cook constitutive model is a commonly used material model for machining simulations. The model includes five parameters that capture the initial yield stress, strain-hardening, strain-rate hardening, and thermal softening behavior of the material. These parameters are difficult to determine using experiments since the conditions observed during machining (such as high strain-rates of the order of $10^5$/sec - $10^6$/sec) are challenging to recreate in the laboratory. To address this problem, several researchers have recently proposed inverse approaches where a combination of experiments and analytical models are used to predict the Johnson-Cook parameters. The errors between the measured cutting forces, chip thicknesses and temperatures and those predicted by analytical models are minimized and the parameters are determined. In this work, it is shown that only two of the five Johnson-Cook parameters can be determined uniquely using inverse approaches. Two different algorithms, namely, Adaptive Memory Programming for Global Optimization (AMPGO) and Particle Swarm Optimization (PSO), are used for this purpose. The extended Oxley’s model is used as the analytical tool for optimization. For determining a parameter’s value, a large range for each parameter is provided as an input to the algorithms. The algorithms converge to several different sets of values for the five Johnson-Cook parameters when all the five parameters are considered as unknown in the optimization algorithm. All of these sets, however, yield the same chip shape and cutting forces in FEM simulations. Further analyses show that only the strain-rate and thermal softening parameters can be determined uniquely and the three parameters present in the strain-hardening term of the Johnson-Cook model cannot be determined uniquely using the inverse method. A combined experimental and numerical approach is proposed to eliminate this determine all parameters uniquely.

1 Introduction

Modeling and simulation are important tools for understanding and optimizing machining processes. Analytical models such as the Oxley machining model [1] and finite element simulations [2,3,4,5,6] are used by researchers for this purpose. Both approaches require a constitutive model for describing the material behavior at the extreme thermomechanical conditions present during machining. The most commonly used material model in machining is the Johnson-Cook constitutive model [7].

Using five material-dependent parameters, the Johnson-Cook model relates flow stress with strain, strain-rate and temperature of the material. Experimentally, these parameters are obtained by fitting the data of the quasi-static tests at various temperatures and dynamic tests at different strain-rates. Tensile tests and Split-Hopkinson Pressure Bar (SHPB) tests are two of the techniques typically used for this purpose [8]. However, the extreme conditions of machining [9] such as strain-rates of the order $10^5$/s to $10^6$/s and high temperatures are challenging to achieve in these experiments. To overcome this difficulty, various researchers have proposed inverse approaches to determine these parameters using the data from the actual machining experiments. However, these methods have been shown to have the drawback of producing non-unique solutions to the Johnson-Cook parameter values [10,11,12].

Machining conditions, experimental observations and simulation results (using finite element analyses or analytical models) are the input to the inverse methods. The simulation results depend on the material model parameters. The goal is to determine these material model parameters by minimizing the objective function consisting of the difference between experimental observations and simulation results. This minimization is achieved by tuning the parameters of the material model using an optimization algorithms. The determined material model parameter set is used in the computational or analytical models and validated with experimental results. Although experiments such as uniaxial, isothermal compression testing of cylindrical specimens [13], laser peening [14], and cold wire drawing [15] have been used for validation purposes, the most widely used experimental technique is based on orthogonal machining.

In this work, the source of non-unique solutions to the inverse problem is identified and a robust approach to determine a unique set of Johnson-Cook parameters is presented. This approach uses the results of orthogonal machining and extended Oxley’s model as the analytical model. Two separate optimization algorithms, Adaptive Memory Programming for Global Optimization (AMPGO) and Particle Swarm Optimization (PSO), are used to minimize the objective function. The consideration of two separate algorithms eliminates any bias that may be present in one particular method. Additionally, this approach replaces the complex Split-Hopkinson Pressure Bar tests by relatively simple orthogonal machining experiments.

2 Literature review

During machining, the workpiece material undergoes plastic deformation. The plastic behavior of the material is modeled using the Johnson-Cook material model:

$$\begin{aligned} \sigma _{eq} =\left( A+B\varepsilon ^{n}_{p}\right) \left[ 1+C\ \ln \left( \frac{\dot{\varepsilon _{p}}}{\dot{\varepsilon }_{0}}\right) \right] \left[ 1-\left( \frac{T-T_{0}}{T_{m} -T_{0}}\right) ^{m}\right] . \end{aligned}$$

(1)

Here, $\sigma _{eq}$ is flow stress, $\varepsilon _p$ is the equivalent plastic strain, $\dot{\varepsilon }_p$ is the plastic strain-rate, $\dot{\varepsilon }_0$ is a reference strain-rate, $T_m$ is the melting temperature, and $T_0$ is a reference temperature. A, B, C, n and m are the material-dependant parameters. A denotes the initial yield strength, B and n describe the strain hardening, C captures the strain-rate sensitivity and m the thermal sensitivity of the material.

The majority of the existing studies that use the inverse approach for determining the Johnson-Cook parameters can be divided into three categories. In the first category, all five parameters of the Johnson-Cook model are taken as optimizing parameters and through optimization algorithms, determination of unique parameter set is claimed. Agmell et al. [16] and Ning et al. [17] performed inverse analysis using a Kalman filter and machining experiments. The relationship between the Johnson-Cook parameters and machining output parameters was developed through multiple FEM simulations. Five discrete values within a range of ± 30 $\%$ of each Johnson-Cook parameter of reference material were used for these simulations. A close agreement between the simulated FEM results and experimental observations was observed using the parameter set obtained through the inverse approach. Ozel et al. [18] used different variations of the PSO method, namely, PSO, PSO-c and CPSO method, to determine the Johnson-Cook parameters. A unique set of parameters were obtained for each method, but the values differ for each method. The parameter set obtained using CPSO showed the best correlation with the experimental results. Eisseler et al. [19] used design of experiments for inverse parameter identification by comparing the cutting force of FEM simulations with 50 Johnson-Cook parameter sets and machining experiments. Two sets of all the five Johnson-Cook parameters were determined for steel SAE-4142 within a maximum difference of less than 3$\%$.

The second category recognizes the non-uniqueness of the parameters obtained by the inverse approach and proposes some suggestions to counter this non-uniqueness. Denkena et al. [10] used Oxley’s machining model and Particle Swarm Optimization (PSO) method using the cutting and thrust forces in an orthogonal slot milling experiment to tune the Johnson-Cook parameters. The optimization was performed without using tensile test data (i.e., all five parameters varied) and with the use of tensile test data (i.e., A, B and n values were obtained from tensile test data and C and n optimized using PSO method). Wide variation was observed in the resulting set of parameters obtained by the two methods. Local minima in the solution domain were suggested to be the reason for this observation. Karkalos and Markopoulos [11] used the Fireworks optimization algorithm for the determination of all the five parameters of Johnson-Cook constitutive material model parameters. Their suggestion was to choose the bounds for optimization variables carefully to avoid premature convergence to a solution far from the optimal point. Pujana et al. [12] varied four parameters (B, n, C and m) of the Johnson-Cook model for the inverse analysis using deterministic minimization techniques. The selection of initial values was found to influence the optimized set of parameters. The use of regularly distributed function evaluations was proposed in order to reach the absolute minimum.

The third category focuses on the non-uniqueness study and attempts to eliminate this by adding experimental results to determine a unique parameter set. Shrot et al. [20] studied the non-unique identification of Johnson-Cook parameters by matching the results of machining experiments and finite element models. The parameters A, B and n were varied in a defined interval. The parameter sets were selected based on the closeness of effective stress-strain plots using the standard Johnson-Cook parameters and test parameters. Similar chip shapes and cutting forces were obtained by the FEM simulation using these identified parameter sets. However, the non-uniqueness was attributed to the measurement error during experiments. The use of different cutting conditions was suggested to obtain a unique parameter set.

Storchak et al. [21] determined the Johnson-Cook parameters using observations of compression tests and machining experiments. The parameters A, B and n were determined by fitting the flow curve to the results of compression tests at room temperature. Then, the parameter m was determined by using the observations of compression tests performed at different temperatures and then averaging all the values. Only the parameter C was obtained using the Oxley theory and machining experiments by comparing the calculated and measured cutting forces. Utilization of actual machining experimental data also takes into the account of the extreme conditions prevailing in machining process tests by relatively simpler orthogonal machining experiments.

These three different approaches coupled with multiple methods to determining unique values of Johnson-Cook parameters via inverse methods show that the origin of non-uniqueness of the parameters (when inverse methods are used) is far from settled. In this paper, we hope to address this issue by considering two different approaches to determine the Johnson-Cook material model parameters uniquely.

3 Methodology

For the inverse approach using orthogonal machining, the observations of machining experiments, the results of machining simulations or an analytical model and a wide range of the Johnson-Cook parameters are used as input. An objective function comprising of the experimental observations and results of the simulation or analytical model is formed. The extended Oxley model is used in this work as the analytical model. This model predicts the machining output for a given set of the Johnson-Cook parameters and the machining conditions. Using the optimization algorithm, the Johnson-Cook parameters are tuned to minimize the objective function. The cutting force ($F_c$), chip thickness ratio ($h_c$ = ratio of chip thickness to uncut chip thickness) and tool-workpiece interface temperature ($T_{int}$) are commonly taken as the variables of the objective function, which is given by

$$\begin{aligned} \text {Err}&= \Bigg [\left( \frac{F_{c,exp}- F_{c,sim}}{F_{c,exp}}\right) ^2+\left( \frac{h_{c,exp}-\ h_{c,sim}}{h_{c,exp}}\right) ^2\\ \nonumber&\qquad +\left( \frac{T_{int,exp}- T_{int,sim}}{T_{int,exp}}\right) ^2 \Bigg ]^{\frac{1}{2}}. \end{aligned}$$

(2)

Here, the label “exp” represents experimental observation and “sim” represents simulated or calculated value. The observations of the machining experiment is assumed to be the same as that obtained from the extended Oxley model using the known values of Johnson-Cook parameters in the literature [22]. This is done to eliminate the measurement uncertainty associated with experiments. Also, the accuracy of the determined Johnson-Cook parameters can be obtained by comparing with these reference values.

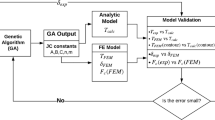
For investigating the reason behind multiple sets of Johnson-Cook parameters obtained using inverse approaches, two approaches (shown in Fig. 1) are taken. In the first approach, all the five Johnson-Cook parameters are considered as the unknown variables. In the second approach, the parameters C and m are considered as the only unknown variables. The motivation behind this is given in Section 5. The parameters A, B and n are considered as known. They are determined using the quasi-static tensile test and their values are taken same as shown in Table 1, under the column “Ref value [22]”. For the unknown Johnson-Cook parameters C and m, a wide range is provided as input to the optimization algorithm. This is based on their values for different materials in the literature [7] and [23]. The ranges considered for the parameters are shown in Table 1. The machining conditions used as input parameters are given in Table 2. Ivester et al. [24] performed orthogonal machining of tubes of 1.6 mm wall thickness. The material of AISI 1045 (chemical composition provided in Table 3) with these machining conditions. Lalwani et al. [25] compared the observations of these experiments with the predicted results of extended Oxley model and observed that the predicted values are close to lower bound values observed in the experiments.This validates the use of extended Oxley model for orthogonal machining conditions.

The Johnson-Cook parameters are obtained with these inputs by minimizing the objective function using the optimization algorithms, AMPGO, and PSO algorithms. In the optimization loop, the extended Oxley model is used to calculate the values of the machining output for a given set of Johnson-Cook parameters. The output of Approach 1 is all the five parameters, whereas the parameters C and m are the output of Approach 2. The uniqueness of the parameter sets is discussed in the results section.

Fig. 1

Two approaches considered for determining the Johnson-Cook parameters

Table 1 Johnson-Cook parameter range used as search space in optimization algorithms

Table 2 Machining conditions used [25] for simulating Approach 1 and Approach 2

Table 3 Chemical composition of AISI 1045 steel (Military specification) [24]. The measured value in [24] conformed to this spec

3.1 Extended Oxley theory

The parallel-sided shear zone theory is a widely used analytical model for predicting the stresses, cutting forces and the average temperature in orthogonal machining. The theory is explained in detail in Oxley and Shaw [1]. The deformation zone consists of two regions: a parallel-sided primary shear zone and a rectangular secondary shear zone at the tool-chip interface of constant thickness. Although further improvement of Oxley model has been done by Karpat and Ozel [26] by incorporating more realistic shape of secondary shear zone, the extended Oxley model has been selected for this work because of its computational simplicity. The focus in this work is primarily given to provide an approach for unique determination of Johnson-Cook parameters. Along with the application of the principle of minimum work, the extended Oxley theory analyses the equilibrium of the shear plane AB (shown in Fig. 2) and the tool-chip interface to determine the physical parameters of the machining process. This is done by tuning three parameters, namely shear angle $\phi$, strain-rate constant at the shear zone $C_0$ and strain-rate constant at the tool-chip interface zone $\delta$. The range of the parameters $C_0$, $\phi$ and $\delta$ are taken from Lalwani et al. [25]. These ranges are large enough to include the values/ ranges obtained by Oxley and Hastings [27] and Ivester et al. [24].

Fig. 2

Chip formation model in Oxley’s theory [1]

3.1.1 Shear Plane AB

Let $t_1$ be the uncut chip thickness, V the cutting velocity and $\alpha$ the rake angle of the tool. Then the length of the shear plane $l_{AB}$, the chip thickness $t_2$, the shear velocity $V_S$, and the chip velocity $V_C$ are given by

$$\begin{aligned} l_{AB}&= \frac{t_1}{\sin \phi }, \end{aligned}$$

(3)

$$\begin{aligned} t_2&= \frac{t_1 \cos (\phi -\alpha )}{\sin \phi }, \end{aligned}$$

(4)

$$\begin{aligned} V_S&= \frac{V \cos \alpha }{\cos (\phi - \alpha )}, \end{aligned}$$

(5)

and

$$\begin{aligned} V_C&= \frac{V \sin \phi }{\cos (\phi - \alpha )}. \end{aligned}$$

(6)

The equivalent shear strain at AB, $\varepsilon _{AB}$, is given by

$$\begin{aligned} \varepsilon _{AB} = \frac{\gamma _{AB}}{\sqrt{3}} = \frac{\cos \alpha }{2 \sqrt{3}\sin \phi \cos (\phi - \alpha )}. \end{aligned}$$

(7)

The equivalent shear strain-rate along AB, $\dot{\varepsilon }_{AB}$, is given by

$$\begin{aligned} \dot{\varepsilon }_{AB} = \frac{\dot{\gamma }_{AB}}{\sqrt{3}} = \frac{C_0 V_S}{\sqrt{3} l_{AB}}. \end{aligned}$$

(8)

Here, $\gamma _{AB}$ and $\dot{\gamma }_{AB}$ are, respectively, the shear strain and shear strain rate along the shear plane.

The shear flow stress, $k_{AB}$ can be obtained from the tensile flow stress, $\sigma _{AB}$ by using the von Mises criterion and the Johnson-Cook material model as

$$\begin{aligned} k_{AB} = \frac{\sigma _{AB}}{\sqrt{3}} \end{aligned}$$

(9)

with

$$\begin{aligned} \sigma _{AB} = \left( A+B\varepsilon _{AB} ^{n}\right) \left[ 1+C\ \ln \left( \frac{\dot{\varepsilon }_{AB} }{\dot{\varepsilon }_{0}}\right) \right] \left[ 1-\left( \frac{T_{AB}-T_{0}}{T_{m} -T_{0}}\right) ^{m}\right] . \end{aligned}$$

(10)

The average temperature along AB, $T_{AB}$ is calculated using

$$\begin{aligned} T_{AB} = T_0 + \eta \Delta T_{SZ}. \end{aligned}$$

(11)

Here, $T_0$ is the initial temperature, $\eta$ is the Taylor–Quinney coefficient and $\Delta T_{SZ}$ is the temperature rise in the primary shear zone. This temperature rise is obtained using the plastic work done in shear zone and is given by

$$\begin{aligned} \Delta T_{SZ} = \frac{(1-\beta ) F_S V_S}{\rho V t_1 w C_p}. \end{aligned}$$

(12)

Here, $F_S$ is the cutting force acting on the shear plane, $V_S$ is the shear velocity of material, $\rho$ is the density of the workpiece, $C_p$ is the specific heat of the workpiece and w is the width of workpiece. The term $\beta$ is the fraction of heat conducted into the workpiece from the shear zone, which is estimated from the empirical equations

$$\begin{aligned} \begin{array}{lll} \beta &{}= 0.5- 0.35 \log (R_T \tan \phi ) &{}\text {for } 0.04 \le R_T \tan \phi \le 10\\ &{}= 0.3- 0.15 \log (R_T \tan \phi ) &{}\text {for } R_T \tan \phi \ge 10.\\ \end{array} \end{aligned}$$

(13)

Here $R_T$ is a non-dimensional number given in terms of the specific heat ($C_p$), cutting velocity (V), uncut chip thickness ($t_1$) and the thermal conductivity of the workpiece (K) by

$$\begin{aligned} R_T = \frac{\rho C_p V t_1}{K}. \end{aligned}$$

(14)

The angles in the chip formulation model (Fig. 2) are related by the expressions

$$\begin{aligned} \theta = \tan ^{-1} \left( 1+ 2 \left( \frac{\pi }{4} - \phi \right) - C_0 n_{eq}\right) , \end{aligned}$$

(15)

and

$$\begin{aligned} \lambda = \theta - \phi + \alpha . \end{aligned}$$

(16)

Here, strain hardening exponent for the Johnson-Cool material model, $n_{eq}$ is expressed by the expression in [25] as

$$\begin{aligned} n_{eq} \approx \frac{n B \varepsilon ^n_{AB}}{A+ B \varepsilon ^n_{AB}}. \end{aligned}$$

(17)

The normal stress at the tool-chip interface is given by

$$\begin{aligned} \sigma _N^\prime = k_{AB} \left( 1+ \frac{\pi }{2} - 2 \alpha -2 C_0 n_{eq} \right) . \end{aligned}$$

(18)

3.1.2 Tool-chip interface

The strain ($\varepsilon _{int}$) and strain-rate ($\dot{ \varepsilon }_{int}$) at tool–chip interface using von Mises criterion are given by

$$\begin{aligned} \varepsilon _{int} = \frac{\gamma _{int}}{\sqrt{3}} = 2 \varepsilon _{AB} + \frac{h}{2 \sqrt{3} \delta t_2} \end{aligned}$$

(19)

and

$$\begin{aligned} \dot{ \varepsilon }_{int} = \frac{\dot{\gamma _{int}}}{\sqrt{3}} = \frac{V_C}{\sqrt{3} \delta t_2}. \end{aligned}$$

(20)

Here, $\gamma _{int}$ and $\dot{\gamma }_{int}$ are, respectively, the shear strain and shear strain rate at tool-chip interface.

The average temperature at the tool–chip interface, $T_{int}$ is given by

$$\begin{aligned} T_{int} = T_0 + \Delta T_{SZ} + \psi \Delta T_M. \end{aligned}$$

(21)

Here, $\psi$ is a factor to account for the average value of $T_{int}$ and a value of $\psi$ = 0.9 is taken in this study [25]. $\Delta T_M$ is the maximum temperature rise of the chip and is calculated using the empirical equation proposed by Boothroyd [28]:

$$\begin{aligned} \log \left( \frac{\Delta T_M}{\Delta T_C}\right) = 0.06- 0.195 \delta \sqrt{\frac{R_T t_2}{t_1}} + 0.5 \log \left( \frac{R_T t_2}{h}\right) \end{aligned}$$

(22)

The tool-chip interface length, h and the average temperature rise in the chip $\Delta T_C$ are given by

$$\begin{aligned} h = \frac{t_1 \sin \theta }{\cos \lambda \sin \phi } \left( 1+ \frac{C_0 n_{eq}}{3 \left( 1+ 2 \left( \frac{\pi }{4} - \phi \right) C_0 n_{eq} \right) } \right) \end{aligned}$$

(23)

and

$$\begin{aligned} \Delta T_C = \frac{F V_C}{\rho V t_1 w C_p}. \end{aligned}$$

(24)

Here F is the frictional force acting at the tool–chip interface.

The flow stress at the tool-chip interface, $k_{chip}$ is calculated using the expression

$$\begin{aligned} k_{chip} =\frac{1}{\sqrt{3}} \left( A+B\varepsilon _{int} ^{n}\right)&\left[ 1+C\ \ln \left( \frac{\dot{\varepsilon }_{int} }{\dot{\varepsilon }_{0}}\right) \right] \\ \nonumber&\times \left[ 1-\left( \frac{T_{int}-T_{0}}{T_{m} -T_{0}}\right) ^{m}\right] . \end{aligned}$$

(25)

3.1.3 Cutting forces

The cutting forces (shown in Fig. 2) are obtained using the following equations.

$$\begin{aligned} F&= R \sin \lambda , \end{aligned}$$

(26)

$$\begin{aligned} N&= R \cos \lambda ,\end{aligned}$$

(27)

$$\begin{aligned} F_S&= R \cos (\phi + \lambda - \alpha ) = k_{AB}l_{AB}w, \end{aligned}$$

(28)

$$\begin{aligned} N_S&= R \sin (\phi + \lambda - \alpha ), \end{aligned}$$

(29)

$$\begin{aligned} F_c&= R \cos (\lambda - \alpha ), \end{aligned}$$

(30)

and

$$\begin{aligned} F_t&= R \sin (\lambda -\alpha ). \end{aligned}$$

(31)

The normal stress $\sigma _n$ and the shear stress $\tau _{int}$ at the tool-chip interface are given by

$$\begin{aligned} \sigma _N = \frac{N}{hw} \end{aligned}$$

(32)

and

$$\begin{aligned} \tau _{int}= \frac{F}{hw}. \end{aligned}$$

(33)

Fig. 3

Determining JC parameters using AMPGO/PSO method

3.2 Calculation flowchart

The flowchart for determining the Johnson-Cook parameters is shown in Fig. 3. There are two loops in the flowchart: the inner loop shown by the dashed line and the outer loop shown by the solid line. The calculation for all the machining parameters for a given Johnson-Cook parameter set is performed in the inner loop. The objective of the inner loop is to minimizing the gap between $k_{chip}$ and $\tau _{int}$, $\sigma _N$ and $\sigma ^\prime _N$ and obtain the minimum cutting force $F_C$ by tuning the parameters $\delta , C_0$ and $\phi$. The detailed derivations and the equations used have been adopted from Lalwani et al. [25]. The difference in the calculation approach in the current work with respect to Lalwani et al. [25] is that instead of varying the values of the parameters ($\delta , C_0 \text { and } \phi$) by discrete values, the optimization is done using the AMPGO algorithm. This eliminates the dependence of the optimization accuracy on the discrete interval.

The optimal Johnson-Cook parameter values are determined using the outer loop. A wide range of Johnson-Cook parameters is provided as input. The objective here is to minimize the objective function of Eq. () by tuning the Johnson-Cook parameters. The minimization is accomplished using both the AMPGO algorithm and PSO algorithm separately, for each of the two approaches shown in Fig. 1.

3.3 Adaptive Memory Programming for Global Optimization (AMPGO) method

Adaptive Memory Programming for Global Optimization (AMPGO) is an optimization algorithm presented by Lasdon et al. [29] for the constrained global optimization problems. It consists of two phases: minimization and tunneling. A local minimum is found using a descent algorithm. Then, using a tunneling loop (See Fig. 4), the objective is to improve the found minimum with the new solution away from the current solution for the next minimization phase. The tunneling function is given by Eq. (34).

$$\begin{aligned} TTf(\mathbf {x}) = \frac{\left( \kern 0.1500emf(\mathbf {x})-\text {aspiration}\right) ^2}{\prod _{\mathbf {s}_i\in \text { Tabulist}}\left( \text {dist}(\mathbf {x},\mathbf {s}_i)\right) ^2}. \end{aligned}$$

(34)

Here, $f(\mathbf {x})$ is the function to be optimized. The aspiration value for the objective function is slightly less than the current best value. Tabulist contains the points from which to move away, i.e., the most recent local solution and recent solutions of tunneling sub-problems that failed to achieve the optimum condition. Also, $\text {dist}(\mathbf {x},\mathbf {s}_i)$ denotes the Eulerian distance .

Fig. 4

Tunneling approach of AMPGO algorithm [29]

3.4 Particle Swarm Optimization (PSO) method

The particle swarm optimization method was first proposed by Kennedy and Eberhart [30]. The method, motivated by the social behavior of bird flocks, can be used to find the minimum or maximum values of an objective function $f\left( \mathbf {X}\right)$, where $\mathbf {X} = [x_1, x_2,... , x_n]$ is a vector of variables, also known as a position vector. In this method, a swarm size is chosen. The optimized solution is found based on the cooperation of these swarm particles in terms of learning and communication among them.

The search movement for optimum solution of each particle, shown in Fig. 5, comprises of a component of current velocity direction $v_t^i$, a movement component toward local best solution from all the previous iterations $c_1\left( p_t^i-x_t^i\right)$ and a movement component toward global best , i.e., the best solution of all the particles in the swarm $c_2\left( g_t^i-x_t^i\right)$. The velocity for the next iteration $(t+1)$ for $i^{th}$ particle of the swarm, represented by $v_{t+1}^i$ is given by Eq. (35).

$$\begin{aligned} v_{t+1}^i=\ {\omega v}_t^i+c_1 r_1\left( p_t^i-x_t^i\right) +\ c_2r_2\left( g_t^i-x_t^i\right) . \end{aligned}$$

(35)

Here, parameter $\omega$ is called inertia weight, $c_1$ is called cognitive learning factor and $c_2$ is called social learning factor. These three parameters control the contribution of each factor in a particle’s movement. $r_1$ and $r_2$ are the random numbers in the range (0,1) and are used to avoid premature convergence. For this work, a swarm size of 20 with equal values to the parameters $c_1$ and $c_2$ is used.

Fig. 5

Movement of particles in PSO algorithm

4 Results

In this section, the results of the parameter determination using Approach 1 and Approach 2 is presented. For each of the approaches, both AMPGO and PSO methods are used. Using Approach 1, multiple sets of Johnson-Cook parameters are obtained by both of the optimization algorithms for different machining conditions of Table 2. Tables 4 and 5 show sets of optimal parameters for the machining condition 4 by AMPGO algorithm and PSO method, respectively. The variation of each parameter over the ten sets is quite large. For example, in Table 4 the parameter A varies from 449.5 MPa to 658.3 MPa. Table 6 shows another example of the parameters calculation using AMPGO algorithm for the machining condition 5 with Approach 1. This machining condition differs widely from the machining condition 4 in cutting speed, rake angle and uncut chip thickness. The determined parameters are not unique.

Table 4 Johnson-Cook parameters obtained using Approach 1 by AMPGO method (for Machining condition 4)

Table 5 Johnson-Cook parameters obtained using Approach 1 by PSO method (for Machining condition 4)

Table 6 Johnson-Cook parameters obtained using Approach 1 by AMPGO method (for Machining condition 5)

Table 7 JC parameters obtained using Approach 2 by AMPGO algorithm for machining conditions shown in Table 2

Table 8 JC parameters obtained using Approach 2 by PSO method for machining conditions shown in Table 2

Using Approach 2, where only the parameters C and m are varied, very close values of the Johnson-Cook parameters are obtained by each of the algorithms. The optimization is done ten times for each of the machining conditions to verify the uniqueness of the parameter set obtained by each algorithm. The deviation of the obtained parameters is within $\pm 2\%$ from the values of the parameters in the literature [22]. The average value of ten optimizations for each of the parameters obtained by the AMPGO and PSO algorithm is given in Tables 7 and 8, respectively.

Fig. 6

Comparison of Johnson Cook parameter C

Fig. 7

Comparison of Johnson Cook parameter m

Comparisons of the optimal values of the Johnson Cook parameters C and m from the optimization algorithms AMPGO and PSO are shown in Figs. 6 and 7, respectively. The solid red lines in the plots represent the range of the parameter provided as an input to the algorithm. Also, the green dashed line indicates the value reported in the literature [22]. The results indicate that the optimization algorithms match the value provided in the literature to a fair accuracy.

5 Discussion on the unique determination of Johnson-Cook parameters

As discussed in the Results section, non-unique sets of the Johnson-Cook parameters are obtained when all the five Johnson-Cook parameters are chosen as unknowns. To investigate further, the machining quantities calculated and compared in Tables 10, 11 and 12 using these Johnson-Cook parameters sets obtained in Tables 4, 5 and 6, respectively. The last row in each Table corresponds to the Johnson-Cook parameters obtained using Approach 2 for the respective machining condition. The variables of the objective function, i.e., the cutting force, chip ratio and the tool-chip interface temperature, agree for all ten sets. In fact, the values of all the other quantities such as the shear strain $\varepsilon _{AB}$ and strain-rate $\dot{\varepsilon }_{AB}$ and average temperature $T_{AB}$ at shear plane AB match with each other and also with the corresponding results calculated using the parameters determined by Approach 2. Additionally, the values of Oxley model parameters, $\delta$, $C_0$ and $\phi$ are also compared. Interestingly, the values of $\delta$ and $\phi$ are very close for all cases for each of Tables 9, 10 and 11, but the values of $C_0$ do not match. However, the values of the product of $C_0$ and $n_{eq}$ remain approximately same for all cases. This result is in agreement with the obtained values of equal phi, as seen in Eq. (15). Also, the effect of different values of $C_0$ is seen in the values of $\dot{\varepsilon _{AB}}$. However, the values of $k_{AB}$ which is a combined effect of all the Johnson-Cook parameters remain approximately same for all cases. These results clearly show that Approach 1 leads to multiple sets of values for the Johnson-Cook parameters while providing the same output.

To further confirm the non-uniqueness resulting from Approach 1, finite element simulations are carried out for Test case 4 using different parameter sets. As a test case, three material parameter sets corresponding to Set no. 1, Set no. 7 and Set no. 10 of Table 4 are selected and used for the simulations. The purpose of these simulations is to demonstrate that similar results are obtained when these different sets of parameters are used while modeling. For brevity and keeping the primary focus on the central idea of the paper, the details of FEM model and other simulation parameters are not presented here. Further details of FEM can be referred in [31, 32]. The predicted cutting forces from these simulations are compared in Fig. 8. Also the corresponding chip profiles, von Mises stress profile and temperature profiles are compared in Fig. 9. Clearly, the results obtained from the simulations using different Johnson-Cook parameter sets are in close agreement.

Table 9 Strain hardening term for Johnson-Cook parameters obtained using Approach 1 for the machining condition 4

Fig. 8

Comparison of cutting force using different JC parameter sets

Fig. 9

Comparison of chip profile, von Mises stress and Temperature profile using different JC parameter sets obtained using Approach 1

Table 10 Machining quantities calculated using Johnson-Cook parameters obtained from Approach 1 using AMPGO method (Machining condition 4). The data in last row corresponds to quantities calculated with the parameters obtained using AMPGO method and Approach 2

Table 11 Machining quantities calculated using Johnson-Cook parameters obtained from Approach 1 using PSO method (Machining condition 4). The data in last row corresponds to quantities calculated with the parameters obtained using PSO method and Approach 2

Table 12 Machining quantities calculated using Johnson-Cook parameters obtained from Approach 1 using AMPGO method (Machining condition 5). The data in last row corresponds to quantities calculated with the parameters obtained using AMPGO method and Approach 2

To investigate the reason for the non-uniqueness of the Johnson-Cook parameters determined using Approach 1, the strain hardening term of the Johnson-Cook constitutive model, i.e., $\left( A + B \varepsilon _p^n \right)$ is calculated for the ten parameters sets in Table 3. It may be recalled that these parameter sets were obtained using Approach 1 for the machining condition 4 of Table 2. The calculated strain hardening term for each of these sets is shown in Table 9. It is observed that in all the cases, this term has approximately the same value. Thus, it may be concluded that the inverse methods discussed here determine the strain-hardening term uniquely but are not able to determine the parameters A, B, and n uniquely.

Summarizing, multiple non-unique sets of the Johnson-Cook parameters are obtained using Approach 1. Using these parameters, variations within a small range are observed in the calculated strain hardening terms and no difference is observed in the results of the Oxley model, such as cutting forces and temperatures. This highlights the inherent shortcoming of the Approach 1, which predicts multiple sets of Johnson-Cook parameters which produce similar simulation/ analytical results. Physically, there cannot be multiplicity of parameters. For example, there cannot be multiple yield strength (denoted by the parameter A) of the same material. Additionally, this observation underscores the importance of analyzing the results while using numerical approaches.

A unique set of Johnson-Cook parameters is obtained using Approach 2 where the parameters A, B and n are determined using the tensile test experiment and the parameters C and m are determined using the inverse method. Thus to determine the Johnson-Cook parameters uniquely, an inverse method comprising of the quasi-static tensile test, orthogonal machining experiments, analytical models or simulations and optimization algorithms can be followed.

6 Conclusion

For simulating the behavior of materials during various manufacturing operations such as machining, the Johnson-Cook material model is widely used. Due to the limitation in achieving the extreme conditions of the actual operation, the parameters of the material model determined using experiments may not be accurate. Various researchers use the inverse method to overcome this difficulty. This work attempts to streamline the three categories and multiple methods currently being used by researchers (discussed in Literature review section) to identify the Johnson-Cook material model parameters. The acceptance of non-unique determination of the parameters, finding the root cause of non-uniqueness and providing a systematic approach for unique determination of these parameters are the major contributions of this work.

Following conclusions can be made based on this work:

• (a) When all five parameters of the Johnson-Cook model are selected as unknowns, multiple sets of values are predicted by the inverse approach. Moreover, these parameters are shown to produce identical machining outputs (Table 10). This result is in contrast to the first category of research studies.

• (b) The root cause of this non-uniqueness is identified in this work, instead of suggesting various possible reasons (as in the second category). Coupling of the parameters A, B and n in a single strain hardening term is shown as the root cause.

• (c) A robust combination of experimental and numerical method (Approach 2) is used to resolve the non-uniqueness issue (in line with the third category). This method is shown to result in unique determination of the parameters. In this approach, the parameters A, B and n are determined using the tensile test experiment and the parameters C and m are determined using the inverse method.

• (d) The benefit of this approach is that orthogonal machining experiments along with uniaxial, quasi-static tensile tests are sufficient for determining the Johnson-Cook parameters. The difficulty of conducting experiments at the extreme high strain-rates and high temperatures observed in machining to determine the thermal softening and strain-rate parameters C and m is eliminated.

• (e) This proposed approach is more robust than the existing methods in terms of a very wide search space used in the inverse method. For example, the search space for the parameter C is [0.001, 0.09] for the actual value of the parameter as 0.0134. This is particularly useful for the parameter determination of new materials, where the range of the parameter is not known.