1 Introduction

Due to the interesting properties and high strength-to-weight ratio, the applications of composite materials have raised considerably in the last decades [15, 27]. They are usually made of multiple plies of fibres (e.g. carbon, glass and/or synthetic fibres), layered up in alternating orientations and held together by resin [10]. Therefore, the laying-up of fibre plies is the fundamental manufacturing phase in the production of composite materials. It is usually performed by human operators, who handle and transport the raw materials, making composite manufacturing time consuming, labour intensive and prone to errors. The manual lay-up process requires skilled workers with knowledge and experience attained over several years. Common techniques used in manual lay-up and further highlighted the complexity and skills involved in the process were discussed in [13], which indicated that laminators need to be trained before operations. This is a problem for long-term sustainability due to a reducing number of skilled workers [34]. Quality is also going to be dependent on the individual, so it is harder to maintain consistent quality with manual lay-up. Different from manual system, automated composite lay-up by robotic system could be performed 24 h a day, which is possible to be more time saving than manual system and is worth investigating as a replacement for manual lay-up. The demand for the phasing in of robotic solutions to improve process efficiency and increase operator safety has grown significantly in recent years. Automated Tape Laying (ATL) [17] and Automated Fibre Placement (AFP) [29, 51] are two popular automated technologies employed in automotive lay-up of composite material. However, limited by the heavy cost of specialised equipment and low flexibility, they are not suitable for making small composite parts [24]. Up to now, investigations on the use of commercially available robotic platforms for composite lay-up are on the rise in composite manufacturing.

Previous works have investigated the viability of using robotic systems in advanced composite manufacturing by exploiting the flexibility of robots to meet the stringent demands of manufacturing processes. In [8] and [38], complete systems for handling and laying up prepreg on a mould were developed. Robotic workcells were demonstrated with different modules. Bjornsson et al. [3] surveyed pick-and-place systems in automated composite handling with regard to handling strategy, gripping technology and reconfigurability etc. This survey indicated that it is hard to find generic design principle and the best solution for handling raw materials for composite manufacture depends on the specific case study. Schuster et al. [42, 43] demonstrated how cooperative robotic manipulators can execute the automated draping process of large composite plies in physical experiments. Similar research has been done by Deden et al., who also addressed the complete handling process from path planning and end-effector design to ply detection [11]. Szcesny et al. [47] proposed an innovative approach for automated composite ply placement by employing three industrial manipulators, where two of them were equipped with grippers for material grasping and the third manipulates a mounted compaction roller for layer compression. A comparable hybrid robot cell was developed by Malhan et al. [25, 26], where rapid refinement of online grasping trajectories was studied. Despite these advances, cooperative/hybrid robotic systems involving mobile robot platforms and fixed-base robotic manipulators have received little attention in the context of advanced composite manufacturing.

Due to the requirement of accurate localisation and fibre orientation detection, an efficient vision system is of great importance for autonomous robotic system in advanced composite manufacturing. Fibre orientation detection is challenging due to the high surface reflectivity and fine weaving of the material, and thus, it has still predominantly been accomplished manually in practice [31, 41]. Traditional machine vision methods for fibre orientation detection of textiles prefer to utilise diffused lighting [45], such as diffuse dome [39] and flat diffuse [22] illumination measuring techniques. Polarisation model approaches have been particularly popular for measuring fibre orientation, where contrast between textile features such as fibres and seams are used to identify the structure of the material relative to the camera [40]. The method presented in [50] used a fibre reflection model to measure fibre orientation from an image and achieved good accuracies and robustness for different types of surfaces. However, when considering the specific application of advanced composite manufacturing, changes in lighting conditions are often unavoidable because of the moving shadow of the robot arm cast on the material. The integration of vision systems with robotics was considered by only few of the previous works. This means systems are inflexible as they are unable to cope with dynamic variations within advanced composite manufacturing processes.

In composite manufacturing, material transport and composite lay-up have not been integrated into a single autonomous robotic system, which is challenging due to the many technologies involved, including path planning, material detection and localisation. Achieving this requires the development of a strategy that combines different modules in a flexible system and provides autonomous material transportation and sufficiently accurate material handling capabilities. This paper presents a case study on robotic material transportation and composite lay-up, which is based on a real-world scenario commonly found in advanced composite manufacturing. Compared to previous works, this research addresses specific challenges that arise from the introduction of different robots that must be coordinated along with the complex set of tasks covering transport, detection, grasping and placement of deformable material for composite manufacturing applications. The aim of this research is to conduct a pilot study on the feasibility of deploying a cooperative robotic system to perform a series of tasks in composite material manufacturing. Therefore, a cooperative mobile robot and manipulator system (Co-MRMS), which consists of an autonomous mobile robot, a fixed-base manipulator and a machine vision sub-system is presented in this paper. The mobile robot transports the material autonomously to a predefined position within the working range of the fixed-base manipulator. The machine vision sub-system then detects the location of the material and estimates the fibre orientation to enable the manipulator to accurately handle the material. This is achieved by employing an ArUco marker detection algorithm [37] to compute the position of the material, and a Fourier transform-based algorithm [1] combined with a least squares line fitting method [49] to calculate the material’s fibre orientation. Afterwards, the manipulator accurately grasps the material and places it onto a mould. Simulated trials and physical experiments are conducted to verify the cooperation behaviours of the Co-MRMS and quantify the accuracy of the vision system.

Modelling and handling of flexible deformable objects have been issues in robotics. To simulate the interactive behaviour between robot actions (such as grasping and transfer actions) and material deformation, various techniques do exist to model non-rigid bodies (i.e. deformable objects), including the finite element method, mass-spring systems and numerical integration methods [2, 18, 44]. In [20], recent advancement of different types of flexible deformable object modelling for robotic manipulation, such as physical-based and mass-spring modelling, was reviewed. Moreover, the approaches of building up deformable object models were presented. Researchers in [33] established a model for deformable cables and investigated robotic cable assembling, addressing collision detection issues. However, the modelling process cannot be performed within (or transferred effectively to) the simulation platforms developed to simulate the physical motion of robots in both static and dynamic conditions. This study adopted particle-based modelling approach [6] to model material deformation within simulation when composite material is grasped and transferred by a manipulator. Another issue of automated handling composite material is end-effector design. Until now, a number of grippers, such as grid gripper and suction cup gripper, have been designed. Suction cup grippers could handle deformable objects without damaging the material and are flexible enough to drape different shapes of composite material to flat or curved moulds. Gerngross et al. [16] developed suction cup-based grippers for handling prepregs in offline programming. The solution of automated handling dry textiles to double curvature mould were verified both in offline programming environment and an industrial scale manufacturing demonstrator. Ellekilde et al. [14] designed a novel draping tool with up to 120 suction cups, which has been tested on draping large aircraft part prepreg. Krogh et al. [23] researched the moving trajectories of suction cup gripper for draping plies with establishing cable model. However, composite material deformation and sagging effects have been few considered in end-effector design. Therefore, a vacuum suction-based end-effector model is developed in this work to simulate sagging effects during grasping, which provides a useful simulation tool for quickly evaluating different gripper designs comprising of an arrangement of multiple suction cups.

In summary, the research gaps of material transport and lay-up in advanced composite manufacturing are listed as follows:

  • Popular automated technologies employed in automotive lay-up of composite material are not suitable for making small composite parts owing to the limits of heavy cost of specialised equipment and low flexibility.

  • In composite manufacturing, a single autonomous robotic system that integrating both of material transport and composite lay-up has not been investigated.

  • Robotic systems without integration of vision systems are inflexible as they are unable to cope with dynamic variations within advanced composite manufacturing processes and this is considered by only few of the previous works.

  • Composite material deformation and sagging effects have been few considered for end-effector design in simulation environment.

The main contributions of this work are listed as follows:

  • An intelligent and cooperative robotic system combining a fixed-base manipulator with a mobile robot is presented for material transport and lay-up in advanced composite manufacturing.

  • A machine vision system integrated with robot for accurate material detection, localisation and fibre orientation identification.

  • Deformable object model was developed in simulation platform and the interactive behaviour between robot actions and material deformation was simulated.

The remaining parts of the paper are organised as follows. First, the framework of the Co-MRMS, the modelling strategy for the interaction with deformable objects and machine vision approaches are described in Section 2. Then, the details of the experimental setup are outlined in Section 3. Section 4 discusses the Co-MRMS evaluation through physical experiments, while Section 5 is devoted to a discussion on the findings, limitations and future directions of the work. Finally, the conclusions are provided in Section 6.

2 The proposed system and approach

2.1 Framework of the cooperative mobile robot and manipulator system (Co-MRMS)

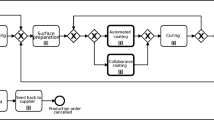
From a hardware perspective, the proposed Co-MRMS involves four components: a mobile robot, a fixed-base robotic manipulator, a vision system and a host PC. The framework of the Co-MRMS is presented in Fig. 1. The mobile robot is responsible for transporting the composite material from a given starting location within the work shop floor (e.g. the storage area) to the robotic manipulator. Aided by the vision system, the estimated position and orientation of the raw material are sent to the fixed-base robot manipulator via the host PC. The manipulator is used for grasping each fibre ply and placing it correctly according to the designed lay-up manufacturing specifications. Robotic path planning for both robots was implemented in MATLAB® [19]. Image processing algorithms were developed by using OpenCV [5], an open-source computer vision and machine vision software library that provides a common infrastructure for computer vision applications and accelerates the development of machine perception capabilities. Being a BSD-licensed product, OpenCV makes it easy for businesses to utilise the library and modify the code. Simulations of the entire process were developed using the CoppeliaSim robotic simulator [36] while the integration of the Co-MRMS was implemented via ROS (Robot Operating System) [35].

Fig. 1
figure 1

The framework of the Co-MRMS

Full size image

2.2 Deformable object modelling and suction cup end-effector design approach

A method based on the particle-based system [6] is developed in this research to simulate the draping behaviour of composite material within the CoppeliaSim robotic simulator. The non-rigid characteristics of composite material was modelled through an array of individual cuboids and associated dummies. A simple 3×3 modelling example of composite material is presented in Fig. 2. Note that these primitive shapes individually behave as rigid bodies. As shown in the Figure, the dummies are attached to cuboids and linked by dynamic constraints linkages. Once the structure is disturbed by an external force, the relative motion between adjacent dummies are constrained by the linkages and material deformation behaviour including bending and stretching are emulated. Note that this approach is a simplified modelling of the particle-based system and does not model shear effects. It is therefore important to note that this model is not intended to replace the more realistic modelling of draping behaviours achieved by the other methods described earlier. Instead, it provides an approximation of the draping effects for visual simulation of the interactions between robot manipulation and draping within a single comprehensive robotic simulation environment for evaluating the high-level behaviours of the Co-MRMS.

Fig. 2
figure 2

Modelling the non-rigid nature of composite material as an array of dynamically linked cuboids

Full size image

Material stiffness parameters have crucial effects on modelling deformable objects. The method presented above for modelling deformable objects in CoppeliaSim enables the stiffness of the overall material to be adjusted by tweaking two different types of model parameters: principle moments of inertia and individual primitive cuboids dimensions. Increasing either the dimensions of the cuboid or the principle moments of inertia produces a higher stiffness material, while reducing either parameters leads to lower stiffness. The parameters chosen in this work are presented in Table 1.

Table 1 Model parameters for composite material deformation
Full size table

Having developed an approach to model composite material as a non-rigid, deformable body within CoppeliaSim, it is also necessary to develop a model for the vacuum suction-based end-effector. CoppeliaSim’s default library provides a simple vacuum suction cup model that enables the simulation of vacuum suction grasping for the manipulation of rigid bodies. However, without any modifications, this model cannot realistically interact with the composite material model as it is developed to grasp only a single rigid body within the simulation environment. When used to grasp the simulated composite material, a numerical-method-induced sagging effect would occur around the vacuum suction cup as the end-effector would pick up the deformable object from a single point corresponding to one cuboid. In reality, however, a suction cup gripper should maintain contact with the entire region of cloth directly underneath the suction cups. Therefore, the default suction cup model was modified to enable compatibility with the approach to modelling deformable materials by ensuring more proper contact behaviour between all elements that lie within the grasp region of a suction cup during grasping operations. The modified suction cup gripper with four suction cups, provides a useful simulation component for quickly evaluating different gripper designs comprising of an arrangement of multiple suction cups. This is an important resource for future design processes that seek to minimise sagging effects during the transfer of composite material sheets of a known shape and size.

The capability of the robot end-effector to deal with ply sagging was tested in simulation environment. Figure 3 shows images of example simulation involving the use of a 4-cup and single-cup vacuum suction gripper to transfer a sheet of composite material across the workspace. Compared with single-cup vacuum suction gripper, 4-cup vacuum suction gripper reduced the sagging effects significantly, reaching satisfactory performance in dealing with ply sagging. It should also be noticed that each suction cup maintains complete contact with the material and sagging effects are minimised in the convex region defined by the four contacts between the gripper and the composite material.

Fig. 3
figure 3

a End-effector mounted with camera and vacuum suction cup in simulation environment. b Image captured from simulation showing the grasping interactions between the vacuum suction cup gripper and composite material model

Full size image

2.3 Localisation and fibre direction identification approach

The aim of the machine vision system is to detect and locate the composite material and identify the orientation of the fibre in the work space according to the requirements of composite material manufacturing processes. The extracted position and orientation of the material are provided to the host PC, which uses the information to plan target coordinates for the robot arm to grasp the composite material transported by the mobile robot. Generally, the position of the material could be approximated continually using wheel encoders of the mobile robot, but substantial error is accumulated over time due to the wheel slippage. This can be compensated by the vision system which provides higher accuracy position information relative to the manipulator end-effector frame and it is necessary to enable accurate localisation of composite material. This corrected position estimation can further be used to eliminate the build-up of error within the wheel odometry-based localisation system. Thus, machine vision plays a crucial role in the Co-MRMS developed for composite material manufacturing. By combining both of the machine vision and wheel odometry-based data, the proposed localisation system could be robust and accurate. Yet the application requires an approach for object detection that is robust to variations in the size and shape of the material. To overcome these challenges, first, a marker-based approach is adopted to enable the Co-MRMS to locate the material accurately. Then, a method for accurate and robust fibre orientation detection is developed. Here it is assumed that the relative position between the marker and the material is fixed. By locating the marker, the position of the material can be inferred from the relative position between the marker and material. This provides the Co-MRMS with a higher accuracy estimation of the position of the fibre material, which does not accumulate error over time. Then, the orientation of fibre is detected to support the composite lay-up process. More details will be given in following sections.

2.3.1 Localisation approach

As shown in Fig. 4, this work uses a single ArUco vision marker for material localisation material. The marker is defined by a 7×7 square array. Horizontal and vertical borders are formed by black squares. All other squares within the array may carry a black or white colour, where the arrangement of black and white interior squares encode a binary pattern. Each ArUco marker has a unique pattern, which can be used to identify the marker. Thus, the digital coding theory system used for detecting these markers proves to be a robust and accurate system producing a low rate of false marker detection. Additionally, the layout of the four corners can be used to identify the orientation of the marker. With this encoded information, the marker can be used robustly to estimate the 3D position and orientation of the marker relative to a monocular camera.

Fig. 4
figure 4

An ArUco marker example

Full size image

The camera can be used to detect and obtain the position of the ArUco vision marker as described below (see Fig. 5). When the image is captured by a camera, it is converted into a grey-scale image. Afterwards, the most prominent contours in the image are detected through the use of a Canny edge detector [9], an efficient edge detection algorithm that provides a binary image containing the border information. The Suzuki algorithm [46] is then used to extract the contours, which are reconstructed by the Douglas-Peucker algorithm [12]. Here contours that do not contain four vertexes or lie too close together are discarded. After these image processing steps, the encoding of the marker is extracted and analysed. To achieve this, the perspective view of the marker must be projected onto a 2D plane. This is achieved through the use of a homography. Otsu’s method [32] was applied using an optimal image threshold value to generate a binarised image. This results in a grid representation of the marker where each cell is assigned a binary value, determined by the average binary value of each pixel belonging to the cell. For example, a value of 1 is assigned if the majority of binarised pixels in the cell possess a value of 1. Cells belonging to the border of the image carry a value of 0, while all inner cells are analysed to obtain the internal encoding, which corresponds to a 6x6 internal grid area. To improve the accuracy of the marker detection, the corners of the marker are refined through subpixel interpolation. Finally, the pose of the camera is estimated by iteratively minimising the reprojection error of the corners using the Levenberg-Marquardt algorithm [28].

Fig. 5
figure 5

Marker detection process

Full size image

As shown in Fig. 6, the material is placed on the x direction of the marker. Using dcc to denote the distance between the centre of the material and the marker (assumed to be known a priority), \(\left (x_{mar},y_{mar} \right )\) to denote the marker position, and Θ to denote the marker orientation in the x-y plane. The relative position of the material can be calculated by:

$$ \left\{\begin{array}{ll} x_{mat}=x_{mar}+d_{cc}\cos({\Theta} )\\ y_{mat}=y_{mar}+d_{cc}\sin({\Theta}) \end{array}\right. $$
(1)

where the final position (xmat,ymat) corresponds to the x and y positions of the material centroid.

Fig. 6
figure 6

Composite material detection

Full size image

Using this approach, the position of the material can be determined robustly regardless of the size and shape of the material. Once the position of the material is detected, target commands are sent to the robot to move the end-effector above this centre position. Additionally, there is no restriction for the size and shape of the material as long as the centre of the fabric is fixed. Thus, this localisation approach is suitable for handling different sizes and shapes of fabric patches.

2.3.2 Fibre orientation detection approach

The orientation of the composite material during placement on a mould must be carefully controlled in a composite lay-up process. This is due to the material being anisotropic, meaning it provides varying strength along different directions across the material. In order to make sure that the plies are layered as designed, strict requirements are imposed for the orientation of each layer of fibres to obtain the expected composite parts. The Fourier Transform [4] is a popular image processing tool that has proven to be effective for a variety of image processing applications such as image enhancement and image compression. In this work, the Fourier Transform is applied for fibre orientation analysis, where an image is converted into the frequency domain to obtain its spatial frequency components. The transformed image can be calculated by:

$$ F_{(\mu,\nu)}={\int}_{-\infty }^{+\infty }{\int}_{-\infty }^{+\infty }f_{(x,y)}e^{-i2\pi (\mu x+\nu y)}dxdy $$
(2)

where μ and ν are spatial frequencies. In order to robustly detect the orientation of fibres from an image using the Fourier transform, a high gradient image possessing strong directional change in intensity must be acquired. This is achieved through the use of a spotlight mounted together with the camera to produce strong reflections from the fibres of the material. The detection process is shown in Fig. 7. An image captured by the camera is first converted to a grey-scale image. Then, the Fourier transform is applied to obtain the frequency domain image. A series of morphological procedures are applied to generate several discrete points that lie along the line in the direction of the fibres. The centre of these points can be analysed by contour detection. Finally, a fitted straight line for this set of points is computed and the orientation of this line is calculated according to its slope. Here curve fitting is achieved through the use of the least squares line fitting method. It should be noted that this approach is inspired by the high surface reflectivity and colour difference between yarn and fibres. Therefore, it’s suitable for materials like carbon fibre while other method need to be considered in detecting low surface reflectivity and colour difference material such as fibreglass.

Fig. 7
figure 7

Fibre orientation detection procedure

Full size image

Assume that the points obtained from the morphological procedures are \(\left (x_{1},y_{1}\right ),...,\left (x_{n},y_{n}\right )\), and the fitted straight line equation is yi = axi + b. The process for curve fitting is to identify appropriate values for \(\left (a,b \right )\) that minimises the total square error E:

$$ E=\sum\limits_{i=1}^{n}\left (y_{i}-ax_{i}-b\right )^{2} $$
(3)

The above equation can be re-expressed as:

$$ E=\left \| Y-XB \right \|^{2}, $$
(4)

where

\(Y=\begin {bmatrix} y_{1}\\ {\vdots } \\ y_{n} \end {bmatrix}, X=\begin {bmatrix} x_{1} & 1\\ {\vdots } & \vdots \\ x_{n} & 1 \end {bmatrix}, B=\begin {bmatrix} a\\ b \end {bmatrix},\)

The explicit expression of E as a function of Euclidean vector norm is:

$$ \begin{array}{lll} E &=\left \| Y-XB \right \|^{2} \\ &=(Y-XB)^{T}(Y-XB)\\ &=Y^{T}Y-2(XB)^{T}Y+(XB)^{T}(XB). \end{array} $$
(5)

According to the stationary condition of E with respects to B requires

$$ \frac{dE}{dB}=2X^{T}XB-2X^{T}Y=0, $$
(6)

which leads to the stationary point

$$ \begin{array}{ll} B=[X^{T}X]^{-1}X^{T}Y. \end{array} $$
(7)

Thus, the original equation can be represented by a least squares solution, B = [XTX]− 1XTY given that [XTX]− 1 exists which depends on the data collection. The values for \(\left (a,b\right )\) are obtained by:

$$ \begin{array}{ll} a=\frac{\sum {x_{i}^{2}}\sum y_{i}-\sum x_{i}(\sum x_{i}y_{i})}{n\sum {x_{i}^{2}}- (\sum x_{i})^{2}} \\ b=\frac{n\sum x_{i}\sum y_{i}-\sum x_{i}(\sum x_{i}y_{i})}{n\sum {x_{i}^{2}}- (\sum x_{i})^{2}} \end{array} $$
(8)

This provides the fitted line, y = ax + b. Using the computed gradient of the line a, the orientation can be calculated by: \({\Theta } =\arctan (a),\) where Θ is the fibre orientation angle in x-y plane taking x-axis as reference position. Therefore, as long as the relative orientation of fibres and yarn is known, the fibre orientation detection could be adapted to different kinds of prepregs. The prepreg used in this work is carbon fibre reinforced polymer (CFRP) composites. The relative orientation of fibres and sewing yarn is known in advance, which is at 90∘.

3 Experimental setup

The composite material used here is a small sheet of fabric prepreg. Both of the simulation-based and physical experiments are described, where the specific robotic layout and designed tools are defined.

3.1 Robot setup

In this paper, the Turtlebot3 Burger differential drive mobile robot was chosen as the mobile robot platform in both simulation and physical experiments due to the unavailability of industry-standard mobile robots. The robot setup in the simulation environment is presented in Fig. 8. As the Turtlebot3 Burger is an open-source mobile robot, low-level access to the robot’s individual functionalities is possible, providing easy access to wheel odometry-based readings that can be sent to the host PC through a ROS network. For the fixed-base robotic manipulator, the 6 degrees of freedom KUKA KR90 R3100 industrial manipulator was chosen for implementation in the simulation environment to model a realistic industrial environment. In physical experiments, a 6 degrees of freedom KUKA KR6 R900 manipulator was used due to its lower scale and availability. Nevertheless, both robots share the same control scheme, allowing algorithms to transfer without modification between the two systems.

Fig. 8
figure 8

a and b are Turtlebot3 Burger and KUKA KR90 R3100 industrial manipulator model in CoppeliaSim respectively while c is the integrated simulation environment

Full size image

3.2 Machine vision system design

The machine vision system comprises a commercial low-cost webcam, a spotlight and a customised camera mounting unit. Localisation of the material and fibre orientation detection are achieved through the use of a spotlight mounted together with the camera to produce strong reflections from the fibres of the material. In order to attach the camera to the end-effector of the fixed-base manipulator and ensure that the camera is orthogonal to the material plane, a camera mounting unit was designed by CAD (Computer-aided design) software and then 3D printed. The CAD design and mounted 3D-printed piece is presented in Fig. 9. During physical experiments, the camera was inserted into the holder facing downwards, while the spotlight was attached to the external surface of the mounting unit facing in the same direction as the camera.

Fig. 9
figure 9

a CAD model and physical dimensions of the module; b and c are the camera mount setup during physical experiments

Full size image

3.3 Host computer and related software

Following the description of the proposed Co-MRMS in Section 2.1, Matlab, CoppeliaSim and OpenCV have been used to support the development of crucial robotic capabilities for this work. The path planning routine for the mobile robot, based upon a bi-directional variant of the Rapidly-exploring Random Tree algorithm [48], was implemented on Matlab. Likewise, the planning of manipulator actions for grasping was developed in Matlab, where reasoning is applied on sensory information to identify target positions and complete motions for the end-effector. The robot was actuated using Point-To-Point movement. A remote API library, developed by Coppelia Robotics, was used to send resulting actuation commands from Matlab to the simulated robots in CoppeliaSim. CoppeliaSim provides an extensive environment for the development of the integrated simulation. In addition, the deformable object was modelled in CoppeliaSim by leveraging its support for the simulation of dynamic behaviours, which is achieved through the Bullet 2.78 physics engine. This handles the complex calculation of composite material deformation during handling operations and enables the visualisation of the material’s deformation behaviours. The integrated simulation environment is presented in Fig. 10, which comprises of the mobile robot, the fixed robotic manipulator, the composite material, a work surface, a cube-shaped mould and the mounted camera. For the physical implementation, the ITRA toolbox [30], developed for the control of KUKA robots, provided the interface for directly sending actuation commands from Matlab to the KUKA robot controller unit for manipulator control, while ROS provided the interface for the actuation of the Turtlebot3 Burger. The vision system relied upon images captured by a webcam mounted on the end-effector of the manipulator to observe the environment. Then the OpenCV library was used for the development of machine vision algorithms that processed images obtained by the camera.

Fig. 10
figure 10

a Simulation environment in CoppeliaSim; b and c are composite material’s placement on mobile robot and mould respectively

Full size image

4 Performance evaluation

The manual lay-up process requires skilled workers with knowledge and experience attained over several years. This is a problem for long-term sustainability due to a reducing number of skilled workers. Quality is also going to be dependent on the individual, so it is harder to maintain consistent quality with manual lay-up. Different from manual system, automated composite lay-up by robotic system could be performed 24 h a day, which is possible to be more time saving than manual system and is worth investigating as a replacement for manual lay-up. System performance is evaluated on the basis of the feasibility of laying up fibre plies, how accurate the plies are placed on the mould and how capable the system deals with uncertainty. To validate the developed system, several experiments were conducted to test the capabilities of the Co-MRMS. Initially, simulation-based experiments were carried out according to the proposed approaches in Section 2 and the accuracy of the vision system was assessed. Subsequently, physical experiments were conducted on an integrated robotic system to validate the combined behaviour of the proposed Co-MRMS and assess the accuracy of machine vision algorithms in real-world scenes.

4.1 Simulation-based experiments

The Co-MRMS, which employs a KUKA KR90 R3100 industrial fixed-base manipulator and a Turtlebot3 Burger differential drive mobile robot, was firstly modelled in CoppeliaSim to verify the performance in fulfilling the transportation and lay-up task of the proposed system. Additionally, an integrated camera and a gripper unit with four suction cups were modelled on the KUKA KR90 end-effector so that the detection and grasping of the material could be simulated. Based on the modelled Co-MRMS, two simulation-based experiments were conducted to evaluate the attainable accuracy of the composite material vision system. First, experiment of evaluating localisation accuracy was assessed. Using the modified bi-directional RRT algorithm [48] to compute a collision-free path, the mobile robot drove autonomously to a randomly generated goal within the manipulator workspace. Then, the vision system was employed to correct the simulated error in the wheel odometry-based positioning system by applying the object localisation algorithm described in Section 2.3.1. To evaluate the repeatability of the localisation results, this experiment was conducted 10 times. In addition, to simulate the accumulation of error in wheel odometry observed in real environments, Gaussian noise was introduced and superimposed with the simulated wheel odometry measurement of the mobile robot’s position relative to its starting position. Gaussian noise has generally been used in signal processing to deal with uncorrelated random noise and is also commonly adopted in neural networks for modelling uncertainties [7]. It is statistically defined by a probability density function (PDF) that is equivalent to a normal distribution (also known as Gaussian distribution). In other words, the odometry error due to wheel slippage was assumed to be Gaussian-distributed.

Setting the mean and standard deviation of the Gaussian distribution to 100 mm and 70 mm, respectively, the wheel odometry position error in x and y are given by:

$$ \begin{array}{ll} Error{(x)}=\frac{1}{\sqrt{2}\sigma \pi }e^{\frac{-(x-\mu)^{2}}{2\sigma^{2}}} \\ Error{(y)}=\frac{1}{\sqrt{2}\sigma \pi }e^{\frac{-(y-\mu)^{2}}{2\sigma^{2}}} \end{array} $$
(9)

where μ is the Gaussian mean and σ is the standard deviation. With the material position data obtained from machine vision system and wheel odometry, the localisation accuracy could be evaluated through Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE). Here the ground truth was retrieved from the simulation. The results are presented in Table 2, where MAE and RMSE of wheel odometry were 158.48 mm and 121.21 mm, respectively, while the MAE and RMSE of the vision system were 11.53 mm and 9.00 mm, respectively. Compared to the wheel odometry-based estimation, the proposed machine vision system reduced the localisation error by 93% and demonstrated its ability in improving the localisation accuracy.

Table 2 Localisation and fibre orientation detection error in simulation environment
Full size table

In the second experiment, the fibre orientation detection algorithm was evaluated by comparing the output of the algorithm against the ground truth. Here the orientation of the material was incremented by 10 degrees between the range of [0∘, 180∘] relative to the camera frame. Like before, the accuracy is expressed by the MAE and RMSE and is shown in Table 2. The MAE and RMSE for fibre orientation detection were found to be 0.70∘ and 0.048∘, respectively. Since the experiments were conducted in a simulation environment, the lighting conditions in the scene could be controlled, which shows that under ideal conditions, the fibre orientation detection algorithm can provide accurate estimates.

4.2 Physical experiments

4.2.1 System interaction behaviour evaluation

The cooperative system interaction behaviour was evaluated by physical experiments, of which a set of execution routines consisting of five active phases and two idle phases were obtained. This corresponds to the complete performance with a duration of approximately 87 s, involving approximately 18 s idle pauses time. Figure 11 plots the time evolution of the x and y positions of the mobile robot (odomx and odomy, respectively), and the x, y and z positions of the manipulator end-effector (kukax, kukay, and kukaz, respectively) across these execution phases recorded from a single trial of the experiment. The first phase consists of the autonomous drive of the mobile robot. The duration of this phase varies according to the start point, goal point and the subsequent path to move between these two points. After the mobile robot arrives at the goal point, it remains stationary to await the machine vision processing phase. This corresponds to a flat curve from the end of phase 1 for odomx and odomy in Fig. 11. After a brief pause where all systems remain idle to indicate that the mobile robot has reached its destination, the host PC sends the wheel odometry estimation of the mobile robot’s position as a target command to drive the manipulator towards the approximate location of the material (phase 2). Here the build-up error in the estimated position arising from wheel slippage causes a misalignment between the centre of the composite material (carried by the mobile robot) and the end-effector of the manipulator. Once the manipulator reaches the target position, both robots remain stationary as the vision system captures an image and runs the localisation algorithm to compute a higher accuracy estimate of the mobile robot’s true position.

Fig. 11
figure 11

Turtlebot3 Burger and KUKA robot positions during the experiment

Full size image

Phase 3 then consists of refining the position of the end-effector using the vision-based estimate of the mobile robot position to reduce the misalignment between the manipulator and composite material. In the fourth phase, the manipulator lowers the z position of the end-effector from 420 mm to 250 mm (relative to the base frame of the manipulator, which is treated as the world coordinate frame) to provide the camera with a close-up view of the composite material. This is necessary to ensure a satisfactory image can be obtained for accurate fibre orientation detection. In the final phase, machine vision parameters are adjusted for the new image depth and the fibre orientation angle of the material is computed using the algorithm described in Section 2. This information is used to rotate the end-effector to correct for the angular offset between the end-effector and composite material. This facilitates the placement of the material in a controlled orientation during grasping operations by ensuring that the fibre direction is always aligned with the z axis rotation of the end-effector.

This experiment demonstrated the capability of the integrated system to correct any manipulator positional offset error that arises from wheel slippage of the mobile robot through higher accuracy estimation provided by machine vision. Compared to the wheel odometry-based localisation, the vision system corrected the position in the x and y direction by 156.87 mm and 23.17 mm in this case.

Due to the high degree of flexibility and wide compatibility of the approach, the fix-based manipulator could be substituted by other industrial robotic manipulator when considering the availability of equipment. As is shown in Fig. 12, experiments including material detection, fibre orientation identification, handling and placement were implemented in 6 degrees of freedom UR 10e with handling tool inspired by tapes. The results indicate that the developed system is capable of performing completed fibre plies lay-up process.

Fig. 12
figure 12

Lay-up experiment

Full size image

4.2.2 Machine vision system accuracy evaluation

To measure the accuracy of the machine vision algorithms in the real world, additional experiments were conducted.

The first experiment was used to quantify the errors in the measured position of the mobile robot using the vision-based localisation algorithm and wheel odometry. The setup for the experiment is shown in Fig. 9, where the camera and spotlight are mounted on the end-effector of the KUKA robot positioned above the Turtlebot3 Burger platform. The mobile robot was driven autonomously to a randomly generated goal within the workspace of the manipulator and the wheel odometry-based position reading was obtained. The fixed-base manipulator was then manually controlled to align the end-effector directly above the centroid of the composite material. The feedback position information of the end-effector was obtained from the KUKA controller and used as the ground truth in this experiment. Finally, the vision-based estimate of the material position was obtained by applying the localisation algorithm with both robots fixed. This experiment was conducted 20 times for statistical significance. For this reason, the mobile robot drove autonomously to a randomly generated goal within the workspace of the manipulator, of which the travelled distances were different each time. The average travelled distance of the mobile robot was 340.9 mm. Table 3 reports the MAE and RMSE for both wheel odometry estimation and vision-based estimation relative to the ground truth. It was found that the MAE and RMSE for wheel odometry was 19.88 mm and 24.72 mm, respectively. This was much larger than the MAE and RMSE for vision-based localisation, which was 4.04 mm and 4.75 mm respectively. Evidently, machine vision reduced the wheel odometry-based error by 80%, which significantly improves the accuracy for localisation when used in conjunction with wheel odometry.

Table 3 Material localisation and fibre orientation detection error
Full size table

The systematic lay-up accuracy is quantified by measuring the deviation between the placement centre and fibre plies. This work uses a single ArUco vision marker for material localisation. As long as the centre of the fabric is fixed, this localisation approach is suitable for handling different sizes and shapes of fabric patches which is shown in Fig. 13. Here, the RMSE of (i) and (ii) are obtained with little difference, which are 5.10 mm and 5.48 mm respectively.

Fig. 13
figure 13

Different sizes and shapes of fabric patches

Full size image

Additionally, experiment was conducted to quantify the accuracy of machine vision for fibre orientation detection. Like the first experiment, a camera and flashlight were mounted on the end-effector of manipulator. A sample piece of composite material was placed in a fixed position in the workspace of the manipulator while the end-effector was positioned directly above the centre of the material with their rotation axes aligned at 0∘. The orientation of the end-effector about the z axis was incrementally increased by 10∘ within the range of [0∘, 180∘]. At each interval the fibre orientation detection algorithm was used to measure the orientation angle of the fibre relative to the camera, which should coincide with the rotation angle of the end-effector under ideal conditions. Thus, the measured angle was compared against the end-effector rotation, used as the ground truth, to compute the MAE and RMSE. Moreover, fibre orientation detection accuracy under three different light conditions (no flash light, low flash light, high flash light) were investigated. Fibre orientation readings shown in Fig. 14 reveal that the identification is more accurate with stronger flash light. The MAE and RMSE for fibre orientation detection are shown in Table 3. Furthermore, manual lay-up was tested by picking and placing the same materials under the same conditions. Table 3 shows the accuracy of the developed Co-MRMS and manual system in lay-up. The placement accuracy differs by 1 mm approximately.

Fig. 14
figure 14

Fibre orientation readings under different light conditions

Full size image

Furthermore, the error in fibre orientation detection in the real world was greater than the simulation results as the composite material was modelled as a non-rigid body, of which the optical features (high specular reflectivity and high absorption of light) of the material were not simulated and the illumination environment in the real world is far more challenging than the simulated environment. Moreover, the alignment between the camera and the normal of the material was not exact in the physical setup, which introduces additional projection errors when detecting the orientation of the fibre as shown in Fig. 15. The investigation shows that the closer the true fibre orientation is to 0∘, the higher the accuracy in fibre orientation detection. This could be overcome by applying a two-step detection strategy as follows. The first step consists of computing an approximate rotation angle for the end-effector to roughly align the camera with the fibre orientation which corresponds to the zero degrees region. Subsequently, a finer tuning on the end-effector rotation is performed by applying a second instance of the fibre orientation detection algorithm, which produces an estimate for the fibre orientation angle with minimal error.

Fig. 15
figure 15

Vision detection error varies with fibre orientation angle

Full size image

The strategy was evaluated in physical experiments. As expected, the performance yielded greater accuracy in fibre orientation detection. The error of the vision system was reduced to 0.23 degree approximately. In comparison, the detection error was around or below 1 degrees by derived fibre reflection model in [50] and the frequency domain machine vision algorithm in [21] showed around 5 degrees error for braid angle measurement. This indicated that the proposed machine vision system with two-step strategy can achieve high accuracy in fibre orientation detection. In addition, the systematic error is approximately 1.84 degrees due to the nonalignment between the camera and fibre orientation and is lower than manual system’s 2.61 degrees. Nevertheless, the system is capable of meeting the high accuracy orientation detection requirements in composite material manufacturing.

5 Discussions

This section discusses the obtained experimental results.

Firstly, it should be noted that the trials incorporating the manipulation actions for grasping the material in physical trials with tapes rather than vacuum suction hardware. Nevertheless, in both the simulation-based and physical experiments, autonomous material transportation, localisation, fibre orientation detection and handling capabilities were achieved. Future work will seek to integrate a vacuum gripper with the existing physical system to further develop material handling capabilities.

Secondly, it could be observed that the mobile robot used in this work was not of an industrial standard. Instead, the educational mobile robot platform Turtlebot 3 Burger was adopted for the investigations conducted. This meant experiments and evaluations were limited to small-scale setups due to the small size of the Turtlebot3 platform. Thus, additional development work is necessary to implement the proposed system framework onto an industrial standard set of hardware to validate the proposed system.

This work has so far focused on the detection and handling of a single sheet of material. Current ongoing work is investigating the lay-up task with the aim of developing an algorithm for autonomous lay-up of composite materials—i.e. working with multiple plies.

Another interesting avenue to examine is the feasibility of developing a method to correct any creases or poor contacts between composite material and the mould in the composite draping process through the use of the manipulator(s), which can maximise the quality of the draping process when performed autonomously using a cooperative robotic system.

6 Conclusions

In this study, a cooperative mobile robot and manipulator system (Co-MRMS), which comprised of a fixed-base manipulator, an autonomous mobile robot and a machine vision sub-system, was developed as a promising strategy for autonomous material transfer and handling tasks to advance composite manufacturing. To demonstrate the feasibility and effectiveness of the proposed Co-MRMS, comprehensive simulations and physical experiments have been conducted. The integrated simulation, developed in CoppeliaSim, simulated a material transfer operation that involves the use of a mobile robot to transport composite material to a robotic manipulator, which grasps and transfers the material to a mould. To realistically simulate the interactions between the robots and the non-rigid nature of composite materials, a method for modelling deformable material within CoppeliaSim has been devised. Physical experiments were performed to evaluate the performance of individual components of the proposed Co-MRMS through a small-scale robotic cell consisting of a 6 degrees of freedom manipulator and the Turtlebot3 Burger mobile robot.

An effective machine vision system has been developed to support the robotic tasks described above by providing the capabilities for object detection, localisation and fibre orientation detection and deals with uncertainties such as size and shape of fibre plies. When compared to the estimation achieved using wheel odometry, the proposed machine vision system reduced the localisation error by 93% and 80% in simulation-based and physical experiments relatively. When compared to the manual system, the proposed machine vision system shows slight difference in localisation and fibre orientation detection accuracy.

Future work will focus on validating the proposed system on industrial standard platforms and improving the system, e.g. integrating a vacuum gripper, quantifying system efficiency, extending the work to multiple plies and developing a method for draping correction.

In conclusion, by exploiting the availability of wheel odometry and integrating this with machine vision algorithms within the proposed Co-MRMS, it is possible to implement a flexible system that provides autonomous material transportation and sufficiently accurate material handling capabilities that extend beyond what is currently adopted in the industry.