Abstract
Warehouse management systems (WMS) track warehousing and picking operations, generating a huge volumes of data quantified in millions to billions of records. Logistic operators incur significant costs to maintain these IT systems, without actively mining the collected data to monitor their business processes, smooth the warehousing flows, and support the strategic decisions. This study explores the impact of tracing data beyond the simple traceability purpose. We aim at supporting the strategic design of a warehousing system by training classifiers that can predict the storage technology (ST), the material handling system (MHS), the storage allocation strategy (SAS), and the picking policy (PP) of a storage system. We introduce the definition of a learning table, whose attributes are benchmarking metrics applicable to any storage system. Then, we investigate how the availability of data in the warehouse management system (i.e. varying the number of attributes of the learning table) affects the accuracy of the predictions. To validate the approach, we illustrate a generalisable case study which collects data from sixteen different real companies belonging to different industrial sectors (automotive, manufacturing, food and beverage, cosmetics and publishing) and different players (distribution centres and third-party logistic providers). The benchmarking metrics are applied and used to generate learning tables with varying number of attributes. A bunch of classifiers is used to identify the crucial input data attributes in the prediction of ST, MHS, SAS, and PP. The managerial relevance of the data-driven methodology for warehouse design is showcased for 3PL providers experiencing a fast rotation of the SKUs stored in their storage systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Warehouse system design pertains the strategic decisions like choosing the storage and handling equipment/technology, the storage layout and space allocation, and the picking policies to adopt [1, 2]. The performance of a storage system is generally measured using key performance indicators (KPIs) regarding the putaway (inbound) or picking (outbound) activities [3]. In the majority of storage systems, the design of the outbound processes deeply affects global performance [4, 5].
The selection of the storage systems and material handling systems is generally linked to the characteristics of the stock-keeping units (SKUs) and the processes connected to the SKUs [6, 7]. Benchmarking can be used to compare the measures of performance of a warehouse with a target efficiency [8, 9]. This selection is generally critical for 3PL operators acquiring the goods of a new client within their existing warehouse. 3PL operators are hardly able to identify the most adequate warehouse configuration to serve the new client efficiently without transforming their existing organisation [10].
This paper approaches the design of a storage system based on the benchmarking of existing warehouses. The measurement of the performance of known warehouses provides the training set to train machine learning algorithms [11,12,13] intended for predicting:
-
1.
an adequate storage system technology (ST), i.e. the suitable system to store the goods, varying the level of automation and the accessibility of the racks (e.g. automated storage & retrieval system AS/RS, block stacking, cantilever racks, miniload, pallet rack, shelves);
-
2.
an adequate material handling system (MHS), i.e. the set of resources to perform material handling (e.g. cart, forklift, operator, order picker);
-
3.
an adequate storage allocation strategy (SAS), i.e. evaluating the duplication of the storage locations of a single SKU to expedite the picking operations (i.e. reserve & forward policy), or simple storage without duplication (i.e. reserve policy);
-
4.
an adequate picking policy (PP), i.e. how picking missions are organised (e.g. single-order or multi-order).
This study explores the following unmet research questions (RQ1 and RQ2) by using a novel data-driven methodology based on descriptive and predictive analytics:
RQ1: how can a data-driven methodology be developed to design a storage system based on existing benchmarks?
RQ2: how can a data-driven methodology support 3PL providers in the configuration and management of a storage system?
The remainder of this paper is organised as follows. Section 2 reviews the relevant literature in the field of ST, MHS, SAS, and PP selection. Section 3 introduces the proposed methodology to classify a storage system and to predict adequate ST, MHS, SAS, and PP, given a set of SKUs. Section 4 applies the methodology to a vast number of warehouses by describing the storage systems, benchmarking their performances, training machine learning algorithms targeting ST, MHS, SAS, and PP, and interpreting the results. Section 5 discusses the results and the managerial implications of this study. Section 6 concludes the paper.
2 Literature review
Scientific contributions in the field of warehousing science have deeply explored many aspects of the warehousing processes, entities, actors and decisions. In this manuscript, we are interested in analysing how these methods evolve in the last three decades and explore machine learning algorithms as the natural enabler of this evolution.
We need to introduce a comprehensive scientific framework that classifies the methodologies used by humans to generate knowledge. According to [14], there are four different paradigms to generate knowledge:
-
1.
Experimental science (pre-renaissance period), empiricism and the description of natural phenomena have a key role in the creation of new knowledge (e.g. Newton’s apple);
-
2.
Theoretical science (pre-computers period), mathematical modelling and generalisation of the theory allows to generate new knowledge (e.g. the Theory of Relativity);
-
3.
Computational science (pre-Big Data), the simulation of complex or chaotic phenomena leads to the creation of new knowledge (e.g. the Finite Elements method);
-
4.
Exploratory science (nowadays), the research of patterns in the available data generates new knowledge (e.g. data mining).
We review the literature, with particular reference to the selection of ST, MHS, SAS and PP and investigating the evolution of these four paradigms in the field of warehouse design.
2.1 Experimental paradigm
Interviews are methods used to collect the knowledge of experts and to analyse it statistically. This method has been used both to benchmark the performance of different STs [15], and to evaluate the improvement of PPs by using different traceability technologies [16].
Data envelopment analysis (DEA) is a method to measure the efficiency of decision-making units, i.e. the effect of multiple decisions (e.g. ST, MHS, SAS or PP) on multiple outputs (e.g. the level of service or the handling cost) [17]. DEA has been used to select ST and PP [18, 19].
2.2 Theoretical paradigm
Frameworks provide the theoretical reference to select design alternatives. Frameworks are provided to select an MHS [20], while [21] identifies a procedure for SAS design. The design and comparison of different STs and PPs have been performed using theoretical frameworks or kinematic models defined in the continuous domain [22,23,24,25,26].
2.3 Computational paradigm
Knowledge-based systems are IT systems fed with a knowledge base on a physical system, used to solve a complex problem. Knowledge-based systems describe the pattern for selecting the MHS [27,28,29]. Similar methodologies based on optimisation provides solutions to SAS design [30,31,32,33]. PP design has been performed by using a knowledge-based system, as well, to improve the picking times [34, 35].
Expert systems are algorithms programmed using symbolic reasoning that mimics the process of human experts and produces decisions associated with an explanation of the decision process [36]. In the field of warehousing, expert systems have been used to select ST by interacting with the user to evaluate the effect of different decisions on the expected performance of the ST [37]. Similar systems allow selecting the MHS by evaluating the impact of different vehicles on the warehouse layout [38,39,40]. Integrations of expert systems with interfaces and decision-making frameworks improve the effectiveness of these decisions [41, 42].
Discrete event simulation (DES) is widely used to support the design and assess the behaviour of complex processes by considering the discrete evolution in time of a process whose parameters are probabilistically defined [43,44,45]. DES has been used to select STs and MHSs by virtualising their behaviour [46, 47].
2.4 Exploratory paradigm
Benchmarking is a method largely used in the field of engineering. Benchmarks provide a quantitative reference of how a system should perform [48]. In general benchmarking allows checking the performance of any aspect of a storage system [49]. A crucial aspect is the definition of the benchmarking metrics used for comparison in the benchmarking procedure [50]. Benchmarking has been used to identify the performance of a process and identify an adequate PP [51, 52] or an adequate MHS [53].
Data-driven algorithms are based on the extraction of knowledge from datasets [54]. In warehousing systems, these algorithms are used to extract similarities between SKUs and solve SAS design using a correlation approach, i.e. locating an SKU close to other SKUs with a high correlation coefficient [55]. Similar approaches can be used to infer the properties of SKUs based on hidden data patterns [56]. Data-driven predictive models are used to forecast the picking workload, and to organise the warehouse zones coherently [57, 58]. The analysis of variance based on picking data is used to design the PP of a storage system [59].
Table 1 classifies the literature contributions identifying the methodology used, the scientific paradigm, and the focus on the design entities (ST, MHS, SAS, PP). Table 1 identifies a direction that goes towards exploratory science over the time (and except for the interviews methodology, that is recently used by the referenced studies to investigate specific managerial qualitative variables). This study aims at moving towards this direction. We built upon the existing KPIs and benchmarking metrics to propose an original data-driven predictive approach of the design variables of a storage system (i.e. ST, MHS, SAS and PP). To the knowledge of the authors, such an approach is novel and missing in the existing literature body.
In this paper, we follow the literature trend identified above, moving a step forward in benchmarking, and data-driven approaches. We aim at providing general benchmarking metrics that can be used as input datasets for the data-driven design of ST, MHS, SAS, and PP. Our methodology focuses on the benchmarking metrics and the definition of an original workflow to use the benchmarking metrics to make predictions of suitable and feasible warehouse configurations.
3 Methodology
The methodology of this study is composed of two steps. The first step applies benchmarking, to characterise the behaviour of a storage system analysing it from four different perspectives (i.e. SKU profiling, Inventory profiling, Workload profiling and Layout profiling). Benchmarking metrics are defined based on well-known KPIs from the warehousing science literature, and original novel indicators introduced in this paper. Benchmarking metrics aim at evaluating the performance of any storage system. Section 3.1 illustrates benchmarking metrics used in the study to compare different storage systems. The second step (see Section 3.2) introduces machine learning models and evaluation metrics to predict the value of ST, MHS, SAS and PP. The benchmarking metrics identified at the previous stage are used to define the learning tables. Two scenarios are considered; a learning table X1 where all needed data are available from the warehouse management system, and a learning table X2 where only an incomplete subset of data is available. Learning tables are used to feed classification models that fit the data while optimising the precision metric. The results are compared between the two scenarios by evaluating the precision of the fitted models in the prediction of ST, MHS, SAS and PP.
Figure 1 summarises the described novel methodology with a block diagram, illustrating the relevant inputs, data flows and outputs.
3.1 Storage system benchmarking
The definition of benchmarks involves the design of metrics and thresholds to set a target performance of an industrial entity (e.g. the number of lines an operator should process within his/her working shift). We introduce a warehouse-specific dashboard whose metrics link to these target performances. These metrics are mostly based on the literature and warehousing science [60, 61], and are designed to efficiently compare the behaviour of different storage systems (e.g. belonging to different industrial sectors or handling different SKUs). We organise these metrics into four macroareas:
-
1.
SKU profiling;
-
2.
inventory profiling;
-
3.
workload profiling;
-
4.
layout profiling.
Table 2 introduces, the parameters and the notation, used to define all the benchmarking metrics.
The benchmarking metrics belonging to SKU profiling aims at classifying the behaviour of each single SKU. This set of metrics includes largely studied indicators in the field of warehousing science: storage assignment coefficients (1) (i.e. Popularity, Turn, Cube-per-order index, Order completion index) [62]; storage allocation coefficients (2) (equal space (EQS), equal time (EQT) and optimal (OPT) coefficients) [60]; coefficients for spare parts classification (3), ADI, and CV2, used to classify the demand patterns of the SKUs [63]. Table 3 summarises all the aforementioned benchmarking metrics.
Inventory profiling aims at describing the behaviour of the saturation of the space of a storage system. Table 4 illustrates the adopted benchmarking metrics of this macroarea. The space saturation should be expressed using a volume unit of measure (e.g. dm3 or m3), or the number of unit loads when the volume is unknown. The definition of the inventory function \(I_{i}\left (t\right )\) of the storage system requires recording the volume vi for each single SKU i. When the volumes of the SKUs are not available, we estimate the trend of the inventory function by using a normalised function \({\hat {I}}_{i}\left (t\right )\), based on the number of parts involved in each movement. The frequency analysis of \(I_{i}\left (t\right )\), or \({\hat {I}}_{i}\left (t\right )\) provides the probability function \(f_{I_{i}}(x)\) (or \(f_{{\hat {I}}_{i}}(x)\)) based on all the observations of the inventory function (e.g. one observation per day). The cumulative function of \(f_{I_{S}}(x)\) (or \(f_{{\hat {I}}_{S}}(x))\) is used to identify the risk of stockout associated with a specific amount of space devoted to the SKUs of a subset S. The inventory covering time distribution identifies, for each SKU, the covering time, i.e. the time before the inventory is consumed by the market demand (i.e. the average time for the consumption of an incoming lot of an SKU).
Workload profiling aims at identifying where and how the workload is distributed. The workload of a storage system can be linked to an entity of the warehouse (e.g. an operator, a handling vehicle or a storage location). The knowledge of the coordinates of the storage locations and the movements associated with them allow calculating the intensity of the workload in terms of the number of lines (i.e. popularity) of the putaway or picking activities. When the volumes vi and weights wi associated with the SKUs are available, it is possible to map an ergonomic workload by representing the cumulative volume or weight associated with the workload of a storage location j. Table 5 illustrates the benchmarking metrics of this macroarea.
Layout profiling aims at identifying how the workload is organised on the plant layout (i.e. how resources are placed within the storage system). Layout profiling allows assessing if there is room for improving the current organisation of the work and space. For this reason, layout profiling involves three graphical KPIs. A graph G(V,A) is defined, with respect to the warehouse layout, considering the connections between aisles and the routing policy within the aisles. All the benchmarking metrics are defined accordingly on the graph G. A traffic graph is a set of weights associated with each arc a ∈ A, depending on the number of times vehicles travel that arc. A popularity bubble graph represents the amount of workload associated with a storage location j, given a storage assignment policy α. By changing the given storage assignment policy (e.g. using an optimal assignment based on a benchmark metric identified in the SKUs profiling) we evaluate an expected behaviour. Similarly, the popularity-distance bubble graph considers the workload associated with each storage location, and its distance from the input-output point [64]. Table 6 illustrates the benchmarking metrics of this macroarea.
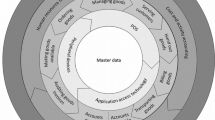
It might occur that the data needed for benchmarking is not tracked by the Warehouse Management System (WMS) of a company. This often happens due to limits of the hardware or the database or lack of interests in precise data collection. Figure 2 introduces an original warehouse framework that matches the set of benchmarking metrics with the input data needed to calculate them. The framework reveals the data attributes (from a generic relational model of a warehouse management system) necessary to calculate the value of the benchmarking metrics. By following the connections of Fig. 2, we understand which input data attribute, generally recorded by a WMS, feeds a specific benchmarking metric. Such connections can help to understand the readiness of a storage system (and its warehouse management system) for the implementation of the data-driven design introduced in the following subsection.
3.2 Data-driven storage system design
The benchmarking metrics permit exploring the performance of a storage system from different perspectives and to compare the behaviour of different warehouses by using the same benchmarking metrics. The definition of common parameters (i.e. the benchmarking metrics) to evaluate the different occurrence of a phenomenon (i.e. the SKUs of a warehouse), recommend implementing machine learning models.
We aim at considering a subset of the benchmarking metrics identified above, referring to the single SKUs, to train classification algorithms able to predict the categorical labels corresponding to the design choices on ST, MHS, SAS, and PP. The input dataset (i.e. the learning table) contains observations of SKUs stored within a storage area with a given label of ST, MHS, SAS, and PP. The benchmarking metrics are used to define a learning table where each row corresponds to a specific SKU and the columns to a benchmarking metric.
The heterogeneity of the input makes quantifying some of the benchmarking metrics challenging. In general, the lack of data results from lacking data collection protocols, poor management of the warehouse management system, recording errors of the operators, and errors or negligence of the operators while using barcode scanners. All these reasons can significantly limit full exploitation of the data-driven approach. We then apply our methodology using two different scenarios, varying the number of attributes (i.e. the columns) of the learning table:
-
1.
scenario 1, where the learning table X1 is composed of all the attributes illustrated in Table 7;
-
2.
scenario 2, where the learning table X2 is composed of a small subset of attributes focused on the outbound (i.e. ADI, CV2, \({C_{i}^{1}}\), \(1/{C_{i}^{1}}\), all the inventory parameters, OCi, \(Pop_{i}^{out}\), and Turni).
This way, we obtain the learning table X1 of scenario 1, with more attributes (i.e. columns), and a smaller number of observations (i.e. rows), and X2 in scenario 2, with fewer attributes, and a higher number of observations. In practice, it is simpler to define the learning table X2, having a smaller number of attributes requiring fewer input data and less pre-processing effort. Consequently, it is possible to investigate if an approach with less data (i.e. Scenario 2) can lead to meaningful results as the one with more data (i.e. Scenario 1). Table 7 identifies the attributes (i.e. the columns) of the learning tables X1, and X2.
The learning tables contain the SKU profiling benchmarking metric, and a number of parameters obtained from the normalised inventory function \({\hat {I}}_{S}\left (t\right )\). These metrics are not affected by the observation time horizon, making it possible to compare and merge information of different storage systems within the same learning table. The productivity and layout profiling metrics are meaningful to benchmark the operations of the storage system; nevertheless, they cannot be referred to the single SKUs (i.e. the rows of the learning table). For this reason, productivity and layout profiling are not considered in the definition of the learning tables. Consequently, X is built on parameters entirely defined by the features of an SKU i.
The learning tables come with four additional attributes, which identify the design target labels, and how the strategic decisions have been addressed in the observed data:
-
1.
ST, e.g. automated storage & retrieval system (AS/RS), automated vertical warehouse, block stacking, cantilever racks, miniload, pallet rack, shelves;
-
2.
MHS, e.g. cart, forklift, operator, order picker.
-
3.
SAS, e.g. reserve & forward, only reserve;
-
4.
PP, e.g. multi-order with batching, multi-order with zoning and sorting, single-order.
We train some different classifiers (linear, non-linear, and ensemble classifier) to select the one that outperforms the others. Some of these classifiers are interpretable, i.e. they produce output coefficients allowing to evaluate the relative importance of the input features. While increasing the complexity of the model, it becomes harder to interpret the choices made during the model training. Table 8 illustrates the selected classification models, the type of method they belong to, and (eventually) the output parameters used to interpret the results. A subset of these models uses randomisation or deep learning techniques that make it difficult to interpret the relative importance of the input features. The mathematical definitions of these models and a discussion of their interpretability can be found in [65]. Table 8 summarises these details. In the case study section, all these models are trained, but the interpretation of the relative importance of the input feature can be performed only on interpretable models.
The choice between the identified classifiers is done based on a performance metric. The classification performance metrics are generally calculated considering the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN). These indicators are tailored on a binary classification problem (i.e. a classification problem with only two target labels: ‘true’ or ‘false’). However, they are easily generalisable by considering the confusion matrix, i.e. a matrix of the observations classified correctly or misclassified, for each target label. There are four main classification metrics:
-
1.
accuracy, measured as \(\frac {TP+TN}{TP+TN+FP+FN}\), indicates the probability that an observation is correctly classified. When using accuracy, it is assumed that the distribution of the labels in the learning table is not skewed and that the misclassification of false positives (FP) and false negatives (FN) have a similar cost;
-
2.
precision, measured as \(\frac {TP}{TP+FP}\), indicates the probability that an observation labelled as “positive” was truly “positive” in the reality (ignoring all the observations labelled as “negative”). When using precision, it is assumed that the cost of a false positive (FP) is higher than the cost of a false negative (FN);
-
3.
recall, measured as \(\frac {TP}{TP+FN}\), indicates the probability that an observation, that is “positive” in the reality, is correctly labelled by the algorithm as “positive”. When using recall, it is assumed that the cost of a false negative (FN) is higher than the cost of a false positive (FP);
-
4.
F1, measured as \(\frac {2(recall\times p r e c i s i o n)}{(recall+precision)}\), considers both the perspectives of precision and recall. While using recall, it is assumed that the distribution of the labels in the learning table is skewed and that the misclassification of false positives (FP) and false negatives (FN) have a similar cost.
In this study, we decided to focus on the precision metric (2.) because it preserves the feasibility of the output more than all the other metrics. Precision focuses only on the “positive” responses of the classification algorithm, assuming the cost of a false positive (FP) being high, compared to the other misclassification costs. The feasibility of the design configuration proposed by the algorithm is mandatory. For example, storing a full-pallet SKU into a miniload is not acceptable.
Since this methodology is data-driven, we test a large amount of real data belonging to different warehouses. The following section implements the benchmarking methods and the prediction procedure to evaluate the impact of the methodology on a real environment, with real data collected on-field.
4 Case study
4.1 Instances description
In this section, the benchmarking and data-driven design methodologies are applied considering 16 warehouses with real operational data provided by 16 companies (6 from distribution centres and 10 from third-party logistics companies), accounting for almost 15 million database records. These traceability data come from different information systems and are inherently heterogeneous. We aim at proving that our benchmarking metrics are generalisable and applicable to any storage system where the relevant data (i.e. the data fields identified with boxes in grey colour in Fig. 2) are recorded. We are interested in interpreting which data attributes are necessary to fit machine learning models predicting the selection of ST, MHS, SAS, and PP. The implementation of this case study is programmed using Python and the scikit-learn library, and developed in Spyder IDE.
Table 9 maps the 16 datasets involved in this study identifying the type of warehouse, the industrial sector and the number of SKUs stored. Table 9 reports a reference year for each dataset, the number of recorded days, the number of movements recorded and the presence or absence of relevant data attributes as:
-
1.
the inbound data (i.e. putaways);
-
2.
the outbound data (i.e. pickings);
-
3.
the layout data (i.e. the ordinal number of rack, bay and level for each storage location);
-
4.
the layout coordinates (i.e. the (x, y, z) Cartesian coordinates for each storage location);
-
5.
the volume data for each SKU;
-
6.
the picking list data (i.e. a common id for all the movements processed within the same putaway or picking route).
In addition, Table 9 analyses the role of the warehouse in the supply chain it belongs. Warehouses act as a buffer of the supply chain; to identify the responsiveness of the storage system to the supply chain, we calculate the percentage of SKUs for each demand pattern based on the ADI, and CV2 classification in [63]. It comes out that 3PL operators experience, on average, more lumpiness (i.e. unpredictability of both the demand quantity and time interval of their SKUs) than distribution centres do.
Table 9 indicates the number of sub-areas for each of the 16 warehouses considered. A sub-area is a zone of the storage system, equipped with a specific technology, and identified by a combination of ST, MHS, SAS and PP. For the warehouse ids dc_auto_1 and tp_manu_1, there is no number of sub-areas in Table 9, due to the fact that the available data do not map the ST, MHS, SAS and PP of these storage systems. For this reason, the dataset of these two instances are used for benchmarking, but not for storage system design. Table 10 identifies the details for each of the 26 sub-areas of the selected warehouses.
As an example, the warehouse id dc_auto_2 is equipped with four different sub-areas. Each sub-area has a different ST (i.e. AS/RS, automated vertical warehouse, pallet rack and shelves) served by two types of MHS (i.e. operator or forklift), and all areas use a forward/reserve SAS, and a multi-order with zoning and sorting PP.
4.2 Instances benchmarking
The benchmarking metrics identified in Section 3.1 are applied to the 16 datasets of the considered warehouses. Since benchmarks are defined graphically on an aggregated basis, this section discusses the insights from the benchmarking of the 16 warehouses, while the graphical representations are found in the Appendixes at the end of the paper.
Appendix 1 represents the SKU profile of each warehouse, mapping the Pareto chartsFootnote 1 of the Popularity, COI, Turn and OC indexes. When inbound data are not recorded, Popularity and COI indexes are limited to the outbound data. Similarly, the COI is not calculated when the SKU master file does not contain the volume for each SKU. The Popout index has a similar pattern for the automotive distribution centres, having very few items producing the majority of pickings. Different behaviour is found in food, beverage, and biomedical warehouses. In these warehouses, a wider number of SKUs determines the majority of the outbound activities. Specific patterns are determined in the popularity of publishing warehouses. There is a strong influence on the seasonality of the academic year, which leads to a high turn index for some SKUs, and complete immobility for others. The OC index is connected to the length of the orders in each warehouse. The automotive, beverage, and manufacturing warehouses have many SKUs ordered alone or ordered frequently. The cardinality of the orders (i.e. the number of lines of an order) tends to be more uniform in food and biomedical warehouses. Turn indexes are different, depending on the operations. High Turn indexes are encountered in distribution centres (that usually have cross-docking areas where SKUs transit fast). A different pattern is found in the 3PL warehouses, depending on the tasks that the operators are required to perform.
Appendix 2 identifies the inventory profile of the 16 warehouses. The inventory profile cannot be identified when the input data lack inbound records. Besides, when the volumes are not recorded, only the normalised inventory function \({\hat {I}}_{S}\left (t\right )\) is calculated. The \({\hat {I}}_{S}\left (t\right )\) can be useful to identify the warehouse saturation trend when the volumes recorded in the SKU master file are not reliable. This is the case of a 3PL provider receiving from its clients bad quality data on the volume of the SKUs (e.g. tp_manu_2).
The inventory profile is highly market-oriented and difficult to generalise. For example, distribution centres have the role to absorb the variability of the market demand by varying their inventory levels. Differently, 3PL providers frequently encounter inventory variability due to changes in the contracts with their customers. The profiles of the distribution centres identify positive or negative trends, while 3PL providers experience a rapid growth (when the client is acquired) followed by an almost stationary profile with stable partners (e.g. tp_manu_2, tp_manu_3, and tp_bio_2), or a rapid decrease with strong seasonality (e.g. tp_pub_2) or e-commerce services (tp_cos).
Appendix 3 identifies the workload profile of the analysed warehouses. The plots represent the workload projected on the plant of the warehouse system or in the space, by considering the coordinates of the storage locations. The graphs are incomplete when the coordinates of the storage locations are omitted. The graphs identify how the workload is distributed in the different areas of the storage system. In distribution centres, a few areas host the majority of the workload, and these areas are mostly placed in the lowest levels, nearby the input/output points. On the contrary, the 3PL providers have fewer locations and a randomly distributed workload, reaching higher levels when picking activities are performed by order pickers.
Appendix 4 illustrates the benchmarking metrics of the layout of the warehouses. The warehouses without layout data are omitted. The popularity bubble graphs and the popularity-distance bubble graphs compare the actual storage assignment policy (asis) with an assignment policy identified by the ranking on the SKUs based on their popularity (tobe). The tobe assignment policy ranks the locations based on their distance from the input and output points. The smaller the distance of a storage location, the higher the popularity of an SKU to be placed there. The traffic graphs identify intense traffic on the front and back corridors when warehouses have picking missions with few stops (i.e. a small number of lines) and the majority of the distance is travelled horizontally to move from the input or output points to the aisles. Differently, the vertical distances result from handling and picking operations performed at the high-levels of the storage system (e.g. dc_furn and tp_manu_3). The popularity bubble graphs identify how the workload should be transferred by passing from an asis to a tobe assignment, given by the popularity ranking.
We see that the workload tends to be organised vertically when the input is placed on the opposite side of the plant, compared to the output; otherwise the workload is concentrated around the same side of the plant. The popularity-distance bubble graphs confirm the change from a distributed workload to an optimised workload where the SKUs with higher popularity are placed in a location with a lower distance.
4.3 Model training for the storage system design
The datasets of the industrial warehouses are used to build the learning tables X1, and X2 in the two scenarios identified by the proposed methodology. Table 11 identifies the number of observations (i.e. the rows) for both the learning tables and the number of observations associated with each label.
Table 11 reports an important piece of information. The input datasets in both the scenarios are skewed, i.e. the labels are not uniformly distributed among the observations, but some labels have more observations than others. This fact may lead to an imbalance of the model and overfitting. For this reason, we resample the dataset before training the machine learning model to work with a similar number of observations for each of the target label. The predictions of each design entity (i.e. ST, MHS, SAS, and PP) are made on a learning table having a number ρ of observations randomly extracted from the learning table X1 or X2, where ρ equals the minimum number of observations having the same label (e.g. 183 in ST predictions within scenario 1, or 6,359 in MHS predictions within scenario 1).
The obtained dataset is split into a training and testing set using 66.7% of the observations to train the models (identified in Table 8), and the remaining 33.3% to test the performance of the trained classification models. Hyperparameter tuning is done using a grid search with 3-fold cross-validation for each model. When predicting ST, MHS and PP, there are more than two classes to predict. For this reason, the problem is multi-class, and the global precision of the algorithm is calculated as the average of the precision of each class. While predicting SAS, there are only two classes in the considered instances (binary classification), then the precision is calculated using the formula in Section 3.2. Table 12 reports the precision of the predictions measured on the test set, for each class of models, identified by the grid search.
Ensemble and non-linear models outperform, on average the linear classifiers. The learning table of scenario 2 (having more observations, but fewer attributes) leads to a higher precision score in 27 out of 44 (i.e. the 59%) of the models identified by our empirical tests. In the remaining, the precision score is comparable to the one obtained in scenario 1. This result indicates that a limited amount of data (e.g. without inbound information and the volume information) is enough to support the design of a storage system using a data-driven approach. The models predicting the PP and the SAS have better performances than the ones predicting ST and MHS. This is due to the fact that an SKU characterised by the same parameters can be stored or handled differently, depending on the practices of a company.
It is hard to understand which input feature is considered more or less important when models are not interpretable (e.g. ensemble and deep learning models, see Table 8). For this reason, additional details on the relevance of the input data attributes come from the interpretation of the results and parameters of the interpretable models. In almost all design entities and scenarios, the best performing interpretable model is the decision tree. A decision tree mimics the engineering design approach by defining thresholds on the parameters, and if-then-else statements based on these thresholds.
When predicting the value of the ST, the decision tree in scenario 1 attributes higher importance to the volume vi, the weight wi, and the standard deviation of the inventory function \(\sigma _{\hat {I}_{S}\left (t\right )}\). When working with the data of scenario 2, the decision tree mostly considers \({C_{i}^{1}}\), \(1/{C_{i}^{1}}\), and \(Pop_{i}^{out}\). This behaviour is similar to the classical engineering approach where volumes and weights of the SKUs are the first information to select feasible storage racks. When these data are not available, the ST is predicted based on its dynamic behaviour, i.e. its productivity (measured using the \(Pop_{i}^{out}\), or the \({C_{i}^{1}}\))
To predict the MHS, the decision tree focuses almost uniquely on the volume vi in scenario 1; while it considers \({C_{i}^{1}},1/{C_{i}^{1}}\), the average inventory \(\overline {\hat {I}_{S} \bar {\left (t\right )}}\), and the ADIi in scenario 2. This behaviour is similar to the prediction of the ST since the volume of a SKU is a discriminant to select a feasible MHS association (e.g. a forklift cannot enter the aisle of a manual shelf hosting small spare parts). When volumes are not available, the inventory profile and the ADIi are mainly used for prediction. This fact suggests that a correlation may exist between the volume of an SKU, and its inventory profile.
Regarding the SAS, the decision tree identifies as the most important features V oli, and \(1/{C_{i}^{1}}\) in scenario 1. In scenario 2, where the volume is not considered by the learning table, \(1/{C_{i}^{1}}\) remains the most relevant feature, slightly assisted by \(Pop_{i}^{out}\). Similarly to the engineering methods for storage allocation, the volume and the dynamics of the demand of an SKU (estimated as \(1/{C_{i}^{1}}\)) are the main drivers to target the SAS.
The decision tree identifies \(Pop_{i}^{in}\) as the most important feature to predict the PP in scenario 1. When dealing with a limited amount of data, the decision tree gives more importance to \({C_{i}^{1}}\), the average inventory \(\overline {\hat {I}_{S} \bar {\left (t\right )}}\), and the \(Pop_{i}^{out}\). Differently from the previous predictions, the selection of the PP is entirely based on the dynamics of the market demand of an SKU focusing on a selection of the picking organisation based on the value of the popularity.
These results suggest that the physical details of the SKUs (i.e. volume) and the dynamics of the demand (i.e. the popularity and \(1/{C_{i}^{1}}\)) are key information to implement a data-driven selection of ST, MHS, SAS and PP.
5 Discussion and managerial implications
The case study results reveal an emerging role of the data-driven approach in the field of warehouse design. We train models to lead complex decision-making through empirical observations. Similarities with the model-driven engineering methods have been found, when interpreting the predictions of the decision trees trained with the data of 16 warehouses.
By considering these pieces of evidence, we are answering research question RQ1, identifying the warehouse benchmarking metrics as the columns of a learning table, able to make predictions of the warehouse configuration to assign to each SKU.
We remark an important limitation of this approach. The predictive models do not point to the optimal decision since they are not trained with optimal assignments. The labels attached to the learning tables indicate the strategic design decisions. These decisions are based on previous observation, i.e. they identify the industrial practices. Industrial practice can be far from optimality but generally requires a high degree of feasibility and flexibility.
We use these models not to predict the optimal storage systems given some estimated parameters (i.e. the traditional model-driven engineering approach), but instead to provide a feasible solution to complex strategic decisions given the current circumstances.
This approach has profound managerial implications for 3PL providers. Generally, 3PL providers experience a rotation of the SKUs due to the expiration of the contracts with their clients. However, in practice, their storage technology cannot easily change together with their client portfolio due to significant investments in technologies that are hard to pay back in the short term. They could benefit from a data-driven approach when they are able to get the data of incoming customers [66]. 3PL providers continuously need forecasts to deal with the unpredictability of their customers’ demand [67]. Literature contributions evidence the impact of prediction models to deal with the operation and allocation of the orders of a 3PL provider [68, 69].
We address research question RQ2 by considering the relevance of our methodology to a set of warehouses of the same 3PL company, in case a 3PL company wants to deploy the models in its real environment. This analysis does not require interpreting the relevance of the features’ dataset. Therefore, we only focus on the precision value to select the most performing model, and we use a neural network to boost the prediction performances. While the case study explores the relevance of the data-driven approach on a multitude of datasets from different players and from a research perspective, this application showcases the managerial implication for a 3PL provider.
A learning table \(X^{2}_{3PL}\) is defined and limited to a number of the datasets involved in the case study regarding the same 3PL provider (i.e. tp_bio_1, tp_bio_2, tp_cos, tp_manu_1, tp_manu_2, tp_pub_1, tp_pub_2). The learning table uses the features of scenario 2, having fewer attributes. Disregarding the interpretability of the model, we are interested in implementing a predictive tool able to suggest to the 3PL a ST, MHS, SAS and PP for an incoming SKU (e.g. provided by a new customer of the 3PL provider). This selection is done by considering the ST, MHS, SAS and PP observed in the learning table, i.e. the storage technologies currently adopted by the 3PL provider. We train the models identified in Table 8 and a deep neural network (NN) whose structure is identified differently for each model in Fig. 3.
The performance of the predictions is evaluated by using the precision metric. Multi-class classification problems are solved as introduced in Section 4.3. The NN predictions significantly outperform the ones of other models while predicting the SS. When dealing with other entities, the predictions of the other models are similar or better than the ones of the NN. The 3PL provider could then provide tailored services to customers even in the presence of a variable inventory mix. Furthermore, the results aid identifying affordable customers to serve, estimating a service level and an operational organisation just looking at the customer’s historical data, before the physical transfer of the SKUs.
6 Conclusions and further research
This paper deals with the design of a storage system from a data-driven perspective. Four design areas are identified: storage system technology (ST), material handling system (MHS), storage allocation strategy (SAS), and picking policy (PP). The literature has been reviewed identifying a lack of data-driven applications in the field of warehouse design.
A novel methodology is proposed and illustrates how to implement machine learning models to predict ST, MHS, SAS and PP, based on a set of benchmarking metrics of the storage systems.
A case study involving a large number of warehouse datasets is used to train the machine learning models predicting ST, MHS, SAS, and PP. The decision tree classifier is used to interpret the relative importance of the input variables. The results of the case study evidence that the features of the SKUs (i.e. the volume and weight), and the dynamics of the market demand of the SKUs (i.e. popularity, and the seasonality) are crucial pieces of information to make accurate predictions.
The role of the predictive warehouse design is discussed for the case of 3PL providers who can benefit from predictions to select ST, MHS, SAS and PP for the organisation of the SKUs of a new client, given the existent infrastructure. The empirical tests show that, when the crucial data are available, machine learning models accurately predict the outcome of strategic decisions, by assigning SKUs to a proper ST, MHS, SAS, and PP. This discovery can help to improve the resilience and the organisation of 3PL providers who need to assign incoming SKUs (e.g. of a new customer) to their existing storage systems.
Further researches should focus on the development of learning tables to support the predictive design of warehousing systems. Learning table using different attributes from the warehouse management system should be tested (e.g. with a focus on the storage locations, or the orders, rather than the SKUs considered in this paper). In addition, other design aspects (e.g. the lane depth of a rack) can be predicted. Finally, the predictive design could be adapted to the strategic design decisions of other supply chain systems (e.g. the design of the layout of a production system or the selection of the fleet vehicles of a distribution network).
Notes
The Pareto Chart (or Pareto curve) represents the cumulative curve of the values in descending order (from the highest value to the lowest value) of a given series of values.
References
Rouwenhorst B, Reuter B, Stockrahm V, van Houtum G, Mantel RJ, Zijm WHM, Van Houtum GJ, Mantel RJ, Zijm WHM, van Houtum G, Mantel RJ, Zijm WHM, Van Houtum GJ, Mantel RJ, Zijm WHM (2000) Warehouse design and control: framework and literature review. Eur J Oper Res 122(3):515–533
Dallari F, Marchet G, Melacini M (2009) Design of order picking system. Int J Adv Manuf Tech 42(1-2):1–12. Cost parameters;Critical analysis;Depth surveys;Design Methodology;Distribution centres;Order picking;Order-picking systems;Warehousing;
Staudt FH, Alpan G, Di Mascolo M, Rodriguez CM (2015) Warehouse performance measurement: a literature review. Int J Prod Res 53(18):5524–5544
Chan FT, Chan HK (2011) Improving the productivity of order picking of a manual-pick and multi-level rack distribution warehouse through the implementation of class-based storage. Expert Syst Appl 38 (3):2686–2700
De Koster R, Le-duc T, Roodbergen KJ (2007) Design and control of warehouse order picking : a literature review. Eur J Oper Res 2006(January):481–501
Gu J, Goetschalckx M, McGinnis LF (2007) Research on warehouse operation: A comprehensive review. Eur J Oper Res 177(1):1–21
Gu J, Goetschalckx M, McGinnis LF (2010) Research on warehouse design and performance evaluation: a comprehensive review, vol 203
Chen P-S, Huang C-Y, Yu C-C, Hung C-C (2017) The examination of key performance indicators of warehouse operation systems based on detailed case studies. J Inf Optim Sci 38(2):367–389
Johnson A, McGinnis L (2011) Performance measurement in the warehousing industry. IIE Transactions (Institute of Industrial Engineers) 43(3):220–230
Baruffaldi G, Accorsi R, Manzini R, Ferrari E (2020) Warehousing process performance improvement: a tailored framework for 3PL, Business Process Management Journal
Kobbacy KA, Vadera S (2011) A survey of AI in operations management from 2005 to 2009. J Manuf Technol Manag 22(6):706–733
Alexopoulos K, Nikolakis N, Chryssolouris G (2020) Digital twin-driven supervised machine learning for the development of artificial intelligence applications in manufacturing. Int J Comput Integr Manuf 33 (5):429–439
Hopkins J, Hawking P (2018) Big Data Analytics and IoT in logistics: a case study. Int J Logist Manag 29(2):575–591
Hey T, Tansley S, Tolle K (2009) The Fourth Paradigm. Data-Intensive Scientific Discovery. Microsoft Research
Makaci M, Reaidy P, Evrard-Samuel K, Botta-Genoulaz V, Monteiro T (2017) Pooled warehouse management: an empirical study. Comput Ind Eng 112:526–536
Hassan M, Ali M, Aktas E, Alkayid K (2015) Factors affecting selection decision of auto-identification technology in warehouse management: an international Delphi study. Prod Plan Control 26(12):1025–1049
Dimitrov S, Sutton W (2010) Promoting symmetric weight selection in data envelopment analysis: a penalty function approach. Eur J Oper Res 200(1):281–288
Johnson A, Chen W-C, McGinnis L (2012) Large-Scale Internet Benchmarking. Technology and Application in Warehousing Operations, SSRN Electronic Journal, no. November
Zimmerman RJ, Bowlin WF, Maurer RA (2001) Benchmarking the Efficiency of Government Warehouse Operations: a Data Envelopment Analysis Approach. J Cost Anal Manag 3(1):19–40
Hassan MM (2010) A framework for selection of material handling equipment in manufacturing and logistics facilities. J Manuf Technol Manag 21(2):246–268
Accorsi R, Manzini R, Bortolini M (2012) A hierarchical procedure for storage allocation and assignment within an order-picking system. A case study. Int J Logist Res Appl 15(6):351–364
Hao J, Shi H, Shi V, Yang C (2020) Adoption of automatic warehousing systems in logistics firms: a technology-organization-environment framework. Sustainability (Switzerland) 12:12
Vidal Vieira JG, Ramos Toso M, da Silva JEAR, Cabral Ribeiro PC (2017) An AHP-based framework for logistics operations in distribution centres. Int J Prod Econ 187:246–259
Battini D, Calzavara M, Persona A, Sgarbossa F (2015) Order picking system design: the storage assignment and travel distance estimation (SA&TDE) joint method. Int J Prod Res 53(4):1077–1093
Bortolini M, Faccio M, Gamberi M, Manzini R (2015) Diagonal cross-aisles in unit load warehouses to increase handling performance. Int J Prod Econ 170:838–849
Lin CH, Lu IY (1999) Procedure of determining the order picking strategies in distribution center. Int J Prod Econ 60:301–307
Fonseca DJ, Uppal G, Greene TJ (2004) A knowledge-based system for conveyor equipment selection. Expert Syst Appl 26(4):615–623
Welgama PS, Gibson PR (1995) A hybrid knowledge based/optimization system for automated selection of materials handling system. Comput Ind Eng 28(2):205–217
Yaman R (2001) A knowledge-based approach for selection of material handling equipment and material handling system pre-design. Turkish Journal of Engineering and Environmental Sciences 25(4):267–278
Bottani E, Cecconi M, Vignali G, Montanari R (2012) Optimisation of storage allocation in order picking operations through a genetic algorithm. Int J Logist Res Appl 15(2):127–146
Manzini R, Accorsi R, Gamberi M, Penazzi S (2015) Modeling class-based storage assignment over life cycle picking patterns. Int J Prod Econ 170:790–800
Taylor P, Lee MK (2007) A storage assignment policy in a man-on-board automated storage / retrieval system. August 2014, pp 37–41
Vickson RG, Lu X (1998) Optimal product and server locations in one-dimensional storage racks. Eur J Oper Res 105(1):18–28
Brynzèr H, Johansson MI (1996) Storage location assignment: using the product structure to reduce order picking times. Int J Prod Econ 46-47:595–603
Valle CA, Beasley JE, da Cunha AS (2017) Optimally solving the joint order batching and picker routing problem. Eur J Oper Res 262(3):817–834
Matsatsinis NF, Doumpos M, Zopounidis C (1997) Knowledge acquisition and representation for expert systems in the field of financial analysis. Expert Syst Appl 12(2):247–262
Park YB (1996) ICMESE: Intelligent Consultant system for material handling equipment selection and evaluation. J Manuf Syst 15(5):325–333
Bookbinder JH (1992) Material-handling equipment selection via an expert system. J Bus Logist 1:1–18
Egbelu PJ, Chu HK, Wu CT (1995) ADVISOR: A computer-aided material handling equipment selection system. Int J Prod Res 33(12):3311–3329
Hassan M (2014) An evaluation of input and output of expert systems for selection of material handling equipment. J Manuf Technol Manag 25(7):1049–1067
Chan FT, Ip RW, Lau H (2001) Integration of expert system with analytic hierarchy process for the design of material handling equipment selection system. J Mater Process Technol 116(2-3): 137–145
Cho C, Egbelu PJ (2005) Design of a web-based integrated material handling system for manufacturing applications. Int J Prod Res 43(2):375–403
Saderova J, Rosova A, Behunova A, Behun M, Sofranko M, Khouri S (2021) Case study: the simulation modelling of selected activity in a warehouse operation. Wireless Networks, vol. 6
Altarazi SA, Ammouri MM (2018) Concurrent manual-order-picking warehouse design: a simulation-based design of experiments approach. Int J Prod Res 56(23):7103–7121
Sadeghi N, Fayek AR, Seresht NG (2016) A fuzzy discrete event simulation framework for construction applications: Improving the simulation time advancement. J Constr Eng Manag 142(12):1–12
Dobos P, Tamás P., Illés B. (2016) Decision method for optimal selection of warehouse material handling strategies by production companies. IOP Conference Series: Materials Science and Engineering, vol. 1:161
Kato T, Kamoshida R (2020) Multi-agent simulation environment for logistics warehouse design based on self-contained agents. Applied Sciences (Switzerland) 10(21):1–20
Zhu J (2009) Quantitative Models for performance evaluation and benchmarking, Operations Research
Kusrini E, Novendri F, Helia VN (2018) Determining key performance indicators for warehouse performance measurement - A case study in construction materials warehouse. MATEC Web of Conferences 154:6–9
Tufano A, Accorsi R, Gallo A, Manzini R (2018) Time and space efficiency in storage systems : a diagnostic framework,” in XXIII Summer School ”Francesco Turco
Guthrie B, Parikh PJ, Kong N (2017) Evaluating warehouse strategies for two-product class distribution planning. Int J Prod Res 55(21):6470–6484
Kłodawski M, Jacyna M, Lewczuk K, Wasiak M (2017) The Issues of Selection Warehouse Process Strategies. Procedia Engineering 187:451–457
Klabusayová N (2013) Support of logistic processes in modern retail chain warehouse. Applied Mechanics and Materials 309:274–279
Li Y, Carabelli S, Fadda E, Manerba D, Tadei R, Terzo O (2020) Machine learning and optimization for production rescheduling in industry 4.0,” International Journal of Advanced Manufacturing Technology, vol. 110, no. 9-10, pp. 2445 – 2463. Classification models;Flexible job-shop scheduling problem;Hybrid Meta-heuristic;Industrial revolutions;Manufacturing process; Optimization algorithms;Production management;Sequence dependent setups
Pang KW, Chan HL (2017) Data mining-based algorithm for storage location assignment in a randomised warehouse. Int J Prod Res 55(14):4035–4052
Tufano A, Accorsi R, Manzini R, Volpe L (2019) Data-driven models to deal with data scarcity in warehousing system design,” in XXIV Summer School ”Francesco Turco
Moshref-Javadi M, Lehto MR (2016) Material handling improvement in warehouses by parts clustering. Int J Prod Res 54(14):4256–4271
van Gils T, Ramaekers K, Caris A, Cools M (2017) The use of time series forecasting in zone order picking systems to predict order pickers’ workload. Int J Prod Res 55(21):6380–6393
van Gils T, Ramaekers K, Braekers K, Depaire B, Caris A (2017) Increasing order picking efficiency by integrating storage, batching, zone picking, and routing policy decisions, International Journal of Production Economics
Bartholdi JJ, Hackman ST (2017) Warehouse & Distribution science
Frazelle E (2002) World-Class warehousing and material handling
Accorsi R, Manzini R, Maranesi F (2014) A decision-support system for the design and management of warehousing systems. Comput Ind 65(1):175–186
Syntetos AA, Boylan JE, Croston JD (2005) On the categorization of demand patterns. J Oper Res Soc 56(5):495–503
Manzini R, Accorsi R, Baruffaldi G, Santi D, Tufano A (2018) Performance assessment in order picking systems : a visual double cross-analysis, The International Journal of Advanced Manufacturing Technology
Hastie T, Tibshirani R, Jerome F (2009) The elements of statistical learning. Data Mining, Inference, and Prediction
Tufano A, Accorsi R, Manzini R (2020) Machine learning methods to improve the operations of 3PL logistics. Procedia Manuf 42(2019):62–69
Papana A (2012) Short-Term Time Series Prediction for a Logistics Outsourcing company pp 150–160
Gurbuz F, Eski I, Denizhan B, Dagli C (2019) Prediction of damage parameters of a 3PL company via data mining and neural networks. J Intell Manuf 30(3):1437–1449
Ren S, Choi TM, Lee KM, Lin L (2020) Intelligent service capacity allocation for cross-border-E-commerce related third-party-forwarding logistics operations: a deep learning approach, Transportation Research Part E: Logistics and Transportation Review, vol. 134, no. September 2019, p 101834
Funding
Open access funding provided by Alma Mater Studiorum - Università di Bologna within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Figure 4 illustrates the graphical benchmarks of the SKU profile of the 16 storage system instances presented in Section 4. Each box of the figure identifies the cumulative Pareto function of the benchmarking metrics identified on the columns (i.e. inbound and outbound Popularity, inbound and outbound COI, Order closing and Turn Index). As detailed in Section 4, the availability of data is partial for some instances; for this reason, some boxes are blank.
Appendix 2
Figure 5 illustrates the graphical benchmarks of the inventory profile of the 16 storage system instances presented in Section 4. Each box of the figure identifies an inventory metric (i.e. the inventory function, the inventory probability distribution, and the inventory stockout distribution). These metrics are only available when the SKU’s volumes are mapped. Otherwise only the normalised counterpart functions are displayed. Estimating these functions requires both the input (i.e. putaway), and output (i.e. picking) movements need to be recorded by the WMS; As a consequence, only the subset of instances meeting these requirements is presented in Fig. 5.
Appendix 3
Figure 6 illustrates the graphical benchmarks of the workload profile of the 16 storage system instances presented in Section 4. Each box of the figure identifies a workload metric. The workload metrics offer 2-dimensional and 3-dimensional views of the warehouse systems. They reflect the workload based on Popularity, volume, or weight of the putaway or picking operations. The presence of volume or weight is necessary to build the corresponding KPIs; for this reason, some boxes are blank. In addition, we define all these metrics only for the subset of instances where the Cartesian coordinates (x, y, z) of the storage locations are known.
Appendix 4
Figure 7 illustrates the graphical benchmarks of the layout profile of the 16 storage system instances presented in Section 4. Each box of the figure identifies a layout metric. These metrics are available when the layout coordinates (or, at least, the progressive number of racks, bays and levels) are known for each storage location. The graphical KPIs shows the layout graph and the traffic on the edges of the warehouse graph (corresponding to the aisles of the warehouse), and the bubble charts identifying the potential margin that can be obtained with a reassignment of the SKUs to the storage locations [64].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tufano, A., Accorsi, R. & Manzini, R. A machine learning approach for predictive warehouse design. Int J Adv Manuf Technol 119, 2369–2392 (2022). https://doi.org/10.1007/s00170-021-08035-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-08035-w