1 Introduction

The plastic deformation of polycrystalline metal samples is a topic of long-standing interest in materials science [1]. It is of immediate importance in the field of mechanical engineering, where plastic deformation processes are involved in the treatment of a workpiece, leading both to residual stresses and to workpiece distortions [2]. The origin and prediction of such distortions are the topic of scientific research [3,4,5,6,7]. To this date, it is still industrial practice to control distortions by trial-and-error tests or repositioning and reclamping.

While machining processes on the microscale are commonly used in ultra-precision engineering [8], nanometer-sized mechanisms are out of reach for most applications. However, in the fields of photolithography, chemical etching, laser machining, atomic force lithography, or focused ion beam lithography, nanofabrication techniques are already being used [9]. Due to its significant future potential, the theory of nanocutting must be systematically developed [10]. It is therefore of interest to widen the understanding of plastic processes by including processes occurring in nanofabrication. Here, atomistic simulation methods based on molecular dynamics simulation, have proven useful [11, 12]. The behavior of samples under homogeneous strain has been investigated best [13,14,15,16,17,18,19,20]. Also several machining processes have been studied, including nanoindentation [21, 22], scratching [23] and nanocutting [24] of surfaces. Several of the results obtained from these studies allowed extension to larger spatial scales (μm-sized samples) for instance the generation of dislocations [22] or the effect of the tip geometry on the plastic processes [23]. Mono- and polycrystalline materials will behave differently in nanomanufacturing processes. For example for microcutting, Shimada et al. [25] used molecular dynamics simulation to show that a worksurface free of residual distortion can be obtained for monocrystalline copper, but nanometrically distorted layers remain on polycrystalline copper worksurfaces.

On the nanoscale, distortion and the generation of residual stresses are based on the plastic processes occurring in the material under mechanical loading. In many metals, plasticity is dominated by dislocations which are activated during loading [1, 26]. In nanocrystalline material, dislocations and grain-boundary-based processes — in particular grain-boundary displacement and rotation — contribute to the plastic deformation [27,28,29,30]. The combination of dislocation and grain-boundary based processes and how they affect distortion has not been investigated up to now.

In the present paper, we will study the mechanical deformation of an Al bar which is compressed in an inhomogeneous way by vice plates [31] (see Fig. 1a). In addition to the plastic deformation, we investigate the processes occurring in the individual grains (i.e., grain displacement and rotation) and the distortion of the bar.

Fig. 1
figure 1

a Schematic setup of the simulation system. The vice plates compress the Al bar laterally. b Two simulation samples containing 180 and 18 grains with average grains sizes of 10 nm and 22 nm, respectively

Full size image

2 Method

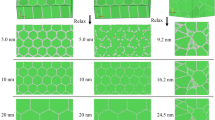
We study an Al block (see Fig. 1a) with sizes of 80 nm × 40 nm × 60 nm in x, y and z directions, consisting of approximately 12 × 106 atoms. The block is subject to periodic boundary conditions in the y direction; the other surfaces are free. The bottom half of the x–z surfaces are held by rigid vice plates. In the course of the simulation, these plates move inward along the x direction with a velocity of 10 m/s for 200 ps, compressing the Al bar from 80 to 78 nm; then the fixtures are held for 200 ps to allow the sample to relax; and finally the vices are released by moving with 10 m/s to their initial positions.

In a previous publication [31], this procedure was applied to a single-crystalline Al block where all surfaces were oriented in {100} directions. In the present work, however, we use polycrystalline Al blocks. In order to understand the effect of grain size, we use two samples (see Fig. 1b): a fine-grained sample consisting of 180 grains with an average size of 10 nm, and a coarse-grained sample with 18 grains of 22 nm size. The small grain size is compatible with the nanoscale dimensions of the sample and is around two orders of magnitude below the grain size encountered in macroscale machining (∼ 1 μm). The samples are generated using Voronoi tesselation [32,33,34]. For the preparation of relaxed samples, first, the samples are heated to 500 K for 50 ps in order to relax the grain boundaries in the samples; then the temperature is kept constant for 50 ps, and finally the temperature is decreased to 300 K for another 50 ps. In a final step, the samples are relaxed for 250 ps at 300 K in an isothermal-isobaric NPT ensemble such that all components of the stress tensor decrease to zero. During the compression and release simulations, the atoms in a stripe of width 1 nm in the middle part of the sample between the vice plates are subjected to a Nose-Hoover thermostat to keep the temperature at 300 K. In addition, the lower part of this stripe with a height of 1 nm has been fixed in order to prevent rigid-body translation and rotation of the entire sample during the release phase.

The vice plates have a thickness of 2 nm and a height of 34 nm. They consist of around 500,000 carbon atoms each, arranged in a rigid diamond-lattice structure.

The Al atoms interact via the Mendelev et al. potential [35] with each other. The Al-carbon interaction is modeled by a purely repulsive potential obtained from a Lennard-Jones potential cut off at its minimum [31].

The simulations are performed with the software LAMMPS [36] and the results are analyzed and visualized using OVITO [37].

3 Results

3.1 Forces

The force on the vices during the pressing, holding and release phases of the simulation are shown in Fig. 2. We show the forces acting on the vice plates on the left- and right-hand side, in order to be able to discuss the asymmetry caused by grain displacements and rotations (see Sections 3.4 and 3.5 below).

Fig. 2
figure 2

Time evolution of the forces acting in x direction on the vices

Full size image

During the pressing phase, initially the force increases in proportion to the distance moved by the plates; however, in the second half of the pressing phase, the forces saturate and even start decreasing. This happens because the yield stress of the material has been reached. The average pressure can be estimated as p = F/A; with the maximum force given by F = 3 μN and the area of the vice plates given by A = 1200 nm2, the pressure is p = 2.5 GPa. This value may be compared to the hardness of single-crystalline Al, which amounts to 6 GPa for the interatomic interaction potential that we employ [38]. The yield stress in nanocrystalline samples has been found to be smaller and is in the range of 1.6 to 3.5 GPa, a value which varies with grain size [15, 39,40,41,42,43]. For the interatomic interaction potential used in the present work, a yield stress of 3.5–4.9 GPa was reported for nanocrystalline samples [44]. These values are considerably above the yield stress of macroscopic polycrystalline Al due to the Hall-Petch effect.

The yield mechanisms in the coarse- and fine-grained samples are different [41, 45], see discussion in Section 3.2 below, and hence the two samples have two different force maxima.

During the holding phase, the force decreases as the material relaxes internally by dislocation- and grain-boundary-based mechanisms (see Section 3.2 below). Stress release is particularly pronounced for the coarse-grained sample, as here dislocations are more active. The dislocation activity is visible in the force evolution by the considerable fluctuations seen that originate from individual dislocation processes occurring in the sample. After around 100–150 ps of holding time, the forces have reached their equilibrium values. The final pressure reached in the coarse-grained sample is only half of that seen during the pressing phase and amounts to only 1.25 GPa.

During release of the vices, the force continuously decreases towards zero. The vices lose contact with the sample after a time of 500 ps, indicating that both samples have shrunk in x direction by around 1 nm due to the plastic deformation in the entire compression and release operation.

We note that the strain rate used in the simulations amounts to 2.5 × 108 s− 1. It has been shown [46, 47] that below strain rates of around 1 × 109 s− 1, elastic and plastic properties — in particular the yield stress — depend only negligibly on strain rate. Above that critical strain rate, dislocation nucleation is prohibited.

3.2 Deformation mechanism

The deformation mechanisms of nanocrystalline materials are known to depend on grain size. In particular, it has been found [47] for fcc Cu that above a grain size of around 15 nm, deformation is governed by dislocation plasticity, which occurs inside grains, and below a grain size of around 15 nm, deformation is governed by grain-boundary processes, such as grain displacement and rotation. Dislocations nucleate in grains as a result of stress concentration at grain boundaries, while the stress in the grain interior is relieved for sufficiently large grains. While the quoted study [47] was on Cu, the grain sizes chosen for this study — 10 and 22 nm — lie clearly below and above the critical grain size, such that we expect to find these distinct behaviors also in Al.

In order to quantify the deformation processes both inside the grains and in the grain boundaries, we use the von Mises shear strain (VMSS) that is readily evaluated for each atom in the sample [48]. Shear strain is the prime agent to nucleate and move dislocations, as well as to shape grain boundaries.

Focusing on the grain-boundary activity first, Fig. 3 shows the fraction of grain-boundary atoms with VMSS > 0.1. The strain at the end of each phase (pressing, holding, and release) is calculated with respect to the configuration at the beginning of the phase. In the fine-grained sample, in each phase more than half of the grain-boundary atoms have been considerably sheared, evidencing a high occurrence of grain-boundary mediated plastic deformation. The fraction of grain-boundary atoms that have been similarly sheared is considerably smaller for the coarse-grained sample. These numbers show that the above distinction made for nanocrystalline Cu is also true for machined Al. Interestingly, the fraction of sheared grain-boundary atoms is largest under the release step. i.e., when the sample is allowed to return to a pressure-free state.

Fig. 3
figure 3

Fraction of grain-boundary atoms with VMSS > 0.1. The reference configurations for holding and releasing are the end of the pressing and the holding phase, respectively

Full size image

Apart from these fractions, the snapshots shown in Fig. 4 demonstrate the occurrence of dislocation-based and grain-boundary-mediated processes in greater detail. In this view on the surface of the sample, dislocations inside the grains are marked and grain boundaries are colored according to whether their shear exceeded VMSS = 0.1. An analysis of the generated dislocations using OVITO [37] shows that these mostly have Burgers vectors of 1/6〈112〉 and 1/2〈110〉, as is common for fcc samples. They glide along 〈110〉 directions and the generated stacking fault planes are {111} planes. We note that the nucleation of dislocations in nanocrystalline samples at grain boundaries under stress does not always follow Schmid’s law, as has been shown in several systematic studies [49, 50].

Fig. 4
figure 4

VMSS map of coarse-grained and fine-grained samples, during pressing, holding and release. The reference configurations are the same as in Fig. 3. In this side view on the sample, dark blue represents atoms in fcc lattice structure inside the grains and light blue represents atoms at grain boundaries. White characterizes grain-boundary atoms with VMSS > 0.1, and red atoms have VMSS > 0.1 and belong to the grain interior. The grain in the coarse-grained sample denoted by “1” serves to discuss dislocation contributions to surface roughness in Section 3.3

Full size image

The number and length of dislocations (Fig. 4) are considerably higher in the coarse-grained sample. Furthermore, the region where dislocations are nucleated extends towards the upper end of the vice plates and even above the vice plates in the coarse-grained sample. Comparatively, the region where the dislocations are nucleated is concentrated towards the lower surface in the fine-grained sample. Not surprisingly, the largest amount of dislocation nucleation is found in the pressing phase, where a previously well-relaxed sample is quickly strained out of equilibrium. However, even the holding and release phases either produce novel dislocations or let already existing dislocations migrate. These findings corroborate the conclusion that dislocation plasticity is more readily found in the coarse- grained sample.

The role of grain-boundary activity can also be analyzed in Fig. 4. After pressing the samples, almost all grain boundaries in the bottom half of the sample are found to be strongly sheared, VMSS > 0.1. Interestingly, the grains close to the vice plates are not as sheared as those in the middle of the samples. This is due to the fact that close to the plates, the stress field is mostly uniaxial, and more shear is expected at the upper ends of the plates and in the middle of the sample. Grain-boundary activities continue during the holding and the release phases, but are more prominent in the fine-grained sample.

Besides shear strain, hydrostatic pressure is an important indicator of the stress fields generated in the sample. Hydrostatic pressure is shown in Fig. 5 in atomic resolution; pressure data are averaged over 0.5 ps to get rid of atomic vibrations. The plots give the same view as Fig. 4. As was noted above, the averaged (uniaxial) stress in the x direction amounts to 2.5 GPa in the bottom half of the sample. The figure shows that even in the bottom half of the sample, the hydrostatic pressure is far from a homogeneous distribution; this is caused by the differing orientations of the grains. While at the end of the pressing phase, the grain interiors are all compressively strained, some regions — in particular regions at grain boundaries are under tensile strain. Grain boundaries act as sources of high stress; some low-angle grain boundaries — can be identified in this figure as a chain of dislocations with their alternating compressive and tensile stress fields. Other grain boundaries are under primarily compressive stress.

Fig. 5
figure 5

Hydrostatic pressure. Negative values denote compressive pressure

Full size image

During the holding phase, pressures equilibrate somewhat in the grains, as can be seen by a stronger mix of compressive and tensile stress regions. This goes in line with the reduction of the forces needed to keep the vice plates in position (Fig. 2). After release, this equilibration process has further proceeded, since now the global pressure vanishes.

The final snapshots in Fig. 5 show the stresses remaining in the sample after the entire process; they constitute the residual stresses. A comparison with Fig. 4 demonstrates that some of the stresses inside the grains may be attributed to the dislocations that have been produced there; other sources of high pressure are in the vicinity of triple junctions of grain boundaries. However, the inhomogeneity of the pressure distribution — which is under vanishing global pressure — is astonishing, since pressures vary between − 1 and + 1 GPa. The coarse-grained system shows stronger residual stresses at some of the grain boundaries than the fine-grained system.

In summary, Figs. 4 and 5 demonstrate that dislocation plasticity is more active in the coarse-grained sample, while grain-boundary processes are important for both samples studied. Defects in the sample — here in particular, grain boundaries — act as stress concentrators and are also the places where residual stresses build up.

3.3 Surface roughness

The snapshots, Figs. 4 and 5, show already strong deformations of the sample surface. During pressing and holding, the upper surface becomes curved in a convex way; this curvature disappears after release. The lower surface becomes rough, and this roughness does not disappear. This is due to the different grain orientations and the various grain rotations (and displacement processes). Another interesting feature is the left-right asymmetry, which develops for the coarse-grained sample in the pressing phase and remains through the holding and release phases and will be discussed in Sections 3.4 and 3.5 below.

We analyze the roughness developing in the bottom surface in greater detail in Fig. 6 which shows the height distribution of the bottom surface profile for the coarse-grained and fine-grained samples. The average and the standard deviation of the distributions are assembled in Table 1. We use the standard deviation of the height profile as a measure of the surface roughness.

Fig. 6
figure 6

Height profile of the bottom sample surface for the a coarse-grained sample and b fine-grained sample. The vertical line indicates the original average surface position. Note the change in scale between the initial and the deformed profiles

Full size image
Table 1 Average (avg) and standard deviation (std) of the surface profiles (Fig. 6)
Full size table

During pressing, the standard deviation increases by a factor of 4.5 (7) with respect to the original value for the coarse-grained (fine-grained) sample. During holding, the roughness increases even further, but reduces somewhat in the release phase. The reason for this surface roughness is grain displacement and rotation and will be discussed in the next two sections. These processes cannot be undone during the release phase. The height profile of the coarse-grained sample (Fig. 6a) differs significantly from a Gaussian profile as it exhibits two peaks in the height spectrum, which are caused by individual grains popping out of the original surface. This feature is even enhanced during the holding phase. There are 42 grains in the fine-grained sample at the bottom surface, but only 13 grains in the coarse-grained sample. Therefore, the multitude of grains contributing to the surface in the fine-grained sample randomize the height profile and lead to a distribution that is closer to a Gaussian profile.

In addition, dislocations contribute to surface roughness. This can be clearly observed in the grain denoted by “1” in the coarse-grained sample in Fig. 4. This grain has a large area on the lower surface and dislocations absorbed on it lead to surface steps which contribute considerably to the surface roughness of this grain.

3.4 Center-of-mass grain displacement

In order to describe the translational motion of grains, we study their center-of-mass displacements, \(\vec {d}\) [27]. Since there is no standard analysis available for this purpose, we proceed as follows. We cut 7 slabs extending in the x–z plane with a thickness of 2 nm in the y direction. The slabs are evenly distributed on the y axis. In these slabs it is possible to analyze the center-of-mass displacement of the grains in the x–z plane, as we can neglect any motion in y direction. We present the resulting translational motions as histograms in Fig. 7. This figure shows the displacements during the pressing, holding and release phases. In each phase, the displacement between the beginning and the end of the phase are shown. The total displacement, \(d_{\text {abs}}= |\vec {d}|\), and the components dx and dz along the x and z axes are also shown.

Fig. 7
figure 7

Normalized distributions of the center-of-mass displacements of grains during the a pressing, b holding, and c release phase

Full size image

Grain displacements during the pressing phase (Fig. 7a) are best described by the component parallel to the force axis, dx. The distributions show two peaks at − 20 Å and + 20 Å, corresponding to grains located close to the vice plates, which are forced to move the entire distance covered by the nearby vice. The majority of the grains, however, suffer only little motion, since they are located in the middle of the sample, between the two vices. Apart from this horizontal motion, a component dz in vertical direction is seen. The majority of the grains are moved upwards and thus contribute to the curvature of the upper surface seen in Fig. 6. In the pressing phase, no large difference between the coarse-grained and the fine-grained samples shows up.

Note that in a purely elastic compression, grain centers initially positioned at x would move by a distance (1 − ε)x, where ε = 0.05 is the applied uniaxial strain. The dx data in Fig. 7a would thus follow a rectangular distribution of constant height. The simulation results thus demonstrate the large deviation of plastic grain flow from this elastic reference case.

Considerable differences are observed during the holding phase (Fig. 7b). Here, grains in the coarse-grained sample are shifted to the right-hand side, dx > 0, with an amplitude of 5 Å. This shift corresponds to the left-right asymmetry shown in Figs. 4 and 5. The fine-grained sample also drifts further in horizontal direction in order to release the compressive strain present in the lower part of the sample; on the other hand, grain movements in the coarse-grained sample are larger in size, but show as much upwards as downwards motion.

The left-right asymmetry showing up here is caused by the individual grain movements. In the coarse-grained sample, an analysis of grain motion shows a relative movement of the upper part of the sample towards the right, accompanied by a downward motion of the grains in the vicinity of the right-hand vice plate. The fine-grained sample does not show a corresponding asymmetry, since here, grain motion is more random.

Also during the release phase, considerable grain movements are observed (Fig. 7c). The curvature of the upper part of the sample is reduced, leading to a downward grain motion, dz < 0. While the grain motion in the x direction is symmetrical for the fine-grained sample, the coarse-grained sample tends to reduce the asymmetric motion that occurred during the holding phase, featuring an average dx < 0.

The asymmetry observed in the grain motion for the coarse-grained sample also shows up when considering the forces acting on the vices (Fig. 2). As the vices are compressed with constant velocity, individual grain movements oppose the vice motion with different forces. Interestingly, this asymmetry is particularly pronounced in the holding stage, but is also visible in the pressing and release stages.

Figure 8 gives an overview over the magnitude and direction of the center-of-mass translation vectors during the pressing phase for the fine-grained sample. A clear flow pattern is established, in which the inward moving vice plates let the grains move inward along the x axis. When these flows converge in the middle of the sample, the grains move upwards along the z axis. In the upper half of the sample, above the vice plates, the flow is everywhere in the z direction, leading to sample expansion in this direction.

Fig. 8
figure 8

Center-of-mass grain displacement during the pressing stage in the fine-grained sample, overlaid with the initial grain structure. The arrows point from the original position of the center of mass to its final position

Full size image

We conclude that grain motion is mainly governed by the movement of the vices and by the upwards expansion of the sample. The coarse-grained sample shows more individuality in grain motions such that an asymmetry with respect to the behavior of the left- and right-hand side begins to appear. In contrast, the grain motion of the fine-grained sample is more randomized and does not show this asymmetry.

3.5 Grain rotation

In the course of pressing, grains are not only translated, but also rotated. We calculate the rotation angle by using a quaternion formulation to identify rotation, which transforms the original orientation of each grain to the final orientation after pressing [51,52,53].

Figure 9 shows the distribution of the rotation angles during the pressing phase. Quite large angles of 8.5∘ are observed with an average value of 1.29∘ (1.40∘) for the coarse-grained (fine-grained) sample. The angles are similar for the 2 samples; however, the largest angles occur for the fine-grained sample. The effect of the grain rotation is the tilting of the grains at the lower sample surface which is visible in Figs. 4 and 5 and leads to the sample roughness discussed in Section 3.3. During the holding and release phase, rotation angles were < 0.01∘, indicating that grains do not rotate back towards their initial orientations. This demonstrates that sizable rotations only occur under immediate sample loading.

Fig. 9
figure 9

Distribution of grain rotation angles during the pressing phase

Full size image

3.6 Sample distortion

The length changes of the sample after release from the fixture are called distortions. We discuss here these length changes in all phases during and after the loading process. The length changes are measured in the vertical direction at 3 positions A, B, C at the left, middle and right of the sample, and at 3 positions in the horizontal direction (D, E, F) in the bottom, middle, and top of the sample (see Fig. 10a). In detail, due to the atomistic roughness of the samples, for the example of position A, we measure the average height of the sample in a slab of width 1 nm extending at a distance of 3 nm from the lateral surface in the z–y plane; this averaging process is performed because of the roughness of the samples due to their nanocrystalline structure (cf. Section 3.3).

Fig. 10
figure 10

a Schematics indicating the positions where vertical (A–C) and horizontal (F–D) sample distortions were measured. b and c show simulation results for distortions for the coarse-grained (b) and fine-grained (c) sample in the pressing, holding and release phase

Full size image

Figure 10 shows the distortions measured as fractional changes of the lengths with respect to their initial values. The sample shrank horizontally under the compressive loading by the vice plates. These induce a compressive strain of − 5% which exactly equals the distortion measured at D in the pressing and holding phase. After release, the sample does not return to its original length, since the deformation was plastic; the final distortion amounts to − 3.8 (− 2.7) % for the coarse-grained (fine-grained) sample. Horizontal distortions in the middle of the sample at position E are considerably reduced, and at the top of the sample, position F, the sample expands in all phases. This expansion is caused by material flow from the lower half of the sample towards the upper half of the sample.

The horizontal narrowing of the sample is accompanied by an expansion in the vertical direction. This expansion is more or less uniform for the fine-grained sample, but shows a considerable left-right asymmetry for the coarse-grained sample, which was already observed and discussed previously (Section 3.4).

We conclude that sample distortions after release are stronger for the coarse-grained than for the fine-grained sample. This is caused by the easier grain movement of the large grains, as evidenced in Section 3.4.

Compared to real applications of nanomanufacturing, the model sample has a larger surface-to-volume ratio. Therefore, it can be assumed that surface effects are less pronounced in real applications. With a higher grain number in real samples, processes in a large number of grains will add up to the total distortion such that the effects in individual grains — while still present — will lose importance for the average distortion in the sample, since variations between individual grains might smoothen out.

4 Summary

This study monitored the plastic deformation processes occurring in a polycrystalline Al bar under external inhomogeneous loading, representing vice plates. The processes occurring in the pressing, the holding and the release phases were analyzed and gave the following results.

  1. 1.

    Fine-grained material (grain size of 10 nm) showed only little dislocation activity inside the grains during plastic deformation, while dislocation activity is strong in the deformation of coarse-grained material (grain size of 18 nm). This result extends previous studies of the deformation of nanocrystalline fcc metals [13, 14, 17, 45, 47], which were mainly based on homogeneous strains in bulk samples, to the case where inhomogeneous strains and free surfaces are relevant.

  2. 2.

    We followed the grain displacements by monitoring their center-of-mass trajectories. The results show strong deviations from a simple affine compaction of the material; rather, grains move in a strongly inhomogeneous way.

  3. 3.

    As a consequence of the nanometric size of the investigated Al bar, grain motions are not symmetric with respect to the bar center, but exhibit a left-right asymmetry. It is caused by grain displacement and rotation and occurs pronouncedly in the coarse-grained sample, while it averages out in the fine-grained sample. It may be expected that this asymmetry will decrease for larger samples.

  4. 4.

    The grains also suffer considerable rotations with an average rotation angle of 1.3∘–1.4∘. These grain rotations only occurred in the pressing phase and not during holding or releasing.

  5. 5.

    These grain rotations lead to a considerable roughening of the bottom surface of the sample, which does not vanish after releasing the vice fixtures.

  6. 6.

    The residual stresses in the material resulting from dislocation activity and grain-boundary processes build up in the pressing phase and do not relax during the holding and release phases.

  7. 7.

    Due to the plastic deformations occurring, the sample shows a distortion after the process. The final distortion at the position where the vice plates acted amounts to around half the applied strain, but decreases in other areas. In the direction perpendicular to the applied strain, the sample grows. The coarse-grained sample shows higher distortion values than the fine-grained sample because of longer-ranged grain displacements.

Our results show that the final sample distortion is based on plastic processes that are mediated both by dislocation glide and grain displacement and rotation. In future work, the results presented here should be extended to other material classes. Besides bcc metals, such as Fe, the distortion processes in alloys would be particularly relevant.