1 Introduction

With the development of aerospace and energy technologies, the nickel alloy has been used extensively. It has high mechanical strength, oxidation resistance, and corrosion resistance at high temperatures. Thus, it is often used in harsh working environments, such as the elements in the high temperature and high pressure environment of aerospace turbine engines, the structures and corrosion-resistant pipelines of nuclear energy, and petrochemical industries. However, for high mechanical strength, low thermal conductivity, and surface hardening property [1], the nickel alloy has worse cutting tool life and machining efficiency than general materials. Thus, how to select reasonable machining parameters affects the quality, cost, and machining time of end products.

In a previous study of cutting parameter, the lathe machining is a common method of machining, where the cutting tool performs lathe machining for the rotating workpiece. It is the most extensively used machine tool processing mode in machine manufacturing and assembly plants. In modern machining process, in order to increase the manufacturing efficiency, selecting appropriate cutting parameters become an important topic. The cutting parameters selected according to the properties of workpiece directly influence the machining time, workpiece surface accuracy, and roughness. Therefore, the machining performance of cutting tool has become one of the key factors in improving the overall process machining efficiency. If the properties of different materials can be mastered and appropriate machining parameters are selected, and a mathematical model is built by using an appropriate statistical method, the cutting tool wear can be controlled effectively, and the manufacturing efficiency can be increased, so as to reduce the production cost and enhance the competitiveness [2,3,4]. Hanasaki et al. [5] used four cutting tools with different coatings to turn nickel alloy, and found that the cutting tool with Al2O3 coating had the minimum cutting tool wear for boundary wear and tool flank wear.

In a previous research of experiment planning, Wright and Chow [6] studied iron base and nickel alloys, and found that the two materials had significantly different machining properties. The calculation of dynamic material strength showed that the nickel alloy had higher strength in primary shear zone and secondary shear zone. In the machining of nickel alloy, the insert edge temperature is very high, and the high mechanical strength of nickel-base material results in high stress on the cutting edge, inducing severe tool flank wear, the tool life is shortened greatly. Ezilarasan et al. [7] tested and analyzed the cutting parameters of nimonic C-263 nickel alloy. They used Taguchi Method to build a machining model, and discussed the relationship of cutting speed, feed rate, and cutting depth to tool flank wear and surface roughness. Moreover, they used response surface methodology to optimize the cutting parameters, and the prediction result was validated by using the optimized cutting parameters. To discuss the optimization of turning parameters for austenitic stainless steel material, Li, Chen, Feng, and Zhong [8] used uniform design method to design a precision lathe machining scheme. Under three different turning cooling conditions, including dry type, environmentally friendly wet type, and low temperature cold air micro oil temperature, the cutting speed, feedrate, back cutting depth, and tool nose radius were used as optimal variables, and the tool life, surface roughness, surface residual stress, cutting temperature, and machining efficiency were used as optimization objective functions, with the experimental table designed by uniform design method, the number of experiments was reduced significantly. The regression analysis was used for modeling of experiment data, and the regression model was obtained for optimizing the turning parameters.

In a previous study of nickel alloy machining, the nickel alloy has very good mechanical properties, oxidation resistance, and resistance to high temperature deformation. However, it has low thermal conductivity and work hardening problems, leading to worse machinability, so that the cutting heat is likely to concentrate on the tool tip during cutting. The cutting tool has serious diffusion wear, oxidative wear, and adhesive wear due to high temperature. The surface hardening of the machined nickel alloy is very severe, the hardness of work hardening is about two times of normal surface hardness. High chip hardness, good ductility, and unlikely fracture result in difficult discontinuous chip in the machining process, so that the tool generates lots of chips (BUE). The material contains a lot of metallic compounds and hard spots, which are likely to induce cutting tool fracture, hard to guarantee the size and accuracy requirements [9]. Muammer et al. [10] used ceramic tool and carbide cutter to turn Inconel-718 alloy, and indicated that the carbide cutter was better than ceramic tool for cutting Inconel-718 alloy. According to the comparison of different cutting speeds, the ceramic tool was applicable to high-speed machining, the carbide cutter was applicable to low-speed machining, and the cutting force was inversely proportional to cutting speed. There have been few papers and research that focus on the relationship between uniform design methodology and nickel alloy machining phenomenon, reviewing date published in literature reveals that the methodology and research reported in this paper has not observed.

2 Research principle and methodology

There are some technical challenges for nickel-based alloy materials machining such as precipitation strengthening, solid solution strengthening, machining hardness, affinity, carbonized precipitation, and thermal conductivity. The purpose of this study is to analyze the significant factors of wear, cutting force, surface roughness, and machining time in cutting tool products using uniform design method. The uniform design and regression method can provide for identifying quickly and accurately the cutting tool life estimate.

2.1 Cutting principle

Using a cutting tool to remove excess material from the workpiece is called machining, and the removed material is called chips. To achieve the predetermined shape and size when the cutting tool is used for cutting material, the machine tool performs appropriate relative movement between material and cutting tool, so as to prepare the required part surface. In terms of turning, under the combined action of material revolution and reciprocating motion of cutting tool, the chips drop off discontinuously or continuously, so as to process the workpiece surface into the expected special surface [11, 12].

According to the definition of ISO [2], for the tungsten carbide cutting tool, the tool life refers to the cutting time when the tool flank wear loss reaches 0.3~0.6mm. When the cutting speed is fixed, Taylor deduced the tool life equation according to experimental results in 1906, expressed as follows[13, 14].

$${\mathrm{VT}}^{\mathrm{n}}=\mathrm{C}$$
(1)

where V is the cutting speed, T is the tool life, m is the constant for describing the cutter material properties, and C is the cutting speed when the tool life is 1 minute. The cutting conditions include cutting speed, feed motion, and depth of cut, which have significant effect on cutting efficiency, cutting force, and tool life. The graph of relation of tool life is shown in Figure 1. When the cutting tool is cutting the workpiece, in the course of chip formation, the required force for the strain on the shear surface at the contact of cutting edge and workpiece material is called cutting resistance. The friction between the machined workpiece surface and the tool flank results in the flank wear land gradually. The flank wear land is parallel to the resultant cutting direction, so the wear spreads to the cutting edge gradually, the cutting force and cutting temperature are increased suddenly, and the cutting tool is damaged. Figure 2 shows the width variation of flank wear land; this curve is divided into three regions for discussion: (1) initial wear region, the rapid wear of sharp cutting edge results in a micro wear region; (2) uniform wear region, the cutting tool is worn at a uniform rate to almost damaged; (3) rapid wear region, the wear width will increase rapidly, so the cutting tool wear region has occupied a considerable proportion of the whole region, very sensitive to the wear resulted from drastic changes in tool temperature, so the cutting tool shall be reground or the insert shall be changed before the surface wear reaches this region.

Fig. 1
figure 1

Graph of relation of tool life

Full size image
Fig. 2
figure 2

Width variation of flank wear land [13]

Full size image

2.2 Composition and characteristics of nickel alloy

The nickel alloy refers to a sort of alloy with Ni content exceeding 30wt% and other elements, as well as higher strength at 650~1000 °C and certain resistance to oxidation and corrosion, so it is often used in harsh working environments. For example, the material of the turbine engines of aerospace industry is required of good mechanical strength at super high temperatures; the common high temperature nickel alloys are A286, Inconel 718/706, Nimonic 80A and Hastelloy X. The structures and corrosion resistant pipelines of nuclear energy and petrochemical industries are required of good resistance to high temperature oxidation, sulfurization, acid and alkali, and aqueous chloride ion corrosion; the corrosion-resistant nickel alloys include Alloy 200, Monel 400, Hastelloy C276, Alloy 625, and Incoloy 925. The composition of the nickel alloy used this time is shown in Table 1. It can be used in molten glass forming tools and molds. The material is made easier for processing by the first heat treatment, and then the material hardness is increased in the second heat treatment. The casting mold made of this material has adequate strength to maintain the shape till the molten alloy is solidified, and it can be separated from the cast when it is rapidly cooled to room temperature. It was usually used in glass forming molds, silencer baffles, plastic transfer printing molds, and so on in the past [15].

Table 1 Nickel alloy material composition
Full size table

2.3 Uniform design method

The uniform design table cannot be used directly, according to the stationing foundation under uniformity principle, the columns in the uniform table are not equivalent, so specific application tables must be proposed for the uniform table for the experiments with different factors, and each uniform table shall have a corresponding application table. The application table stationing principle of Un(nm) assumes n to be the number of experiments (level number), and m to be the number of columns in Un   table. Now, there are S factors, each has n levels. In general condition (S ≤ m), let a1, a2, ……, as; b1, b2, ……, bs be two groups of positive integers, and ai ≠ aj, bi ≠ bj, i ≠ j, (ai, n) = (bi, n) = 1, i, j = 1, 2, …, S, two S columns in Un table can be generated according to the rule of uniform table, the following two equations can be obtained by theoretical derivation[16, 17].

$$\mathrm{f}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots \dots, {\mathrm{a}}_{\mathrm{s}}\right)=\frac{1}{\mathrm{n}}\sum \limits_{\mathrm{k}=1}^{\mathrm{n}}{\prod}_{\mathrm{v}=1}^{\mathrm{s}}\left[1-\frac{2}{\uppi}\ln \left(2\sin \uppi \left(\frac{{\mathrm{a}}_{\mathrm{v}\mathrm{k}}}{\mathrm{n}+1}\right)\right)\right]$$
(2)
$$\mathrm{f}\left({\mathrm{b}}_1,{\mathrm{b}}_2,\dots \dots, {\mathrm{b}}_{\mathrm{s}}\right)=\frac{1}{\mathrm{n}}\sum \limits_{\mathrm{k}=1}^{\mathrm{n}}{\prod}_{\mathrm{v}=1}^{\mathrm{s}}\left[1-\frac{2}{\uppi}\ln \left(2\sin \uppi \left(\frac{{\mathrm{b}}_{\mathrm{v}\mathrm{k}}}{\mathrm{n}+1}\right)\right)\right]$$
(3)

where

$${a}_{vk}\equiv {ka}_v,{b}_{vk}\equiv {kb}_v,\left(\operatorname{mod}\ \mathrm{n}\right),\left(\mathrm{v}=1,2,\dots \dots, \mathrm{S}\right)$$

If f(a1, a2, ……, as) ⁢f(b1, b2, ……, bs), meaning the S column composed of a1, a2, ……, as has higher uniformity than the S column composed of b1, b2, ……, bs. In the uniformity principle, if there are m natural numbers satisfying (ai, n) = 1, the probability of taking S from m is Sm, the combination which can minimize the f(a1, a2, ……, as) value is selected from the S columns, and used for planning the experimental table. In the case of ai = 1, the first column of Un table must be contained, as long as (S − 1)m − 1 conditions are compared, in order to obtain the application table of S factors, S of m natural numbers ai satisfying (ai, n) = 1, (i = 1, 2, ……, m) are selected according to uniformity principle, the application table can be derived from ai = 1 using the following Eq. (4):

$${P}_n(K)=\left({K}_{a1},{K}_{a2},\dots \dots, {K}_{as}\right)\ \Big)$$
(4)

where: K=1,2,……,n.

To meet the requirement of multifactor multilevel experiments, Wang and Wang [3] proposed a new Design of Experiment combined with mathematical theory and multivariate statistical method based on orthogonal design, which is known as uniform design. The orthogonal design is characterized by designing experiments with “uniform dispersion” and “orderly comparability.” The uniform dispersion means the experimental points are uniformly dispersed in the scope of experiment, and the orderly comparability aims at easy compilation of experiment data and easy analysis of the influence of various factors on experiment and the law of variation, each level of each factor must be tested over and over. However, overall experiment is required in order to achieve orderly comparability, so the number of experiments for orthogonal design is increased.

The uniform design starts from the view of experimentally uniform dispersion, the orderly comparability is abandoned in order to reduce the number of experiments, only the uniform dispersion remains, each level of each factor is tested once, so the significance of each experimental point after planning is enhanced, and the number of experiments is reduced a lot. Table 2 compares the number of experiments of orthogonal design with that of uniform design.

Table 2 Numbers of experiments of orthogonal design and uniform design
Full size table

However, the uniform table cannot be used correctly until it is combined with the fitted application table. The design of experiments using uniform design method approximately comprises the following steps.

  • Step (1):

    Select an appropriate uniform table. This experiment has three factors and eleven levels, the U11(1110) table is applicable.

  • Step (2):

    According to the application table requirement of U11(1110), columns 1, 5, and 7 of U11(1110) table are selected to form U11(113) table.

  • Step (3):

    The three factors are placed above the three columns in U11(113) table respectively, and the specific experimental conditions corresponding to the factors are filled in U11(113) table, and then the planning of experimental program is completed.

3 Experimental equipment and planning

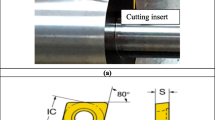
For the parameter selection of nickel alloy turning parameters, this study uses uniform design method to design machining experiments to reduce the number of experiments; Figure 3 shows the experimental workpiece plan, and the experimental equipment is listed in Table 3. Three independent variables are allocated according to cutting conditions, which are cutting speed (Vc = 20~100 M/min), feed motion (feed = 0.1~0.4 mm/rev), and cutting depth (dp = 0.5~1.0 mm). As this experiment requires 11 levels and selects three factors, columns 1, 5, and 7 are selected according to U11 application table to arrange cutting conditions, as shown in Table 4. Four dependent variable data must be recorded during experiment, which are the cutting tool wear (VB), surface roughness (Ra), machining time (T), and cutting force (N). Finally, the machining experiment log sheet is established. Taking Experiment 11 as an example, it is recorded every 50 mm according to the machining stroke, till the total run is 250 mm. Finally, the nickel-base material turning parameter model and regression equation are built by regression analysis, so as to further discuss the I/O relationship among various combinations of variables. The experimental plan is shown in Figure 4.

Fig. 3
figure 3

Experimental layout

Full size image
Table 3 Experimental equipment
Full size table
Table 4 Experiment condition plan
Full size table
Fig. 4
figure 4

Experimental plan

Full size image

4 Results and discussion

4.1 Influence of cutting parameters on tool flank wear

In this stage of experiment, the cutting parameters are designed by uniform design method. The real machining is performed according to the obtained experimental plan, so as to observe the cutting tool wear-travel curve of this experiment, as shown in Figure 5. It is found that the cutting tool wear has a fixed trend for analyzing and predicting data as the machining travel increases.

Fig. 5
figure 5

Cutting tool wear-travel curve

Full size image

This experiment is a quantitative experiment, when the total run of machining is 600 mm (Table 3), according to ISO standard, the experiment stops if the uneven wear VBmax >0.6mm. The changes in the tool flank wear and machining travel of Experiment 9 are shown in Figure 6. As seen, the tool flank wear goes through three stages as the machining travel increases. It enters initial wear region in Stage I, the sharp cutting edge is worn rapidly, resulting in micro wear. Afterwards, it increases at a uniform rate in Stage II wear. Finally, in Stage III, the tool flank is worn till VBmax >0.6mm damaged.

Fig. 6
figure 6

Relationship between tool flank wear and machining travel in Experiment 9

Full size image

The increase of cutting length will cause increasing flank wear and cutting force and vice versa; the experiments No. 2 and No. 10 curve have same Taylor’s tool life curve, as shown in Figure 7 and Figure 8.

Fig. 7
figure 7

Relationships of cutting length to cutting force and flank wear in Experiment 2

Full size image
Fig. 8
figure 8

Relationships of cutting length to cutting force and flank wear in Experiment 10

Full size image

Sikdar and Chen [18] discussed the relationship between cutting tool wear and cutting force in single-point turning; the tool flank generates rubbing effect in cutting; it is worn gradually, and the wear results in higher cutting resistance, so that the cutting force is increased, as shown in Figure 9.

Fig. 9
figure 9

Relationship of tool flank wear to cutting force [18]

Full size image

According to machining Experiment 11, the relationships of tool flank wear to cutting force and surface roughness are shown in Figure 10. It is observed that the tool flank wear increases cutting resistance, and the cutting force increases accordingly, and the wear damages the original geometric shape of tool nose, leading to unstable cutting, and the surface roughness is increased.

Fig. 10
figure 10

Relationships of cutting tool wear to cutting force and surface roughness in Experiment 11

Full size image

The uniform design is a concept of uniform dispersion, and the levels in the experiment are planned uniformly, but the factors which have important influence on output parameters will generate different trends in the scatter diagram of coincidence relation. The trends of physical phenomena in the scatter diagram are analyzed below.

  1. (a)

    Relationship between cutting tool wear and cutting speed:

According to cutting tool Taylor Eq. 5-1, the cutting speed (V) is the major factor in tool life. When the cutting speed and tool flank wear in the experiment data are discussed together, the relationship between tool flank wear and cutting speed can be obtained, as shown in Figure 11, and an exponential forecasting line is made to judge the trend of the relationship. It is known that the cutting tool wear increases greatly with cutting speed, meaning the cutting speed is a factor which influences cutting tool wear; their relationship meets the description of Taylor’s equation.

Fig. 11
figure 11

Relationship between tool flank wear and cutting speed

Full size image
  1. (b)

    Relationship between surface roughness and feedrate:

The theoretical surface roughness is expressed as Eq. 5-2, the feedrate (mm/rev) is one of the major factors in surface roughness (h). If the feedrate and surface roughness in the experiment data are discussed together, the relationship between surface roughness and feedrate can be obtained, as shown in Figure 12, and an exponential forecasting line is made to judge the trend of the relationship. It is observed that the surface roughness increases greatly with feedrate, meaning the feedrate is one of the key factors influencing the surface roughness.

$$\mathrm{h}=\frac{f^2}{8\mathit{\operatorname{Re}}}\times 1000$$
(5)
Fig. 12
figure 12

Relationship between surface roughness and feedrate

Full size image

where h is the surface roughness (μm); f is the feed-rate(mm/rev); Re is the tool nose radius (mm)

  1. (iii)

    Relationships of cutting force to feed-rate and cutting depth:

The cutting force (F) can be derived from Eq. 2-3, but the accuracy is poor in practical application, because there are many hypotheses of various conditions which influence the cutting force in the equation, and it is difficult to find the value correctly. Therefore, to figure out the cutting force accurately, the empirical equation must be determined by experiment, the cutting force is measured by dynamometer, and the data are processed by graphical method and linear regression, and then the empirical equation of cutting force can be obtained. According to the equation, the feedrate (f) and cutting depth (dp) are the key factors which influence the cutting force. In terms of main cutting force (Fc), expressed as Eq. 6 [19], the feed motion and feedrate are the major factors which influence the cutting force. The cutting force, feedrate, and cutting depth are discussed in the experiment data, and the relationships of cutting force to feedrate and cutting depth are obtained, as shown in Figure 13. The cutting force increases with feed-rate and cutting depth.

$${F}_c={C}_{F_c}\ast {dp}^{x_{F_c}}\ast {f}^{y_{F_c}}$$
(6)
Fig. 13
figure 13

Relationships of cutting force to feedrate and cutting depth

Full size image

where Fc is the main cutting force (N);\({C}_{F_c}\) is a constant

\({x}_{F_c}\) and \({y}_{F_c}\) are the slopes of Fc − dp line and Fc − f line

4.2 Establishment of regression model and test methods

This study uses uniform design method for planning and design of turning parameters, and the experimental results are used for regression analysis; the regression model is built, and the insignificant terms are removed by reverse scalping method to obtain the regression equation. The ANOVA is used for analysis and test, under the standard of statistical significanceα = 0.05, the coefficient of determination R2 is calculated by statistical software, the f-test and independence t-test are used for decision, and the related analysis diagrams are drawn, e.g., normal distribution diagram and residual analysis chart, so as to check whether the regression model is proper. The combination of 3 factors and 11 levels for the machining experiment in this study can fit the second-order regression model:

$$Y={\beta}_0+{\beta}_1{X}_1+{\beta}_2{X}_2+{\beta}_3{X}_3+{\beta}_4{X}_1{X}_2+{\beta}_5{X}_1{X}_3+\kern2em {\beta}_6{X}_2{X}_3+{\beta}_7{X_1}^2+{\beta}_8{X_2}^2+{\beta}_9{X_3}^2$$
(7)

where X1   is the cutting speed   (Vc);X2   is the feedrate   (f);X3   is the cutting depth(ap);

$${\beta}_0{}^{\backprime}{\beta}_1{}^{\backprime}\dots \dots {}^{\backprime}{\beta}_9\ \mathrm{are}\ \mathrm{the}\ \mathrm{coefficients}\ \mathrm{of}\ \mathrm{various}\ \mathrm{terms};$$

The regression model uses reverse scalping method to eliminate insignificant terms before ANOVA, and the regression model significance F-test hypotheses for significant relationship between terms and Y are:

$${H}_0:{\beta}_i=0,\kern0.5em i=1,2,\dots, n$$
$${H}_1:\mathrm{at}\ \mathrm{least}\ \mathrm{one}\ \mathrm{coefficient}\ \mathrm{of}\ {\beta}_i\ \mathrm{is}\ \mathrm{unequal}\ \mathrm{to}\ 0,i=1,2,\dots, n$$

If rejecting the null hypothesis H0 is tenable, the sampling distribution of MSR/MSE is proved to comply with F distribution, when F   value >Fα, n, n − p − 1 statistical value, rejecting the null hypothesis H0 is tenable, meaning the regression equation is significant, so the Y value of prediction equation is effective on the independent variables in the scope of experiment.

When the significance of regression model is confirmed by F-test, the marginal T-test for individual regression coefficients is performed to discuss whether the β coefficient of individual independent variables is zero or not. The independent variables have explanatory ability only if the coefficient is not 0, hypothesized as follows:H0 : βi = 0, i = 1, 2, …, n

$${H}_a:{\beta}_i\ne 0,i=1,2,\dots, n$$

Under bilateral statistical significance, when t ratio >tα/2, the regression coefficient βi has statistical significance. When the discriminant coefficient R2 is a percentage the regression model can explain, the larger the value is, the better is the fitness of regression model. Use F value and t value to test in regression model, observe predictive ability and confidence interval, and make the estimation model achieve improved precision.

4.2.1 Tool flank wear modeling

When the objective function is tool flank wear (VB), the variable factors in cutting are the spindle speed, feedrate, and depth of cut, the regression analysis is used for analysis after experiment. The significance level is set as α = 0.05 for this experiment, and according to ANOVA of the second-order regression model, F = 11.94 ⁢F(0.05,8, 2) = 19.4 in F-test has not passed test, meaning the regression model is insignificant. Afterwards, two terms with less contribution are subtracted by using reverse scalping method.

The insignificant terms are removed by reverse scalping method, the ANOVA of tool flank wear regression model is obtained, as shown in Table 5, and individual coefficient analysis is shown in Table 6.

Table 5 Adjusted ANOVA of second-order tool flank wear regression model
Full size table
Table 6 Adjusted individual coefficient analysis sheet of second-order tool flank wear regression model
Full size table

The insignificant terms are eliminated by reverse scalping method, the ANOVA of tool flank wear regression model is obtained, and individual coefficient is analyzed as follows.

$$\mathrm{F}=26.0>{\mathrm{F}}_{\left(\mathrm{0.05,6},4\right)}=6.16$$
(8)

The significance P value ⁢0.01 and F-value is 26.0 after ANOVA, according to Eq. 5-3, F >F(0.05,6, 4), so the null hypothesis is rejected. According to calibration coefficient R2 = 0.9750, 97.5% of total variation of regression model can be explained by independent variables, and the regression model fitness is high. The T-value of various coefficients has exceeded the value tα/2 = t0.025 = 2.365 of bilateral t distribution, so the coefficients have statistical significance. Therefore, the regression equation is

$$\mathrm{Tool}\ \mathrm{wear}=0.095-0.04193\ {\mathrm{X}}_1+15.55\ {\mathrm{X}}_2-1.442\ {\mathrm{X}}_3+0.0641\ {\mathrm{X}}_1\ast {\mathrm{X}}_3-7.65\ {\mathrm{X}}_2\ast {\mathrm{X}}_3-21.77\ {{\mathrm{X}}_2}^2$$
(9)

The error test method is to perform residual analysis for the built regression model to check whether the model has normality, homogeneity of variance, and independence, as shown in Figure 14, related graphs have not violated the hypothetic variation trend, so the regression model conforms to the hypothesis.

Fig. 14
figure 14

Residual plots for flank wear

Full size image

4.2.2 Surface roughness modeling

When the objective function is surface roughness (Ra), the variable factors in cutting are spindle speed, feedrate, and depth of cut. The regression analysis is used for analysis after experiment. The significance level is set as α = 0.05 for this experiment, in the ANOVA of the second-order regression model, F = 38.84 >F(0.05,8, 2) = 19.4 in F-test has passed test, but P-value >0.05 of various terms (X1~X22), meaning the relationship of predictor variable to response variable is insignificant, so there are four terms with less contribution to be deducted by using reverse scalping method.

$$\mathrm{F}=45.63>{\mathrm{F}}_{\left(\mathrm{0.05,4},6\right)}=4.53$$
(10)

The significance P value ⁢0.01 and F-value is 45.63 after ANOVA, F >F(0.05,4, 6) according to Eq. 5-5, so the null hypothesis is rejected. According to calibration coefficient R2 = 0.9682, 96.82% of total variation of regression model can be explained by independent variables, the regression model fitness is high. Therefore, the coefficients have statistical significance. The regression equation is

$$\mathrm{Surface}\ \mathrm{roughness}=10.44-59.3\ {\mathrm{X}}_2-9.61\ {\mathrm{X}}_3+47.1\ {\mathrm{X}}_2\ast {\mathrm{X}}_3+92.3\ {{\mathrm{X}}_2}^2$$
(11)

The error test method is to perform residual analysis for the built regression model to check whether the model has normality, homogeneity of variance, and independence, as shown in Figure 15, related graphs have not violated the hypothetic variation trend, so the regression model conforms to the hypothesis.

Fig. 15
figure 15

Residual plots for surface roughness

Full size image

4.2.3 Machining time modeling

When the objective function is machining time (T), the variable factors in cutting are speed, feedrate, and depth of cut. The regression analysis is used for analysis after experiment. The significance level is set as   α = 0.05 for this experiment. In the ANOVA of the second-order regression model, as F = 10.50 ⁢F(0.05,8, 2) = 19.4 in F-test has not passed test, and the P-value of various terms (X1~X22) is larger than 0.05, meaning the relationship of predictor variable to response variable is insignificant, so there are five terms with less contribution to be deducted by using reverse scalping method.

$$\mathrm{F}=62.54>{\mathrm{F}}_{\left(\mathrm{0.05,3},7\right)}=4.35$$
(12)

The significance P value ⁢0.01 and F-value is 62.54 after ANOVA, F >F(0.05,3, 7) according to Eq. 5-7, so the null hypothesis is rejected. The calibration coefficient R2 = 0.9682, meaning 96.82% of total variation of regression model can be explained by independent variables, the regression model fitness is high. Therefore, various coefficients have statistical significance, and the regression equation is

$$\mathrm{Machining}\ \mathrm{time}=1748-27.72\ {\mathrm{X}}_1-1712\ {\mathrm{X}}_2+0.1776\ {{\mathrm{X}}_1}^2$$
(13)

The error test method is to perform residual analysis for the built regression model to check whether the model has normality, homogeneity of variance and independence, as shown in Figure 16, related graphs have not violated the hypothetic variation trend, so the regression model conforms to the hypothesis.

Fig. 16
figure 16

Residual plots for machining time

Full size image

4.2.4 Cutting force modeling

When the cutting force (N) is objective function, the variable factors in cutting are spindle speed, feedrate, and depth of cut. The regression analysis is used for analysis after experiment. The significance level is set as   α = 0.05 for this experiment. In the ANOVA of the second-order regression model, F = 31.51 >F(0.05,8, 2) = 19.4 in F-test has passed test, but P-value >0.05 of terms (X1~X22), meaning the relationship of predictor variable to response variable is insignificant, so there are four terms with less contribution to be deducted by using reverse scalping method.

$$\mathrm{F}=29.77>{\mathrm{F}}_{\left(\mathrm{0.05,4},6\right)}=4.53$$
(14)

The significance P value ⁢0.01 and F-value is 29.77 after ANOVA, F >F(0.05,4, 6) according to Eq. 5-9, so the null hypothesis is rejected, as the calibration coefficient R2 = 0.9520, meaning 95.2% of total variation of regression model can be explained by independent variables, the regression model fitness is high. The T-value of coefficients has exceeded the value tα/2 = t0.025 = 2.365 of bilateral t distribution, so the coefficients have statistical significance. Therefore, the regression equation is

$$\mathrm{Cutting}\ \mathrm{force}=111-9.29\ {\mathrm{X}}_1+906\ {\mathrm{X}}_2+351.5\ {\mathrm{X}}_3+0.0791\ {{\mathrm{X}}_1}^2$$
(15)

The error test method is to perform residual analysis for the built regression model to check whether the model has normality, homogeneity of variance, and independence, as shown in Figure 17, related graphs have not violated the hypothetic variation trend, so the regression model conforms to the hypothesis.

Fig. 17
figure 17

Residual plots for cutting force

Full size image

4.3 Model verification experiment

The regression equation of output parameters is found out after regression analysis, and the verification experiment is performed to confirm whether the regression equation can estimate the performance of output variables in different cutting parameter combinations. Therefore, three untested cutting parameter level combinations are selected in verification experiment, as shown in Table 7. The verification experiment uses the operations of 95% confidence interval (CI) to confirm whether the data of verification experiment fall into the CI of regression equation estimated value, the 95% CI is expressed as follows:

$$95\%\mathrm{CI}=\mathrm{sample}\ \mathrm{mean}\pm \left(1.96\times \frac{S}{\sqrt{n}}\ \right)$$
(16)
Table 7 Cutting parameter combinations for verification experiment
Full size table

According to three verification experiments, the estimated values of regression prediction equation for cutting tool wear, surface roughness, cutting time, and cutting force fall in the 95% CI, as shown in Table 8 and Table 9. Therefore, the estimation model of this study has high-accuracy estimation ability, the cutting tool wear (VB) is 2.72~6.18%, the surface roughness (Ra) is 4.10~7.72%, the machining time (T) is 3.75~8.82%, the cutting force (N) is 1.54~7.42%, and the errors of various dependent variables are approximately less than 10%.

Table 8 Verification experiment result analysis
Full size table
Table 9 Cutting tool wear and cutting force of verification experiment
Full size table

5 Conclusions

This study used uniform design method to plan the machining parameter selection problem in turning nickel alloy material. The nickel alloy material is a hard-to-cut material, so the approach and the results of this study will be beneficial in the assessment of performance of the estimate system of cutting nickel alloy material. In comparison to orthogonal design planning, the uniform design method planning in multi-factor cutting parameters can be reducing the number of experiments. The results of three verification experiments, the estimated values of prediction equation have less than in the 95% CI. In the lathe machining, the uniform design is used to arrange the experimental combination of cutting parameters (cutting speed, feedrate, cutting depth), and the model of the output data (tool flank wear, surface roughness, machining time, cutting force) derived from experiment is built by regression analysis, and the regression equation is worked out, hoping to predict appropriate prediction values conforming with statistical method effectively in different cutting parameter combinations. This study is concluded as follows [20].

  1. 1.

    According to the data of experimental combination after uniform planning, whether there is reasonable coincidence relation between variables can be discussed statistically, the relationship between tool flank wear and cutting speed, the relationship between surface roughness and feedrate and the relationships of cutting force to feedrate and cutting depth conform to correlation equation, and the number of experiments is only 20% of orthogonal array.

  2. 2.

    Which variable is a significant factor in the equation can be known according to the regression equation, in actual machining, the parameters that would affect the machining results should be taken into consideration. Therefore, the machining parameter combination suitable for different conditions can be found by simple calculation.

  3. 3.

    According to the results of three verification experiments, the estimated values of prediction equation have less than in the 95% CI, meaning the values estimated by the regression equation through the operations and test of statistical method are reliable. In terms of the errors between actual values of verification experiments and prediction values, the cutting tool wear (VB) is 2.72~6.18%, the surface roughness (Ra) is 4.10~7.72%, the machining time (T) is 3.75~8.82%, the cutting force (N) is 1.54~7.42%, and the errors of various dependent variables are approximately less than 10%. In the future, the use of regression analysis to integrate with CNC controllers has achieved the purpose of smart manufacturing