1 Introduction

Vacuum bagging is an essential process step in the manufacturing of high-performance composite components for aerospace applications. Hermetic sealing of the composite layup against the environment is crucial for part quality during curing in an autoclave. Therefore, a high effort is taken to detect leakages during vacuum bagging and before the curing process. Faulty vacuum bags might lead to complex repair work and severe impairment of the laminate quality. This case has to be avoided as good as possible.

Actual leakage detection methods are, e.g., based on the automated two-stage leakage detection process which has been patented by The Center for Lightweight Production Technology (ZLP®;) of the German Aerospace Center in Stade. The first step locates a possible leak-affected area with a sensor system which is afterwards examined by an infrared thermography system to localize the leak. But this method still has its limits and disadvantages. A new approach is introduced here which can lead to a much faster detection process with higher accuracy. Due to the exploitation of precise sensor data, there also might be the potential for the application of machine learning approaches to increase the level of automation. The data can also be used for process documentation in a digital life data sheet.

2 State of the art

2.1 Vacuum bagging for prepreg components

In the production process of composite components produced in an open-mold process, a vacuum bag is required for the curing of the part. Its primary purpose is to establish a hermetic border between the laminate and the ambient to allow a homogeneous pressure distribution onto the part to be cured. Forces created by the pressure difference are applied uniformly and normal to the surface due to the flexibility of the vacuum bag material and the principle of isostatic pressure, even if the part geometry is complex (e.g., due to reinforcement with stiffening elements). For this purpose, the vacuum film must fit as perfectly and tensionless as possible on the component in order to ensure a uniform pressure at each point. Ideally, the vacuum film will lie flat, smooth, and without wrinkles on any part geometry to prevent tentering or bridging [1].

Pressure onto the laminate is desired to compress the fiber bed and in some cases force out excess resin. This is required to gain components with high fiber volume content as needed for high-performance applications. With the help of the consolidation pressure difference during curing, the laminate adapts to the tool geometry [2]. In consequence, entrapped air is displaced and reduced from in between fiber layers and the formation of pure resin regions is counteracted. Both phenomena would otherwise result in loss of mechanical properties of the composite structure. Likewise, volatile constituents of the resin system that outgas during curing and could prevent proper bonding of the layers are displaced and transported out of the laminate by the evacuation process [3].

The effective pressure peff acting onto the laminate is described by the difference of absolute ambient pressure \(p_{\infty }\) and absolute pressure inside the vacuum bag pvac; see Eq. (1).

$$ p_{eff}=p_{\infty}-p_{vac} $$
(1)

A high degree of evacuation is needed to achieve high forces onto the laminate. During autoclave curing, the pressure acting onto the laminate is further increased by elevating the ambient pressure inside the autoclave. As evident from Eq. (1), pressure can only act onto the laminate as long as there is an existing pressure difference between the ambient and the vacuum bag. Therefore, it is essential that no leakages inside the vacuum bag allow for pressure equalization between the two volumes. The detection of a potential leakage before and during the curing process becomes thus a crucial point [4,5,6].

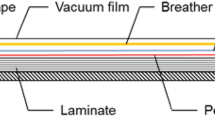
The elements of commonly used vacuum bagging systems are shown in Fig. 1. The vacuum film, the sealant tape, and the breather cloth are especially relevant for the detection of leakages, as the breather acts as the air-conducting layer inside the vacuum bag [5].

Fig. 1
figure 1

Schematic setup of a vacuum bag (based on [5])

Full size image

2.2 Leakage detection

Leakage detection in the current serial process for aircraft components mostly consists of an ultrasonic microphone and a pressure increase test. During evacuation of the vacuum bag, the sensitive ultrasonic microphone is used to detect possible leakages along the sealant tape. The flow of air leaking into a vacuum bag contains supersonic turbulent flow that can be detected with the help of this manually operated sensor.

After evacuation and holding the vacuum inside the vacuum bag for 15 to 20 min using a vacuum pump, a vacuum drop test is performed over the course of a specified amount of time (e.g., 5 min). This is the simplest method of leakage detection. Once the desired vacuum level is reached, the vacuum lines are disconnected from the vacuum bag and the pressure increase for a specified time is metered with a pressure gauge. Leakages lead to a pressure increase inside the vacuum bag while no pressure increase indicates an airtight bagging. In industrial processes, an acceptable threshold value for pressure increase is commonly given and varies between 5 and 15 mbar/min. Should the pressure increase exceed the given threshold, the leakage must be located and repaired. In older aircraft programs, this is commonly done using the previous mentioned ultrasonic microphone [7]. For specific larger parts, helium leakage detection and a test dye are used as a subsequent step to the ultrasonic detector. The functional principle of these methods is described in reference [8].

As soon as leakages are detected, they are repaired with adhesive or sealing tape. If the leakages are not detectable or too large for reworking, the vacuum film must be replaced. This process is very time-consuming and extremely dependent on the experience of the employees, which leads to additional leakage-related costs of approx. 50.5–70.5k € per year and component type [8]. Therefore, a faster and more robust process for leak detection in vacuum bags is required.

New developments range from volumetric flow measurement [3] to leakage detection with thermographic cameras [9].

3 Advanced leakage detection

In 2017, the German Aerospace Center (DLR) filed an application for a two-stage leakage detection process for high performance composite parts [10]. With the two-stage process, it is possible to reduce detection times and automate the leakage detection procedure. Right after the vacuum bagging is finished, a sensor system is used during the evacuation process to check if a leakage appears in the bag. In contrast to the pressure increase test, the system does not need any extra time (Fig. 2). Furthermore, an exact criterion for the evaluation of the airtightness is used. If a leak is detected, the sensor system identifies the area in the vacuum film where the leakages are presumably located. In the second step, a thermographic camera is used only in the determined areas to indicate the exact position of the leak. This process is expected to result in considerable time savings and has a high potential for automation. In Fig. 2, the two-stage process is compared to the conventional process.

Fig. 2
figure 2

Two-stage leakage detection process as patented by DLR; cf. [10]

Full size image

With the introduction of another test method, the volumetric flow rate measurement, the time-consuming pressure increase test can be eliminated. It is possible to draw three conclusions from the flow rate measurement during the evacuation process of the vacuum bag.

  • The existence of a leakage (identification)

  • The pressure increase caused by a leakage (severity)

  • The position of a leakage (localization)

Instead of multiple independent leakage detection methods that are used in sequence without taking each other into account, the methods used in the two-stage process are interlinked.

After identification of a leakage during evacuation, the severity of the leakage should be clear. Should the measurement exceed part specifications, an area for thermographic inspection is identified using multiple flow meters. Subsequently, a thermographic camera would be applied to locate the leakage position exactly.

4 Volumetric flow measurement

To evaluate the tow-stage leak detection process and the feasibility of the three main goals: identification of a leak, severity of the leakage (in terms of size and impact), and localization, three groups of experiments are performed. The following gives an overview about the trials related to each objective:

  • Identification

    • Flow rate behavior for (faulty) vacuum bag

    • Correlation of flow rate and leakage area

  • Severity

    • Check of vacuum loss model for fixed volume

    • Vacuum bag volume change during evacuation

    • Application of vacuum loss model onto vacuum bag

  • Localization

    • Trilateration experiments

4.1 Measurement technology

Flow rate is a physical quantity used to quantify bulk fluid movement. It describes the amount of substance or volume of a fluid that passes through an observed tubing per time unit [11]. Measurement devices used for flow measurements are divided into mass flow meters and volume flow meters based on the respective physical quantity that is used to quantify the flow. The volumetric flow rate is defined by the limit

$$ \dot{V} = \lim_{\Delta t \rightarrow 0} \frac{\Delta V}{\Delta t} = \frac{dV}{dt} $$
(2)

and directly correlated to the mass flow rate \(\dot {m}=\frac {dm}{dt}\) by the fluid’s density ρ

$$ \dot{m} = \rho\dot{V} $$
(3)

The SI units for volumetric flow rate and mass flow rate are \([\dot {V}] = \frac {\mathrm {m}^{3}}{\mathrm {s}}\) and \([\dot {m}] = \frac {\text {kg}}{\mathrm {s}}\), respectively. Furthermore, volumetric flow rate is commonly represented by the symbol Q.

In addition to direct measurement, a variety of different physical effects can be used to indirectly determine flow rates by measuring correlated physical quantities such as particle speed, for instance [11]. Furthermore, in industrial flow measurement, it is not uncommon to use relation (3) to convert a measured mass flow rate into volume flow rate that is displayed as a measurement reading [12].

Thermal flow measurement is an indirect measurement method that uses a temperature or a temperature difference to assess the mass flow rate via the specific heat capacity of the flowing medium [13, 14]. All design options of thermal mass flow meters consist of a heating unit and one or more points for temperature measurement [12, 13]. Thermal mass flow meters cover a wide measurement range down to small flow rates and show quick response behavior with only moderate costs [11]. Especially the former is of great benefit for leakage detection as the magnitude of volumetric flow rates caused by leakages varies depending on both amount and size of leakages and is small by industrial standards. Additionally, thermal mass flow meters include no moving parts, making them unsusceptible to fatigue and provide a nearly unobstructed flow path. Because volume flow rate of the medium is measured via its mass flow rate, the measurement is largely independent of process-related temperature and pressure fluctuations [11, 12].

Depending on application and magnitude of flow rate, different design options for thermal mass flow meters exist. Figure 3 shows a schematic of the measurement devices used in the course of this work, and a capillary-type sensor is used for small flow rates by industrial standards.

Fig. 3
figure 3

Bypass sensor, schematically; cf. [12]

Full size image

Two temperature measurements are performed in the flume of the sensor, while a heating unit of constant power in between emits a constant amount of heat Q (not to be confused with the volumetric flow rate as discussed earlier in this chapter) per unit time that is transferred to the flow. The temperature increase ΔTs = T − T0 of a substance is correlated to the absorbed heat ΔQ via the specific heat capacity c of that substance:

$$ {\Delta} Q = c \cdot m \cdot {\Delta} T_{s} $$
(4)

Differentiation with respect to time of Eq. 4 and rearranging yields:

$$ \dot{m} = \frac{\dot{Q}}{c{\Delta} T_{s}} $$
(5)

For constant power of the heating unit \(\dot {Q}\), the mass flow rate \(\dot {m}\) of the fluid can be computed directly based on the temperature increase, the latter being measured by the temperature sensors adjacent to the heating unit. For small mass flow rates, the molecules of the substance passing through the flume reside in proximity to the heating unit for a longer time, thus absorbing more heat and the measured temperature difference increases. Correspondingly, a high mass flow rate leaves less time for the molecules to absorb heat; thus, a smaller temperature increase is measured. A schematic of the sensor and discussed physical quantities is displayed in Fig. 4.

Fig. 4
figure 4

Physical working principle of thermal mass flow measurement, cf. [14]

Full size image

Albeit the physical quantity measured by the thermal measurement principle is the mass flow rate, the sensors used for this work are calibrated to give volumetric flow rate readings based on equation (3) using air standard density (0∘C, 1.01325 barabs) [12]. Presentation of volumetric flow rates in standardized liters (ℓn) per minute is widespread in industry because it makes measurements independent of local process temperature and pressure fluctuations possible.

4.2 Leakage detection

The first field of application of the volumetric flow meters is the identification of leakages through the flow rate. If the flow rate measurement can be used for the identification of leakages in a vacuum bagging, it would mean, that it is possible to identify leaks during the evacuation process. This can eliminate the extra process for the pressure increase step and therefore reduce production time.

To evaluate if the flow rate measurement is capable of identifying leaks a more precise understanding of its progression during evacuation of a vacuum bag with and without leakages is necessary. Flow rates from the evacuation of airtight and leaky vacuum bags, where the leaks are introduced before and after evacuation, are evaluated. Different sizes of leakages are investigated to create a possible correlation between the flow rate measurement and the leakage dimension. To create a leakage, single-use hypodermic needles of different diameters are used to puncture the vacuum film. The inserted needle remains in the vacuum film to ensure a constant and reproducible leak size with minimum deviation to the insertion process. These tests are carried out to assess whether a leakage in the vacuum bag can be identified and if the volume flow gives an indication of the size of the leakage.

When a leakage is present in the vacuum bag, a complete evacuation is not possible, due to a constant airflow into the leak. When connecting a vacuum pump, the flawed vacuum bag will evacuate until equilibrium of incoming leakage flow and outflowing air through the pump is reached. Due to the conservation of mass, in a state of equilibrium, the incoming air flow through the leakage Qin must equal the outgoing flow Qout which is shown in Fig. 5 and Eq. 6.

Fig. 5
figure 5

Premise: equilibrium of incoming and outgoing flow after sufficient evacuation

Full size image
$$ Q_{Leakage}=Q_{in}=Q_{out}=Q_{Pump} $$
(6)

If the vacuum bag is airtight, the volumetric flow rate converges towards zero with progressing evacuation process. After reaching the upper measurement limit, the volumetric flow rate measurement decreases fast in the initial process. With ongoing evacuation, the decease of volumetric flow rate per time unit reduces and causes the measurement curve to flatten. The progression of the magnitude of the volumetric flow rate for an airtight and flawed bag is shown in Fig. 6, where the different colors represent various measurements.

Fig. 6
figure 6

Flow rate progression with and without leakage and after leakage introduction with a Ø1,2-mm hypodermic needle

Full size image

As can be seen in Fig. 6, a leakage in a vacuum bag causes a notably elevated volumetric flow rate compared to an airtight bag. It makes no difference if the leak is created before or after evacuation; the volumetric flow rate converges towards the same value if the leakage is of the same size. This finding confirms that existing leakages as well as leakages that occur during the vacuum bagging process or handling of the auxiliary materials can be identified and distinguished based on the volumetric flow rate progression. Furthermore, the time required to identify a flawed vacuum bag with this method is significantly lower than the common pressure increase test that is performed after evacuation of the bag.

It can be seen that different leakage sizes in the vacuum bag cause volumetric flow rates of distinct values. Figure 7 displays the linear correlation resulting when plotting the equilibrium flow rate values over the leakage area. It was noticeable that readings for leakages created by larger hypodermic needle diameter showed more scatter in comparison to the other needle diameters. This deviation can be explained by fluctuations in the experiments, as the injection needles are inserted manually into the vacuum structure. It can happen that the size of the hole deviates from the specified size due to the insertion process. It is also possible to calculate the resulting volumetric flow for a specific leakage area by using the orifice plate equation. The results are shown in Fig. 7.

Fig. 7
figure 7

Dependency of equilibrium flow on leakage area

Full size image

As the level of equilibrium flow rate is proportional to the leakage diameter, the assumption that leakages behave like very short pipes in terms of fluid dynamics can be confirmed. Based on the observed linear correlation, a leakage area ALeakage can directly be assessed by the measured flow rate equilibrium, with cAir being the velocity of the air.

$$ Q_{Leakage}=c_{Air}\cdot A_{Leakage} $$
(7)

The experiments also show that the resulting volumetric flow rate is independent of the vacuum bag size and leakage position.

4.3 Severity of leakages

On the basis of the first tests and the fast convergence of the volumetric flow rate towards a tight or flawed level as shown in Fig. 6, a reasonable time saving is expected by replacing the current leakage detection method. To substitute the common pressure increase test described in Section 2.2, the severity of a leakage needs to be known. As the common test is based on the pressure increase rather than on a defined leakage size, it is necessary to convert the current specifications for the pressure increase per time into flow rates. A correlation between the two parameters must be found.

Since the air inside the vacuum bag can be treated as an ideal gas, as the pressure is atmosphere or lower and the temperature is room temperature, the pressure inside the bag is directly dependent on the amount of air substance inside the vacuum bag. The two sizes are connected by the ideal gas law:

$$ pV_{A}=nRT $$
(8)

Where n is the amount of air taking the volume VA inside the vacuum bag. T and p are temperature and pressure, respectively, and R is the universal gas constant.

A pressure increase over time within a fixed volume at constant temperature is only possible if the number of molecules of the gaseous substance increases simultaneously.

$$ \frac{\Delta p}{\Delta t}V_{A}=\frac{\Delta n}{\Delta t}RT $$
(9)

The left-hand side of equation (9) is commonly defined as the so-called leakage rate (10) [15].

$$ q_{L}=\frac{\Delta p}{\Delta t}V; [q_{L} ]=\frac{(mbar\cdot\ell)}{s} $$
(10)

With the introduction of the leakage rate, it is possible to quantify leakages in evacuated or pressurized containers. A leakage rate of \(q_{L}=1 \frac {(mbar\cdot \ell )}{s}\) causes the pressure inside an evacuated or pressurized volume of 1 L to increase or decrease by 1 mbar in 1 s, respectively.

Using the relation of mass, amount of substance, and molar mass \(n=\frac {m}{n}\) and rearranging yields the mass of air that has to be introduced into the vacuum bag to cause a given pressure increase.

$$ \frac{\Delta m}{\Delta t}=\frac{\Delta pV_{A}M}{\Delta tRT} $$
(11)

The connection of mass to volume by the density ρ allows the reformulation of the equation (11) in terms of volume that is to be added to cause a given pressure increase inside the vacuum bag over time.

$$ \frac{\Delta V}{\Delta t}=\frac{\Delta pV_{A}M}{\Delta tRT\rho} $$
(12)

The volume of air that is flowing into the vacuum bag through a leakage is measured by the volumetric flow rate Q. Approximating Q to be constant throughout the process, i.e., \(Q=\frac {dV}{dt}=\frac {\Delta V}{\Delta t}\), then a correlation of volumetric flow rate and pressure increase is given as:

$$ Q=\frac{\Delta pV_{A}M}{\Delta tRT\rho} $$
(13)

An evacuated vacuum bag of volume VA will experience a pressure increase of Δp per time Δt if a constant volumetric flow rate of air Q enters through a leakage.

The accuracy of the pressure increase model is estimated to be faim = ± 10% which would be acceptable for manufacturing purposes.

The functionality of the model is verified experimentally for a rigid container within the expected accuracy. The purpose of this experiment is the controlled introduction of a leakage into a rigid vessel and the measurement of the occurring volume flow and the associated pressure increase inside this container (see Figs. 8 and 9).

Fig. 8
figure 8

Resin trap: experimental setup

Full size image
Fig. 9
figure 9

Progression of pressure inside the resin trap; leakages created with different hypodermic needle diameters

Full size image

Unlike a rigid container, a vacuum bag has flexible borders and changes its volume during the evacuation process. This phenomenon is caused by the breather material, which is compressed under vacuum and relaxes at a low pressure difference, resulting in a non-linear progression of the pressure increase over time, as shown in Figs. 10 and 11.

Fig. 10
figure 10

Vacuum bag: experimental setup

Full size image
Fig. 11
figure 11

Progression of pressure inside the vacuum bag; leakages created with different hypodermic needle diameters

Full size image

A second experiment is performed to prepare the use of the pressure increase model for variable size vacuum bags. The outflow volume of a vacuum bag is measured for evacuation from different absolute pressures. As seen in Figs. 12 and 13, below a pressure of 600 mbar, it is found that vacuum bags constructed with an Airtec Ultraweave 1332 breather [16] behave like a hypothetical rigid container that has a volume of 1.3 ℓn for every square meter of breather inside the vacuum bag.

Fig. 12
figure 12

Vacuum bag air content throughout evacuation process

Full size image
Fig. 13
figure 13

Resin trap air content throughout evacuation process

Full size image

To verify the correlation between the volumetric flow rate and the pressure increase over time, a third experiment is performed. Different sized vacuum bags are punctured with hypodermic needles of various nominal diameters to introduce controlled leakages. The resulting pressure increase is logged to calculate pressure differences over distinct time periods. With the knowledge gained from the previous tests, it is possible to calculate the resulting volumetric flow rates on the basis of the given pressure increase over time and vice versa. Here, too, an accuracy of ± 10% below an absolute pressure of 600 mbar has been confirmed and can be achieved under special conditions:

  • Consideration of remaining volumetric flow rate for small leakages during evacuation

  • Prevention of pressure gradient formation in large vacuum bags by using vacuum channels or flow aids

No influence of the vacuum bag size on the functionality of the vacuum loss model can be detected, with the exception of small vacuum bags with large leaks. The rapid aeration does not allow the formation of a linear pressure rise in the available measurement resolution and the pressure rise model is not applicable.

The position of a leak in a vacuum bag does not affect the functionality of the pressure increase model.

The results show that the volumetric flow rate measurement is a worthwhile replacement of the commonly used pressure increase test. The current part specification for the acceptable pressure increase over a certain period of time can be converted into a volumetric flow rate. By measuring the flow rate during evacuation, it can be checked whether the pressure inside the vacuum bag would exceed the allowable pressure threshold. With this model, all sizes and shapes of vacuum bags are covered, if specific equivalent rigid volumes are used. For serial production, it is advisable to measure the actual equivalent rigid volume of the part to be tested, as for specific vacuum setups, especially for complex geometries, the volume might vary.

4.4 Leakage localization

To speed up the detection process, the localization of the leakage when using multiple volumetric flow meters is desired. If the incoming air flow through the leak is divided in a certain pattern into separate vacuum lines depending on their distance to the leakage, it would be possible to draw conclusions about its location. To achieve this, it would be necessary to measure and compare the individual volumetric flow rates at several distributed vacuum connections.

The position of a point in two-dimensional space is sufficiently described by its distance to three fixed reference points. This method of localization is called trilateration and depicted in Fig. 14. The leakage is located in the intersection of the resulting radii. The more accurate the measurements, the smaller the resulting area.

Fig. 14
figure 14

Principal of trilateration

Full size image

Based on the trilateration localization principle, a vacuum bag in the shape of an equilateral triangular is used for the first trial, as shown in Fig. 15 [17]. Since conservation of mass holds true, the incoming flow through the leakage equals the sum of the individual subflows for an equilibrium state:

$$ Q_{in}=Q_{Leakage}=Q_{1}+Q_{2}+...+Q_{n}=Q_{out} $$
(14)
Fig. 15
figure 15

Experimental setup with triangular vacuum bag

Full size image

It is observed that the volumetric flow rate caused by a leakage is divided among the three vacuum connections in a distinct pattern. As seen in Fig. 16, the distribution is related to the respective distance of leakage to the vacuum ports. The leakage size has no influence on the resulting pattern.

Fig. 16
figure 16

Distribution of volumetric flow rate for a single Ø 0.8 mm needle leakage at different locations with three vacuum lines

Full size image

A qualitative comparison of the flow rate distribution at different leakage positions enabled the triangle to be divided into twelve sectors, as shown in Fig. 17. The affected area with the leakage can be identified and investigated with further detection methods.

Fig. 17
figure 17

Qualitative partitioning approach for determination of leakage area

Full size image

In a first attempt of trilateration, the measured flow percentage of a vacuum connection is correlated to its distance to the introduced leak. This correlation results in a radius around a specific vacuum connection on which the leakage is located. The calculation works with an acceptable accuracy as long as the leak and vacuum port are located in the same of the three large sectors. Once the leak is outside the sector, a significant loss of accuracy is observed, which is shown in Fig. 18.

Fig. 18
figure 18

Decreasing accuracy with increasing leakage distance when using analytical trilateration

Full size image

To refine the localization with trilateration, further trials are required. Nevertheless, combined with the partitioning approach, it can be used to further define the position of the leakage in a previously narrowed down area. Once a section with a potential leakage position has been identified, the trilateration approach can be used to obtain a radius around the nearest vacuum port. In this way, the possible leak position is reduced to a radius segment limited by the section borders.

This principle is universal and can be applied to all possible forms of vacuum setups. A prerequisite for this is the use of breather material over the wide area within the vacuum assembly and a minimum number of three vacuum connections on the component, positioned as far apart as possible and evenly distributed over the component.

5 Thermographic leakage detection

The theory of infrared (IR) thermography is based on the fact that the total radiation Wtot that is received by the camera sensor is compiled from three sources: object radiation, Wobj, radiation that is reflected from the objects surroundings, Wref and atmospheric radiation, Watm [18,19,20,21]. Equation 15 describes this context.

$$ W_{tot} = W_{obj}+W_{ref}+W_{atm} $$
(15)

Expanded, Eq. (2) looks as follows

$$ W_{tot} = \varepsilon\tau\sigma T^{4}_{obj} + (1-\varepsilon)\tau\sigma T^{4}_{ref} + (1-\tau)\sigma T^{4}_{atm} $$
(16)

where σ is the Stefan–Boltzmann constant and equal to \(5.67\cdot 10^{-8}\frac {W}{mK^{4}}\), ε being the emissivity of the object, τ being the atmosphere transmittance parameter, Tobj being the temperature of the object, Tref being the temperature of the object surroundings reflected toward the camera, and Tatm being the atmospheric temperature.

For the leakage detection, the vacuum bag is scanned with the thermographic camera. The vacuum film on top has a transmission for IR-radiation of 60–90%, depending on the vacuum film used. The camera is able to detect the temperature of the breather material beneath, and thus show a temperature deviation due to a leakage [22].

The leakage detection system using infrared thermography and patented by DLR is based on the Joule-Thomson effect [9]. The effect describes how the air as a non-ideal gas also undergoes changes in temperature during an isenthalpic pressure reduction. Air flowing into the vacuum bag through a leakage expands inside the lower pressurized vacuum bag, thereby cooling itself and the surrounding material down [23]. This local temperature decrease in direct proximity to the leakage can be identified as a cold spot in the image acquired by the thermal camera. To achieve a well-detectable decrease in temperature, it is beneficial to evacuate a faulty vacuum bag to the maximum achievable degree.

This technique is simple to use, and a contact-free process meaning its application for leakage detection has no impact on the composite part quality or the vacuum bag. As an imaging method, it allows for quick and exact identification of the leakage position. In addition, leakages have a characteristic temperature profile, which facilitates automated recognition and analysis of the thermal image [22]. The thermogram of a leakage and a characteristic temperature profile are shown in Fig. 19.

Fig. 19
figure 19

Thermogram of a leakage and characteristic temperature profile

Full size image

6 Conclusion

To improve the two-stage leakage detection process for a more reliable and automated identification of leaks, volumetric flow rate measurement was investigated. The tests showed that volumetric flow meters are not only able to detect the presence of a leakage in a vacuum bag, but can also provide information on the severity and location of the leakage.

Since the sensors are integrated outside of the vacuum bag into the vacuum line, they do not interfere with the ancillary materials or the part itself and are removed before the autoclave process. A measurement during the autoclave curing can be performed if the flow meters are installed outside of the autoclave in the vacuum lines. In processes with resin infusion, precautions must be taken to avoid contact of the resin with the volumetric flow meters.

Originally, volume flow measurement was intended exclusively for the identification of defective areas of a vacuum bag in preparation for thermographic leak detection. However, further investigations showed that the interpretation of volume flow measurements offered additional applications. In addition to leakage localization, volume flow meters have proven to be useful as a replacement for the usual pressure increase test after appropriate preparatory work.

In combination with infrared thermography, a complete leak location process could be realized, as shown in Fig. 20.

Fig. 20
figure 20

Conceivable application of volumetric flow measurement in automated leakage detection

Full size image

The implementation of volumetric flow meters for leakage detection is expected to offer a high savings potential. As the flow rate is measured directly during the evacuation process, the time for the pressure increase test can be eliminated. This is associated with a saving of approx. 15 min per part, as each component must pass a leak test before the autoclave process. The process effort for leak detection and localization can be reduced, whereby the latter can even be skipped depending on the assessed severity of the leakage. By interlinking the detection and localization methods in the two-stage leakage detection, the process time can be reduced from about 5 h to only 1 h conservatively calculated for a 60-m large part. This results in a process time reduction of up to 80%. In combination with an evaluation algorithm and thermographic leakage localization, volume flow measurement is a promising sensor system for fully automatic leakage detection.