A mechanical model of axial and circumferential bidirectional deformation for large thin-walled pipes in the process of continuous and synchronous calibration of roundness and straightness by three rollers

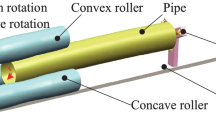
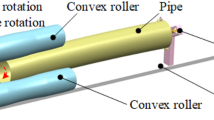
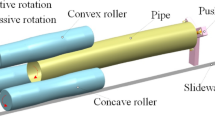
Abstract

In this paper, a mechanical model of axial and circumferential bidirectional deformation has been developed by considering two factors: roller shape and radial reduction. Since the calibration of the roundness and that of the straightness of pipes are currently separate processes, the established mechanical models are based on a single direction. However, the established bidirectional mechanical model can describe not only the stress-strain distribution of the pipe in deformation to determine the position of the stress concentration but also the deformation curve of the pipe in different directions. As a result, it can serve as a theoretical basis for setting process parameters and optimizing roller shape. A large thin-walled pipe of Al6063 is modeled and then numerically simulated with FEM software of ABAQUS, and the results are compared with the model. Then, the process is fabricated and tested experimentally. The results are compared with the mechanical and numerical models. The distribution of equivalent stress and equivalent strain obtained by the model has a good match with the simulation results, and the maximum relative error is not more than 25%. The axial and circumferential deformation curve calculated by the mechanical model coincides well with the simulation and experimental results, and the maximum error is not greater than 3.0 mm. Obviously, both the experiment and the simulation have verified a superior validity of the model.

Graphical abstract

Appendices

Equation (30) can be simplified as follows:

$$ {a_1}^6+{a_1}^4\left(3{b_1}^2-3{r}^2\right)+{a_1}^2\left(3{b_1}^4-7{b_1}^2{r}^2+3{r}^4\right)+{b_1}^6-3{b_1}^4{r}^2+3{b_1}^2{r}^4-{r}^6=0 $$

(44)

If a is made to be 3b₁² − 3r², b is 3b₁⁴ − 7b₁²r² + 3r⁴, c is b₁⁶ − 3b₁⁴r² + 3b₁²r⁴ − r⁶, and a₁² is y, the following equations can be obtained.

$$ {y}^3+{ay}^2+ by+c=0 $$

(45)

By substituting y = x − a/3 into Eq. (45), the form of x³ + px + q = 0 can be given as follows:

$$ {x}^3+\left(b-\frac{a^2}{3}\right)x+\frac{2{a}^3}{27}+c-\frac{ab}{3}=0 $$

(46)

where $p=b-\frac{a^2}{3}$; $q=\frac{2{a}^3}{27}+c-\frac{ab}{3}$. A real number solution is given by Eq. (46), such as Eq. (47).

$$ x=\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}} $$

(47)

The following conclusions can be drawn, as shown in Eq. (48).

$$ {a_1}^2=y=\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3} $$

(48)

The curve PQ can be obtained by substituting Eqs. (48) and (28) into Eq. (26).

$$ \left.\begin{array}{l}\frac{{x_1}^2}{\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}}+\frac{{y_1}^2}{{\left(r-H\right)}^2}=1\\ {}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\kern1.00em \left(-{m}_1\le {x}_1\le {m}_1;{y}_{m_1}\le {y}_1\le r-H\right)\end{array}\right\} $$

(49)

Substituting Eq. (37) into Eq. (36), and making a ₂ ² = z, x ₂ ² = z + m ₂ ², the cubic equation with a variable z can be expressed as follows:

$$ {z}^3+{z}^2\left(6{m_2}^2-{r}^2\right)+12{m_2}^4z+8{m_2}^6=0 $$

(50)

where ${m}_2=r\sin \frac{2\pi -6\arcsin \frac{m_1}{r}}{6}$ (see Appendix C for details). Similarly, the following can be obtained by making e = 6m₂² − r², f = 12m₂⁴, and g = 8m₂⁶.

$$ {z}^3+{z}^2e+ zf+g=0 $$

(51)

Let $z=x-\frac{e}{3}$ and substitute it into Eq. (51); Eq. (52) can be obtained.

$$ {x}^3+\left(f-\frac{e^2}{3}\right)x+\frac{2{e}^3}{27}+g-\frac{ef}{3}=0 $$

(52)

where ${p}_1=f-\frac{e^2}{3}$, ${q}_1=\frac{2{e}^3}{27}+g-\frac{ef}{3}$. A real number solution is given by Eq. (52), such as Eq. (53).

$$ x=\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}} $$

(53)

The following conclusions can be drawn, as shown in Eq. (54).

$$ {a_2}^2=z=\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3} $$

(54)

By substituting Eq. (54) into Eq. (35), the curve WT can be expressed as follows:

$$ \left.\begin{array}{l}{x_2}^2-{y_2}^2=\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3}\\ {}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\kern1.00em \left({a}_2\le {x}_2\le {x}_{m_2};-{m}_2\le {y}_2\le {m}_2\right)\end{array}\right\} $$

(55)

As can be seen from the fact that three reverse bending regions and three positive bending regions are evenly distributed across the circular cross-section of the pipe, the angle corresponding to the region is also evenly distributed.

$$ {\theta}_{\mathrm{T}}+{\theta}_{\mathrm{F}}=\frac{2\pi }{3} $$

(56)

where θ_T is the angle corresponding to the reverse bending region, and θ_F is the angle corresponding to the positive bending region. The geometric relationship can be obtained in Fig. 13 and Fig. 14.

$$ \left.\begin{array}{l}\sin \frac{\theta_{\mathrm{T}}}{2}=\frac{m_1}{r}\\ {}\sin \frac{\theta_{\mathrm{F}}}{2}=\frac{m_2}{r}\end{array}\right\} $$

(57)

Equation (57) is substituted into Eq. (56), and Eq. (58) and Eq. (59) can be obtained.

$$ {\theta}_{\mathrm{F}}=\frac{2\pi }{3}-2\arcsin \frac{m_1}{r} $$

(58)

$$ {m}_2=r\sin \frac{2\pi -6\arcsin \frac{m_1}{r}}{6} $$

(59)