1 Introduction

Maraging steels are categorized as FeNi alloys with dominating martensitic microstructure at room temperature. This class of alloys can be hardened through a uniform precipitation mechanism, reflecting the name maraging steel (martensitic + ageing). Maraging steels are usually graded by the nominal axial tensile strength in the imperial unit ksi (or sometimes in MPa), which depends on the chemical composition. In additive manufacturing (AM), specifically laser beam powder bed fusion (PBF-LB/M), maraging steel grade 300 is the most commonly used grade [1]. The steel is also known as 18% Ni maraging 300 (USA), 1.2709 (Europe), and X3NiCoMoTi 18-9-5 (Germany). The material is easily machined in its annealed state, while higher strength and hardness can be obtained after proper ageing heat treatment [2, 3], making it suitable for several applications. Among other applications, the PBF-LB/M material is used in the tooling industry such as injection moulding [4] and aluminium casting [5,6,7].

The mechanical properties of maraging steel grade 300 (hereafter denoted as 18Ni300) processed by PBF-LB/M depends on several variables in the AM process chain. In the AM value chain, three factors, namely, feedstock properties, PBF-LB/M process parameters, as well as post-processing conditions, influence the mechanical response of the material. Feedstock properties such as particle size distribution and morphology, chemical composition, and apparent density directly affect the processability of the material [8], while laser processing parameters such as laser power (P), laser scan velocity (v), hatch spacing (h), layer thickness (t), and scan strategy influence the relative density, microstructure, and mechanical properties. Post-processing such as solution annealing will soften the material and allow for easy machining [2], while precipitation hardening will increase the hardness and strength [9, 10] at the expense of bulk ductility.

Unique to AM and PBF-LB/M in particular, materials develop a fine-grained columnar microstructure due to the rapid and directional cooling conditions and epitaxial growth [10]. Because of the disproportional grain geometry, the columnar microstructure may result in anisotropic behaviour [11,12,13]. Due to increased geometrical complexity, understanding the influence of build orientation on the mechanical response of the additively manufactured materials is of great importance. Table 1 summarizes the tensile properties of PBF-LB/18Ni300. There is significant variation in elastic modulus, yield strength, ultimate tensile strength, and elongation at fracture between the different studies. Build orientation, processing parameters, and heat treatment schemes all influence the mechanical properties. Mooney et al. [9] investigated the influence of build orientation and heat treatments on the plastic anisotropy of PBF-LB/18Ni300 and observed considerable anisotropy in the material, especially in the as-built condition. They reported that tailored heat treatments can reduce the anisotropy at the expense of material’s yield strength. Vishwakarma et al. [14] demonstrates how the ductility can be significantly approved (elongation at fracture above 10%), but at the cost of a large reduction in strength. With the exception of the latter study, the elongation at fracture ranges between 1.7 and 6.1%. The yield strength and ultimate tensile strength are in the range of 1700–2100 MPa. The elastic modulus ranges from 142.5 GPa found by Wu et al. [15] to 219 GPa found by Becker et al. [16]. The ageing temperature of 550 °C in the latter study might explain the low elastic modulus.

Table 1 Summary of orientation-dependent tensile properties of PBF-LB/18Ni300
Full size table

There are two main sources of anisotropy: preferred crystallographic orientation and alignment in the microstructure of secondary phases and inclusions [21]. The latter is typically the main contributor to plastic anisotropy, while the former is often observed in elastically anisotropic materials. The PBF-LB/M is known to bring on both sources of anisotropy in a range of materials [9, 11, 13, 21,22,23]. In metals with cubic crystal structure, the plastic anisotropy resulting from preferred crystallographic orientation is limited because of numerous slip planes that can be activated in different orientations. This suggests that microstructural alignment of the secondary phases and inclusions are more likely to prevail. Xiong et al. observed that the fracture occurred along the melt pool boundaries (MPB) and that the fraction of load-bearing MPBs in the cross-section can be a source of anisotropic plastic tensile response [24].

The heat treatment for PBF-LB/18Ni300 is typically (as suggested by material vendors) a two-stage treatment starting with a solution treatment followed by ageing. The standards are not developed for AM applications. However, the recommended solution treatment, ageing temperatures, and holding times might not be appropriate for the PBF-LB/M material. Bai et al. [10] investigates the effect of temperature and holding time for solution treatment and ageing of PBF-LB/18Ni300 and finds that a good combination of hardness and strength is achieved with a direct ageing at 520 °C for 6 h. As shown by Mooney et al. [9], this heat treatment scheme also reduces the plastic anisotropy, yet higher strength can be achieved with lower ageing temperatures.

Although plastic anisotropy of PBF-LB/18Ni300 is set forth in preceding articles, this study provides a systematic investigation of the strain behaviour in both the elastic and plastic regions of the flow curve of tensile specimens built in seven different orientations in the PBF-LB/M process subjected to two different heat treatments. Digital image correlation (DIC) is utilized to capture the strain fields on the surface of rectangular tensile specimens. By using tensile tests with DIC combined with microstructure investigation, this study demonstrates how the fraction of load bearing melt pool boundaries directly influences the transverse strain anisotropy. Furthermore, it is demonstrated how this effect can be minimized by opting for a solution annealing heat treatment prior to precipitation hardening.

2 Material and methods

2.1 Specimen preparation

A total of 42 tensile specimens were prepared in a Concept Laser M2 Cusing PBF-LB/M machine in a nitrogen atmosphere with monitored oxygen content below 0.2%. The feedstock material was supplied by Sandvik Osprey®. The nominal chemical composition is provided in Table 2. The powder morphology was analysed with a Malvern Morphologi G3 system. A particle size distribution with a mean diameter of 24 μm, a lower cut-off at 5 μm, and upper cut-off at 63 μm was characterized. The average circularity of the powder particles is 0.93, where a circularity of 1 indicates a perfect circle [25]. Laser parameters for the PBF-LB/18Ni300 specimens were determined in a previous study [26] and are summarised in Table 3.

Table 2 Nominal chemical composition of 18Ni300
Full size table
Table 3 Processing parameters [26]
Full size table

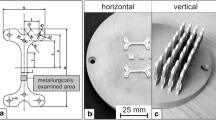
The tensile specimens were prepared in two sets of 21 specimens, subjected to different heat treatments (HT). Within each set, three identical specimens were prepared at 0°, 15°, 30°, 45°, 60°, 75°, and 90° angles with respect to the building plate. The specimens were built using the ‘island’ scan strategy from concept laser with 5 mm × 5 mm islands with an angular shift of 45° and XY shift of 1 mm. Following PBF-LB/M processing, the tensile specimens were machined to target standard dimensions according to Fig. 1 in order to preclude the process induced surface roughness effects. The two different heat treatments are solution treatment (815 °C, 1 h) plus ageing (500 °C, 5 h), denoted as SA + A, and direct ageing (500 °C, 5 h), denoted as DA. All specimens were rotated 5° around the Z-axis to avert the re-coater colliding with long flat edges of the samples, intending to mitigate powder coating failures. The specimens were built in two separate builds, depending on the HT. Overhanging samples were built with block-type support structures, which were removed using electrical discharge machining (EDM). Figure 2 illustrates the orientations of all the specimens.

Fig. 1
figure 1

Dimensions of tensile specimens. All dimensions in mm. AOI 1 and 2 indicate the strain fields captured with the digital image correlation system

Full size image
Fig. 2
figure 2

Illustration of the specimens on the build plate

Full size image

2.2 Mechanical evaluation

The tensile tests were carried out in an MTS 809 Axial Test System with a 100 kN load cell at room temperature, equipped with a DIC system from Vic3D to capture the evolution of strain fields. A detailed description of the DIC setup is provided in [27]. Post-processing of the DIC data was performed in a combination of Vic3D Version 7 and self-developed MATLAB code.

2.3 Microstructure investigation

The microstructure was characterised using scanning electron microscopy (SEM) after electro-etching of the samples using Struers A2 electrolyte solution with vendor's recommended steel etching parameters. The fracture surfaces after tensile testing were also investigated by SEM. A selective area of the material in the SA + A was investigated by the electron backscattered diffraction (EBSD) technique to understand the crystal orientation and microstructure of the material. The EBSD maps were acquired from an area of 300 μm × 300 μm and scanned with a step size of 200 nm corresponding to 2000 datapoints. The details of the microscopy and EBSD methods are given in [11] by the current authors.

3 Results and discussion

3.1 Mechanical properties

Figure 3 shows the engineering stress and Lagrange strain for one tensile specimen for each orientation for direct ageing (a) and solution treatment + ageing (b). Except for elongation at fracture, the flow curves are relatively homogeneous with respect to HT and orientation. The elongation at fracture is comparable for the two HT conditions, except for the 90° orientation in the SA + A condition, which is significantly lower compared to the DA condition. The elongation at fracture for the 15° orientation is also significantly lower compared to the other orientations for both HT conditions.

Fig. 3
figure 3

Engineering stress and Lagrange strain plotted for a selected specimen of each orientation for direct ageing (a) and solution treatment + ageing (b)

Full size image

Figure 4 shows selected tensile properties plotted against the build orientation for the two HT conditions. The average elastic modulus is 179 ± 5.0 GPa and 180 ± 2.0 GPa for DA and SA + A conditions respectively, slightly below the reference value at 183 GPa for bar stock aged at 482 °C [17]. The results suggest that the build orientation slightly influences the elastic modulus in the DA condition. It appears that the material is slightly stiffer when loaded at angles around 45°. Both the magnitude and orientation dependency of the elastic modulus are consistent with previously reported findings with similar HT procedures [9]. The stiffest orientation (60°) is approximately 8% stiffer compared to the least stiff orientation at 90°. In the plastic region of the flow curve, a yield strength of 1900 ± 30 MPa and 1920 ± 10 MPa and ultimate tensile strength of 1960 ± 30 MPa and 1990 ± 20 MPa for DA and SA + A conditions respectively are observed. This is within the expected values reported in the literature (Table 1) and compares well with the reference values in the Metallic Materials Properties Development and Standardization (MMPDS-11) report [17]. There is no obvious dependency on build orientation in the yield strength and ultimate tensile strength. The elongation at fracture is 4.23 ± 1.83% and 4.24 ± 1.48% for DA and SA + A respectively, with a significant variation at certain orientations. In the literature elongation at fracture, values are reported in a range between 1.7 and 6.1% depending on HT and processing conditions (Table 1), with a design value indicated at 4% at 0° increasing to 5% at 90° [17]. The elongation at fracture at 15° orientation is considerably lower compared to the remaining orientations (except for SA + A 90°).

Fig. 4
figure 4

Elastic modulus (a), yield strength (b), elongation at fracture (c), and ultimate tensile strength (d) plotted against build orientation for both HT conditions. Reference values are for bar stock aged at 482 °C [17]

Full size image

Due to the relatively homogeneous elastic and plastic tensile properties with respect to orientation, it is hard to draw any conclusions about anisotropy based on the tensile tests as shown in Fig. 3 and Fig. 4. Further investigation of the DIC strain fields as well as SEM imaging with EBSD is needed to shed light on the subject.

3.2 Strain field analysis

To investigate the anisotropy, the strain fields captured by DIC are analysed. The DIC setup captures the strains in the local X, Y, and Z directions of the specimens as indicated in Fig. 1. Each specimen is oriented such that the local XY plane of each specimen is parallel to the build direction, and the local YZ surface is built at the indicated angles (Fig. 2). In an isotropic material, the transverse strains in the specimen Y and Z directions should be equal, in both the elastic and plastic regions of the flow curve. The transverse strain ratio, or Lankford coefficient, in the plastic range of the flow curve has been used to quantify anisotropy in sheet metal since the early 1950s [28]. The Lankford coefficient, r, can be expressed as r = Δϵy/Δϵz for an axial load in the X direction, where Δϵy is the change in strain in the specimen Y direction and Δϵz is the change in specimen Z direction (see specimen directions in Fig. 1). If the Lankford coefficient is unequal to one, the material must be considered anisotropic in the plastic region. Recent works by Mooney et al. have utilized the Lankford coefficient to quantify plastic anisotropy in PBF-LB/18Ni300 [9, 29]. A similar approach is shown in Fig. 5 where the measured plastic strain ratio is shown with solid lines (measured between the yield strength and 2% elongation for each sample). The dashed lines in Fig. 5 represent the elastic strain ratios measured in the elastic part of the flow curve for each sample. The calculated elastic strain ratios (dotted lines) are estimated from the elastic constants of the compliance matrix in Hooke’s law [30], using the relationship described in Eq. (1) assuming ϵxx = ϵyy in the machine coordinate system.

$$ {r}_{el}\left(\theta \right)=\frac{{\mathit{\cos}}^2\left(\theta \right){\mathit{\sin}}^2\left(\theta \right)\left(\frac{2}{E_{xx}}-\frac{2}{G_{xy}}\right)+\left({\mathit{\cos}}^4\left(\theta \right)+{\mathit{\sin}}^4\left(\theta \right)\right)\frac{-{\nu}_{xy}}{E_{xx}}}{{co\mathrm{s}}^2\left(\theta \right)\frac{-{\nu}_{xz}}{E_{zz}}+{\mathit{\sin}}^2\left(\theta \right)\frac{-{\nu}_{zx}}{E_{zz}}} $$
(1)
Fig. 5
figure 5

Elastic and plastic strain ratios as a function of build orientation, shown with polynomial fits. An isotropic material would have a transverse strain ratio of 1

Full size image

In Eq. (1), Exx is the elastic modulus of the 0° specimen, and Ezz is the elastic modulus of the 90° specimen. θ is the specimen build angle with respect to the build plate. Gxy = Exx/2(1 + νxy ), and νxy, νzx, νxz are Poisson ratios determined using the strains in the respective directions according to the different specimen orientations. The measured elastic strain ratios are determined as Rel = Δϵz/Δϵy, where z and y denote the local specimen directions indicated in Fig. 1.

3.2.1 Plastic transverse strain ratios

The plastic strain ratios of the 0° specimens are close to rpl = 1 for both HT conditions, indicating isotropic straining at this orientation. rpl takes a value of approximately 0.8 at 45° for the DA HT condition, and rpl = 0.75 for the SA + A HT condition. For the 90° specimens, the plastic strain ratio is slightly higher than rpl = 0.8 for both HT conditions. Mooney et al. [9] reports plastic strain ratios of approximately 0.6 for the 0° specimens and between 0.5 to 0.6 for the 90° specimens depending on the HT condition. The same trend is observed, where the plastic strain ratio for the 45° specimens is lower compared to the 0° and 90° specimens. Figure 6 shows the transverse strain field of a DA45° specimen, where it is clearly indicated that the transverse strain in the specimen Y direction is significantly higher than the Z direction in the plastic part of the flow curve. Even though the tensile properties do not indicate plastic anisotropy, the DIC strain fields reveal that the material favours straining in certain directions depending on the build orientation.

Fig. 6
figure 6

Transverse strain field of DA 45° specimen in the plastic region. Note the high strain in the y direction compared to the z direction

Full size image

3.2.2 Elastic transverse strain ratios

The calculated elastic strain ratio is estimated based on the assumption that the material is transversely isotropic, i.e., ϵxx = ϵyy in the machine coordinate system. This leads to rel,c = 1 for the 0° and 90° specimens. As illustrated in Fig. 5, this assumption is not valid for either of the HT conditions at 90° since the measured transverse strain ratio is unequal to one. Even though νxy ≠ νzx, the calculated transverse strain ratio for the 0° specimens suggests isotropic straining. The latter holds true for the SA + A HT condition, but for the DA condition, the material heavily favours straining on the surface parallel to the build direction, particularly for the low angle specimens. In the DA condition, the material has close to isotropic straining in the 60° build orientation, whereas the SA + A condition has close to isotropic straining in the 0° build orientation.

A potential explanation to the favoured straining can be found in the number of melt pool boundaries (MPB) in the different directions. The number of MPBs in the specimen Y and Z directions can be approximated geometrically. Consider the schematic in Fig. 7 where the laser tracks are indicated on the specimen surface. The number of laser tracks in the build plane can be expressed by the specimen height, H, specimen width, w, layer thickness, t, hatch spacing, h, and the angle from the build plate θ. For any θ between 0° and 90°, the number of MPBs in the specimen Y direction can be expressed as H/t × sinθ + w/h × cosθ. The number of MPBs in the specimen Z direction can be expressed as w/h.Note that this assumes only one MPB for each laser line, since only the fraction of MPBs are of interest. The fraction of MPBs in the specimen Y direction over MPBs in the specimen Z direction is shown in Fig. 7. The measured elastic transverse strain ratio in the DA condition (Fig. 5) clearly indicates that when the fraction of MPBs in the specimen Y direction is low, the material favours straining in that direction, and as the fraction of MPBs increase, the straining is more uniform in the two directions. As will be discussed later, the MPBs are clearly present in the DA condition, while not visible in the SA + A condition. A consequence of this observation is that the anisotropy cannot be accurately modelled under the assumption that the material is transversely isotropic, with symmetry around the axis of the build direction.

Fig. 7
figure 7

Fraction of MPBs in the specimen Y direction over specimen Z direction as a function of specimen orientation

Full size image

The solution treatment before ageing appears to partially reduce the elastic anisotropy, although it is not eliminating it completely. In the plastic part of the flow curve, the solution treatment seems to have a negligible effect on the anisotropic straining. A potential explanation for why the elastic anisotropy is reduced by solution treatment is that the microstructure is textured in the as-built condition, which is recrystallized in the SA treatment, and thus the texture strength is reduced. This would also explain why only the elastic anisotropy is reduced by SA treatment, assuming that the source of the plastic anisotropy is strongly related to MPB or grain boundary decoration and not texture.

3.3 Microstructure investigation

To understand the underlying mechanism of unequal straining, the microstructure has been investigated using SEM and EBSD. Figure 8 shows a micrograph of the as-built microstructure, with several distinct process induced features. A cellular microstructure is observed, and the coarseness of the structure is dependent on the thermal cycling history of the specific area. Arrow 1 shows a fine cellular structure that is formed in the middle of the fused area, namely, the molten pool, while arrow 2 shows a coarser structure. Arrow 3 shows a melt pool boundary (fusion line) crossing a previously molten area. In the vicinity of the fusion line, the material undergoes a thermal cycle without being melted. In those regions, the temperature reaches the austenitization temperature of the material, and the grains transform to austenite. For the given time interval, the grains grow, and upon martensite transformation, coarser microstructure is formed. Such coarsening could be observed between the fusion lines in the illustrated cross section. Arrow 4 points to precipitates assumed to form only when the material is kept above a critical temperature for an extended period of time [31]. The precipitates observed in the microstructure are likely contributing to the anisotropy, as reported by several authors [9, 21, 22], where the precipitates are dispersed along elongated grain boundaries and block the movement of dislocations within the crystal structure.

Fig. 8
figure 8

SEM image of the as-built microstructure. (1) Indicates a fine cellular structure; (2) indicates a heat affected zone with cell growth; (3) shows a melt pool boundary; (4) precipitates in the AB condition

Full size image

When the material is heat treated, some of the process induced features tend to abate. Figure 9 shows the microstructure after DA (a) and SA + A (b) heat treatments. In the direct ageing condition, the melt pool boundaries are still distinctive, but not to the extent that was observed in the as-built condition. Furthermore, the microstructure is composed of lamellas, which appears to align with the heat flux direction during initial solidification (indicated by arrows in Fig. 9a). This provides a potential reason for the anisotropy in the angled specimens. When the material first solidifies during the PBF-LB/M process, the high atomic density vector <110> of the primary austenite face-centred cubic (FCC) crystal structure aligns with the direction of the heat flux [32]. As martensite transformation happens during cooling, the orientations of the martensite plates are directed by the Kurdjumov-Sachs (K-S) orientation relationship [33], and the martensite plates align with the heat flux direction. Furthermore, as seen in Fig. 10 a and b, the precipitates formed during ageing are dispersed on the martensite plates, acting as barrier against dislocation movement along the heat flux direction. This is exemplified in the DA0° specimen, which favoured elastic straining on the surface parallel to the build plate, perpendicular to the martensite plates, as can be seen from the transverse strain ratio in Fig. 5. Even though there is local anisotropy, there is no significant variation in yield stress with respect to build orientation (Fig. 4). Only one component of the stress tensor is influenced by this, and the overall yield stress of the differently oriented specimens conforms to the same magnitude.

Fig. 9
figure 9

SEM images of a DA condition; b SA + A condition. Arrows in (a) suggest the solidification direction

Full size image
Fig. 10:
figure 10

SEM image of a DA condition; b SA + A condition at higher magnification showing precipitation along the martensite plates

Full size image

When the material is solution treated before ageing, the microstructure recrystallizes, and the melt pool boundaries are no longer vividly visible. Nevertheless, the strain ratios still indicate plastic anisotropy, likely due to the precipitates dispersed on the martensite plates. The solution treatment brings the material up to a temperature allowing for complete austenite reversion. However, the observed carbide precipitates in the as-built condition are not expected to dissolve at that temperature range and dwelling time. Due to the crystal orientation of the primary austenite grains, martensitic transformation has a memory effect. This means that the martensite laths will remain in the same orientation, morphology, and location over several numbers of austenitization and martensite transformation episodes [34]. The martensite lath boundaries will become preferred sites for precipitation, and therefore the precipitates will align along the morphological orientation of the plates, which have a relationship with the primary austenite grains, which are originally affected by the solidification conditions affected by the heat flux direction.

Figure 11 shows an inverse pole figure orientation map of a selected area from an ‘as-built’ sample of the material. It is clear that there is texture in the individual pockets, as highlighted in areas 1 to 4. The K-S orientation relationship [32] for the respective areas is shown as individual pole figures on the right-hand side of the figure and corresponds well with the theoretical pattern indicated in red. As previously mentioned, the <110> direction of the primary austenite aligns with the direction of the heat-flux, and the K-S orientation relationship dictates the direction of the martensite plates. The texture is limited to individual pockets, which orientations are affected by the laser scan strategy, giving a stochastic global microstructure, thus isotropic behaviour.

Fig. 11
figure 11

Inverse pole figure (IPF-Z) orientation map of a selective area from the AB sample. Smaller pockets of the transformed material show K-S orientation relationship as shown in their pole figures

Full size image

Figure 12 shows the Taylor factor mapping of the same area as Fig. 11. In polycrystalline materials, the arithmetic mean of the Taylor factors (M) is calculated from the ratio between the material’s flow stress over the critical resolved shear stress. Therefore, grains with low M will deform more easily than the ones with higher M. However, grains with low M cannot deform until the harder ones are also deforming plastically. Moreover, the grains with high M will not deform unless a combination of stress and work hardening conditions are met.

Fig. 12
figure 12

Taylor factor mapping of the mapped area when loaded along X direction (a), loaded along Y direction (b), and loaded along the Z direction. The darker red colour shows higher Taylor factor (more difficult to deform), and the brighter colour is representing the weaker grains under the given loading direction

Full size image

The weighted average of the Taylor factors along X, Y, and Z are shown in Fig. 13. The frequency of grains with high Taylor factors indicates that the investigated area is approximately 3.2% stronger if loaded in the Y direction compared to the X direction, and approximately 1% weaker if loaded in the Z direction compared to the X direction. These values suggest that there is a mild anisotropy in the microstructure level.

Fig. 13
figure 13

Histogram of the Taylor factor when the mapped area is loaded along X, Y, and Z. When the external load is aligned along Y direction, the frequency of grains with high M increases

Full size image

3.3.1 Fracture surface analysis

The strain ratios captured by the DIC system indicates anisotropic straining, but this is only observed in the tensile tests for the elastic part of the flow curve. The variation in yield strength, ultimate tensile strength, and elongation at failure with respect to build orientation is not systematic enough to draw conclusions about anisotropy. The yield strength and ultimate tensile strength are fairly uniform, but there is significant scatter in the elongation at failure. To better understand the root cause of scattering, fracture surface analysis was carried out on the specimens performing poorly. The specimens selected were the 0° and 15° from the DA condition, and the 90° specimen from the SA + A condition. SEM images of the fracture surfaces of the respective specimens are compiled in Fig. 14.

Fig. 14
figure 14

SEM images of the fracture surfaces of the tensile tests. a–b DA 0°, c–d DA 15°, and e–f SA + A 90° specimens

Full size image

Figure 14 a, c, and e show low magnification images of the fracture surface. The surfaces have flat regions in the centre and pronounced shear lips around the edges, typically seen when there is a large reduction in cross-section area prior to failure [35]. Even though the relative density is measured to be above 99.94%, traces of porosity are visible on all the surfaces. The higher magnification images reveal process specific defects in addition to the porosity. In the DA-0° specimen, lines parallel to the layers are visible throughout the cross-section, highlighted in Fig. 14b. The defect extends for lines with lengths of approximately 3 mm and appears to be process-parameter related, as they are evenly spaced and parallel to each other. At first glance, the defects appear to be lack-of-fusion (LOF) defects, but further investigation suggests that it could be a result of micro-segregation. Figure 15 shows the fracture surface after polishing, and Table 4 shows the corresponding EDS spectra and chemical composition. The EDS analysis reveals a higher concentration of Ti and O in the defect. Micro-segregation in PBF-LB/18Ni300 has been reported by several authors [36,37,38], where certain elements, such as Ti, segregate towards the front of the melt pool. Furthermore, Ti has one of the highest affinities to oxygen of the remaining elements composing the 18Ni300 material [39]. When a sufficiently high concentration of oxygen is present, Ti-oxides can form. As described in section 2.1, the material is processed with the ‘island’ scan strategy with an island size of 5 mm. The contour of each island is scanned in a continuous line, consistent with the lines observed in the fracture surface of the 0° specimen. Thijs et al. [40] also observed a higher concentration of oxides at the contour of the islands. Based on the EDS spectra and the length and spacing of the defects in Fig. 14 a and b, a compelling argument can be made that the defects are a result of micro-segregation leading to Ti-oxide formation, in combination with a laser scan strategy where the phenomena are amplified. Furthermore, this type of defect is only observed in the 0° orientation specimen, where the loading direction is within the plane of the islands.

Fig. 15
figure 15

Polished SEM image with corresponding EDS spectrum of a DA-0° after fracture

Full size image
Table 4 Chemical composition of EDS spectra as indicated in Fig. 15
Full size table

Defects are observed in the DA-15° and SA + A-90° specimens as well. In the DA 15° specimen, a defect is found with what appears to be partially melted powder particles. This could in fact be a LOF defect, if for instance a re-coater issue leads to a high local layer thickness. In the SA + A-90° specimen, a LOF region of approximately the same size is observed, despite that non-melted powder particles are not present. In addition to the LOF defect, a crack is visible. Defects of this sort highlight the importance of process-parameter optimization. The defects are assumed to not be detrimental for the yield strength but are expected to influence the fatigue life of the material.

4 Conclusions

In this study, the anisotropy of PBF-LB/18Ni300 maraging steel subjected to two different heat treatments has been investigated using techniques such as tensile testing, digital image correlation (DIC), and microstructure and fracture surface analysis with scanning electron microscopy. Strain field analysis with DIC reveals elastic and plastic anisotropy for both direct ageing (DA) and solution treatment + ageing (SA+A) heat treatment conditions.

Based on the results and discussions in this study, it is concluded that the elastic anisotropy is likely a result of process induced features such as melt pool boundaries (MPB) decorated with precipitates, which limits the dislocation movement. In addition, the martensite plates decorated with precipitates align with the primary austenite grain orientation, which is related to the direction of the heat flux during solidification. In the DA condition, the elastic anisotropy is significant, and the elastic modulus varies with the build orientation. In the SA + A condition, the MPBs are no longer vividly visible, and the elastic modulus has only a very slight dependency on the specimen build orientation. The DIC analysis reveals anisotropic straining, which cannot be represented by Hooke’s law under the assumption that PBF-LB/M materials are transversely isotropic.

The EBSD analysis shows a strong texture within individual pockets, but the global microstructure appears to be heterogeneous. This further supports the conclusion that the anisotropy is due to process induced features related to the MPBs and that there is no globally preferred crystallographic orientation causing anisotropic tensile properties.

Plastic anisotropy was observed in the strain field analysis but did not have a significant influence on the yield strength and ultimate tensile strength. The elongation at fracture was significantly lower for specimens at low-angle orientations, which is mainly attributed to MPB effects.

Based on the results presented for grain orientation and transformation relationships, future work can include in-depth studies to delineate the effect of transformation-induced crystal plasticity on the anisotropic behaviour. The results in this study contribute to establishing computational models, where the effect of anisotropy, transformation-induced plasticity, and residual stresses can be studied in isolation to provide a better understanding of the thermal cycles and pre-heating conditions for AM parameter optimization in phase transforming steels of similar type.