Use of 450-808 nm diode lasers for efficient energy absorption during powder bed fusion of Ti6Al4V

Abstract

The additive manufacturing process selective laser melting (SLM) uses a powder bed fusion approach to fully melt layers of powdered metal and create 3D components. Current SLM systems are equipped with either single or multiple (up to four) high-power galvo-scanning infrared fibre laser sources operating at a fixed wavelength of 1064 nm. At this wavelength, a limited laser energy absorption takes place for most metals (e.g. alloys of aluminium have less than 10% absorption and titanium 50-60% absorption). The lower absorption of 1064-nm laser sources requires higher laser powers to compensate for the loss of energy due to reflectivity and fully melt the feedstock material. This makes the use of 1064-nm lasers within current powder bed fusion SLM systems energy inefficient. Further to this, there is limited potential for scale-up of these laser sources within an SLM system architecture due to physical space requirements and high economic cost, placing further limitations on current state-of-the-art SLM productivity. This research investigates the use of low power, highly scalable fibre coupled diode laser sources and the influence of shorter laser wavelengths (450–808 nm) on material absorption and processing efficiency using a diode area melting (DAM) approach. It was found that when processing Ti6Al4V, absorption was 11% higher using 450-nm lasers when compared to using 808-nm lasers and 14% higher than 1064-nm lasers. The maximum powder bed temperature for irradiation at 450 nm and 808 nm was 1920 ⁰C and 1760 ⁰C respectively when using only 3.5 W of laser power. Due to the speed at which the DAM process scans the powder bed, the melt pool cooling rate was much slower (750–1400 ⁰C/s) than traditional SLM (10⁵–10^{6 0}C/s). This encouraged the development of β phases within the formed Ti6Al4V component. The low power, low cost, highly compact short wavelength diode laser is viable energy source for future powder bed fusion additive manufacturing systems, with potential for productivity scale-up using a DAM methodology.

Background

Laser-based additive manufacturing (AM) technologies have developed to a stage where they are routinely used to manufacture end-use high value components from a variety of materials. Compared with traditional fabrication techniques, AM processes are known for their ability to fabricate geometrically complex components that can be easily customised without significant additional cost or lead time delay. Among the various AM techniques for fabricating metal components, selective laser melting (SLM) is the most widely used within aerospace, automotive and medical sectors. Classified as a powder bed fusion (PBF) process, it is capable of producing near net shape metal components through melting successively deposited thin metal powder layers using a high power, highly focused scanning laser.

Though industrial uptake of the technology has grown in recent years, SLM has drawn criticism due to limits on productivity, this specifically being the rate at which a volume of material can be successfully laser processed per second. To address this challenge, researchers have explored two methods to improve the production rate and overcome the limitations of SLM; either by using high power lasers to maintain higher energy densities whilst scanning the surface of the powder faster. The second method is via the integration of multiple laser sources within the build chamber to increase the surface area of the powder that can be processed simultaneously.

Influence of laser power and wavelength on SLM

Energy input can be increased in SLM systems by either using a single high power fibre laser module (1 kW) [1] or multiple lasers (100–400 W each) [2] to increase production speed and/or process highly reflective metals similar to work undertaken by Jadhav et al. [3]. Buchbinder et al. investigated the impact of laser power on AlSi10Mg parts [1]. They concluded that the production rate can be increased by a factor of × 4 (from 5 to 21 mm³/s) by increasing the power from 200–400 W to 1 kW. Jadhav et al. successfully produced dense copper parts (exceeding 96% density) through use of a 1-kW laser [3]. However, damage to the SLM optical mirror was observed in this case, reportedly caused by sustained back reflection from the copper (absorption 9% versus reflection 91%). Typically, SLM systems are equipped with a fibre laser emitting a 1064-nm wavelength. At these wavelengths, only a small portion of the supplied optical energy is absorbed and converted into thermal energy due to the high reflectance of light at this wavelength from the metal [4]. Use of higher laser powers to overcome the challenge of poor absorption is not an efficient solution. Furthermore, increasing laser power leads to larger temperature gradients and build-up of residual stress during the process, which may also indirectly cause the formation of cracks, keyholes, spatter, material vaporisation as studied by Bertoli et al. [5]. In contrast, it has been reported that reducing the scan speed (in combination when using high laser power) reduces the temperature gradient [6], cooling cycles [7] and residual stress [8], which in turn reduces geometric deformation and crack formation. However, moving the laser more slowly limits system productivity.

The interaction between the laser beam and metallic surface can be characterised by either reflectivity (R) or absorptivity (A), which are critical parameters for determination of laser melting efficiency. As reported by Sun and Brandt, the absorptivity of various metals generally increases as the wavelength shortens [9]. Ehlers et al. observed that the absorptivity of aluminium can be increased by up to 13% when using a 800-nm high power diode laser (HPDL) compared with 1064-nm fibre lasers [10]. Yadroitsev et al. considered the relationship between the conductivity of the material and its absorption to be one of the most important material properties, influencing the ability to be processed by SLM [11]. Traditional SLM lasers have low electrical to optical efficiency resulting in high overall energy consumption, with the laser consuming ~ 68% of the overall energy within an SLM system [12]. Only 10–30% of the electrical power consumed by the laser is converted into optical energy, making it inefficient and uneconomical. System cost and power consumption can increase significantly with the addition of multiple fibre laser sources within the SLM system.

Use of diode lasers for efficient wavelength targeted materials processing

Recent studies have attempted to overcome the limitations of low absorption and efficiency by using a shorter wavelength laser to process powdered metal [13, 14]. Semiconductor diode lasers offer a broad range of laser wavelengths (405–3300 nm) and are among the most efficient lasers sources with up to 60% wall-plug efficiency (Nd:YAG and fibre lasers offer up to 20% and 30% efficiency respectively) [15, 16]. The key advantage of diode lasers over a fibre laser is the potential to decrease the operational cost whilst also benefitting from high wall-plug efficiency. Additionally, diode laser hardware (laser module, power/cooling hardware) occupies a fraction of the space compared to a fibre lasers offering more potential for scale-up and integration of multiple laser sources when using a traversing laser PBF approach [14]. Material processing applications such as surface heating and welding have already shown performance improvements such as increased homogeneity in heating areas, greater consistency and repeatability by using a diode laser [16, 17]. All these advantages can be utilised in the development of SLM systems. However, the direct use of diode lasers within SLM systems remains out of scope due to their limited power and beam quality. The highly asymmetric beam divergence of diode lasers requires the separate collimation in the two perpendicular axes, with careful matching of focal lengths to obtain a symmetric spot. This limited the working distance as a low F-theta lens is needed to focus the beam over the processing area, which is not practical within the current SLM process. The beam divergence for a typical diode laser is approximately 85 mrad x 200 mrad compared to the fibre laser (1064 nm) which is (1–5 mrad) [16]. In order to use diode lasers in material processing, Hengesbach et al. mentioned that the beam quality of the diode lasers has to be improved to less than 10 mm*mrad at an output greater than 200 W [17]. Recently, Matthews et al. developed a diode-based additive manufacturing system (DiAM) by optically addressing the beam over a specific area (2 x 2 mm²) [13]. Four continuous-wave (CW) diode modules were used in the DiAM system to generate a total power of 5 kW at a wavelength of 1007 nm. A liquid crystal light valve was used to homogenise the non-uniform output beam in conjunction with a Q-switched Nd: YAG laser beam as a hybrid laser at a wavelength of 1064 nm to selectively melt an area of (2–3 mm) in a single exposure for each layer. However, the complexity of the optical system and the short pulse of the laser through the photomask limited the maximum processing area. In addition to this, the wavelength range of the system and the output power available limit the process to only low melting temperature materials (Sn) as demonstrated in this study. In work undertaken by Zavala et al., a new process known as diode area melting (DAM) was developed [14]. DAM uses a traversing array of multi-laser diode spots to selectively melt material from a powder bed. In this investigation, a 50-W diode laser bar comprising 19 emitters at 2.5 W each and a wavelength of 808 nm was used to laser process 316L stainless steel powder at a power density of 4.21 x 10³ W/cm². The investigators used micro-lenses to collimate the light and focus the laser energy onto a 4.75 mm x 0.25 mm linear strip (area of 1.18 mm²), as shown in Fig. 1. The investigators were able to fully melt 316L stainless steel and create multi-layer components with 99% density using low power individual laser spots [18].

Fig. 1

Diode area melting developed by Zavala et al. [14], individually controllable emitters within moving diode laser bar over powder

With theory underpinning the increase in metal absorption at shorter wavelengths, and preliminary work using low powered 808-nm lasers to successfully process steel powder, there is a clear opportunity to explore the impact of short-wavelength diode lasers within the SLM process.

This investigation will study the effect of using low power 450-nm and 808-nm diode lasers during the PBF of Ti6Al4V, one the most widely/commonly used materials in SLM processing. A DAM methodology will be employed, with the diode laser physically traversing in the x/y plane to raster scan the surface of the powder bed. However, compared with the work of Zavala et al. [14], an optical fibre pigtailed diode laser will be used to deliver a flexible and improved beam quality within the PBF test rig. The effect of laser wavelength on melt pool characteristics will be studied for comparable energy densities. Consequently, if the technique is effectively demonstrated in Ti6Al4V, then a wide range of materials can also be expected to be processed effectively.

Methodology

Diode laser processing test rig

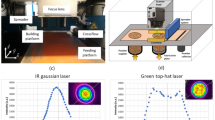
A custom-built, fully enclosed powder deposition system was used to provide flexibility and strict control over the processing environment. The enclosure was purged with Argon prior to processing, with oxygen content maintained below 0.2% to avoid oxidation. The system employed a fully automated powder delivery system embedded with a conductive heater, which allows the substrate temperature to be raised up to 300 °C. Powder layers of 50 μm (± 5 μm) were deposited using a silicon wiper. The optical system (discussed in section 2.2) was mounted on a motorised stage to transverse the X-Y axes over the powder bed. A schematic of the system is shown in Fig. 2. An IR-pyrometer (Single colour - CTLM-2H, MICRO-EPSILON UK Ltd) was integrated into the system to monitor the surface temperature during the process. The IR-pyrometer was static with an angle of 45⁰ to monitor a specified laser impact zone whilst the laser passes over. The IR-Pyrometer has a temperature range of 350 to 2000 ⁰C, and the field of view can be adjusted to 500 μm. The central wavelength of the transmission spectrum is 1.6 μm, with a 5-ms recording time. A temperature analysis software (Compact Connect) was used to calibrate the inputs and signal processing to obtain results in brightness temperature, not in arbitrary units.

Fig. 2

Schematic illustration of diode area melting system (the key components of the system and cross-section of optical system) used in this work

Previous work studying the use of low power diode lasers for processing metal powder by Zavala et al. [18] encountered challenges in bonding the first powder layer onto the substrate platform due to the use of a low energy input and large substrate heat-sink. Additionally, Yadroitsev et al. reported an absence of adhesion between the substrate and powder layers at powers below 25W due to heat dissipation through the bulk substrate as a result of using low power lasers [11]. Poor wettability can lead to separation between adjacent layers or to misalignment of layers during the deposition of subsequent layers. Because of this, modifications were made to the substrate plate (Ti6Al4V Grade 5) to alleviate these issues, as shown in Fig. 3. An array of 1-mm diameter holes was drilled into the substrate (Fig. 3a) to a depth of 1 mm. During the SLM process, the holes fill with powder. As the laser beam passes over the targeted area, the molten material seeps inside the holes and upon solidification acts as an anchorage for the subsequent layers to be built upon. This substrate configuration improved surface wettability, better adherence to the substrate and less thermal deformation (warpage) compared to a flat substrate.

Fig. 3

Schematic illustrates (a) the substrate holes array configuration and (b) scanning strategy used in this study (zig-zag)

Laser specifications and beam characterisation

This research compares the processing of Ti6Al4V feedstock using two multimode fibre-coupled diode lasers (808 nm, 450 nm). The optical ratio method (focusing lens to collimation lens) was adopted to reduce the spot size with a focal length comparable to SLM processing, as shown in Fig. 2. The 808-nm laser provided a maximum power of 3.5 W, delivered via an optical fibre with a numerical aperture (N.A.) of 0.22 and core diameter of 105 μm. The output beam was collimated to a diameter of 8 mm, with full angle beam divergence of 0.001⁰ using a fixed optical collimator (Thorlabs F810FC-850). Finally, the beam was focused using an achromatic doublet lens (Thorlabs - AC254-060) to a spot size of 175 μm (1/e²) at a focal distance of 60 mm. The 450-nm laser module provided a maximum laser power of 3.5 W, delivered using a fibre optic with N.A. of 0.22 and a core diameter of 200 μm. The beam was collimated to a diameter of 6.7 mm with a full angle beam divergence of 0.001⁰ using a fixed collimator (Thorlabs F810SMA-405). An achromatic lens (Thorlabs - AC254-030) focused the beam to a spot size of 175 μm (1/e²) and focal distance of 30 mm.

Both lasers were characterised using a scanning slit (NanoScan2sPryo/9/5). The beam parameters were calculated by measuring the beam profile at several axial positions Z, calculating beam width value w(z), and then minimum square fitting was used to obtain w₀, z₀, and M². The beam radius was measured as a function of Z position by measuring the laser diameter along the Z-axis with an incremental increase of 10 μm until the ISO standard (11146-1) distance was reached. As presented in Table 1, the smallest spot size achieved for both lasers are about 175 μm. The beam profile of both the 808-nm (Fig. 4a) and 450-nm (Fig. 4b) lasers have a Gaussian distribution profile, demonstrated in the figure by superimposing a Gaussian fit over the measured profile in red.

Table 1 Specifications of lasers used in this study

Fig. 4

Beam profiles and Gaussian fit of (a) 808-nm laser module and (b) 450-nm laser module

Materials

Gas-atomised Ti6Al4V powder (supplied by LPW Ltd, UK) with a particle size of 15–50 μm was used within this work. The chemical composition and material properties correspond to the ASTM standard F13608 as presented in Table 2. SEM images demonstrating the shape and size distribution of powder particles are presented in Fig. 5a. The majority of particles are spherical in shape. Their size distribution was measured using a laser particle distribution analyser (Malvern Mastersizer 3000 PSA). The result was (d10: 23.5 μm; d50: 33.3 μm; d90: 47.3 μm) as presented in Fig. 5b.

Table 2 The chemical composition and properties of Ti-4Al-4V [19]

Fig. 5

a Ti-6Al-4V powder morphology; b particle size distribution

The absorptivity of Ti6Al4V powder was measured and compared with Cu (15–45 μm) and AlSi12 (15–45 μm) powder using a spectrophotometer (Ocean HDX Vis NIR), utilising spectralon as a 100% reflective reference material. The measurement was performed at room temperature within the wavelength range of 380–1100 nm. Equation (1) was used to calculate the absorptivity as a function of wavelength, by assuming zero transmission and averaging 10 reflectively measurements.

$$ A\left(\%\right)=100-\mathrm{measured}\ \mathrm{refectivity}\ \left(\%\right) $$

(1)

Experimental procedure

This research was conducted in two stages. The first stage was to assess the ability of lasers to melt the Ti6Al4V using different laser powers and scan speed; whilst measuring the surface temperature and analysing the single-track morphology (melt pool depth, width and density). The second stage was to determine processing parameters for three dimensional manufacturing using a process energy normalisation approach developed by Thomas et al. [20].

Single track laser processing and characterisation

To study the influence of energy density at different wavelengths, a series of single tracks was produced by varying the scanning speed (v), and maintaining laser power at 3.5 W. The process parameters used are listed in Table 3. Seven single tracks were produced with a length of 15 mm for each laser wavelength (with x3 repeats). The selected scanning speed ranges were chosen to provide sufficient energy input. This was based on calculation of the linear energy density (LED), using the most effective processing parameters as shown in Eq. (2). P is the laser power in Watts and V is the scanning speed in mm/min.

$$ \mathrm{LED}=\frac{P}{v}\ \left(\frac{J}{mm}\right) $$

(2)

Table 3 SLM processing parameters used in this study for single-track formation

This approached was adapted from work undertaken by Wang et al. [19] on Ti6Al4V, where the energy density falls within the range of 0.2 < LED< 0.5, which can be achieved in this study for a given laser power by varying the scanning speed between 10 mm/min and 500 mm/min. In this research, the layer thickness was kept constant at 1 mm and the substrate was preheated to 200 °C before laser irradiation. During the processing, the surface temperature was measured using the pyrometer to measure the temperature profiles of the process and correlate it to the wavelength laser absorption. The top surface morphology of the melt pool was characterised using SEM (Tescan Vega3 LMU) with 15-keV beam intensity. The tracks were then hot mounted, polished and cross-sectioned to examine the melt pool morphology in terms of the width and depth of each track. Geometric shapes of each cross-section were analysed using SEM and quantified using ImageJ (NIH, Bethesda, MD, USA). For each track, the measurement was conducted for two different cross-sections and their results averaged.

Normalisation

Conventional SLM processing contains a large number of parameters that influence the thermodynamic cycle during the process. Most SLM users define the energy input density using four factors: laser power (P); Scanning speed (v); layer thickness (l ); and hatch distance (H_d). However, these factors alone are not sufficient to predict the real energy input since we must also include the effect of the material properties such as Absorptivity (A), and thermal diffusivity (D). Therefore, SLM processing parameters are not directly comparable between different systems and materials by using the volumetric energy density VED method. Bertoli et al. investigation on reliability of volumetric energy density showed that VED is insufficient to define the process parameters as it does not take into account the complex physics such as hydrodynamic instabilities, recoil pressure and Marangoni flow [5]. By summarising the processing parameters and the optimal energy density from the literature in Table 4, it was found that each work has different processing values and optimal energy densities. For this reason, a normalisation approach has been adopted in this research. This normalisation approach enables transfer of known process parameters from one study to other. Additionally, it includes the influence of the wavelength on energy input which is a key parameter of this study. The normalised processing diagram takes into account the properties of the material (i.e. absorptivity, thermal conductivity, etc.) as described by the following equations:

$$ {E}^{\ast }=\frac{P^{\ast }}{v^{\ast }\ {l}^{\ast }}=\frac{AP}{2 vl{r}_B\ \uprho\ {C}_{\uprho}\left({T}_m-{T}_0\right)} $$

(3)

Where E^∗ represents the normalised volumetric energy density (VED) required to melt the material. P^∗, v^∗, h^∗ and l^∗ are the normalised primary SLM parameters. In this study, the average thermal properties of the Ti6Al4V were adopted at the approximate powder bed melting temperature (T_m) 1604 ⁰C (1877K) as presented in Table 2. Following the work done by wang et al. [19] and Thomas et al. [20], the thermo-physical properties (D-thermal diffusivity, C_ρ - specific heat, ρ - material density) were assumed unchanged by the melting temperature variation during the process. Where the thermal conductivity (k) was calculated as follows:

$$ \mathrm{k}=14.307+0.0181\ {T}_m-6\ x\ {10}^{-6}\ {T}_m^2 $$

(4)

Table 4 Summary of processing parameters for SLM of Ti6Al4V from literature

Normalised beam power:

$$ {\mathrm{P}}^{\ast }=\frac{\mathrm{AP}}{{\mathrm{r}}_{\mathrm{B}}\ \mathrm{k}\ \left({\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_0\right)} $$

(5)

Normalised scanning speed:

$$ {v}^{\ast }=\frac{v\ {r}_B}{D} $$

(6)

Normalised layer thickness:

$$ {l}^{\ast }=\frac{l}{r_B} $$

(7)

Normalised hatch distance:

$$ {h}^{\ast }=\frac{H_d}{r_B} $$

(8)

To compare and summarise the processing parameters of Ti6Al4V as used in the various references from the literature (Table 4), the normalised processing data was calculated and is presented in Fig. 6. In the figure, 1/h^∗ is plotted as a function of q^∗/v^∗.l^∗ to assist in plotting ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ as the diagonal dash lines on the graph. ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ represents the energy density required to melt the material. In this way, it is possible to compare the processing parameters from different studies to define the broad range of the ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ for this study. Thus, enabling this study to define a processing window for the material. From this plot, it be seen that the energy density required to ensure > 99.0% density is in the range 2$<{\boldsymbol{E}}_{\mathbf{0}}^{\ast }<8$. When ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }>8\kern0.5em$the material will be exposed to excessive energy, leading to over-melting, whilst ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }<2$ leads to insufficient melting, as demonstrated by Thomas et al. [20]. In this study, the processing parameters were tuned to obtain ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ within these limits.

Fig. 6

Normalised processing diagram for SLM of Ti6Al4V constructed using Eqs. (5)–(8) and processing parameter data from Table 4

To characterise the manufactured samples, the density was measured using a Mettler Toledo density metre, based on the Archimedes principle, as suggested by Spierings et al. [26]. All manufactured samples were measured five times independently and the results averaged. Samples exhibiting densities > 90% were hot mounted, polished and cross-sectioned to be examined visually for porosity, XRD and mechanical properties. XRD (D2 Phaser -Bruker) was used to conduct phase and microstructure analysis with Cu Kα radiation. Scans were carried out in the range of 2θ = 20⁰ - 100⁰ with steps of 0.02⁰, based on previous work done by Wang et al. [19]. Finally, nanoindentation tests were performed using a Triboindenter with a Berkovich tip of 100-nm radius and at an angle of 142.3°. The test was performed with a 4 × 4 matrix using an open-loop trapezoidal method of loading and unloading, with 5-s hold per stage at 13000 μN maximum loads. With load and depth plots obtained from the experiments, the sample elastic modulus was calculated using:

$$ \frac{1}{E_r}=\frac{1-{v}_i^2}{E_i}+\frac{1-{v}_s^2}{E_s} $$

(9)

Where Poisson’s ratio of indenter v_i =0.07; Elastic modulus of indente E_s=1140 GPa; Poisson’s ratio of Ti- 6Al-4V V_s=0. 342. The hardness is calculated by the following:

$$ H=\frac{P_{\mathrm{max}}}{A} $$

(10)

Results and discussions

Influence of wavelength on laser absorption

Absorption of laser energy by a material is highly dependent on the laser’s operating wavelength, the size of feedstock particles and its material properties. Given the importance of laser wavelength for PBF processing, there have been very few studies on the effect of wavelength on metal powder feedstock. Previous studies relied on the absorptivity of bulk material [20] [27]. Therefore, for this study, it was important to measure the physical absorptivity of the powder used instead of using absorption for bulk materials available in literature. Figure 7 presents the optical (laser) absorption coefficients for common SLM materials within the range of 400 to 1100 nm, measured using an Ocean HDX Vis NIR as specified in section 2.3. Powder absorption is seen to vary significantly with laser wavelength. For instance, the absorptivity of Ti6Al4V increases by 14% when using a 450-nm laser source compared with a 1064-nm fibre laser. However, for highly reflective and conductive materials such as copper, absorption is increased by 78% when using a 450-nm laser source. Since this study focuses on Ti6Al4V, the absorptivity at 808 nm and 450 nm will be used to calculate the normalised energy density as discussed in section (2.4.2).

Fig. 7

The optical absorption of Ti6Al4V, AlSi12 and Cu within the wavelength range of 400 to 1100 nm

Influence of wavelength on surface temperature

As the first stage of this study, the surface temperature of Ti6Al4V powder was measured to determine the maximum achievable temperature and to monitor the thermal cycle. The surface temperature increases as the laser beam enters the measurement spot, rapidly reaching peak temperature before slowly receding to room temperature after the laser spot has passed. Three temperature transients were recorded and averaged for a range of scan speeds (10 mm/min to 500 mm/min). The maximum temperature attained is plotted in Fig. 8 for laser irradiation at both 808 nm and 450 nm. For both wavelengths, higher temperatures were recorded at slower scanning speeds, due to the higher energy input generated. The maximum temperature reached at each scanning speed is noticeably different for the two wavelengths, with the maximum surface temperature reached at 450 nm higher by approximately 12% compared to that at 808 nm. At 10 mm/min, the maximum temperature for 450 nm was 1920 ⁰C and for 808 nm was 1760 ⁰C. This 12% higher average temperature correlates well with the measured 11% higher absorption for the shorter wavelength light.

Fig. 8

The maximum temperature measured during laser processing at various scanning speeds for 808-nm and 450-nm wavelengths

Temperature transients are plotted in Fig. 9 for 808-nm and 450-nm laser irradiation at a speed of 50 mm/min, showing the temperature within the measurement spot as the laser beam passes through. The 450-nm laser achieved a maximum temperature within 260 ms whereas the 808-nm laser achieved this after 530 ms. This phenomenon can be related to the absorption spectrum of Ti6Al4V powder, where more energy is absorbed and converted to heat at a shorter wavelength, allowing the shorter wavelength laser source to achieve a maximum temperature faster. However, at speeds of 50 mm/min or below, a large fluctuation in temperature of approximately ± 100 ⁰C was observed, as can be seen in Fig. 9. This is possibly due to keyhole formation caused by the increase in interaction time, similar to the effect reported by Matthews et al. [28].

Fig. 9

Temperature measurement at speed of 50 mm/min

Influence of the wavelength on the morphology of single laser tracks

Single tracks were processed using 450-nm and 808-nm wavelength lasers in order to determine the influence of wavelength, and therefore absorptivity, on single-track geometric features. Surface morphology and cross-sectional geometric characteristics of single tracks were investigated. Table 5 documents the melt-pool depth and width for 14 sets of laser parameters that produced reportable results, i.e. some amount of melting was observed. The table represents the melt pool depth, width and the feature produced for different parameters.

Table 5 A summary of single-track processing parameters and resultant melt pool characteristics

Melt pool top surface morphology

Figure 10 shows the top surface morphology of single tracks produced by the two different wavelength lasers for a range of scan speeds at fixed power (3.5 W). This determines whether the surface will exhibit a continuous smooth morphology, a coarse irregular morphology or contain a number of keyholes. Increasing the scanning speed results in narrower track width for both 450 nm and 808 nm. Further reduction of the scanning speed results in keyhole formation due to excessive energy input.

Fig. 10

Morphology of top surface under different scanning speeds for 808-nm and 450-nm wavelength laser processing

Morphology varied significantly with scan speed for both laser wavelengths. At high speeds above 300 mm/s, both lasers had insufficient energy to form a melt pool, and solid structures were not possible. This was a result of the lower peak temperature reached due to the rapidly moving laser source. Powder was sintered to some extent, but the resultant samples had little or no mechanical strength and easily crumbled when physically handled. Similar behaviour was observed at very low scan speeds of 10 mm/min or slower, in this case producing non-periodic keyholes. The keyholes can be attributed to the higher incident energies, where a high melt pool temperature is attained at slow scanning speeds.

For the 450-nm laser, the process window is much wider compared to that at 808 nm. This is due to higher absorptivity at the shorter wavelength. At 450 nm, a continuous and smooth top surface was formed at scanning speeds ranging from 50 to 200 mm/min (Fig. 10). However, at scanning speeds above 200 mm/min, the balling phenomena starts to appear until the energy input is insufficient to melt powder at speeds above 400 mm/min. This phenomenon is commonly observed for metals processed with lower energy densities, as reported by Yadroitsev et al. [29], where energy density was insufficient to melt powder at high scanning speeds resulting in severe balling. On the contrary, a stable process window for 808 nm is observed from 50 to 100 mm/min, with keyholes forming at 50 mm/min or below. Between 100 and 300 mm/min, we observe discontinuous melt pools with balling. Above 300 mm/min, the energy was found to be insufficient to form melt pools.

The width of the track generally increased with energy density; for the 450-nm laser, the track was generally wider than at 808 nm, due to higher absorption. This is illustrated by Fig. 11, which plots the average width of the melt pool track measured at the top surface as a function of scanning speed. For example, at 100 mm/ min, the width of the track was 208.2 μm when the 450-nm laser was used, compared to 182.8 μm for the 808-nm laser. The width of tracks processed using the 450-nm laser remained above 200 μm for speeds below 200 mm/min, whereas for 808 nm, the track width narrowed below 200 μm at speeds above 50 mm/min.

Fig. 11

Effect of scanning speed on melt pool width

Four hundred fifty-nanometre lasers produced better track surface quality at a scan speed of 100 mm/min at 3.5 W compared to 808-nm laser as observed in Fig. 10. This power is substantially lower than that currently used in commercial SLM systems (typically 100–900 W) and anything reported in the literature. The 808-nm laser produced satisfactory results in terms of morphology, but at a slower speed of 50 mm/min due to its lower absorption compared to 450 nm. All of this has been achieved whilst exhibiting a high wall plug efficiency of 70% compared to the typical 20% of fibre lasers.

Morphology of cross-sectioned tracks

Scanning speed affects energy density and is therefore a dominant parameter in influencing the shape and morphology of a single track. When the scanning speed was below 50 mm/min, the energy input was high enough for lasers at both wavelengths to penetrate deeply and create keyholes. Figure 12 shows the cross-section of tracks processed with the 450-nm and 808-nm lasers at different scanning speeds, allowing comparison of the depth and width characteristics of the tracks. The depth and width of tracks reduce with increasing scan speed for both wavelengths. Furthermore, it can be noted that the penetration depth is 20–40% deeper for the 450-nm laser compared to 808 nm. Figure 13 shows the relation between the geometric features of single tracks and scanning speed, plotting the reduction in melt pool depth (a) and width (b) as scanning speed increases from 10 to 400 mm/min. For the same scanning speed, tracks produced using 450 nm light are generally wider than those using 808 nm (Fig. 13b). The track narrows from 416 to 165 μm with increasing scanning speed up to 400mm/min for 450 nm, whereas for 808 nm, the track width narrows from 395 to 281 μm for a maximum speed of 300 mm/min.

Fig. 12

Cross-section morphology of melt pool at different scanning speeds

Fig. 13

Variation of melt pool (a) depth and (b) width with scan speed for 450- and 808-nm lasers

Wavelength also has a significant influence on the melt pool depth. This can be described using Fig. 13a, which plots the melt pool depth as a function of scan speed. At the same scan speed, keyhole formation occurred with a deeper penetration depth when processed with 450 nm compared with 808 nm. In addition, keyhole formation for 450 nm was more prominent at speeds below 50 mm/min, whereas for 808 nm, keyholes were observed for speeds below 10 mm/min. Four hundred fifty nanometre also exhibited deeper penetration than 808 nm. Generally, there is a wider processing window for 450 nm compared to 808 nm. This provides flexibility in terms of process adaptability and capacity to improve the SLM process. It also allows the use of lower powers and makes it possible to scan at faster speeds.

Multilayer fabrication

Processing regions for 450–808 nm powder bed fusion of Ti6Al4V

Several variables need to be considered in order to achieve high part density in SLM, such as scan speed, layer thickness, power and hatch distance. The combination of these variables needs to be carefully explored for any given laser power to avoid the introduction of defects related to insufficient wettability or poor overlapping. Results from the single-track experiments can provide an estimate of the melt pool morphology under different processing parameters, allowing a selection of suitable process parameters for fabrication of multilayer samples. In this section, the effect of wavelength on microstructure, part density and processing parameters is investigated.

According to our analysis of the dimensionless processing data (normalisation) discussed in Section 2.2.2, the key SLM parameters and their interaction with each other were considered to determine the minimum energy required to melt Ti6Al4V. Laser power P ( 3.5 W), scanning speed v (25–400 mm/min) hatch spacing H_d (100–200 μm) and layer thickness l (50–100 μm) were selected and normalised as summarised in Table 6. Multilayer samples were processed to a size of 7 mm × 7 mm × 2 mm. Figure 14 shows the normalised processing diagram, which represents the required energy input,${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$, to be absorbed by a material for specific volume 2r_Bl^∗ as isopleth dashed lines. The y-axis $\frac{\mathbf{1}}{{\boldsymbol{h}}^{\ast}}$ , where E₀ on x-axis as log₁₀ scale.

Table 6 Experimental parameters investigated for Ti6Al4V

Fig. 14

Normalised diagram showing the location of the experimental parameters and the visible region for given laser power

Accordingly, it was evident that a high value of (${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ > 8) would lead to excessive energy input which results in the formation of voids and keyholes. In contrast, low energy input (${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$<2) will be insufficient to fuse the material or generate sufficient wettability, leading to imperfect parts. The highest density samples of density greater than 90% were produced in a region between 2 < ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$< 8 for selected laser power and wavelengths.

The effect of v^∗ was more pronounced than h^∗on the density of the parts. For instance, increasing the v^∗ will provide${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ values below the threshold of the material. Adjustment of hatch distance to maintain the optimal${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ within the range of (2<${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ < 8) was not sufficient to improve the density of parts. As the scanning speed increased above v^∗ = 0.072 (equivalent to 300 mm/min), an inconsistent melt pool was formed, as shown in Fig. 15. The optimal results were achieved at scanning speeds below v^∗ < 0.048 (equivalent to 200 mm/min), whilst spattering was observed at v^∗ < 0.012 (equivalent to 50 mm/min) as a result of excessive energy input. The maximum processing range was generally higher for 450 nm compared to 808 nm.

Fig. 15

The effect of the scanning speed on the top surface of the specimen

The effect of the normalised h^∗was noticeable when the v^∗ was within the effective range from 0.012 to 0.048 (equivalent to 50–200 mm/min). In general, the hatch distance affects the thermal history of the process, and therefore influences the microstructure, density and process efficiency [20]. As can be seen in Fig. 16, decreasing the overlap of laser paths by selecting a normalised overlap 1/h^∗> 0.5 leads to excessive energy being delivered into the powder. This high energy causes vaporisation spatter and the formation of keyholes, which reduces part density, as shown in Fig. 16c. Reducing the 1/h^∗ to <0.3 leads to poor weldability between the tracks resulting in sintered powder between tracks that deteriorates density and mechanical properties (Fig. 16a).

Fig. 16

The effect of hatch distance on the top surface of the specimens. a H_d 200 μm increase the separation between the tracks. b H_d = 157 μm is the optimal value to provide better joint and re-melting between tracks. c H_d100 μm reduces the processing efficiency and excessive energy

The normalised overlapping 1/h^∗ within the range of 0.3–0.5 was found to be optimal for increased part density which also showed smoother surface finish as can be seen in Fig. 16b.

The layer thickness significantly affected the required energy to melt the material ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$. The excessive${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ points on the normalised diagram were shifted from the “optimal” region to “insufficient” region when a layer thickness of 100 μm was applied. Correspondingly, the experimental results at a layer thickness of 100 μm showed insufficient bonding between layers. In contrast, the use of 50-μm layer thickness showed solid bonding and higher density parts. Therefore, a wider range of feasible processing parameters is permitted for layer thicknesses of 50 μm and below.

Microstructure and mechanical properties

Part density

By selecting the appropriate processing parameters associated with the SLM process, high density parts (> 90%) can be achieved. Figure 17a represents the density values of parts fabricated utilising 808-nm laser within the normalised range of 2 <${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ < 8. The density varies from 79.15 to 93.42% of the theoretical value implying the presence of deficiencies. The highest density of 93.42% was achieved at a scanning speed of 75 mm/s, hatch distance of 157 μm and 50-μm layer thickness, as shown in Fig. 18a. For a thick layer of 100 μm, higher energy input is needed to achieve sufficient bonding between layers. Such input cannot be achieved using this level of laser power even when scanning speeds are reduced. The density of specimens reduced as a consequence of applying excessive energy when a scanning speed of 50 mm/min was used or 100 μm hatch distance was applied.

Fig. 17

Density of parts fabricated using (a) 808 nm and (b) 450 nm

Fig. 18

Top surface porosity of specimen fabricated using (a) 808 nm and (b) 450 nm

The density of specimens fabricated using the 450-nm laser was similar to that of specimens fabricated with the 808-nm laser. Over the range of scanning speeds from 50 to 200 mm/min, the density of samples processed using 450nm varied between 83.31 and 94.16% of that of bulk material, as shown in Fig. 17b. For 450 nm, at a scanning speed of 25 mm/min, large holes and over-melting were evident in the specimen, resulting from excessive energy input. The maximum density of 94.16% was achieved at a scanning speed of 75 mm/min, as shown in the top surface microscope image in Fig. 18b. A maximum density of 93% is observed in specimens fabricated using 808 nm. This density can be achieved at 450 nm at a scanning speed of 100 mm/min. The slower scanning speeds can be expected to allow the melt pool to settle for longer in its molten state, resulting in a wider melt pool, with lower cooling rates potentially reducing stresses and resulting in an overall improved surface. By using 3.5 W laser of 450-nm wavelength, this study was able to manufacture parts of density above 94%, with further improvement, approaching comparable densities of > 99% manufactured by conventional 200–1000 W lasers. Therefore, as an alternative to ever-increasing laser powers in order to improve processing speed and part density (particularly for reflective materials), laser wavelength offers a further variable enabling low power diode lasers to process materials effectively. In general, defects in the sample which lower the density of fabricated parts in this study can be related to several “real world” uncertainties, such as instability in the laser focal length as the laser traverses the powder bed and the inaccuracy of the deposition system.

Microstructure (XRD)

The microstructure of Ti6Al4V is characterised by a combination of α phases and β phases at room temperature. These phases are related to the thermal gradient and the solidification of the melt pool in the SLM process [30]. Generally, parts produced by SLM predominantly show the ά martensite microstructures only, as a result of the fast cooling rate associated with the process [31]. In comparison to SLM, for Ti6Al4V by EBM, the temperature of the powder bed is normally held at 600 °C, which is above the temperature of martensitic transformation (575 °C). This leads to lamellar (α+ β) microstructure in the as-manufactured microstructure. The cooling rate is the influential factor that controls the transformation of ά martensite to (α+ β) during the process. As reported by Ahmed et al. [32], the ά phase forms at rapid cooling rates higher than 410 °C/s, which is exceeded in the SLM process. However, a cooling rate between 20 and 410 °C/s would give time for the β phase to form, which can either be achieved by maintaining the powder bed temperature above 575 °C or slow processing speed in order to reduce the cooling rate.

In this study, the relatively slow scanning speed of the diode laser maintains the temperature above β transus for a longer period of time compared to SLM, thereby reducing the cooling rate and promoting the development of the β phase. As a result, the XRD pattern in Fig. 19 shows a presence of two types of microstructures: ά phase and β phase with both laser wavelengths (450 and 808 nm).

Fig. 19

XRD profile for 808 nm and 450 nm

The cooling rate in this study was calculated using Eq. (11). The pyrometer was used to measure the temperature transient. The cooling rate was calculated from the time taken for the temperature to drop from the β transus temperature (T_{β transus} = 994 °C) to the end of the martensitic transformation temperature (T_ms= 575 °C), as described for Ti6Al4V by Ahmed and Rack [32]. In this study, the range of parameters used developed a cooling rate in the range of 750 to 1400 ^oC/S. Even though the cooling rate of the DAM process exceeded the critical cooling rate of 410 ^oC/s, it is still comparatively slower than SLM and EBM. Table 7 summarises the different processes and both the cooling rate and microstructure associated with the different process parameters. The high absorptivity of 450-nm and 808-nm lasers allows the use of low powers at slow scanning speeds ranging from 75 to 100 mm/min. This maintains the temperature above the β transus for a longer period of time, thus reducing the cooling rate and developing the β phase in as-built samples, similar to results achieved by Simonelli et al. [33]. The author successfully obtained α + β microstructure in the SLM process by reducing laser power and scanning speed, which as a result increased the diffusion time and reduced the cooling rate.

$$ \mathrm{Cooling}\ \mathrm{rate}\ \left({}^{\circ}\mathrm{C}{s}^{-1}\right)=\frac{\Delta \mathrm{T}}{\Delta \mathrm{t}}=\left|\frac{{\mathrm{T}}_{\upbeta\ \mathrm{transus}}\ \left({}^{\circ}\mathrm{C}\right)-{\mathrm{T}}_{\mathrm{ms}}\ \left({}^{\circ}\mathrm{C}\right)}{{\mathrm{t}}_{\upbeta\ \mathrm{transus}}\left(\mathrm{s}\right)-{\mathrm{t}}_{\mathrm{ms}}\left(\mathrm{s}\right)}\right| $$

(11)

Table 7 A comparsion of cooling rate and corresponding microstructures of Ti6Al4V processed using SLM ,EBM and DAM

The polarised light micrograph was used to identify the top surface microstructure of specimens as shown in Fig. 20. The microstructure was dominated by a mixture of Widmanstätten and Martensite. Figure 20b shows that ά has decomposed into equilibrium (α+β) basketweave microstructure with different sizes and orientations, using the 450-nm laser. Similar results obtained with a slightly higher amount of martensite ά microstructure compared with 450 nm, as shown in Fig. 20a. This can be related to the high absorption of 450 nm which is prolonging the time above the transus temperature and decreasing the cooling rate.

Fig. 20

Ti6Al4V microstructure. a 808 nm. b 450 nm

Nanoindentations (hardness and elastic modulus)

In this section, the top surface of the highest density parts is further investigated for their hardness and elastic properties using the nanoindentation technique suggested by Fischer-Cripps [35]. In general, the formation of the microstructure (Widmanstätten and Martensite) in final parts has a significant influence on mechanical properties. According to He et al., the presence of Martensite (ά) microstructure leads to increase hardness of parts and decrease elasticity [36]. The measured microhardness by Thijs et al. of SLM parts has a Vickers hardness within the range of 381–479 (3.70–4.69 GPa) [31]. He et al. also reported the microhardness to be 395 Hv (3.7GPa) and the elastic modulus was 107 GPa [36]. On the other hand, the microhardness of EBM parts was around 3.2–3.5 GPa and the elastic modulus was 118 GPa as reported by Facchini et al. [37]. In this study, the nanoindentation hardness of parts processed using the 450-nm laser and 808 nm was found to be 4.59 GPa and 4.7 GPa, respectively. The elastic modulus for 450 nm and 808 nm was measured to be 114 GPa and 111 GPa, respectively. Figure 21 plots the average hardness and elastic modulus for samples produced at laser power of 3.5 W, scanning speed 75 mm/min and hatch distance 157 μm.

Fig. 21

Ti6Al4V mechanical properties. a Elastic modulus. b Hardness

Conclusions

Ti6Al4V powdered feedstock was successfully processed using 808-nm and 450-nm wavelength lasers using a diode area melting approach. It was found that low laser powers of 3.5 W were sufficient in generating temperatures capable of forming melt pools with energy densities comparable to those generated using traditional selective laser melting. For Ti6Al4V powder, the absorption was 11% higher using 450-nm laser sources compared to 808 nm. This increased absorption resulted in an average of 12% higher temperatures with a maximum surface temperature of 1920 ⁰C generated. Effective control over the width and depth of the melt pool was achieved with a Normalisation model and parametric study. Parts with a density greater than 90% were manufactured in the range of 2 <${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ < 8 and 0.018 < V* < 0.048 which correlated with established processing windows for conventional SLM processing of Ti6Al4V. The width and depth of melt pool tracks varied between 150 and 520 μm and were generally 5–10% wider and 20–40% deeper using 450-nm laser sources compared to 808-nm laser. The higher penetration depth caused the formation of keyholes for both lasers at low scan speeds; with the 450-nm laser, the keyhole formation was observed at speeds below 50 mm/min, whereas for 808 nm, the keyholes started to appear below 10 mm/min. These keyholes were generally formed for high energy densities ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$ > 8 and insufficient fusing of material at energy density values ${\boldsymbol{E}}_{\mathbf{0}}^{\ast }$<2. Normalised overlapping 1/h^∗ within the range of 0.3–0.5 was found to be optimal for increased part density with a hatch distance of 0.157 μm. Microstructure analysis revealed the presence of two types of microstructures; ά phase and β phases were formed during DAM processing compared to only the ά prime that is formed in commercial SLM systems. DAM processing generates much slower cooling rates (~ 750–1400 ^oC/S) compared to SLM, allowing β phases to form. The mechanical properties of parts manufactured by the 3.5-W, 450-nm and 808-nm lasers should in future be comparable to SLM parts manufactured with 100–1000 W systems as part density values increase to above 99% (through further system development). This research has demonstrated the potential for using low power short wavelength diode lasers within metal PBF processes. Further potential exists for processing highly reflective materials and significant scale-up/productivity opportunities when combining the DAM approach with low-cost highly versatile diode laser sources.