1 Introduction

Additive manufacturing (AM), commonly known as 3D printing, has attracted the interest of the academic and industrial research community because of its ability to fabricate objects with complex geometries at relatively low cost and with high flexibility [1,2,3,4,5,6,7,8,9]. It is an emerging technology where structures are printed layer by layer with the help of computer-aided design (CAD) models. Popular AM techniques include fused filament fabrication (FFF) [4, 10,11,12,13], selective laser sintering (SLS) [14, 15], digital light processing (DLP) [16,17,18] and stereolithography (SLA) [19,20,21,22,23,24]. FFF has several advantages including simplicity of operation, lower cost of fabrication compared to conventional methods, e.g. injection moulding, fast processing and the ability to process a versatile range of thermoplastics with complex structures [25,26,27,28,29,30]. The feedstock used in FFF is usually a thermoplastic polymer–based filament of a specific diameter. As the printing occurs in a layer-by-layer fashion by local welding of discrete extruded layers, the printing direction (aka raster angle) and the choice of the infill pattern play an important role in the mechanical response of 3D-printed thermoplastic structures processed via FFF. The layered structure of the FFF print forms discrete bonds between adjacent beads and typically includes a significant amount of interlayer porosity, which affects the mechanical properties of the printed parts [31], and results in build orientation- and raster angle–dependent fracture properties.

Several phenomenological studies have been reported in the literature to foster understanding of the process-property relationships associated with 3D-printed thermoplastics [32,33,34]. Aliheidari et al. [35] studied the effect of process parameters (melt temperature, bed temperature, layer height and layer width) on the fracture resistance of acrylonitrile butadiene styrene (ABS) and found that the critical J-integral is strongly correlated with the process parameters through both the interlayer adhesion and the mesostructure. Sood et al. [36] used a surface optimization method and found that the tensile, flexural and impact strength of 3D-printed ABS samples can be enhanced by altering the printing parameters such as layer height, width, air gap and orientation. Tymark et al. [37] optimized the layer height and printing orientation for enhanced tensile strength, strain and modulus of polylactic acid (PLA). Durgun et al. [38] reported that the out-of-plane orientation has a greater influence on the mechanical properties of 3D-printed parts than in-plane orientation of layers. Gurrla et al. [39] suggested a simplified mathematical model to understand the neck growth between cylindrical filament layers. By using ultimate tensile strength values obtained for two different print directions, they established the simulation output with experimental data and concluded that neck growth between layers has a dominant effect on the strength of printed parts. Yang et al. [40] studied the effect of thermal processing conditions in FFF on crystallinity and mechanical properties of PEEK samples in order to develop the relation among them. Arif et al. [41, 42] evaluated the influence of the print orientation and raster angle on the tensile, flexural, thermal and fracture behaviour of FFF PEEK. McLouth et al. [43] studied the effect of print orientation and raster pattern on fracture toughness of ABS matrix and analysed variations of the fracture toughness with mesostructure. They concluded that, as alignment of printing filament changed from 0 to 90° (parallel to perpendicular) with respect to crack plane, the fracture toughness increased by 54%. It was also observed that the printing orientation significantly affects the fracture toughness. A decrease of 11% was observed in fracture toughness for printing orientation of 0/90° compared to + 45/− 45°. Recently, Cuesta et al. [44] used the essential work of fracture (EWF) approach to examine the mechanical behaviour and fracture properties of 3D-printed polymeric materials, including fibre-reinforced plastics, and proposed a new miniature test specimen for measuring the fracture properties of polymers processed via AM. Moreover, Lorenzo-Bañuelos et al. [45] examined the effect of raster orientation on the fracture properties of thin polypropylene (PP) components processed via material extrusion AM, and found that the printing orientation can have a significant effect on the essential work of fracture of the 3D-printed PP.

As the applications of FFF processes are expanding, good knowledge and understanding of the relationship between the printing orientation and the mechanical performance is becoming more important from the process and product design point of view to achieve high-quality prints. Although previous studies have provided useful guidelines on the process-property relationship of FFF-enabled parts, there is a need to combine experiments and modelling to understand how the printing direction and build orientation affect the crack initiation resistance of 3D-printed thermoplastics that undergo significant inelastic deformation before the onset of fracture. Herein, we study the fracture properties of ABS thermoplastics processed via FFF using the concept of essential work of fracture (EWF) [46,47,48]. The effect of the raster angle on the EWF and non-essential work of fracture (non-EWF) of 3D-printed ABS are assessed via both experimental and numerical approaches. Tensile tests are performed on double-edge-notched tension (DENT) specimens printed with different raster angles (0°, 90° and + 45/− 45°), and the essential and non-essential work of fracture is determined from the obtained measurements. Moreover, the evolution of the strain fields in the ligaments of the specimens is examined via digital image correlation (DIC), and scanning electron microscopy (SEM) images are obtained from the fracture surfaces to identify dominant failure mechanisms and correlate them with the results extracted from the macroscopic fracture tests. The experimental results are further corroborated with the predictions from a 2D plane-stress FE model, considering the anisotropic elastic response and failure properties associated with the FFF print.

2 Experimental methods

2.1 Sample fabrication via fused filament fabrication 3D printing

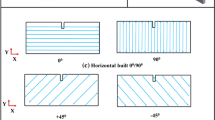
Acrylonitrile butadiene styrene (ABS) is a rubber-toughened, amorphous polymer with exceptional printability. ABS filament feedstocks (diameter 1.75 mm) supplied by leapfrog MAXX PRO, Netherlands, with a batch number A-22-003 were used for the preparation of DENT specimens via FFF 3D printing [49]. As shown in Fig. 1, CAD models of double DENT specimens (length h = 90 mm, width W = 30 mm, thickness t = ~ 1 mm) were prepared in 3D printable STL format and a slicing tool (Simplify3D) was used to convert them into a G-code which the 3D printer (Creator Pro Flash Forge) can process and execute prints. Four different ligament lengths (L = 4, 6, 8 or 12 mm) were considered, and for each choice of L, three different specimens were printed with raster angles of 0°, 90° and + 45/− 45° (see Fig. 1), respectively, giving a total of 12 different specimens. The process parameters such as nozzle tip temperature (230 °C), bed temperature (105 °C), layer height (0.17 mm), infill density (100%), extrusion width (0.4 mm) and number of layers (6) were kept constant for all the samples [50]. To examine possible changes in the crystallinity of the polymer as a result of the 3D printing process, wide-angle X-ray diffraction (WAXD) analysis was performed on ABS samples before and after 3D printing (see Section S1, Supplementary Information).

Fig. 1
figure 1

a Schematic illustration of the 3D-printed specimens with different raster angles; b SEM micrographs showing the surface texture of specimens for each choice of raster angle

Full size image

2.2 Measurement of the elastic constants of 3D-printed ABS

It is known that the mechanical properties of components processed via FFF are anisotropic and are dependent on the printing direction. Since all infill patterns in this work are rectilinear (see Fig. 1), we consider our 3D-printed ABS as a transversely isotropic solid composed of vertically stacked layers of fused beads. To determine their elastic properties, we performed quasi-static tensile tests on dog bone specimens printed with the same raster angles as the DENT specimens (0°, 90° and + 45/− 45°), as described in Section S2 (Supplementary Information). The engineering stress vs. strain responses for specimens with the aforementioned raster angles are shown in Fig. S2 (Supplementary Information). The in-plane Young’s moduli with respect to the printing direction, E11, and the transverse direction, E22, were found by measuring the initial slopes of the stress-strain responses associated with the 0° and 90° samples, respectively, while the in-plane Poisson’s ratio, ν12 =  − ε22/ε11, was measured from the slope of the transverse strain, ε22, vs. longitudinal strain, ε11, plot which was constructed using the DIC results for the 0° sample. The in-plane shear modulus, G12 = τ12/γ12, was found by measuring the slope of the shear stress vs. shear strain responses deduced from the tensile test results for the + 45/− 45° sample via

$$ {\tau}_{12}=\frac{P}{2A}\ \mathrm{and}\ {\gamma}_{12}={\varepsilon}_{yy}-{\varepsilon}_{xx} $$
(1)

where P is the applied load, A is the cross-sectional area, and εyy and εxx represent, respectively, the strains in longitudinal and transverse direction of the specimen. Since the elastic properties in the 2-3 plane are considered isotropic, we may write E22 = E33, G12 = G13 and ν12 = ν13, while Poisson’s ratio ν23 and shear modulus G23 are given by

$$ {\nu}_{23}={\nu}_{32}={\nu}_{12}\frac{1-{\nu}_{21}}{1-{\nu}_{12}}\ \mathrm{and}\ {G}_{23}=\frac{E_{22}}{2\left(1+{\nu}_{23}\right)} $$
(2)

where ν21 = ν12E22/E11. The elastic constants for the transversely isotropic 3D-printed ABS are listed in Table 1.

Table 1 Elastic constants for the transversely isotropic 3D-printed ABS
Full size table

2.3 Essential work of fracture assessment

The essential work of fracture (EWF) concept has been widely used to describe the fracture behaviour of ductile materials [48, 51,52,53] and is employed here to quantify directional changes in the fracture properties of the 3D-printed ABS. The EWF concept is based on the idea that the fracture process zone (FPZ) within the ligament of a DENT specimen can be divided into (i) the inner fracture process zone (IFPZ), in which energy is absorbed through the separation of atomic bonds and the creation of new surfaces, and (ii) the outer plastic deformation zone (OPDZ), where energy is absorbed primarily through plastic deformation processes. Thus, the total work of fracture, Wf, can be additively decomposed as

$$ {W}_f={W}_e+{W}_p\kern0.24em $$
(3)

where We is the essential work of fracture, representing the work needed to advance the crack through the material in the IFPZ, while Wp denotes the non-essential work of fracture associated with plastic deformation within the OPDZ. Assuming that We is proportional to the cross-sectional area of the ligament, AL = Lt, and that Wp scales with the volume of the material undergoing plastic deformation, the above equation can be re-written in terms of the fracture energy or specific work of fracture (energy per unit area), wf, as follows

$$ {w}_f={w}_e+\beta {w}_pL\kern0.24em $$
(4)

where we is the fracture initiation energy, i.e. essential work of fracture (EWF); wp is the specific plastic work (energy per unit volume) required to yield the material around the ligament, i.e. non-essential work of fracture (non-EWF); L is the ligament length; and β is a plastic zone shape factor.

To determine wf and βwp experimentally, multiple fracture tests were performed on DENT specimens with different ligament lengths (L = 4, 6, 8 and 12 mm) and raster angles (0°, 90° and + 45/− 45°) using a Zwick-Roell universal testing machine (2.5-kN load cell) with a constant crosshead speed of 1 mm/min. Five repeat tests for each sample were conducted to generate statistically consistent results. To enable strain field measurements via DIC, all DENT specimens were spray-coated with solvent-dispersed black dye prior to testing. Images of the specimen’s surface were recorded during the test using a CCD camera of 5.0 MP at 2 Hz. The obtained images were analysed using VIC-2D software and the nominal average strains in the loading direction, εyy, and transverse direction, εxx, were evaluated. Note that the average strains were measured in an area within the gauge length of the sample over a width slightly less than the specimen width to reduce the error in strain calculation at the boundaries. The total work of fracture, Wf, was evaluated for each specimen by calculating the area under the measured load-displacement curve. Then, the specific work of fracture, wf, was calculated by dividing Wf by the respective ligament area AL, and the obtained data was used to construct a wf vs. L plot. Since the EWF theory predicts a linear relationship between wf and L (see Eq. (4)), the EWF and non-EWF can be determined by fitting a regression line to the wf vs. L plot, where the intercept and slope represent the we and βwp, respectively. Furthermore, the fracture surface morphologies of the DENT specimens were characterized through scanning electron microscopy (SEM) using a Nova Nano SEM (50 series) operated at 10 kV. Each sample was gold sputter coated prior to the SEM examination.

3 Finite element modelling

To better understand the experimental results and to develop a simple tool for strength prediction of notched samples, finite element (FE) models were developed in ABAQUS 6.14. The 3D-printed ABS is treated as a transversely isotropic solid with elastic properties chosen according to the measurements given in Table 1. The criteria for damage initiation in the 3D-printed ABS are based on Hashin’s theory [54], which was originally developed for fibre-reinforced composite materials but can also be used for analysis of orthotropic materials [55] by using the definitions of the directions as described in Eqs. (5–8). In this model, the print direction is treated analogous to the fibre direction and the transverse to the print direction is treated as the transverse direction. The Hashin damage theory is available in ABAQUS, and introduces four damage initiation criteria associated with different damage mechanisms [54]:

Axial direction tension:

$$ {F}_{fT}={\left(\frac{{\overline{\sigma}}_{11}}{\sigma_{1\mathrm{T}}^{\ast }}\right)}^2+\alpha {\left(\frac{{\overline{\tau}}_{12}}{\tau_{12}^{\ast }}\right)}^2\ \mathrm{for}\ {\overline{\sigma}}_{11}\ge 0 $$
(5)

Axial direction compression:

$$ {F}_{fC}={\left(\frac{{\overline{\sigma}}_{11}}{\sigma_{1\mathrm{C}}^{\ast }}\right)}^2\ \mathrm{for}\ {\overline{\sigma}}_{11}<0 $$
(6)

Transverse direction tension:

$$ {F}_{mT}={\left(\frac{{\overline{\sigma}}_{11}}{\sigma_{1\mathrm{C}}^{\ast }}\right)}^2\ \mathrm{for}\ {\overline{\sigma}}_{22}\ge 0 $$
(7)

Transverse direction compression:

$$ {F}_{mC}={\left(\frac{{\overline{\sigma}}_{22}}{2{\tau}_{13}^{\ast }}\right)}^2+\left[{\left(\frac{\sigma_{2C}^{\ast }}{2{\tau}_{13}^{\ast }}\right)}^2-1\right]\left(\frac{{\overline{\sigma}}_{22}}{\sigma_{2C}^{\ast }}\right)+{\left(\frac{{\overline{\tau}}_{12}}{\tau_{12}^{\ast }}\right)}^2\ \mathrm{for}\ {\overline{\sigma}}_{22}<0 $$
(8)

Here, \( {\overline{\sigma}}_{11} \), \( {\overline{\sigma}}_{22} \), \( {\overline{\tau}}_{12} \) and \( {\overline{\tau}}_{13} \) are the stress components of the effective stress tensor with respect to the material coordinate system (1,2,3) where 1 denotes the printing (or longitudinal) direction, 2 the transverse direction and 3 the through-thickness direction. The material strength of the transversely isotropic material is represented by \( {\sigma}_{1\mathrm{T}}^{\ast } \), \( {\sigma}_{1C}^{\ast } \), \( {\sigma}_{2\mathrm{T}}^{\ast } \), \( {\sigma}_{2C}^{\ast } \), \( {\tau}_{12}^{\ast } \) and \( {\tau}_{13}^{\ast } \) where the subscripts ‘T’ and ‘C’ denote tension and compression, respectively, and α in Eq. (5) is a parameter that quantifies the effect of the in-plane shear stress on the damage initiation criterion for fibre tension. The values for the tensile strength in the longitudinal, and transverse, direction were taken from the stress-strain curves (see Fig. S2, Supplementary Information) obtained for dog bone specimens with 0° and 90° raster angles, \( {\sigma}_{1\mathrm{T}}^{\ast }=39.6\;\mathrm{MPa} \) and \( {\sigma}_{2\mathrm{T}}^{\ast }=25.6\;\mathrm{MPa} \), respectively, while the longitudinal shear strength was taken equal to half of the tensile strength measured for the specimen with + 45/− 45° raster angle, \( {\tau}_{12}^{\ast }=31.2/2=15.6\kern0.5em \mathrm{MPa} \). The compressive strength is assumed to be the same as the tensile strength in both the longitudinal and transverse direction, \( {\sigma}_{1\mathrm{T}}^{\ast }={\sigma}_{1C}^{\ast } \) and \( {\sigma}_{2\mathrm{T}}^{\ast }={\sigma}_{2C}^{\ast } \). The transverse shear strength \( {\tau}_{13}^{\ast } \) is assumed to be the same as in-plane shear strength, and α was set to 0.

The effective stress tensor is defined as

$$ \overline{\boldsymbol{\upsigma}}=\left[\begin{array}{ccc}1/\left(1-{d}_f\right)& 0& 0\\ {}0& 1/\left(1-{d}_m\right)& 0\\ {}0& 0& 1/\left(1-{d}_s\right)\end{array}\right]\boldsymbol{\upsigma} $$
(9)

where σ is the Cauchy stress tensor [34]. The parameters df, dm and ds are damage variables associated with axial, transverse and shear damage, respectively, and are used to compute the damaged material response as follows:

$$ \sigma =\frac{1}{D}\left[\begin{array}{ccc}\left(1-{d}_f\right){E}_1& \left(1-{d}_f\right)\left(1-{d}_m\right){\nu}_{21}{E}_1& 0\\ {}\left(1-{d}_f\right)\left(1-{d}_m\right){\nu}_{12}{E}_2& \left(1-{d}_m\right){E}_2& 0\\ {}0& 0& \left(1-{d}_s\right) GD\end{array}\right]\varepsilon . $$
(10)

In the latter equation, G is the in-plane shear modulus and D = 1 − (1 − df)(1 − dm)ν12ν21. The fibre, matrix and shear damage variables are defined as

$$ {d}_f=\left\{\begin{array}{c}{d}_{fT}\kern0.24em \mathrm{for}\kern0.24em {\overline{\sigma}}_{11}\ge 0\\ {}{d}_{fC}\kern0.24em \mathrm{for}\kern0.24em {\overline{\sigma}}_{11}<0\end{array}\right. $$
(11)
$$ {d}_m=\left\{\begin{array}{c}{d}_{mT}\kern0.24em \mathrm{for}\kern0.24em {\overline{\sigma}}_{22}\ge 0\\ {}{d}_{mC}\kern0.24em \mathrm{for}\kern0.24em {\overline{\sigma}}_{22}<0\end{array}\right. $$
(12)
$$ {d}_s=1-\left(1-{d}_{fT}\right)\left(1-{d}_{fC}\right)\left(1-{d}_{mT}\right)\left(1-{d}_{mC}\right) $$
(13)

where dfT, dfC, dmT and dmC are damage variables associated with the four modes of failure (see Eqs. (5)–(8)). Note that the latter damage variables take values between 0 (undamaged state) and 1 (fully damaged state) and are initially set to 0 to obtain a linear elastic response prior to the initiation of damage, as seen from Eq. (10). Once a specific damage criterion (Eqs. (5)–(8)) is met, the corresponding damage variable is activated and evolves as a function of the deformation state [56]. Here, the evolution equations for the damage variables are chosen such to obtain a linear stress softening response for each failure mode, ensuring that a certain amount of fracture energy is dissipated when the fully damaged state is reached (see [56] for further information). The fracture energies associated with longitudinal tension, \( {G}_{1T}^{\ast } \), and transverse tension, \( {G}_{2T}^{\ast } \), were taken equal to 90% of the total area under the stress-strain curve measured in uniaxial tension for the specimens with 0° and 90° raster angles, respectively, and the latter values were assumed to be identical for both tension and compression; hence, \( {G}_{1T}^{\ast }={G}_{1C}^{\ast } \) and \( {G}_{2T}^{\ast }={G}_{2C}^{\ast } \). The parameters chosen for the Hashin failure criteria and the progressive damage model are summarized in Table 2.

Table 2 Parameters chosen for the progressive damage model
Full size table

The DENT specimen is modelled as 2D plane-stress continuum. The thickness of the samples is small (only ~ 1 mm) and thus plane-stress assumptions were made. Plane-strain assumption is typically made if out-of-plane dimension is significantly larger than the in-plane dimensions and hence not valid in this case. Moreover, the Hashin Failure criterion implementation in ABAQUS is limited to plane-stress elements. This is likely due to the fact that the implementation of the Hashin Failure criterion implementation in ABAQUS was primarily aimed at composite laminates (which like our experimental samples are quite thin). To mimic the loading conditions applied in the tests, Dirichlet boundary conditions were applied on the DENT specimen by constraining all DOFs of the nodes at one end, while imposing a linear ramp on the axial displacements on all nodes at the opposite end. The characteristic element size in the finite element mesh was chosen as 0.25 mm throughout the specimen (see Fig. S3, Supplementary Information). The latter choice was ascertained by performing a sensitivity study on the L = 4 mm DENT specimen with 0° raster angle, which showed that further decreases in the mesh size led to less than 3–5% change in the calculated strength. The element type chosen is CPS4R, which is a 4-node bilinear plane-stress quadrilateral element with reduced integration and hourglass control, and the total number of elements is about 42,000.

4 Results and discussion

4.1 Load-displacement responses

In Fig. 2a–c, we plot the predicted (dashed lines) and measured (solid lines) load–displacement curves of DENT specimens with raster angles of 0°, 90° and + 45/− 45°; the contours included in each figure relate to specimens with different ligament length L = 4, 6, 8 or 12 mm. The curves in Fig. 2a–c show an initial linear elastic response followed by a blunt peak and a steep drop in load, coinciding with the propagation of a crack through the IFPZ that had formed in the ligament of the DENT specimen. For the 90° infill pattern, the ultimate loads are generally lower, and the peaks appear to be sharper than those associated with the 0° and + 45/− 45° raster angles, suggesting that the 90° specimens fracture in a more brittle manner. We also observe that the measured load-displacement curves generally follow a pattern of self-similarity with the total area under the curve (Wf), the peak load (Pmax), and the extension at break (Δb), increasing with increasing ligament length (L). Note that the latter self-similarity of the load-displacement curves is an important criterion for the validity of the EWF method and ensures that the cracks propagate under similar conditions [57,58,59]. Similar trends are predicted numerically by the FE model which is capable of replicating some of the measured load-displacement curves with good accuracy, particularly those shown in Fig. 2a for the 0° raster angle and for specimens with lower ligament length. However, the model consistently under-predicts the measured peak loads for the specimens corresponding to ligament length, L = 12 mm. Further details on the predicted failure modes are provided in Fig. S3 (Supplementary Information), showing contour plots of the damage variables df, dm and ds at the onset of fast fracture. The predicted and measured failure (or peak) loads, Pmax, are plotted as function of the ligament length L in Fig. 2d–f for 0°, 90° and + 45/− 45° raster angles, respectively. The FE model predicts a nearly linear relation between Pmax and L, due to the observed self-similarity in the load-displacement curves (see Fig. 2a–c), and similar trends are observed for the measurements.

Fig. 2
figure 2

a–c Measured and predicted load vs. displacement curves for different raster angles and ligament lengths L; d–f ultimate load plotted as a function of ligament length

Full size image

4.2 Visualization of ligament strains via DIC

Figure 3a shows the measured load-displacement curve for a DENT specimen with L = 12 mm and 0° raster angle along with contour plots of the longitudinal strain εyy in the vicinity of the ligament, as measured in situ using DIC. During the initial phase of the response, the ligament strains resemble the Mode-I strain field of a linear-elastic isotropic solid [60], as seen from frames I and II. A close examination of the strain field reveals that a small plastic zone exists at the tip of the notch where the strains exceed the material’s yield strain (εY = 1.9% for the 0° raster angle). This is observed even at low values of displacement (i.e. frames I and II), due to the stress concentration effect produced by the notch. As the applied load approaches the peak load, the intensity of the strain field in the ligament increases significantly and the strain starts to localize in the form of two strip-shaped zones within the ligament (see frame IV), which are the precursors to the propagation of a straight crack through the ligament, as shown in Fig. S4 (Supplementary Information). Similar information is shown in Fig. 3b–c for the case of 90° and + 45/− 45° raster angles (both with L = 12 mm). At small displacements, the DENT specimen with + 45/− 45° raster angle (frames I and II in Fig. 3c) shows similar strain contours as those associated with the response of the 0° specimen (see Fig. 3a). However, the zone of localized strains (i.e. the red zone in the contour plot) starts to expand further outside the ligament in the + 45/− 45° specimen as the peak load is approached (see frame IV in Fig. 3c); this is not observed for the 0° specimen. The latter observation can be explained by the fact that the + 45/− 45° specimen fractures in a zigzag pattern along the relatively weak interfaces between adjacent beads which are subjected to a combination of tensile and shear loads, as shown in Fig. S4 (Supplementary Information). Due to the brittle behaviour of the DENT specimen with 90° raster angle, the strain field could not be clearly resolved within the strain ranges shown in Fig. 3b but will be further discussed below.

Fig. 3
figure 3

Load versus displacement curves and contour plots of longitudinal strain in the vicinity of the notch measured via DIC for different raster angles (L = 12 mm): a 0°, b 90° and c + 45/− 45°

Full size image

In Fig. 4, we compare the strain fields of the three different raster angles for DENT specimens with L = 4 mm (shortest ligament) and L = 12 mm (longest ligament), respectively. Note that the strain fields in Fig. 4 were evaluated via DIC at the point of ultimate failure. Here, an effort was made to illustrate changes in the shape and size of the plastic zones by selecting a strain range limited by the yield strain measured in uniaxial tension for each raster angle. Note that the yield strain is defined here as the total strain where the plastic strain would reach 0.2% upon unloading and was determined from the stress-strain curves in Fig. S2 (Supplementary information) as 1.9%, 1.6% and 2.0% for specimens with raster angles of 0°, 90° and + 45/− 45°, respectively. Hence, the red zones in the contour plots shown in Fig. 4 can be considered equal to the size of the plastic zone in the ligament. For DENT specimens with L = 4 mm, a strip-shaped plastic zone exists for all raster angles considered here, while for L = 12 mm, the plastic zones occupy significantly more material volume, particularly at the centre of the ligaments, due to the fact that the plastic work scales (theoretically) with the square of the ligament length, Wp ∼ L2 (see discussion in Section 2.3). For all choices of L and raster angles shown in Fig. 4, the material in the ligament has fully yielded before undergoing fracture, giving us confidence that the EWF concept is applicable for the DENT samples analysed in this study. However, for the 90° specimen with the largest ligament size L = 12 mm, we notice an elastic core zone at the ligament centre. While the existence of the an elastic core might alter the fracture behaviour of the specimen, the Wp ∼ L2 scaling, as required by the EWF concept, remains unaffected, since this core region is surrounded by plastically deformed material.

Fig. 4
figure 4

Contour plots of surface strain showing the sizes of the yield zones (in red colour) at the onset of failure for different raster angles: (a) 0°, (b) + 45/− 45° and (c) 90°

Full size image

4.3 Essential work of fracture assessment

Having analysed the load-displacement curves and the strain fields induced in the DENT specimens, we proceed to evaluate the essential and non-essential work of fracture associated with each raster angle. The total work of fracture, Wf, is evaluated by calculating the area under the load-displacement curves for each DENT specimen (see Fig. 2) while the specific work of fracture wf is obtained by dividing Wf by the ligament area:

$$ {W}_f=\underset{0}{\overset{\varDelta_f}{\int }} Pd\varDelta\ \mathrm{and}\ {w}_f=\frac{W_f}{Lt}. $$
(14)

Here, Δ is the displacement applied on the specimen boundary, P is the induced load and Δf is the displacement at ultimate failure.

In Fig. 5a–c, we plot the predicted and measured total work of fracture, Wf, as a function of the ligament length, L, for 0°, 90° and + 45/− 45° raster angles, respectively, while the corresponding wf vs. L trends are presented in Fig. 5d–f. The trend lines in Fig. 5d–f represent Eq. (4) and were obtained through least square fits to the predictions and measurements, respectively. It is found that that the linear fitting lines indeed provide a good description of the measured and predicted wf vs. L trends, in line with the EWF theory [59]. For the 0° and 90° raster angles, very good agreement is reported between the predictions and measurements; however, larger discrepancies are observed for the specimens with + 45/− 45° raster angle.

Fig. 5
figure 5

Measured and predicted work of fracture (a–c) and specific work of fracture (d–f) for different raster angles

Full size image

The intercepts and slopes of the fitting lines in Fig. 5d–f were used to determine the essential work of fracture (EWF) and non-EWF, and are denoted as we and βwp, respectively, in accordance with Eq. (4). The predicted and measured EWF and non-EWF of specimens with 0°, 90° and + 45/− 45° raster angle are listed in Table 3 and plotted in Fig. 6. The experimental data show that the 0° and + 45/− 45° specimens possess a comparable EWF of 7.24 and 7.40 kJ m−2, respectively, while the ones with 90° raster angle possess a significantly lower EWF of only 3.61 kJ m−2 (see Table 3 or Fig. 6a). Similar trends are observed experimentally for the non-EWF, reporting 0.71, 0.46 and 0.80 kJ m−3 for 0°, 90° and + 45/− 45° specimens, respectively (see Table 3 or Fig. 6b). The FE model predicts a higher EWF for the 0° and 90° specimens, but under-predicts the EWF of the + 45/− 45° specimen (see Fig. 6a), in line with what was observed from Fig. 5d–f. Furthermore, the FE predictions of the non-EWF lie below the measured data by a considerable margin for all choices of raster angles, as shown in Fig. 6b. Although the FE model is capable of predicting the total specific work of fracture, wf, of the 0° and 90° specimens with good accuracy (see Fig. 2d–f), it is unable to correctly decompose wf into essential (we) and non-essential (βwp) components (see Fig. 6a–b), reporting an over-prediction in EWF and an under-prediction in non-EWF. The latter observation can be explained by the fact that the formulation of the model does not permit a clear distinction between the plastic dissipation in the OFPZ and the energy required to propagate the crack through the IFPZ, which would require a different constitutive description. For the specimens with + 45/− 45° raster angle, the FE model under-predicts the total specific work of fracture, wf (see Fig. 5f), which, in turn, causes the predicted values of EWF and non-EWF to lie below the corresponding measurements (see Fig. 6). In the load-displacement curves, the slope of the predicted curve matches well with that of experimental curves for low displacements (see Fig. 2a–c), suggesting that the choice of orthotropic material behaviour is reasonable. The significant mismatch of predicted fracture toughness values with those of experiments is likely due to one of the following two reasons: (i) the damage modelling capabilities in ABAQUS FEA, namely the Hashin Failure criterion, is based on simplistic assumptions and (ii) the simplifications and assumptions involved in the choice of parameters used for the analysis (see Table 2, for example, the value of the compressive strength is assumed to be the same as tensile strength). Parametric study with different values of α and exploring more advanced failure theories like phase field criteria is left to subsequent work. The deviations are primarily due to non-repeatable microstructure (rather, defect-structure) of the specimens stemming from the non-uniform quality of the filament feedstocks, under the same processing conditions. We note that the EWF values listed in Table 3 are comparable to those reported by Luna et al. [61] for compression moulded ABS polymer which were found to range between 3.4 and 4.7 kJ m−2 at room temperature.

Table 3 Essential and non-essential work of fracture evaluated for the three different raster angles considered in this study
Full size table
Fig. 6
figure 6

Predicted and measured EWF (a) and non-EWF (b) for different raster angles

Full size image

Figure 7 presents SEM scans of the fracture surfaces of DENT specimens with 0°, + 45/− 45° and 90° raster angles. All fracture surfaces are microscopically rough and show a combination of dimples and fibrillated structures. It is likely that the formation of the dimples resulted from extensive cavitation inside the polymer particles which then coalesced to form larger cavities, as those visible in the micrographs, while the fibrillated structures appear as a result of continued stretching and tearing of the ligaments between the cavities [62]. The fibrillated structures are most pronounced in the specimen with 0° raster angle (see Fig. 7a) where individual fibrils reach a length of > 10 μm. For a raster angle of 90°, however, the dimples on the fracture surface appear to be smaller and the formation of fibrils cannot be clearly observed which suggests that plastic flow was highly restricted and led to fracture of the ligaments soon after cavitation commenced, in line with the results obtained from our macroscopic mechanical tests (see Fig. S2, Supplementary Information). The information presented in this section allows concluding that the choice of raster angle does not only affect the macroscopic fracture properties of the 3D-printed ABS but can also alter the microscopic deformation mechanisms operative during the fracture process.

Fig. 7
figure 7

SEM scans of fracture surfaces for different raster angles. a 0°, b 90° and c + 45/− 45°

Full size image

5 Conclusions

In this study, we examined experimentally and numerically the effect of the raster angle on the essential and non-essential work of fracture of acrylonitrile butadiene styrene (ABS) thermoplastics processed via FFF AM. Tensile tests were conducted on DENT specimens with three different raster angles (0°, + 45/− 45° and 90°), and their essential and non-essential work of fracture (EWF and non-EWF) were determined via least square fits to the experimental data. To examine the effect of the raster angle on the details of the ligament strain field, digital image correlation (DIC) analysis was performed in situ, and contour plots of the longitudinal strains in the vicinity of the ligament were constructed. In addition, we developed a 2D FE model to predict the response of the 3D-printed DENT specimens, taking into account the anisotropic elastic response and fracture properties associated with the FFF printed specimens. The measurements show that the resistance to fracture initiation of 3D-printed DENT specimens is substantially higher when the printing direction is perpendicular to the crack plane (0° raster angle) as compared to the samples where the printing direction is parallel to the crack (90° raster angle), reporting EWF values of 7.24 kJ m−2 and 3.61 kJ m−2 for the 0° and 90° infill patterns, respectively. A high EWF value was also reported for the + 45/− 45° raster angle (7.40 kJ m−2) where the beads of the FFF print are subjected to pronounced shear loading. The DIC analysis showed that connected plastic zones existed in the ligament of the DENT specimens prior to the onset of fracture, and this was corroborated by SEM fractography which showed that fracture proceeded by a ductile mechanisms involving void growth and coalescence followed by drawing and ductile tearing of fibrils. The ultimate strength and fracture properties predicted by the FE model were found in good agreement with the measurements obtained for the different DENT specimens, while larger discrepancies were reported when the ligament length was L = 12 mm. Future work should involve in-depth study of the effects of the different parameters of the Hashin criteria and explore the efficacy of different failure criteria such as the Tsai Wu, Puck etc. The results presented in this study offer physical insights into the fracture mechanisms of 3D-printed ABS and provide useful guidelines for the design of fracture-resistant thermoplastics processed via fused filament fabrication AM.