Abstract
To date, slicing algorithms for additive manufacturing is the most effective for favourable triangular mesh topologies; worst-case models, where a large percentage of triangles intersect each slice plane, take significantly longer to slice than a like-for-like file. In larger files, this results in a significant slicing duration, when models are both worst cases and contain more than 100,000 triangles. The research presented here introduces a slicing algorithm which can slice worst-case large models effectively. A new algorithm is implemented utilising an efficient contour construction method, with further adaptations, which make the algorithm suitable for all model topologies. Edge matching, which is an advanced sorting method, decreases the number of sorts per edge from n total number of intersections to two, alongside additional micro-optimisations that deliver the enhanced efficient contour construction algorithm. The algorithm was able to slice a worst-case model of 2.5 million triangles in the 1025s. Maximum improvement was measured as 9400% over the standard efficient contour construction method. Improvements were also observed in all parts in excess of 1000 triangles. The slicing algorithm presented offers novel methods that address the failings of other algorithms described in literature to slice worst-case models effectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Additive manufacturing (AM) can be defined as a technology where a three-dimensional (3D) object is constructed by the sequential creation of two-dimensional (2D) layers [1]. The creation of components can be performed using a range of methods and materials; however, all AM processes consist of three distinct stages: (i) construction of a digital model; (ii) application of pre-processing algorithms, converting the model into 2D layers then generating the machine toolpath [2]; and (iii) creation of the part by either depositing or fusing material to the preceding layer. The benefits of AM include increased design possibilities over subtractive manufacturing and increase in efficiency and cost in small volumes [3].
Of the three primary file formats for AM (*.STL, *.AMF, *.3MF) [4, 5], all construct geometry using triangular meshes. Meshes in AM always consist of tessellated triangles which connect at the vertices, each vertex defined as a 3D floating point coordinate and are ordered counter-clockwise when observing the part from the outside [6]; an associated outward-facing normal is attributed to each triangle, which can be utilised during slicing or when graphically rendering the part [7]. As technology has advanced and the resolution and accuracy of machines have improved [8], the meshes in AM files required to capture the more detailed geometric features have increased in complexity and become finer [9]. The slicing algorithm required to convert modern AM models into 2D contours must continue to improve, to slice what was once considered exceptionally large files efficiently.
Part models that are the worst case from a slicing algorithmic perspective are those containing a large percentage of triangles intersecting on any given layer. The slicing process consists of two operations calculating the intersections between the triangles and the slice plane and then sorting the intersection into contiguous contours. Worst-case parts are particularly difficult to slice due to the sorting process, increasing in duration exponentially by each additional triangle in the layer. The research presented here builds on the efficient contour construction (ECC) method [10] that exploits the triangular mesh format adding features that address the inability to handle worst-case parts effectively.
2 Review of related works
Slicing is the process of converting the 3D model into a series of layers containing the 2D perimeter boundaries characterised by a closed loop of connected points [11]. Xu et al. [12] offer a basic description of the stages involved in the slicing process (Fig. 1), consisting of calculating all the intersections for one slice plane then sorting them into a continuous contours method that works very well for simple geometries but becomes highly inefficient as complexity increases, due to the consideration of triangles that do not intersect with the slice plane. Tian et al. [13] describe a method where pre-grouping triangles according to whether they fall into a collection of slice planes using a binary search to reduce such considerations. Whilst a significant increase in efficiency can be observed, it would be better if consideration of redundant triangles could be eliminated entirely.
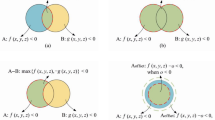
In the standard slicing model (Fig. 1), sorting of the generated intersections relies on comparison of end points of the generated line segment when intersecting the triangle with the slice plane, as described by Steuben et al. [14] taking the form of a connected graph search [15] causing false matches due to models where more than two triangles converge on one point (Fig. 2). This causes the algorithm to either fall into a continuous loop or produce a failed output, for which a better method of sorting is required.
Typically, layer thickness is constant during the slicing process; however, there are a number of examples for adaptive slicing [16,17,18] where the layer height is decreased when slicing regions of high detail or increased when there are less geometric features to be captured. These methods can increase the efficiency of the slicing process; however, use is only appropriate where one model is produced per build cycle. In larger AM machines, such as selective laser sintering (SLS), stereolithography (SL), or selective laser melting (SLM), where conventionally, multiple models are tessellated into the build area. Increasing or decreasing the slice depth for one model will likely be to the detriment of other models on the layer. Li and Xu [19] acknowledge that adaptive slicing is primarily useful for fused deposition modelling (FDM) and can therefore not be considered suitable for a universally efficient slice engine.
Several slicing algorithms produce an optimal output for specific methods of AM. Ding et al. [20] suggest slicing in multiple orientations for wire-feed-based AM, primarily with the goal of increasing part integrity and minimising support structures. There is similar research attempting to optimise the slicing process for powder bed fusion technology [21]; however, similar, more significant improvements in this regard can be seen in the optimising model orientation and arrangement [22,23,24] and should therefore not be the responsibility of the slicing algorithm.
Combining the slicing algorithm with tool path generation [25] can improve the efficiency of the overall process by removing the need to write to an intermediary slice file but limits the possibilities of the output of the algorithm to the specific application, due to the varying nature of the toolpath input format. There have been a number of efforts to compensate for low-quality models, containing errors or incorrect geometric features using the slicing process; Zhao et al. [26] aimed to reduce the error caused by discretising the CAD model into the triangular mesh file using contour approximation, and Luo and Wang [27] similarly aimed to minimise the impact of defects such as cracks and overlapping edges in the model during the slicing process.
Zhang’s [10] ECC algorithm presents a comprehensive universal slicing algorithm that is both time- and memory-efficient; their method exploits the clockwise nature of a triangular mesh, allowing for only one intersection per slice plane per triangle to be computed, reducing the memory requirement of the slicing algorithm by half. Additionally, the dynamic sorting method is utilised where intersections are inserted directly into the contour as they are calculated rather than using an intermediary data structure to hold the unsorted line segments, again reducing the memory requirement of the algorithm. The sorting method enables lines to be connected so that only the start and end of the connected line segments need to be checked, drastically reducing the number of sorts and therefore the amount of time taken for sorting than the end-to-end line segment sort detailed in Fig. 1.
3 Methods
3.1 ECC algorithm implementation
Zhang et al. [10] offer a robust ECC algorithm, which is efficient for some part geometries. The algorithm relies on calculating the intersections for each triangle from top to bottom along either the longest edge or the two shorter edges (Fig. 3). The decision is reliant on the order in which the vertices of the longest edge appear in each triangle. On calculation of the intersection, it is stored in an intersection node (IN), which contains the 2D coordinates of the intersection, an edge pointer (EP) containing the memory address of the vertices of the two edges of the triangle intersecting the slice plane, and the next and previous pointer, which locates a following or preceding IN in the list, respectively (Fig. 4). A series of linked INs are held in an intersection linked list (ILL) data structure, which contains a pointer to the subsequent ILL and a pointer to the first and last element in the list.
Following the creation of the IN, it must be inserted into an ILL. All the existing ILLs of the first and last element’s edge pointers are compared with the edge pointer of the IN for insertion. The IN is then inserted according to the following scenarios:
-
1.
There are no existing ILLs, the IN is the first calculated intersection on that layer, and the IN is inserted in a new ILL;
-
2.
One match is found with the first IN in an ILL, and the IN is inserted at the front of the list;
-
3.
One match is found with the last IN in an ILL, and the IN is inserted at the back of the list;
-
4.
Two matches are found, in separate lists, at the first element in one ILL and the last element in a second ILL; the IN connects the two lists; and the second list is deleted;
-
5.
Two matches are found in the same list, the IN is inserted at the back of the matched list, and this indicates the matched list has been completed;
-
6.
No match is found in any of the existing ILLS, and the IN is inserted in a new ILL.
Once the IN has been inserted into an ILL, the following intersection on the edge is calculated and sorted. Once all the intersections on the triangle have been computed and inserted into ILLs, the subsequent triangle is considered until all triangles in the mesh have been considered, and slicing reaches completion. The data in the ILLs can then be written into a slice file format, or the ILL list format can be used directly for generation of the toolpath.
Upon implementation of the ECC algorithm and a traditional strategy based on the flowchart detailed in Fig. 1 [12], in the C++ language, comprehensive testing was performed on the *.STL files shown in Figs. 5 and 6, and the results are given in Table 1. The ECC algorithm shows improvements over the conventional slicing method between 9000 and 1150% for all three parts. The result was especially impressive for Fig. 6, taking under 575 ms to slice the part. However, in both the conventional and the ECC methods, there is a disparity between the slice durations for Figs. 5a and 6 despite consisting of a similar number of triangles, took in excess of 237,000 ms and 2,752,181 ms for the ECC and conventional algorithms, respectively—413 times longer to slice for the ECC method and 494 times longer for the conventional algorithm.
Figure 5b slice time is 20.9 and 19.2 times less than that of Fig. 5a for the ECC and conventional algorithm, respectively, indicating that the direction of slicing interacting with the topology of the part has a significant impact on the effectiveness of both the algorithms. A possible solution is to analyse parts and orient them in a way that is optimal for the slicing algorithm; however, this does not present a good result as the optimal orientation for slicing is unlikely to be the optimal orientation for building the part [28]. An algorithm capable of slicing the parts efficiently, regardless of the orientation, is essential.
Analysis of the topology of Fig. 5a indicated that the average percentage of triangles intersecting on each layer is 33% equating to 34,000 triangles, meaning that the part can be identified as the worst case, whereas for Fig. 5b, an average of less than 2% or 2056 triangles intersect on each layer. The total number of intersections of the entire part remains the same for both cases. It can be derived that the sorting procedure when a large number of triangles are present per layer is the cause of inefficiency.
3.2 Edge matching
The sorting process in the ECC algorithm relies on comparing the edge pointer at the start and end of each list of connected vertices for a match with the current IN. This process can be further optimised using the fact that triangular meshes can only be matched edge to edge and vertex to vertex; therefore, one triangle only shares edges with exactly three others, one on each edge. Consequently, once a match has been made for one intersection on an edge, the matched triangle will be the same for the rest of that edge (Fig. 7). The standard ECC algorithm was adjusted to account for this to reduce the number of sorting procedures required for each edge from n, the total number of intersections of the edge to one.
The IN data structure was modified to contain an edge link pointer (Fig. 8), holding the memory location address which points to the ILL containing the IN of the subsequent intersection on the triangle. The procedure of using the edge link is described in the flowchart in Fig. 9. The first intersection is inserted into the ILL using the method for the standard ECC algorithm, and following this, the subsequent IN (INi) is inserted into the ILL under four cases depending on the outcome of the sorting of the previous IN (INprev):
-
1.
If the INprev is inserted into a new ILL, the current IN for consideration INi will also be inserted into a new ILL, and the address of the ILL containing INi will be saved as INprev’s edge link pointer;
-
2.
If INprev is inserted at the back of a list, INi will be inserted into the back of the list that is located at the edge pointer of the last IN in the list that INprev is connected to;
-
3.
If INprev is inserted at the front of a list, INi will be inserted into the front of the list that is located at the edge pointer of the first IN in the list that INprev is connected to;
-
4.
Finally, if INprev connected two lists, INi will connect the two lists contained in the edge pointers of the last IN in the ILL that INprev follows and the first IN that INprev precedes once connected.
In cases 1 to 3, the memory location address of the ILL that INi has been inserted into is assigned as the edge link of the INprev. In case 4, it is unnecessary to assign the edge link, as INprev is on the middle of an ILL and therefore will not be checked in future IN insertions. The impact of implementing the edge link pointer into the algorithm is that the number of intersections that undergo the checking process per triangle is reduced from n (the total number of intersections on the triangle) to one. The values recorded in counter were temporarily implemented within each algorithm detailing the number of times the matching process of the standard ECC has undergone for each algorithm is given in Table 2.
3.3 Additional modifications and edge matching
Transferring completed ILLs from the active sorting CLL to a separate CLL containing only completed lists was expected to increase efficiency by reducing the number of sorts. In some cases, all the triangles in one connected multi-shell triangular mesh appear successively in the file; therefore, the contour or contours associated with that shell will be completed first, and consequently, any further INs generated by the remaining shells will check the completed ILL on each search iteration. On initialisation of the algorithm, two versions of the CLL are created: the standard CLL where all sorting and IN insertions take place and a second complete CLL where ILLs are transferred by modifying the memory location pointers, when the IN is found to match in the same list twice.
Micro-optimisation in the order that case variables are assessed in the IF/ELSE-case loop provided a noticeable time saving. The order the case variables appear was restructured to ensure that the most likely case arises first. To test which case is the most likely, a series of integer values were created to count the number of times each case variable appeared. Table 3 shows the number of occurrences of each case recorded using integer counters when running the ECC algorithm with edge matching.
Table 4 shows that the most dominant case is largely dependent on the topology of the triangles in the mesh, revealed by a comparison of the rotated test sheets in Fig. 5 presenting differing case occurrences despite having triangles of identical geometry and connections. Table 5 contains the average likelihood of a case occurring for all models considered in this paper. It was determined that the order of the automatic insertion processes in the IF/ELSE loop would follow the most probable to the least probable occurrence outlined in Table 4.
4 Results, analysis, and discussion
The modifications to the ECC algorithm create the enhanced efficient contour construction (EECC) algorithm, to assess the successfulness of this method; several parts were sliced using the standard ECC algorithm, the ECC algorithm with edge matching, and the completed EECC algorithm, and the results are shown in Table 5. The most impactful improvement is shown in the identified worst-case parts (Figs. 12, 13, 14, and 15). In the largest worst-case model that could be sliced using the ECC algorithm (Fig. 15), the EECC algorithm is 9400% faster than the standard ECC algorithm. Of the parts tested, only models containing under 1000 triangles witnessed a significant percentage increase in comparison to the original slicing time of 180% for Fig. 10. This is an acceptable increase due to the imperceptible slicing times both with the ECC and EECC algorithms and can be explained due to the implementation of edge-point testing taking more time than its saves; only a negligible decrease is seen in Fig. 11 for the same reason.
Figures 11, 12, and 13, 16 represent the largest of the files tested using the standard ECC algorithm, which underwent the slicing process for over 4 h but never reached completion due to the program being terminated after this time, as it was unacceptably long. This indicated that these parts would have seen even larger improvements than those witnessed in Fig. 14, if completion was indeed possible.
Table 6 offers a comparison of open-source slicers with the enhanced ECC algorithm; slicing was precisely timed by downloading the open-source software and including timing modifications. The EECC algorithm was at least twice as fast for all instances.
4.1 Space and time complexity
The standard ECC sort procedure can be defined under three cases: worst case, best case, and average case, if there are k number of lists in the CLL, m intersections per triangle, and n triangles in the model; the complexity of the sorting algorithm is detailed in Table 7.
The introduction of the enhanced ECC algorithm reduces the number of sorts per triangle from m intersections on the triangle to 2 in all cases, and therefore, the time complexity become O(2n), O(2kn), and O(kn) for the best, worst, and average cases, respectively. This demonstrates that the improvements to the ECC algorithm have the greatest impact on the worst-case triangular meshes, and the least on the best case. The worst-case sort procedure can be differentiated from previously identified worst-case models where the k value would be very large, up to 67% of the total number of triangles n, when compared with a best-case model where k would be less than 1% of the total number of triangles.
There was a slight increase in space complexity in the enhanced ECC algorithm in comparison to the standard ECC algorithm due to the implementation of the edge link pointer, where each pointer is 8 bytes on a 64-bit system. The total space requirement for one intersection is 4 bytes each for the X and Y coordinates of the intersection and the five pointers, two edge pointers, one edge link pointer, and two pointers which link the contour together, which is a total of 48 bytes per intersection, an increase of 8 bytes or 16.67% over the standard ECC algorithm. As there are m intersections per triangle and n triangles in the model, the total RAM requirement can be defined as 48-nm bytes. This slight increase in space complexity can be justified by the improvements in efficiency.
4.2 Industrial context
Lattice structures have been identified that offer significant advantages over solid infill products and design dependently, and they can offer the same or better material properties, e.g., tensile and compressive strength at a considerably reduced part weight and volume. These types of parts have seen significant advantages in areas where a high strength to weight ratio is desirable, examples include aerospace and sport performance products. Lattice structure models can often be categorised as the worst-case models, especially when the lattice is in one layer running from top to bottom in the direction of construction.
One industrial example of lattice structures in AM is 3D printed shoes [29, 30], Figure 17 shows the Adidas Alphaedge 4D shoes currently available on the mass market, featuring a lattice structure on the sole of the shoe. Increasingly, these shoes are manufactured custom to a scan of the wearers’ foot, meaning that each CAD model is different and will need to be sliced individually, resulting in overall very lengthy slice times. Figure 18 shows a model of the sole of shoe intended that is intended for production using additive manufacturing. This part can be considered both the worst case, with an average of 24% triangles intersecting on each layer and a large *.stl file. The results in Table 5 demonstrate enhanced ECC algorithm that offers significant advantage on this part that would be manufactured in an industrial application. The part shows an improvement of over 100% on the standard ECC algorithm and an improvement of at least 15,200% over the traditional end-to-end line sort algorithm.
Adidas Alphaedge 4D [29]
5 Conclusion
The objective of this research was to generate a slicing algorithm for AM that is capable of efficiently slicing worst-case geometric parts, defined as triangular mesh models where a high percentage of the parts of triangles intersect on each layer. An adaption of the ECC algorithm, including reduction in the number of sorts for each triangle, and micro-optimisations through structuring, formed the enhanced ECC algorithm. Efficiency tests were conducted on a set of *.STL files (however, any other triangular mesh files could be used in the algorithm) and found a maximum improvement of 9400% on the largest worst-case file. It was also found that *.STL files that were previously too time-inefficient to complete slicing using the standard ECC algorithm took less than 300 s to slice.
The enhanced ECC algorithm addresses the failings of the other algorithms to slice very large worst-case parts, which are becoming more prevalent in the AM sector [31] in reproduction of scanned real-world objects [32] or highly detailed, large-scale AM components. Improvements to the slicing process will have to evolve as the models grow in complexity and size; whilst the enhanced ECC algorithm may be able to slice all parts efficiently now, and further developments will be necessary in the future.
Data availability
Not applicable.
References
Gibson I, Rosen D, Stucker B (2014) Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing: Springer, New York. pp. 1–25
King B, Bennett GR, Rennie AEW (2017) Comparison of galvanometer and polygon scanning systems on component production rates in selective laser sintering. In: Proceedings of the 15th Rapid Design, Prototyping & Manufacturing Conference (RDPM2017), Newcastle
Mohsen A (2017) The rise of 3-D printing: the advantages of additive manufacturing over traditional manufacturing. Bus Horiz 30(5):677–688
Garden J (2016) Additive manufacturing technologies: state of the art and trends. Int J Prod Res 54(10):3118–3152
Paul R, Anand S (2015) A new Steiner patch-based file format for additive manufacturing processes. Comput Aided Des 63:86–100
Cătălin I, Daniela I, Alin S (2010) From Cad model to 3d print via “Stl” file format. Fiabilitate Durab, l 1(5):73–80
Adnan FA, Romlay FRM, Shafiq M (2018) Real-time slicing algorithm for Stereolithography (STL) CAD model applied in additive manufacturing industry, IOP conference series Materials Science and Engineering 342(1):012016
Engstrom D, Porter B, Pacios M, Bhaskaran H (2014) Additive nanomanufacturing - a review. J Mater Res 29(17):1792–1816
Zha W, Anand S (2015) Geometric approaches to input file modification for part quality improvement in additive manufacturing. J Manuf Process 20:465–477
Zhang Z, Joshi S (2015) An improved slicing algorithm with efficient contour construction using STL files. Int J Adv Manuf Technol 80(5–8):1347–1362
Brown A, De Beer D (2013) Development of a stereolithography (STL) slicing and G-code generation algorithm for an entry-level 3-D printer, 2013 AFRICON, pp 1–5
Xu H, Jing W, Li M, Li W (2016) A slicing model algorithm based on STL model for additive manufacturing processes. IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC) : 1607–1610
Tian R, Liu S, Zhang Y (2018) Research on fast grouping slice algorithm for STL model in rapid prototyping. J Phys: Conf Ser. https://doi.org/10.1088/1742-6596/1074/1/012165
Steuben J, Iliopoulos A, Michopoulos J Implicit slicing for functionally tailored additive manufacturing. Comput Aided Des 77:107–119
Hopcroft J, Tarjan R (1973) Efficient algorithms for graph manipulation. Commun ACM 16(6):372–378
Hu B, Jin G, Sun L (2018) A novel adaptive slicing method for additive manufacturing. CSCWD, Nanjing, pp 218–223
Wang W, Chao H, Tong J, Yang Z, Tong X, Li H, Liu X, Liu L (2015) Saliency-preserving slicing optimization for effective 3D printing. Comput Graph Forum 34(6):148–160
Pan X, Chen K, Zhang Z, Chen D, Li T (2013) Adaptive slicing algorithm based on STL model. Appl Mech Mater 288:241–245
Li Q, Xu XY (2015) Self-adaptive slicing algorithm for 3D printing of FGM components. Mater Res Innov 19(S5):635–641
Ding D, Pan Z, Cuiuri D, Li H, Larkin N, Van Duin S (2016) Automatic multi-direction slicing algorithms for wire based additive manufacturing. Robot Comput Integr Manuf 37:139–150
Singhal SK, Jain PK, Pandey PM (2008) Adaptive slicing for SLS prototyping. Comput-Aided Des Appl 5(1–4):412–423
Pereira S, Vaz A, Vicente L (2018) On the optimal object orientation in additive manufacturing. Int J Adv Manuf Technol 98(5):1685–1694
Golmohammadi AH, Khodaygan S (2019) A framework for multi-objective optimisation of 3D part-build orientation with a desired angular resolution in additive manufacturing processes. Virtual Phys Prototyp 14(1):19–36
Yang G, Liu W, Wang W, Qin L (2010) Research on the rapid slicing algorithm based on STL topology construction. Adv Mater Res 97-101:3397–3402
Eragubi E (2013) Slicing 3D model in STL format and laser path generation. Int J Innov Manag Technol 4(4):410–413
Zhao G, Ma G, Feng J, Xiao W (2018) Nonplanar slicing and path generation methods for robotic additive manufacturing.(Report). Int J Adv Manuf Technol 96(9–12):3149
Luo N, Wang Q (2016) Fast slicing orientation determining and optimizing algorithm for least volumetric error in rapid prototyping. Int J Adv Manuf Technol 83(5):1297–1313
Zhang Y, De Backer W, Harik R, Bernard A (2016) Build orientation determination for multi-material deposition additive manufacturing with continuous fibers. Proc CIRP 50:414–419
Cătălin A, Zapciu A, Popescu D (2019) 3D-printed shoe last for bespoke shoe manufacturing. MATEC Web Conf 290:4001
Perry A (2018) 3D-printed apparel and 3D-printer: exploring advantages, concerns, and purchases. Int J Fash Des Innov 11(1):95–103
Barnett E, Gosselin C (2015) Large-scale 3D printing with a cable-suspended robot. Addit Manuf 7(C):27–44
Tóth T, Živčák J (2014) A comparison of the outputs of 3D scanners. Proc Eng 69:393–401
Funding
This study was partly funded by the Low Carbon in Lancashire Hub (grant reference 19R16P01012 and Euriscus Ltd.).
Author information
Authors and Affiliations
Contributions
BK undertook the development of the algorithm presented in this paper, supervised by AR. Models for testing were supplied by GB.
Corresponding author
Ethics declarations
Conflict of interest
This research is sponsored by Euriscus Ltd. of which Graham Bennett is the CTO.
Ethical approval
This study complies with the ethical standards set out by Springer.
Consent to participate
Not applicable.
Consent to publish
Not applicable.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
King, B., Rennie, A. & Bennett, G. An efficient triangle mesh slicing algorithm for all topologies in additive manufacturing. Int J Adv Manuf Technol 112, 1023–1033 (2021). https://doi.org/10.1007/s00170-020-06396-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-020-06396-2