1 Introduction

Conventional machining processes such as turning, drilling and milling have achieved a dominant position in the aerospace and automotive industries, as they contribute to the rendering of a large variety of necessary features on mechanical components with sufficient efficiency. Although these processes were proven effective for the commonly used engineering materials, the rise of utilization of various hard-to-cut materials such as steel, titanium alloys, nickel superalloys, ceramics or metal matrix composites in the aforementioned industries due to their superior mechanical properties, wear and corrosion resistance, has posed new difficulties such as increased tool wear, which require more advanced methods in order to be overcome [19, 37, 38]. Furthermore, the limitations on, feed and cutting speed, related to conventional machining of hard-to-cut materials reduce the productivity and profit in industrial practice. In order to improve machining of difficult-to-cut materials, assistance of conventional machining processes by non-conventional technologies was proposed, in the form of energy-assisted hybrid machining processes such as vibration-assisted machining (VAM), thermal-assisted machining (TAM) or magnetic-assisted machining (MAM), among others [19, 37, 43].

In the area of TAM, laser-assisted machining (LAM) is one of the most important processes. LAM is a hybrid machining process in which the surface of the workpiece is scanned by a laser beam, which is a high power, localized heat source, heating the workpiece before cutting without leading to thermal damage or phase transition [20, 37]. At higher temperatures, the material strength is usually lower, as well as the cutting energy and plastic deformation is enhanced, something that improves machinability [19, 20, 37]. The regulation of workpiece temperature can be managed by properly adjusting the values of process parameters, such as cutting speed and feed as well as laser parameters such as power, spot size, incident angle and tool-beam distance [37, 40]. Moreover, material properties, such as thermal conductivity, specific heat, reflectivity and phase transition of the materials play a significant role to LAM [19]. One of the basic factors determining the benefits of the use of laser assistance in machining is the reduction of the cutting forces, which are required to carry out the cutting process of the workpiece.

A considerable amount of work has already been conducted in the field of laser-assisted machining of various hard-to-cut materials, such as nickel-based alloys, steel, composites and titanium alloys. Anderson et al. [4] confirmed in their research the great economic benefits of the use of LAM in the case of machining of Inconel 718 alloy. With regard to nickel alloys, there is a lot of research in the field of LAM technology [6, 45],in which its beneficial effect on cutting force during machining of Inconel 718 alloy [46] was demonstrated. More specifically, studies show that with the difficult-to-cut Inconel 718 alloy, often used in aviation technology, a beneficial effect of laser assistance has been observed on cutting force components [44, 46], surface roughness [41, 46], cutting zone temperature [44], microhardness [41] and residual stresses [6]. Regarding LAM of steels, Panjehpour et al. conducted a study of AISI 52100 pulsed laser-assisted steel processing [27]. They found that at an increased laser power value, 25% decrease of specific cutting energy could be achieved but higher power values were unfavorable due to increase of tool wear rate. Xavierarockiaraj and Kuppan observed a reduction of workpiece strength by about 40% due to the use of LAM in the case of tool steel turning [47]. Moreover, Ahn et al. tested the effectiveness of LAM for AISI 1045 steel by predicting the possibility of a wide application of this technology for difficult-to-cut materials, including heat-resistant and heat-resistant alloys [3]. Przestacki et al. and Bejjani et al. expanded the investigations regarding the machining in LAM conditions to titanium- and aluminum-based metal matrix composites [7, 29].

Also in the case of titanium alloys, research in the field of LAM machining can be found [40]. Braham-Bouchnak et al. [8] studied the effect of laser assistance on the machinability of the Ti533-3 alloy. They showed a reduction in cutting forces with increasing temperature, which is significantly influenced by cutting parameters and laser power. The surface roughness, in this case, was almost insensitive to the laser. Dandekar et al. [9] improved the machinability of the Ti-6Al-4V alloy by using LAM and additionally cryogenic cooling of the tool surface, showing, in addition to improving quality indicators, the economic benefits of such technology. Sun et al. studied laser-assisted processing of technical titanium [38] and Ti-6Al-4V alloy [39]. They showed that in the case of pure titanium, power density had a major impact on the reduction of cutting force components. Less dynamic forces were obtained for both titanium and its alloy due to continuous deformation during chip formation. They determined that in order to achieve maximum reduction of cutting force, with constant laser power, it is necessary to properly set the angular position of the laser determining the distance between the cutting place and the laser spot ahead of it. The distance required for machining under LAM conditions for the Ti-6Al-4V alloy was greater than that for technical titanium and was dependent on the cutting speed.

Habrat [15] conducted research on the impact of laser assistance during turning of a titanium alloy on selected machinability indicators. In addition, Habrat et al. [14] developed models for the cutting force components in the finishing process. Rashid et al. [30] observed when machining the titanium alloy Ti-6Cr-5Mo-5V-4Al, a significant effect of laser power on cutting forces in the entire range of cutting speeds tested. The higher the laser power, the greater the reduction in cutting forces compared with conventional machining. Gao et al. [12] conducted an interesting study regarding the machinability of near-alpha titanium alloy BTi-6431S compared with that of Ti-6Al-4V during laser-assisted milling. For the preheating of the BTi-6431S workpiece, temperature values of 200 ∘C and 300 ∘C were selected and experiments were conducted under various levels of cutting speed and feed rate. Increased laser power was found to lead to lower cutting forces in each case but it was shown that the highest cutting force reduction was obtained for Ti-6Al-4V due to its relatively lower strength at elevated temperatures. Regarding feed rate, it was observed that the laser beam effect was significant only above a critical feed rate value whereas regarding cutting speed the effect of laser heating was almost similar for the entire range of cutting speeds. Moreover, it was found that the tool wear mechanism was changed from flank wear and chipping to diffusion wear in the case of LAM and that LAM did not contribute much to the tool life in the case of BTi-6431S machining, compared with that of Ti-6Al-4V.

Rahman Rashid et al. [31] also investigated the effect of laser beam assistance to turning of Ti-10V-2Fe-3Al beta titanium alloy. Cutting forces were shown to be lower during LAM but the difference between force during conventional turning (CT) and LAM was reduced at high cutting speeds, whereas this difference was almost the same within the entire range of feed rates. Cutting temperature during LAM showed an opposite trend compared with that in CT as it was reduced at higher cutting speeds, where it was found to be close to the temperature during CT. A similar trend was found to exist regarding feed rates but the difference between LAM and CT temperatures was much larger and it was also found that over 800 ∘C thermal softening had more influence than strain hardening. However the machinability of this alloy was found to be almost 33% of that achieved for α and α-β alloys. Regarding the same alloy, the same research group expanded their study under various values of laser power, as although laser power needs to be over a certain limit in order to have an observable effect, very high power values may lead to adverse effects [32]. The authors concluded that the range 800–1200 W was the recommended laser power range for LAM of the specific alloy. However, it is important to note that machining of titanium alloys is also risky due to the possibility of ignition [13], especially in conditions of dry machining with an additional source of heat, as in the case of LAM. Therefore, it is important to specify process models for optimizing cutting parameters.

Apart from the experimental studies, during the last decades, studies including the finite element (FE) modeling of LAM processes were presented, focusing mainly on laser-assisted milling and laser-assisted turning with a view to act complementary to the experimental studies towards the study of fundamental thermo-mechanical phenomena and the optimization of LAM process. The majority of the presented models are related to laser-assisted milling and especially the effect of laser heating on the substrate, e.g., [26, 49], whereas fewer works deal with the coupled thermo-mechanical problem, e.g., [21, 50].

Yang et al. [49] used a FE model for laser-assisted milling with a view to predict the volume of HAZ. In their model they calculated emissivity and absorptivity based on experimental data and managed to predict HAZ under various process conditions. Although laser scanning is usually performed in a linear path in laser-assisted milling simulations, Pan et al. [26] simulated a rotating laser scanning path for the laser scanning and absorption ratio was approximated based on the melting area prediction. In the work of Liu and Shi [21] the effect of laser beam preheating was calculated analytically and then considered as an initial temperature boundary condition for the machining process which was solved sequentially with the temperature field inserted in the cutting model after some time intervals. Zamani et al. [50] created a coupled thermo-mechanical model with simultaneous laser heating and cutting.

Regarding laser-assisted turning, relatively fewer works have been conducted. Most of them consider the thermo-mechanical problem of laser-assisted turning as an extension of the established orthogonal cutting model [5, 48] or simplified 3D turning models [36], in which both contributions from laser heating and material removal are considered. However, these models cannot present in detail the heat transfer phenomena during laser-assisted turning for a real cylindrical workpiece in respect to the variation of cutting speed, feed rate and laser beam characteristics. Thus, several authors have employed 3D thermal models in order to study in detail the characteristics of laser heating process during LAM. Rozzi et al. [34, 35] conducted the earliest numerical studies on laser-assisted turning by using a model which transformed the heat transfer problem on the cylindrical part to a heat transfer problem on a flat surface and managed to determine the effects of cutting speed, feed rate, laser beam diameter and power on workpiece temperature. Later, Pfefferkorn et al. [28] employed a similar model for laser-assisted turning focusing also on the effect of parameter uncertainties on the results, showing that laser absorptivity and convective heat transfer play a significant role on the accuracy of the model. Moreover, although their model predicted the effect of laser power and feed rate accurately, the effect of depth of cut was difficult to be captured. Tian and Shin [42] presented a complex 3D model regarding LAM of a cylindrical workpiece with variable diameter and found that the model showed good agreement with experimental results under various laser power, feed rate and cutting speed values.

While most early laser-assisted turning models involved simplifications or special element deactivation methods, Jung and Lee [17] and Roostaei and Movahhedy [33] presented a fully 3D LAM model with moving heat source on the cylindrical workpiece. Ding and Shin [10] developed a thermal LAM model for a hollow cylindrical workpiece with varying diameter and achieved sufficient accuracy and Abdulgani et al. [1] presented a comprehensive study on the effect of laser power, preheating time, cutting speed and feed rate during LAM. Dong and Shin [11] developed a coupled thermo-mechanical model for laser-assisted turning with a view to predict thermal cracks due to laser heating on the workpiece. Kashani et al. created a model for turning carbon steel for the initial phase of machining in laser-assisted conditions [18] and compared the results of the FE with an analytical solution. They noted that the errors of both models were below 10% and stressed the necessity of use a systematic approach for laser absorptivity determination in order to improve model accuracy. Finally, Nadim et al. [24] investigated the thermal phenomena during LAM with a FE model, including the effect of air jet cooling and different laser beam power profile. After validating the model with various experimental data, they were able to determine also the thermal penetration depth in each case. It was observed that in most of the aforementioned models, the authors concentrated on studying the thermal effects of LAM on ceramic workpiece materials with only two studies conducted on steel workpieces. Moreover, in most studies on laser-assisted turning only the variation of the temperature field was discussed and little or no work has been conducted to determine heat-affected zones and microstructure alterations.

In the present study, a comprehensive experimental study on the laser-assisted turning of Ti-6Al-4V is conducted. The parameters varied in this study include laser spot size and workpiece diameter, apart from cutting speed, which are not commonly studied in existing works. Thus, experiments are conducted under various cutting speed, laser spot size and workpiece diameter values in order to determine the effect of laser assistance on cutting forces, tool life and surface microstructure of the workpieces. The experimental study is complemented by a 3D thermal model for laser heating of the workpiece in order to observe the heat transfer phenomena during this phase of LAM, which was performed for the first time regarding titanium alloys. After validation of the model with experimentally measured data regarding temperature field on the workpiece surface, the variation of heating and cooling rate in the workpieces is determined, revealing the important factors which affect the thermal phenomena during LAM and for the first time, the computed values of temperature rate are employed to explain the observed microstructural alterations of the workpiece.

2 Experiment and simulation condition

2.1 Material and cutting tool

The workpiece for the study was made of Ti-6Al-4V titanium alloy with the α + β microstructure and chemical composition: 90% Ti, 6% Al, 4% V, max 0.25% Fe, max 0.2%O. It has the following mechanical properties: tensile strength of 950 MPa, compressive yield strength of 970 MPa, Young’s modulus of 113.8 GPa and average hardness of 36 HRC. The cutting tool adopted for testing is a CNMG 120412-UP cutting insert made of cemented carbide KC5010, coated with a layer of PVD-Al0.55Ti0.45N with a thickness of about 3 μm. It is made of WC sub-microcrystalline carbide. It is widely used in the aviation industry due to the relatively low cost of mass use. Ternary transition metal nitrides such as PVD-TiAlN coatings can effectively reduce abrasive wear during both wet and dry machining. However, their thermo-mechanical properties and machining efficiency depend on many factors, including mainly the stoichiometry ratio.

2.2 Laser-assisted turning conditions and measuring methodology

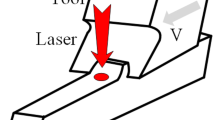
Laser-assisted turning is a hybrid machining process in which the surface of the workpiece is scanned with a laser beam, which is a heat source, heating the workpiece before cutting (Fig. 1). When the workpiece surface has a higher temperature, the cutting energy required for material removal is lower due to material softening, which improves machinability. One of the basics characteristics of the laser-assisted cutting process is to that it leads to the reduction of the cutting force components necessary for machining.

Fig. 1
figure 1

Schematic of the laser-assisted turning

Full size image

The process conditions utilized in the laser-assisted turning tests are listed in Table 1. Laser scanning speed and cutting speed are the same due to process kinematics, as the rotating motion is performed by the workpiece only, with the laser beam moving in a similar way as the cutting tool, with the same constant feed. In every case, the laser is forward-shifted against the cutting tool by the value of the laser spot radius so that there is no impact of the laser on the already machined surface. Two series of experiments are conducted, the first one comprising only laser scanning of the workpiece surface and the second comprising cutting as well. This approach was necessary in order to observe separately and explain the thermal phenomena occurring during LAM and then try to explain the effect of combined laser heating and cutting action. The adopted range of cutting parameters covers the typical range for applications in the aviation industry [14]. The cutting speed range is narrow due to the decreasing impact of laser assistance on the process quality indicators as the speed increases. The laser power value has been adopted as the average value from initial tests and taking into consideration that, for higher laser power values, the risk of ignition of the workpiece material increases. The workpiece diameter range adopted for testing results from the geometry of the available blank used for the tests and the need for metallographic specimens with a specific diameter. Moreover, the minimum diameter used was selected in a way that it can ensure the required rigidity of the workpiece.

Table 1 Test conditions
Full size table

The laser-assisted turning tests were performed on a specially adapted MAG VDF 220 CD turning center. The source of radiation was the TRUMPF TruDiode 3006 laser with a maximum power of 3 kW (Fig. 2a). Three orthogonal components of the resultant cutting force (Fc, Fp and Ff) were measured using a Kistler 9257B piezoelectric dynamometer and a Kistler 5019 signal amplifier to amplify the generated force signals. The dynamometer was clamped in the turret using a VDI clamping system. The signals were transmitted to the DAQ board using a NI 6062E A/D transducer by National Instruments. The measured data were recorded with the frequency of 2000 Hz using a Cut Pro data acquisition program.

Fig. 2
figure 2

Work area of the laser-assisted lathe (a) and measuring position of the thermal imaging camera (b)

Full size image

The FLIR X6540sc thermal imaging camera was used to measure temperature, recording the image in the working area through a special window with sapphire glass (Fig. 2b). The recorded films were analyzed with a view to determine the maximum temperature in selected zones. In the case of non-cutting laser scanning, the maximum laser scanning temperature, intermediate temperature between the laser heating point and cutting zone, and the temperature in the cutting zone were measured (Fig. 3a). In addition, the maximum chip temperature was measured during laser-assisted turning as a result of the laser’s impact on the workpiece and the material removal process in the cutting zone (Fig. 3b). An emissivity factor of 0.48 was adopted for the analysis, determined on the basis of [25].

Fig. 3
figure 3

Areas of maximum temperature analysis on the workpiece for laser scanning (a) and laser-assisted turning (b)

Full size image

2.3 The numerical model

For the simulation of heat transfer phenomena during the stage of laser heating of titanium workpiece prior to the cutting process, a 3D transient heat transfer finite element model was developed. By simulating cases where only laser heating was performed, focus can be primarily set on the thermal phenomena caused by the interaction between the laser beam and workpiece. Determination of the temperature field in the workpiece during LAM is important, as it can reveal the intensity of repeating heating and cooling cycles and lead to the selection of optimum conditions for LAM. In this model, the real 3D geometry of the workpiece and a moving heat source are included in order to accurately represent the effect of heating of the workpiece surface by the laser beam. The trajectory followed by the laser beam is computed according to the equation of a helix, due to the simultaneous horizontal feed of the laser beam and the rotation of the workpiece; as the latter is considered fixed in the present model, the rotational velocity is taken into account by the moving heat source. For the computation of temperature field in the workpiece, the governing differential equation for the transient heat transfer problem is solved, formulated as follows:

$$ \rho C_{p}\ \ \partial T/\partial t+\rho C_{p}\ \mathbf{u}\bullet\nabla T+\nabla\bullet(-k \nabla T)=Q $$
(1)

where ρ represents material density in kg/m3, Cp represents the specific heat in J/(kg K), k is the thermal conductivity in W/(m K) and Q is a heat source term. The laser heat source has a Gaussian spatial distribution, with its maximum heat flux being on the laser spot center. The laser heat flux is computed as [1, 33]:

$$ {q}=\frac{2{P}}{{\pi}{r}_{\mathrm{b}}^{\mathrm{2}}}\mathrm{e}^{\mathrm{-}\frac{\mathrm{2}{r}^{\mathrm{2}}}{{r}_{\mathrm{b}}^{\mathrm{2}}}} $$
(2)

where P is the laser power in W, rb is the radius of the laser spot and r is the distance of a point on the workpiece from the position of the laser beam spot center. Due to reflectance from the workpiece surface, the actual power is reduced; in this work the laser beam wavelength can be varied in the range of 900–1032 μm as per the manufacturer and thus reflectivity for Ti-6Al-4V is assumed as 0.614 [16].

However, due to a part of the laser beam irradiation being reflected back from the workpiece surface, the real heat flux imposed on the workpiece surface is properly reduced. As in the current work the heat source is moving, the center position is calculated each moment as (x0, y0, z0) = (Rcosω t, Rsinω t, vft), where R is the workpiece radius, ω the rotational velocity of the workpiece and vf the feed speed. Material properties for the titanium workpiece such as thermal conductivity, density and specific heat were assumed as temperature-dependent, as the significant increase of temperature of the workpiece causes a considerable change in material properties’ value. Although the temperatures observed in LAM are in every case lower than melting point, time-dependent properties at least up to the melting point can ensure that the effect of microstructure alterations such as the transition between alpha and beta phases can be taken into consideration. The initial temperature of the workpiece prior to the laser heating process was 293K and boundary conditions on the workpiece surface, depicted in the schematic of Fig. 4 include heat losses qhl, both due to natural convection from the outer workpiece surface with the surrounding air and due to radiation from the workpiece surface, as follows [1]:

$$ \begin{array}{ll} q_{hl}={q_{conv}+q_{rad}=\ h}_{air}\left( T_{surf}-T_{amb}\right)+\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad+\varepsilon B({T}_{surf}^{4}-{T}_{amb}^{4}) \end{array} $$
(3)

where hair is the convective heat transfer coefficient between air and the workpiece surface, ε is surface emissivity and B is the Stefan-Boltzmann constant. Thus, the convection heat transfer is regulated by the temperature difference between surface temperature Tsurf and ambient temperature Tamb, which is equal to 293K, whereas the radiation heat transfer is also dependent on the emissivity of workpiece material. The two end faces of the cylindrical workpiece are considered adiabatic, as it is commonly assumed in the relevant literature [18, 33].

Fig. 4
figure 4

Schematic of the numerical model features

Full size image

Mesh size is also of fundamental importance for a FE model, as it is directly related to the accuracy of the model and consequently its degree of realism. A coarse mesh leads to inaccuracy of the predicted process outcomes, such as forces or temperature field but an extremely fine mesh leads usually to a high computational cost. Thus a trade-off between accuracy and affordable computational cost is necessary for the determination of appropriate mesh size. In the current work, mesh quality was calculated as the ratio of the inscribed and circumscribed circles for the polytope corresponding to the corner of each element, with a value of 1 indicating the highest quality. From preliminary test simulations, it was shown that necessary mesh quality could be attained with relatively moderate number of elements; thus, additional criteria were set such as the accuracy of representation of heat source which means that mesh size should be smaller than the size of the heat source and the mesh size in the feed and radial direction should be adjusted in order to capture the effect of temperature gradients to the heat penetration depth and the potential development of the heat-affected zone which causes microstructure alterations or phase changes. The mesh size is the same in simulations with the same workpiece diameter but for larger workpiece diameters, it is essential that a larger size of mesh is required in order for the aforementioned criteria to be met.

In every model the 3D finite elements are hexahedra (bricks). At first, the cylindrical surface as well as top and bottom end surfaces are meshed with 2d quadratic elements and then the 3D mesh is built with a sweep technique along the direction of a generatrix. For the simulations with a 10 mm diameter workpiece, the average element size is 4.4e-4 mm with average element quality 0.89, for the simulations with a 30 mm diameter workpiece the average element size is 8.6e-4 mm with average element quality 0.895 and for the simulations with a 50 mm diameter workpiece the average element size is 1.3e-3 mm with average element quality 0.896. The average element size was increased with an increasing diameter as, using a very fine mesh in areas where thermal phenomena are not significant leads to a considerably high computational cost in the cases with large workpieces.

As the laser beam traversing path length was 10 mm in the laser scanning experiments, for the simulations the same length was used. The total length of the workpiece in the simulation is 20 mm in each case. The timestep is determined in respect to the spindle speed in each simulation, in order to use a sufficient number of timesteps within each rotation of the workpiece and be able to accurately represent the heat source trajectory.

3 Results and discussion

Additional energy sources when turning the Ti-6Al-4V alloy in the form of laser heating strongly affect thermo-mechanical phenomena. The configuration used in the present work, in which the laser head is positioned in the opposite side of the workpiece than the cutting tool was essential in order to be able to analyze the impact of laser heating power density expressed in terms of spot diameter and scanning speed, as well as the workpiece diameter, on selected indicators of laser-assisted turning efficiency. The effect of changing the diameter of the workpiece is actually related to the frequency of heating the same position on the workpiece surface and also depends on the heat capacity of the workpiece material.

3.1 Thermal effect of laser scanning

The laser heating of the workpiece surface is depending on the ratio of the diameter D of the laser spot to the feed f, as the same positions of the workpiece surface can be heated several times before the laser spot is irradiating adjacent positions with the heating frequency resulting from the rotational speed of this workpiece in accordance with the relationship:

$$ n=\frac{1000v_{ls}}{\pi D} $$
(4)

where vls is laser scanning speed. Thus, for workpieces with different diameters or when cutting speed values are different, the workpiece surface is subjected to laser heating under completely different conditions, resulting in different temperature and heating or cooling rate values in each case.

Over time, as the laser beam in moving along the workpiece, depending on the process parameters, the surface temperature of the workpiece recorded in the laser scanning zone stabilizes over time. Figure 5 shows the maximum temperatures in the laser scanning zone on the workpiece for the various diameters of the workpiece and selected process parameters.

Fig. 5
figure 5

Maximum laser scanning temperature on the workpiece for different diameters of the workpiece

Full size image

The highest temperature was measured for a diameter D = 10 mm. As the workpiece diameter increased, the maximum laser scanning temperature decreased. A 50% reduction in temperature was found for the workpiece with a diameter of 50 mm. A change in the diameter of the laser spot in the adopted range resulted in an insignificant variation of the temperature (max. 3%). Increasing the scanning speed resulted in a slight decrease in the temperature of laser scanning (max. 8%). Analysis of the microstructure of the Ti-6Al-4V alloy after laser scanning confirms the impact of the laser beam on the microstructure. The boundary of the influence of the laser heating and the zone in which the solid-state phase transformation occurred and the martensite (α′ phase) was formed are identified (Fig. 6). Martensitic transformation in titanium and its alloys proceeds during fast cooling from the temperature range of β phase stability. The transformation in titanium alloys is unique—it differs significantly from the martensitic transformation in iron-based alloys [22, 23].

Fig. 6
figure 6

Microstructure of surface layer of Ti-6Al-4V alloy after laser scanning with speed vls = 90 m/min and laser spot diameter dls = 1.2 mm for workpiece diameter D = 10 mm

Full size image

For the smallest workpiece diameter D = 10 mm, laser scanning speed vls = 60 m/min and laser spot diameter dls = 0.8 mm, damages of the surface layer structure were observed, interrupting the martensite zone at various positions (Fig. 7a). This is justified due to the fact that in this case the highest temperature was recorded and the impact of the laser heating was among the highest. Reducing the heating frequency by increasing the diameter of the workpiece ensured a clear martensite zone without damaging the surface (Fig. 7b).

Fig. 7
figure 7

Microstructure of surface layer of Ti-6Al-4V alloy after laser scanning with speed vls = 60 m/min and laser spot diameter dls = 0.8 mm for workpiece diameter D = 10 mm (a) and D = 50 mm (b)

Full size image

The maximum temperature measurement in the cutting zone showed lower values in relation to the maximum laser scanning temperature with the lowest decrease observed for D = 10 mm up to even 48% in the case of D = 50 mm (Fig. 8).

Fig. 8
figure 8

Maximum temperature of cutting zone for different diameters of the workpiece

Full size image

Comparison of the heat losses in the distance between laser scanning point, intermediate zone and cutting zone for selected process conditions shows a rapid temperature drop in the first half of the distance (Fig. 9). A comparison of the graphs of temperature dependence on the workpiece diameter for different laser scanning speeds and laser spot diameters shows the largest differences for the workpiece diameter D = 10 mm. Among the three process parameters, the workpiece diameter has the greatest impact in every case as different cutting speed or laser beam diameter values affect the temperatures in each zone to a much lesser extent. The production of heat in the workpiece as a result of laser scanning involves the introduction of an appropriate amount of laser irradiation. The spot of the laser beam determines the size of the irradiated surface area which is comparable to the cross-sectional area of the laser beam. Surface power density indicates the amount of power per unit of time which is delivered per unit of area. The product of surface power density and the duration of the treatment results in surface energy density. This is how the amount of energy through irradiation is calculated for lasers operating in continuous mode. In the case of heating as for the experiments presented in the current work, the surface energy density results from the heating frequency described by Eq. (4). From this formula, it occurs that, for smaller diameters, the frequency of heating is higher, resulting in higher temperatures in the workpiece. The other two parameters, namely laser spot diameter and cutting speed, have a considerably less significant effect on temperature. The slightly lower values of temperature for increased cutting speed can be justified as the increase of cutting speed, which is related to the increase of revolutions per minute of the shaft, increases the actual feed (in mm/min) and thus the time of irradiation of the workpiece surface becomes lower.

Fig. 9
figure 9

Differences in the max. laser scanning temperature ts and the temperature in the cutting zone tcz (together with the intermediate temperature ti) for selected process conditions

Full size image

As the laser scanning zone is on the opposite area of the workpiece than the cutting zone, the temperature difference between these zones, which is around 200 ∘C in each case indicates a considerable heat loss from the workpiece surface as the laser beam moves away from the irradiated region. The fast heat loss from the workpiece surface justifies the formation of a martensite zone.

Analysis of changes in the morphology of the phase components of the microstructure showed a strong relationship between the depth of the martensite zone and process parameters and the diameter of the workpiece (Fig. 10). A heat-affected zone greater than the thickness of the martensite layer was observed for the workpiece diameter D = 10 mm. For the smaller diameter of the laser spot, the thickness of the martensite zone is larger with even distribution and decreases as the diameter of the workpiece increases. For the laser spot diameter dls = 1.2 mm, the uneven thickness of the martensite layers were obtained, as it is clearly observed in the micrographs of Fig. 10.

Fig. 10
figure 10

Microstructure of surface layer of Ti-6Al-4V alloy after laser scanning for selected process conditions

Full size image

The reduction in the depth of the heat-affected zone for a larger diameter of the workpiece and the diameter of the laser spot occurs mainly due to the reduction of linear energy - power density (the ratio of the laser power affecting the surface of the workpiece and the frequency of heating). The thermal conductivity of the Ti-6Al-4V alloy and changes in radiation absorption during heating are also important for the changes of the heat-affected zone and martensite zone dimensions under the selected conditions.

The combination of laser scanning with the cutting process causes that the temperature in the cutting zone increases significantly. In the case of tests, this temperature was defined as the temperature of the chip coming out of contact with the cutting tool. Measured differences in the maximum chip temperature for different diameter of the workpiece are much smaller (do not exceed 26%) - especially for diameters of 30 and 50 mm (Fig. 11). This indicates compensation based on the one hand on the increase of the temperature as a result of laser scanning and on the other hand on reducing the heat generated during cutting because the reduction of plastic stress at higher temperatures results in less energy needed for cutting.

Fig. 11
figure 11

Maximum temperature of chip for different diameters of the workpiece

Full size image

3.2 Components of cutting forces

The beneficial effect of an additional energy source in the form of laser heating of the workpiece material before the cutting process of the Ti-6Al-4V alloy on the components of the cutting forces has been confirmed by the authors in most of the aforementioned earlier works. As part of this research, it was limited to analyzing the impact of factors other than laser power but still technologically significant, i.e., workpiece diameter, laser spot diameter and cutting speed.

Figure 12 shows the impact of selected technological parameters on the cutting force Fc for different diameter sizes of the workpiece. The differences in the value of the force Fc resulting from changes in the diameter of the laser spot or cutting speed in the adopted ranges did not exceed 4%. Similar results (not exceeding 5%) were obtained for the passive force Fp (Fig. 13). However, increasing the diameter of the workpiece caused about 15% increase in cutting force and even 28% increase in passive force.

Fig. 12
figure 12

The impact of selected technological parameters on the cutting force Fc for different diameters of the workpiece

Full size image
Fig. 13
figure 13

The impact of selected technological parameters on the passive force Fp for different diameters of the workpiece

Full size image

The dependencies obtained are correlated with the thermal effect as a result of laser heating. Comparing the relationships shown in Fig. 13 with Fig 11, it can be seen that the most beneficial effects were obtained for a diameter of 30 mm. In this case, a large reduction in force was obtained at a relatively lower temperature in the cutting zone.

The effect of too much laser heating energy for the diameter D = 10 mm affects the morphology of the phase components of the microstructure (Fig. 14a). For this diameter of the workpiece, an α phase layer appeared on the surface of the workpiece (α-case) and the depth of deformation was about 30 μm. At the same process parameters for the workpiece diameter D = 30 mm, microstructure morphology without plastic deformation was obtained (Fig. 14b).

Fig. 14
figure 14

Microstructure of surface layer of Ti-6Al-4V alloy after laser-assisted turning with speed vc = 60 m/min and laser spot diameter dls = 0.8 mm for workpiece diameter D = 10 mm (a) and D = 30 mm (b)

Full size image

In the case of feed force, the obtained values also depend on the diameter of the workpiece, however, the values of this component of the cutting force are much smaller than the others (Fig. 15).

Fig. 15
figure 15

The impact of selected technological parameters on the feed force Ff for different diameters of the workpiece

Full size image

Analyzing the mechanisms which have a decisive effect on the reduction of cutting force components, it can be seen that the dominating factor is the reduction of the plastic stress along with the temperature increase due to laser heating.

3.3 Thermo-mechanical effect on tool wear

The course of wear during turning in LAM conditions was a consequence of increasing the temperature in the cutting zone as a result of an additional heat source in the form of laser heating and the lack of heat dissipation via the coolant. Figure 16 shows SEM images of the rake surface of a worn cutting tool with EDX spectra. The analysis showed the detachment of a large coating TiAlN area of the cutting insert including a layer of carbide substrate (white color) and adhesion of the workpiece material to the surface of the damage (gray color).

Fig. 16
figure 16

SEM pictures of the fragments of worn rake surface and EDX spectra for selected points after laser-assisted turning with laser power P = 1000 W

Full size image

The flank surface (Fig. 17) of a worn cutting tool has a large proportion of adhesive wear mechanisms and a significant lowering of the cutting edge (approximately 0.12 mm).

Fig. 17
figure 17

SEM pictures of the fragments of worn flank surface after laser-assisted turning with laser power P = 1000 W

Full size image

The beneficial effect of reducing the plasticizing stress has been decreased by the intensive wear of the cutting tool. For this reason, it is necessary to look for ways to reduce the temperature of the cutting tool and apply better coatings that provide an adequate thermal barrier.

3.4 Modeling of the laser-assisted turning

After the simulations were conducted analysis of the results was performed. Using the computational model, the effect of the studied process parameters such as cutting speed and workpiece diameter not only on temperature field which was experimentally measured but also on temperature rate is able to be determined. The results regarding the temperature field can be useful in most cases in order to qualitatively determine the variation of cutting forces, as higher temperatures lead usually to lower forces and the results regarding heating and cooling rate can be used to determine the occurrence of microstructure alterations, e.g., martensite formation when high cooling rates are observed after the workpiece has reached a critical temperature. Then, the appropriate range for cutting conditions can be selected so that cutting forces and tool wear are kept low and unfavorable microstructural alterations are avoided.

In Table 2, the details of the simulation cases are presented. In Fig. 18, the temperature field on the workpiece surface for case 3 at different time steps is depicted. As it was anticipated, the laser source heats progressively the circumference of the workpiece and as time passes laser heating affects also other parts of the workpiece in the axial direction as the laser moves along it. At each moment, the highest temperatures occur in the region close to the irradiated area and afterwards, temperature becomes lower due to heat losses. The already heated regions retain a high temperature even after the irradiation and heat is transferred to adjacent regions of the workpiece due to conduction. At these temperatures and laser intensity values, heat losses by convection or radiation are not significant at least for some time after laser beam has irradiated a specific region. By comparing the temperature profile near the position of the laser beam in Fig. 18a, it can be seen that it is very similar to the experimental one, depicted in Fig. 3a, thus this is a first qualitative indication that the developed model can produce realistic results.

Fig. 18
figure 18

Snapshots of the laser heating process of case 3: a at t = 2.35 s, b at t = 4.7 s, c at t = 7.05 s and d at t = 9.4 s. Temperature values are in ∘C in every case

Full size image
Table 2 Details regarding simulation cases
Full size table

As it was shown in the laser scanning experiments, process parameters have a direct impact on the development of the temperature field and subsequently on the heat transfer phenomena within the workpiece. In Fig. 19, the maximum temperatures from the simulation are presented, also compared with the experimental values. The determination of maximum temperature from the simulation is conducted by analyzing the time evolution of temperature at various points along a generatrix of the cylindrical workpiece. From these results, it can be deduced that the increase of cutting speed results to a decrease of maximum temperatures in any case and that the increase of workpiece diameter leads also to a decrease of maximum temperatures, as it was anticipated by the experimental findings. These effects were observed experimentally in other works in the relevant literature as well [31]. Moreover, by comparing the experimental with the simulation results regarding maximum temperature it can be observed that a good agreement between them exists, as the percentage error is clearly below 10% in most cases, indicating that the proposed model was successfully validated. More specifically, the lowest percentage error is 2.51% in case 6 and the maximum percentage error is 11.5% in case 4. Thus, the simulation results can be further analyzed to provide information that is not possible to be experimentally determined.

Fig. 19
figure 19

Maximum temperatures from the experimental and numerical results

Full size image

More specifically, the heating and cooling rates will be also presented for each simulation. The heating and cooling rates are calculated in a representative point on a generatrix of the cylindrical workpiece, at 7.5 mm distance from the initial position of the laser beam. The maximum values of the heating and cooling rates for each case are presented in Fig. 20a and b, respectively. For the heating rate, it can be seen that its values vary considerably with the workpiece diameter, as higher heating rates are observed for the cases with the smaller diameter and then a large decrease is observed for the workpiece with 30 mm diameter, whereas the heating rate is slightly lower for the workpiece with 50 mm diameter. Moreover a smaller variation is found to occur between cases with different cutting speed values; in the case with D = 10 mm a slight increase occurs in the heating rate with an increase of cutting speed whereas in the two other cases, a clear decrease is observed instead. For the cooling rate, similar trends were generally observed; an increase of workpiece diameter led to a significant decrease of cooling rate at first but differences between the two larger diameters are much lower. Moreover, in every case, the increase of cutting speed led to lower cooling rate. These findings indicate that lower workpiece diameter and lower cutting speed generally increases the intensity of the repeating heating/cooling cycles, leading possibly to more intense alterations of the workpiece microstructure and integrity.

Fig. 20
figure 20

Maximum heating rate (a) and maximum cooling rate (b) for every simulated case

Full size image

In the present work, this effect was confirmed by the results presented in Section 3, depicted also in Fig. 10, where a larger martensite zone was formed at workpieces with smaller diameter. Moreover, the strong dependence of heating-related phenomena on the workpiece diameter is justified, as a consequence of the significant differences regarding the heating and cooling rate values between cases with different workpiece diameters, as observed in the simulations.

Another confirmation of the validity of the simulation results is that the cooling rates are consistent with the ones required for the formation of martensite α’ phase near the surface of the titanium workpiece given that all other necessary conditions are met, something that was observed in the microstructural analysis of the workpiece. In literature works, e.g., [2], the limit heat rate value for martensite formation in the case of Ti-6Al-4V is reported to be 525 ∘C/s, which is far lower compared with the one predicted by the simulations.

4 Conclusions

In the present work, a comprehensive study regarding laser-assisted turning was conducted under various process conditions in order to determine their effect on cutting forces, temperature, tool wear and workpiece microstructure. Moreover, a finite element model was created for the simulation of laser heating process in order to gain a deeper insight into the thermal phenomena occurring during LAM. From this study, the following conclusions were drawn:

  • Maximum workpiece temperatures during laser heating were mainly affected by the workpiece diameter and to a lesser extent by cutting speed and laser spot diameter. Maximum temperature was found to decrease with increasing workpiece diameter or increasing laser spot diameter, whereas it also generally decreases with increasing cutting speed. Temperature has the highest value at the center of the laser beam spot, drops considerably at some distance from the laser beam position and has a small further drop until the opposite point from the center of the laser beam spot.

  • Due to high temperatures obtained during laser-assisted turning and rapid cooling rates, martensitic transformation was shown to occur at the top of the heat-affected zone of the workpiece. In cases with small workpiece diameter, damage can occur in the surface layer, whereas for higher workpiece diameter, the martensite zone is more clear due to lower heating frequency. For the smaller laser spot diameter the martensite zone is thicker with an even distribution and decreases with larger workpiece diameter. For larger spot diameter an uneven distribution of the martensite layer occurs.

  • Regarding cutting and passive forces, the workpiece diameter effect was shown to be more important than that of the cutting speed or the laser spot beam. The reduced force values were attributed to the beneficial effect of the laser heating, leading to material softening and reduced stresses. High temperatures occurring during some cases led to more intensive tool wear instead of providing a beneficial effect to it.

  • Finally, by conducting FE simulations, the time evolution of the temperature field on the workpiece surface was determined after the model was successfully validated by comparison with the experimental data, the heating and cooling rates during LAM were determined. These rates were mainly affected by the workpiece diameter, as higher workpiece diameter caused lower magnitudes of heating and cooling rates, while cutting speed played a less significant role. Moreover, the high cooling rates, which clearly exceed the limit for diffusionless transformation, justify the creation of the martensite phase.